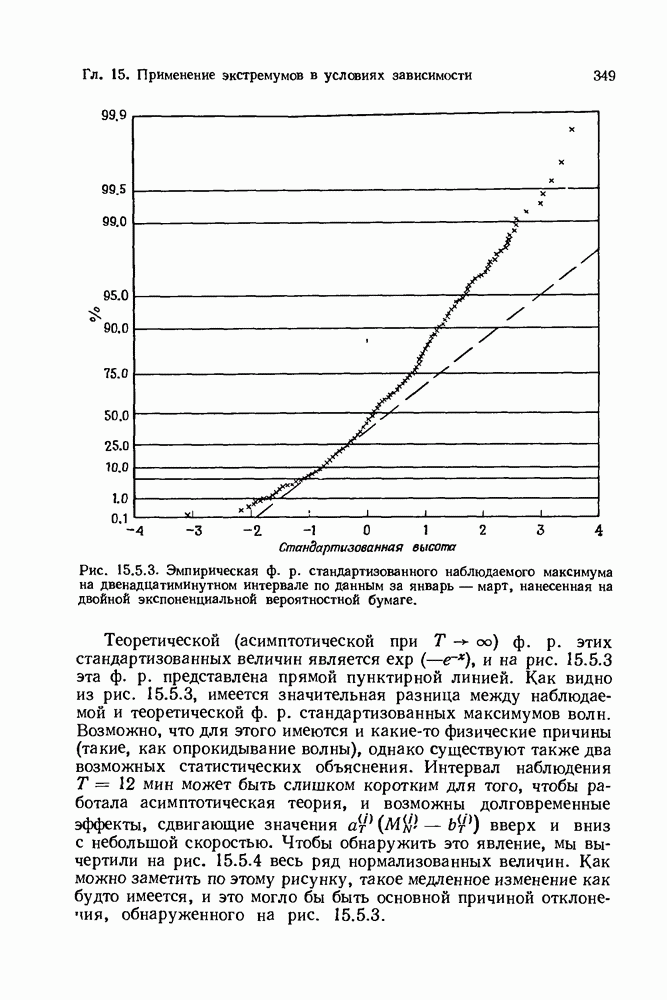
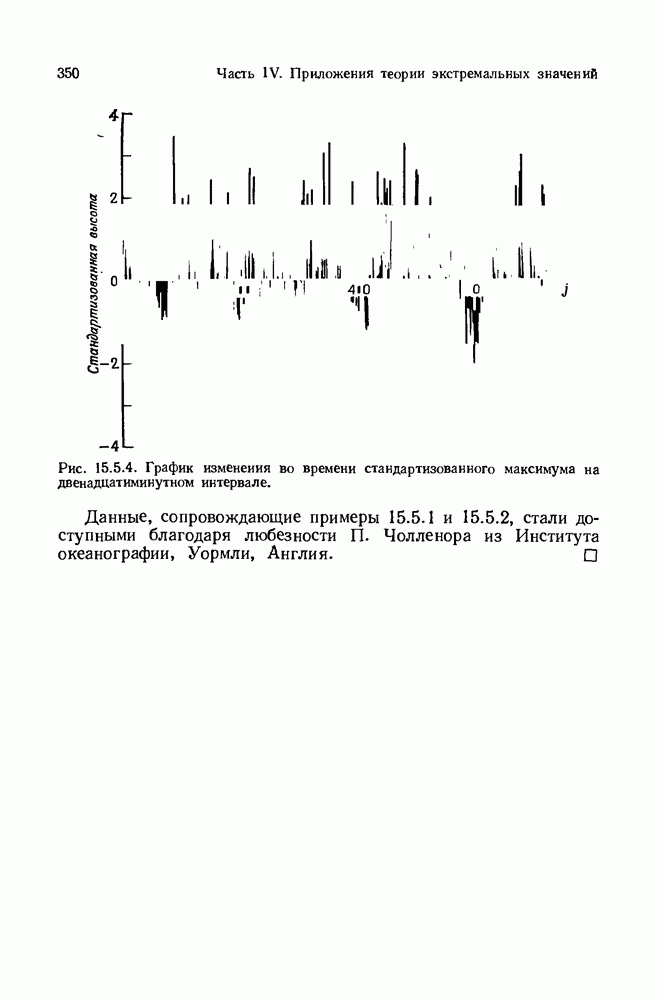
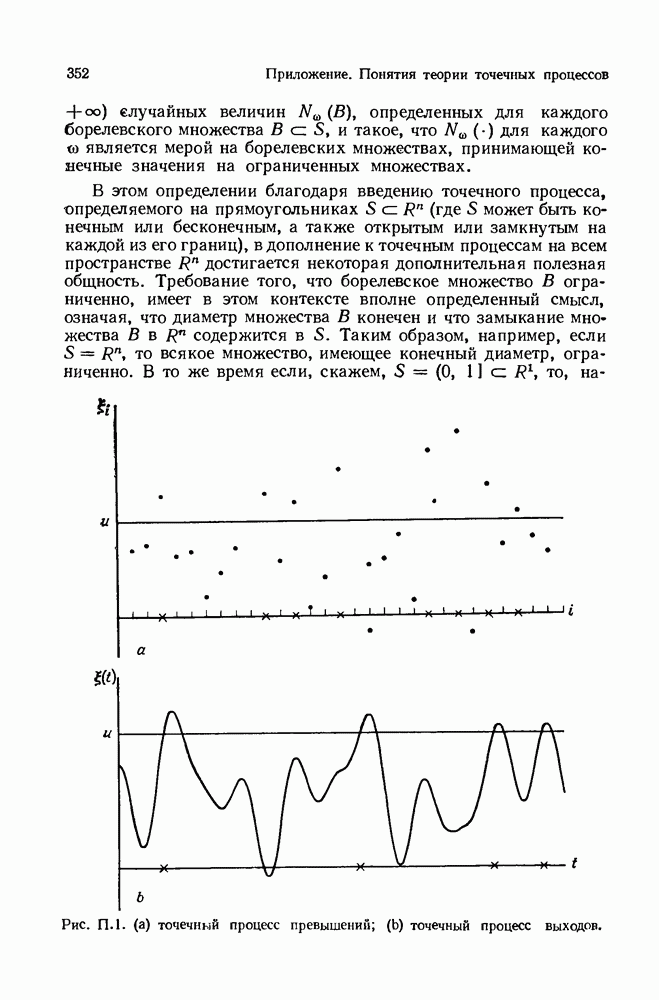
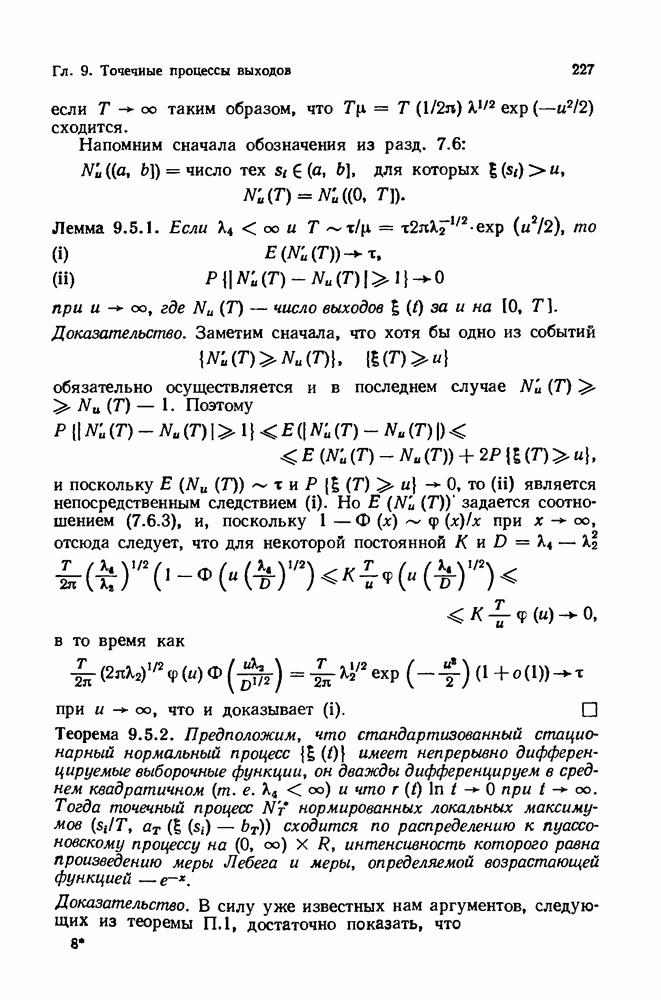| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.5. Маркированные пересечения
Материал оставшейся части этой главы не будет использоваться вплоть до гл. 9 и следующих за ней глав. При желании читатель может перейти непосредственно к гл. 8, возвратившись к этому разделу, когда это понадобится.
Рассмотрим ситуации, когда мы регистрируем не только момент выхода, но также и значение какой-нибудь другой случайной величины, связанной с этим выходом. Мы можем, например, интересоваться значениями производной  в точках
в точках  выходов
выходов  за уровень и или значениями
за уровень и или значениями  в точках
в точках  входов
входов
производной  под нулевой уровень, т. е. в точках, где
под нулевой уровень, т. е. в точках, где  имеет локальный максимум. Мы будем говорить о них как о маркированных пересечениях и рассматривать, скажем
имеет локальный максимум. Мы будем говорить о них как о маркированных пересечениях и рассматривать, скажем  как метки (или марки), приписываемые пересечениям в точках
как метки (или марки), приписываемые пересечениям в точках  Изложим здесь методы работы с такими метками, подобные тем, которые привели нас к формуле Райса (хотя и несколько более сложные).
Изложим здесь методы работы с такими метками, подобные тем, которые привели нас к формуле Райса (хотя и несколько более сложные).
Через  будем обозначать совместно стационарные процессы, имеющие непрерывные выборочные функции, и рассмотрим пересечения уровня процессом
будем обозначать совместно стационарные процессы, имеющие непрерывные выборочные функции, и рассмотрим пересечения уровня процессом  маркированные посредством
маркированные посредством  В приведенных выше примерах в качестве
В приведенных выше примерах в качестве  выступали бы соответственно
выступали бы соответственно  а в качестве
а в качестве  соответственно
соответственно  Пусть
Пусть  выходы процесса
выходы процесса  за уровень и, и пусть для произвольного интервала
за уровень и, и пусть для произвольного интервала  величина
величина  равна числу таких
равна числу таких  в I, для которых
в I, для которых  Мы будем писать
Мы будем писать  Обозначения
Обозначения  будут иметь тот же смысл, что и прежде, например
будут иметь тот же смысл, что и прежде, например  Определим, далее,
Определим, далее,

Лемма 7.5.1. Пусть I — ограниченный интервал,  при
при  и пусть
и пусть  число таких точек вида
число таких точек вида  для которых
для которых

Тогда
(i) если А — открытый интервал, то

(ii) если для каждого 

то для любого интервала А

(iii) если А — открытый интервал, то

и если выполнено (7.5.1) и  то
то 

и для 

Доказательство, (i) Предположим, что  и что
и что  имеет выходы за уровень и в точках
имеет выходы за уровень и в точках  принадлежащих внутренности интервала
принадлежащих внутренности интервала  и при этом
и при этом  непрерывности распределения
непрерывности распределения  в концевых точках интервала
в концевых точках интервала  выходов нет.) Поскольку выборочные функции
выходов нет.) Поскольку выборочные функции  непрерывны, а интервал
непрерывны, а интервал  открытый, можем окружить указанные точки
открытый, можем окружить указанные точки  непересекающимися подынтервалами
непересекающимися подынтервалами  из
из  в которых
в которых  Отсюда, как и в доказательстве леммы 7.2.2 (ii), следует, что
Отсюда, как и в доказательстве леммы 7.2.2 (ii), следует, что 
Предположим сначала, что  и пусть
и пусть  такие же, как и в
такие же, как и в  Если
Если  внутренность интервала
внутренность интервала  то в силу
то в силу  не могут равняться ни а ни
не могут равняться ни а ни  так что
так что  и мы поэтому можем взять непересекающиеся интервалы
и мы поэтому можем взять непересекающиеся интервалы  в которых
в которых  Введем обозначение
Введем обозначение  для множества таких
для множества таких  для которых и
для которых и  принадлежат
принадлежат  для некоторого
для некоторого  и
и  -для множества таких
-для множества таких  для которых
для которых  принадлежат
принадлежат  но
но  Ясно, что
Ясно, что  является единственным выходом
является единственным выходом  за уровень и для
за уровень и для  следовательно, по лемме
следовательно, по лемме 

где

Кроме того, если

то для произвольно больших  существуют
существуют  следовательно, такая последовательность целых чисел
следовательно, такая последовательность целых чисел  что
что  Из непрерывности
Из непрерывности  следует, что
следует, что  и поэтому, согласно (7.5.1),
и поэтому, согласно (7.5.1),  Итак,
Итак,  при
при  для некоторого
для некоторого  которое можно взять столь малым, чтобы
которое можно взять столь малым, чтобы  Далее, для достаточно больших
Далее, для достаточно больших  величины
величины  и
и  принадлежат
принадлежат  Следовательно, по лемме
Следовательно, по лемме  имеет выход за уровень и в
имеет выход за уровень и в  что противоречит предположению
что противоречит предположению  Это показывает, что
Это показывает, что

а это вместе с (7.5.2) доказывает, что  п. н. Поскольку к тому же из (7.5.1) вытекает, что
п. н. Поскольку к тому же из (7.5.1) вытекает, что  то часть (i) дает
то часть (i) дает

Поэтому  н., как и утверждалось. Если
н., как и утверждалось. Если  то искомое заключение вытекает из части (i) с заменой А на
то искомое заключение вытекает из части (i) с заменой А на  поскольку
поскольку  согласно (7.5.1).
согласно (7.5.1).
(iii) Первое заключение сразу вытекает из леммы Фату и части (i), в то время как из части (ii) следует, что  поскольку
поскольку  по предположению. Далее, если
по предположению. Далее, если  то существует приблизительно
то существует приблизительно  точек
точек  так что
так что

Поскольку последовательность  произвольна, отсюда получаем последнее утверждение в (iii).
произвольна, отсюда получаем последнее утверждение в (iii).
Мы вычислим теперь предал для  в случае, когда
в случае, когда  совместно нормальные процессы с нулевыми средними. Пусть
совместно нормальные процессы с нулевыми средними. Пусть  обозначает ковариационную функцию процесса
обозначает ковариационную функцию процесса  Как отмечалось ранее, если процесс
Как отмечалось ранее, если процесс  дифференцируем в среднем квадратичном,
дифференцируем в среднем квадратичном,  случайные величины
случайные величины  независимы при каждом
независимы при каждом  и нормальны, а их совместная плотность равна
и нормальны, а их совместная плотность равна

Кроме того, можно показать, что три процесса  совместно нормальны и что их ковариации и взаимные ковариации могут быть получены как пределы, например
совместно нормальны и что их ковариации и взаимные ковариации могут быть получены как пределы, например

Мы можем определить также условные распределения, используя отношения функций плотности, когда они существуют. Например, для измеримого множества А мы определяем

где  функция плотности случайных величин
функция плотности случайных величин  В последующем условные вероятности всегда будут пониматься определенными именно таким образом.
В последующем условные вероятности всегда будут пониматься определенными именно таким образом.
Лемма 7.5.2. Пусть  такие совместно нормальные процессы с нулевыми средними, что с. в.
такие совместно нормальные процессы с нулевыми средними, что с. в.  имеют невырожденное распределение. Предположим, кроме того, что
имеют невырожденное распределение. Предположим, кроме того, что  имеет непрерывные выборочные функции и что
имеет непрерывные выборочные функции и что  дифференцируем в среднем квадратичном. Тогда для любого измеримого множества А и любого и
дифференцируем в среднем квадратичном. Тогда для любого измеримого множества А и любого и

Доказательство. Обозначим  и введем, как и в теореме 7.3.1, независимые нормальные с. в.
и введем, как и в теореме 7.3.1, независимые нормальные с. в.  с дисперсиями
с дисперсиями  Заметим, что
Заметим, что

Чтобы найти предел условной нормальной вероятности

при  заметим, что, поскольку
заметим, что, поскольку  совместно нормальные процессы, условное распределение с. в.
совместно нормальные процессы, условное распределение с. в.  при заданных значениях
при заданных значениях  также нормальное и имеет среднее
также нормальное и имеет среднее

и дисперсию

см., например, Рао (1973, с. 467).
Поскольку  в среднем квадратичном при
в среднем квадратичном при  отсюда следует, что
отсюда следует, что  при
при  Поскольку к тому же
Поскольку к тому же  невырождены по предположению мы имеем
невырождены по предположению мы имеем
 Обозначая
Обозначая  имеем
имеем

и поэтому мажорированная сходимость дает нам, что для всех 

при  Опять из мажорированной сходимости следует, что
Опять из мажорированной сходимости следует, что

что в силу (7.5.3) и является заключением леммы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- ЧАСТЬ 1. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭКСТРЕМУМОВ
- Глава 1. Асимптотические распределения экстремумов
- 1.2. Обратные функции и теорема Хинчина о сходимости
- 1.3. Максимум-устойчивые распределения
- 1.4. Теорема об экстремальных типах
- 1.5. Сходимость вероятностей
- 1.6. Общая теория областей притяжения
- 1.7. Примеры
- 1.8. Минимумы
- Глава 2. Превышения уровней и k-е наибольшие максимумы
- 2.1. Пуассоновские свойства превышений
- 2.2. Асимптотическое распределение k-х наибольших значений
- 2.3. Совместное асимптотическое распределение наибольших максимумов
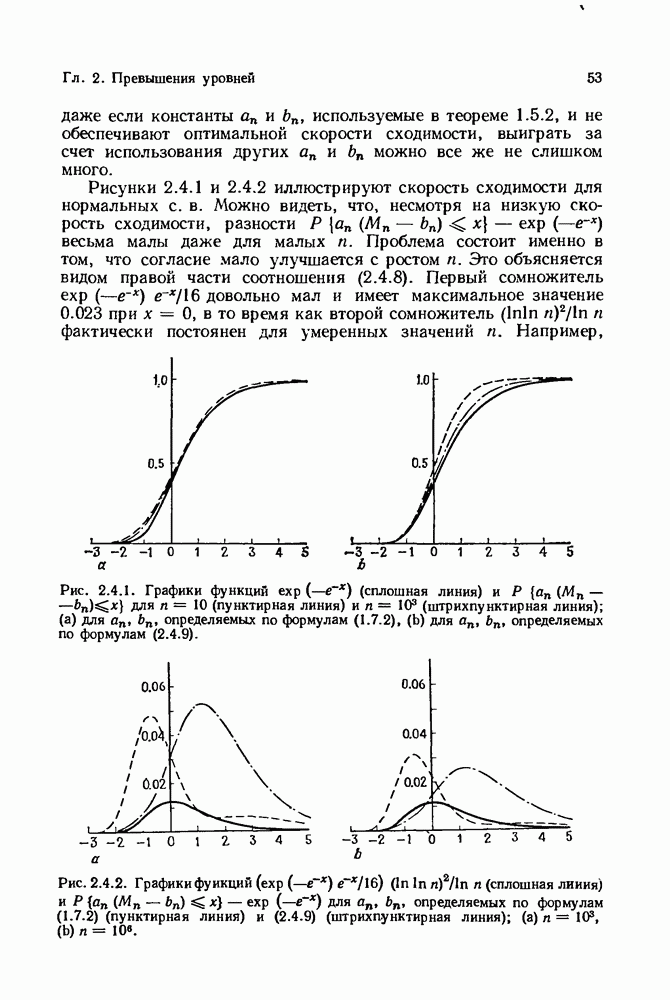
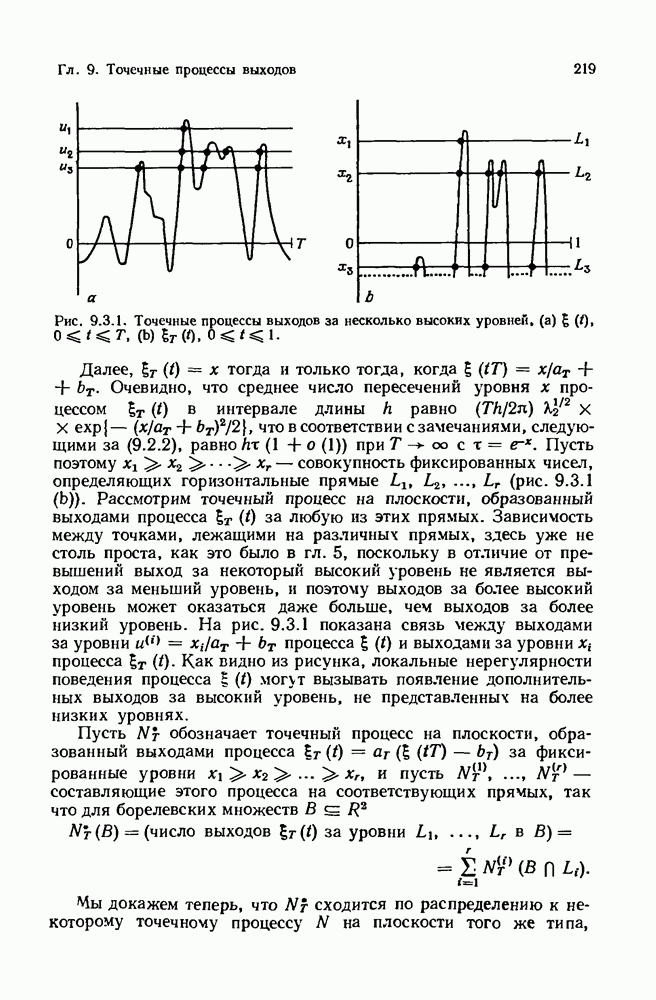
- 2.4. Скорость сходимости
- 2.5. Возрастающие ранги
- 2.6. Центральные ранги
- 2.7. Промежуточные ранги
- Часть II. СВОЙСТВА ЭКСТРЕМУМОВ ЗАВИСИМЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- Глава 3. Максимумы стационарных последовательностей
- 3.1. Ограничения на зависимость для стационарных последовательностей
- 3.2. Перемешивание по распределениям
- 3.3. Теорема об экстремальных типах для стационарных последовательностей
- 3.4. Сходимость последовательности … при наличии зависимости
- 3.5. Сопровождающие независимые последовательности и области притяжения
- 3.6. Максимумы на произвольных интервалах
- 3.7. О роли условий …
- 3.8. Максимумы скользящих средних устойчивых величин
- Глава 4. Нормальные последовательности
- 4.2. Нормальная лемма сравнения
- 4.3. Теория экстремальных значений для нормальных последовательностей — прямой метод
- 4.4. Условия … для нормальных последовательностей
- 4.5. Более слабые предположения о зависимости
- 4.6. Скорость сходимости
- Глава 5. Сходимость точечных процессов превышений и распределений k-x наибольших максимумов
- 5.2. Сходимость превышений высокого уровня к пуассоновскому процессу
- 5.3. Асимптотическое распределение k-x наибольших значений
- 5.4. Независимость максимумов на непересекающихся интервалах
- 5.5. Превышения множества уровней
- 5.6. Совместное асимптотическое распределение наибольших максимумов
- 5.7. Полная пуассоновская сходимость
- 5.8. Моменты рекордов и процессы экстремумов
- Глава 6. Нестационарные и сильно зависимые нормальные последовательности
- 6.1. Нестационарные нормальные последовательности
- 6.2. Асимптотическое распределение максимума
- 6.3. Сходимость вероятностей … при наиболее слабых условиях на …
- 6.4. Стационарные нормальные последовательности с сильной зависимостью
- 6.5. Пределы для превышений и максимумов в случае …
- 6.6. Распределение максимума в случае, когда …
- ЧАСТЬ III. ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ В СЛУЧАЕ НЕПРЕРЫВНОГО ВРЕМЕНИ
- Глава 7. Основные свойства экстремумов и пересечений уровня
- 7.2. Пересечения уровня и их основные свойства
- 7.3. Пересечения нормальными процессами
- 7.4. Максимумы нормальных процессов
- 7.5. Маркированные пересечения
- 7.6. Локальные максимумы
- Глава 8. Максимумы дифференцируемых в среднем квадратичном нормальных процессов
- 8.2. Двойное экспоненциальное распределение максимума
- Глава 9. Точечные процессы выходов и локальные максимумы
- 9.1. Пуассоновская сходимость выходов
- 9.2. Взаимная независимость максимумов на непересекающихся интервалах
- 9.3. Выходы за несколько смежных уровней
- 9.4. Положение максимумов
- 9.5. Высота и положение локальных максимумов
- 9.6. Максимумы при более общих условиях
- Глава 10. Свойства выборочных функций в точках выходов
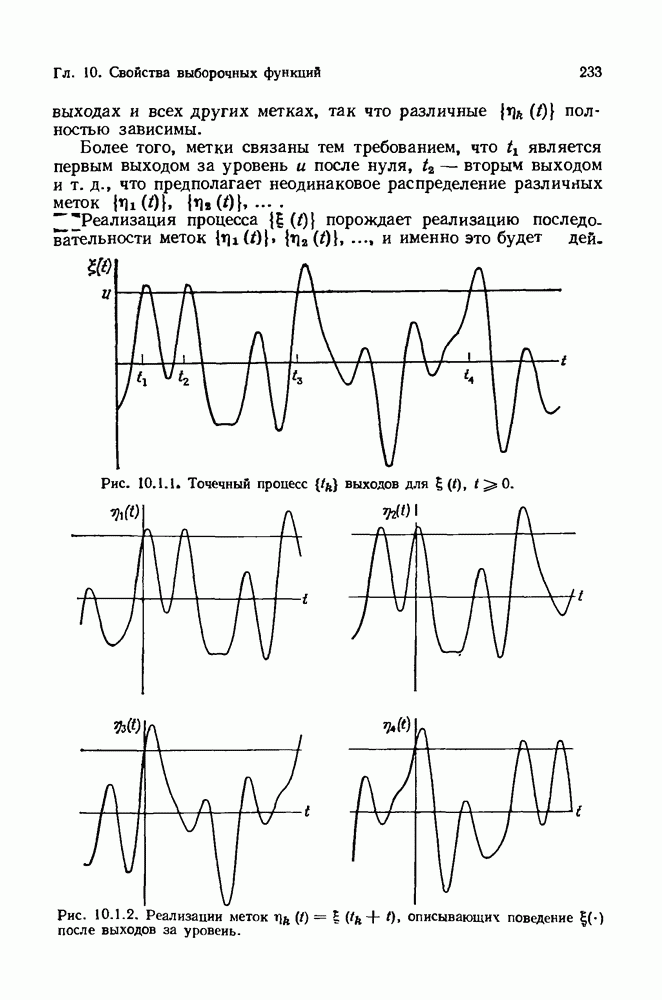
- 10.2. Эмпирические распределения меток в точках выходов
- 10.3. Модельный процесс Слепяна
- 10.4. Выбросы за высокий уровень
- Глава 11. Максимумы и минимумы и теория экстремумов для зависимых процессов
- 11.2. Экстремальные значения и пересечения для зависимых процессов
- Глава 12. Максимумы и пересечения недифференцируемых нормальных процессов
- 12.2. Максимумы на конечных интервалах
- 12.3. Максимумы на расширяющихся интервалах
- 12.4. Асимптотические свойства e-выходов
- 12.5. Более слабые условия на бесконечности
- Глава 13. Экстремумы стационарных процессов с непрерывным параметром
- 13.2. Сходимость вероятностей …
- 13.3. Сопровождающая последовательность независимых величин
- 13.4. Стационарные нормальные процессы
- 13.5. Процессы с конечными интенсивностями выходов
- 13.6. Пуассоновская сходимость выходов
- 13.7. Интерпретация функции …
- ЧАСТЬ IV. ПРИЛОЖЕНИЯ ТЕОРИИ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ
- Глава 14. Теория экстремальных значений и прочность материалов
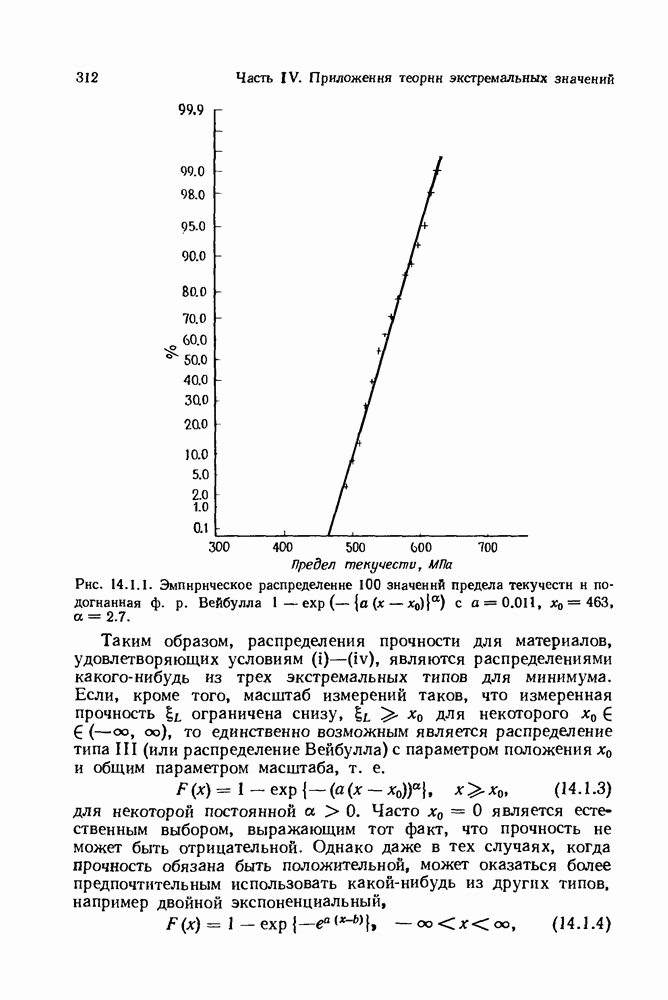
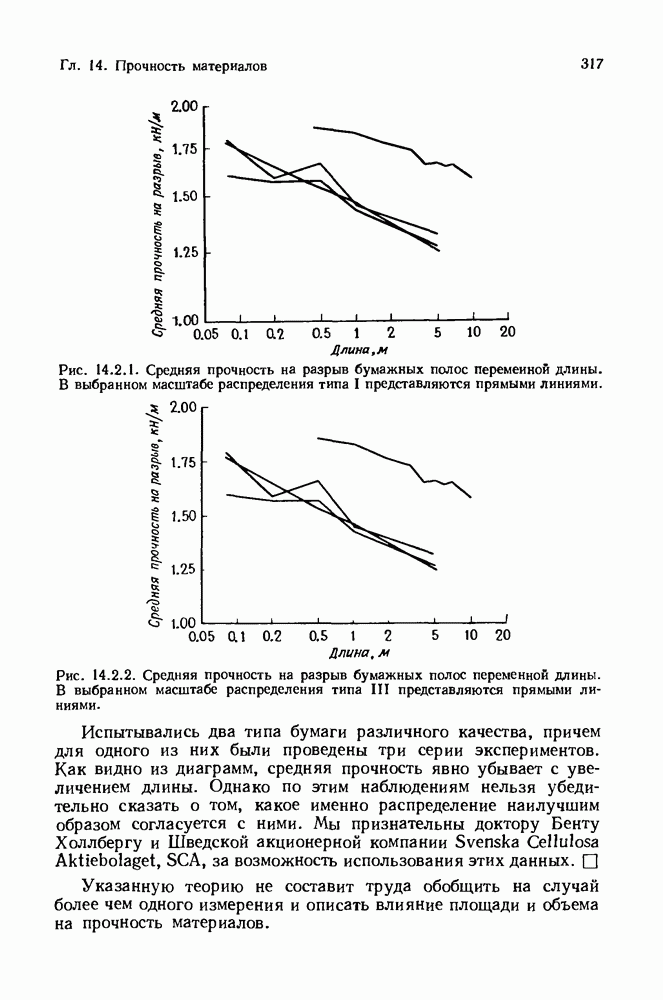
- 14.1. Характеризации распределений экстремальных значений
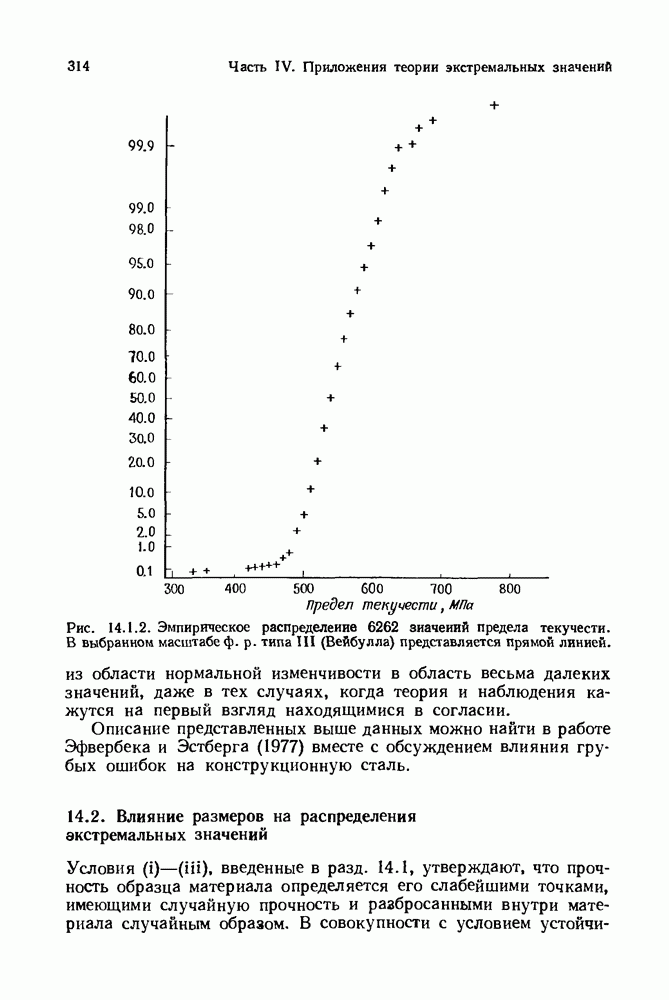
- 14.2. Влияние размеров на распределения экстремальных значений
- Глава 15. Применение экстремумов и пересечений в условиях зависимости
- 15.2. Пуассоновские превышения и показательные времена ожиданий
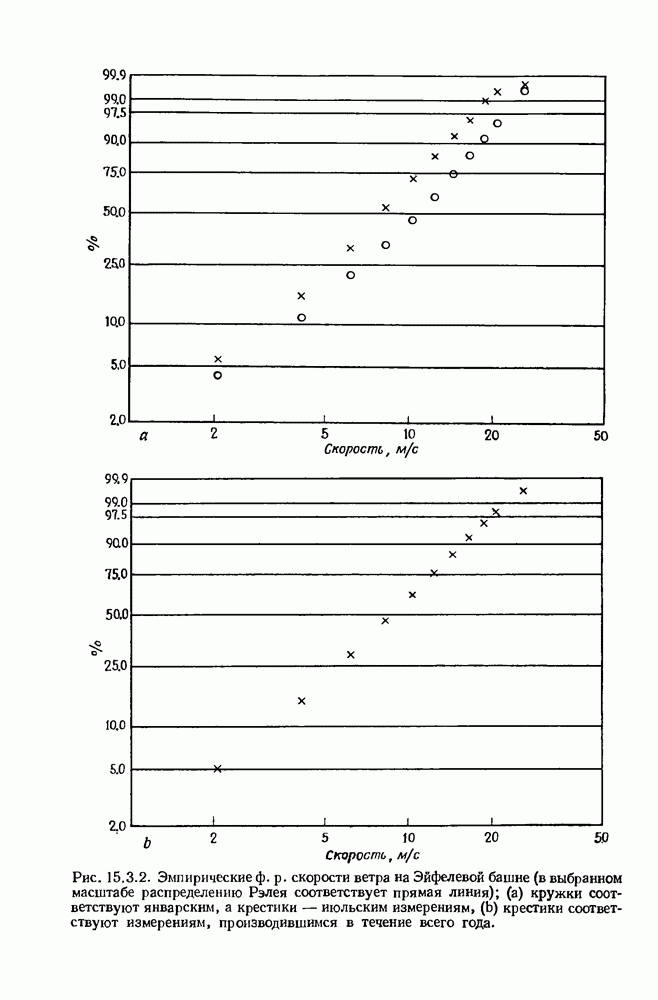
- 15.3. Области притяжения и экстремумы для смесей распределений
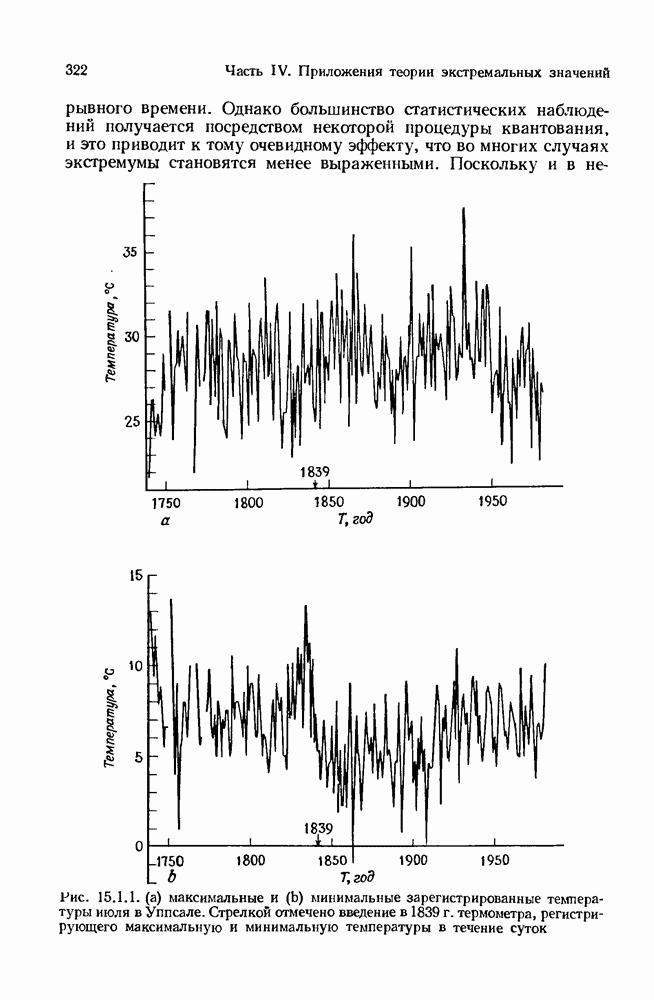
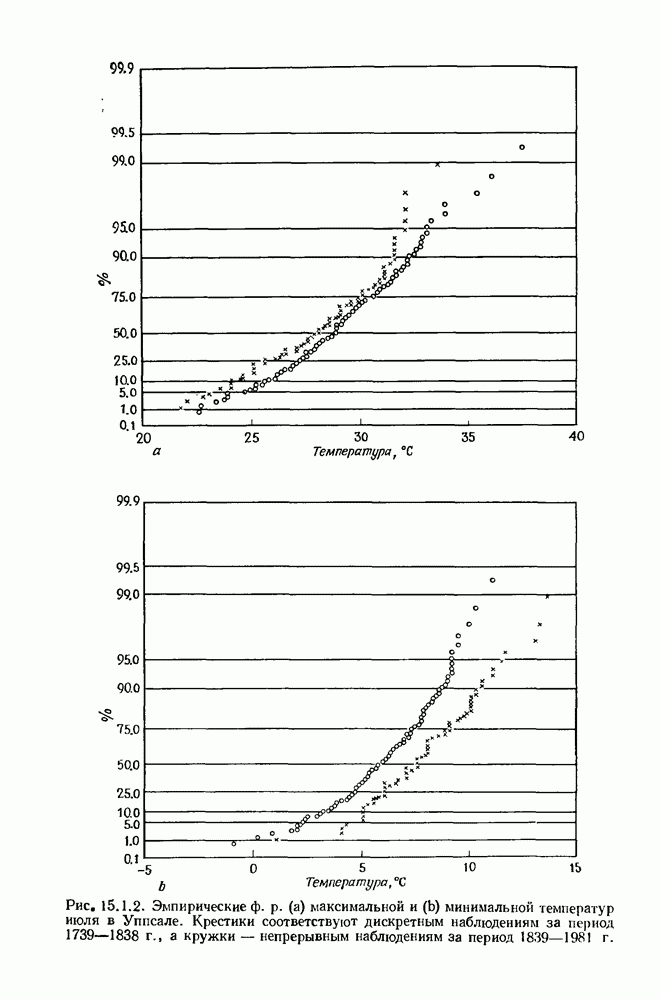
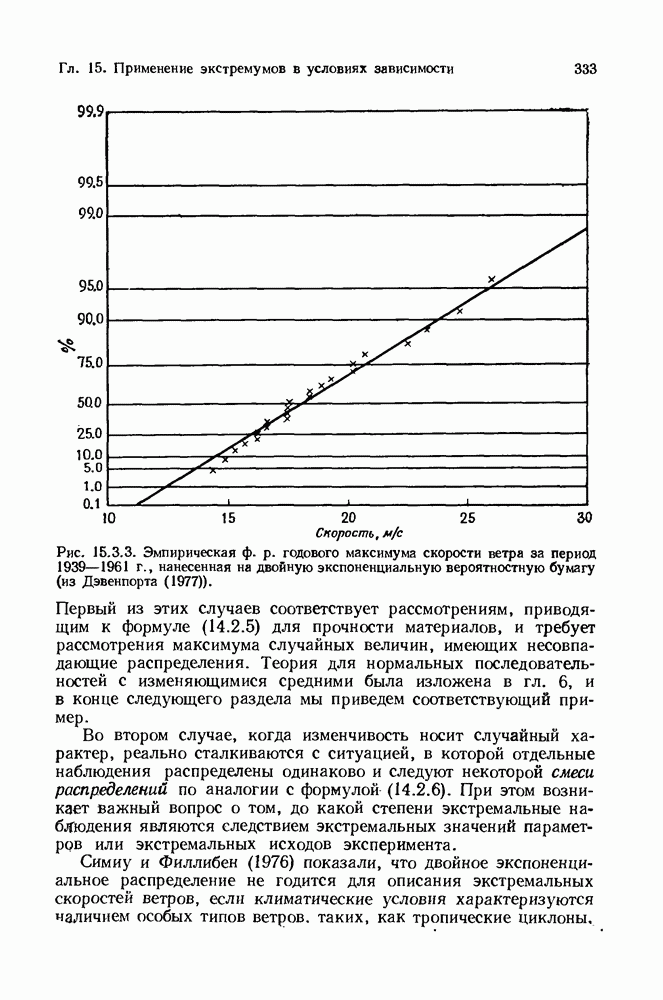
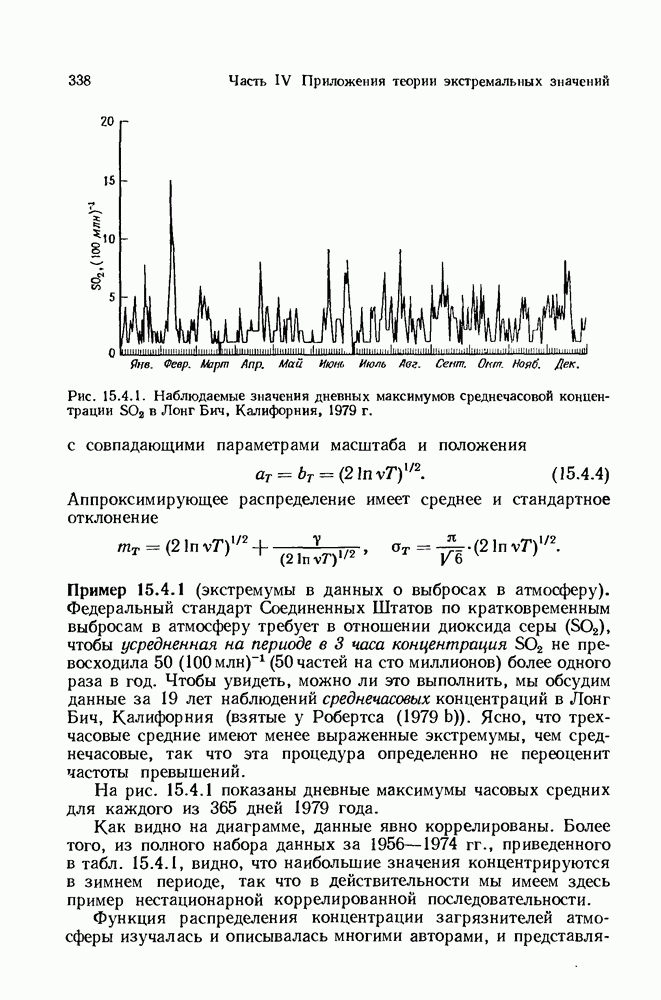
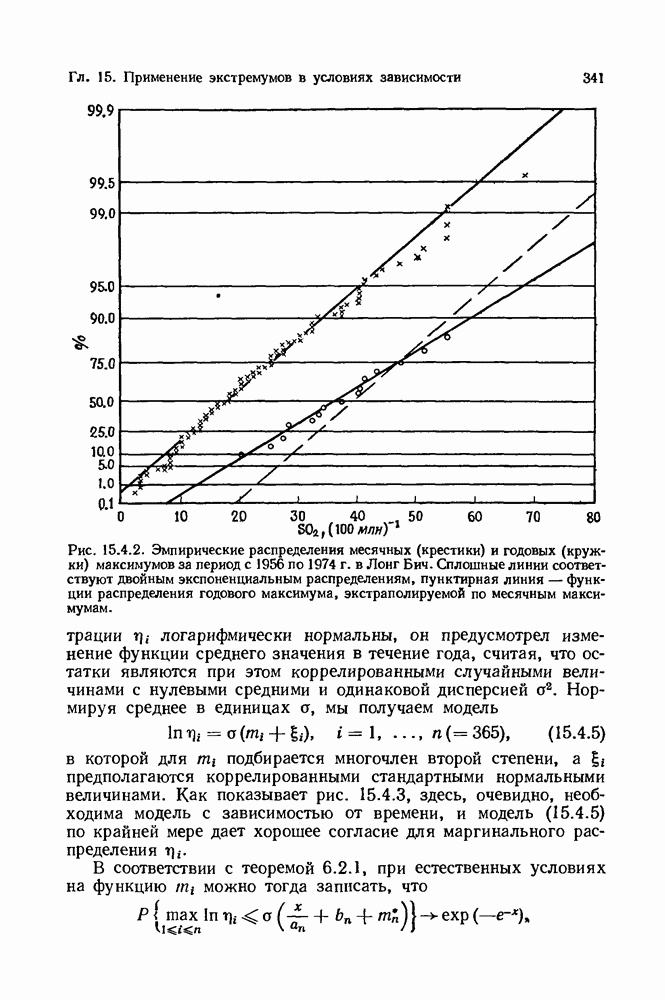
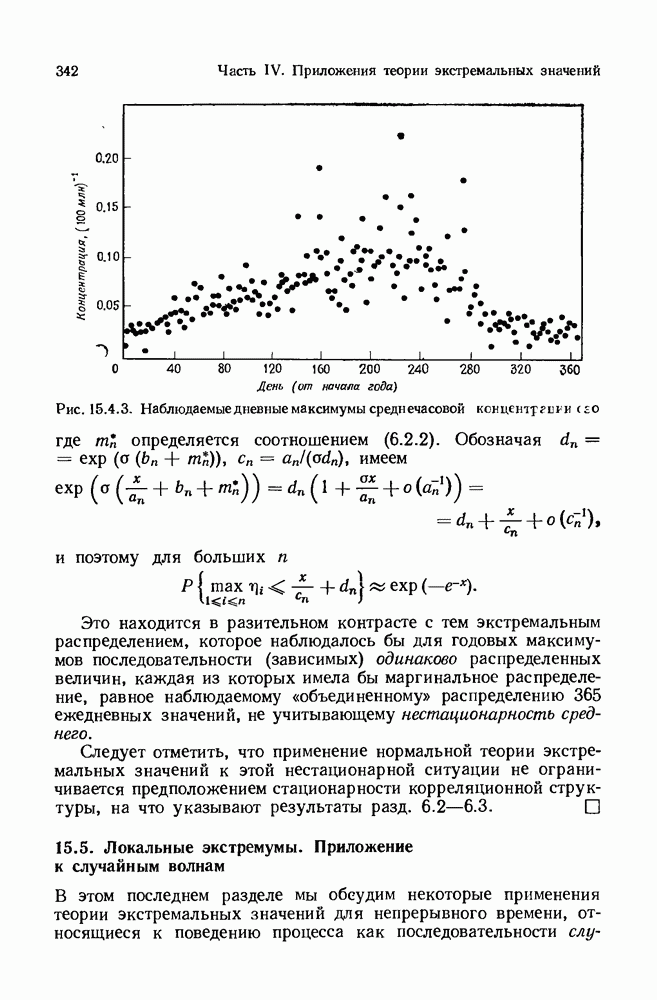
- 15.4. Экстраполирование экстремумов на более обширный период времени
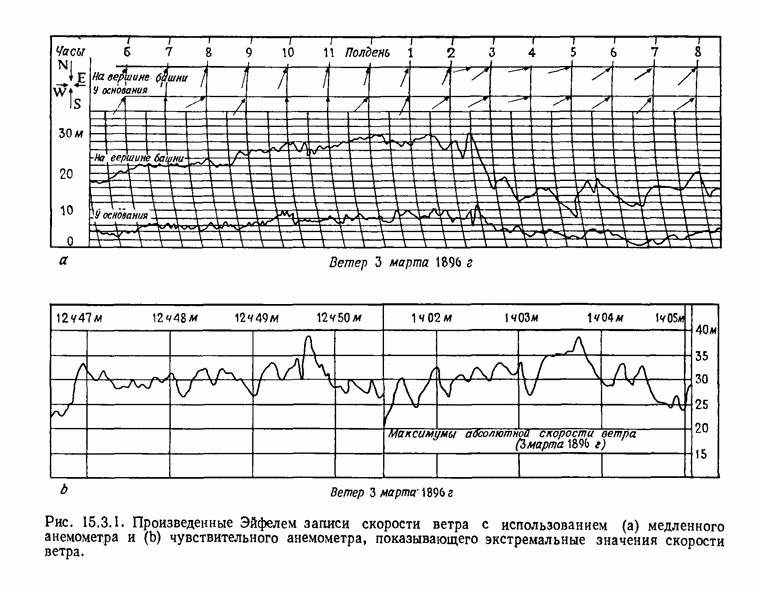
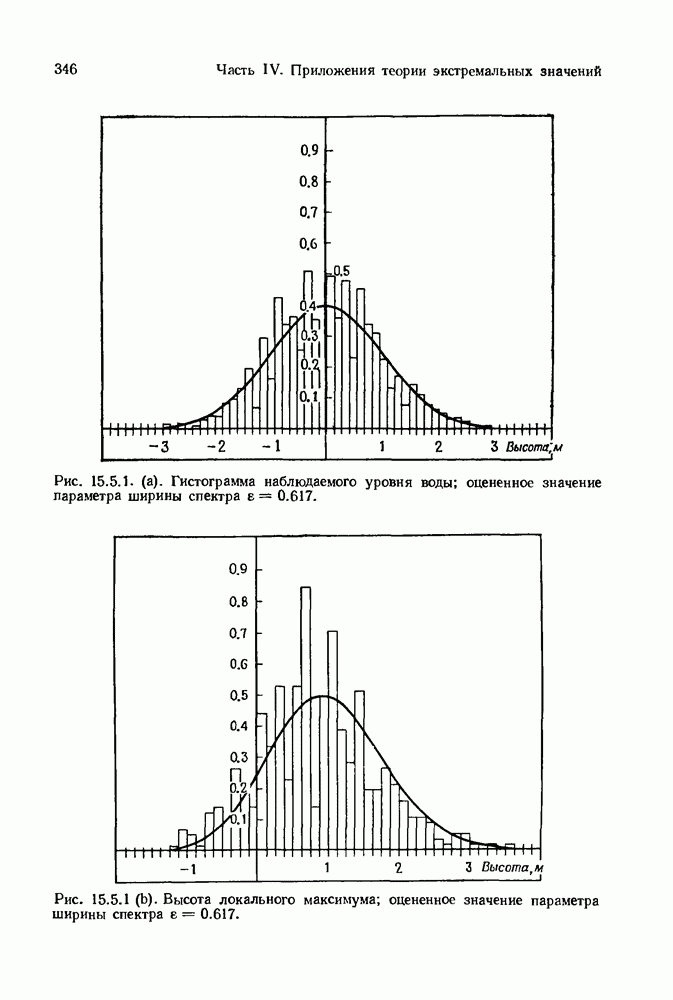
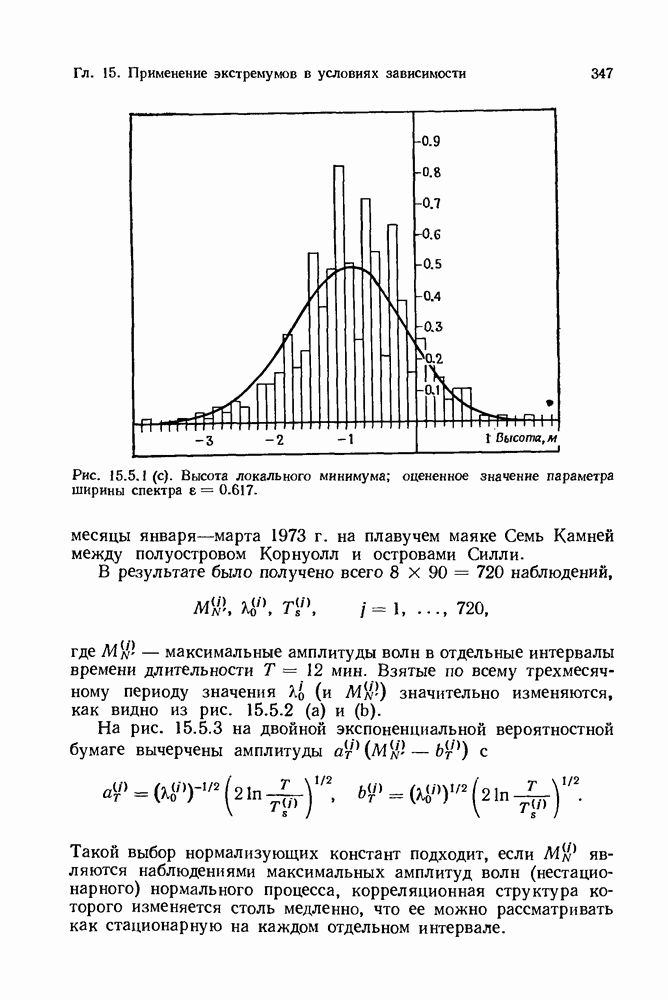
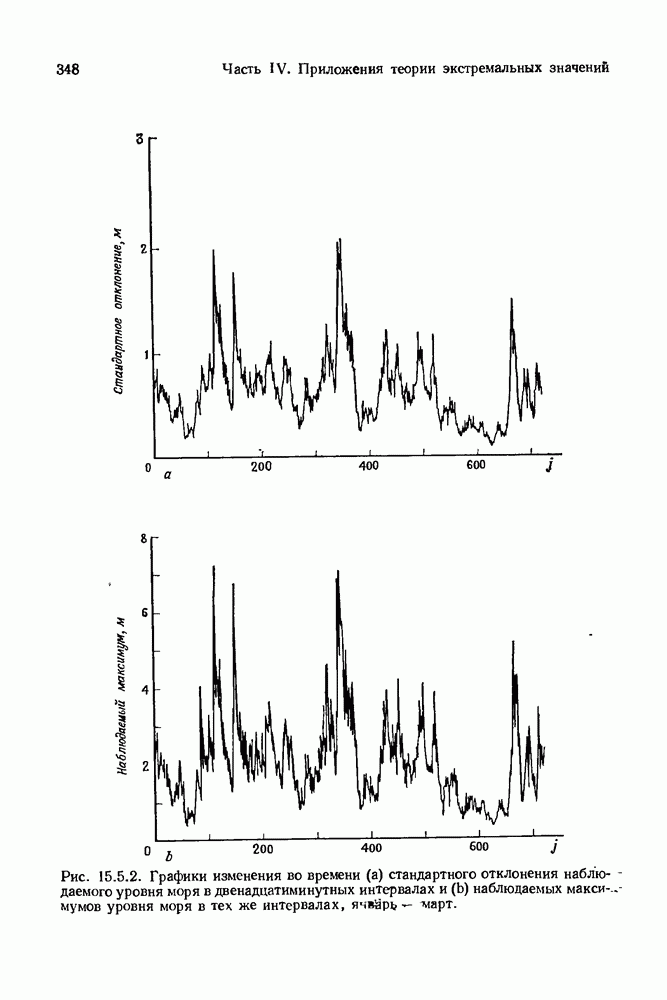
- 15.5. Локальные экстремумы. Приложение к случайным волнам
- Приложение. Некоторые основные понятия теории точечных процессов