| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Преобразование гауссова пучка в линзовой системе.
Гауссов пучок (рис. 2.50) распространяется от плоскости  до плоскости
до плоскости  и проходит при этом через линзу с фокусным расстоянием
и проходит при этом через линзу с фокусным расстоянием  — расстояние от
— расстояние от  до линзы,
до линзы,  — расстояние от линзы до
— расстояние от линзы до  Сначала пучок преобразуется в свободном пространстве от
Сначала пучок преобразуется в свободном пространстве от  до линзы; согласно (2.8.7)
до линзы; согласно (2.8.7)

Затем пучок преобразуется в линзе; согласно (2.8.8)

или


Рис. 2.50
Наконец, пучок Преобразуется в свободном пространстве от линзы до  согласно (2.8.7)
согласно (2.8.7)

Объединяя (2.8.9) — (2.8.11), получаем следующее правило для преобразования пучка при его распространении от плоскости  (параметр пучка
(параметр пучка  до плоскости
до плоскости  (параметр пучка
(параметр пучка 

Закон ABCD — закон преобразования гауссовых пучков в линзовых системах. Любое преобразование гауссова пучка в линзовой системе может быть представлено в виде

где  — соответственно начальный и конечный параметры пучка. Матрица описывает систему, обеспечивающую рассматриваемое преобразование пучка.
— соответственно начальный и конечный параметры пучка. Матрица описывает систему, обеспечивающую рассматриваемое преобразование пучка.
Так, преобразованию пучка в свободном пространстве протяженности  отвечает матрица (ср. (2.8.7) и (2.8.13))
отвечает матрица (ср. (2.8.7) и (2.8.13))

Преобразованию пучка в линзе с фокусным расстоянием  отвечает матрица (ср. (2.8.10) и (2.8.13))
отвечает матрица (ср. (2.8.10) и (2.8.13))

Преобразованию пучка в линзовой системе, показанной на рис. 2.50, отвечает матрица (ср. (2.8.12) и (2.8.13))

Если преобразование гауссова пучка есть последовательность нескольких преобразований, то его матрица представляет собой произведение матриц составляющих преобразований, записанных в порядке, обратном порядку, в каком выполняются эти преобразования. Легко убедиться, например, что

Выражаемый соотношением (2.8.13) закон ABCD позволяет легко находить правило преобразования гауссова пучка в произвольной линзовой системе. АВСО-матрица соответствующего преобразования определяется как произведение матриц типа (2.8.14) и (2.8.15), записанных в определенном порядке. Принимая во внимание аналогию между линзовыми волноводами и открытыми резонаторами, можно распространить закон ABCD и на резонатор, при условии, что рассматриваются резонаторы, в которых световые пучки являются гауссовыми. Матрица, описывающая

Рис. 2.51
преобразование гауссова пучка при его отражении от сферического зеркала с радиусом кривизны  имеет вид
имеет вид

который формально следует из (2.8.15), если 
Сопоставляя результаты, полученные в данном параграфе, с результатами, полученными в § 2.4 при рассмотрении преобразований светового луча, нетрудно обнаружить интересную аналогию между оптикой гауссовых пучков и геометрической оптикой. Дело в том, что используемая в законе ABCD для гауссовых пучков  -матрица, описывающая некоторую оптическую систему, совпадает с описывающей эту же систему матрицей передачи светового луча. Эта матрица выражается через произведение записанных В определенном порядке «элементарных» матриц (для свободного пространства, линзы, сферического зеркала), имеющих одинаковый вид как в геометрической оптике, так и в оптике гауссовых пучков. Можно получить
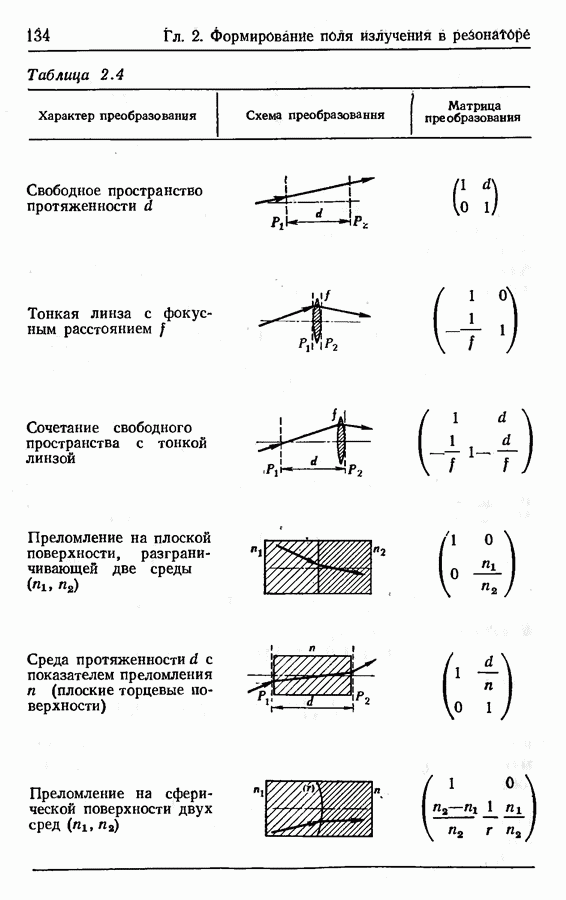
-матрица, описывающая некоторую оптическую систему, совпадает с описывающей эту же систему матрицей передачи светового луча. Эта матрица выражается через произведение записанных В определенном порядке «элементарных» матриц (для свободного пространства, линзы, сферического зеркала), имеющих одинаковый вид как в геометрической оптике, так и в оптике гауссовых пучков. Можно получить  -матрицу, рассматривая поведение световых лучей в оптической системе, и затем применить эту матрицу к гауссовым пучкам. Собранные в табл. 2.4 матрицы передачи луча используются при рассмотрении гауссовых пучков.
-матрицу, рассматривая поведение световых лучей в оптической системе, и затем применить эту матрицу к гауссовым пучкам. Собранные в табл. 2.4 матрицы передачи луча используются при рассмотрении гауссовых пучков.
Впрочем аналогию между лучевой оптикой и оптикой гауссовых пучков не следует преувеличивать. Аналогия имеет место лишь постольку, поскольку речь идет о виде

Рис. 2.52
АВCD-матрицы для рассматриваемой оптической системы. Что же касается характера выполняемого  -матрицей преобразования, то он различен для луча и гауссова пучка. Преобразование луча описывается выражением (2.4.16), тогда как гауссов пучок преобразуется в соответствии с законом
-матрицей преобразования, то он различен для луча и гауссова пучка. Преобразование луча описывается выражением (2.4.16), тогда как гауссов пучок преобразуется в соответствии с законом  описываемым выражением (2.8.13); см. рис. 2.51.
описываемым выражением (2.8.13); см. рис. 2.51.
В заключение заметим, что закон  применим также при распространении гауссова пучка в среде, показатель преломления которой изменяется в поперечном к оптической оси направлении по квадратичному закону
применим также при распространении гауссова пучка в среде, показатель преломления которой изменяется в поперечном к оптической оси направлении по квадратичному закону

Для сред с произвольным (неквадратичным) законом изменения показателя преломления закон  неприменим. Он неприменим также в случаях, когда необходимо принимать во внимание аберрации линз. Во всех этих случаях в результате преобразования световой пучок перестает быть гауссовым [7].
неприменим. Он неприменим также в случаях, когда необходимо принимать во внимание аберрации линз. Во всех этих случаях в результате преобразования световой пучок перестает быть гауссовым [7].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. СПОСОБЫ ПОЛУЧЕНИЯ ИНВЕРТИРОВАННЫХ АКТИВНЫХ СРЕД
- Квантовый выход и коэффициент полезного действия лазера.
- Условие инверсии для четырехуровневой модели (стационарная накачка).
- Механизмы заселения уровней (механизмы возбуждения).
- Механизмы очищения уровней (механизмы релаксации).
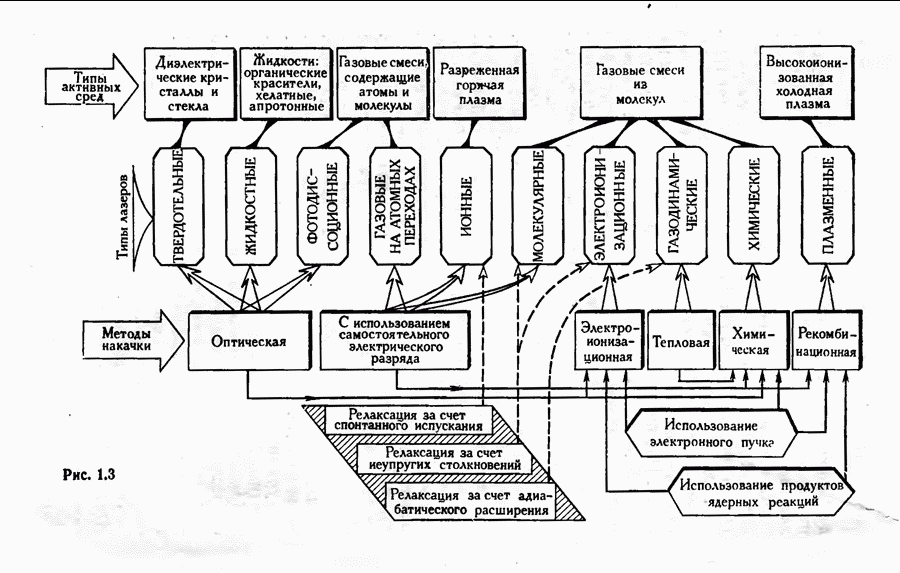
- Классификация лазеров с учетом различных методов накачки.
- Некоторые проблемы, возникающие при непрерывной генерации; столкновительные лазеры.
- Преимущества импульсной накачки; генерация на самоограниченных переходах.
- Лазеры на разлетных молекулах.
- 1.2. Оптическая накачка. Твердотельные лазеры
- Условия реализации стационарной инверсии при оптической накачке.
- Твердотельные лазеры: вопросы практической реализации оптической накачки, рабочие схемы лазеров.
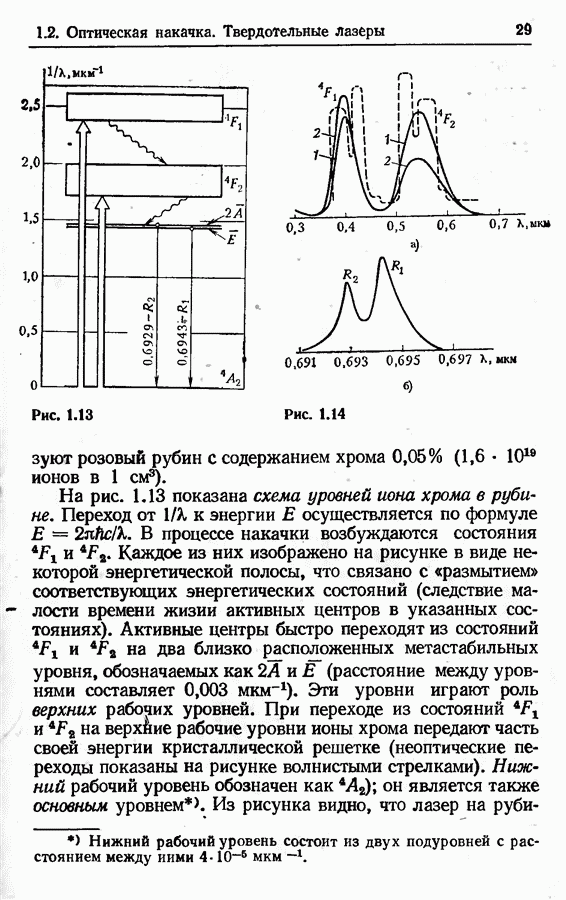
- Лазер на рубине.
- Лазер на иттрий-алюминиевом гранате с неодимом.
- Оптическая накачка полупроводниковым лазером или светодиодом.
- 1.3. Лазеры на органических красителях
- Оптическая накачка лазеров на красителях.
- Схема уровней и основные переходы.
- Перестройка длины волны генерации; селективные резонаторы.
- Проблема расширения диапазона перестройки длины волны генерации.
- 1.4. Газовые лазеры с широкополосной оптической накачкой
- Возможность широкополосной оптической накачки в газах; фотодиссоционные лазеры.
- Фотодиссоционный йодный лазер.
- Проблема прямого преобразования солнечной энергии в лазерное излучение.
- 1.5. Накачка с использованием самостоятельного электрического разряда в разреженных газах
- Электрические разряды, применяемые в газоразрядных лазерах.
- Аргоновый лазер [39].
- Механизм возникновения инверсии в аргоновом лазере.
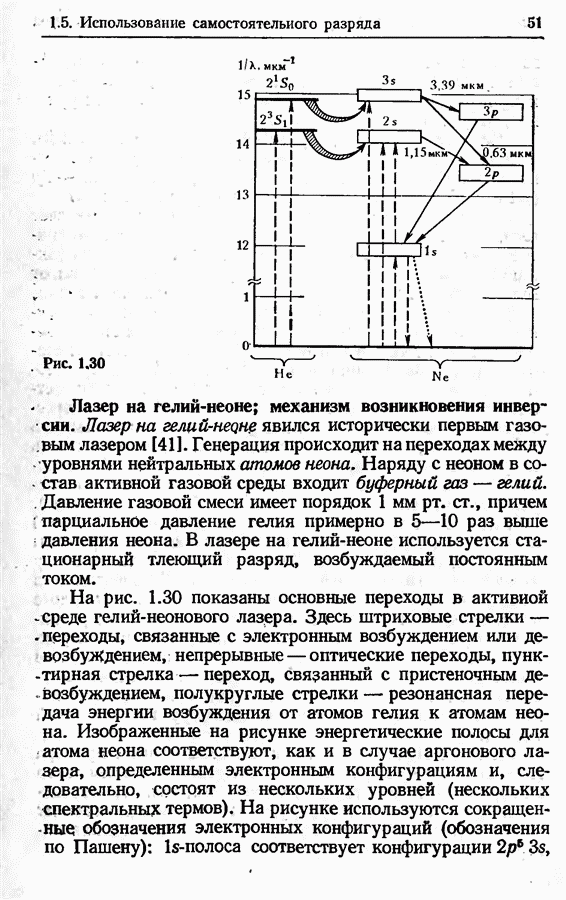
- Лазер на гелий-неоне; механизм возникновения инверсии.
- Лазер на парах меди [5].
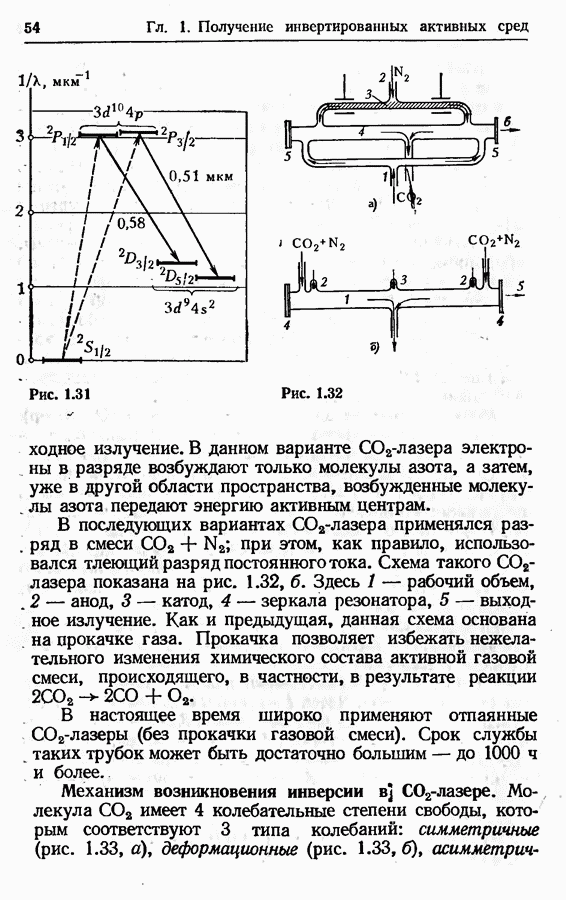
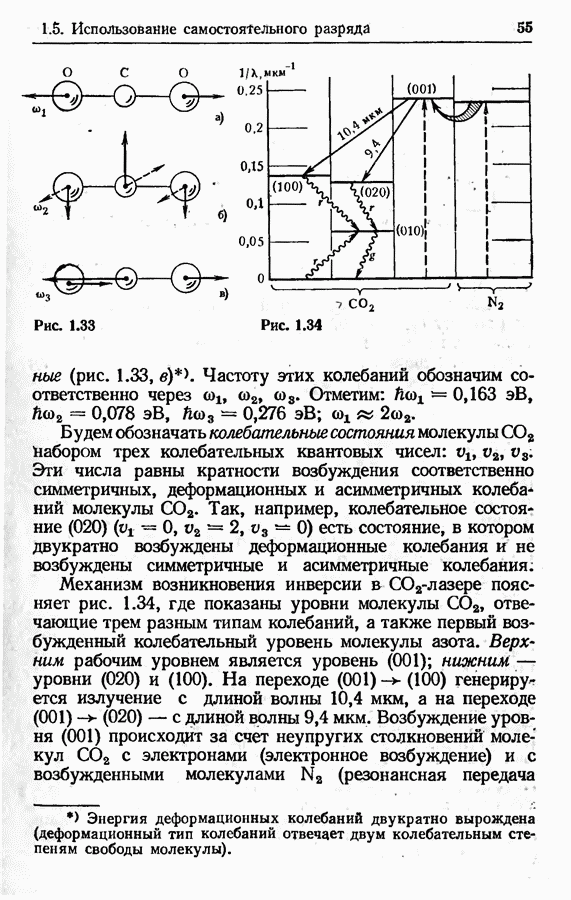
- Молекулярный лазер на двуокиси углерода (CO2-лазер).
- Механизм возникновения инверсии в CO2-лазере.
- 1.6. Электроионизационные лазеры
- Электроионизационный метод накачки газовых лазеров высокого давления.
- Электроионизационный CO2-лазер.
- Использование различных активных сред.
- Способы ионизации.
- 1.7. Газодинамические лазеры (тепловая накачка)
- Газодинамический CO2-лазер.
- Механизм возникновения инверсии в газодинамическом CO2-лазере.
- Пути повышения КПД газодинамических лазеров.
- 1.8. Химические лазеры
- Цепной характер химических реакций; химическая и лазерная длина цепи.
- Лазеры с прямым и непрямым образованием инверсии.
- Химический лазер на фторводородной смеси с непрямым образованием инверсии [63].
- Химические лазеры на сероуглероде (химические СО-лазеры).
- Химические лазеры на электронных переходах молекул.
- 1.9. Плазменные лазеры (рекомбинационная накачка)
- Принципиальные вопросы создания лазера на рекомбинирующей плазме.
- «Открытая» двухуровневая модель плазменного лазера.
- Проблема очищения нижнего рабочего уровня.
- Импульсные плазменные лазеры.
- Плазменные лазеры с использованием жестких ионизаторов; реактор-лазер.
- Плазмодинамические лазеры.
- Плазмохимические лазеры.
- Список литературы
- Глава 2. ФОРМИРОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ В РЕЗОНАТОРЕ ЛАЗЕРА
- Начальный коэффициент усиления для оптически разрешенных и запрещенных рабочих переходов.
- Зависимость начального коэффициента усиления от скорости накачки.
- Зависимость начального коэффициента усиления от частоты.
- 2.2. Онтический резонатор и лазерное излучение (начальные сведения)
- Резонансные частоты.
- Моды (типы колебаний) оптического резонатора.
- Роль оптического резонатора в лазере.
- Пассивные и активные резонаторы.
- 2.3. Общие замечания об открытых резонаторах
- Добротность резонатора.
- Добротность и моды открытого резонатора.
- Дифракционные потери. Число Френеля.
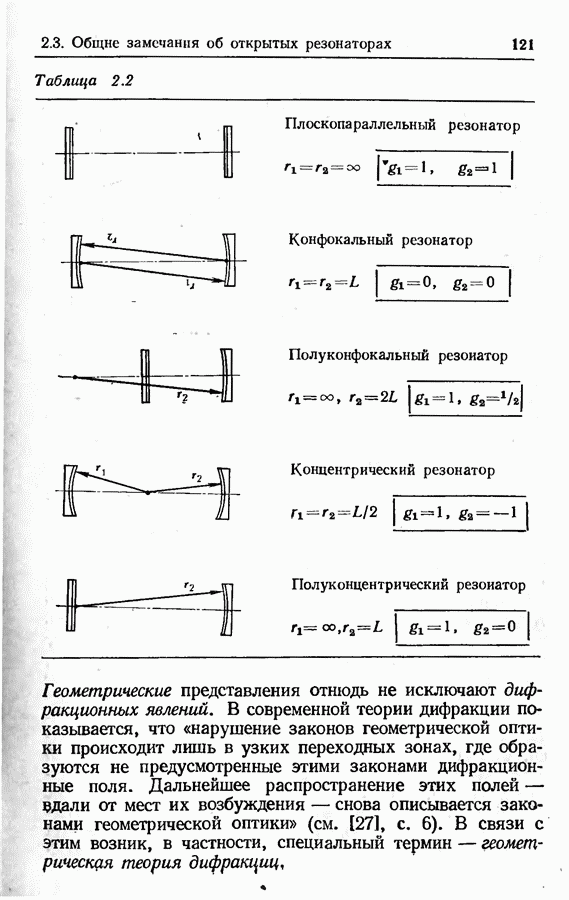
- Основные параметры пассивного резонатора, образованного двумя зеркалами (сферическими либо плоскими).
- Геометрическое приближение.
- 2.4. Линзовые волноводы и открытые резонаторы (приближение геометрической оптики)
- Условие устойчивости для линзового волновода с чередующимися линзами.
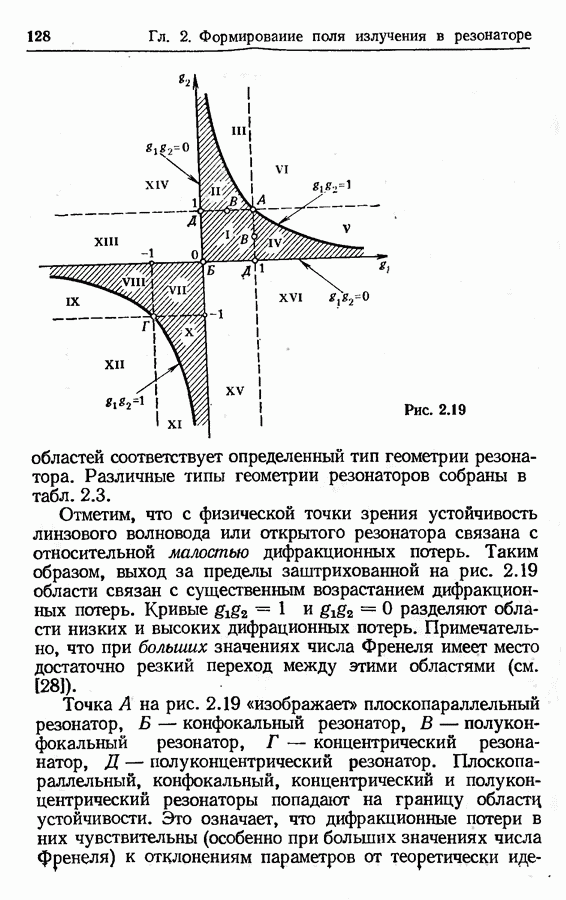
- Устойчивые и неустойчивые открытые резонаторы; диаграмма устойчивости.
- Матрица передачи светового луча.
- Матрица передачи луча для двойного прохода резонатора.
- 2.5. Расстройка открытого резонатора
- Резонатор с разъюстированным оптическим элементом.
- 2.6. Рассмотрение открытых резонаторов на основе итерационного метода Фокса — Ли. Эквивалентные резонаторы
- Интегральное уравнение Фокса — Ли.
- Поперечные моды открытого резонатора.
- Резонатор, образованный двумя сферическими зеркалами.
- Конфокальный резонатор
- Учет величины апертуры зеркал резонатора.
- Эквивалентные резонаторы.
- Резонатор, эквивалентный резонатору с внутренней линзой.
- Резонатор с диафрагмой.
- 2.7. Гауссовы пучки
- Распространение гауссова пучка в свободном пространстве.
- Радиус кривизны поверхности постоянной фазы.
- Основные соотношения, связывающие параметры гауссова пучка.
- Комплексные параметры гауссова пучка.
- Гауссов пучок как решение параболического уравнения.
- Обобщение на моды высоких порядков.
- 2.8. Преобразование и согласование гауссовых пучков
- Линза как фазовый корректор.
- Преобразование гауссова пучка в линзе.
- Преобразование гауссова пучка в линзовой системе.
- Преобразование гауссова пучка в квадратичной среде.
- Согласование гауссовых пучков.
- 2.9. Гауссовы пучки в устойчивых резонаторах
- Гауссов пучок в резонаторе (большие апертуры зеркал).
- Замечания, связанные с учетом апертуры зеркал.
- Фазовый сдвиг для гауссова пучка и спектр резонансных частот.
- Применение закона ABCD к рассмотрению поля в резонаторе.
- Неопределенность каустики конфокального резонатора с неограниченными апертурами зеркал.
- Конфокальный резонатор с конечными апертурами зеркал.
- Конфокальный резонатор с диафрагмой.
- 2.10. Неустойчивые резонаторы
- Потери в неустойчивом резонаторе по геометрооптической теории.
- Применение закона ABCD к неустойчивым резонаторам.
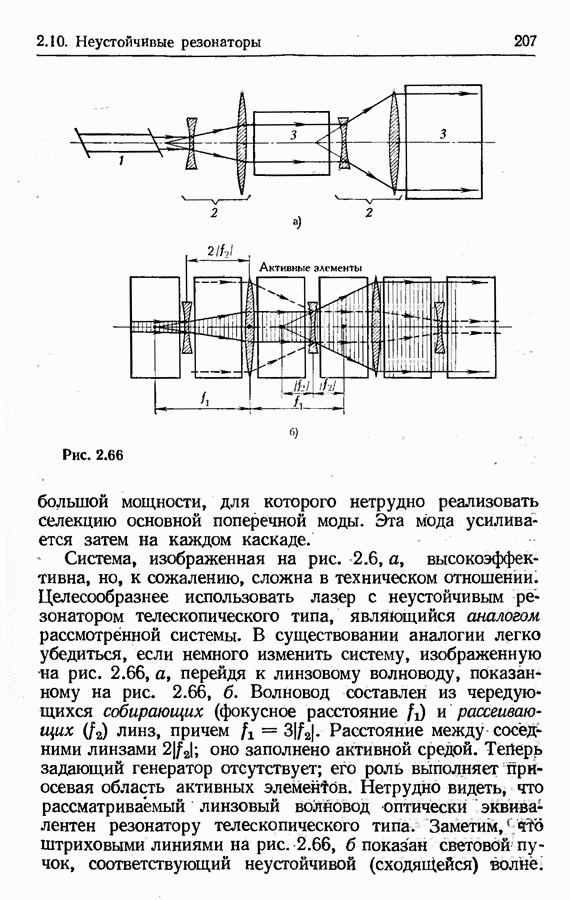
- Лазер с неустойчивым резонатором телескопического типа.
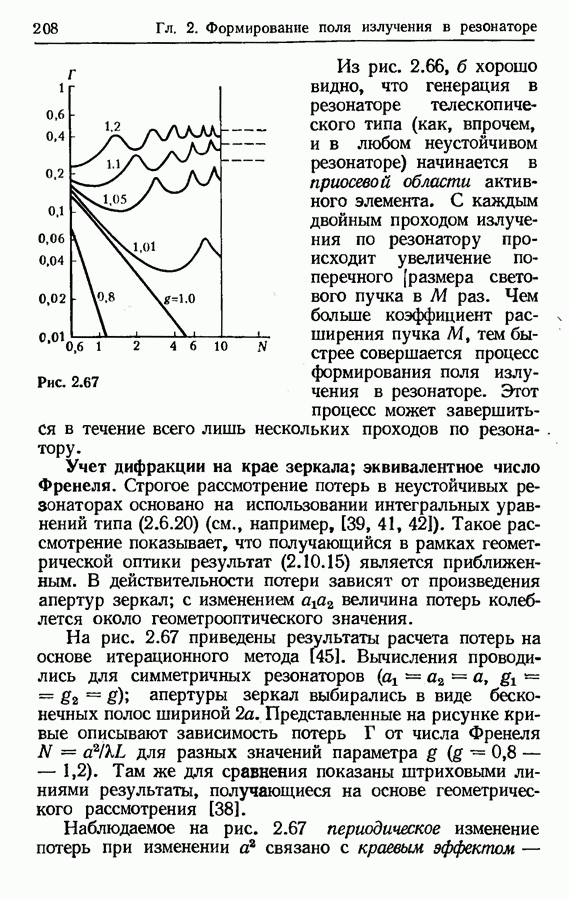
- Учет дифракции на крае зеркала; эквивалентное число Френеля.
- Преимущества неустойчивых резонаторов.
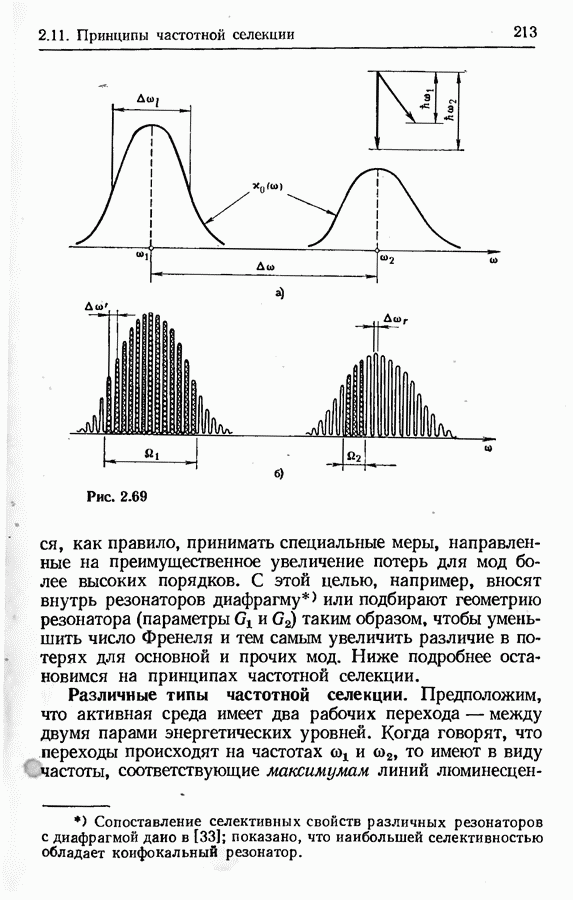
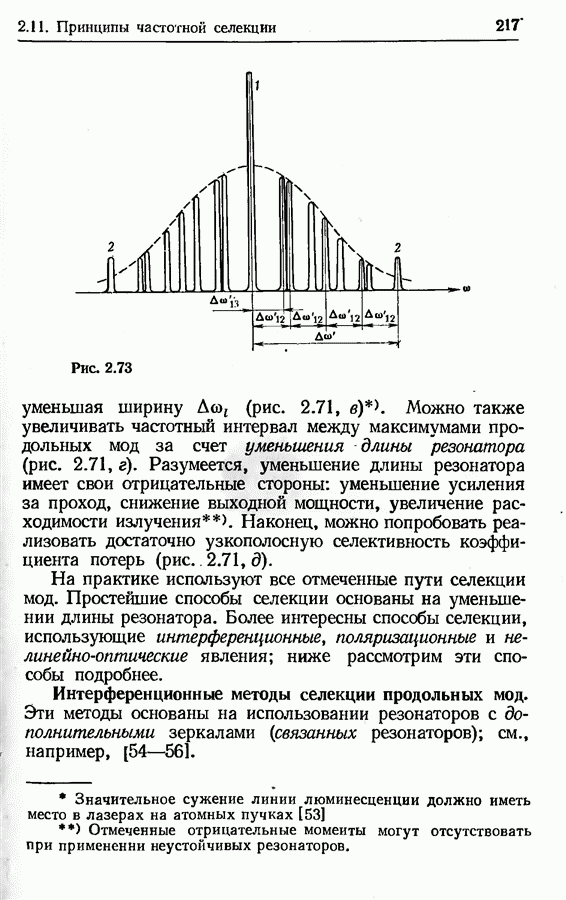
- 2.11. Принципы частотной селекции
- Применение широкополосных поглощающих фильтров и дисперсионных элементов.
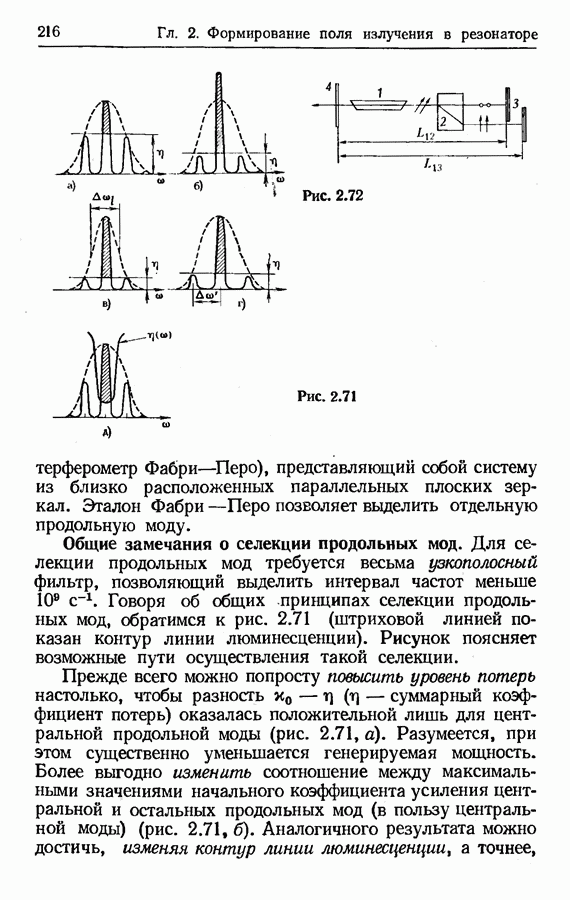
- Общие замечания о селекции продольных мод.
- Интерференционные методы селекции продольных мод.
- Резонаторы с анизотропными элементами.
- Нелинейно-оптический метод частотной селекции.
- 2.12. Эффекты «выгорания дыр» и затягивания частот
- Насыщение усиления при однородном и неоднородном уширении линий; эффект «выгорания дыр».
- Специфика рассмотрения насыщения усиления при неоднородном уширении линнн перехода.
- Эффект затягивания частот.
- Эффект затягивания частот для случаев однородного и неоднородного уширения.
- 2.13. Тепловая линза
- Термоупругие напряжения; термические искажения резонатора.
- Фокусное расстояние и главные плоскости тепловой линзы.
- Учет тепловой линзы в лазерных системах.
- 2.14. Волноводные резонаторы
- Число волноводных мод в резонаторе.
- Волноводный резонатор половинного типа.
- Преимущества волноводных резонаторов.
- 2.15. Оптическое излучение в тонкопленочном волноводе. Распределенная обратная связь
- Волноводные моды в тонкой пленке.
- Число волноводных мод в пленке.
- Распределение поля в волноводных модах.
- Методы ввода и вывода излучения для тонкопленочного волновода.
- Принцип действия элемента связи призма — пленка.
- Распределенная обратная связь.
- Пленочные РОС-лазеры.
- Пленочные лазеры с периодической структурой в качестве зеркала резонатора.
- Список литературы
- Глава 3. ДИНАМИКА ПРОЦЕССОВ В ЛАЗЕРЕ
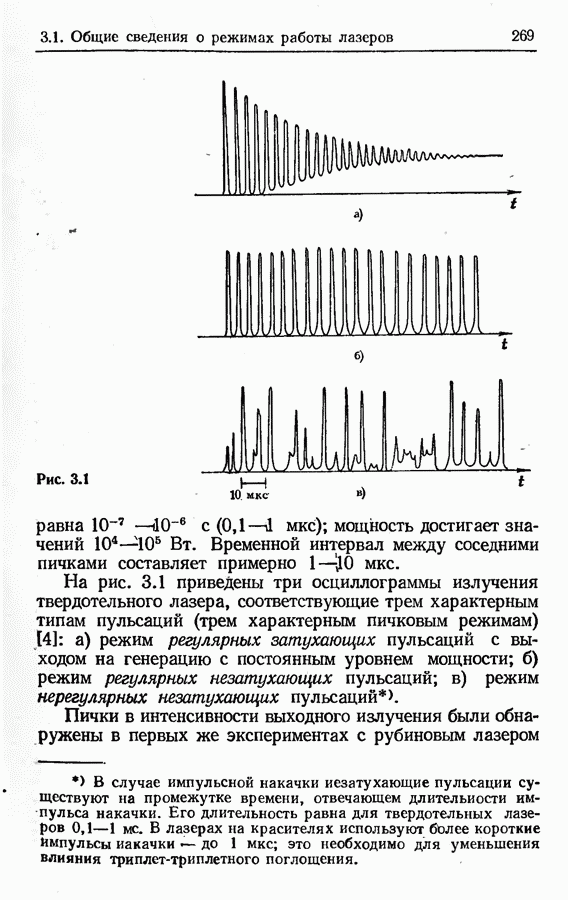
- 3.1. Общие сведения о режимах работы лазеров
- Режим свободной генерации.
- Режим генерации гигантских импульсов при активной модуляции добротности резонатора.
- Режим генерации гигантских импульсов при пассивной модуляции добротности резонатора.
- Режим синхронизации продольных мод (режим генерации сверхкоротких световых импульсов).
- Режим синхронизации поперечных мод.
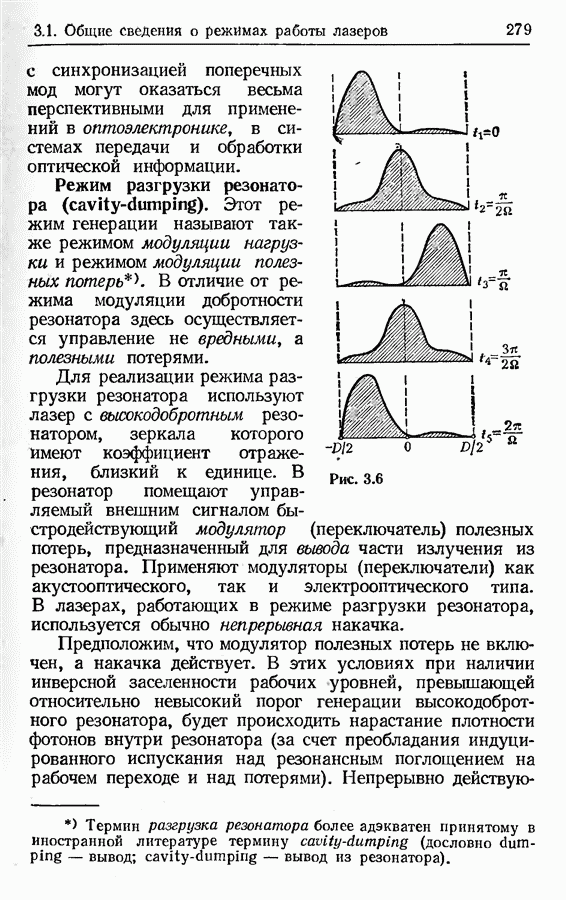
- Режим разгрузки резонатора (cavity-dumping).
- Генерация последовательности импульсов в лазерах с непрерывной накачкой.
- Использование отрицательной обратной связи для получения импульсов микросекундной длительности.
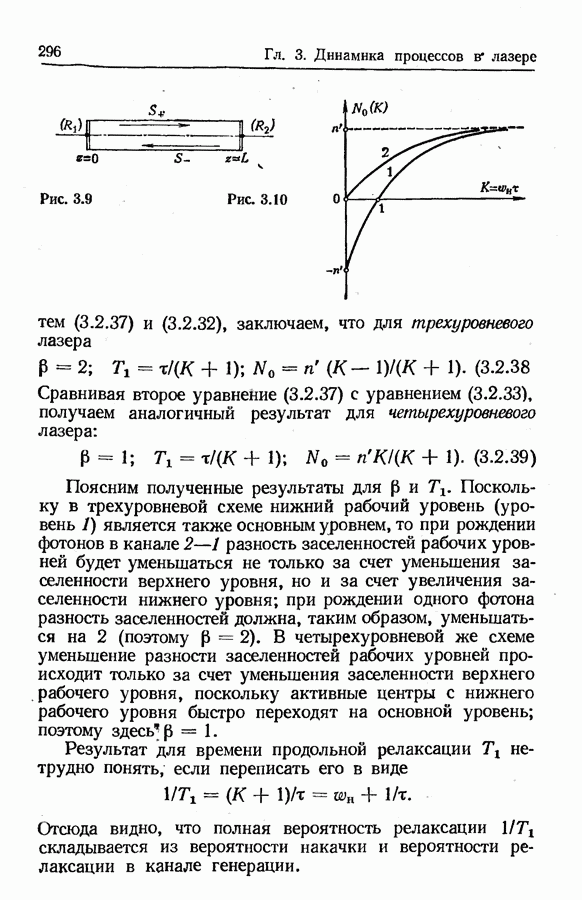
- 3.2. Приближенные уравнения для описания динамики процессов в лазерах (балансные уравнения)
- Дифференциальные уравнения для плотности инверсной заселенности (трехуровневый и четырехуровневый лазеры).
- Полная система балансных уравнений в частных производных.
- Усредненные балансные уравнения (скоростные уравнения).
- Уравнения Статца — Де Марса.
- Сопоставление уравнений Статца — Де Марса и системы усредненных балансных уравнений.
- Пороговая плотность инверсной заселенности и условие генерации.
- Безразмерная форма записи уравнений Статца—Де Марса.
- Учет вклада спонтанного излучения в интенсивность поля.
- Общие замечания о методе балансных уравнений.
- Лазер как распределенная автоколебательная система.
- 3.3. Режим свободной генерации. Регулярные затухающие пульсации мощности излучения
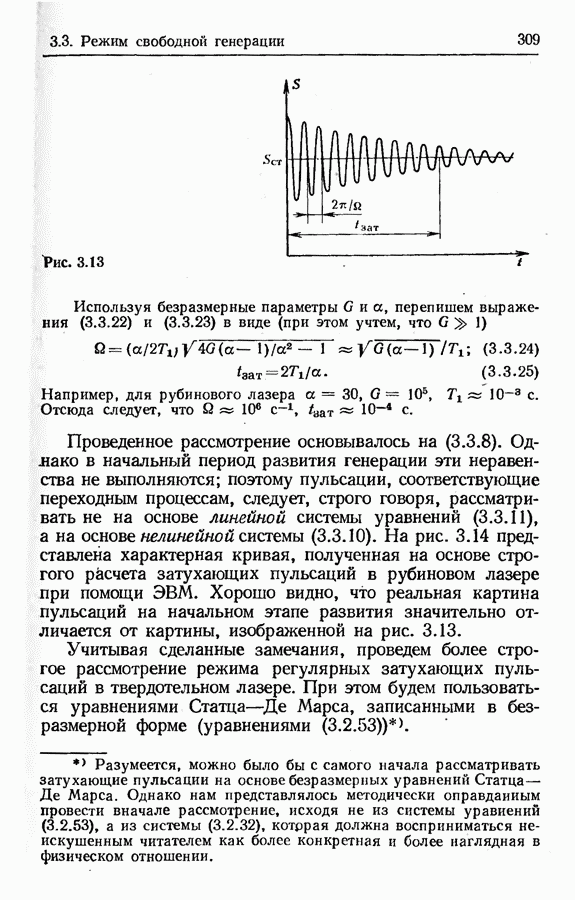
- Переходные процессы, сопровождающие возникновение генерации (регулярные затухающие пульсации мощности излучения).
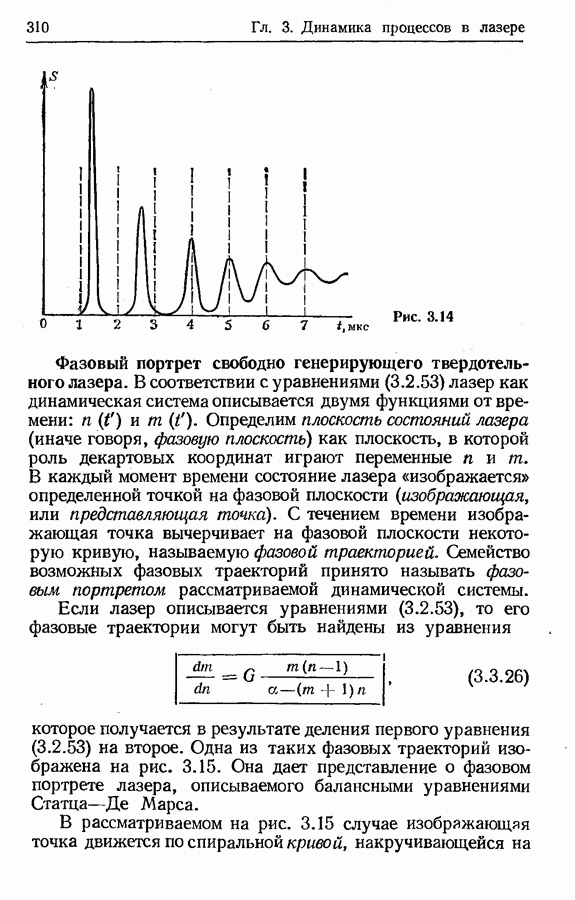
- Фазовый портрет свободно генерирующего твердотельного лазера.
- Выявление структуры фазового портрета лазера.
- Замечания о свободной генерации в многомодовом лазере.
- 3.4. Лазер с нестационарным резонатором. Незатухающие пульсации мощности излучения
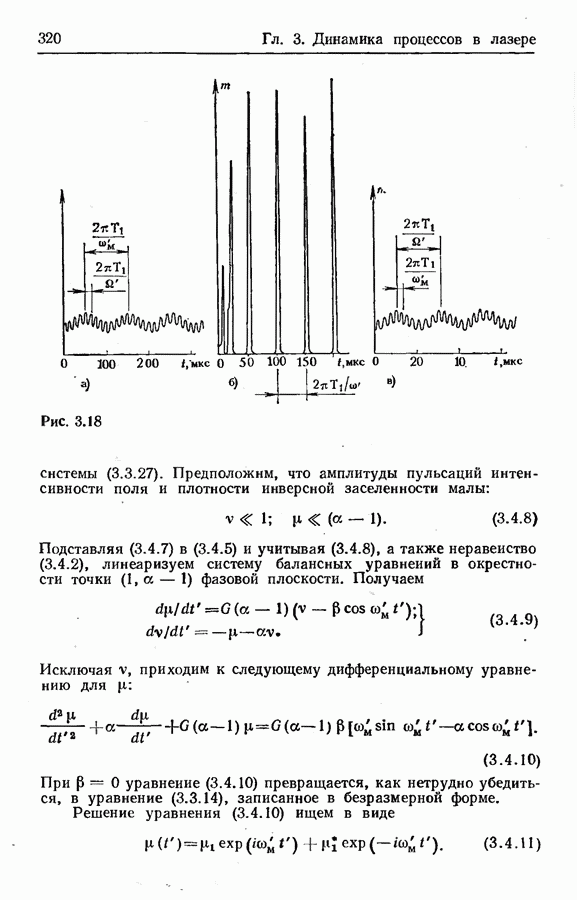
- Пульсации малой амплитуды.
- Замечания о возможности реализации незатухающих пульсаций большой амплитуды.
- Периодическая модуляция добротности при равномерном движении отражающей плоскости.
- Природа незатухающих пульсаций в режиме свободной генерации.
- 3.5. Активная модуляция добротности резонатора
- Электрооптическая модуляция добротности.
- Акустооптическая модуляция добротности.
- Акустооптическая и электрооптическая модуляция добротности (сопоставление).
- Модуляция полезных потерь.
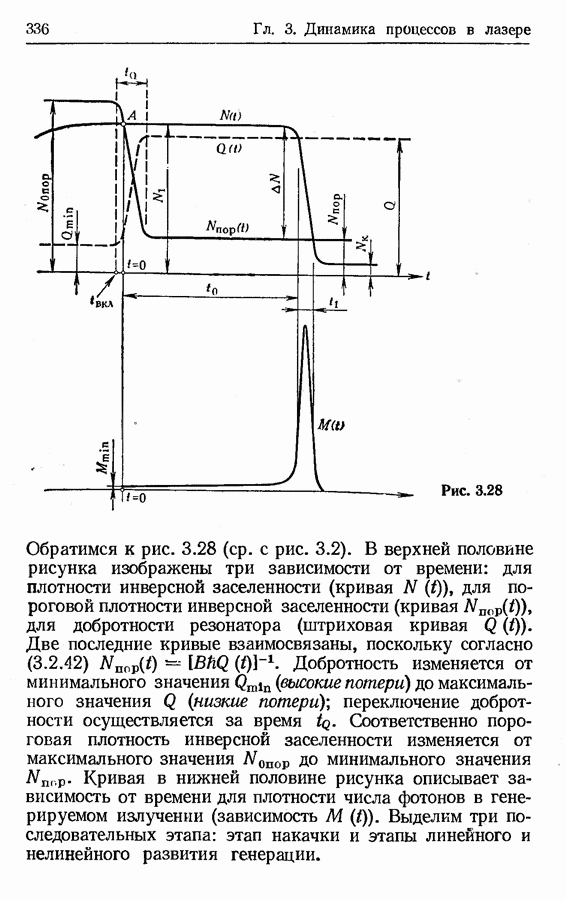
- 3.6. Режим генерации гигантских импульсов при активной модуляции добротности резонатора
- Балансные уравнения. Мгновенное включение добротности.
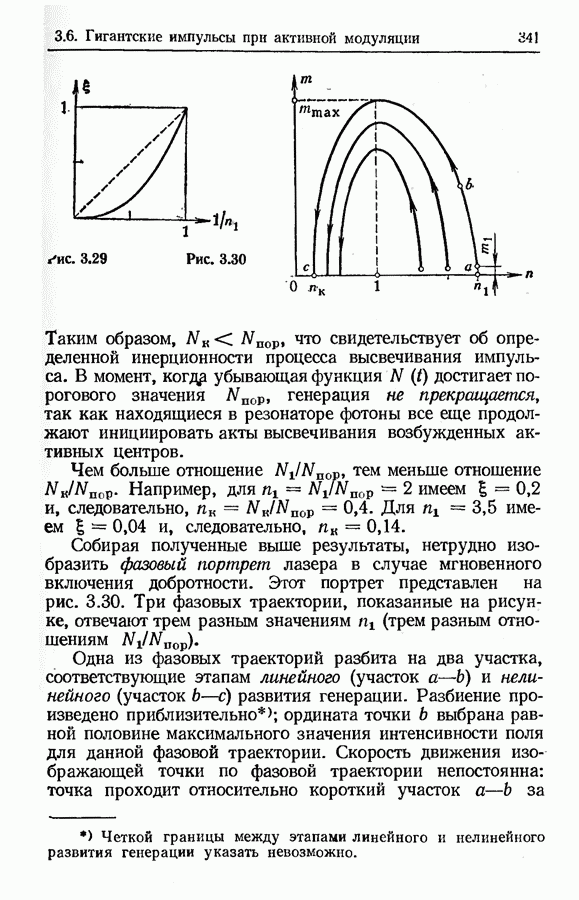
- Фазовый портрет лазера при мгновенном включении добротности.
- Анализ этапа линейного развития генерации.
- Энергетические характеристики гигантского импульса.
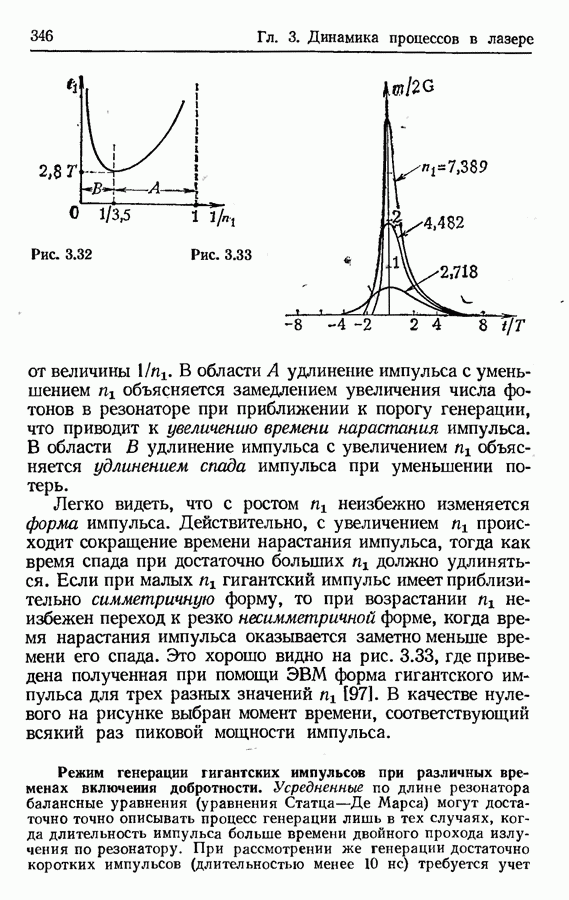
- Длительность и форма гигантского импульса.
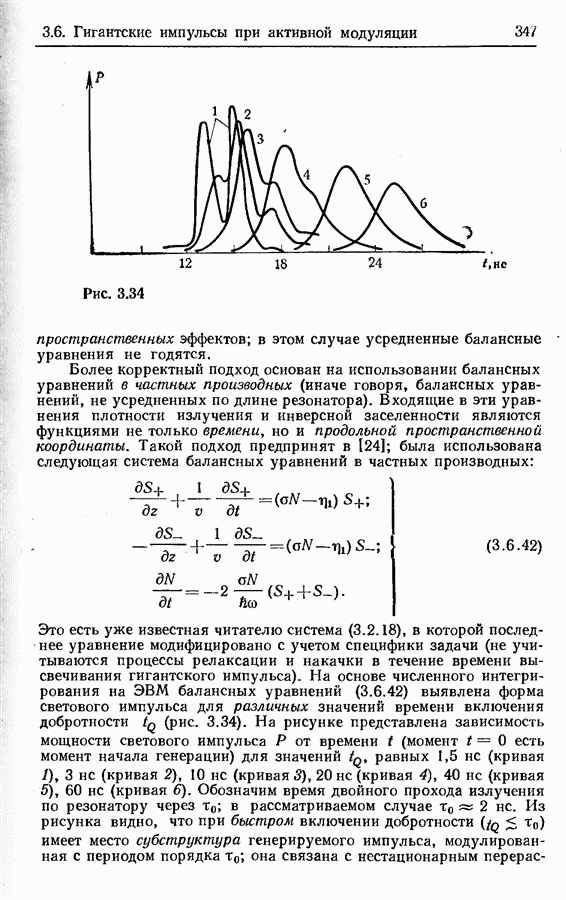
- Режим генерации гигантских импульсов при различных временах включения добротности.
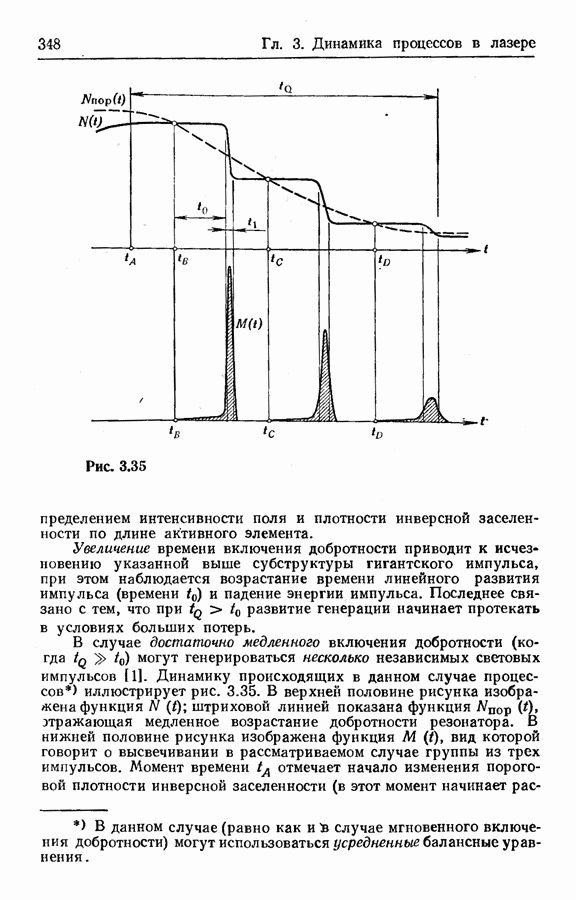
- Замечания о развитии импульса в поперечном к оси резонатора направлении.
- 3.7. Лазеры с просветляющимся фильтром
- Дифференциальное уравнение для усредненной плотности светового потока.
- Полная система балансных уравнений для лазера с просветляющимся фильтром.
- Стационарные решения системы балансных уравнений.
- Неустойчивость исходного стационарного состояния и условие самовозбуждения генерации в лазере с просветляющимся фильтром.
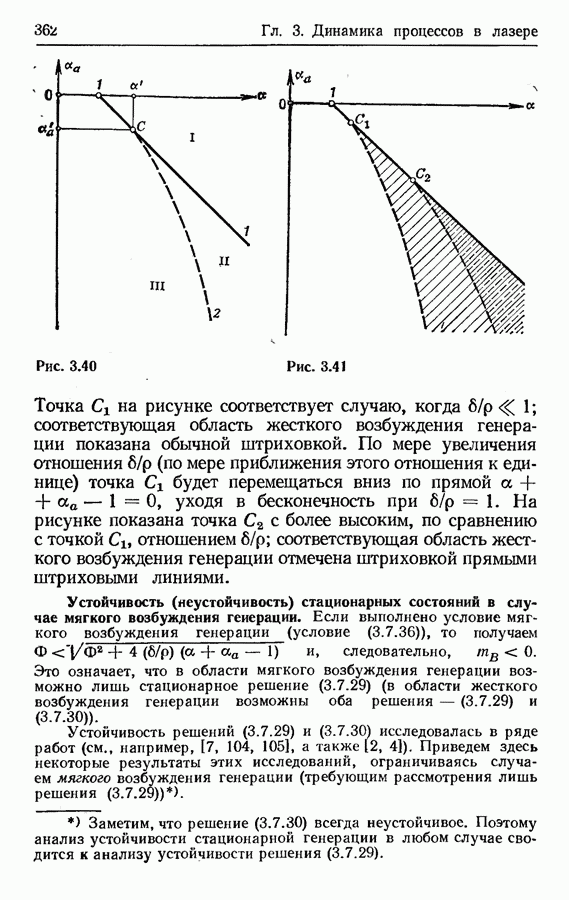
- Мягкое и жесткое возбуждение генерации.
- Устойчивость (неустойчивость) стационарных состояний в случае мягкого возбуждения генерации.
- Режимы генерации лазера с просветляющимся фильтром.
- 3.8. Режим генерации гигантских импульсов при пассивной модуляции добротности резонатора
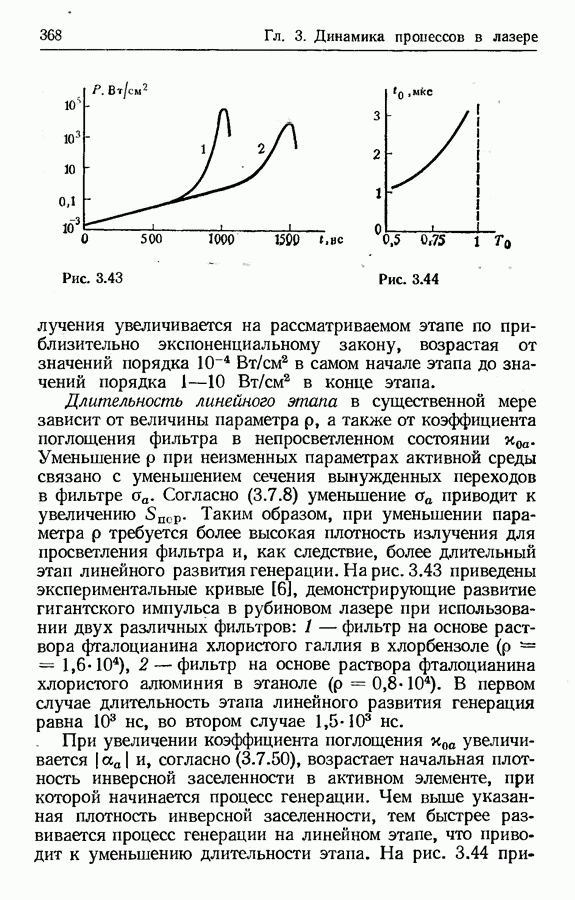
- Развитие гигантского импульса в лазере с просветляющимся фильтром.
- Балансные уравнения; аналогия со случаем мгновенного включения добротности.
- Сопоставление режимов генерации гигантских импульсов при активной и пассивной модуляции добротности; комбинированная модуляция добротности.
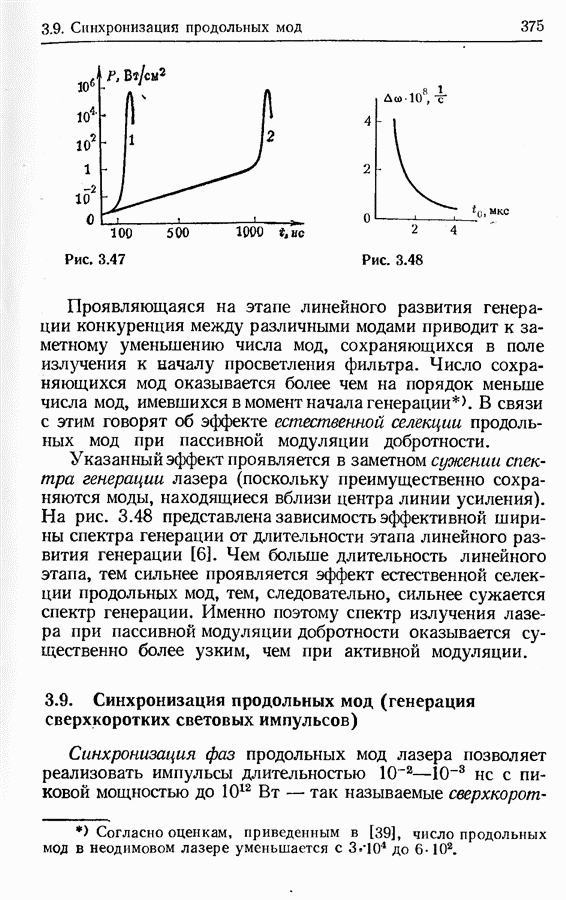
- Естественная селекция продольных мод при пассивной модуляции добротности.
- 3.9. Синхронизация продольных мод (генерация сверхкоротких световых импульсов)
- Неселективный резонатор.
- Активная синхронизация мод.
- Пассивная синхронизация мод (самосинхронизация мод).
- Комбинированный метод синхронизации мод.
- Способы уменьшения времени релаксации просветляющихся фильтров.
- Влияние эффекта самофокусировки света.
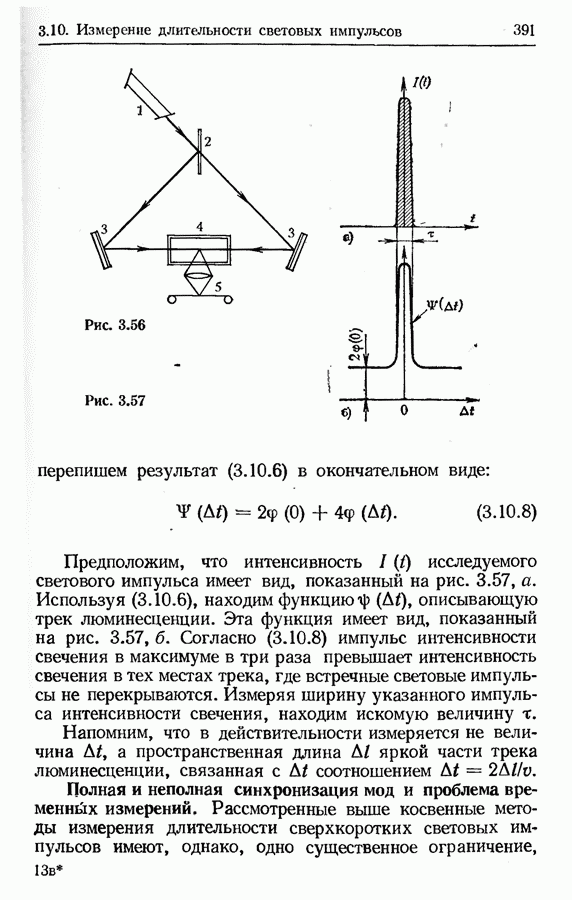
- 3.10. Измерение длительности сверхкоротких световых импульсов
- Метод, использующий генерацию второй гармоники.
- Двухфотонная методика.
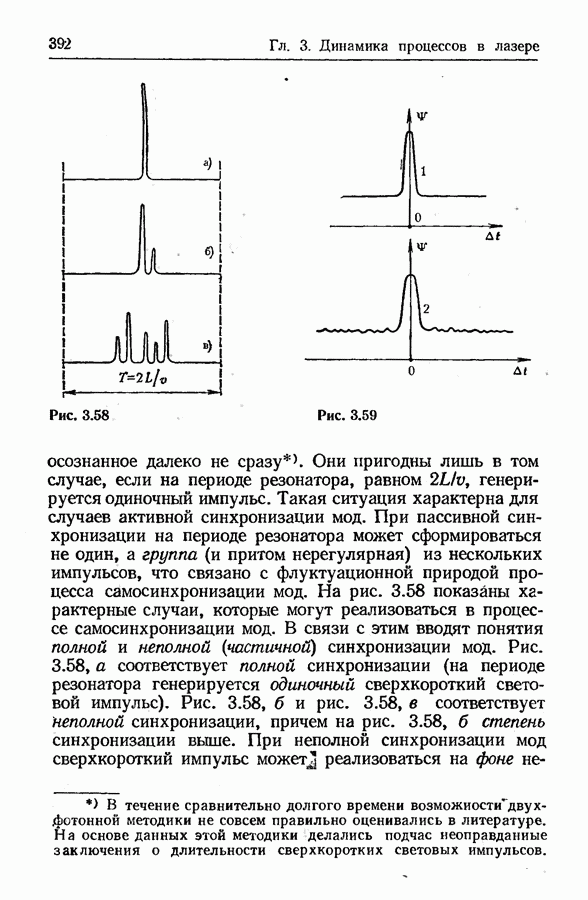
- Полная и неполная синхронизация мод и проблема временных измерений.
- Методика, основанная на измерении структуры спектра сигнала.
- 3.11. Рассмотрение самосинхронизации продольных мод в лазере с просветляющимся фильтром на основе флуктуационных представлений
- О спектральном и временном описании синхронизации мод.
- Исходный профиль поля излучения.
- Показатель нелинейности.
- Преобразование профиля поля при взаимодействии излучения с фильтром на этапе просветления.
- О возможности синхронизации мод в случае генерации второй гармоники.
- Условия полной самосинхронизации мод.
- 3.12. Временное описание активной синхронизации продольных мод в лазере с однородно уширенной линией усиления
- Изменение светового импульса при его прохождении через активный элемент и модулятор.
- Система дифференциальных уравнений, описывающая процесс установления режима синхронизации мод.
- Замечания о фазовых (электрооптических) и амплитудных (акустооптических) синхронизаторах мод.
- Список литературы
- ПРИЛОЖЕНИЕ 1. ПОЛИНОМЫ ЭРМИТА
- ПРИЛОЖЕНИЕ 2. ГАУССОВ ПУЧОК В СВОБОДНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ 3. УСТОЙЧИВАЯ И НЕУСТОЙЧИВАЯ СФЕРИЧЕСКИЕ ВОЛНЫ В НЕУСТОЙЧИВОМ РЕЗОНАТОРЕ
- ПРИЛОЖЕНИЕ 4. МАТРИЦЫ ДЖОНСА
- ПРИЛОЖЕНИЕ 5. ОСОБЫЕ ТОЧКИ ДВУМЕРНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ