| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 7. Характеристические кривые ячейки
При высокочастотном титровании измеряют электрические (и магнитные) параметры исследуемых растворов в зависимости от их состава; подобные зависимости называются характеристическими.
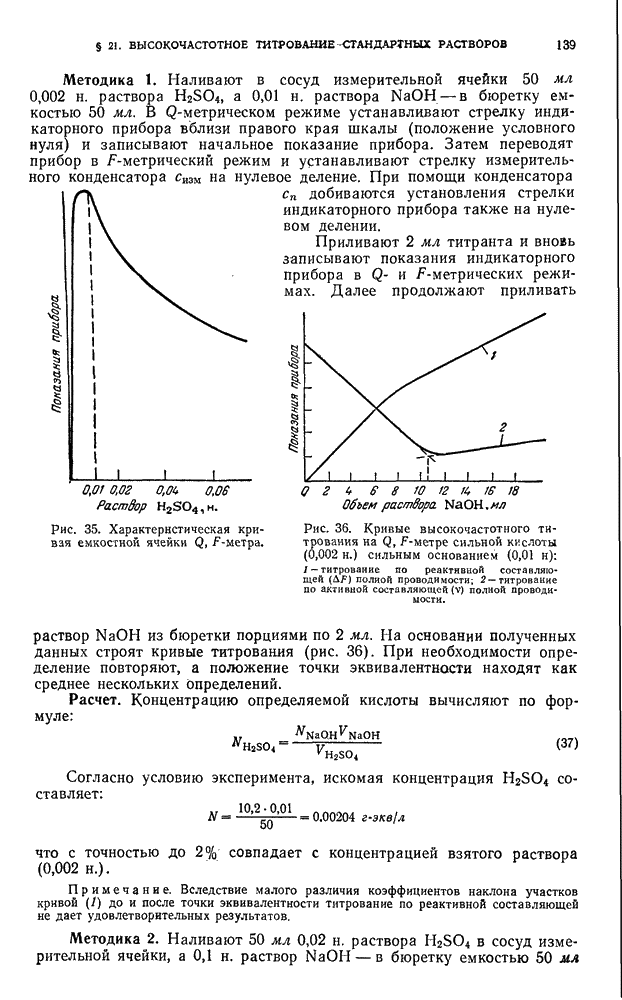
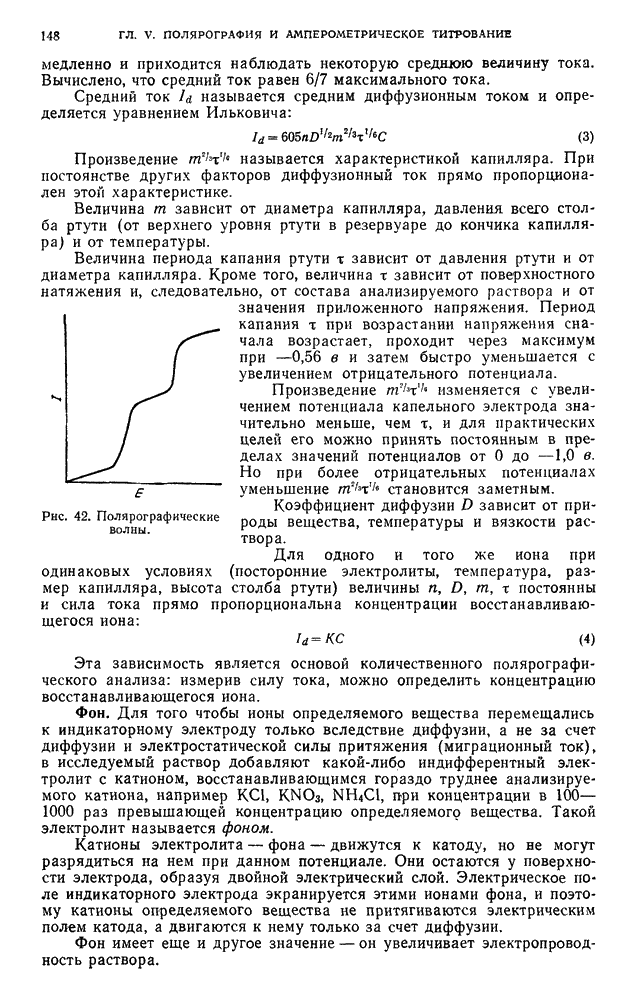
Две характеристические зависимости описываются уравнениями (16) и (17). Они являются сложной функцией величины k. Кривая 1, выраженная уравнением (16), имеет максимум (рис. 21, а). Очевидно, что аналогичные характеристические кривые будут получены и при использовании значений концентрации  или удельной низкочастотной электропроводности
или удельной низкочастотной электропроводности  . вместо значения k, поскольку эти параметры связаны друг с другом зависимостью, близкой к линейной.
. вместо значения k, поскольку эти параметры связаны друг с другом зависимостью, близкой к линейной.
Характеристическая кривая активной составляющей полной проводимости ячейки емкостного типа. Положение максимума на кривой может быть найдено дифференцированием уравнения (16), приравниванием к нулю его первой производной но k и решением полученного выражения относительно  :
:

Выражения (16) и (19) позволяют сделать следующие очень важные выводы.
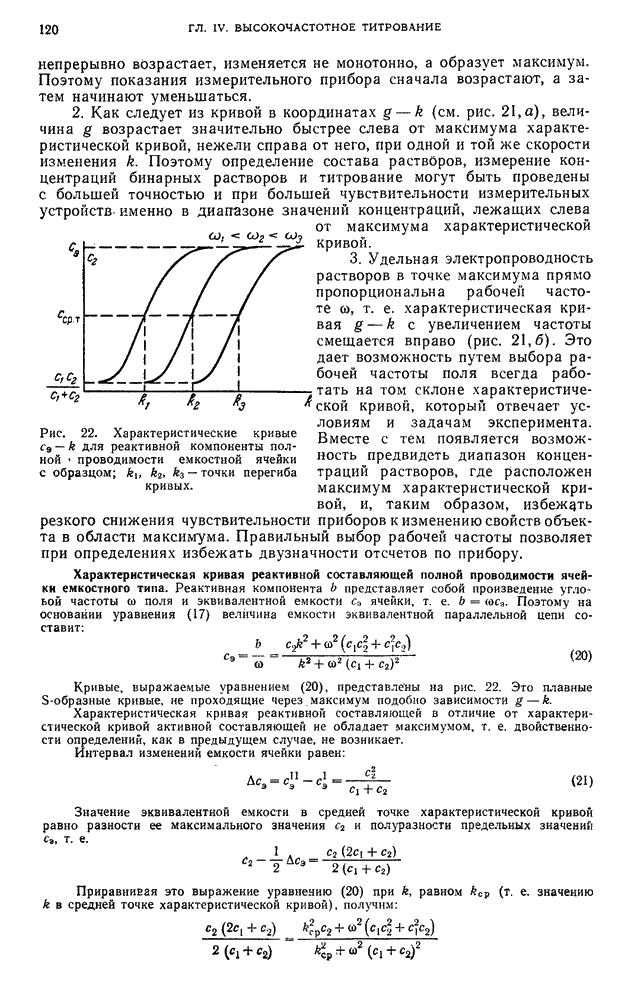
1. Активная составляющая высокочастотной (полной) проводимости измерительной ячейки с образцом, электропроводность которого непрерывно возрастает, изменяется не монотонно, а образует максимум.

Рис. 21. Характеристическая кривая емкостной ячейки для активной компоненты полной проводимости: а — общий вид; б — смещение с увеличением частоты; 1 — в прямых координатах; 2 — в полулогарифмических координатах.
Поэтому показания измерительного прибора сначала возрастают, а затем начинают уменьшаться.
2. Как следует из кривой в координатах  (см. рис. 21,а), величина g возрастает значительно быстрее слева от максимума характеристической кривой, нежели справа от него, при одной и той же скорости изменения k. Поэтому определение состава растворов, измерение концентраций бинарных растворов и титрование могут быть проведены с большей точностью и при большей чувствительности измерительных устройств, именно в диапазоне значений концентраций, лежащих слева от максимума характеристической кривой.
(см. рис. 21,а), величина g возрастает значительно быстрее слева от максимума характеристической кривой, нежели справа от него, при одной и той же скорости изменения k. Поэтому определение состава растворов, измерение концентраций бинарных растворов и титрование могут быть проведены с большей точностью и при большей чувствительности измерительных устройств, именно в диапазоне значений концентраций, лежащих слева от максимума характеристической кривой.
3. Удельная электропроводность растворов в точке максимума прямо пропорциональна рабочей частоте о, т. е. характеристическая кривая g — k с увеличением частоты смещается вправо (рис. 21,6). Это дает возможность путем выбора рабочей частоты поля всегда работать на том склоне характеристической кривой, который отвечает условиям и задачам эксперимента. Вместе с тем появляется возможность предвидеть диапазон концентраций растворов, где расположен максимум характеристической кривой, и, таким образом, избежать резкого снижения чувствительности приборов к изменению свойств объекта в области максимума. Правильный выбор рабочей частоты позволяет при определениях избежать двузначности отсчетов по прибору.
Характеристическая кривая реактивной составляющей полной проводимости ячейки емкостного типа. Реактивная компонента  представляет собой произведение угловой частоты
представляет собой произведение угловой частоты  поля и эквивалентной емкости
поля и эквивалентной емкости  ячейки, т. е.
ячейки, т. е.  . Поэтому на основании уравнения (17) величина емкости эквивалентной параллельной цепи составит:
. Поэтому на основании уравнения (17) величина емкости эквивалентной параллельной цепи составит:

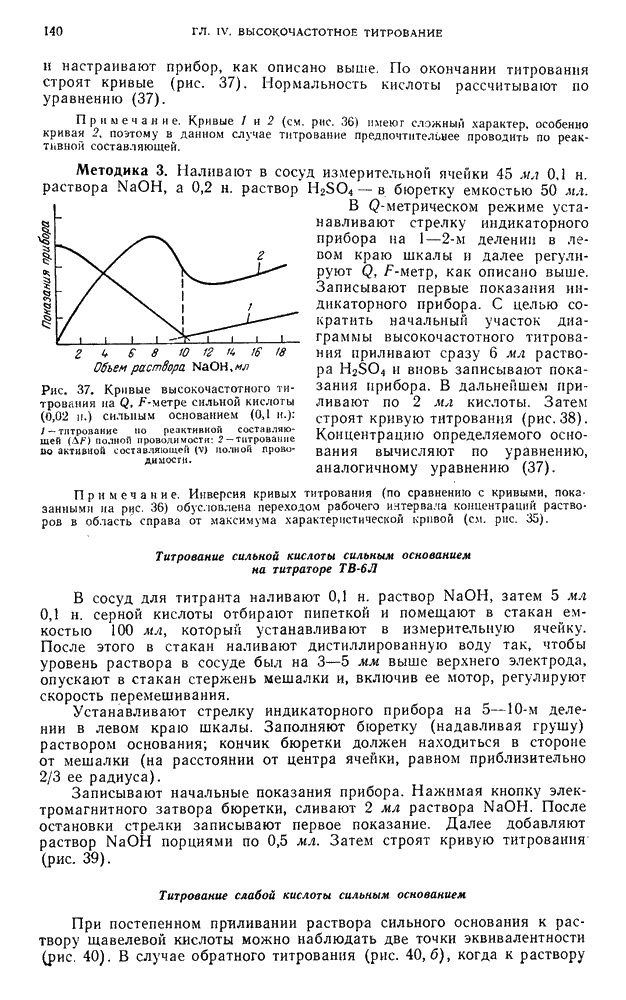
Кривые, выражаемые уравнением (20), представлены на рис. 22. Это плавные  -образные кривые, не проходящие через максимум подобно зависимости
-образные кривые, не проходящие через максимум подобно зависимости  .
.
Характеристическая кривая реактивной составляющей в отличие от характеристической кривой активной составляющей не обладает максимумом, т. е. двойственности определений, как в предыдущем случае, не возникает.
Интервал изменений емкости ячейки равен:

Значение эквивалентной емкости в средней точке характеристической кривой равно разности ее максимального значения  и полуразности предельных значений
и полуразности предельных значений  , т. е.
, т. е.

Приравнивая это выражение уравнению (20) при к, равном  (т. е. значению к в средней точке характеристической кривой), получим:
(т. е. значению к в средней точке характеристической кривой), получим:


Рис. 22. Характеристические кривые  для реактивной компоненты полной проводимости емкостной ячейки с образцом;
для реактивной компоненты полной проводимости емкостной ячейки с образцом;  — точки перегиба кривых.
— точки перегиба кривых.
Откуда

Уравнение (22) идентично уравнению (19). Следовательно, положение максимума характеристической кривой g — k для активной составляющей и положение средней точки характеристической кривой  для реактивной составляющей полной проводимости ячейки с образцом совпадают. Это совпадение может быть использовано при проведении исследований, когда необходимо перейти от одной характеристической кривой к другой.
для реактивной составляющей полной проводимости ячейки с образцом совпадают. Это совпадение может быть использовано при проведении исследований, когда необходимо перейти от одной характеристической кривой к другой.
Максимальная чувствительность измерительной установки, с помощью которой определяют эквивалентную емкость  , соответствует области наиболее крутого подъема характеристической кривой, т. е. вблизи ее точки перегиба. Положение точки перегиба находят, приравнивая нулю вторую производную уравнения (20) и решая полученное выражение относительно значения электропроводности к в точке перегиба (
, соответствует области наиболее крутого подъема характеристической кривой, т. е. вблизи ее точки перегиба. Положение точки перегиба находят, приравнивая нулю вторую производную уравнения (20) и решая полученное выражение относительно значения электропроводности к в точке перегиба ( ). После преобразований получаем:
). После преобразований получаем:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВЫ ФИЗИКО-ХИМИЧЕСКИХ (ИНСТРУМЕНТАЛЬНЫХ) МЕТОДОВ АНАЛИЗА
- § 1. Особенности физико-химических методов анализа
- § 2. Области применения инструментальных методов анализа
- § 3. Анализ веществ высокой чистоты
- § 4. Повышение чувствительности и точности методов определения следов примесей
- § 5. Инструментальные методы титрования
- § 6. Применение физико-химических методов анализа для определения индивидуальных соединений
- § 7. Применение физико-химических методов для анализа смесей веществ
- § 8. Классификация инструментальных количественных методов анализа
- § 9. Электрохимические методы анализа
- § 10. Спектральные (оптические) методы анализа
- § 11. Хроматографические методы анализа
- § 12. Радиометрические методы анализа
- § 13. Масс-спектрометрические методы анализа
- § 14. Физико-химический анализ по Н. С. Курнакову
- § 15. Другие методы анализа
- ГЛАВА II. ПОТЕНЦИОМЕТРИЯ И ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Зависимость величины электродных потенциалов от концентрации (активности)
- § 2. Применение потенциометрического метода анализа
- § 3. Потенциометрическое титрование
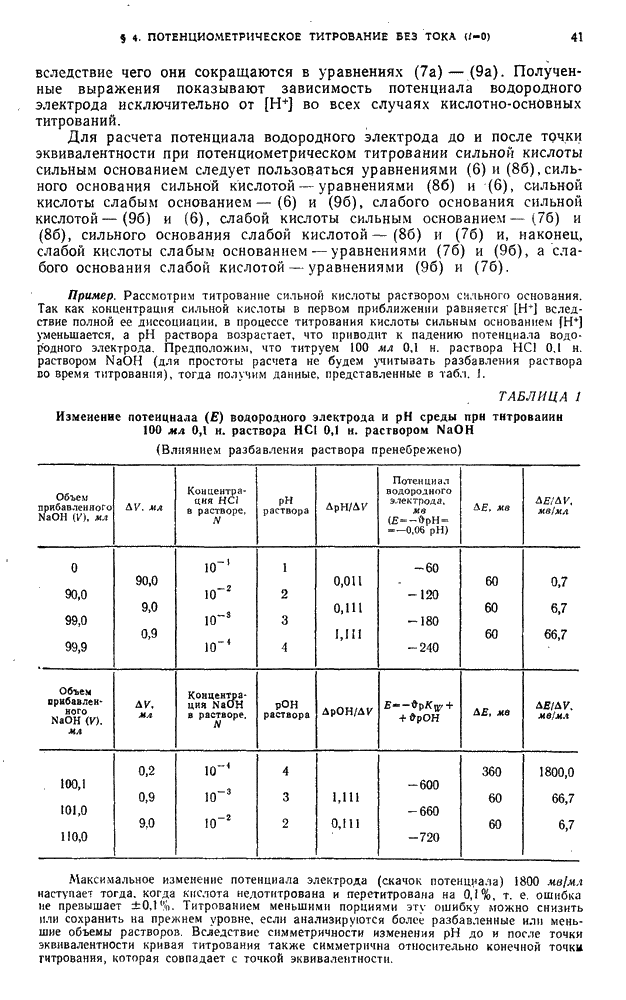
- § 4. Потенциометрическое титрование без тока (i=0)
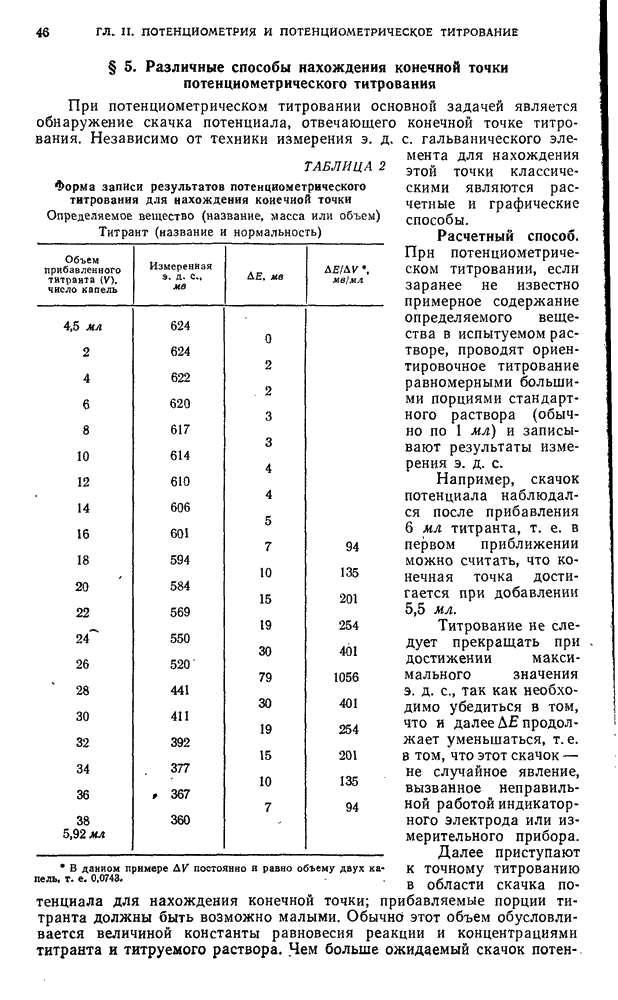
- § 5. Различные способы нахождения конечной точки потенциометрического титрования
- § 6. Некомпенсационный метод потенциометрического титрования
- § 7. Потенциометрическое титрование под током (i != 0)
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 8. Измерение электродвижущей силы
- § 9. Установка для поляризации электродов при потенциометрическом титровании под током
- § 10. Некоторые приборы, применяемые в потенциометрическом титровании
- § 11. Электроды
- В. ПРАКТИЧЕСКИЕ РАБОТЫ ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ БЕЗ ТОКА (i=0)
- § 12. Кислотно-основное титрование
- § 13. Титрование по методу окисления — восстановления
- § 14. Титрование по методу осаждения
- § 15. Титрование по методу комплексообразования
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ ПОД ТОКОМ (i != 0)
- § 16. Титрование по методу окисления — восстановления
- ГЛАВА III. КОНДУКТОМЕТРИЯ и КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Удельная и эквивалентная электропроводность
- § 2. Кондуктометрическне методы анализа
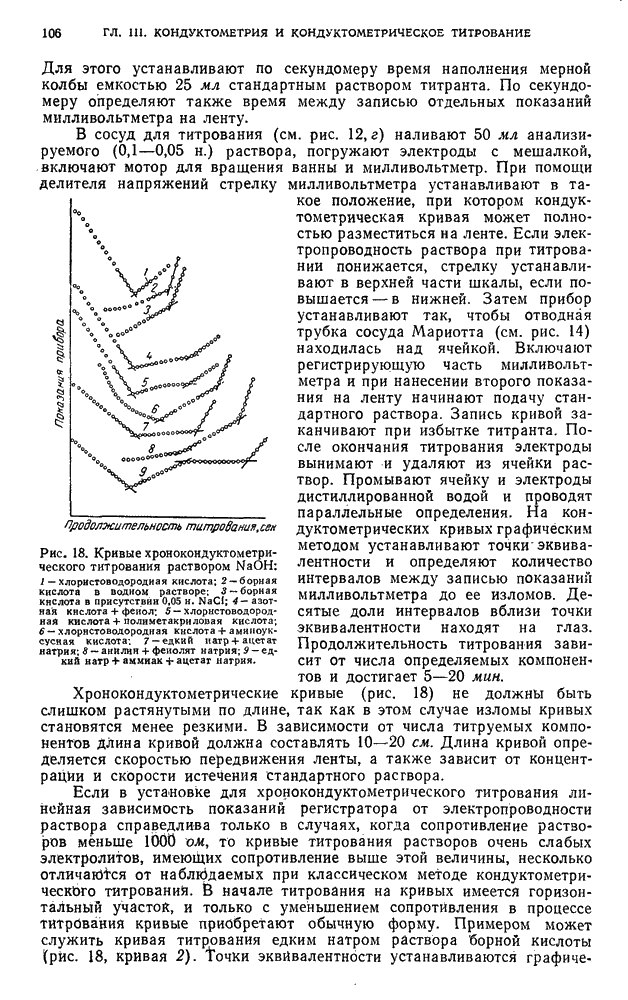
- § 3. Кислотно-основное титрование
- § 4. Титрование, основанное на реакциях осаждения
- § 5. Титрование, основанное на реакциях окисления — восстановления
- § 6. Титрование, основанное на реакциях комплексообразования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 7. Измерение электропроводности растворов
- § 8. Конструкции электролитических ячеек
- § 9. Измерения в хронокондуктометрическом титровании
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 10. Подготовка к определению
- §11. Определение индивидуальных кислот методом кондуктометрического титрования
- § 12. Определение индивидуальных оснований методом кондуктометрического титрования
- § 13. Анализ смесей оснований методом кондуктометрического титрования
- § 14. Определение солей методом кондуктометрического титрования
- § 15. Анализ смесей кислот и солей слабых оснований методом кондуктометрического титрования
- § 16. Анализ смесей кислот методом хронокондуктометрического титрования
- § 17. Анализ смесей оснований и солей слабых кислот методом хронокондуктометрического титрования
- ГЛАВА IV. ВЫСОКОЧАСТОТНОЕ ТИТРОВАНИЕ
- § 1. Общие положения теории высокочастотного титрования
- § 2. Физические основы и погрешности метода высокочастотного титрования
- § 3. Физические основы метода диэлкометрического титрования
- § 4. Погрешности метода диэлкометрического титрования
- ТЕОРИЯ ИЗМЕРИТЕЛЬНЫХ ЯЧЕЕК ЕМКОСТНОГО ТИПА
- § 5. Электрическая эквивалентная схема ячейки и физические процессы, протекающие в ее объеме
- § 6. Импеданс и полная проводимость ячейки
- § 7. Характеристические кривые ячейки
- § 8. Чувствительность ячейки
- § 9. Критерий применимости и постоянная с-ячейки
- ТЕОРИЯ ИЗМЕРИТЕЛЬНЫХ ЯЧЕЕК ИНДУКТИВНОГО ТИПА
- § 10. Электрическая эквивалентная схема ячейки
- § 11. Импеданс и характеристические кривые ячейки
- § 12. Критерий применимости и постоянная L-ячейки
- § 13. Влияние на характеристические кривые ячейки ее некомпенсированного электрического поля
- ДИАГРАММЫ СООТВЕТСТВИЯ
- § 14. Диаграмма соответствия для титрования по активной составляющей полной проводимости
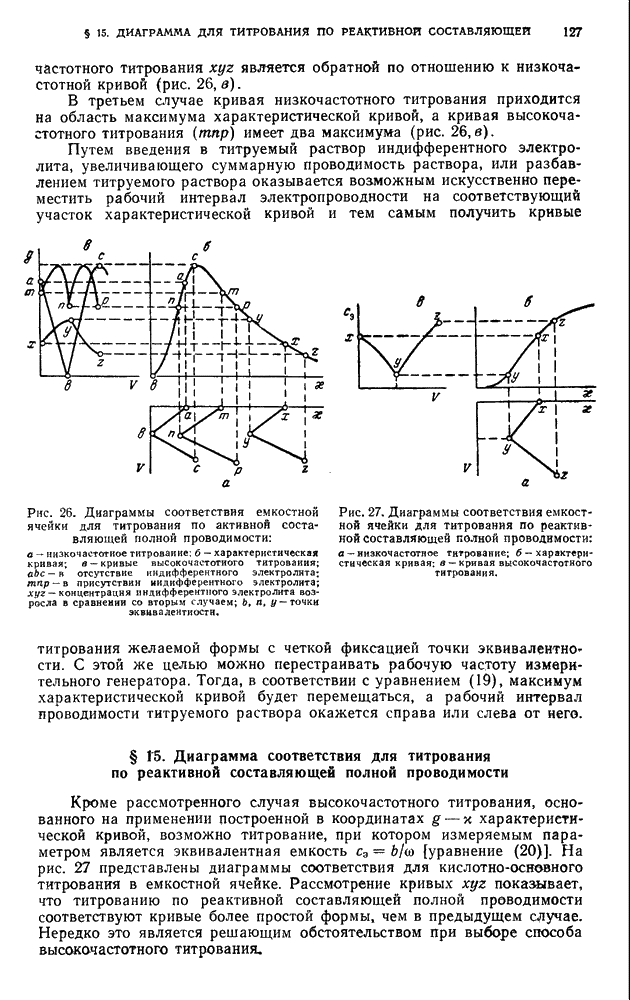
- § 15. Диаграмма соответствия для титрования по реактивной составляющей полной проводимости
- § 16. Выбор типа диаграмм
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
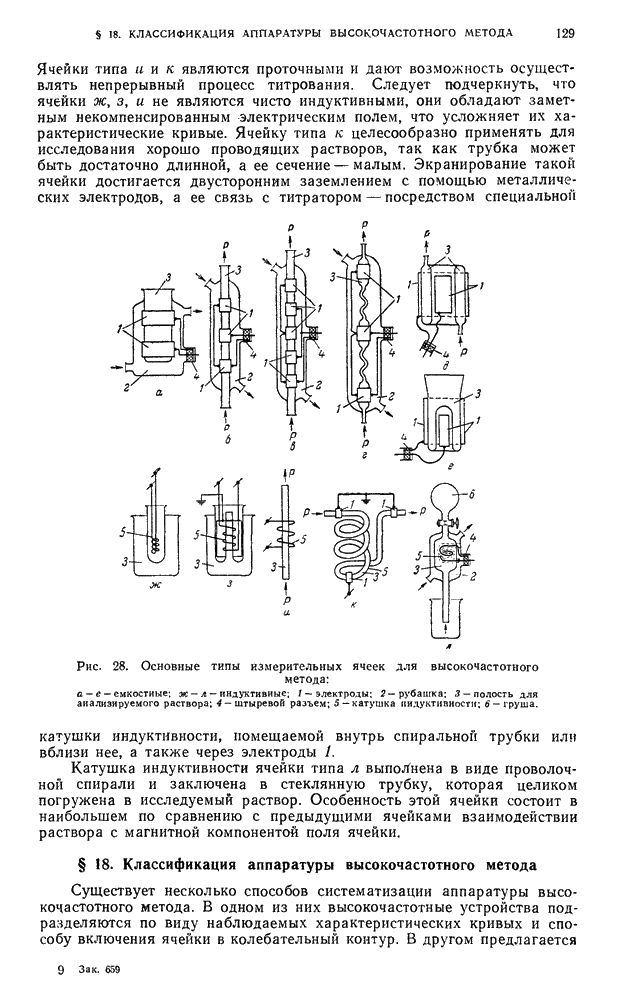
- § 17. Измерительные ячейки (датчики) высокочастотного метода и области их применения
- § 18. Классификация аппаратуры высокочастотного метода
- § 19. Высокочастотные титраторы
- § 20. Общие правила работы с приборами для высокочастотного анализа
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 21. Высокочастотное титрование стандартных растворов
- § 22. Высокочастотное титрование растворов неизвестной концентрации
- ГЛАВА V. ПОЛЯРОГРАФИЧЕСКИЙ МЕТОД АНАЛИЗА И АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Предельный, или диффузионный, ток
- § 2. Возникновение диффузионного тока на твердых микроэлектродах
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ ПОЛЯРОГРАФИЧЕСКОГО АНАЛИЗА
- § 3. Полярографы
- § 4. Электролитическая ячейка
- § 5. Электролизеры
- § 6. Электроды сравнения
- § 7. Снятие полярограммы на полярографической установке с визуальным полярографом
- § 8. Методы количественного полярографического анализа
- § 9. Правила техники безопасности при работе с металлической ртутью
- В. НОВЫЕ НАПРАВЛЕНИЯ В ПОЛЯРОГРАФИИ
- § 10. Амальгамная полярография с накоплением
- § 11. Осциллографическая полярография
- § 12. Переменнотоковая полярография
- Г. ПРАКТИЧЕСКИЕ РАБОТЫ С ПРИМЕНЕНИЕМ ПОЛЯРОГРАФИЧЕСКОГО МЕТОДА АНАЛИЗА
- § 13. Примеры полярографических определений
- АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 14. Особенности амперометрического титрования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АМПЕРОМЕТРИЧЕСКОГО ТИТРОВАНИЯ
- § 15. Схема установки и применяемые электроды
- § 16. Амперометрическое титрование с двумя индикаторными электродами
- В. ПРАКТИЧЕСКИЕ РАБОТЫ С ПРИМЕНЕНИЕМ АМПЕРОМЕТРИЧЕСКОГО ТИТРОВАНИЯ
- § 17. Примеры амперометрического титрования
- ГЛАВА VI. КУЛОНОМЕТРИЯ И КУЛОНОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Сущность и классификация кулонометрических методов
- ПРЯМАЯ КУЛОНОМЕТРИЯ
- § 2. Прямая кулонометрия при постоянном потенциале рабочего электрода (прямая потенциостатическая кулонометрия)
- § 3. Использование прямой потенциостатической кулонометрии
- § 4. Прямая кулонометрия при постоянной силе тока электролиза (прямая амперостатическая кулонометрия)
- § 5. Использование прямой амперостатической кулонометрии
- КУЛОНОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 6. Кулонометрическое титрование при постоянной силе тока электролиза
- § 7. Использование амперостатического кулонометрического титрования
- § 8. Кулонометрическое титрование првд постоянном потенциале рабочего электрода
- § 9. Особенности кулонометрических методов анализа
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 10. Электроды
- § 11. Электролизеры
- § 12. Приборы для измерения количества электричества, израсходованного на электролиз вещества
- § 13. Приборы, обеспечивающие стабильность потенциала рабочего электрода или силы тока электролиза, и установки для кулонометрического анализа
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 14. Работы, выполняемые методом прямой кулонометрии
- § 15. Работы, выполняемые методом косвенной кулонометрии, или кулонометрического титрования, при постоянной силе тока электролиза
- ГЛАВА VII. СПЕКТРАЛЬНЫЕ (ОПТИЧЕСКИЕ) МЕТОДЫ АНАЛИЗА
- § 1. Общая характеристика метода
- § 2. Классификация методов эмиссионного спектрального анализа
- § 3. Качественный спектральный анализ
- § 4. Полуколичественные методы спектрального анализа
- § 5. Количественный спектральный анализ
- § 6. Основы фотографического метода эмиссионного количественного анализа
- § 7. Зависимость между почернением фотопластинки и интенсивностью излучения
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 8. Источники возбуждения спектров
- § 9. Спектральные приборы
- § 10. Вспомогательные приборы и принадлежности
- § 11. Микрофотометр МФ-2
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 12. Качественный анализ при помощи стилоскопа
- § 13. Качественный анализ фотографическим методом при помощи спектра железа в ультрафиолетовой области
- § 14. Полуколичественный анализ
- § 15. Количественный анализ
- СПЕКТРОФОТОМЕТРИЯ ПЛАМЕНИ
- § 16. Общая характеристика метода
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 17. Схема установки, применяемой для анализа методом спектрофотометрии пламени
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 18. Определения по методу спектрофотометрии пламени
- АТОМНО-АБСОРБЦИОННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 19. Общая характеристика метода
- МОЛЕКУЛЯРНО-АБСОРБЦИОННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 20. Общая характеристика метода
- § 21. Законы поглощения света
- § 22. Отклонения от закона Бугера—Ламберта—Бера
- § 23. Качественный анализ спектрофотометрическим методом
- § 24. Количественный анализ спектрофотометрическим методом
- § 25. Методы определения концентрации веществ, поглощающих в видимой и ультрафиолетовой областях спектра
- § 26. Определение нескольких компонентов в растворе
- § 27. Определение концентрации вещества в растворе дифференциальным методом
- § 28. Выбор толщины слоя и оптимальной концентрации исследуемого раствора
- § 29. Выбор длины волны поглощаемого излучения при спектрофотометрических измерениях
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 30. Приборы, применяемые для спектрофотометрического анализа в ультрафиолетовой и видимой областях спектра
- § 31. Приборы, применяемые для колориметрического анализа
- § 32. Приборы, применяемые для спектрофотометрического анализа в инфракрасной области спектра
- § 33. Нулевые растворы
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 34. Определение в ультрафиолетовой области спектра
- § 35. Определение в видимой области спектра
- § 36. Определение в инфракрасной области спектра
- СПЕКТРОФОТОМЕТРИЧЕСКИЕ (ФОТОМЕТРИЧЕСКИЕ) МЕТОДЫ ТИТРОВАНИЯ
- § 37. Общая характеристика метода
- § 38. Кривые спектрофотометрического титрования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ ТИТРОВАНИЯ
- § 39. Установки для спектрофотометрического титрования
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 40. Спектрофотометрическое титрование
- НЕФЕЛОМЕТРИЧЕСКИЙ И ТУРБИДИМЕТРИЧЕСКИЙ МЕТОДЫ АНАЛИЗА
- § 41. Общая характеристика методов
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 42. Приборы, применяемые для нефелометрических и турбидиметрических измерений
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 43. Нефелометрические и турбидиметрические определения
- § 44. Фототурбидиметрическое и фотонефелометрическое титрование
- ГЛАВА VIII. ХРОМАТОГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
- § 1. Классификация хроматографических методов анализа
- § 2. Адсорбционная хроматография
- § 3. Разновидности газовой хроматографии
- § 4. Распределительная хроматография
- § 5. Ионообменная хроматография
- § 6. Константа ионного обмена
- § 7. Осадочная хроматография
- § 8. Окислительно-восстановительная хроматография
- § 9. Адсорбционно-комплексообразовательная хроматография
- § 10. Хроматографические колонки, применяемые в адсорбционно-жидкостной хроматографии
- § 11. Аппаратура, применяемая в газовой хроматографии
- § 12. Приборы и материалы, применяемые в распределительной хроматографии
- § 13. Колонки, применяемые в ионообменной хроматографии
- § 14. Колонки, применяемые в осадочной и окислительновосстановительной хроматографии
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 15. Работы по методу адсорбционной (жидкостной и газовой) хроматографии
- § 16. Работы по методу распределительной хроматографии
- § 17. Работы по методу ионообменной хроматографии
- § 18. Работы по методу осадочной хроматографии
- § 19. Работы по методу окислительно-восстановительной хроматографии
- § 20. Работы по методу адсорбционно-комплексообразовательной хроматографии
- ГЛАВА IX. РАДИОМЕТРИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
- § 1. Виды радиоактивного распада
- § 2. Скорость распада
- § 3. Взаимодействие излучения с веществом
- § 4. Ошибки при измерении радиоактивности
- Б. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ ПРИ РАБОТЕ С РАДИОАКТИВНЫМИ ВЕЩЕСТВАМИ
- § 5. Понятия и единицы измерения
- § 6. Классификация источников радиоактивного излучения и радиоактивных изотопов
- § 7. Классификация химических операций с радиоактивными веществами
- § 8. Устройство лабораторий и классификация работ
- § 9. Специальное оборудование для работ с радиоактивными веществами
- § 10. Средства индивидуальной защиты
- § 11. Проведение работ в химической лаборатории с радиоактивными веществами
- § 12. Правила работы с радиоактивными веществами
- В. МЕТОДЫ РЕГИСТРАЦИИ РАДИОАКТИВНОГО ИЗЛУЧЕНИЯ
- § 13. Ионизационные методы
- § 14. Сцинтилляционный метод
- Г. АППАРАТУРА И ТЕХНИКА ИЗМЕРЕНИЯ РАДИОАКТИВНОСТИ
- § 15. Радиометрические установки
- § 16. Измерение радиоактивности
- § 17. Измерение дозы на рабочем месте, индивидуальной дозы, полученной работающим, и загрязненности рабочих поверхностей, рук и одежды
- § 18. Абсолютные и относительные измерения активности
- Д. РАДИОМЕТРИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
- § 19. Приготовление раствора с заданной активностью
- § 20. Прямое определение ионов химических элементов в растворе с помощью радиоактивных реагентов
- § 21. Практические работы, выполняемые методом прямого определения
- § 22. Метод радиометрического титрования
- § 23. Практические работы, выполняемые методом радиометрического титрования
- § 24. Метод изотопного разбавления
- § 25. Практические работы, выполняемые методом изотопного разбавления
- § 26. Метод активационного анализа
- § 27. Практические работы, выполняемые методом активационного анализа
- § 28. Фотонейтронный метод
- § 29. Практические работы, выполняемые фотонейтронным методом
- § 30. Методы определения содержания химических элементов по излучению их естественных радиоактивных изотопов
- § 31. Практические работы по определению содержания химических элементов методом измерения излучения их естественных радиоактивных изотопов
- § 32. Методы анализа, основанные на поглощении излучения
- § 33. Практические работы, выполняемые по методу анализа, основанному на поглощении излучения
- § 34. Метод, основанный на отражении бетта-излучения
- § 35. Практические работы, выполняемые по методу, основанному на отражении бетта-излучения
- ГЛАВА X. ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ КОЛИЧЕСТВЕННОГО ОПРЕДЕЛЕНИЯ РЕДКИХ ЭЛЕМЕНТОВ
- § 1. Работы, выполняемые методом амперометрического титрования
- § 2. Работы, выполняемые полярографическим методом
- § 3. Работы, выполняемые фотометрическим методом
- § 4. Работы, выполняемые экстракционно-фотометрическим методом
- § 5. Работы, выполняемые спектрофотометрическим методом
- § 6. Работы, выполняемые флуориметрическим методом
- § 7. Работы, выполняемые методом потенциометрического титрования
- ГЛАВА XI. ФИЗИКО-ХИМИЧЕСКИЕ (ИНСТРУМЕНТАЛЬНЫЕ) МЕТОДЫ АНАЛИЗА НЕВОДНЫХ РАСТВОРОВ
- § 1. Влияние химической природы и физико-химических свойств растворителей на свойства растворенного вещества
- § 2. Классификация неводных растворителей по их протонно-донорно-акцепторным свойствам
- § 3. Классификация неводных растворителей по признаку их влияния на относительную силу электролитов
- § 4. Дифференцирующее действие растворителей
- § 5. Константы диссоциации, потенциалы полунейтрализации в неводных средах и относительная шкала кислотности
- § 6. Шкала pH и константы автопротолиза неводных растворителей
- § 7. Абсолютная (единая) шкала кислотности растворителей
- § 8. Химико-аналитическое использование неводных растворителей
- Б. АППАРАТУРА И ТЕХНИКА ТИТРОВАНИЯ НЕВОДНЫХ РАСТВОРОВ
- § 9. Установки, используемые при амперометрическом титровании неводных растворов
- § 10. Установки, используемые при потенциометрическом титровании неводных растворов
- § 11. Установки, используемые при кондуктометрическом титровании неводных растворов
- § 12. Установки, используемые при высокочастотном титровании неводных растворов
- § 13. Установки, используемые при спектрофотометрическом титровании неводных растворов
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 14. Очистка и обезвоживание неводных растворителей
- § 15. Титранты, применяемые для титрования кислот и оснований в неводных растворах
- § 16. Амперометрическое титрование
- § 17. Методы прямого потенциометрического титрования
- § 18. Методы косвенного потенциометрического титрования
- § 19. Дифференцированное потенциометрическое титрование
- § 20. Комбинированные методы потенциометрического титрования
- § 21. Хронопотенциометрическое титрование
- § 22. Кондуктометрическое титрование
- § 23. Хронокондуктометрическое титрование
- § 24. Спектрофотометрическое титрование