| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 12. Критерий применимости и постоянная L-ячейки
Параметр  относительное уменьшение высокочастотной энергии в колебательном контуре за один период его колебаний, в радиотехнике называется добротностью:
относительное уменьшение высокочастотной энергии в колебательном контуре за один период его колебаний, в радиотехнике называется добротностью:


Рис. 24. Измерительная ячейка индуктивного типа: а — схема; б — электрическая эквивалентная схема (трансформаторная); в — преобразование схемы б (последовательная схема).
Возможны два случая:  . В первом случае на основании уравнений (29) и (30) имеем:
. В первом случае на основании уравнений (29) и (30) имеем:

Во втором случае:

При переходе от измерений при  [уравнения (32а) и (32б)] к измерениям при
[уравнения (32а) и (32б)] к измерениям при  [уравнения (32в) и (32г)] характеристические кривые претерпевают инверсию, изменяясь от обратных зависимостей по
[уравнения (32в) и (32г)] характеристические кривые претерпевают инверсию, изменяясь от обратных зависимостей по  т. е. от
т. е. от

к прямым, т. е. к выражениям

где F — функциональная зависимость.
Полученные выражения показывают, что если метод измерения активной составляющей в обоих случаях одинаково целесообразен, то титрование по реактивной составляющей во втором случае оказывается более перспективным. Это заключение следует из того, что величина  , поэтому второе слагаемое уравнения (32г) более «весомо» по сравнению со вторым слагаемым уравнения (32б); его прирост при изменении параметров раствора значительно сильнее отражается на измеряемой величине
, поэтому второе слагаемое уравнения (32г) более «весомо» по сравнению со вторым слагаемым уравнения (32б); его прирост при изменении параметров раствора значительно сильнее отражается на измеряемой величине  . С другой стороны, множитель а снижает роль первого слагаемого уравнения (32г), что также способствует применимости случая
. С другой стороны, множитель а снижает роль первого слагаемого уравнения (32г), что также способствует применимости случая  . Кроме того, поскольку для наиболее употребительных размеров ячейки (
. Кроме того, поскольку для наиболее употребительных размеров ячейки ( см,
см,  см) интервал изменений
см) интервал изменений  составляет 102— 105 ом, величина второго слагаемого в уравнении (326) может оказываться значительно меньше, чем в уравнении (32г).
составляет 102— 105 ом, величина второго слагаемого в уравнении (326) может оказываться значительно меньше, чем в уравнении (32г).
Таким образом, высокочастотное титрование с помощью измерительной ячейки индуктивного типа более целесообразно в случае, когда параметр  . Выясним, как практически можно выполнить условие
. Выясним, как практически можно выполнить условие  или
или  .
.
Допустим, что короткозамкнутый виток проводника — раствора обладает индуктивностью, описываемой полуэмпирическим выражением:

где N — число витков;  — толщина витка (длина сосуда); d — диаметр витка (диаметр сосуда).
— толщина витка (длина сосуда); d — диаметр витка (диаметр сосуда).
Подставляя значение  из уравнения (33) в уравнение (31), находим:
из уравнения (33) в уравнение (31), находим:

В этих выражениях  — геометрический фактор (фактор заполнения) и
— геометрический фактор (фактор заполнения) и  — величина, характеризующая глубину проникновения поля в раствор, являются безразмерными величинами, а коэффициент
— величина, характеризующая глубину проникновения поля в раствор, являются безразмерными величинами, а коэффициент  — геометрический фактор (фактор заполнения);
— геометрический фактор (фактор заполнения);  - относительная величина, характеризующая глубину проникновения поля в раствор.
- относительная величина, характеризующая глубину проникновения поля в раствор.
Величина  , является константой высокочастотной индуктивной ячейки; ее размерность, как и в случае емкостной ячейки, выражается в сантиметрах.
, является константой высокочастотной индуктивной ячейки; ее размерность, как и в случае емкостной ячейки, выражается в сантиметрах.
Произведенные выкладки позволяют сделать следующие заключения о применимости  -ячеек:
-ячеек:
1) для повышения параметра  ячейки с раствором необходимо увеличить размеры сосуда;
ячейки с раствором необходимо увеличить размеры сосуда;
2) чем выше удельная электропроводность раствора  и чем выше рабочая частота
и чем выше рабочая частота  , тем выше значение
, тем выше значение  и тем эффективнее методы измерения активной составляющей
и тем эффективнее методы измерения активной составляющей  , согласно уравнениям (32а) и (32в);
, согласно уравнениям (32а) и (32в);
3) при малых значениях частоты поля и проводимости раствора параметр  имеет незначительную величину. Для его повышения в этом случае необходимо использовать большие количества раствора. В этих же условиях можно применять метод измерения эффективных значеннй индуктивности ячейки, согласно уравнениям (326) и (32г).
имеет незначительную величину. Для его повышения в этом случае необходимо использовать большие количества раствора. В этих же условиях можно применять метод измерения эффективных значеннй индуктивности ячейки, согласно уравнениям (326) и (32г).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ОСНОВЫ ФИЗИКО-ХИМИЧЕСКИХ (ИНСТРУМЕНТАЛЬНЫХ) МЕТОДОВ АНАЛИЗА
- § 1. Особенности физико-химических методов анализа
- § 2. Области применения инструментальных методов анализа
- § 3. Анализ веществ высокой чистоты
- § 4. Повышение чувствительности и точности методов определения следов примесей
- § 5. Инструментальные методы титрования
- § 6. Применение физико-химических методов анализа для определения индивидуальных соединений
- § 7. Применение физико-химических методов для анализа смесей веществ
- § 8. Классификация инструментальных количественных методов анализа
- § 9. Электрохимические методы анализа
- § 10. Спектральные (оптические) методы анализа
- § 11. Хроматографические методы анализа
- § 12. Радиометрические методы анализа
- § 13. Масс-спектрометрические методы анализа
- § 14. Физико-химический анализ по Н. С. Курнакову
- § 15. Другие методы анализа
- ГЛАВА II. ПОТЕНЦИОМЕТРИЯ И ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Зависимость величины электродных потенциалов от концентрации (активности)
- § 2. Применение потенциометрического метода анализа
- § 3. Потенциометрическое титрование
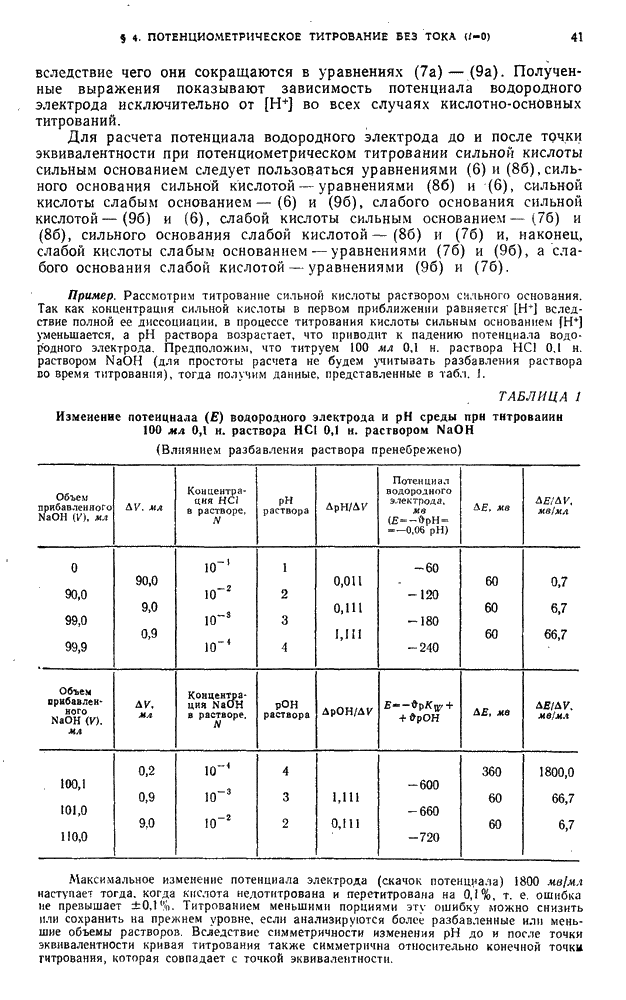
- § 4. Потенциометрическое титрование без тока (i=0)
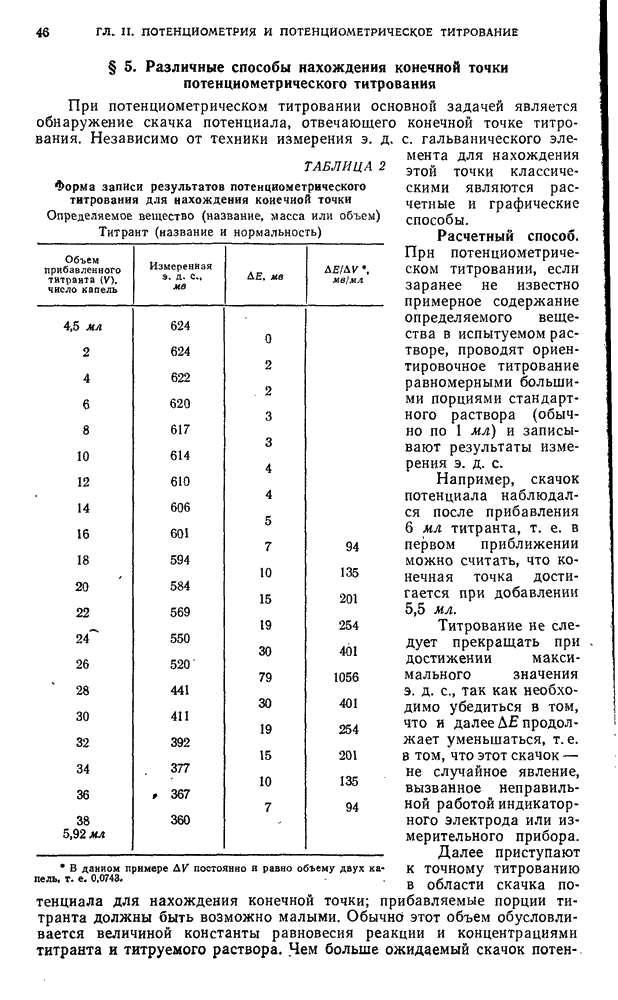
- § 5. Различные способы нахождения конечной точки потенциометрического титрования
- § 6. Некомпенсационный метод потенциометрического титрования
- § 7. Потенциометрическое титрование под током (i != 0)
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 8. Измерение электродвижущей силы
- § 9. Установка для поляризации электродов при потенциометрическом титровании под током
- § 10. Некоторые приборы, применяемые в потенциометрическом титровании
- § 11. Электроды
- В. ПРАКТИЧЕСКИЕ РАБОТЫ ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ БЕЗ ТОКА (i=0)
- § 12. Кислотно-основное титрование
- § 13. Титрование по методу окисления — восстановления
- § 14. Титрование по методу осаждения
- § 15. Титрование по методу комплексообразования
- ПОТЕНЦИОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ ПОД ТОКОМ (i != 0)
- § 16. Титрование по методу окисления — восстановления
- ГЛАВА III. КОНДУКТОМЕТРИЯ и КОНДУКТОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Удельная и эквивалентная электропроводность
- § 2. Кондуктометрическне методы анализа
- § 3. Кислотно-основное титрование
- § 4. Титрование, основанное на реакциях осаждения
- § 5. Титрование, основанное на реакциях окисления — восстановления
- § 6. Титрование, основанное на реакциях комплексообразования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 7. Измерение электропроводности растворов
- § 8. Конструкции электролитических ячеек
- § 9. Измерения в хронокондуктометрическом титровании
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 10. Подготовка к определению
- §11. Определение индивидуальных кислот методом кондуктометрического титрования
- § 12. Определение индивидуальных оснований методом кондуктометрического титрования
- § 13. Анализ смесей оснований методом кондуктометрического титрования
- § 14. Определение солей методом кондуктометрического титрования
- § 15. Анализ смесей кислот и солей слабых оснований методом кондуктометрического титрования
- § 16. Анализ смесей кислот методом хронокондуктометрического титрования
- § 17. Анализ смесей оснований и солей слабых кислот методом хронокондуктометрического титрования
- ГЛАВА IV. ВЫСОКОЧАСТОТНОЕ ТИТРОВАНИЕ
- § 1. Общие положения теории высокочастотного титрования
- § 2. Физические основы и погрешности метода высокочастотного титрования
- § 3. Физические основы метода диэлкометрического титрования
- § 4. Погрешности метода диэлкометрического титрования
- ТЕОРИЯ ИЗМЕРИТЕЛЬНЫХ ЯЧЕЕК ЕМКОСТНОГО ТИПА
- § 5. Электрическая эквивалентная схема ячейки и физические процессы, протекающие в ее объеме
- § 6. Импеданс и полная проводимость ячейки
- § 7. Характеристические кривые ячейки
- § 8. Чувствительность ячейки
- § 9. Критерий применимости и постоянная с-ячейки
- ТЕОРИЯ ИЗМЕРИТЕЛЬНЫХ ЯЧЕЕК ИНДУКТИВНОГО ТИПА
- § 10. Электрическая эквивалентная схема ячейки
- § 11. Импеданс и характеристические кривые ячейки
- § 12. Критерий применимости и постоянная L-ячейки
- § 13. Влияние на характеристические кривые ячейки ее некомпенсированного электрического поля
- ДИАГРАММЫ СООТВЕТСТВИЯ
- § 14. Диаграмма соответствия для титрования по активной составляющей полной проводимости
- § 15. Диаграмма соответствия для титрования по реактивной составляющей полной проводимости
- § 16. Выбор типа диаграмм
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 17. Измерительные ячейки (датчики) высокочастотного метода и области их применения
- § 18. Классификация аппаратуры высокочастотного метода
- § 19. Высокочастотные титраторы
- § 20. Общие правила работы с приборами для высокочастотного анализа
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 21. Высокочастотное титрование стандартных растворов
- § 22. Высокочастотное титрование растворов неизвестной концентрации
- ГЛАВА V. ПОЛЯРОГРАФИЧЕСКИЙ МЕТОД АНАЛИЗА И АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Предельный, или диффузионный, ток
- § 2. Возникновение диффузионного тока на твердых микроэлектродах
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ ПОЛЯРОГРАФИЧЕСКОГО АНАЛИЗА
- § 3. Полярографы
- § 4. Электролитическая ячейка
- § 5. Электролизеры
- § 6. Электроды сравнения
- § 7. Снятие полярограммы на полярографической установке с визуальным полярографом
- § 8. Методы количественного полярографического анализа
- § 9. Правила техники безопасности при работе с металлической ртутью
- В. НОВЫЕ НАПРАВЛЕНИЯ В ПОЛЯРОГРАФИИ
- § 10. Амальгамная полярография с накоплением
- § 11. Осциллографическая полярография
- § 12. Переменнотоковая полярография
- Г. ПРАКТИЧЕСКИЕ РАБОТЫ С ПРИМЕНЕНИЕМ ПОЛЯРОГРАФИЧЕСКОГО МЕТОДА АНАЛИЗА
- § 13. Примеры полярографических определений
- АМПЕРОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 14. Особенности амперометрического титрования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АМПЕРОМЕТРИЧЕСКОГО ТИТРОВАНИЯ
- § 15. Схема установки и применяемые электроды
- § 16. Амперометрическое титрование с двумя индикаторными электродами
- В. ПРАКТИЧЕСКИЕ РАБОТЫ С ПРИМЕНЕНИЕМ АМПЕРОМЕТРИЧЕСКОГО ТИТРОВАНИЯ
- § 17. Примеры амперометрического титрования
- ГЛАВА VI. КУЛОНОМЕТРИЯ И КУЛОНОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 1. Сущность и классификация кулонометрических методов
- ПРЯМАЯ КУЛОНОМЕТРИЯ
- § 2. Прямая кулонометрия при постоянном потенциале рабочего электрода (прямая потенциостатическая кулонометрия)
- § 3. Использование прямой потенциостатической кулонометрии
- § 4. Прямая кулонометрия при постоянной силе тока электролиза (прямая амперостатическая кулонометрия)
- § 5. Использование прямой амперостатической кулонометрии
- КУЛОНОМЕТРИЧЕСКОЕ ТИТРОВАНИЕ
- § 6. Кулонометрическое титрование при постоянной силе тока электролиза
- § 7. Использование амперостатического кулонометрического титрования
- § 8. Кулонометрическое титрование првд постоянном потенциале рабочего электрода
- § 9. Особенности кулонометрических методов анализа
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 10. Электроды
- § 11. Электролизеры
- § 12. Приборы для измерения количества электричества, израсходованного на электролиз вещества
- § 13. Приборы, обеспечивающие стабильность потенциала рабочего электрода или силы тока электролиза, и установки для кулонометрического анализа
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 14. Работы, выполняемые методом прямой кулонометрии
- § 15. Работы, выполняемые методом косвенной кулонометрии, или кулонометрического титрования, при постоянной силе тока электролиза
- ГЛАВА VII. СПЕКТРАЛЬНЫЕ (ОПТИЧЕСКИЕ) МЕТОДЫ АНАЛИЗА
- § 1. Общая характеристика метода
- § 2. Классификация методов эмиссионного спектрального анализа
- § 3. Качественный спектральный анализ
- § 4. Полуколичественные методы спектрального анализа
- § 5. Количественный спектральный анализ
- § 6. Основы фотографического метода эмиссионного количественного анализа
- § 7. Зависимость между почернением фотопластинки и интенсивностью излучения
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 8. Источники возбуждения спектров
- § 9. Спектральные приборы
- § 10. Вспомогательные приборы и принадлежности
- § 11. Микрофотометр МФ-2
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 12. Качественный анализ при помощи стилоскопа
- § 13. Качественный анализ фотографическим методом при помощи спектра железа в ультрафиолетовой области
- § 14. Полуколичественный анализ
- § 15. Количественный анализ
- СПЕКТРОФОТОМЕТРИЯ ПЛАМЕНИ
- § 16. Общая характеристика метода
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 17. Схема установки, применяемой для анализа методом спектрофотометрии пламени
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 18. Определения по методу спектрофотометрии пламени
- АТОМНО-АБСОРБЦИОННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 19. Общая характеристика метода
- МОЛЕКУЛЯРНО-АБСОРБЦИОННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ
- § 20. Общая характеристика метода
- § 21. Законы поглощения света
- § 22. Отклонения от закона Бугера—Ламберта—Бера
- § 23. Качественный анализ спектрофотометрическим методом
- § 24. Количественный анализ спектрофотометрическим методом
- § 25. Методы определения концентрации веществ, поглощающих в видимой и ультрафиолетовой областях спектра
- § 26. Определение нескольких компонентов в растворе
- § 27. Определение концентрации вещества в растворе дифференциальным методом
- § 28. Выбор толщины слоя и оптимальной концентрации исследуемого раствора
- § 29. Выбор длины волны поглощаемого излучения при спектрофотометрических измерениях
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 30. Приборы, применяемые для спектрофотометрического анализа в ультрафиолетовой и видимой областях спектра
- § 31. Приборы, применяемые для колориметрического анализа
- § 32. Приборы, применяемые для спектрофотометрического анализа в инфракрасной области спектра
- § 33. Нулевые растворы
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 34. Определение в ультрафиолетовой области спектра
- § 35. Определение в видимой области спектра
- § 36. Определение в инфракрасной области спектра
- СПЕКТРОФОТОМЕТРИЧЕСКИЕ (ФОТОМЕТРИЧЕСКИЕ) МЕТОДЫ ТИТРОВАНИЯ
- § 37. Общая характеристика метода
- § 38. Кривые спектрофотометрического титрования
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ ТИТРОВАНИЯ
- § 39. Установки для спектрофотометрического титрования
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 40. Спектрофотометрическое титрование
- НЕФЕЛОМЕТРИЧЕСКИЙ И ТУРБИДИМЕТРИЧЕСКИЙ МЕТОДЫ АНАЛИЗА
- § 41. Общая характеристика методов
- Б. АППАРАТУРА И ТЕХНИКА ВЫПОЛНЕНИЯ АНАЛИЗА
- § 42. Приборы, применяемые для нефелометрических и турбидиметрических измерений
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 43. Нефелометрические и турбидиметрические определения
- § 44. Фототурбидиметрическое и фотонефелометрическое титрование
- ГЛАВА VIII. ХРОМАТОГРАФИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
- § 1. Классификация хроматографических методов анализа
- § 2. Адсорбционная хроматография
- § 3. Разновидности газовой хроматографии
- § 4. Распределительная хроматография
- § 5. Ионообменная хроматография
- § 6. Константа ионного обмена
- § 7. Осадочная хроматография
- § 8. Окислительно-восстановительная хроматография
- § 9. Адсорбционно-комплексообразовательная хроматография
- § 10. Хроматографические колонки, применяемые в адсорбционно-жидкостной хроматографии
- § 11. Аппаратура, применяемая в газовой хроматографии
- § 12. Приборы и материалы, применяемые в распределительной хроматографии
- § 13. Колонки, применяемые в ионообменной хроматографии
- § 14. Колонки, применяемые в осадочной и окислительновосстановительной хроматографии
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 15. Работы по методу адсорбционной (жидкостной и газовой) хроматографии
- § 16. Работы по методу распределительной хроматографии
- § 17. Работы по методу ионообменной хроматографии
- § 18. Работы по методу осадочной хроматографии
- § 19. Работы по методу окислительно-восстановительной хроматографии
- § 20. Работы по методу адсорбционно-комплексообразовательной хроматографии
- ГЛАВА IX. РАДИОМЕТРИЧЕСКИЕ МЕТОДЫ АНАЛИЗА
- § 1. Виды радиоактивного распада
- § 2. Скорость распада
- § 3. Взаимодействие излучения с веществом
- § 4. Ошибки при измерении радиоактивности
- Б. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ ПРИ РАБОТЕ С РАДИОАКТИВНЫМИ ВЕЩЕСТВАМИ
- § 5. Понятия и единицы измерения
- § 6. Классификация источников радиоактивного излучения и радиоактивных изотопов
- § 7. Классификация химических операций с радиоактивными веществами
- § 8. Устройство лабораторий и классификация работ
- § 9. Специальное оборудование для работ с радиоактивными веществами
- § 10. Средства индивидуальной защиты
- § 11. Проведение работ в химической лаборатории с радиоактивными веществами
- § 12. Правила работы с радиоактивными веществами
- В. МЕТОДЫ РЕГИСТРАЦИИ РАДИОАКТИВНОГО ИЗЛУЧЕНИЯ
- § 13. Ионизационные методы
- § 14. Сцинтилляционный метод
- Г. АППАРАТУРА И ТЕХНИКА ИЗМЕРЕНИЯ РАДИОАКТИВНОСТИ
- § 15. Радиометрические установки
- § 16. Измерение радиоактивности
- § 17. Измерение дозы на рабочем месте, индивидуальной дозы, полученной работающим, и загрязненности рабочих поверхностей, рук и одежды
- § 18. Абсолютные и относительные измерения активности
- Д. РАДИОМЕТРИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
- § 19. Приготовление раствора с заданной активностью
- § 20. Прямое определение ионов химических элементов в растворе с помощью радиоактивных реагентов
- § 21. Практические работы, выполняемые методом прямого определения
- § 22. Метод радиометрического титрования
- § 23. Практические работы, выполняемые методом радиометрического титрования
- § 24. Метод изотопного разбавления
- § 25. Практические работы, выполняемые методом изотопного разбавления
- § 26. Метод активационного анализа
- § 27. Практические работы, выполняемые методом активационного анализа
- § 28. Фотонейтронный метод
- § 29. Практические работы, выполняемые фотонейтронным методом
- § 30. Методы определения содержания химических элементов по излучению их естественных радиоактивных изотопов
- § 31. Практические работы по определению содержания химических элементов методом измерения излучения их естественных радиоактивных изотопов
- § 32. Методы анализа, основанные на поглощении излучения
- § 33. Практические работы, выполняемые по методу анализа, основанному на поглощении излучения
- § 34. Метод, основанный на отражении бетта-излучения
- § 35. Практические работы, выполняемые по методу, основанному на отражении бетта-излучения
- ГЛАВА X. ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ КОЛИЧЕСТВЕННОГО ОПРЕДЕЛЕНИЯ РЕДКИХ ЭЛЕМЕНТОВ
- § 1. Работы, выполняемые методом амперометрического титрования
- § 2. Работы, выполняемые полярографическим методом
- § 3. Работы, выполняемые фотометрическим методом
- § 4. Работы, выполняемые экстракционно-фотометрическим методом
- § 5. Работы, выполняемые спектрофотометрическим методом
- § 6. Работы, выполняемые флуориметрическим методом
- § 7. Работы, выполняемые методом потенциометрического титрования
- ГЛАВА XI. ФИЗИКО-ХИМИЧЕСКИЕ (ИНСТРУМЕНТАЛЬНЫЕ) МЕТОДЫ АНАЛИЗА НЕВОДНЫХ РАСТВОРОВ
- § 1. Влияние химической природы и физико-химических свойств растворителей на свойства растворенного вещества
- § 2. Классификация неводных растворителей по их протонно-донорно-акцепторным свойствам
- § 3. Классификация неводных растворителей по признаку их влияния на относительную силу электролитов
- § 4. Дифференцирующее действие растворителей
- § 5. Константы диссоциации, потенциалы полунейтрализации в неводных средах и относительная шкала кислотности
- § 6. Шкала pH и константы автопротолиза неводных растворителей
- § 7. Абсолютная (единая) шкала кислотности растворителей
- § 8. Химико-аналитическое использование неводных растворителей
- Б. АППАРАТУРА И ТЕХНИКА ТИТРОВАНИЯ НЕВОДНЫХ РАСТВОРОВ
- § 9. Установки, используемые при амперометрическом титровании неводных растворов
- § 10. Установки, используемые при потенциометрическом титровании неводных растворов
- § 11. Установки, используемые при кондуктометрическом титровании неводных растворов
- § 12. Установки, используемые при высокочастотном титровании неводных растворов
- § 13. Установки, используемые при спектрофотометрическом титровании неводных растворов
- В. ПРАКТИЧЕСКИЕ РАБОТЫ
- § 14. Очистка и обезвоживание неводных растворителей
- § 15. Титранты, применяемые для титрования кислот и оснований в неводных растворах
- § 16. Амперометрическое титрование
- § 17. Методы прямого потенциометрического титрования
- § 18. Методы косвенного потенциометрического титрования
- § 19. Дифференцированное потенциометрическое титрование
- § 20. Комбинированные методы потенциометрического титрования
- § 21. Хронопотенциометрическое титрование
- § 22. Кондуктометрическое титрование
- § 23. Хронокондуктометрическое титрование
- § 24. Спектрофотометрическое титрование