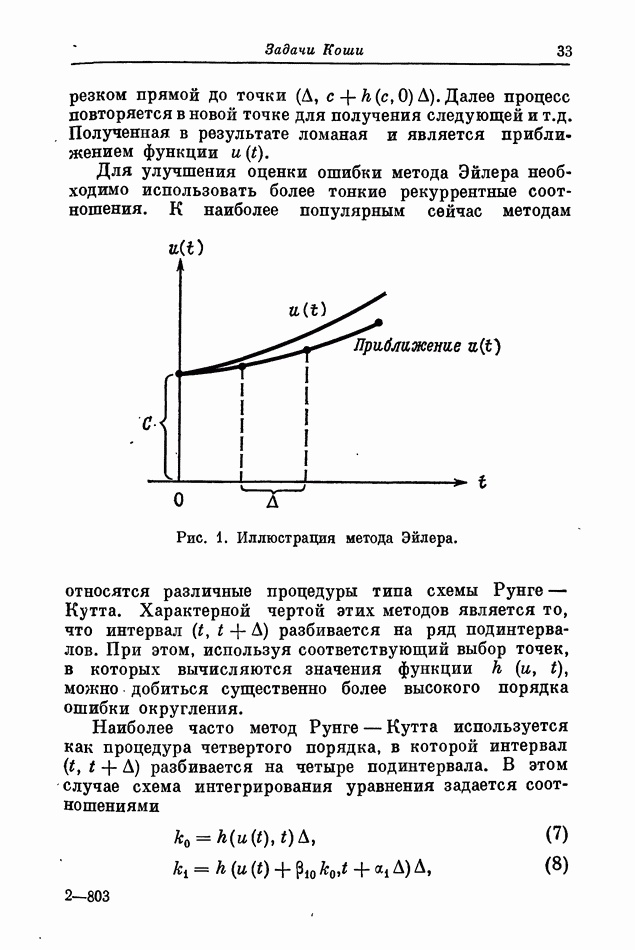
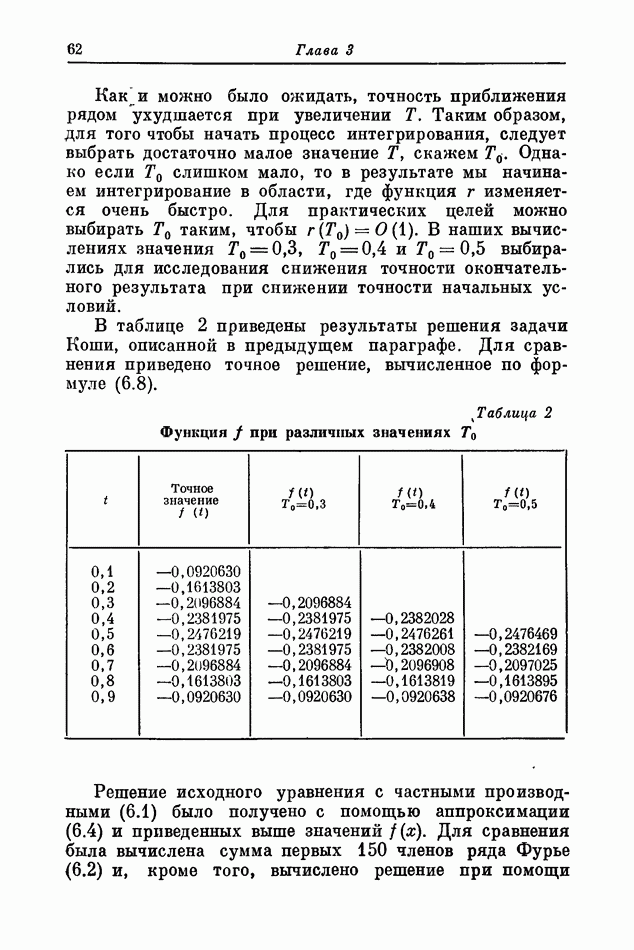
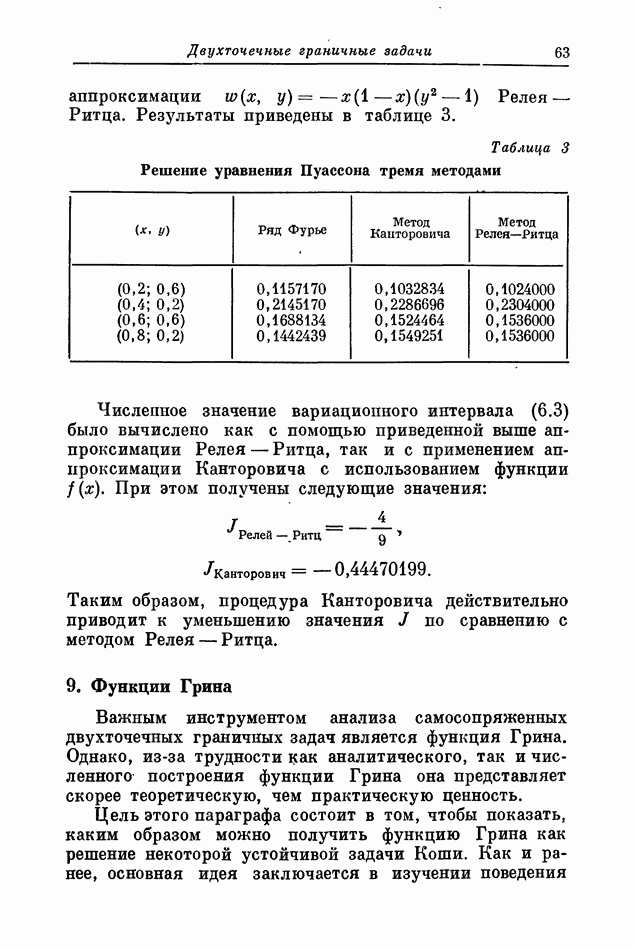
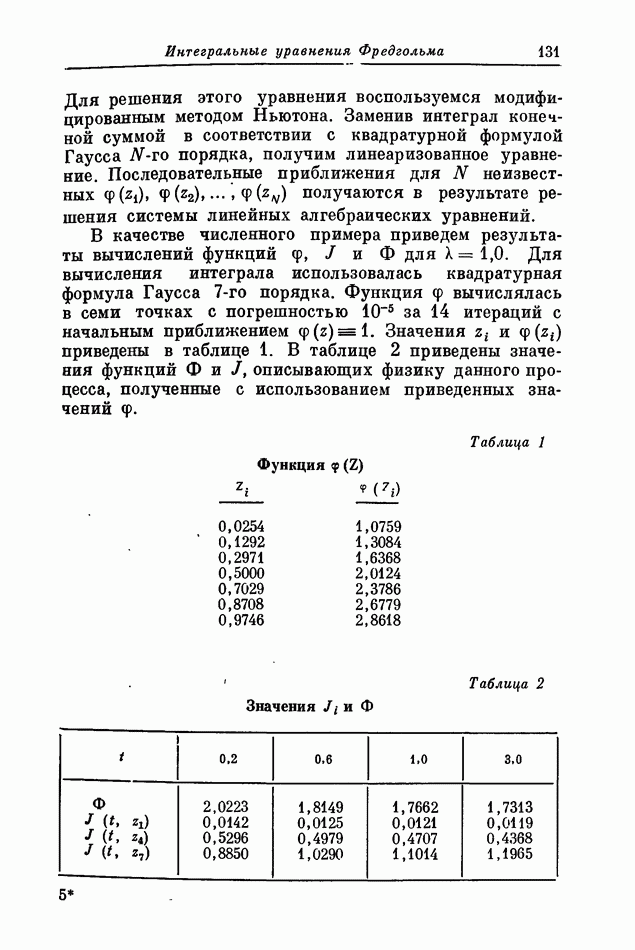
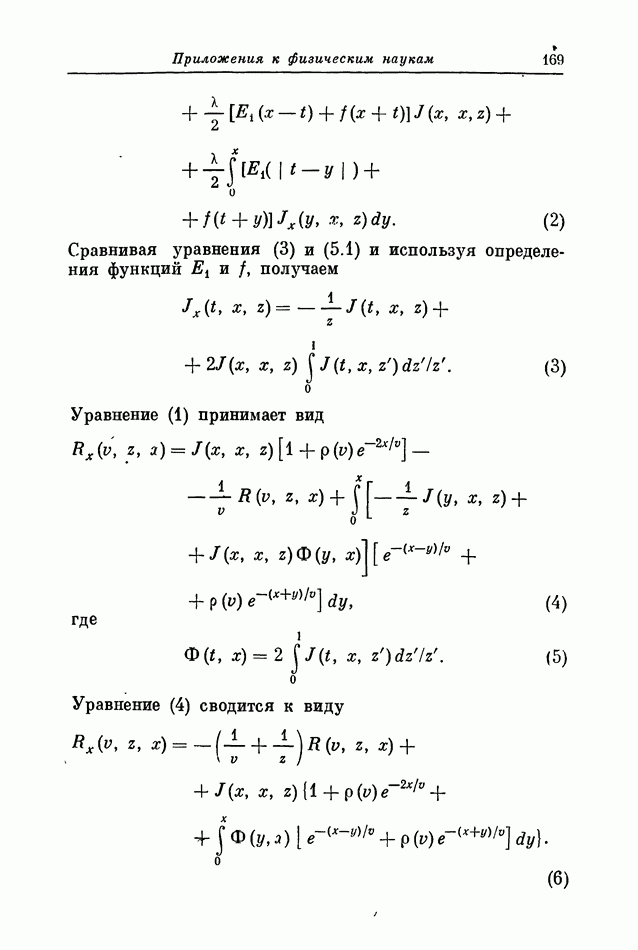| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
Быстродействие современных цифровых вычислительных машин измеряется наносекундами. Эти машины позволяют с высокой точностью и достаточно быстро решать системы из сотен обыкновенных дифференциальных уравнений. Что же дают эти воистину грандиозные возможности для решения научных, технических, экономических и социальных задач, которые встают ныне перед человечеством? Естественно, что для ответа на этот вопрос сейчас прилагаются огромные усилия.
В некоторых областях пока еще невозможно адекватно описать изучаемые процессы на языке математических уравнений. Здесь машину можно использовать лишь для моделирования процесса и, быть может, для оценки эффективности той или иной стратегии управления. В других областях математическое описание построить можно, но полученные уравнения с трудом поддаются численному решению. Возникающие при этом трудности иногда можно преодолеть непосредственно, а если это не удается, можно попытаться переформулировать исходную задачу так, чтобы она лучше согласовывалась с возможностями машины. Математика постоянно стимулируется такого рода деятельностью и, с другой стороны, сама стимулирует развитие вычислительной техники.
Каждое возрастание порядка быстродействия и размеров памяти вычислительных машин требует ревизии существующих численных методов и изучения новых классов задач, для которых появилась надежда на решение.
В книгах этой серии будут отражены современные взгляды на постановки задач, методы их анализа и численные схемы их решения.
Лос-Анджелес, Калифорния Роберт Калаба
Апрель, 1973
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
После выхода в свет в 1973 г. английского издания этой книги появилось много книг и статей, в которых развиваются темы, лишь затронутые в нашей работе. Можно отметить, в частности, обширные исследования по проблеме собственных значений дифференциальных и интегральных операторов, разнообразные приложения к механике сплошных сред и распространение общих идей погружения на дифференциальные операторы с частными производными. Инвариантное погружение все чаще используется в работах прикладного характера. Все это подтверждает наше давнее мнение о том, что теория инвариантного погружения нашла лишь первые применения и что в дальнейшем она послужит средством анализа великого множества математических, физических и технических задач.
Нам особенно приятно, что между выходом в свет оригинала и появлением русского перевода прошло совсем немного времени. Очень многие из самых существенных идей теории инвариантного погружения возникли в работах советских ученых и было бы более естественно, если бы оригиналом служила книга на русском языке, а перевод делался на английский. Мы отмечаем в связи с этим лишь работы В. А. Амбарцумяна и
В. В. Соболева в области астрофизики, хотя крупный вклад внесли и многие другие советские ученые. Мы надеемся, что, прочитав эту книгу, советский читатель
не только познакомится с многочисленными приложениями теории инвариантного погружения (помимо задач распространения излучения), но и глубже проникнет в основные ее идеи и методы.
Мы считаем своим приятным долгом поблагодарить ааших советских коллег Р. В. Гамкрелидзе, по инициативе которого книга была принята к переводу, и С. П. Чеботарева за нелегкую работу по ее переводу. Без их настойчивых усилий она, вероятно, так и осталась бы лишь на английском языке»
Апрель 1975
Лаксенбург, Австрия Джон Касти
Лос-Анджелес, Калифорния Роберт Калаба
| Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
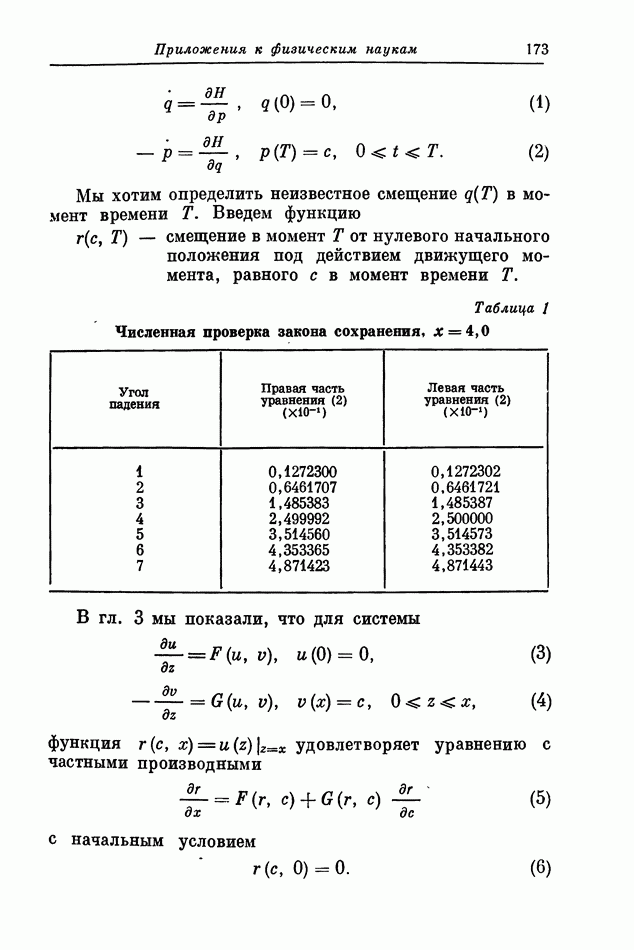
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)