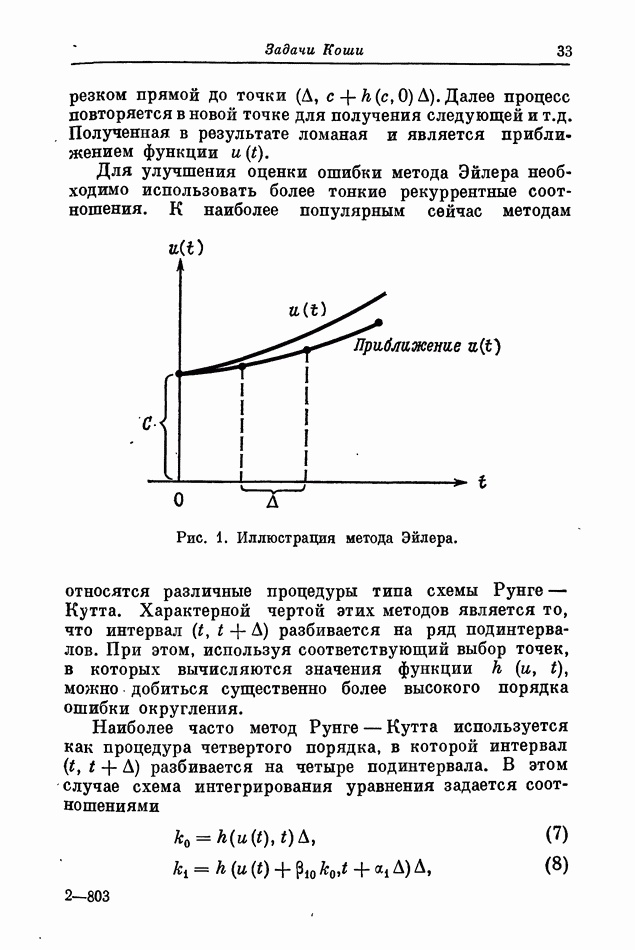
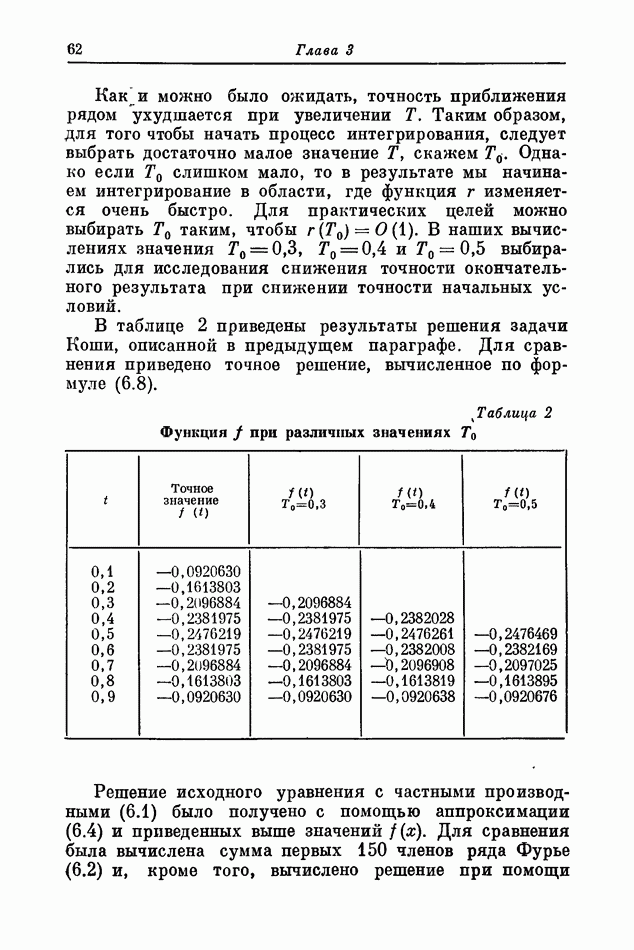
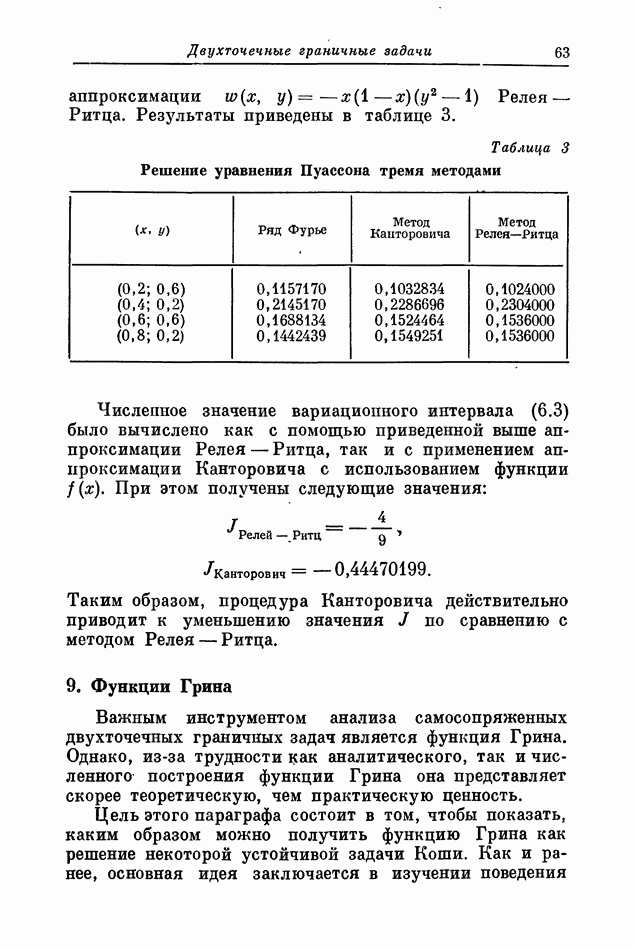
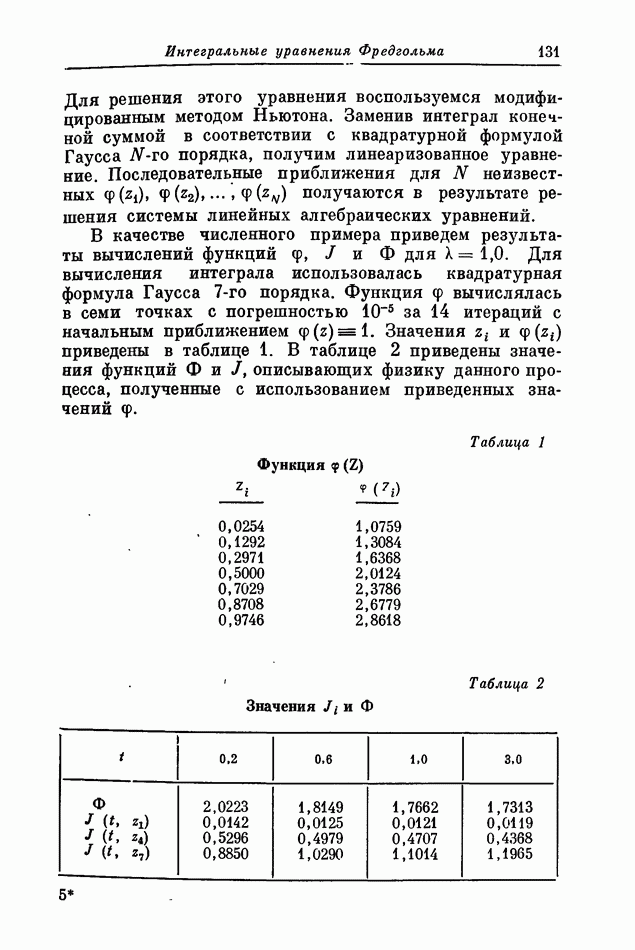
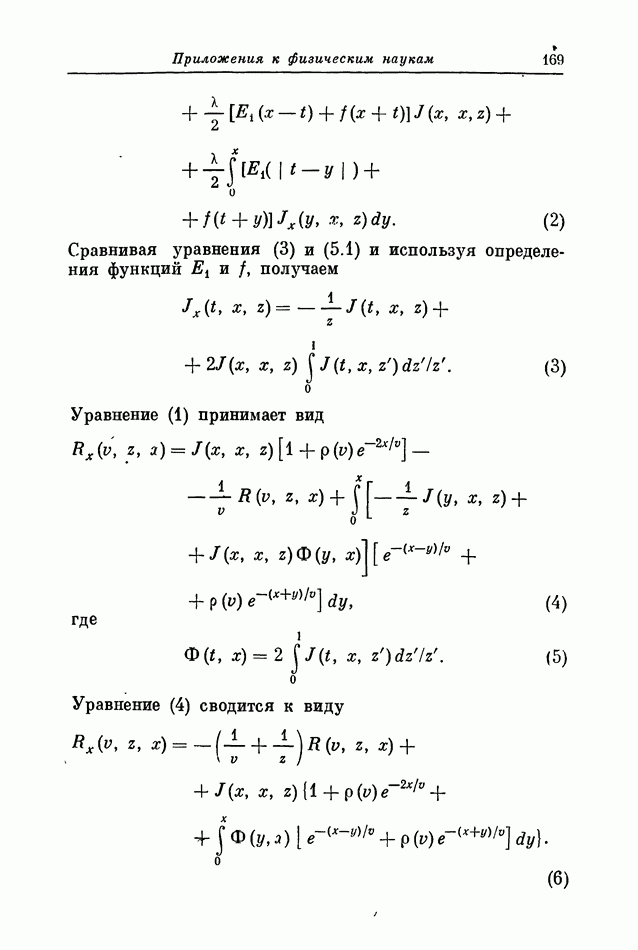| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Линейные двухточечные граничные задачи
Мы начинаем изучение двухточечных граничных задач с рассмотрения скалярных уравнений

где  непрерывны на
непрерывны на  постоянны. Хотя уравнения (1) — (2) и не являются наиболее общей формой линейной двухточечной граничной задачи, тем не менее в эту схему укладывается большинство интересных задач физики и техники. Читатель, заинтересованный в задачах более общего вида, включающих многомерные аналоги задачи (1) — (2) или отличающихся от них другой формой задания граничных условий, сможет без труда распространить излагаемый ниже подход и на эти случаи. Некоторые результаты в этом направлении мы приведем в § 12.
постоянны. Хотя уравнения (1) — (2) и не являются наиболее общей формой линейной двухточечной граничной задачи, тем не менее в эту схему укладывается большинство интересных задач физики и техники. Читатель, заинтересованный в задачах более общего вида, включающих многомерные аналоги задачи (1) — (2) или отличающихся от них другой формой задания граничных условий, сможет без труда распространить излагаемый ниже подход и на эти случаи. Некоторые результаты в этом направлении мы приведем в § 12.
Поскольку полный набор условий, позволяющих определить  единственным образом, задан не в одной, а в двух точках
единственным образом, задан не в одной, а в двух точках  задача
задача  называется двухточечной граничной задачей. Такая двухточечная система задания условий весьма усложняет как анализ, так и численное решение задачи (1) — (2), поскольку в каждой из этих точек в отдельности не содержится достаточной информаций для полного определения векторного поля
называется двухточечной граничной задачей. Такая двухточечная система задания условий весьма усложняет как анализ, так и численное решение задачи (1) — (2), поскольку в каждой из этих точек в отдельности не содержится достаточной информаций для полного определения векторного поля  . С вычислительной точки зрения это соответствует ситуации, когда непосредственное применение различных схем численного интегрирования, таких, как методы Рунге-Кутта, Адамса-Мултона и т.д., невозможно из-за отсутствия в начальной точке информации, необходимой для «запуска» алгоритма. Стоит ли говорить, что эти трудности становятся еще более острыми в случае, нелинейных задач.
. С вычислительной точки зрения это соответствует ситуации, когда непосредственное применение различных схем численного интегрирования, таких, как методы Рунге-Кутта, Адамса-Мултона и т.д., невозможно из-за отсутствия в начальной точке информации, необходимой для «запуска» алгоритма. Стоит ли говорить, что эти трудности становятся еще более острыми в случае, нелинейных задач.
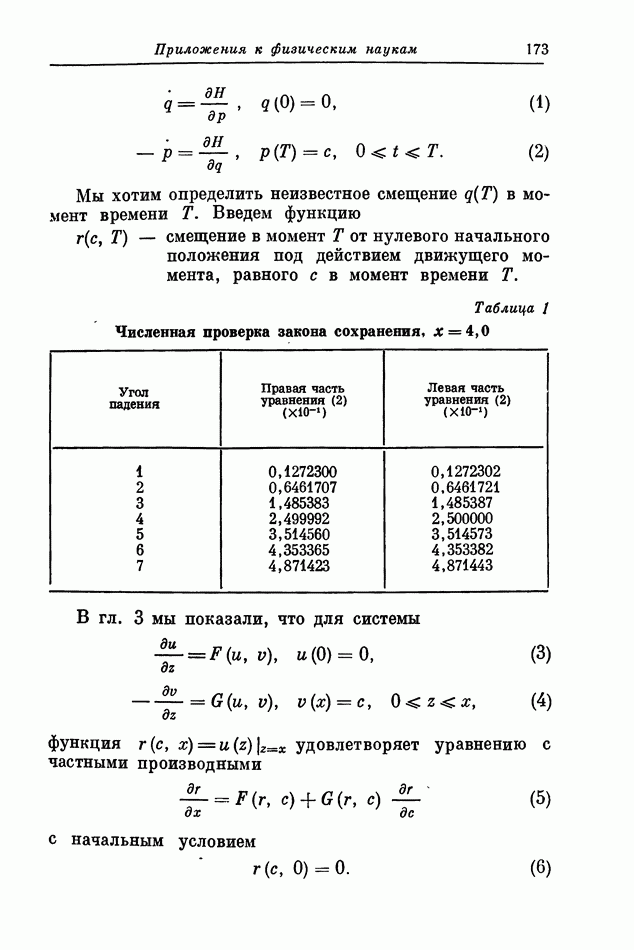
Наша цель состоит в том, чтобы сформулировать задачу Коши (вместо двухточечной граничной задачи), которая «представляла» бы решение задачи  Под термином «представляет» мы понимаем тот факт, что решение задачи Коши единственным образом определяет решение граничной задачи и наоборот. Иными словами, эти задачи изоморфны и в результате любые свойства,
Под термином «представляет» мы понимаем тот факт, что решение задачи Коши единственным образом определяет решение граничной задачи и наоборот. Иными словами, эти задачи изоморфны и в результате любые свойства,
установленные для одной из задач, автоматически оказываются верными и для другой. Поскольку мы преследуем в основном педагогические цели, большинство наших результатов мы будем получать, оставляя в стороне тонкие моменты (которые в некоторых случаях оказываются весьма нетривиальными). Итак, вернемся к нашей задаче.
Параметром погружения, который мы будем использовать при построении задачи Коши, является длина интервала  Поэтому перепишем (1) — (2), чтобы явно подчеркнуть зависимость решения от Т:
Поэтому перепишем (1) — (2), чтобы явно подчеркнуть зависимость решения от Т:

Для лучшего понимания изложения воспользуемся линейностью системы  и рассмотрим две системы уравнений:
и рассмотрим две системы уравнений:
Система 

и
Система 11

Принцип суперпозиции для линейных систем позволяет записать

Поэтому рассмотрим системы I и II по отдельности.
Рассмотрим сначала функции и и  системы
системы  Нас интересует, как изменяются кривые решения в фиксированной точке
Нас интересует, как изменяются кривые решения в фиксированной точке  при изменении длины интервала
при изменении длины интервала  Дифференцируя (5) — (6) по
Дифференцируя (5) — (6) по  получим
получим

Здесь точка сверху обозначает дифференцирование по  -дифференцирование по
-дифференцирование по  Сравнивая (11) - (12) с (7) — (8), видим, что
Сравнивая (11) - (12) с (7) — (8), видим, что

Рассмотрим квадратную скобку из (13), (14). Подставив  в (5) — (6), получим
в (5) — (6), получим

Введем теперь новые переменные тип:

Учитывая  достаточно определить функции
достаточно определить функции  рассмотрим сначала
рассмотрим сначала 
Продифференцируем уравнение (13) и получим

Аналогично для  получаем
получаем

Из уравнений (19) и (20) видно, что мы должны рассмотреть величины 
Дифференцируя (7) и (8) по  получим
получим

Сравнивая  получаем
получаем

Для использования этих соотношений заметим, что из (7) и (8) при  вытекает
вытекает

Пусть функции  определяются равенствами
определяются равенствами

Выведем теперь задачу Коши для  Прежде всего продифференцируем
Прежде всего продифференцируем  по
по 

Аналогично получим уравнение для 

Элементарными преобразованиями (29) и (30) приводятся к системе

Начальные условия при  получаются из уравнений (7) и (8) как решение системы
получаются из уравнений (7) и (8) как решение системы

Очевидно, отсюда получается! условие разрешимости  гарантирующее существование единственного решения.
гарантирующее существование единственного решения.
Знание  позволяет получить
позволяет получить  решая задачу Коши
решая задачу Коши  Соответствующие уравнения
Соответствующие уравнения  этом имеют вид
этом имеют вид

Начальными условиями при  являются
являются

Возвращаясь теперь к уравнениям (19) и (20) для функций  мы видим, что
мы видим, что

Начальные условия при  определяются из уравнений (5) и (6) как
определяются из уравнений (5) и (6) как

Уравнения для функций и и и через  имеют вид
имеют вид

При  имеем
имеем

Этим завершается вывод полной задачи Коши для определения функций и,  необходимых для получения решения х и у задачи
необходимых для получения решения х и у задачи 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)