4. Численное решение задачи Коши

Рассмотрим теперь вопрос получения численного решения задачи Коши на цифровой вычислительной машине. Допустим, мы собираемся решить скалярное уравнение

Поскольку цифровая вычислительная машина способна выполнять лишь арифметические операции сложения, вычитания, умножения и деления, наша первая задача состоит в сведении трансцедентной операции

дифференцирования к арифметическим. Весьма простой и далеко не самый эффективный способ состоит в аппроксимации уравнения (1) конечно-разностной схемой

где А — «малый» параметр. Знание начального значения и позволяет с помощью уравнения (2) последовательно вычислять значения а это как раз та задача, для решения которой ЭЦВМ идеально приспособлена.

Как обычно бывает в случае замены точного соотношения приближенным, здесь необходимо исследовать вопрос о точности аппроксимации. Разлагая, например, левую часть (2) по степеням получим

Следовательно, мы видим, что локальная ошибка при вычислении и с помощью уравнения (2) при заданном и составляет

В качестве примера того, как ценой небольших усилий можно уменьшить ошибку, воспользуемся для аппроксимации производной центральными разностями:

Разложение и по стеценям в точке дает локальную ошибку

которая на порядок меньше, чем (4).

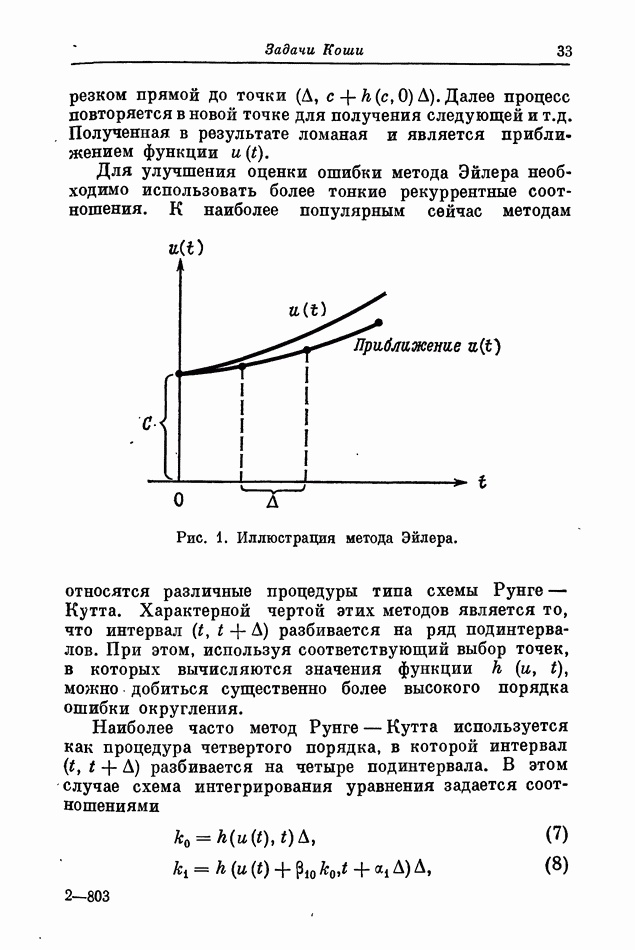
Аппроксимация типа (2) восходит еще к Эйлеру и обычно называется методом Эйлера. На рис. 1 приведена графическая иллюстрация этого метода. Сначала вычисляется наклон функции и в начальной точке затем он используется для аппроксимации функции

отрезком прямой до точки . Далее процесс повторяется в новой точке для получения следующей и т.д. Полученная в результате ломаная и является приближением функции

Для улучшения оценки ошибки метода Эйлера необходимо использовать более тонкие рекуррентные соотношения.

Рис. 1. Иллюстрация метода Эйлера.

К наиболее популярным сейчас методам относятся различные процедуры типа схемы Рунге — Кутта. Характерной чертой этих методов является то, что интервал разбивается на ряд под интервалов. При этом, используя соответствующий выбор точек, в которых вычисляются значения функции можно добиться существенно более высокого порядка ошибки округления.

Наиболее часто метод Рунге — Кутта используется как процедура четвертого порядка, в которой интервал разбивается на четыре подинтервала. В этом случае схема интегрирования уравнения задается соотношениями

Значения некоторых параметров, входящих в соотношения (7)—(11), можно определить, приравнивая выражение для и разложению и в ряд Тейлора в точке Приравнивая члены соответствующих степеней до четвертого порядка включительно, получаем ошибку округления Среди бесчисленного множества возможных вариантов выбора параметров приведем один, первоначально предложенный Рунге:

Функция сначала вычисляется на левом конце интервала, затем дважды в экстраполированных внутренних точках и, наконец, на экстраполированном правом конце интервала. В процедуре Рунге интервал подразделяется на четыре подинтервала которые служат весами значений функции в соответствующих точках.

Метод Рунге — Кутта и метод Эйлера обладают тем общим свойством, что для начала процедуры решения необходимо знать значение функции лишь в одной точке. Подобные методы иногда называют «пошаговыми» или «открытыми» методами. Основной недостаток

методов Рунге — Кутта заключается в том, что в них на каждом шаге интегрирования необходимо несколько раз вычислять значение функции Это увеличивает время, необходимое для получения решения. Главный недостаток метода Эйлера состоит в довольно большой ошибке округления.

Для того чтобы избавиться от недостатков, свойственных методам Эйлера и Рунге — Кутта, необходимо воспользоваться более тонким подходом. В описанных выше методах предполагается, что наклон и постоянен на интервале что почти никогда не встречается на практике. Ясно поэтому, что более точной процедурой мог бы быть метод, в котором наклон аппроксимируется набором многочленов, которые используются для предсказания значения и Получив предсказание для можно с помощью итеративной процедуры, использующей значение полученное из уравнения (1), уточнить его. Такие методы называются методами типа «предсказание-уточнение» и, как мы увидим далее, часто позволяют преодолеть трудности, вознцкающие при применении метода Эйлера или

Для получения предсказания проведем интерполяционный многочлен через известных точек

Д) и затем продолжим результирующую функцию на весь интервал интегрирования. Для того чтобы начать интегрирование, с помощью какой-либо другой процедуры, скажем метода Рунге — Кутта, необходимо получить первые точек.

Используя в ряде предыдущих точек, мы можем для вычисления и использовать интерполяционную формулу

где —оператор обратной разности . Интегрируя (17) по интервалу получим формулу Адамса — Бэшфорта

Аналогично, интегрируя (17) по интервалу получаем формулу Адамса — Мултона V

или, заменяя разности их выражениями через и и заменяя на получим, сохраняя лишь члены до третьего порядка включительно,

Проводя интерполяционный многочлен через точек и можно получить формулу для итеративного уточнения, использующую значение Воспользовавшись обратной интерполяционной формулой Грегори-Ньютона (более подробное изложение см. в соответствующей литературе, указанной в конце главы), окончательно получаем

где

Интегрирование уравнения (1) с заменой на по интервалу дает

Заменяя конечные разности их определением и сохраняя лишь члены до третьего порядка включительно, получим

Только что выведенная схема Адамса — Мултона как вариант общего метода «предсказание-уточнение» и используется в дальнейшем во всех численных примерах. При этом (20) используется для предсказания, а (23) — для уточнения. Программа этого метода для ЭЦВМ приведена в приложении.

Оценка локальной ошибки для схемы интегрирования Адамса — Мултона в предположении, что меняется на интервале не слишком быстро, дается формулой

Сравнивая эту величину с оценкой ошибки метода Рунге—Кутта, мы видим, что обе имеют порядок Анализируя, однако, выражения (20) и (23), легко видеть, что в методе Адамса-Мултона функция вычисляется только дважды в то время, как в методе Рунге — Кутта на каждом шаге интегрирования требуются четыре значения этой функции. Таким образом, при той же точности процедура Адамса — Мултона приблизительно вдвое быстрее, чем метод Рунге — Кутта.

При этом несколько увеличивается объем необходимой памяти, поскольку необходимо хранить предыдущие точки.

Поскольку дифференциальное уравнение второго или более высокого порядка сродится к системе уравнений первого порядка введением дополнительных переменных, изложенные выше методы можно применять как к одномерным, так и к многомерным задачам. Если, например, для решения системы двух дифференциальных уравнений вида

используется описанный выше метод Рунге - Кутта, то интегрирование проводится по формулам

и

Аналогичные формулы имеют место и для систем более высокой размерности. Точно так же можно вывести и многомерный аналог формул (20), (23) для метода Адамса — Мултона.