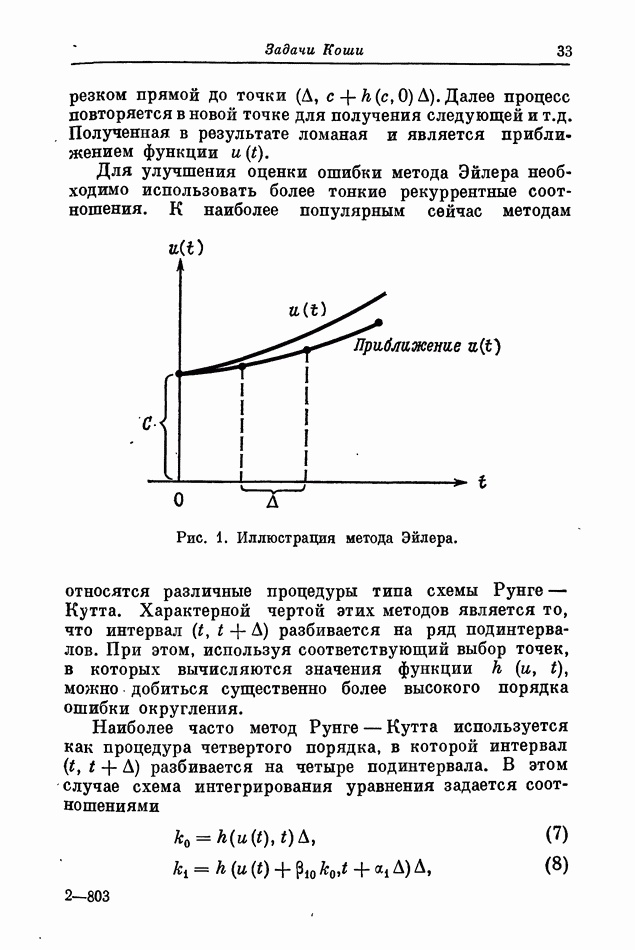
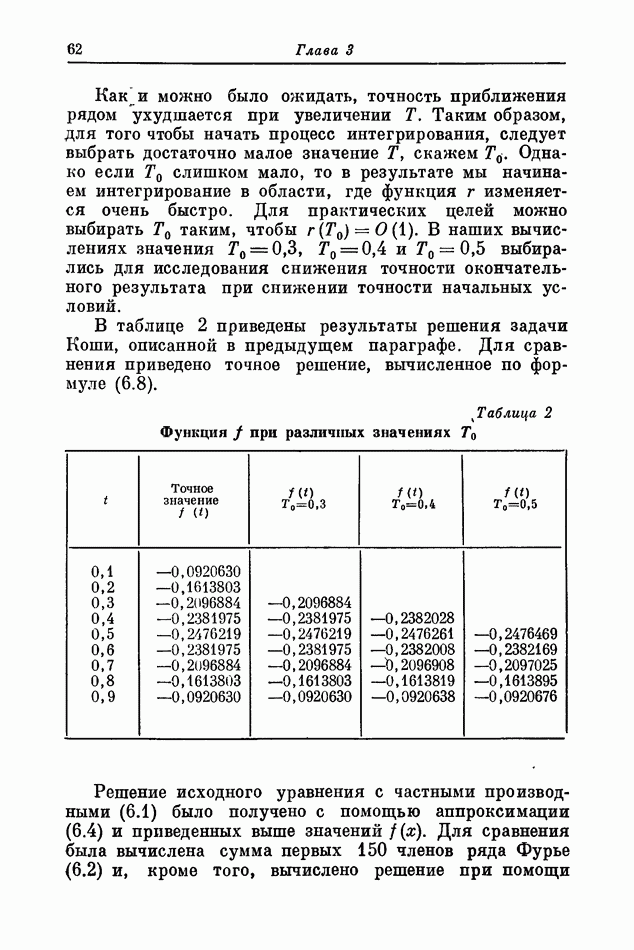
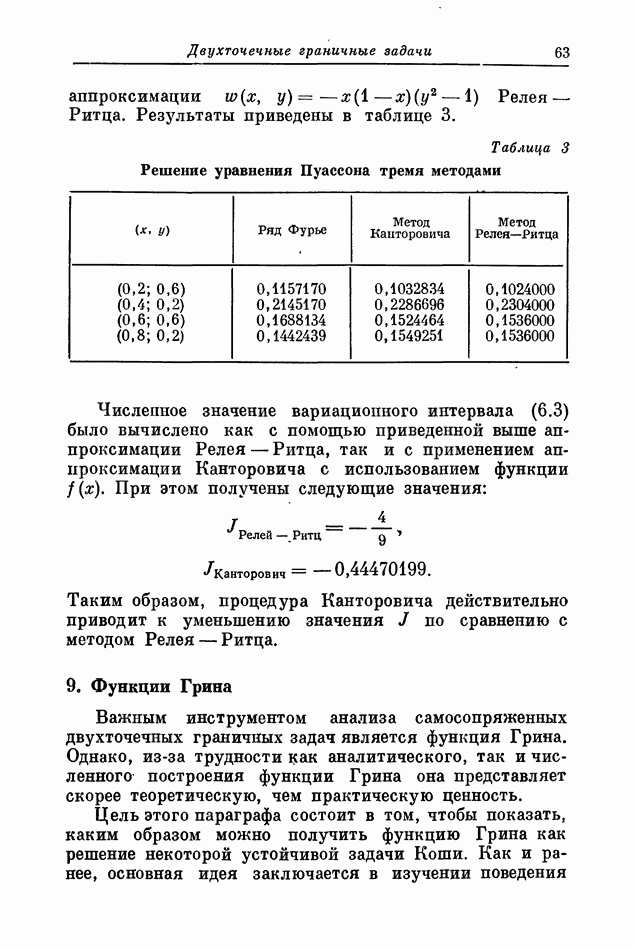
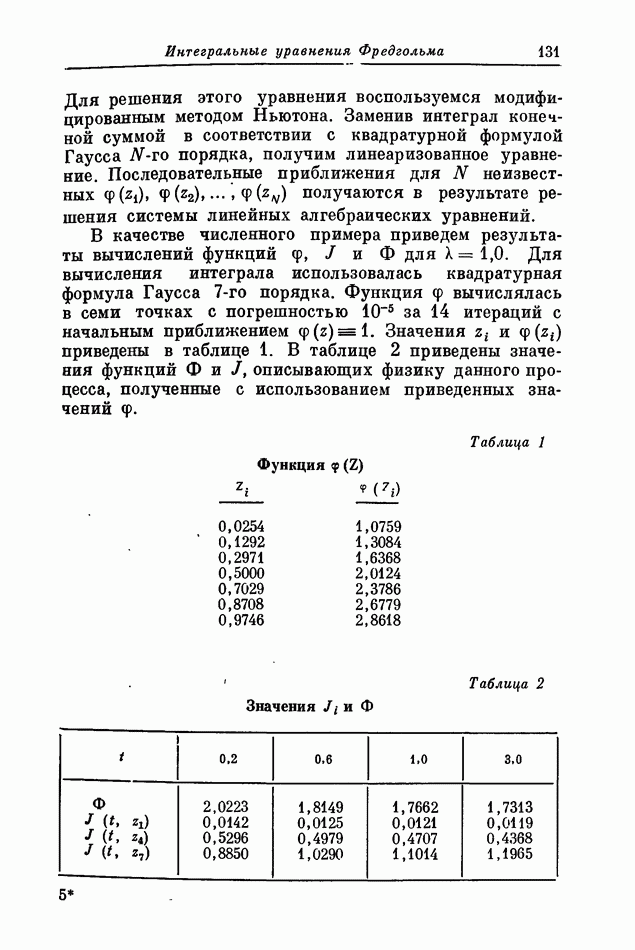
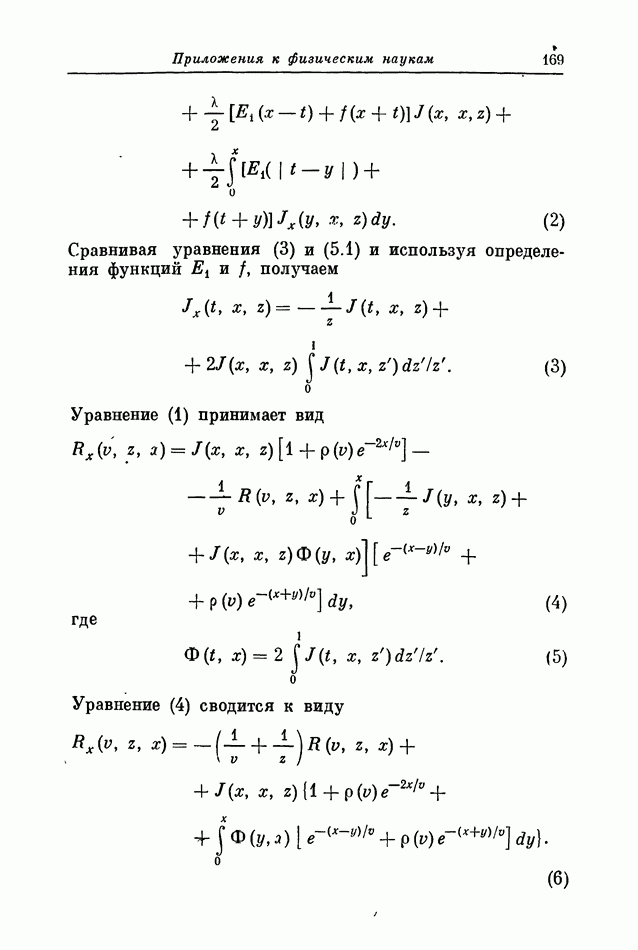| << Предыдущий параграф | Следующий параграф >> |
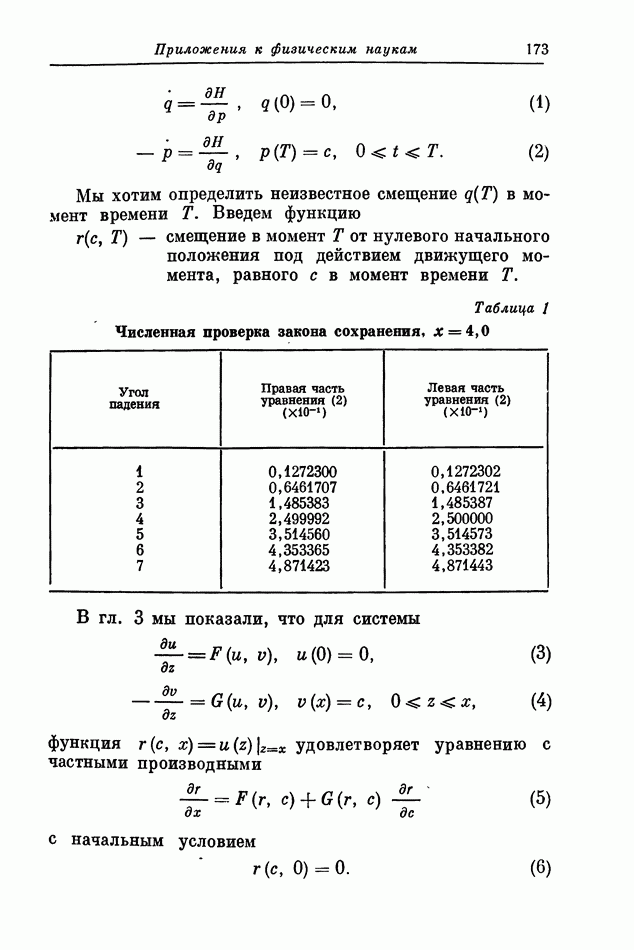
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ
По выражению фон Неймана «математические идеи рождаются из эмпирики». Под влиянием окружающего мира возникают различные математические модели действительности и появляются новые теории. Эти теории, разрастаясь и вливаясь в главный поток математической мысли, позволяют объединить на общей основе значительные классы математических задач и дать ответы на ряд вопросов, которые ранее и не ставились. Математическую теорию от набора конкретных методов отличают два основных признака: универсальность и ясность идей и понятий.
Одним из наиболее эффективных стимулов возникновения новых теорий на всем пути развития математики была необходимость получения численных ответов на численно поставленные вопросы. Можно смело сказать, что большая часть того, что сейчас называют классической прикладной математикой, обязана своим появлением желанию избавиться от трудоемких вычислений. Теперь с ростом возможностей вычислительных машин центр тяжести переместился: основное внимание уделяется не полному освобождению от арифметических расчетов, а поискам наиболее эффективных и удобных способов их проведения.
Исходная идея этой книги состоит в том, что вычислительные машины по самой природе являются наиболее эффективным средством для решения дифференциальных уравнений, начальные условия которых заданы в одной точке, т. е. так называемых «задач Коши». С другой стороны, многие задачи, возникающие в математической физике, технике, биологии, экономике и исследовании операций, по своей природе являются граничными задачами, поскольку необходимые для однозначного определения решения условия задаются в двух или более точках. Но надо сказать, что цифровые вычислительные машины, вообще говоря, не слишком хорошо приспособлены для численного решения таких задач. Основная мысль, развиваемая в этой книге, состоит в следующем: формулируя математически какую-либо задачу, следует учитывать имеющиеся вычислительные средства, ибо часто существуют иные эквивалентные формулировки задачи, которые в вычислительном отношении выгодно отличаются от начальной. Очень часто традиционная математическая формулировка задачи принимается как единственно возможная, будто бы она предложена неким математическим Соломоном, мудрость, рассудительность и способность предвидения которого не вызывают сомнений.
Развивая одну математическую идею, возникшую при изучении распространения излучения в атмосфере, мы стараемся показать, как можно воспользоваться первыми плодами математической теории инвариантного погружения для переформулировки широкого класса граничных
задач в виде задач Коши. Наша основная задача — пополнить арсенал ученого еще одним мощным средством решения важных задач, возникающих в области его деятельности, но, кроме этого, мы приводим также ряд идей, которые, вероятно, могут сформироваться в одно из ведущих направлений современной прикладной математики.
Чтобы сделать книгу доступной наиболее широкому кругу читателей, мы намеренно предпочли строгому изложению изложение математически формальное. Хотя «пуристы» от математики, вероятно, неодобрительно отнесутся к этому решению, мы считаем, что при таком изложении, иллюстрированном разнообразными примерами, основные идеи видны лучше, чем при строгом изложении, обремененном искусственными математическими препонами. Разумеется, для обоснования рассматриваемых методов под них необходимо подвести строгую математическую базу. Тем не менее, мы решили привести только наиболее важные теоремы, оставив многое для следующей книги. Надеемся, что это решение не только сделает книгу более доступной, но и стимулирует дальнейшие теоретические исследования: нам кажется, что если придерживаться чуть более строгой манеры изложения, то на эту тему можно написать множество журнальных статей, книг и диссертаций. Во всяком случае большинство приведенных в книге рассуждений будет без труда воспринято читателем, знакомым с начальным курсом по теории обыкновенных дифференциальных уравнений. Перейдем теперь к краткому описанию содержания отдельных глав книги.
В первой главе на примере конечно-разностных уравнений вводятся те основные идеи, которые будут использоваться в дальнейшем. Мы приводим краткий анализ «задачи о разорении игрока», излагаем ее
нетрадиционную постановку и метод решения и показываем, что новая постановка обладает определенными вычислительными (и аналитическими) преимуществами перед обычной. Далее, основываясь на разобранном примере, мы применяем эти идеи для решения неоднородной системы линейных разностных уравнений общего вида.
Чтобы сделать изложение независимым, в гл. 2 мы приводим краткий обзор идей и методов численного решения задач Коши. Здесь же рассматриваются стандартные схемы численного интегрирования типа методов Рунге — Кутта и Адамса — Мултона, а также вопросы численной устойчивости,
Изложение основных результатов начинается в гл. 3, где исследуются линейные и нелинейные двухточечные граничные задачи. Мы показываем, что широкий класс таких задач можно переформулировать в виде задач Коши, и, кроме того, излагаем некоторые результаты, полезные для вычисления функции Грина. На конкретном примере кратко рассматривается вопрос численной устойчивости предлагаемого метода, а также приводятся результаты нескольких численных экспериментов, поставленных для его подтверждения.
Четвертая глава посвящена интегральным уравнениям Фредгольма. В основном мы рассматриваем уравнения с ядрами  удовлетворяющими условию
удовлетворяющими условию  Мы ограничились этим классом задач, поскольку такие уравнения очень часто возникают во многих областях физики, астрономии, техники и биологии, а, кроме того, можно ожидать, что специальный вид ядра позволит получить более глубокие результаты, чем в общем случае. В конце главы приводятся ссылки на работы, содержащие аналогичные исследования для случаев вырожденных и полувырожденных ядер более общего вида.
Мы ограничились этим классом задач, поскольку такие уравнения очень часто возникают во многих областях физики, астрономии, техники и биологии, а, кроме того, можно ожидать, что специальный вид ядра позволит получить более глубокие результаты, чем в общем случае. В конце главы приводятся ссылки на работы, содержащие аналогичные исследования для случаев вырожденных и полувырожденных ядер более общего вида.
Вариационные задачи и задачи оптимального управления являются объектом исследований пятой главы. Показано, как можно изучать широкие классы задач безусловной оптимизации и оптимизации с ограничениями, не пользуясь уравнением Эйлера, динамическим программированием или принципом максимума. Однако мы отмечаем (и подтверждаем конкретным примером), что комбинация различных методов может привести к более эффективной вычислительной процедуре, чем каждый из этих методов в отдельности.
Последняя глава посвящена приложениям методов, описанных в предыдущих главах, к различным разделам физики. Показано, что идеи погружения приводят к новым формулировкам и новому подходу к задачам, возникающим в теории распространения излучения, аналитической механике, теории оптимальной фильтрации и теории нелокального взаимодействия волн.
Если взглянуть на ссылки в конце каждой главы, становится ясно, что большая часть изложенных в этой книге результатов получена совместно с другими авторами. Поэтому вполне можно сказать, что книга принадлежит и им. В этой связи мы хотим поблагодарить, в частности, С. Уэно и X. Кагиваду за полезные обсуждения и сотрудничество по вопросам, связанным с распространением излучения, Р. Сридхара за плодотворные дискуссии по теории фильтрации и оценивания и А. Шумицки за полезные предложения в области интегральных уравнений. Мы крайне признательны Э. Энджелу и М. Джанкоза за критические замечания и предложения по вопросам численного анализа и М. Скотту за помощь в области задач на собственные значения. Особенно мы благодарны Р. Веллману: его влияние ощущается во всем, без его заинтересованности, поддержки и
энтузиазма остались бы в области несбыточных мечтаний как теория инвариантного погружения, так и эта книга.
Кроме того, мы хотим выразить свою благодарность многочисленным машинисткам в РЭНД Корпорейшн, Системз Контрол Инкорпорейтид и Университете Южной Калифорнии за терпеливое печатание и перепечатывание различных разделов этой книги. В частности, мы хотели бы отметить вклад Канды Кюнце, которой удалось собрать воедино разрозненные куски первого варианта рукописи.
Март 1973
Туесон, Аризона Джон Каспги
Лос-Анджелес, Калифорния Роберт Калаба
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)