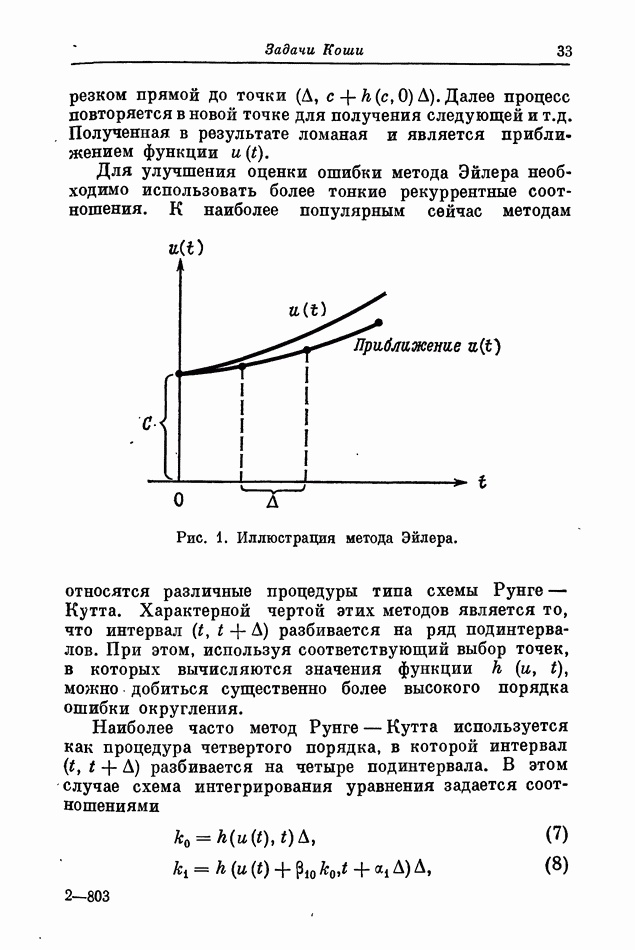
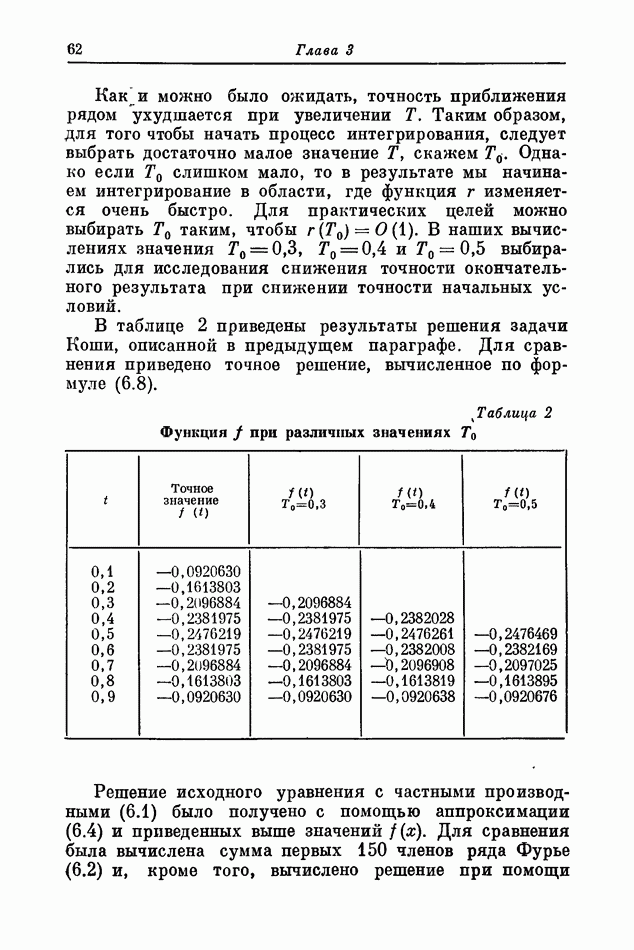
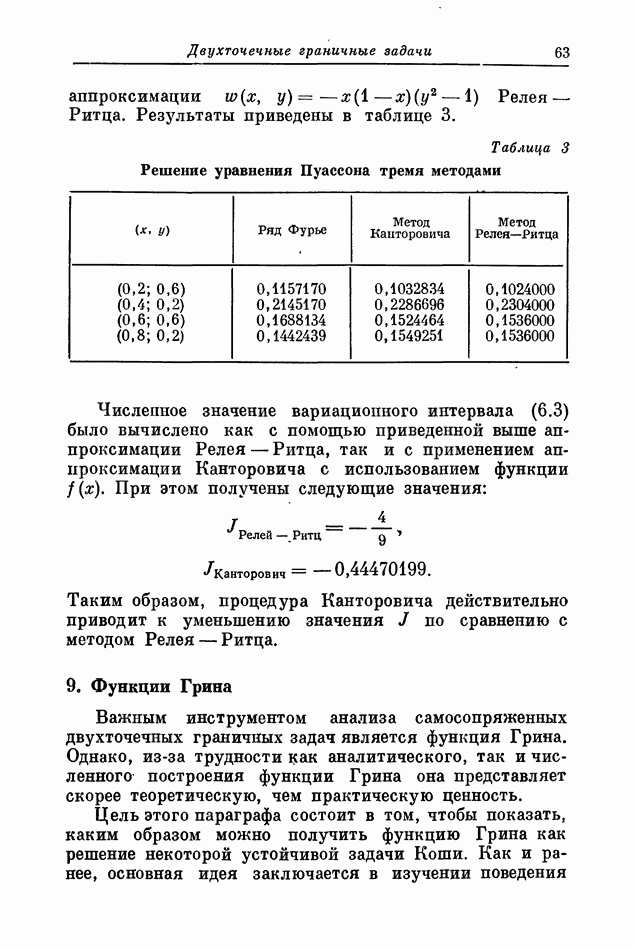
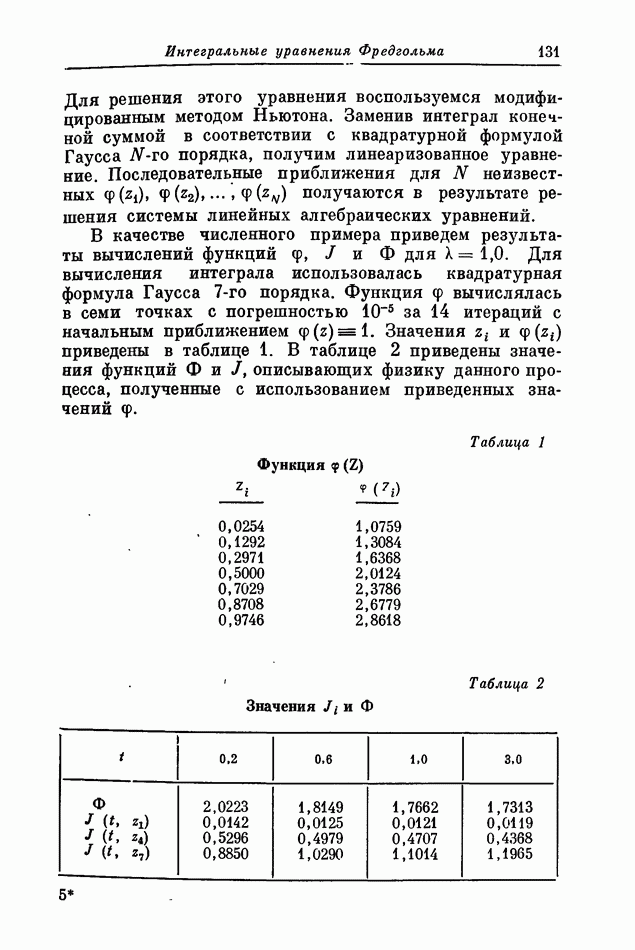
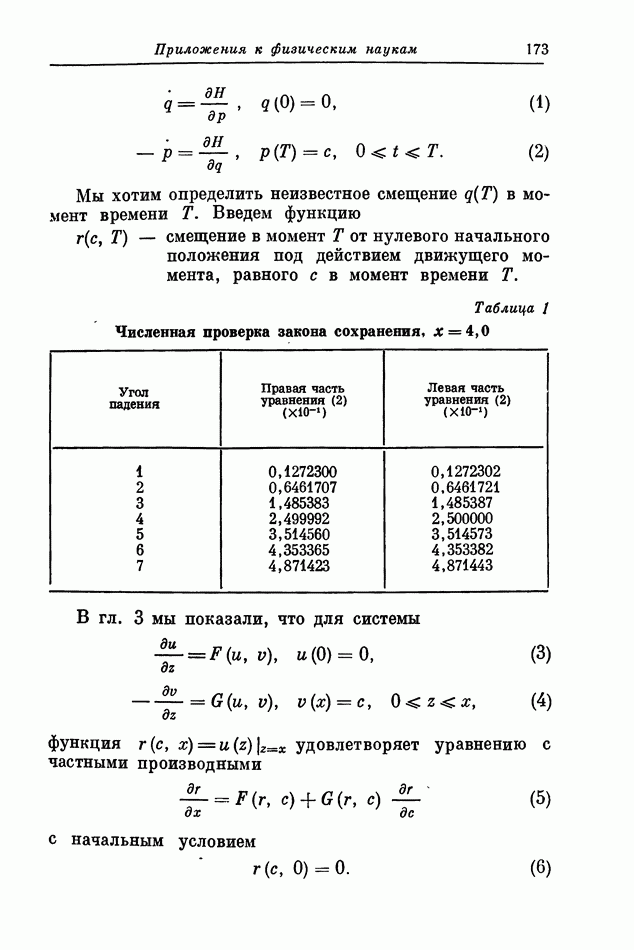
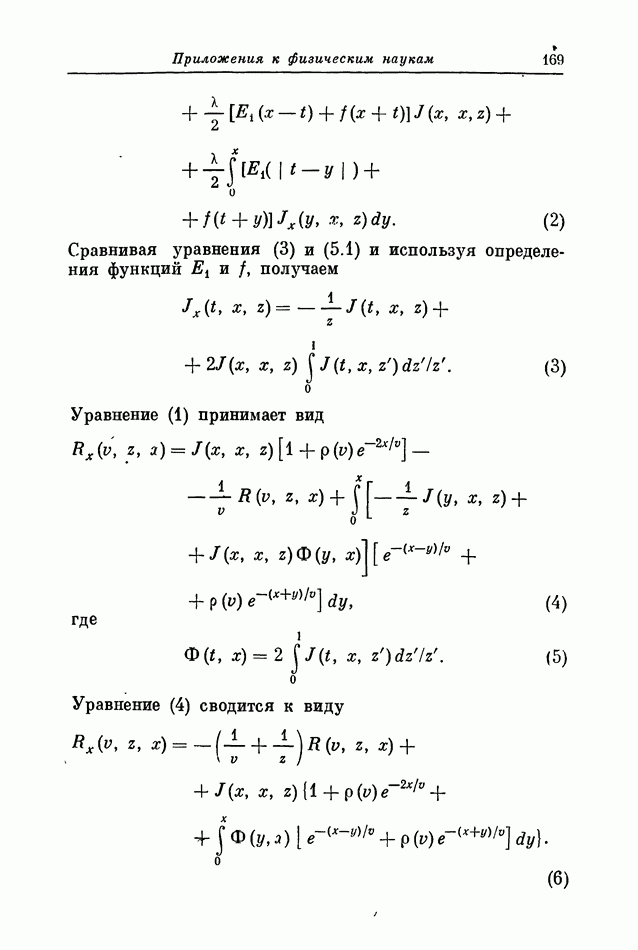| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
В оставшихся параграфах мы введем еще один усложняющий элемент в задачи, которые мы рассматривали до сих пор. А именно, мы займемся задачами оптимального управления с ограничениями на управляющие переменные. Эти ограничения вполне естественно возникают во многих случаях и часто соответствуют той ситуации, когда управляющие переменные описывают количество имеющихся ресурсов. Ясно, что в этом случае эти ограничения просто отражают тот факт, что для управления системой мы не можем тратить больше, чем у нас есть. Разумеется, существует множество типов ограничений такого рода, однако, мы рассмотрим лишь случай, когда управление просто ограничено по абсолютной величине. Затем мы укажем некоторые многообещающие подходы к решению более общих задач таких, как задачи с нестационарными ограничениями, с фазовыми ограничениями и т. д.
Класс задач, который мы подробно рассматриваем, относится к тому типу задач оптимального управления с ограничениями, для анализа которых обычно привлекается принцип максимума Понтрягина. Соответствующую данному случаю задачу Коши можно рассматривать как распространение классической теории Гамильтона — Якоби на вариационные задачи с ограничениями.
Обозначим значение переменной состояния системы в момент времени  через у и запишем уравнения движения в виде
через у и запишем уравнения движения в виде

где  - переменная управления. Предположим, что на управление наложено ограничение
- переменная управления. Предположим, что на управление наложено ограничение
 действительное число. (3)
действительное число. (3)
Функционал, который требуется минимизировать, имеет вид

Целью управления, естественно, является выбор управления  удовлетворяющего ограничению (3) и минимизирующего
удовлетворяющего ограничению (3) и минимизирующего  Мы будем предполагать, что функции
Мы будем предполагать, что функции  достаточно гладкие на достаточно малом интервале
достаточно гладкие на достаточно малом интервале  так что применение дальнейших операций обосновано.
так что применение дальнейших операций обосновано.
В соответствии с принципом максимума Понтрягина решение данной задачи можно получить, введя переменную X и функцию  , такие, что
, такие, что

и решая двухточечную граничную задачу

где

Наша цель состоит в сведении решения этой граничной задачи к решению соответствующей задачи Коши.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)