9. Невариационные принципы динамики

Обобщим результаты предыдущего параграфа, следуя тому пути, которым шел Якоби при обобщении теории Гамильтона. Важно иметь в виду, что наш подход здесь применяется к общему случаю, когда может и не существовать вариационного принципа, лежащего в основе уравнений (8.1) и (8.2).

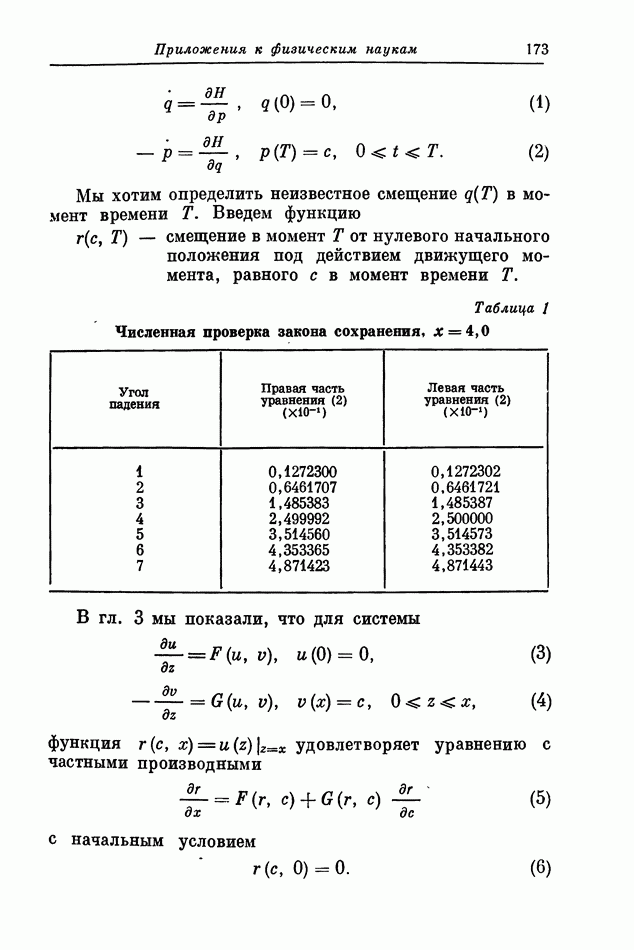
Рассмотрим для простоты систему уравнений движения

Раньше мы показали, что функции

удовлетворяют уравнениям с частными производными первого порядка

с начальными условиями

Следуя идеям Якоби, используем функции для определения решений Пусть

является решением уравнения (5) для произвольных значений параметра а, и пусть а) является решением уравнения (6), куда а входит через Тогда можно утверждать следующее: уравнения

образуют систему уравнений, неявно определяющую как функции от при этом удовлетворяют уравнениям (1) и (2).

Проверим справедливость этого утверждения. Продифференцировав (10) по , получим

откуда в силу (6) вытекает равенство

при условии, что Уравнение (13) является одним из нужных соотношений. Продифференцировав (11) по получим

или

откуда с учетом уравнения (5) получаем