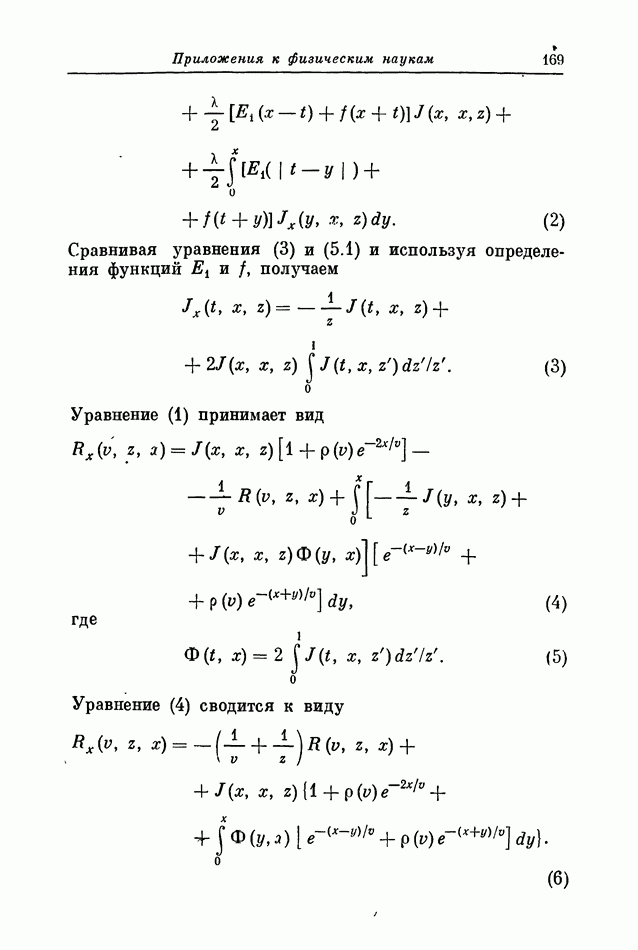| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)
1. Описание
В программе предполагается, что ядро  имеет вид, как в уравнении (2.2) из гл. 4, и
имеет вид, как в уравнении (2.2) из гл. 4, и  Пользователь должен написать подпрограмму KERNEL, вычисляющую функцию
Пользователь должен написать подпрограмму KERNEL, вычисляющую функцию  где
где  абсциссы квадратурной формулы Гаусса из интервала
абсциссы квадратурной формулы Гаусса из интервала  (порядок квадратурной формулы определяется пользователем),
(порядок квадратурной формулы определяется пользователем),  соответствующие весовые коэффициенты. Значения
соответствующие весовые коэффициенты. Значения  хранятся в массиве AKERN(I). Кроме того, пользователь должен написать подпрограмму ESUM1, которая вычисляет значения функции
хранятся в массиве AKERN(I). Кроме того, пользователь должен написать подпрограмму ESUM1, которая вычисляет значения функции  Параметром процедуры ESUM1 является текущее значение независимой переменной
Параметром процедуры ESUM1 является текущее значение независимой переменной  Результат вычислений хранится в ячейке E1SUM.
Результат вычислений хранится в ячейке E1SUM.
Обращение к программе имеет вид: CALL INTEQ (NQUAD, NIPTS, PTS, ALEN(K), TDEL, OUTPT, T, K, INDM1), при этом пользователь задает численные значения следующих параметров:
NQUAD - порядок квадратурной формулы, целое число от 3 до 15;
NIPTS - целое число от 1 до 76, указывающее число точек из интервала интегрирования, в которых требуется определить решение;
PTS - одномерный массив из 76 ячеек, в которых в порядке возрастания хранятся указанные точки;
ALEN(K) - действительная переменная, указывающая длину интервала интегрирования;
TDEL - действительная переменная, указывающая длину шага интегрирования (шаг интегрирования должен быть больше 0,001);
OUTPT - одномерный массив из 76 ячеек, в которых хранятся значения решения в заданных точках (элементы массива OUTPT находятся в однозначном соответствии с элементами PTS);
Т - одномерный массив дополнительной памяти из 12610 ячеек;
NTL - число интервалов интегрирования.
Пользователь должен помнить, что элементы массива  являются произведениями шага TDEL на целые числа.
являются произведениями шага TDEL на целые числа.
По окончании вычислений с заданным шагом TDEL длина шага автоматически уменьшается вдвое и задача решается еще раз для проверки точности решения, если переменной  присвоено некоторое целочисленное значение, отличное от нуля. В этом случае пользователь может получить результат из контрольного счета, заменив в основной программе вектор OUTPT на вектор
присвоено некоторое целочисленное значение, отличное от нуля. В этом случае пользователь может получить результат из контрольного счета, заменив в основной программе вектор OUTPT на вектор  Если пользователь хочет получить значения вспомогательных переменных
Если пользователь хочет получить значения вспомогательных переменных  или
или  он может обратиться к массиву
он может обратиться к массиву  где эти переменные расположены в следующем порядке:
где эти переменные расположены в следующем порядке:

Если требуется получить решение более, чем в 76 точках, то необходимо ввести в программу следующие изменения:
1. Увеличить длину массивов  и OUTPT до желаемой длины.
и OUTPT до желаемой длины.
2. Увеличить длину массива  от 12610 до
от 12610 до 
3. Увеличить длину массива  от (76, 15) до
от (76, 15) до  .
.
4. В подпрограммах  и
и  изменить длину массива
изменить длину массива  от 1310 до
от 1310 до 
2. Расположение и формат числового материала
Формат и расположение числового материала имеют следующий вид
Формат

В этой программе используется процедура «предсказание-уточнение» Адамса — Мултона четвертого порядка. При этом для получения начальной точки используется метод Рунге — Кутта четвертого порядка.
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф |
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
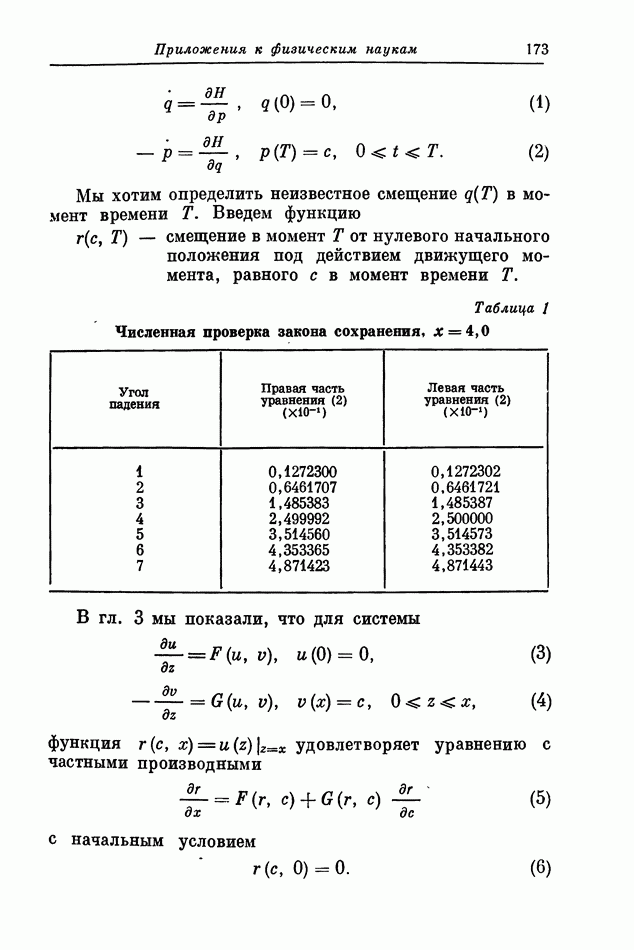
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)