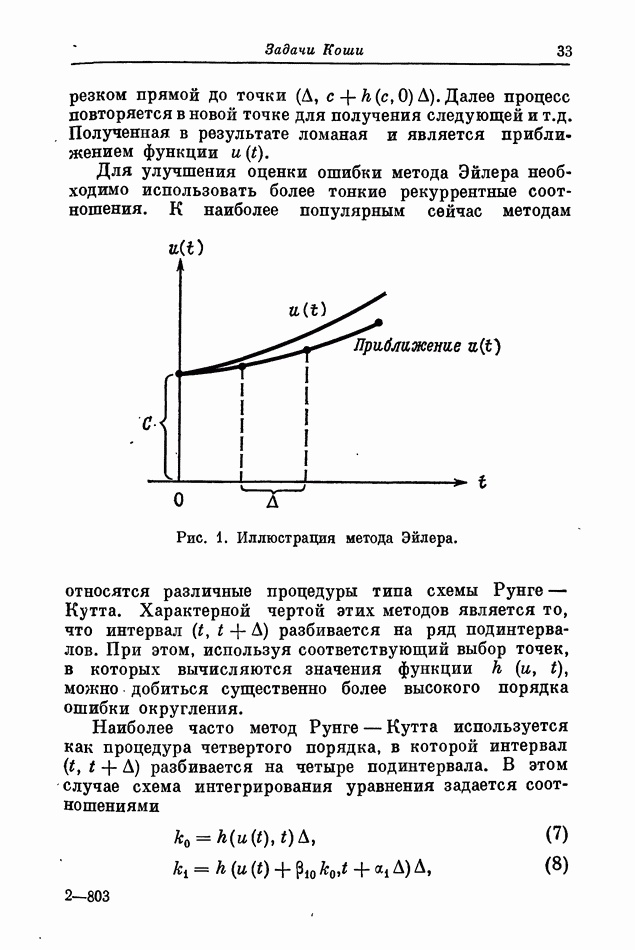
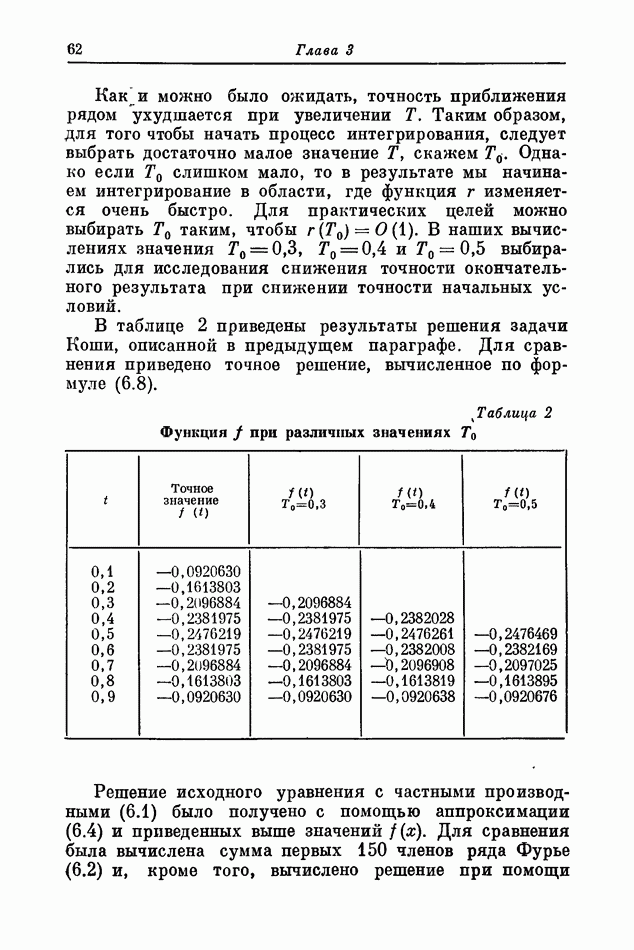
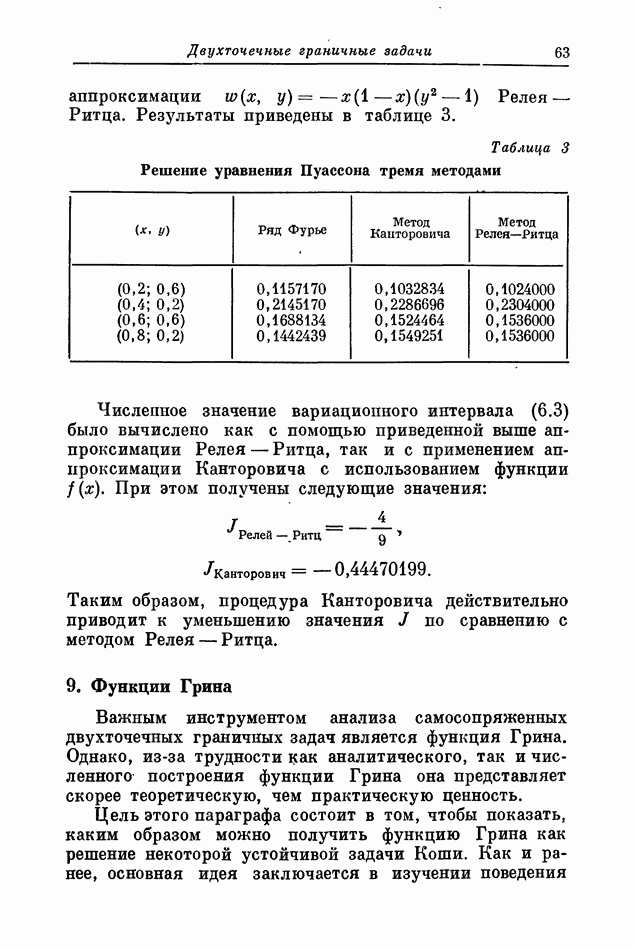
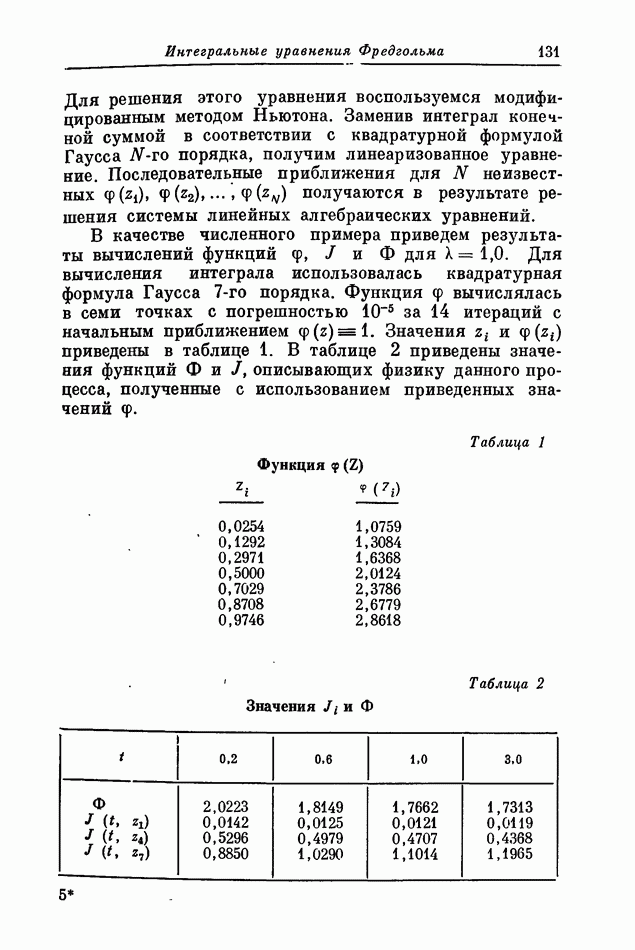
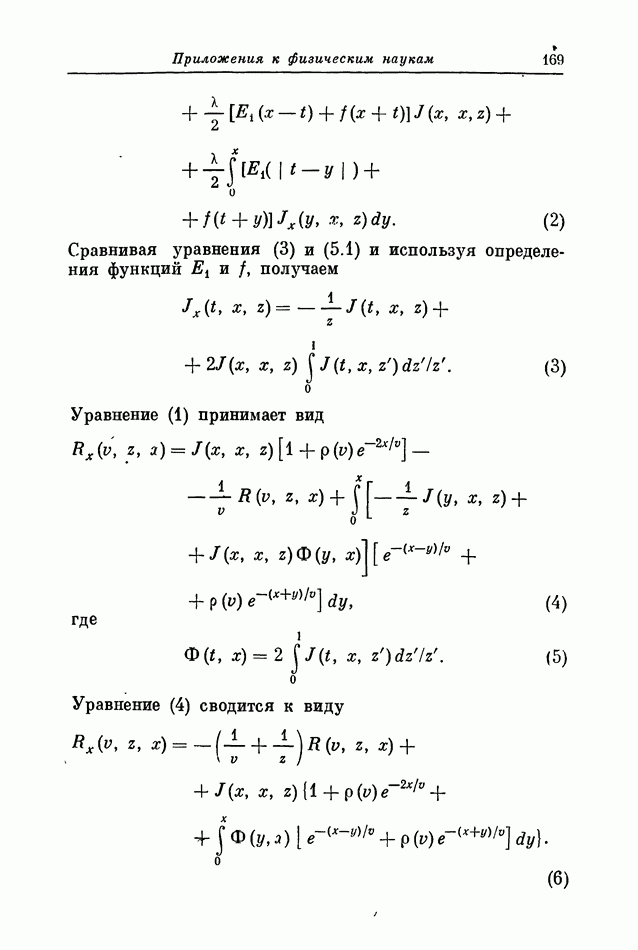| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
1. Введение
Учитывая, что теория инвариантного погружения с успехом справляется с двухточечными граничными задачами, и имея в виду тесную связь этих задач с интегральными уравнениями Фредгольма, попробуем теперь применить наши процедуры к различным типам линейных интегральных уравнений. Центральным объектом наших исследований будет интегральное уравнение типа уравнений в свертках

которое возникает в теории оптимальной фильтрации, химии полимеров, распространении излучения и многих других областях физики и техники.
Прежде всего мы покажем, что введением некоторого подходящего параметра погружения можно выразить решение уравнения (1) через дополнительную функцию Ф. При выводе формулы для представления функции и через Ф будут получены некоторые неклассические результаты, касающиеся резольвенты Фредгольма.
Далее будет описан один численный метод решения уравнения (1) с помощью уравнений погружения и приведен наглядный пример.
Затем будет изложено доказательство того, что введенная задача Коши действительно дает решение задачи (1). По ходу доказательства будет введено несколько новых функций, которые представляют интерес сами по себе.
Наконец, в завершение главы мы рассмотрим различные вопросы теории интегральных уравнений и ее связи
с теорией инвариантного погружения. Мы увидим, что собственные функции и собственные значения могут быть вычислены из уравнений погружения и что с помощью задачи Коши можно вычислить резольвенту Фредгольма. Тесная связь между идеей погружения и этими хорошо изученными областями классического анализа открывает путь для гораздо более глубокого понимания теории инвариантного погружения.
2. Основная задача
Чтобы упростить изложение основных идей насколько это возможно и тем не менее покрыть широкий класс нетривиальных и важных задач, пока ограничимся рассмотрением интегрального уравнения Фредгольма

где ядро к представимо в виде

Более того, будем предполагать, что функция  (такова, что уравнение (1) обладает единственным решением на интервале
(такова, что уравнение (1) обладает единственным решением на интервале  для всех непрерывных внешних воздействий
для всех непрерывных внешних воздействий 
3. Погружение
По аналогии с двухточечной граничной задачей постараемся погрузить уравнение (1) в семейство задач, для которого можно вывести соотношения, связывающие соседние члены этого семейства, и такое, что для него можно найти соответствующее «начальное условие».
4. Производящая функция
Для получения решения задачи (2.1) мы привлекаем одно из мощных средств анализа — производящую функцию. Мы постараемся получить некоторую функцию,
которую можно вычислить и через которую может быть выражено решение семейства интегральных уравнений.
Пусть функция  определяется интегральным уравнением
определяется интегральным уравнением

Определим, кроме того, функцию  формулой
формулой

Тогда мы утверждаем, что решение семейства интегральных уравнений

выражается формулой

Доказательство проводится очень просто. Продифференцировав обе части уравнения (3) по  получим
получим

Рассматривая уравнение (5) как интегральное уравнение относительно функции  видим, что его решением является
видим, что его решением является

Проинтегрировав это уравнение, приходим к уравнению

Для  можно записать
можно записать

Перемйожив уравнения (1) и (3) крест на крест, проинтегрировав полученное равенство  до
до  воспользовавшись симметрией ядра к, получаем
воспользовавшись симметрией ядра к, получаем

Таким образом, уравнение (8) принимает вид

Тогда уравнение (7) приводится к виду 

что и требовалось доказать.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА СЕРИИ
- ПРЕДИСЛОВИЕ
- Глава 1. КОНЕЧНО-РАЗНОСТНЫЕ УРАВНЕНИЯ
- 2. Задача «о разорении игрока»
- 3. Классическая формулировка
- 4. Подход на основе инвариантного погружения
- 5. Стандартный пример
- 6. Линейные разностные уравнения
- 7. Инвариантное погружение
- 8. Задача Коши
- 9. Неоднородный случай
- Замечания и литература
- Глава 2. ЗАДАЧИ КОШИ
- 2. Векторно-матричные обозначения
- 3. Существование и единственность
- 4. Численное решение задачи Коши
- 5. Устойчивость и анализ ошибок
- 6. Сравнение задачи Коши с двухточечной граничной задачей
- Глава 3. ДВУХТОЧЕЧНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Линейные двухточечные граничные задачи
- 3. Окончательный вид задачи Коши
- 4. Пример неустойчивой задачи
- 5. Многомерные системы
- 6. Уравнение Пуассона и численная неустойчивость
- 7. Другой вид задачи Коши
- 8. Численные результаты
- 9. Функции Грина
- 10. Задача Коши для определения функции Грина
- 11. Численный пример
- 12. Нелинейные двухточечные граничные задачи
- 13. Формулировка задачи Коши
- 14. Вычислительные методы
- 15. Обоснование задачи Коши
- Глава 4. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА
- 5. Уравнение Веллмана-Крейна
- 6. Вычисление функции Ф(t,x)
- 7. Задачи Коши для функции J
- 8. Первый способ вывода уравнения для X
- 9. Иной вывод уравнения для функции X
- 10. Окончательный вид задачи Коши
- 11. Процедура решения
- 12. Численные примеры
- 13. Доказательство адекватности задачи Коши
- 14. Общая схема доказательства
- 15. Дифференциальные уравнения для M и P
- 16. Частные производные функций J и W
- 17. Связь между W и J
- 18. Соотношения между P, Q, X и Y
- 19. Интегральные уравнения для J и Ф
- 20. Внешнее воздействие произвольного вида
- 21. Окончательный вид задачи Коши
- 22. Доказательство адекватности задачи Коши, II
- 23. Начальное условие для функции A
- 24. Обсуждение
- 25. Однородная задача
- 26. Продолжение за особые точки
- 27. Бесконечный интервал, I
- 28. Бесконечный интервал, II
- 29. Бесконечный интервал. Пример
- Глава 5. ВАРИАЦИОННЫЕ ЗАДАЧИ
- 2. Квадратичная вариационная задача
- 3. Задача Коши
- 4. Вычислительная схема
- 5. Простые примеры
- 6. Распространение и обобщение результатов
- 7. «Квазиквадратичные» задачи
- 8. Уравнения Эйлера и минимальность
- 9. Уравнение Беллмана — Гамильтона — Якоби
- 10. Задачи оптимального управления
- 14. Полное описание задачи Коши
- 15. Квадратичные задачи с линейными уравнениями движения
- 16. Задачи оптимального управления с ограничениями и принцип максимума Понтрягина
- 17. Построение задачи Коши
- 18. Замечания
- Глава 6. ПРИЛОЖЕНИЯ К ФИЗИЧЕСКИМ НАУКАМ
- 2. Функция источника
- 3. Задача Коши для J
- 4. Внешние и внутренние поля излучения
- 5. Отражающие поверхности
- 6. Отражение и преломление
- 7. Некоторые численные результаты
- 8. Аналитическая механика и уравнения Гамильтона
- 9. Невариационные принципы динамики
- 10. Еще раз о гармоническом осцилляторе
- 11. Равновесие тонкого стержня
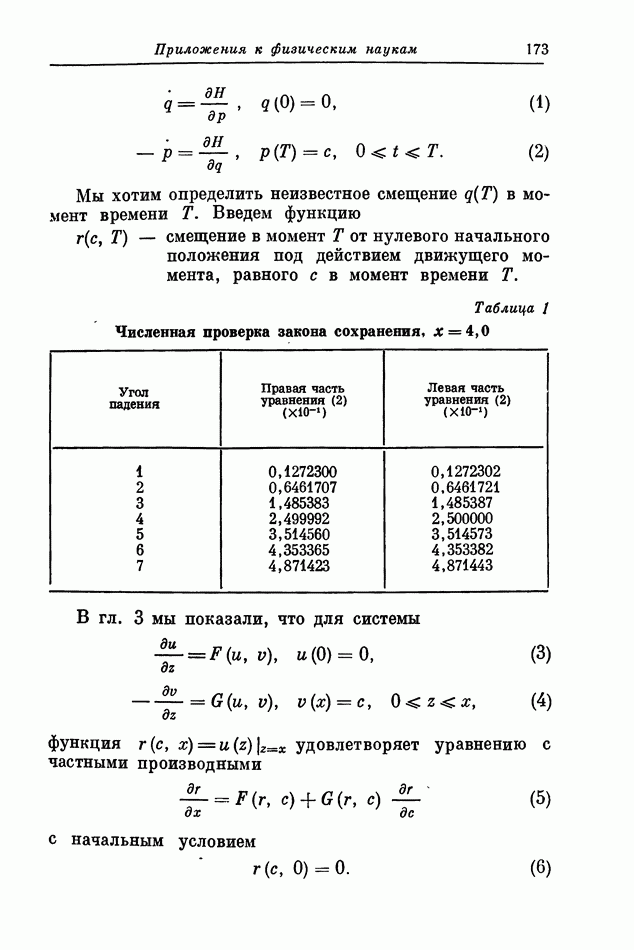
- 13. Оптимальное оценивание и фильтрация
- 14. Инвариантное погружение и фильтрация в реальном масштабе времени
- 15. Некоторые аспекты нелинейного сглаживания
- 16. Последовательное сглаживание
- 17. Линейные системы
- 18. Интегро-дифференциальные уравнения и нелокальное взаимодействие волн
- 19. Описание задачи Коши
- 20. Вывод задачи Коши
- Приложение А. ПРОГРАММА ДЛЯ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ЯДРАМИ ВИДА k(t,y) = k(|t-y|)