| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Частотные методы исследования устойчивости линейных управляемых систем
1. Преобразование характеристического определителя замкнутой управляемой системы.
Как показано в § 2 (2.10), характеристический определитель замкнутой управляемой системы имеет следующий вид:

Здесь  — характеристические определители звеньев управляемой системы, причем согласно (2.21) произведение этих определителей представляет собой определитель разомкнутой управляемой системы
— характеристические определители звеньев управляемой системы, причем согласно (2.21) произведение этих определителей представляет собой определитель разомкнутой управляемой системы

Таким образом, определитель замкнутой управляемой системы можно записать так:
 (3.1)
(3.1)
Согласно (2.7) и (2.8)
 (3.2)
(3.2)
то
 (3.3)
(3.3)
Матрица  является квадратной матрицей типа
является квадратной матрицей типа  и в соответствии с выражением (3) все элементы матрицы
и в соответствии с выражением (3) все элементы матрицы
 (3.4)
(3.4)
представляют собой дробно-рациональные функции от оператора дифференцирования D, у каждой из которых знаменатель равен  .
.
Матрица  имеет вид
имеет вид
 (3.5)
(3.5)
Определитель этой матрицы можно привести к следующему виду:
 (3.6)
(3.6)
где  — дробно-рациональная функция от
— дробно-рациональная функция от 
 (3.7)
(3.7)
а  - некоторый полином от D. Из выражений (6) и (1) следует, что
- некоторый полином от D. Из выражений (6) и (1) следует, что
 (3.8)
(3.8)
или согласно (7)
 (3.9)
(3.9)
Так как  - целая функция (поскольку она представляет собой определитель замкнутой управляемой системы), то очевидно, что
- целая функция (поскольку она представляет собой определитель замкнутой управляемой системы), то очевидно, что
 (3.10)
(3.10)
где  - некоторый полином от
- некоторый полином от  .
.
Таким образом,
 (3.11)
(3.11)
Выражение (8) теперь принимает вид
 (3.12)
(3.12)
Для того чтобы управляемая система была асимптотически устойчивой, необходимо, чтобы все нули полинома  были расположены в левой полуплоскости комплексного переменного
были расположены в левой полуплоскости комплексного переменного  .
.
Необходимые и достаточные условия, при которых эти требования выполняются, даются критерием Гурвитца [17, 21]. Большие возможности, однако, дает критерий Найквиста, который позволяет судить об устойчивости замкнутой управляемой системы по частотным характеристикам разомкнутой системы.
Частотной характеристикой разомкнутой управляемой системы называется функция

где  - матричная передаточная функция разомкнутой системы, которая определена в § 2 формулой (2.28).
- матричная передаточная функция разомкнутой системы, которая определена в § 2 формулой (2.28).
Так как, согласно (2.28)

где  и
и  - матричные передаточные функции звеньев системы, то
- матричные передаточные функции звеньев системы, то

и для построения частотной характеристики разомкнутой управляемой системы требуется лишь знание частотных характеристик ее звеньев. Последние же, если неизвестно аналитическое выражение функций  , могут быть определены экспериментально, как это показано ниже. Таким образом, основная ценность критерия Найквиста состоит в том, что он позволяет судить об устойчивости замкнутой управляемой системы не только по аналитическим, но и по экспериментальным характеристикам разомкнутой системы. Этот критерий, излагаемый ниже, был предложен Найквистом [13] для усилителей с обратной связью и применен А. В. Михайловым [65] и др. к регулируемым системам.
, могут быть определены экспериментально, как это показано ниже. Таким образом, основная ценность критерия Найквиста состоит в том, что он позволяет судить об устойчивости замкнутой управляемой системы не только по аналитическим, но и по экспериментальным характеристикам разомкнутой системы. Этот критерий, излагаемый ниже, был предложен Найквистом [13] для усилителей с обратной связью и применен А. В. Михайловым [65] и др. к регулируемым системам.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
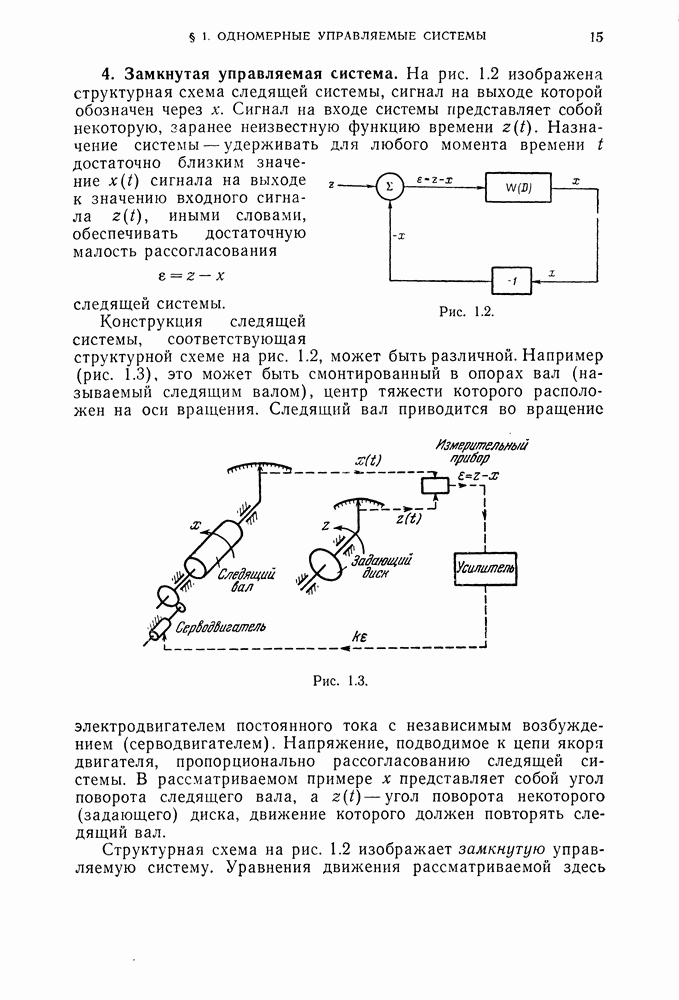
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
- 8. Логарифмические частотные характеристики.
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА