| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
Как указано выше, принцип максимума представляет собой необходимое условие оптимальности. Следовательно, принцип максимума позволяет выделить траектории, которые могут быть оптимальными.
Для линейных систем в задаче о быстродействии доказана [72] теорема существования оптимальной траектории и теорема об единственности траектории выделяемой принципом максимума. Таким образом, в этом случае принцип максимума однозначно определяет траекторию, которая может быть оптимальной; эта траектория и является единственной оптимальной траекторией, соединяющей две заданные в фазовом пространстве точки.
Для нелинейных систем (а также для линейных систем в задачах, отличных от задачи о быстродействии) вопрос о том, приводит ли синтез управления, осуществленный на основе принципа максимума, к оптимальным траекториям, решается полученной В. Г. Болтянским теоремой о достаточных условиях оптимальности. Эта теорема позволяет, как правило, утверждать, что синтез, осуществленный на основе принципа максимума, действительно приводит к оптимальным траекториям.
В теореме В. Г. Болтянского основным условием является осуществление регулярного синтеза для векторного дифференциального уравнения (20.1), описывающего управляемую систему. В связи с этим заметим, что условия А-Е (стр. 280) регулярного синтеза фактически не накладывают ограничений на систему, описываемую векторным дифференциальным уравнением (20.1), а постулируют те обычные обстоятельства, которые имеют место при осуществлении синтеза. В нижеследующей теореме доказано, что синтез, осуществленный на основе принципа максимума, при выполнении условий А-Е действительно приводит к оптимальным траекториям. В этом смысле принцип максимума является достаточным условием оптимальности.
Теорема В. Г. Болтянского. Если в множестве D осуществлен регулярный синтез для уравнения (20.1) (в предположении существования непрерывных производных и справедливости соотношения  , то все отмеченные траектории являются оптимальными (в области D). В этом смысле принцип максимума является достаточным условием оптимальности.
, то все отмеченные траектории являются оптимальными (в области D). В этом смысле принцип максимума является достаточным условием оптимальности.
Доказательство теоремы. Приведенное ниже доказательство дано в статье [14] В. Г. Болтянского в 1964 г. Ограничимся здесь случаем, когда в выражении (17.3) функция

что имеет место в задаче о быстродействии.
В этом случае функционал Q представляет собой время движения изображающей точки от точки  до точки
до точки  .
.
Обозначим через  время движения изображающей точки вдоль отмеченной траектории от точки
время движения изображающей точки вдоль отмеченной траектории от точки  до точки
до точки  .
.
Множество  обозначим через М.
обозначим через М.
Если доказать, что  является функцией Беллмана с особым множеством М, то доказываемая здесь теорема будет вытекать из теоремы, доказанной в § 15 на стр. 241.
является функцией Беллмана с особым множеством М, то доказываемая здесь теорема будет вытекать из теоремы, доказанной в § 15 на стр. 241.
Таким образом, достаточно доказать, что функция  , которая введена здесь, дифференцируема на множестве
, которая введена здесь, дифференцируема на множестве  и удовлетворяет уравнению Беллмана (15.7)
и удовлетворяет уравнению Беллмана (15.7)

Пусть х — произвольная точка, принадлежащая некоторой  -мерной клетке
-мерной клетке  , и пусть траектория системы (20.3)
, и пусть траектория системы (20.3)

которая исходит в момент времени U из указанной здесь точки  , проходит в момент времени
, проходит в момент времени  через точку
через точку  клетки
клетки  .
.
Из общих теорем о дифференцируемости решений дифференциальных уравнений по параметрам следует, что функции  и
и  — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от  .
.
Для рассмотренного в § 20 примера линейной системы явный вид функций  и
и  определен выражениями (20.42) и (20.43). В общем случае функции
определен выражениями (20.42) и (20.43). В общем случае функции  и
и  можно найти из решения векторного дифференциального уравнения, описывающего попятное движение
можно найти из решения векторного дифференциального уравнения, описывающего попятное движение

Решение уравнения (1) будет

где  . Уравнение
. Уравнение

однозначно разрешимо при  , близких к
, близких к  , так как соответствующий функциональный определитель отличен от нуля. (В рассмотренном в §20 примере уравнения попятного движения имеют вид (20.44), а упомянутый функциональный определитель имеет вид
, так как соответствующий функциональный определитель отличен от нуля. (В рассмотренном в §20 примере уравнения попятного движения имеют вид (20.44), а упомянутый функциональный определитель имеет вид  . Найденные из (3) функции
. Найденные из (3) функции  и
и  будут непрерывно дифференцируемыми по
будут непрерывно дифференцируемыми по  .
.
Из точки  траектория продолжается по клетке
траектория продолжается по клетке  или
или  . Аналогично устанавливается, что точка
. Аналогично устанавливается, что точка  в которой траектория покидает клетку
в которой траектория покидает клетку  или
или  , и время
, и время  движения по этой клетке — дифференцируемые функции от
движения по этой клетке — дифференцируемые функции от  следовательно, и от
следовательно, и от  .
.
Общее время  . движения по отмеченной траектории из точки
. движения по отмеченной траектории из точки  в точку
в точку  , таким образом, будет (внутри клетки
, таким образом, будет (внутри клетки  ) непрерывно дифференцируемой функцией точки
) непрерывно дифференцируемой функцией точки  .
.
Из изложенного следует, что функция  непрерывно дифференцируема на множестве
непрерывно дифференцируема на множестве  .
.
Теперь надо показать, что на множестве  М функция
М функция  удовлетворяет уравнению Веллмана (15.7).
удовлетворяет уравнению Веллмана (15.7).
Пусть  . Через
. Через  обозначим отмеченную траекторию, которая исходит в момент
обозначим отмеченную траекторию, которая исходит в момент  из точки
из точки  , а в момент
, а в момент  попадает в точку а.
попадает в точку а.
Через S обозначим множество, состоящее из всех точек  , удовлетворяющих условию
, удовлетворяющих условию

Вблизи точки  множество S представляет собой гладкую гиперповерхность в D с нормальным к ней вектором
множество S представляет собой гладкую гиперповерхность в D с нормальным к ней вектором

Функция  , где
, где  время движения по отмеченной траектории из точки
время движения по отмеченной траектории из точки  в точку а. Для всякой текущей точки
в точку а. Для всякой текущей точки  отмененной траектории функция
отмененной траектории функция  , откуда следует, что
, откуда следует, что  . Так как в соответствии с (20.3)
. Так как в соответствии с (20.3)

то

или

Из (5) следует, что

Согласно условию Д регулярного синтеза, отмеченная траектория удовлетворяет принципу максимума. Через

обозначим вектор-функцию, соответствующую траектории  в силу принципа максимума.
в силу принципа максимума.
Можно показать, что вектор  ортогонален гиперповерхности S в точке
ортогонален гиперповерхности S в точке  , то есть
, то есть

или, что то же,

В соответствии с (17.21) и (20.3) функция Н здесь имеет вид

Из (9), (8) и (4) следует, что

Так как согласно (17.27)

то из (10) и п.  теоремы 2 (стр. 255) следует, что
теоремы 2 (стр. 255) следует, что  . Из (7) следует, что
. Из (7) следует, что  , так как иначе было бы
, так как иначе было бы  . Таким образом,
. Таким образом,
 (21.11)
(21.11)
Из принципа максимума следует, что для любого 
 (21.12)
(21.12)
Из (12), (4), (8), (10) и (11) найдем, что для любого 

Из (13) вытекает соотношение
 (21.14)
(21.14)
которое совпадает с уравнением Беллмана (15.7), так как в качестве начальной точки  можно принять любую (принадлежащую множеству
можно принять любую (принадлежащую множеству  точку
точку  отмеченной траектории.
отмеченной траектории.
Таким образом, если выполнено условие (7), то функция  удовлетворяет на множестве
удовлетворяет на множестве  уравнению Беллмана (15.7).
уравнению Беллмана (15.7).
Для завершения доказательства теоремы надо еще показать справедливость соотношения (7)

Отмеченная траектория  исходит в момент времени
исходит в момент времени  из точки
из точки  , которая находится внутри клетки первого рода
, которая находится внутри клетки первого рода  .
.
Обозначим через  траекторию системы (20.3)
траекторию системы (20.3)

исходящую из некоторой внутренней точки  той же клетки
той же клетки  . Будем считать, что точка
. Будем считать, что точка  расположена достаточно близко от точки
расположена достаточно близко от точки  и при этом лежит на гиперповерхности S. Из последнего следует, что обе траектории
и при этом лежит на гиперповерхности S. Из последнего следует, что обе траектории  и
и  , выходящие в момент
, выходящие в момент  соответственно из точек
соответственно из точек  и
и  , приходят в точку а в один и тот же момент времени
, приходят в точку а в один и тот же момент времени  .
.
Обозначим через  расстояние между точками
расстояние между точками  и
и  и будем считать
и будем считать  достаточно малым.
достаточно малым.
Так как точки  и
и  лежат в одной и той же клетке
лежат в одной и той же клетке  то траектории
то траектории  и
и  придут в точку
придут в точку  , проходя по одной и той же последовательности клеток
, проходя по одной и той же последовательности клеток  , где
, где  — одномерная клетка, примыкающая к точке
— одномерная клетка, примыкающая к точке  .
.
Выше было показано, что моменты времени  перехода отмеченной траектории
перехода отмеченной траектории  из одной клетки в другую и соответствующие точки траектории
из одной клетки в другую и соответствующие точки траектории  дифференцируемым образом зависят от начальной точки
дифференцируемым образом зависят от начальной точки  .
.
Обозначим через  промежуток времени
промежуток времени

полагая при этом, что то  .
.
Из того, что  и
и  дифференцируемым образом зависят от точки
дифференцируемым образом зависят от точки  (а
(а  и
и  дифференцируемым образом зависят от точки
дифференцируемым образом зависят от точки  ), следует, что существует такая положительная константа С, что любой из промежутков времени
), следует, что существует такая положительная константа С, что любой из промежутков времени  не превосходит по модулю
не превосходит по модулю  , а траектории
, а траектории  и
и  находятся друг от друга на расстоянии порядка
находятся друг от друга на расстоянии порядка  :
:
 (21.15)
(21.15)
Выполним теперь некоторые преобразования. Как и выше, через  обозначим вектор-функцию, соответствующую в силу принципа максимума траектории
обозначим вектор-функцию, соответствующую в силу принципа максимума траектории  .
.
Так как  , то будем иметь
, то будем иметь

Таким образом,

где

Если обозначить через  некоторую точку отрезка, соединяющего точки
некоторую точку отрезка, соединяющего точки  и
и  , то на основании известной теоремы Лагранжа будем иметь следующее соотношение:
, то на основании известной теоремы Лагранжа будем иметь следующее соотношение:

Поэтому выражение (17) можно переписать так:
 (21.19)
(21.19)
Так как  и
и  представляют собой отмеченную траекторию и соответствующее ей управление, которые согласно условию Д регулярного синтеза удовлетворяют принципу максимума, то в силу соотношения (17.28)
представляют собой отмеченную траекторию и соответствующее ей управление, которые согласно условию Д регулярного синтеза удовлетворяют принципу максимума, то в силу соотношения (17.28)
 (21.20)
(21.20)
Из соотношений (19) и (20) следует, что
 (21.21)
(21.21)
где

Рассмотрим теперь следующие два случая. В первом случае точка  принадлежит одному из интервалов времени
принадлежит одному из интервалов времени  , в течение которого
, в течение которого  и
и  находятся в одной и той же клетке
находятся в одной и той же клетке  , на которой функция
, на которой функция  непрерывно дифференцируема. Учитывая (15) будем иметь оценку
непрерывно дифференцируема. Учитывая (15) будем иметь оценку
 (21.23)
(21.23)
Так как точка  расположена на отрезке, соединяющем точки
расположена на отрезке, соединяющем точки  , то в соответствии с (15) имеем
, то в соответствии с (15) имеем
 (21.24)
(21.24)
Так как функция непрерывна по своим аргументам, то при  разность
разность

будет бесконечно малой величиной порядка  и вместе с
и вместе с  будет стремиться к нулю.
будет стремиться к нулю.
Из (15) и (22) поэтому имеем 

Отсюда следует, что
 (21.26)
(21.26)
где  — начало интервала
— начало интервала  .
.
Во втором случае точка t принадлежит одному из интервалов времени  , в течение которого
, в течение которого  и
и  находятся в двух соседних клетках
находятся в двух соседних клетках  и
и  . Здесь уже нельзя утверждать, что разность (25) бесконечно мала вместе с
. Здесь уже нельзя утверждать, что разность (25) бесконечно мала вместе с  , так как точки
, так как точки  и
и  принадлежат разным клеткам, а при переходе от клетки к клетке управление
принадлежат разным клеткам, а при переходе от клетки к клетке управление  может терпеть разрывы.
может терпеть разрывы.
Однако разность (25) при всех t остается ограниченной в силу ограниченности траектории  . Поэтому в соответствии с (15)
. Поэтому в соответствии с (15)

Так как длина отрезка  не превосходит
не превосходит  (см. стр. 296), то
(см. стр. 296), то
 (21.27)
(21.27)
Складывая соотношения (26) и (27), получим
 (21.28)
(21.28)
Пусть теперь точка  приближается к точке
приближается к точке  по поверхности S, касаясь некоторого вектора
по поверхности S, касаясь некоторого вектора  . Тогда будем иметь
. Тогда будем иметь
 (21.29)
(21.29)
Согласно (16), (21) и (28) будем иметь
 (21.30)
(21.30)
При  траектория
траектория  , и обусловленная неравенством (20) разность
, и обусловленная неравенством (20) разность
 (21.31)
(21.31)
может быть представлена выражением, аналогичным (18). Повторяя рассуждения, при помощи которых получено соотношение (28), найдем, что
 (21.32)
(21.32)
откуда в соответствии с (30) получим, что для любого касательного гиперповерхности S в точке  вектора
вектора  будет иметь место соотношение
будет иметь место соотношение
 (21.33)
(21.33)
Из (33) вытекает соотношение (7), то есть рассматриваемая теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
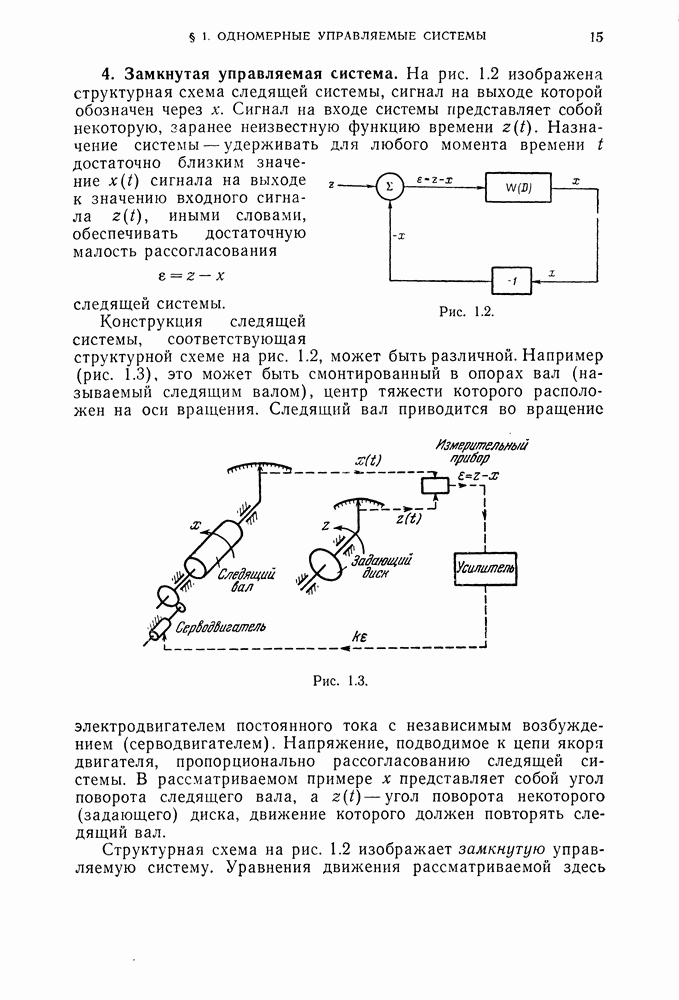
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
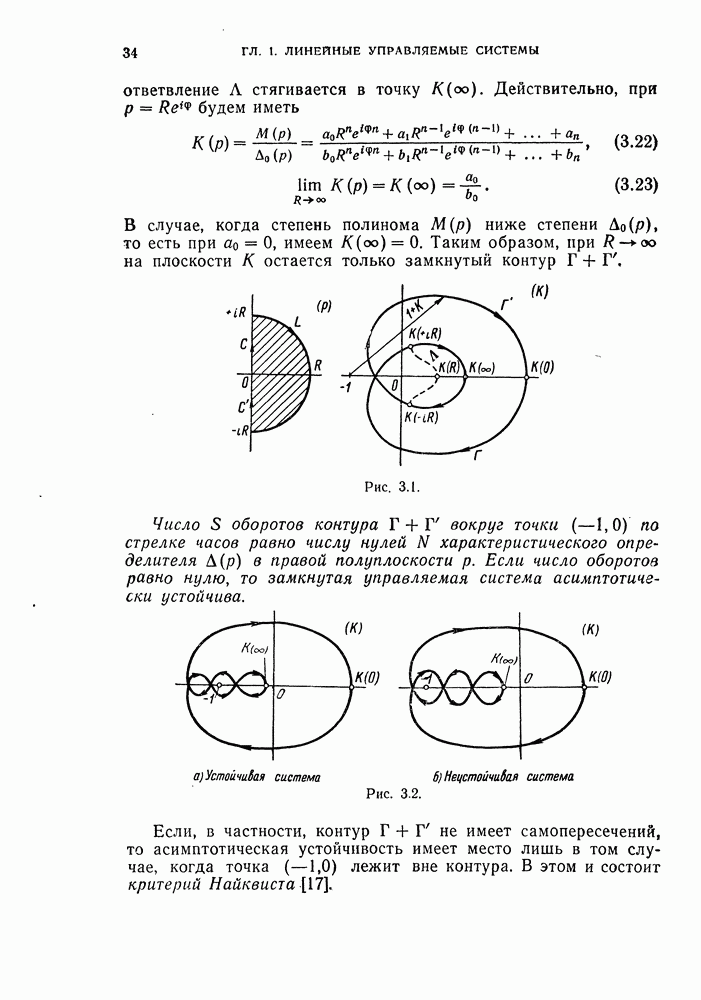
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
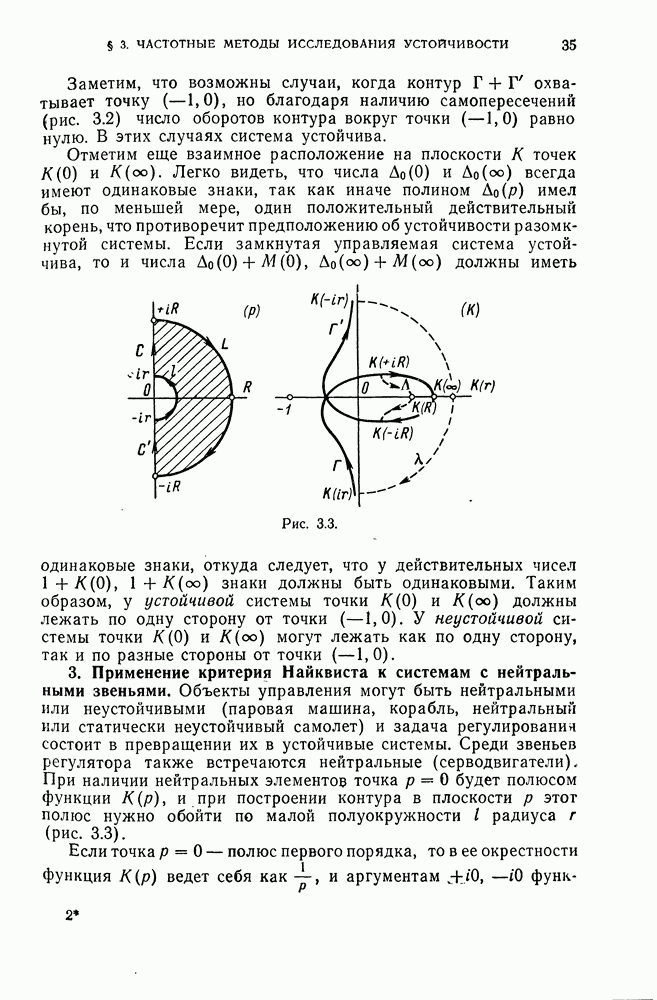
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
- 8. Логарифмические частотные характеристики.
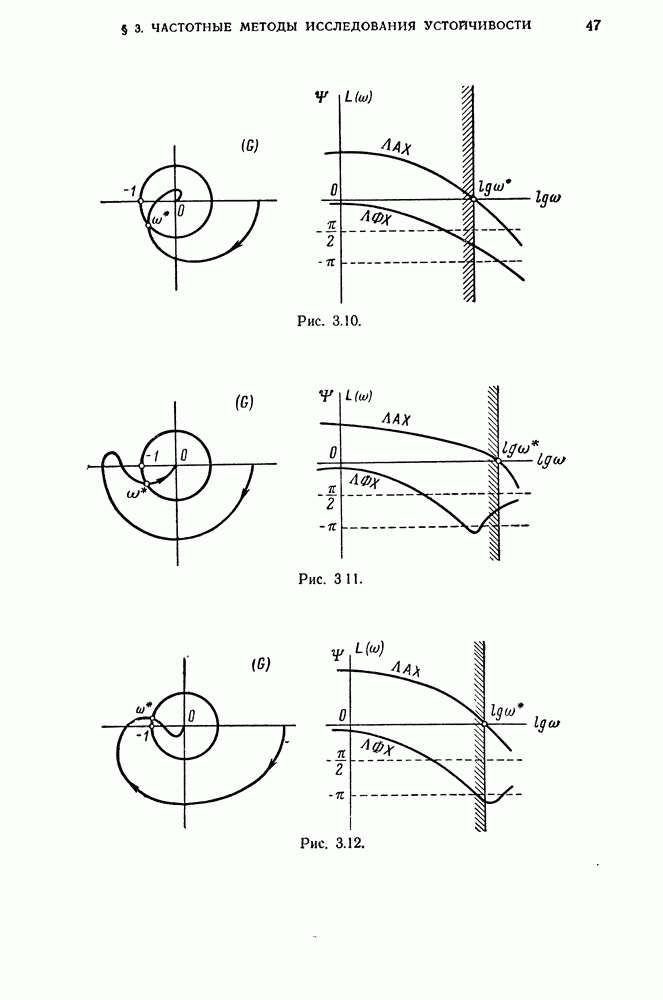
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА