| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
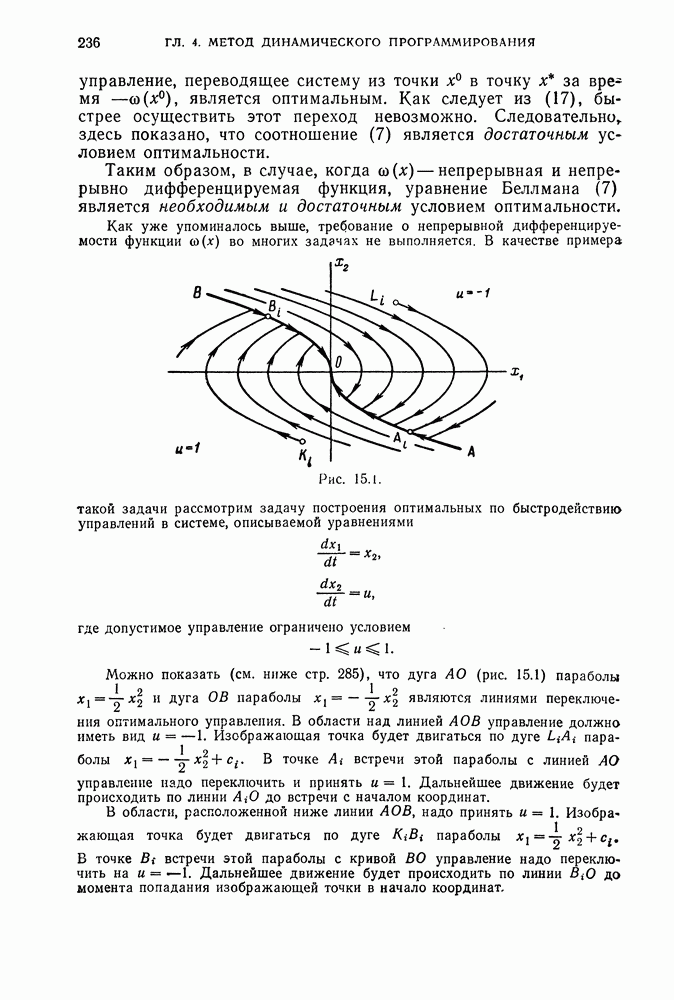
12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
Найдем решение системы линейных дифференциальных уравнений
 (10.118)
(10.118)
при начальных условиях
 (10.119)
(10.119)
Здесь  - некоторые постоянные (вообще комплексные) величины.
- некоторые постоянные (вообще комплексные) величины.
Введем матрицы
 (10.120)
(10.120)
Так как при дифференцировании (интегрировании) матриц дифференцируется (интегрируется) каждый элемент матрицы, то систему скалярных дифференциальных уравнений (118) можно заменить векторным дифференциальным уравнением
 (10.121)
(10.121)
Начальные условия (119) можно записать так:
 (10.122)
(10.122)
Искомый вектор  представим в виде ряда Маклорена по степеням
представим в виде ряда Маклорена по степеням  :
:
 (10.123)
(10.123)
Дифференцируя левую и правую части уравнения (121), найдем
 (10.124)
(10.124)
Соотношения (121) и (124) имеют место для любого значения аргумента t. При  они принимают вид
они принимают вид
 (10.125)
(10.125)
Ряд (123), таким образом, принимает вид
 (10.126)
(10.126)
то есть согласно (101)
 (10.127)
(10.127)
Так как
 (10.128)
(10.128)
то непосредственной подстановкой в дифференциальное уравнение (121) убеждаемся, что выражение (127) является решением этого уравнения, удовлетворяющим начальным условиям (122).
Так как из (127) следует, что

а согласно (116)

то можно преобразовать выражение (127) к виду
 (10.129)
(10.129)
Выражение (129) представляет собой решение векторного дифференциального уравнения (121), удовлетворяющее начальным условиям
 (10.130)
(10.130)
Обратимся теперь к выражению (71). Полагая
 (10.131)
(10.131)
будем иметь
 (10.132)
(10.132)
В соответствии с (71), (131) и (132) функция  может быть записана так:
может быть записана так:
 (10.133)
(10.133)
и решение (127) может быть приведено к форме, содержащей компоненты матрицы А.
Учитывая соотношение (133), нетрудно убедиться, что полученное применением функций от матриц решение системы дифференциальных уравнений (118) совпадает (как это и должно быть) с полученным в § 4 решением (4.124). (В § 4 рассмотрена система более общего вида.) Это соответствие в какой-то мере мотивирует принятое в теории матриц определение (45) функции от матрицы.
Рассмотрим теперь систему неоднородных линейных уравнений
 (10.134)
(10.134)
Систему скалярных дифференциальных уравнений (134) можно заменить векторным дифференциальным уравнением
 (10.135)
(10.135)
где через  обозначен вектор
обозначен вектор

Решение уравнения (135), удовлетворяющее начальным условиям (130) будем искать в виде
 (10.136)
(10.136)
где
 (10.137)
(10.137)
Элементы вектора  подлежат определению.
подлежат определению.
Подставляя выражение (136) в уравнение (135), получим

или
 (10.138)
(10.138)
Отсюда
 (10.139)
(10.139)
где С — вектор из произвольных постоянных
 (10.140)
(10.140)
Выражение (136) принимает теперь вид
 (10.141)
(10.141)
Из выражения (141) следует, что

откуда, учитывая начальные условия (130), получим
 (10.142)
(10.142)
Подставляя в (141) найденное значение С, найдем
 (10.143)
(10.143)
Это и есть решение векторного дифференциального уравнения (135) при начальных условиях (130).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
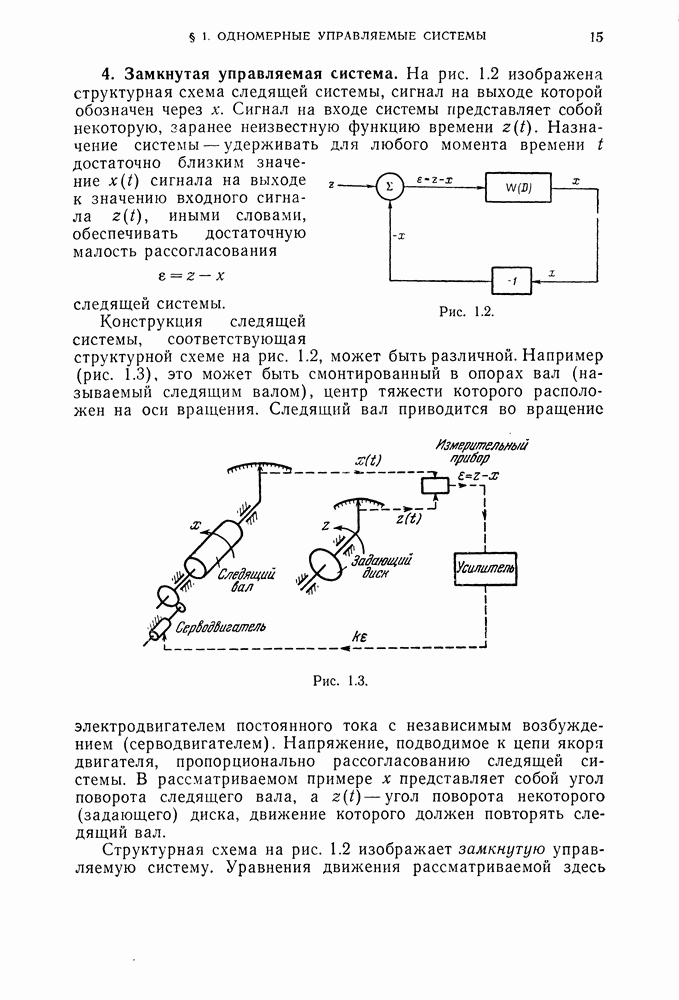
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
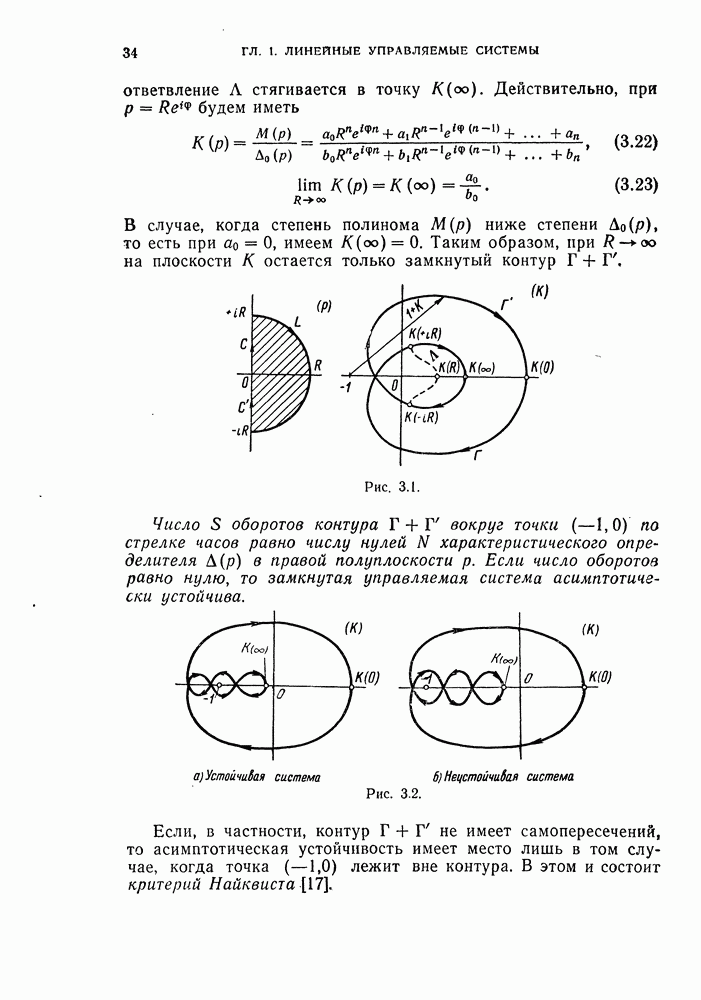
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
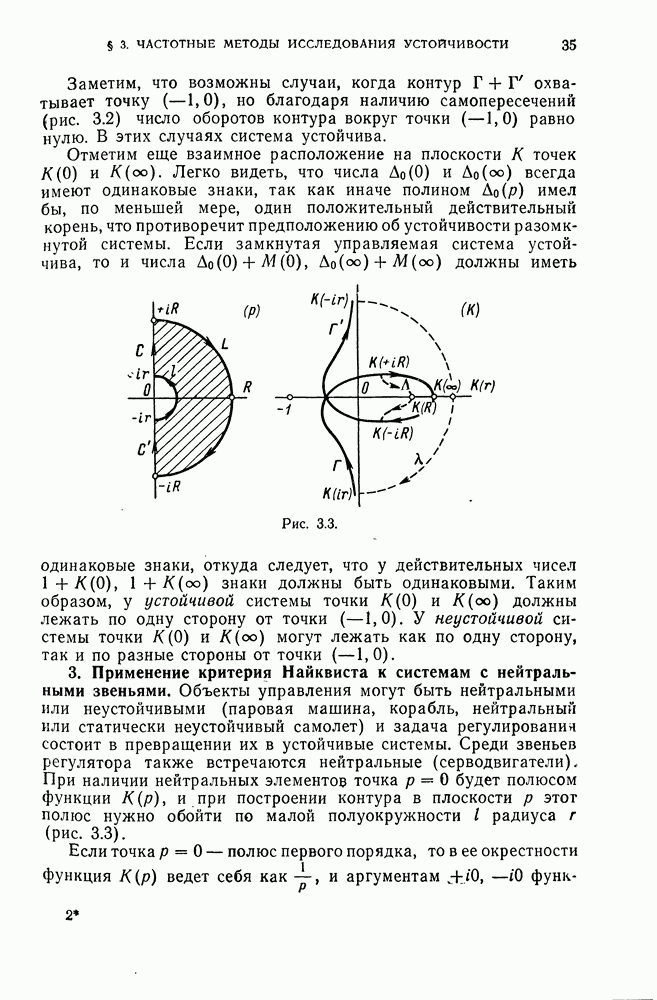
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
- 8. Логарифмические частотные характеристики.
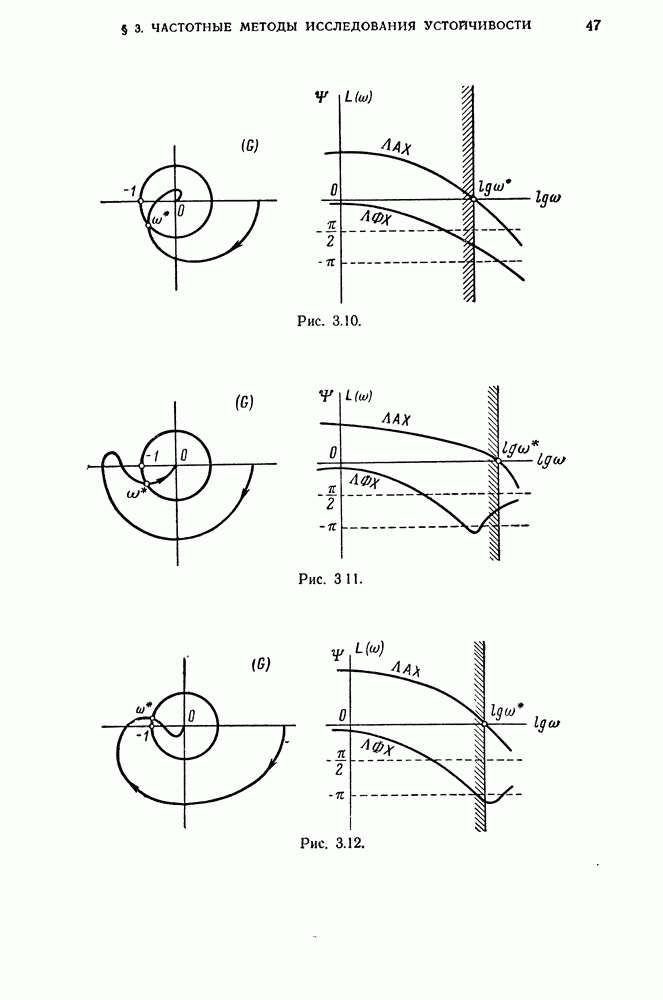
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА