| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Теорема В. Г. Болтянского для задачи о быстродействии.
Перейдем к отысканию достаточных условий отпимальности. Предложенный В. Г. Болтянским метод состоит в следующем. Функция  рассматривается теперь с иной точки зрения, чем выше, а именно в качестве исходного принимается соотношение (8). При помощи этого соотношения можно дать оценку времени перехода системы из любого начального состояния в заданное конечное состояние. При этом будем считать, что правые части дифференциальных уравнений (1) определены, непрерывны и имеют непрерывные производные
рассматривается теперь с иной точки зрения, чем выше, а именно в качестве исходного принимается соотношение (8). При помощи этого соотношения можно дать оценку времени перехода системы из любого начального состояния в заданное конечное состояние. При этом будем считать, что правые части дифференциальных уравнений (1) определены, непрерывны и имеют непрерывные производные  в любой точке
в любой точке  , когда
, когда  .
.
Лемма 1. Предположим, что на некотором открытом множестве D пространства X задана непрерывная и непрерывно дифференцируемая функция  , удовлетворяющая для всех
, удовлетворяющая для всех  неравенству вида (8)
неравенству вида (8)
 (15.13)
(15.13)
Тогда если  — допустимое (то есть
— допустимое (то есть  ) управление, переводящее изображающую точку из положения
) управление, переводящее изображающую точку из положения  в положение
в положение  , причем соответствующая траектория
, причем соответствующая траектория  расположена целиком в множестве D, то время
расположена целиком в множестве D, то время  перехода из точки
перехода из точки  в точку
в точку  оценивается неравенством
оценивается неравенством

Доказательство. Пусть  — точки, в которых управления
— точки, в которых управления  терпят разрыв, причем
терпят разрыв, причем

Обозначим еще

Точки разрыва управлений обязательно будут иметь место, если, например, ограничения (4), наложенные на управление, имеют вид

На каждом из интервалов  функция
функция  непрерывна.
непрерывна.
Согласно (8) и (1)
 (15.15)
(15.15)
Внутри каждого из интервалов времени  функция
функция  непрерывна и в соответствии с условием леммы имеет непрерывную производную по
непрерывна и в соответствии с условием леммы имеет непрерывную производную по  , удовлетворяющую неравенству (15)
, удовлетворяющую неравенству (15)

Отсюда следует, что

Складывая левые и правые части этих соотношений, написанных для интервалов  , получим
, получим

что совпадает с соотношением (14). Таким образом, лемма доказана.
Так как прибавление любой константы к функции  не изменяет соотношения (8), то можно принять, что функция
не изменяет соотношения (8), то можно принять, что функция  удовлетворяет условию
удовлетворяет условию
 (15.16)
(15.16)
При этом неравенство (14) примет вид
 (15.17)
(15.17)
Заметим теперь, что соотношение (7), представляющее собой уравнение Беллмана в задаче о быстродействии, было получено выше как необходимое условие оптимальности.
Здесь, при тех же предположениях о непрерывности и непрерывной дифференцируемости функции  и условии
и условии  , доказано, что если соотношение (8) имеет место, то управление, переводящее систему из точки
, доказано, что если соотношение (8) имеет место, то управление, переводящее систему из точки  в точку
в точку  за время
за время  , является оптимальным.
, является оптимальным.
Как следует из (17), быстрее осуществить этот переход невозможно. Следовательно, здесь показано, что соотношение (7) является достаточным условием оптимальности.
Таким образом, в случае, когда  - непрерывная и непрерывно дифференцируемая функция, уравнение Беллмана (7) является необходимым и достаточным условием оптимальности.
- непрерывная и непрерывно дифференцируемая функция, уравнение Беллмана (7) является необходимым и достаточным условием оптимальности.

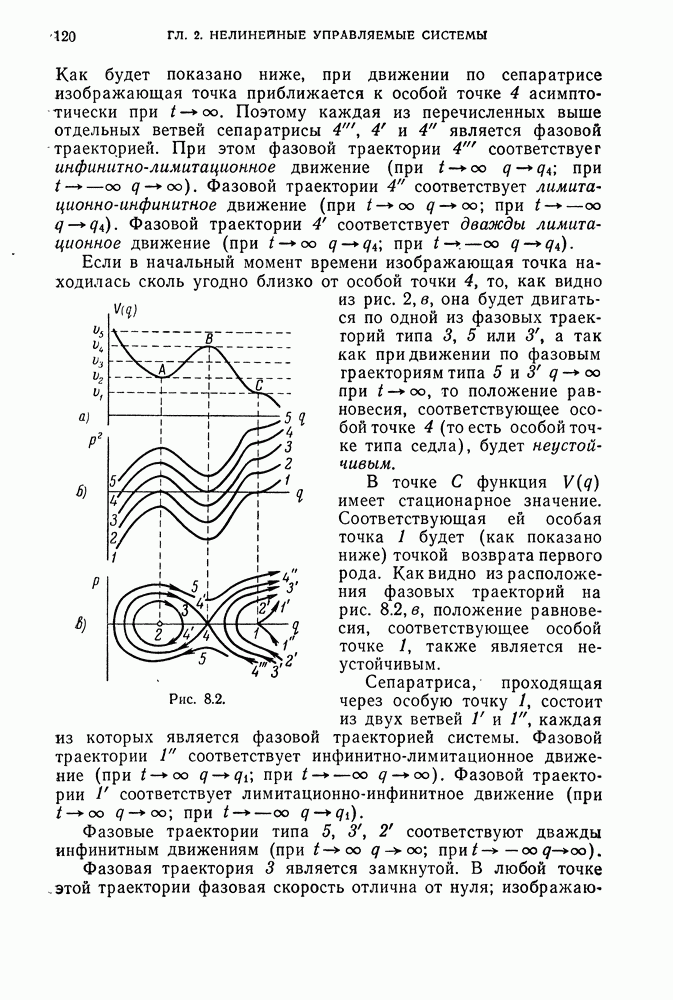
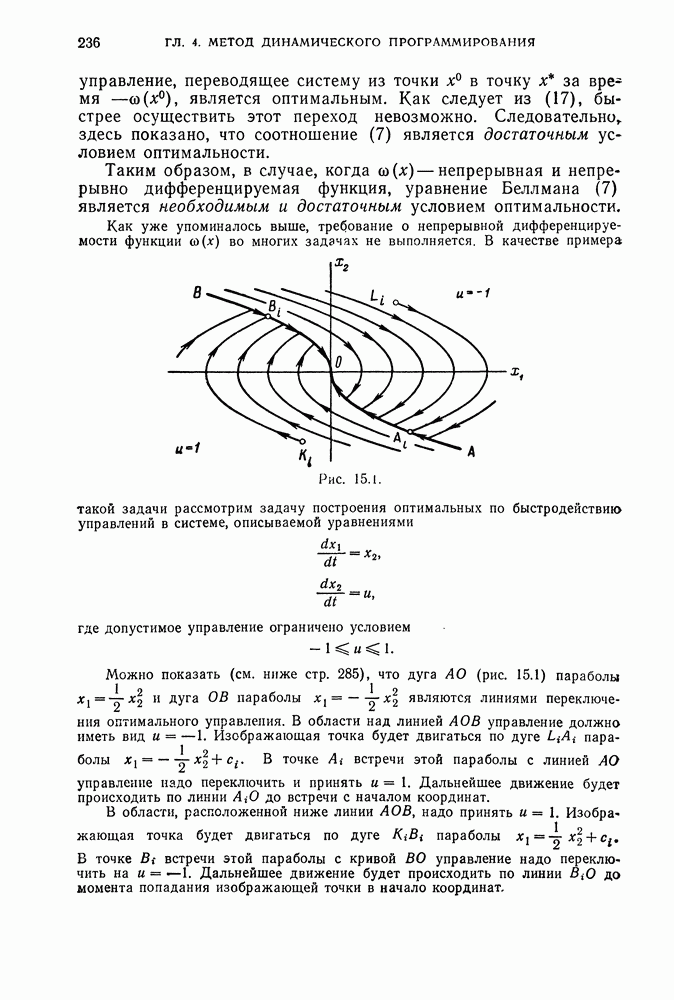
Рис. 15.1.
Как уже упоминалось выше, требование о непрерывной  функции
функции  во многих задачах не выполняется. В качестве примера такой задачи рассмотрим задачу построения оптимальных по быстродействию управлений в системе, описываемой уравнениями
во многих задачах не выполняется. В качестве примера такой задачи рассмотрим задачу построения оптимальных по быстродействию управлений в системе, описываемой уравнениями

где допустимое управление ограничено условием

Можно показать (см. ниже стр. 285), что дуга АО (рис. 15.1) параболы  и дуга OB параболы
и дуга OB параболы  являются линиями переключения оптимального управления. В области над линией АОВ управление должно иметь вид и
являются линиями переключения оптимального управления. В области над линией АОВ управление должно иметь вид и  . Изображающая точка будет двигаться по дуге
. Изображающая точка будет двигаться по дуге  параболы
параболы  . В точке
. В точке  встречи этой параболы с линией АО управление надо переключить и принять и
встречи этой параболы с линией АО управление надо переключить и принять и  . Дальнейшее движение будет происходить по линии
. Дальнейшее движение будет происходить по линии  до встречи с началом координат.
до встречи с началом координат.
В области, расположенной ниже линии АОВ, надо принять и  . Изображающая точка будет двигаться по дуге
. Изображающая точка будет двигаться по дуге  параболы
параболы  .
.
В точке  встречи этой параболы с кривой ВО управление надо переключить на и
встречи этой параболы с кривой ВО управление надо переключить на и  . Дальнейшее движение будет происходить по линии
. Дальнейшее движение будет происходить по линии  до момента попадания изображающей точки в начало координат.
до момента попадания изображающей точки в начало координат.
Траектория  и аналогично траектория
и аналогично траектория  будут оптимальными по быстродействию траекториями для начальных положений изображающей точки, расположенных на линии и
будут оптимальными по быстродействию траекториями для начальных положений изображающей точки, расположенных на линии и  соответственно.
соответственно.
Ниже (стр. 288) показано, что функция  непрерывна во всей фазовой плоскости
непрерывна во всей фазовой плоскости  . Частные производные
. Частные производные  и
и  существуют во всех точках фазовой плоскости
существуют во всех точках фазовой плоскости  , за исключением точек линии переключения АОВ. Ни в одной из точек линии переключения АО В частные производные
, за исключением точек линии переключения АОВ. Ни в одной из точек линии переключения АО В частные производные  и
и  не существуют.
не существуют.
Предположим теперь в общем случае, что в множестве D, на котором задана функция  , выделено некоторое множество М ("осободе множество" функции
, выделено некоторое множество М ("осободе множество" функции  ) и что функция
) и что функция  непрерывна на всем множестве D, а непрерывные частные производные
непрерывна на всем множестве D, а непрерывные частные производные  имеет лишь в тех точках множества D, которые не принадлежат М.
имеет лишь в тех точках множества D, которые не принадлежат М.
Лемма 2. Пусть D — открытое множество фазового пространства X и М — некоторое множество, содержащееся в D. Предположим, что на множестве D задана непрерывная функция  , которая в точках, не принадлежащих множеству М, имеет непрерывные частные производные и удовлетворяет неравенству (8)
, которая в точках, не принадлежащих множеству М, имеет непрерывные частные производные и удовлетворяет неравенству (8)

Пусть, далее,  — допустимое управление, переводящее изображающую точку из положения
— допустимое управление, переводящее изображающую точку из положения  в положение
в положение  причем соответствующая траектория
причем соответствующая траектория  расположена целиком в D и пересекается с множеством М лишь в конечное число моментов времени. Тогда оценка (14)
расположена целиком в D и пересекается с множеством М лишь в конечное число моментов времени. Тогда оценка (14)

остается справедливой.
Доказательство  . Заметим, что оценка (14) остается справедливой, если траектория
. Заметим, что оценка (14) остается справедливой, если траектория  пересекается с множеством М лишь в моменты времени
пересекается с множеством М лишь в моменты времени  или в один из этих моментов. Действительно, в этом случае полностью проходит доказательство леммы 1, поскольку функция
или в один из этих моментов. Действительно, в этом случае полностью проходит доказательство леммы 1, поскольку функция  по-прежнему непрерывна, а когда t заключено внутри интервалов
по-прежнему непрерывна, а когда t заключено внутри интервалов  (границы которых суть моменты времени, в которых управления
(границы которых суть моменты времени, в которых управления  терпят разрыв), точка
терпят разрыв), точка  лежит вне множества М и, следовательно, на этих интервалах производные
лежит вне множества М и, следовательно, на этих интервалах производные  существуют и непрерывны.
существуют и непрерывны.
 . Пусть теперь
. Пусть теперь  — все принадлежащие интервалу
— все принадлежащие интервалу  моменты встречи траектории
моменты встречи траектории  с множеством
с множеством  причем
причем  . Обозначим еще
. Обозначим еще

К каждому из отрезков  применимо сделанное выше
применимо сделанное выше  замечание, и потому
замечание, и потому

Складывая левые и правые части этих соотношений, написанных для отрезков времени  , получим соотношение
, получим соотношение

которое совпадает с требуемым в условии леммы неравенством (14). Таким образом, лемма доказана.
Отметим теперь, что ситуация, которая имеет место в задаче о быстродействии (см. пример на рис. 15.1), не охватывается условиями леммы 2.
Действительно, в этом примере (рис. 15.1, 15.2) не отдельные точки, а дуга оптимальной траектории расположена на линии переключения АОВ, то есть по терминологии леммы 2 целый участок оптимальной траектории расположен в множестве М. По условию леммы 2 допускается пересечение оптимальной траектории с множеством М лишь в конечное число моментов времени. Здесь же оптимальная траектория в течение некоторого промежутка времени находится в множестве М.
Выход из создавшейся трудности дается в приведенной ниже лемме 3.

Рис. 15.2.
Лемма 3. Сохраним предположения о функции  , сделанные в лемме 2. Пусть
, сделанные в лемме 2. Пусть  — допустимое управление, переводящее изображающую точку из положения
— допустимое управление, переводящее изображающую точку из положения  в положение
в положение  , причем соответствующая траектория
, причем соответствующая траектория  расположена целиком в D. Предположим еще, что как угодно близко к
расположена целиком в D. Предположим еще, что как угодно близко к  найдется такая точка
найдется такая точка  , что траектория
, что траектория  , исходящая из точки
, исходящая из точки  и соответствующая тому же управлению
и соответствующая тому же управлению  , пересекается с М лишь в конечное число моментов времени. Тогда оценка (14)
, пересекается с М лишь в конечное число моментов времени. Тогда оценка (14)

остается справедливой.
Доказательство. Выберем произвольное число  , и пусть
, и пусть  и
и  (рис. 15.2) — такие окрестности точек
(рис. 15.2) — такие окрестности точек  и
и  соответственно, что
соответственно, что

Согласно теореме  зависимости решений дифференциальных уравнений от начальных условий, существует такая окрестность
зависимости решений дифференциальных уравнений от начальных условий, существует такая окрестность  точки
точки  , что всякое решение системы уравнений, аналогичной системе (1) (с тем же управлением
, что всякое решение системы уравнений, аналогичной системе (1) (с тем же управлением  )
)
 (15.19)
(15.19)
для которого  определено на всем отрезке
определено на всем отрезке  и удовлетворяет соотношению
и удовлетворяет соотношению  .
.
По условию доказываемой леммы указанное решение  системы (19) с начальными данными
системы (19) с начальными данными  , пересекается с М лишь в конечном числе точек. Из этого вытекает в силу леммы 2, что имеет место неравенство
, пересекается с М лишь в конечном числе точек. Из этого вытекает в силу леммы 2, что имеет место неравенство
 (15.20)
(15.20)
Далее, так как у  то
то  Следовательно, в соответствии с (18) имеем
Следовательно, в соответствии с (18) имеем
 (15.21)
(15.21)
Из соотношений (21) следует, что
 (15.22)
(15.22)
Складывая левые и правые части неравенств (20) и (22), получим
 (15.23)
(15.23)
Отсюда в виду произвольности  вытекает неравенство (14).
вытекает неравенство (14).
Лемма 3 дает наиболее общие условия, при выполнении которых оценка (14) справедлива. Однако условия леммы 3 сформулированы отдельно для каждого управления  . Остается еще показать справедливость этих условий для всевозможных управлений
. Остается еще показать справедливость этих условий для всевозможных управлений  .
.
В. Г. Болтянским в цитированных выше работах показано, что при наложении некоторых условий на множество М сформулированные в лемме 3 условия выполняются для любых допустимых управлений  .
.
В частности, это .имеет место, если М — кусочно-гладкое множество размерности  .
.
Приведем определение кусочно-гладкого множества [15]. Пусть К — некоторый ограниченный  -мерный выпуклый многогранник
-мерный выпуклый многогранник  , расположенный в векторном пространстве
, расположенный в векторном пространстве  переменных и рассматриваемый вместе с границей (то есть замкнутый). Предположим, что в некотором открытом множестве пространства
переменных и рассматриваемый вместе с границей (то есть замкнутый). Предположим, что в некотором открытом множестве пространства  , содержащем многогранник К, заданы
, содержащем многогранник К, заданы  непрерывно дифференцируемых функций
непрерывно дифференцируемых функций
 (15.24)
(15.24)
обладающих тем свойством, что функциональная матрица

имеет в каждой точке  ранг s. Функции (24) осуществляют гладкое отображение
ранг s. Функции (24) осуществляют гладкое отображение  многогранника К в пространстве X по формулам
многогранника К в пространстве X по формулам
 (15.25)
(15.25)
Если это отображение взаимно однозначно (то есть различные точки многогранника К переводит в различные точки пространства X), то образ  многогранника К называется криволинейным
многогранника К называется криволинейным  -мерным многогранником в пространстве X. Очевидно, что криволинейный многогранник является замкнутым и ограниченным множеством пространства
-мерным многогранником в пространстве X. Очевидно, что криволинейный многогранник является замкнутым и ограниченным множеством пространства  .
.
Пусть теперь D — некоторое открытое множество фазового пространства X. Всякое множество Май, представляющееся в виде объединения конечного или бесконечного числа криволинейных многогранников, расположенных таким образом, что с каждым замкнутым ограниченным множеством, лежащим в D, пересекается лишь конечное число этих многогранников, называется кусочно-гладким множеством в D. (К границе множества D многогранники могут скапливаться.)
Если среди криволинейных многогранников, объединением которых является кусочно-гладкое множество М, имеется хотя бы один многогранник размерности k, а все остальные многогранники имеют размерность, меньшую или равную k, то кусочно-гладкое множество называется  -мерным. В частности, всякая замкнутая в D гладкая поверхность размерности, меньшей чем
-мерным. В частности, всякая замкнутая в D гладкая поверхность размерности, меньшей чем  , является кусочно-гладким множеством в D (ибо ее можно разбить на криволинейные многогранники). Из изложенного следует, что кусочно-гладкое в D множество размерности, меньшей чем
, является кусочно-гладким множеством в D (ибо ее можно разбить на криволинейные многогранники). Из изложенного следует, что кусочно-гладкое в D множество размерности, меньшей чем  , не содержит внутренних точек.
, не содержит внутренних точек.
В качестве примера укажем, что при  кусочно-гладкими множествами размерности <2 являются линии, состоящие из отдельных дифференцируемых кусков (например, линия АОВ на рис. 15.1).
кусочно-гладкими множествами размерности <2 являются линии, состоящие из отдельных дифференцируемых кусков (например, линия АОВ на рис. 15.1).
Следующую лемму приведем без доказательства. Доказательство этой леммы требует привлечения ряда понятий теории гладких многообразий и дано в цитированных работах В. Г. Болтянского [15].
Лемма 4. Пусть М — кусочно-гладкое в D множество размерности  . Пусть далее
. Пусть далее  - допустимое управление, переводящее изображающую точку из положения
- допустимое управление, переводящее изображающую точку из положения  в положение
в положение  , причем соответствующая траектория
, причем соответствующая траектория  расположена целиком в множестве D.
расположена целиком в множестве D.
Тогда в любой окрестности  точки
точки  найдется такая точка
найдется такая точка  , что траектория
, что траектория  , исходящая из точки
, исходящая из точки  и соответствующая управлению
и соответствующая управлению  , целиком расположена в D и пересекается с М лишь в конечном числе точек, то есть существует лишь конечное число моментов времени
, целиком расположена в D и пересекается с М лишь в конечном числе точек, то есть существует лишь конечное число моментов времени  для которых
для которых  .
.
Из леммы 4 и леммы 3 вытекает непосредственно справедливость следующей основной леммы.
Основная лемма. Пусть М — кусочно-глад кое множество размерности  расположенное в открытом множестве D фазового пространства X. Предположим, что на множестве D задана непрерывная функция
расположенное в открытом множестве D фазового пространства X. Предположим, что на множестве D задана непрерывная функция  , которая в точках, не принадлежащих множеству М, имеет непрерывные производные и удовлетворяет неравенству (8):
, которая в точках, не принадлежащих множеству М, имеет непрерывные производные и удовлетворяет неравенству (8):

Тогда если  - допустимое управление, переводящее изображающую точку из положения
- допустимое управление, переводящее изображающую точку из положения  в положение
в положение  , причем соответствующая траектория
, причем соответствующая траектория  расположена целиком в множестве D, то для времени перехода справедлива оценка (14)
расположена целиком в множестве D, то для времени перехода справедлива оценка (14)

Изложенные выше результаты приводят к следующей  , представляющей собой необходимое и достаточное условие оптимальности в форме метода динамического программирования.
, представляющей собой необходимое и достаточное условие оптимальности в форме метода динамического программирования.
Теорема В. Г. Болтянского. Пусть М — кусочно-гладкое множество размерности  , расположенное в фазовом пространстве X, и
, расположенное в фазовом пространстве X, и  — непрерывная функция, заданная на X и имеющая в точках, не принадлежащих множеству М, непрерывные производные. Пусть, далее,
— непрерывная функция, заданная на X и имеющая в точках, не принадлежащих множеству М, непрерывные производные. Пусть, далее,  для некоторой точки
для некоторой точки  . Предположим, что для каждой отличной от
. Предположим, что для каждой отличной от  точки
точки  существует допустимое управление
существует допустимое управление  , переводящее изображающую точку из положения
, переводящее изображающую точку из положения  в положение
в положение  за время
за время  .
.
Для того чтобы все  управления
управления  были оптимальными, необходимо и достаточно, чтобы во всех точках не принадлежащих множеству М, функция
были оптимальными, необходимо и достаточно, чтобы во всех точках не принадлежащих множеству М, функция  удовлетворяла уравнению Беллмана (7)
удовлетворяла уравнению Беллмана (7)

или, что то же самое, неравенству (8)

Доказательство. Необходимость приведенного в теореме условия доказывается так же, как и на стр. 235. Приведенное там доказательство применимо ко всякой точке  , в которой производные
, в которой производные  существуют и непрерывны.
существуют и непрерывны.
Достаточность вытекает из основной леммы. Действительно, из основной леммы следует, что если соотношение (8) удовлетворяется во всех точках  , не принадлежащих множеству М, а, кроме того,
, не принадлежащих множеству М, а, кроме того,  , то управление, приводящее систему из точки
, то управление, приводящее систему из точки  в точку
в точку  за время
за время  , будет оптимальным. При
, будет оптимальным. При  оценка времени перевода системы из точки
оценка времени перевода системы из точки  в точку
в точку  при любом допустимом управлении будет
при любом допустимом управлении будет

то есть быстрее чем за время  осуществить этот перевод невозможно.
осуществить этот перевод невозможно.
В доказанной теореме требования о непрерывной  функции
функции  столь серьезно ослаблены, что теорема применима к весьма большому кругу задач. Это и позволяет ее считать обоснованием метода динамического программирования.
столь серьезно ослаблены, что теорема применима к весьма большому кругу задач. Это и позволяет ее считать обоснованием метода динамического программирования.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
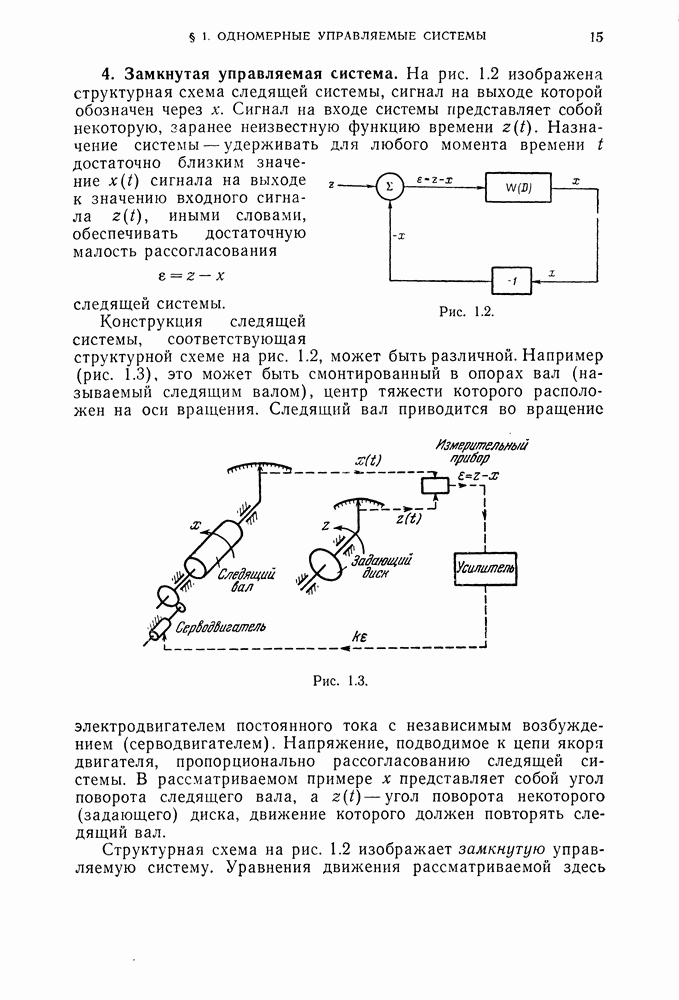
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
- 8. Логарифмические частотные характеристики.
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА