| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11. Управляемость и наблюдаемость линейных систем
1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
Рассмотрим систему, описываемую векторным дифференциальным уравнением

где

Через  здесь обозначены переменные, определяющие состояние системы:
здесь обозначены переменные, определяющие состояние системы:  - приложенные к системе управляющие силы, называемые также «управлениями». Элементы матриц А и G предполагаются здесь постоянными.
- приложенные к системе управляющие силы, называемые также «управлениями». Элементы матриц А и G предполагаются здесь постоянными.
Векторное дифференциальное уравнение (1) эквивалентно системе скалярных дифференциальных уравнений

Уравнения (3) являются линейными дифференциальными уравнениями с постоянными коэффициентами, и их можно интерпретировать, например, как уравнения в вариациях относительно установившегося движения (или относительно состояния равновесия) некоторой системы материальных точек. Пусть  число степеней свободы этой системы, а
число степеней свободы этой системы, а  — ее обобщенные координаты. Ранг системы уравнений (3) при этом будет
— ее обобщенные координаты. Ранг системы уравнений (3) при этом будет

Переменные  в уравнениях (3) могут быть фазовыми координатами или каноническими переменными (обобщенными координатами и обобщенными импульсами) рассматриваемой системы материальных точек или быть связанными с ними при помощи некоторого линейного преобразования.
в уравнениях (3) могут быть фазовыми координатами или каноническими переменными (обобщенными координатами и обобщенными импульсами) рассматриваемой системы материальных точек или быть связанными с ними при помощи некоторого линейного преобразования.
Так как у системы материальных точек число приложенных обобщенных сил не может превышать числа степеней свободы, то число г управляющих сил  в дифференциальных уравнениях (3) должно удовлетворять условию
в дифференциальных уравнениях (3) должно удовлетворять условию

Заметим еще, что те из уравнений системы (3), которые выражают лишь зависимость между переменными  папример уравнения вида
папример уравнения вида

в случае, когда  — фазовые координаты системы, требуют выполнения тождеств
— фазовые координаты системы, требуют выполнения тождеств

для чего необходимо, чтобы соответствующие строки матрицы G состояли из нулевых элементов

Обычно управляемая система имеет, однако, более сложную структуру. В ее состав входят еще устройства для формирования управляющих сигналов и др. При этом в число уравнений (3) могут входить также дифференциальные уравнения, описывающие программы включенных в состав системы вычислительных управляющих устройств и т. п. Эти уравнения могут содержать и свои управляющие воздействия. В этом случае будет иметь место соотношение  , где под s здесь подразумевается число степеней свободы лишь совокупности механических звеньев, входящих в систему (3), а также может оказаться, что
, где под s здесь подразумевается число степеней свободы лишь совокупности механических звеньев, входящих в систему (3), а также может оказаться, что  .
.
Рассмотрим сейчас вопрос о том, можно ли систему, описываемую уравнением (1), перевести из любого заданного начального состояния в любое желаемое состояние за конечный промежуток времени, выбирая надлежащим образом закон изменения управляющих сил  .
.
Сформулированное здесь свойство получило название управляемости. Системы, обладающие этим свойством, называются вполне управляемыми.
Так как управляемость системы определяется строением матриц А и G, то понятие управляемости относят также к этим матрицам, говоря, что пара  вполне управляема, или соответственно неуправляема.
вполне управляема, или соответственно неуправляема.
Перейдем к решению поставленной задачи. Согласно (10.143) закон движения системы, описываемой уравнением (1), будет следующим:

Предположим, что существует такой закон изменения управляющих сил  , который обеспечивает приведение системы к моменту времени
, который обеспечивает приведение системы к моменту времени  в начало координат, то есть обеспечивает выполнение условия
в начало координат, то есть обеспечивает выполнение условия

Так как согласно (7)

то в соответствии с (8) будем иметь следующее соотношение:
 (11.10)
(11.10)
Умножая левую и правую части соотношения (10) на  получим
получим
 (11.11)
(11.11)
Согласно (10.58)
 (11.12)
(11.12)
где  — степень минимального полинома
— степень минимального полинома  матрицы А, а
матрицы А, а  — коэффициенты интерполяционного полинома Лагранжа— Сильвестра
— коэффициенты интерполяционного полинома Лагранжа— Сильвестра  , построенного для функции
, построенного для функции  , которая определена на спектре матрицы А.
, которая определена на спектре матрицы А.
Соотношение (11) можно, учитывая выражение (12), переписать так:
 (11.13)
(11.13)
или
 (11.14)
(11.14)
Каждое из слагаемых в левой части соотношения (14) является вектором типа  .
.
Левую часть соотношения (14) можно представить в виде произведения двух матриц и переписать соотношение (14) так:
 (11.15)
(11.15)
Так как  есть матрица типа
есть матрица типа  , то матрица
, то матрица
 (11.16)
(11.16)
является коагулированной (блочной) матрицей типа  .
.
Сделаем сейчас следующее замечание. Согласно (10.29) минимальный полином матрицы А имеет вид

или

Так как  является аннулирующим полиномом для матрицы А, то есть
является аннулирующим полиномом для матрицы А, то есть

то будем иметь

Отсюда следует, что

то есть матрица  является линейной комбинацией матриц
является линейной комбинацией матриц  .
.
Так как  и степени матриц коммутативны при умножении, то приходим к следующему результату.
и степени матриц коммутативны при умножении, то приходим к следующему результату.
Если степень минимального полинома матрицы А равна m, то матрица  является линейной комбинацией матриц
является линейной комбинацией матриц  :
:

Обратимся теперь к матрице (16). Так как матрица  , где
, где  матрица типа
матрица типа  , может быть представлена в виде
, может быть представлена в виде

то у расширенной матрицы

образующейся прибавлением к матрице  элементов
элементов  , ранг остается таким же,
, ранг остается таким же,  и у матрицы
и у матрицы  .
.
Подставляя в (16) вместо  соответствующие матрицы, получим матрицу типа
соответствующие матрицы, получим матрицу типа  , где
, где
 (11.17)
(11.17)
элементы которой являются скалярами
 (11.18)
(11.18)
Матрица
 (11.19)
(11.19)
представляет собой матрицу-столбец (вектор) типа  и является коагулированной матрицей, так как каждый ее элемент есть
и является коагулированной матрицей, так как каждый ее элемент есть  -мерный вектор, поскольку согласно (2)
-мерный вектор, поскольку согласно (2)

Обозначая

можно представить матрицу (19) так:

то есть в виде  -мерного вектора
-мерного вектора  , элементы которого
, элементы которого  являются скалярами.
являются скалярами.
Векторное уравнение (15), таким образом, принимает вид
 (11.22)
(11.22)
где W и U определены выражениями (18) и (21), Уравнение (22) эквивалентно следующей системе скалярных уравнений:
 (11.23)
(11.23)
Далее будем считать, что число управлений  выбрано так, что выполняется условие
выбрано так, что выполняется условие
 (11.24)
(11.24)
Здесь, как указано выше,  — степень минимального полинома
— степень минимального полинома  матрицы А (причем
матрицы А (причем  , а r — размерность вектора управлений u.
, а r — размерность вектора управлений u.
Если обозначить через  векторы-столбцы матрицы (18)
векторы-столбцы матрицы (18)

то систему скалярных уравнений (23) можно заменить следующим векторным уравнением:
 (11.26)
(11.26)
где  и
и 
 -мерные векторы, а
-мерные векторы, а  — скаляры, причем согласно (24)
— скаляры, причем согласно (24)  . Таким образом, вектор
. Таким образом, вектор  представляет собой линейную комбинацию векторов
представляет собой линейную комбинацию векторов  .
.
Так как в качестве  может быть выбран любой вектор
может быть выбран любой вектор  -мерного пространства
-мерного пространства  то из соотношения (26) следует, что для того, чтобы система (1) была вполне управляемой, необходимо и достаточно, чтобы среди векторов
то из соотношения (26) следует, что для того, чтобы система (1) была вполне управляемой, необходимо и достаточно, чтобы среди векторов  имелось
имелось  линейно-независимых векторов.
линейно-независимых векторов.
Иными словами, условие управляемости [36] системы (1) состоит в том, что ранг матрицы (16)

долокен быть равен  .
.
Система значений  удовлетворяющая уравнениям (23), в случае, когда
удовлетворяющая уравнениям (23), в случае, когда  будет не единственной. При выборе решения уравнений (23) необходимо еще учитывать зависимости, которые накладывают на
будет не единственной. При выборе решения уравнений (23) необходимо еще учитывать зависимости, которые накладывают на  формулы (20). (Так, например, как видно из (20), у
формулы (20). (Так, например, как видно из (20), у  и
и  подынтегральные функции содержат один и тот же множитель
подынтегральные функции содержат один и тот же множитель  и т. д.)
и т. д.)
Определив значения  надо из соотношений (20) найти закон управления
надо из соотношений (20) найти закон управления  . Последняя задача также допускает не единственное решение.
. Последняя задача также допускает не единственное решение.
Указанные обстоятельства открывают возможность наложения дополнительных условий, обеспечивающих тот или иной характер движения системы — каких-либо условий оптимальности и т. п.
Покажем, что одним из возможных управлений  например, управление
например, управление

где

а символом  обозначена транспонированная матрица.
обозначена транспонированная матрица.
Проверим, что  приводит систему (1) к моменту времени Г в начало координат. Для этого подставим
приводит систему (1) к моменту времени Г в начало координат. Для этого подставим  в левую часть соотношения (11)
в левую часть соотношения (11)

Таким образом, соотношение (11) удовлетворяется, откуда в соответствии с (9) следует, что  .
.
Здесь мы предполагали, что матрица  существует. В п. 6 будет доказано, что если система управляема, то R является положительно-определенной матрицей, и, следовательно, обратная матрица
существует. В п. 6 будет доказано, что если система управляема, то R является положительно-определенной матрицей, и, следовательно, обратная матрица  существует.
существует.
Пример. Рассмотрим систему, описываемую скалярным дифференциальным уравнением

Здесь управление  принимает вид
принимает вид

Левая часть соотношения (11) теперь будет

то есть соотношение (11) удовлетворяется, и согласно (9) будем иметь  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
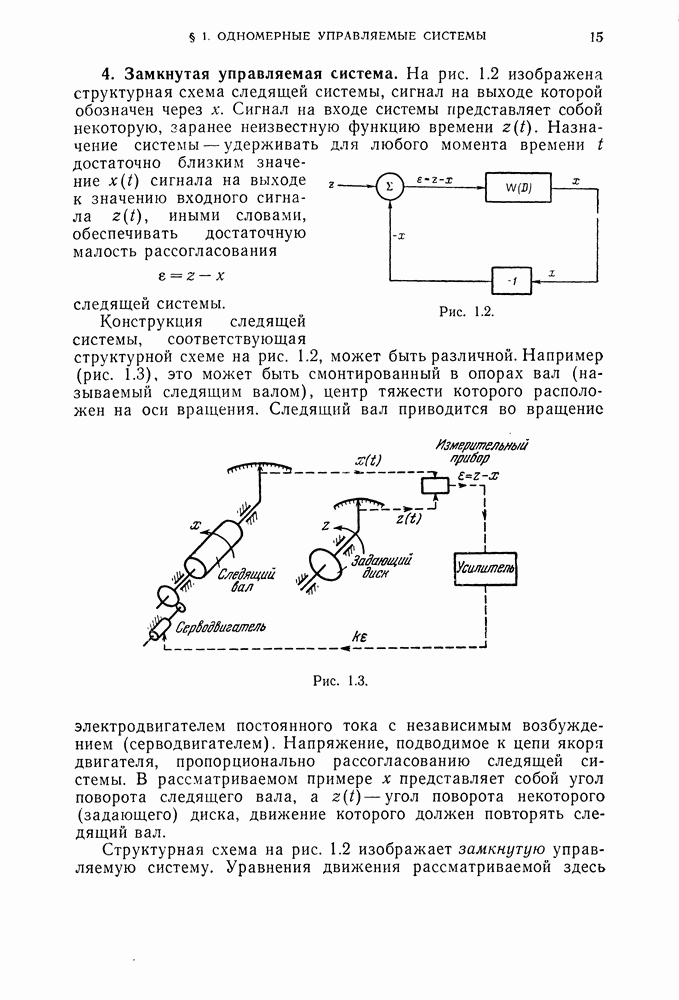
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
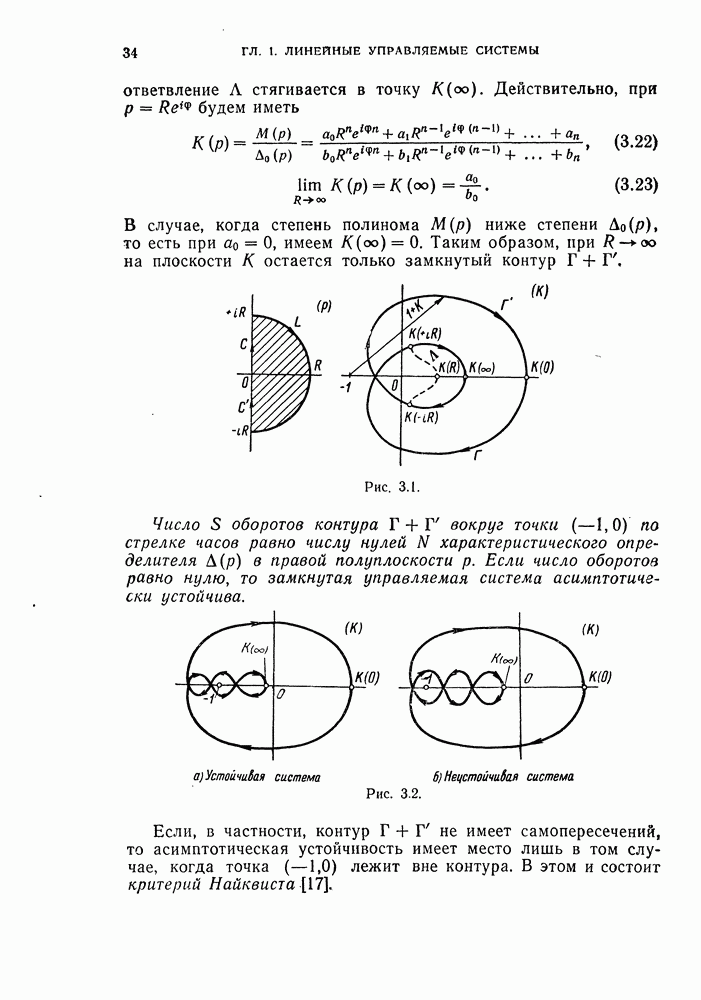
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
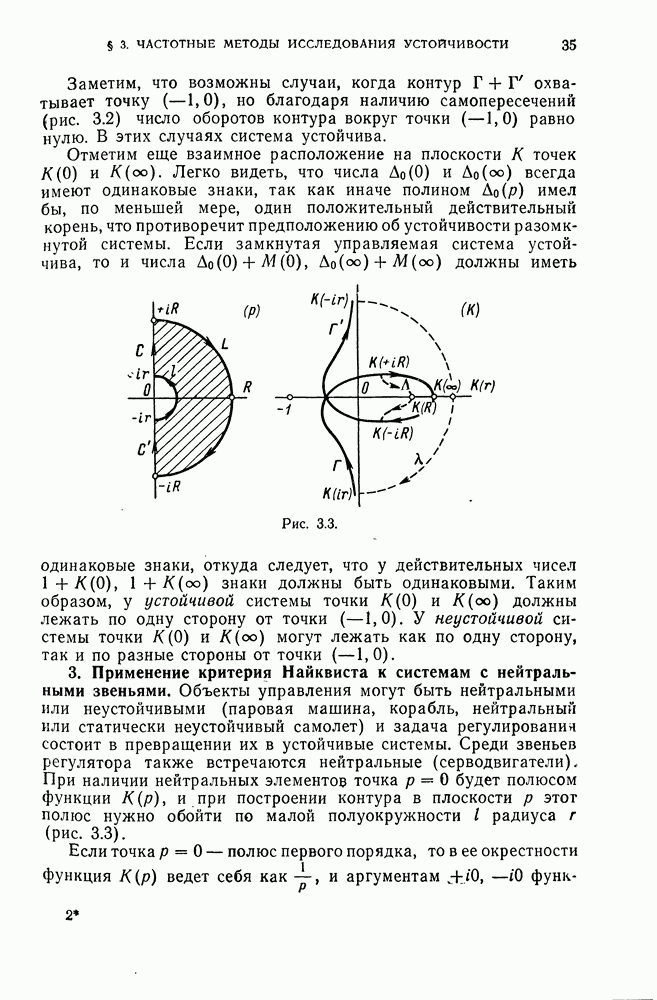
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
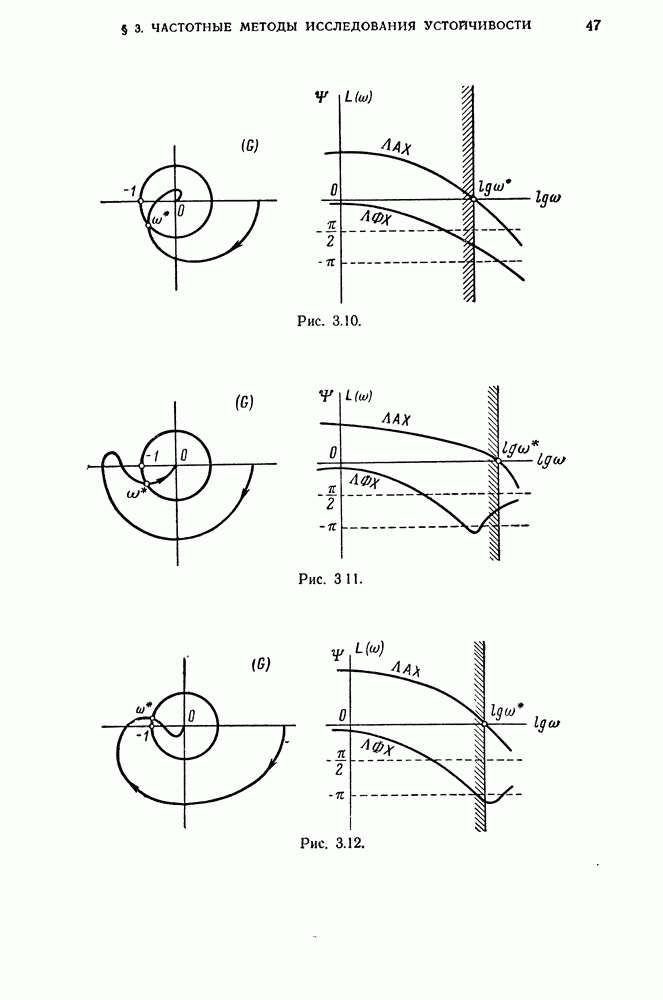
- 8. Логарифмические частотные характеристики.
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА