| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 20. Понятие регулярного синтеза в теории оптимальных систем
Понятие регулярного синтеза, введенное В. Г. Болтянским [14], для системы, описываемой дифференциальными уравнениями (17.1)

или эквивалентным векторным уравнением

где  , для которых теперь предполагается непрерывность производных
, для которых теперь предполагается непрерывность производных

состоит в следующем.
Предположим, что заданы кусочно-гладкое (см. § 15, стр. 240) множество N размерности  , кусочно-гладкие множества
, кусочно-гладкие множества

и функция  , определенная в D и принимающая значения в
, определенная в D и принимающая значения в  .
.
Множества (2) и функция  осуществляют регулярный синтез для уравнения (1) в области D, если выполнены следующие условия, сформулированные В. Г. Болтянским.
осуществляют регулярный синтез для уравнения (1) в области D, если выполнены следующие условия, сформулированные В. Г. Болтянским. 
А. Множество  содержит точку а
содержит точку а  и не имеет предельных точек в открытом множестве D. Каждая компонента множества
и не имеет предельных точек в открытом множестве D. Каждая компонента множества  представляет собой
представляет собой  -мерное гладкое многообразие в
-мерное гладкое многообразие в  эти компоненты называются
эти компоненты называются  -мерными клетками. Точки множества
-мерными клетками. Точки множества  называются нульмерными клетками. Функция
называются нульмерными клетками. Функция  непрерывна и непрерывно дифференцируема на каждой клетке и может быть продолжена в непрерывно дифференцируемую функцию на окрестности клетки.
непрерывна и непрерывно дифференцируема на каждой клетке и может быть продолжена в непрерывно дифференцируемую функцию на окрестности клетки.
Б. Все клетки распределены на клетки первого и второго рода. Все  -мерные клетки являются клетками первого рода, все нульмерные — клетками второго рода.
-мерные клетки являются клетками первого рода, все нульмерные — клетками второго рода.
В. Если  — некоторая
— некоторая  -мерная клетка первого рода, то через каждую точку этой клетки проходит единственная траектория уравнения
-мерная клетка первого рода, то через каждую точку этой клетки проходит единственная траектория уравнения

(проходящая по клетке  ). Существует такая
). Существует такая  -мерная клетка
-мерная клетка  , что каждая траектория системы (3), идущая в клетне
, что каждая траектория системы (3), идущая в клетне  , через конечное время покидает клетку
, через конечное время покидает клетку  , упираясь под нулевым углом в клетку
, упираясь под нулевым углом в клетку  и подходя к ней с ненулевой фазовой скоростью.
и подходя к ней с ненулевой фазовой скоростью.
Если  — одномерная клетка первого рода, то она представляет собой кусок фазовой траектории системы (3), подходящей с ненулевой фазовой скоростью к некоторой нульмерной клетке
— одномерная клетка первого рода, то она представляет собой кусок фазовой траектории системы (3), подходящей с ненулевой фазовой скоростью к некоторой нульмерной клетке  .
.
Если  — некоторая
— некоторая  -мерная клетка второго рода, отличная от точки
-мерная клетка второго рода, отличная от точки  , то существует такая
, то существует такая  -мерная клетка
-мерная клетка  , являющаяся клеткой первого рода, что из любой точки клетки
, являющаяся клеткой первого рода, что из любой точки клетки  исходит единственная траектория системы (3), идущая по клетке
исходит единственная траектория системы (3), идущая по клетке  , причем функция
, причем функция  непрерывна и непрерывно дифференцируема на
непрерывна и непрерывно дифференцируема на  .
.
Г. Перечисленные выше условия обеспечивают возможность продолжения траекторий системы (3) от клетки к клетке: из клетки  в клетку
в клетку  , если клетка
, если клетка  первого рода, и из клетки
первого рода, и из клетки  в клетку
в клетку  , если клетка
, если клетка  второго рода. Требуется, чтобы каждая такая траектория шла лишь по конечному числу клеток (то есть чтобы «протыкание» клеток второго рода происходило для каждой траектории конечное число раз). При этом любая траектория кончается в точке
второго рода. Требуется, чтобы каждая такая траектория шла лишь по конечному числу клеток (то есть чтобы «протыкание» клеток второго рода происходило для каждой траектории конечное число раз). При этом любая траектория кончается в точке  .
.
Указанные траектории называются отмеченными.
Таким образом, из каждой точки множества  исходит единственная отмеченная траектория, ведущая в точку
исходит единственная отмеченная траектория, ведущая в точку  . Требуется также, чтобы из каждой точки множества N исходила (возможно, не единственная) траектория системы (3), ведущая в точку
. Требуется также, чтобы из каждой точки множества N исходила (возможно, не единственная) траектория системы (3), ведущая в точку  и также называемая отмеченной.
и также называемая отмеченной.
Д. Все отмеченные траектории удовлетворяют принципу максимума.
Е. Значение функционала Q (см. (17.3)), вычисленное вдоль отмеченных траекторий (кончающихся в точке  ), является непрерывной функцией начальной точки
), является непрерывной функцией начальной точки  .
.
В частности, если из точки  исходят несколько отмеченных траекторий, то значение функционала Q для них одинаково.
исходят несколько отмеченных траекторий, то значение функционала Q для них одинаково.
Пример регулярного синтеза. Задача о быстродействии в линейной системе. Все известные примеры синтеза оптимального по быстродействию управления в линейных системах являются частными случаями регулярного синтеза.
Покажем это на сравнительно простом примере линейной системы, рассмотренной в § 15, стр. 236.
Уравнения движения системы имеют следующий вид:

На управление и наложено следующее ограничение:

Требуется перевести систему из заданного начального состояния  в состояние
в состояние  в наименьшее возможное время.
в наименьшее возможное время.
Промежуток времени, в течение которого удастся привести систему в состояние  , существенно зависит от наложенных на управляющую силу и ограничений:
, существенно зависит от наложенных на управляющую силу и ограничений:  .
.
В соответствии с (1) и (4) в рассматриваемом примере

Функция  согласно (17.21) здесь принимает вид
согласно (17.21) здесь принимает вид

где  и
и  в соответствии с (17.23) удовлетворяют следующим дифференциальным уравнениям:
в соответствии с (17.23) удовлетворяют следующим дифференциальным уравнениям:

Из (7) следует, что для любого момента времени  при ограничении (5) наибольшее возможное значение функции
при ограничении (5) наибольшее возможное значение функции  переменного и, где
переменного и, где  доставит управление
доставит управление

Таким образом, оптимальное управление будет согласно (9) следующим:

Согласно (8) функции  и
и  будут иметь следующий вид:
будут иметь следующий вид:
 (20.10)
(20.10)
где через  и
и  обозначены начальные значения функций
обозначены начальные значения функций  и
и  соответственно.
соответственно.
Если бы начальные значения  и
и  были известны, то в соответствии с (9) и (10) задача синтеза оптимального управления была бы завершена. Отыскание начального значения
были известны, то в соответствии с (9) и (10) задача синтеза оптимального управления была бы завершена. Отыскание начального значения  вектор-функции
вектор-функции  является основной трудностью в общей задаче синтеза оптимального управления по принципу максимума.
является основной трудностью в общей задаче синтеза оптимального управления по принципу максимума.
В рассматриваемом здесь простом примере задачу удается решить благодаря возможности явного определения на фазовой плоскости  кривой
кривой  , на которой управление и (модуль которого согласно (9) остается постоянным
, на которой управление и (модуль которого согласно (9) остается постоянным  должно изменять знак. Кривая
должно изменять знак. Кривая  называется линией переключения управления.
называется линией переключения управления.
Так как согласно (9)
и  (20.11)
(20.11)
а функция  изменяет свой знак лишь один раз в момент времени
изменяет свой знак лишь один раз в момент времени  , то оптимальное управление
, то оптимальное управление  изменяет свой знак не более одного раза на отрезке времени
изменяет свой знак не более одного раза на отрезке времени  , где
, где  — момент попадания изображающей точки в начало координат.
— момент попадания изображающей точки в начало координат.
Таким образом, оптимальное управление и  является кусочно-постоянной функцией (модуль этой функции
является кусочно-постоянной функцией (модуль этой функции  которая имеет не более двух интервалов постоянства.
которая имеет не более двух интервалов постоянства.
Указанное свойство оптимального управления  в рассматриваемом примере позволяет построить семейство оптимальных траекторий на фазовой плоскости
в рассматриваемом примере позволяет построить семейство оптимальных траекторий на фазовой плоскости  .
.
На отрезке времени, на котором управление и  , уравнения (4) принимают вид
, уравнения (4) принимают вид

откуда следует, что

Интегрируя это уравнение, получим семейство парабол
 (20.13)
(20.13)
зависящее от параметра  . При
. При  получим параболу
получим параболу
 (20.14)
(20.14)
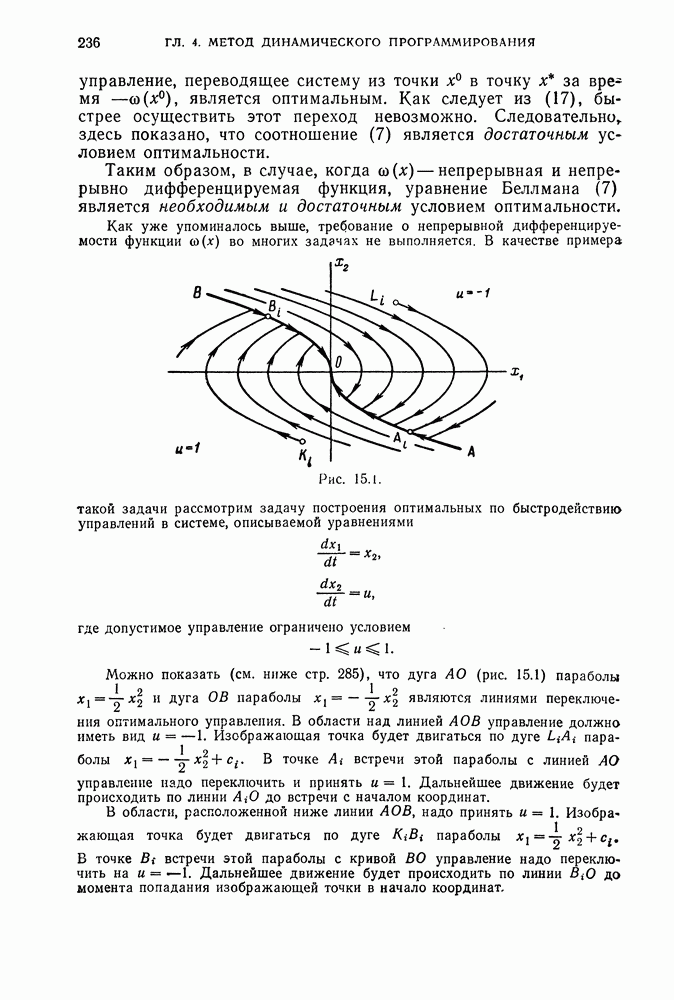
проходяшую через начало координат. Дуга АО параболы (14) показана на рис. 20.1. Линии  являются дугами парабол (13), которые соответствуют различным значениям параметра
являются дугами парабол (13), которые соответствуют различным значениям параметра  .
.

Рис. 20.1.
Аналогично при и  уравнения (4) принимают вид
уравнения (4) принимают вид
 (20.15)
(20.15)
откуда следует, что

Интегрируя это уравнение, найдем семейство парабол
 (20.16)
(20.16)
зависящее от параметра  . При
. При  получим параболу
получим параболу
 (20.17)
(20.17)
проходящую через начало координат. Дуга ВО параболы (17) показана на рис. 20.1. Линии  являются дугами парабол (16), которые соответствуют различным значениям параметра
являются дугами парабол (16), которые соответствуют различным значениям параметра  .
.
Обозначим теперь через Г линию, состоящую из дуг AO и ОВ. Линия Г делит фазовую плоскость  на две области
на две области  и
и  , расположенные над линией Г и под ней соответственно.
, расположенные над линией Г и под ней соответственно.
Если в начальный момент времени  изображающая точка находится
изображающая точка находится  области
области  например в точке
например в точке  , то надо принять и
, то надо принять и  . Тогда изображающая точка будет двигаться по дуге
. Тогда изображающая точка будет двигаться по дуге  параболы (16), проходящей через точку
параболы (16), проходящей через точку  . В момент времени, когда изображающая точка попадет в точку
. В момент времени, когда изображающая точка попадет в точку  , надо изменить управление на и
, надо изменить управление на и  . Изображающая точка будет тогда продолжать движение по дуге
. Изображающая точка будет тогда продолжать движение по дуге  , по которой и придет в начало координат. Кривая
, по которой и придет в начало координат. Кривая  , состоящая из
, состоящая из  и является оптимальной траекторией, соответствующей начальному состоянию
и является оптимальной траекторией, соответствующей начальному состоянию  В соответствии с теоремой о единственности оптимальной траектории в задаче о быстродействии в линейных системах [72] время движения по траектории
В соответствии с теоремой о единственности оптимальной траектории в задаче о быстродействии в линейных системах [72] время движения по траектории  будет наименьшим по сравнению с временем движения по любой другой траектории, ведущей из точки
будет наименьшим по сравнению с временем движения по любой другой траектории, ведущей из точки  в начало координат.
в начало координат.
Аналогично, если в начальный момент времени изображающая точка находится в области  , например в точке
, например в точке  , то надо принять и
, то надо принять и  . Изображающая точка будет двигаться по дуге
. Изображающая точка будет двигаться по дуге  параболы (13). В точке
параболы (13). В точке  надо переключить управление на и
надо переключить управление на и  . Дальнейшее движение будет происходить по дуге
. Дальнейшее движение будет происходить по дуге  , по которой изображающая точка придет в начало координат. Таким образом, для начального состояния
, по которой изображающая точка придет в начало координат. Таким образом, для начального состояния  оптимальной будет траектория
оптимальной будет траектория  .
.
Как указано выше, для задачи о быстродействии в линейных системах доказана теорема о единственности оптимальной траектории [72] выделяемой принципом максимума.
В рассматриваемом примере единственность найденной выше оптимальной траектории можно доказать непосредственно [15]. Обозначим через  момент попадания изображающей точки в начало координат. Тогда время движения по траектории
момент попадания изображающей точки в начало координат. Тогда время движения по траектории  будет
будет  . Через
. Через  обозначим момент переключения управления.
обозначим момент переключения управления.
Предположим, что существует другое управление  , где
, где  которое приводит систему в начало координат за время — где
которое приводит систему в начало координат за время — где  Траекторию, соответствующую управлению (9), обозначим по-прежнему через
Траекторию, соответствующую управлению (9), обозначим по-прежнему через  , а управлению
, а управлению  — через
— через  . Таким образом, будем иметь следующие соотношения:
. Таким образом, будем иметь следующие соотношения:

Траектории  и
и  определяются уравнениями движения
определяются уравнениями движения

и соответственно

Обозначим теперь

Так как

то

Из приведенных выше соотношений следует, что

Производные по t от  и
и  будут
будут

Так как на траектории  управление
управление  удовлетворяет условиям
удовлетворяет условиям

то

Нетрудно видеть, что для любого другого управления  , где
, где  будет иметь место неравенство
будет иметь место неравенство

Из полученных соотношений следует, что

откуда найдем, что

Таким образом,

а так как  , а кроме того,
, а кроме того,  , то будем иметь
, то будем иметь

С другой стороны, поскольку мы предполагали, что  , то, учитывая, что
, то, учитывая, что  , можно получить такое соотношение:
, можно получить такое соотношение:

откуда следует, что

Мы получили противоречие. Следовательно, невозможно, чтобы было меньше, чем  . Таким образом, доказана единственность (при ограничении
. Таким образом, доказана единственность (при ограничении  оптимального управления (9) и единственность соответствующей этому управлению оптимальной траектории для заданного начального состояния системы.
оптимального управления (9) и единственность соответствующей этому управлению оптимальной траектории для заданного начального состояния системы.
Найдем теперь функцию Беллмана для рассматриваемой задачи
 (20.18)
(20.18)
Здесь
 (20.19)
(20.19)
есть время движения изображающей точки по оптимальной траектории из начального положения  в начало координат
в начало координат  .
.
Пусть в начальным момент времени  изображающая точка находится в точке
изображающая точка находится в точке  плоскости
плоскости  , то есть
, то есть  и
и  являются координатами точки
являются координатами точки  . Уравнение параболы, дугой которой является линия
. Уравнение параболы, дугой которой является линия  будет в соответствии с (16) иметь вид
будет в соответствии с (16) иметь вид
 (20.20)
(20.20)
Точка  , в которой переключается управление, является точкой пересечения парабол (20) и (14). Ордината точки
, в которой переключается управление, является точкой пересечения парабол (20) и (14). Ордината точки  удовлетворяет соотношению
удовлетворяет соотношению

Так как дуга АО расположена ниже оси абсцисс, то надо принять

При движении изображающей точки по дуге  имеют место уравнения (15). Второе из этих уравнений имеет вид
имеют место уравнения (15). Второе из этих уравнений имеет вид

откуда, учитывая, что здесь координаты точки  обозначены через
обозначены через  , найдем
, найдем
 (20.22)
(20.22)
где  — момент времени, в который переключается управление.
— момент времени, в который переключается управление.
Из (22) следует, что

При движении изображающей точки по дуге  имеет место согласно (12) уравнение
имеет место согласно (12) уравнение

откуда следует, что
 (20.24)
(20.24)
где  — момент времени, в который изображающая точка попадает в начале координат. Из (24) найдем, что
— момент времени, в который изображающая точка попадает в начале координат. Из (24) найдем, что

Из (23) и (25) следует, что

В соответствии с (21) выражение (26) принимает вид
 (20.27)
(20.27)
Выражение (27) имеет место, когда точка  лежит в области
лежит в области  то есть в любой точке фазовой плоскости над линией АОВ.
то есть в любой точке фазовой плоскости над линией АОВ.
Однако нетрудно видеть, что выражение (27) сохраняется, если точка  лежит на линии АО. Действительно, в этом случае
лежит на линии АО. Действительно, в этом случае  и выражение (26) принимает для точек линии АО следующий вид:
и выражение (26) принимает для точек линии АО следующий вид:

что совпадает с выражением (25) для времени движения изображающей точки по дуге  .
.
Аналогичным путем можно найти  для случая, когда точка
для случая, когда точка  лежит в области
лежит в области  и на линии ВО.
и на линии ВО.
В случае, когда точка  лежит в области
лежит в области  , то есть в любой точке фазовой плоскости под линией АОВ, будем иметь
, то есть в любой точке фазовой плоскости под линией АОВ, будем иметь
 (20.28)
(20.28)
Если изображающая точка в начальный момент времени находится на линии ВО в точке  то время приведения системы в начало координат будет следующим:
то время приведения системы в начало координат будет следующим:

Из формул (28) и (27) следует, что для симметричных начальных точек  и
и  время приведения в начало координат одинаково, как это, естественно, и должно быть.
время приведения в начало координат одинаково, как это, естественно, и должно быть.
Нетрудно видеть, что в точках линии АО функции (27) и (28) принимают одинаковое значение. Действительно, так как АО является дугой параболы (14)

то в точках линии АО функция (27) принимает значение, которое, учитывая, что линия АО расположена ниже оси абсцисс, можно записать так
 (20.30)
(20.30)
Функция (28) в точках линии АО принимает значение
 (20.31)
(20.31)
Значения (30) и (31) совпадают. Аналогично можно показать, что значения функций (27) и (28) будут совпадать и в точках линии  принимаемэе ими значение будет равно
принимаемэе ими значение будет равно  .
.
Таким образом, функция  , которая определена в областях
, которая определена в областях  и
и  соответственно выражениями (27) и (28), сохраняет непрерывность на всей фазовой плоскости
соответственно выражениями (27) и (28), сохраняет непрерывность на всей фазовой плоскости  .
.
Частные производные от функции (27) по ее аргументам будут
 (20.32)
(20.32)
Аналогично частные производные от функции (28) будут
 (20.33)
(20.33)
Найдем значения, которые принимают функции (32) и (33) в точке  , то есть положим, что
, то есть положим, что

Так как согласно (21)

то значения функций (32) в точке  будут
будут
 (20.34)
(20.34)
Значения функций (33) в точке  в которой, как на всей линии
в которой, как на всей линии
 (20.35)
(20.35)
Из (34) и (35) видно, что значения функций (32) и (33) на линии АО (то есть на кривой  ) будут различными. На линии BO (то есть на кривой
) будут различными. На линии BO (то есть на кривой  ) значения функций (32) и (33) также будут различными.
) значения функций (32) и (33) также будут различными.
Таким образом, в точках линии АОВ функция  , а, следовательно, и функция
, а, следовательно, и функция  не имеют частных производных
не имеют частных производных  своим аргументам
своим аргументам  и
и  .
.
Нетрудно убедиться в том, что оптимальные траектории, построенные в рассматриваемом здесь примере (рис. 20.1), удовлетворяют сформулированным выше (стр. 280) условиям регулярного синтеза.
Заметим при этом, что в рассматриваемом примере множество  , то есть множество
, то есть множество  содержит лишь точку
содержит лишь точку  .
.
Множество  , где через Г обозначена линия, состоящая из АО и ОB (то есть линия переключения управления).
, где через Г обозначена линия, состоящая из АО и ОB (то есть линия переключения управления).
Множество  где D — вся фазовая плоскость
где D — вся фазовая плоскость  .
.
Множество N в рассматриваемом примере является пустым. Таким образом, здесь  , то есть объединение множеств
, то есть объединение множеств  и N представляет собой линию АОВ (линию переключения управления Г).
и N представляет собой линию АОВ (линию переключения управления Г).
Линии АО и ОВ представляют собой две одномерные клетки первого рода. Области  и
и  , на которые линия Г разбивает фазовую плоскость, представляют собой две двумерные клетки первого рода.
, на которые линия Г разбивает фазовую плоскость, представляют собой две двумерные клетки первого рода.
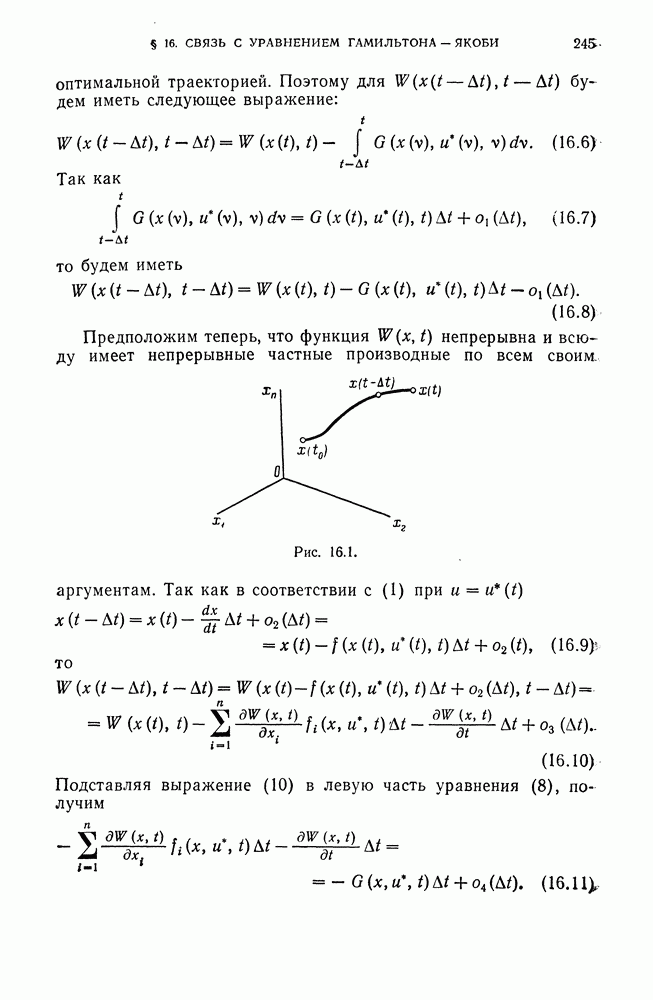
Отметим еще некоторые свойства оптимальных траекторий, достаточно очевидные в рассматриваемом примере.

Рис. 20.2.
На рис. 20.2 через  обозначена точка, в которой находилась
обозначена точка, в которой находилась  момент времени
момент времени  , и изображена оптимальная траектория, которая ведет из точки
, и изображена оптимальная траектория, которая ведет из точки  в начало координат. Положение точки
в начало координат. Положение точки  которой переключается управление) на кривой АО зависит от начального состояния
которой переключается управление) на кривой АО зависит от начального состояния  системы. Так как точки кривой АО удовлетворяют соотношению (14)
системы. Так как точки кривой АО удовлетворяют соотношению (14)

то, обозначая

можно представить координаты точки  на плоскости так:
на плоскости так:

Таким образом, положение точки  (принадлежащей линии АО, то есть одномерной клетке первого рода) определяется лишь одним параметром
(принадлежащей линии АО, то есть одномерной клетке первого рода) определяется лишь одним параметром  , который является функцией от начального состояния системы
, который является функцией от начального состояния системы
 (20.37)
(20.37)
Согласно (21) и (36)
 (20.38)
(20.38)
Равным образом и промежуток времени
 (20.39)
(20.39)
за который система проходит из точки  в точку
в точку  , есть функция от начального состояния системы
, есть функция от начального состояния системы  :
:
 (20.40)
(20.40)
Согласно (23)

В соответствии с (21) это выражение принимает вид
 (20.41)
(20.41)
Как видно из (38) и (41), функции  и
и  являются непрерывными и непрерывно дифференцируемыми функциями своих аргументов
являются непрерывными и непрерывно дифференцируемыми функциями своих аргументов  и
и  (то есть координат вектора
(то есть координат вектора  ).
).
Так как в качестве начальной точки  может служить любая точка
может служить любая точка  дуги оптимальной траектории в области то выражения (38) и (41) можно переписать так
дуги оптимальной траектории в области то выражения (38) и (41) можно переписать так
 (20.42)
(20.42)
 (20.43)
(20.43)
Рассмотрим теперь попятное движение изображающей точки от точки  к точке
к точке  . Это движение мы получим, обратив время t. В соответствии с (15) попятное движение будет описываться дифференциальными уравнениями
. Это движение мы получим, обратив время t. В соответствии с (15) попятное движение будет описываться дифференциальными уравнениями
 (20.44)
(20.44)
Решение уравнений (44) будет следующим:
 (20.45)
(20.45)
Так как в попятном движении начальная точка  лежит на линии АО, то согласно (14)
лежит на линии АО, то согласно (14)
 (20.46)
(20.46)
Поэтому решение (45) можно привести к виду

где через  обозначено
обозначено
 (20.48)
(20.48)
Так как
 (20.49)
(20.49)
то уравнения (47) можно разрешить относительно  и
и  .
.
Заметим еще, что если  является начальным состоянием в исходном движении (от точки
является начальным состоянием в исходном движении (от точки  к точке
к точке  ), то, подставляя в (47) вместо
), то, подставляя в (47) вместо  и
и  величины
величины

получим

то есть если попятное движение началось (как следует из (36)) из точки  , то по истечении промежутка времени
, то по истечении промежутка времени  изображающая точка придет в точку
изображающая точка придет в точку  , как это, естественно, и должно быть.
, как это, естественно, и должно быть.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
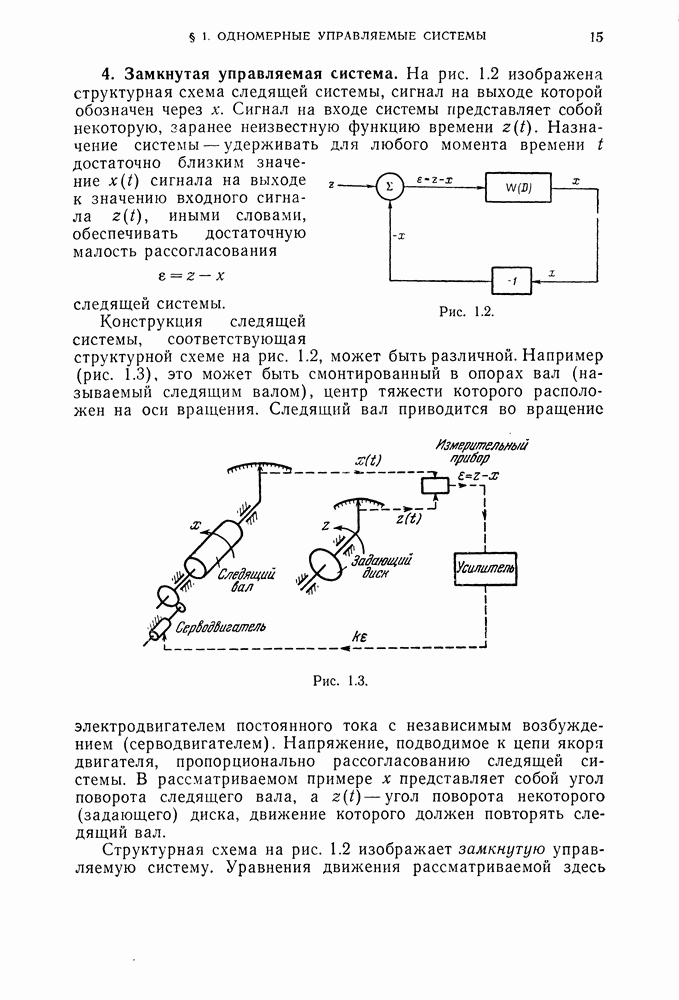
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
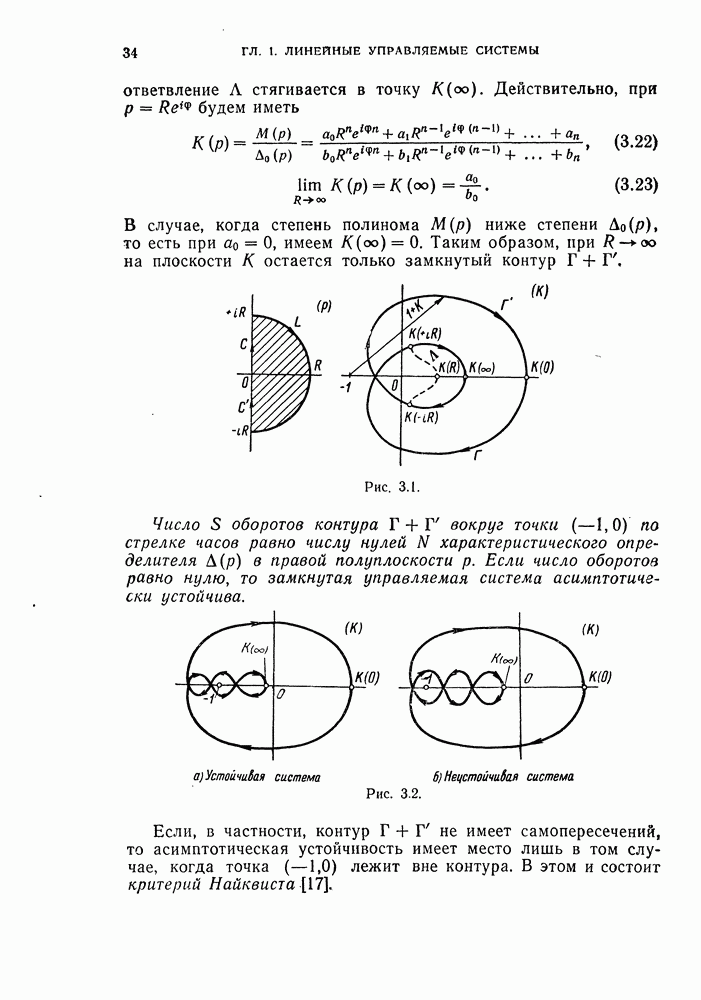
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
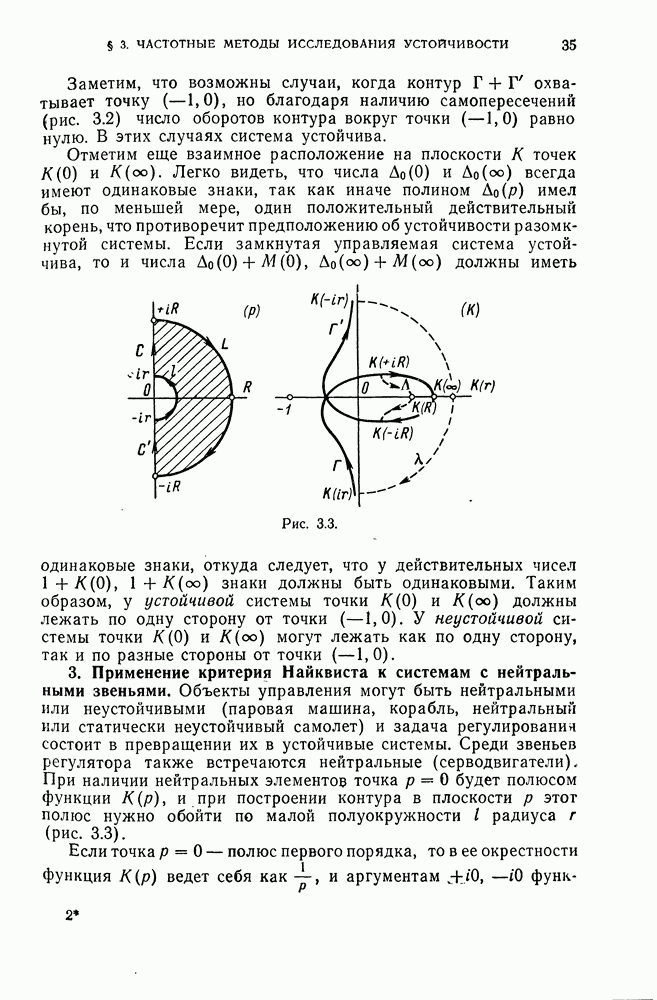
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
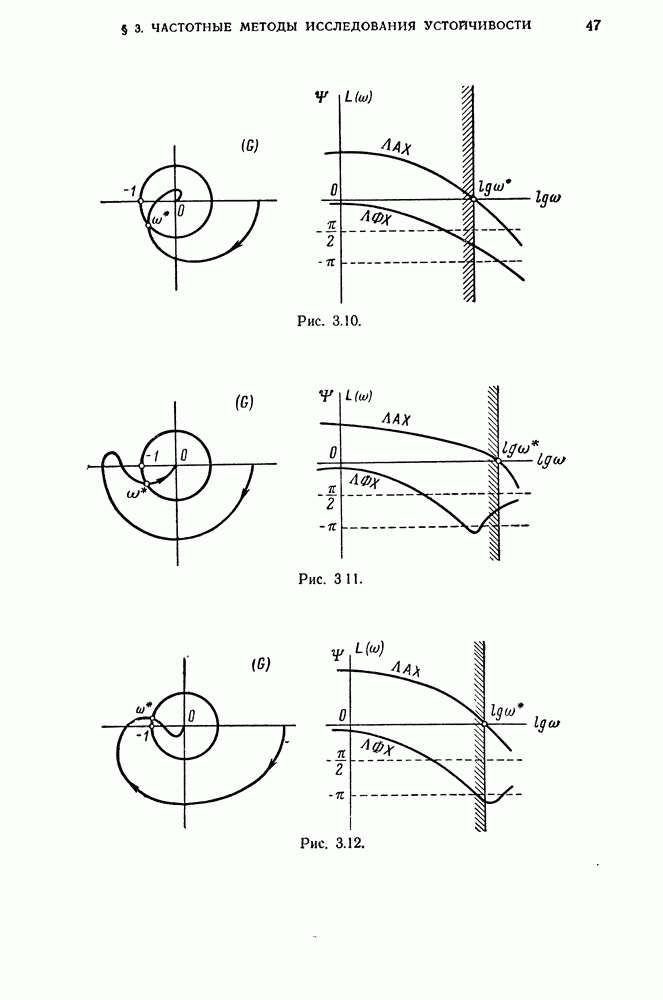
- 8. Логарифмические частотные характеристики.
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА