| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
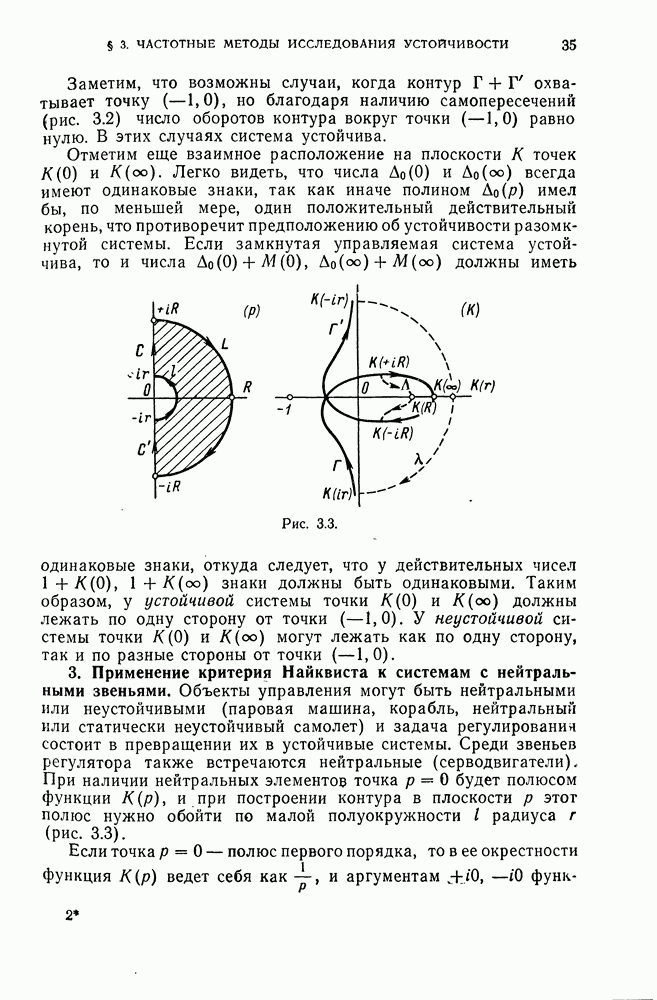
3. Применение критерия Найквиста к системам с нейтральными звеньями.
Объекты управления могут быть нейтральными или неустойчивыми (паровая машина, корабль, нейтральный или статически неустойчивый самолет) и задача регулирования состоит в превращении их в устойчивые системы. Среди звеньев регулятора также встречаются нейтральные (серводвигатели). При наличии нейтральных элементов точка  будет полюсом функции
будет полюсом функции  , и при построении контура в плоскости
, и при построении контура в плоскости  этот полюс нужно обойти по малой полуокружности
этот полюс нужно обойти по малой полуокружности  радиуса
радиуса  (рис. 3.3).
(рис. 3.3).
Если точка  — полюс первого порядка, то в ее окрестности Функция
— полюс первого порядка, то в ее окрестности Функция  ведет себя как
ведет себя как  , и аргументам
, и аргументам  функции
функции  соответствуют ветви кривых
соответствуют ветви кривых  , уходящие в бесконечность вдоль мнимой оси.
, уходящие в бесконечность вдоль мнимой оси.
Полуокружность  отображается на кривую, близкую к полуокружности бесконечно большого радиуса, описываемую по стрелке часов и смыкающуюся с бесконечными ветвями кривых
отображается на кривую, близкую к полуокружности бесконечно большого радиуса, описываемую по стрелке часов и смыкающуюся с бесконечными ветвями кривых  . Когда
. Когда  , дуга
, дуга  , отображающая полуокружность
, отображающая полуокружность  , стягивается в точку
, стягивается в точку  , а дуга X, отображающая малую полуокружность
, а дуга X, отображающая малую полуокружность  , уходит в бесконечность.
, уходит в бесконечность.
В итоге опять остается кривая  , бесконечные ветви которой нужно представлять себе замкнутыми полуокружностью бесконечно большого радиуса, расположенной в правой полуплоскости К. К полученному замкнутому контуру по-прежнему применяем критерий Найквиста.
, бесконечные ветви которой нужно представлять себе замкнутыми полуокружностью бесконечно большого радиуса, расположенной в правой полуплоскости К. К полученному замкнутому контуру по-прежнему применяем критерий Найквиста.
Диаграмма Найквиста, изображенная на рис. 3.3, относится к устойчивой системе, у которой точка  является полюсом первого порядка. Для показанного на рис. 3.3 случая имеет место соотношение
является полюсом первого порядка. Для показанного на рис. 3.3 случая имеет место соотношение
 (3.24)
(3.24)

Рис. 3.4.
Показанная на рис. 3.4 диаграмма Найквиста относится к устойчивой системе, у которой точка  является полюсом
является полюсом  -го порядка.
-го порядка.
Если точка  есть полюс
есть полюс  порядка, то кривая
порядка, то кривая  должна быть замкнута бесконечно удаленной линией, состоящей из
должна быть замкнута бесконечно удаленной линией, состоящей из  полуокружностей, пробегаемых по стрелке часов. Это следует из того, что в окрестности точки
полуокружностей, пробегаемых по стрелке часов. Это следует из того, что в окрестности точки  функция
функция  ведет себя
ведет себя  как
как  , то есть
, то есть  угол в плоскости К в
угол в плоскости К в  раз больше полярного угла в плоскости
раз больше полярного угла в плоскости  в
в  раз. В рассматриваемом случае имеет место соотношение
раз. В рассматриваемом случае имеет место соотношение
 (3.25)
(3.25)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 1. Одномерные управляемые системы
- 2. Функция веса и передаточная функция.
- 3. Частотная характеристика.
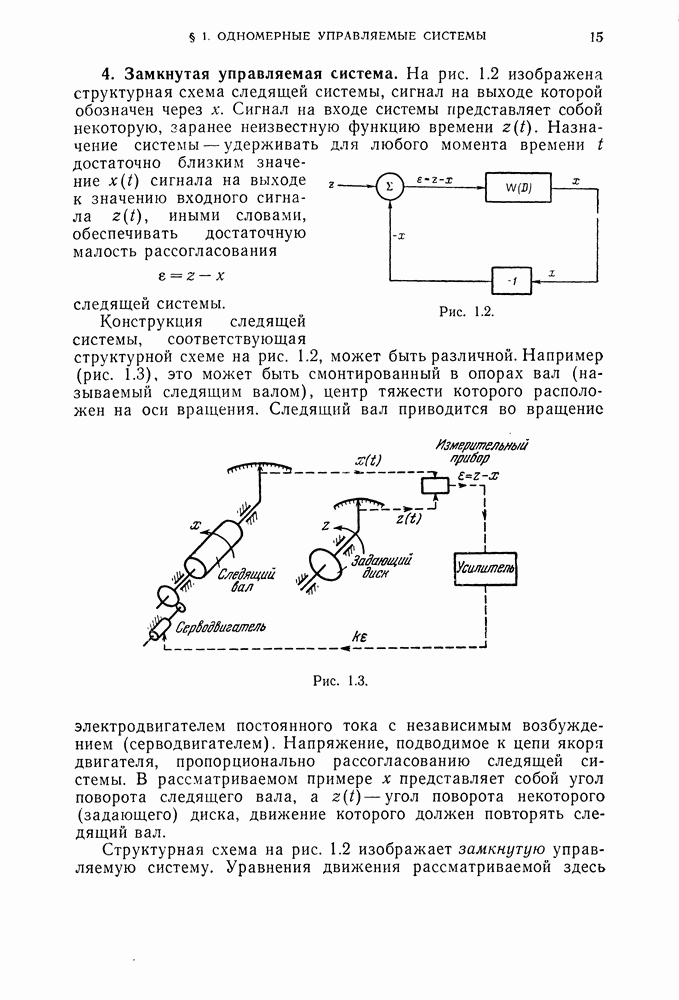
- 4. Замкнутая управляемая система.
- 5. Разомкнутая управляемая система.
- 6. Воспроизведение преобразованного входного сигнала.
- 7. Одномерная управляемая система с конечным числом степеней свободы.
- 8. Одно замечание об интегрировании уравнений движения одномерной системы.
- § 2. Многомерные управляемые системы
- 1. Замкнутая управляемая система.
- 2. Характеристический определитель замкнутой управляемой системы.
- 3. Уравнение автоматического управления.
- 4. Разомкнутая управляемая система.
- 5. Интерпретация матричных операторов.
- 6. О воспроизведении входного сигнала в многомерной управляемой системе.
- § 3. Частотные методы исследования устойчивости линейных управляемых систем
- 1. Преобразование характеристического определителя замкнутой управляемой системы.
- 2. Критерий асимптотической устойчивости замкнутых управляемых систем, содержащих лишь устойчивые звенья (критерий Найквиста).
- 3. Применение критерия Найквиста к системам с нейтральными звеньями.
- 4. Применение критерия Найквиста к системам с неустойчивыми звеньями.
- 5. Частотные характеристики управляемых систем и их экспериментальное определение.
- 6. Пример построения диаграммы Найквиста.
- 7. Управляемые системы, содержащие звенья с запаздыванием и критерии устойчивости этих систем.
- 8. Логарифмические частотные характеристики.
- 9. Определение устойчивости замкнутой управляемой системы по логарифмическим частотным характеристикам разомкнутой управляемой системы.
- § 4. Функция веса и переходная функция стационарной линейной системы
- 1. Одномерная управляемая система.
- 2. Одномерная управляемая система, у которой передаточная функция является неправильной дробью.
- 3. Многомерные управляемые системы.
- § 5. Переходные и установившиеся процессы в замкнутых управляемых системах
- 1. Определение функции веса по частотной характеристике замкнутой системы.
- 2. Определение переходной функции по частотной характеристике замкнутой системы.
- 3. Минимально-фазовые системы.
- 4. Установившиеся процессы в замкнутых управляемых системах. Коэффициенты ошибок.
- 5. Установившиеся процессы в следящей системе.
- Глава 2. НЕЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ СИСТЕМЫ
- § 6. Устойчивость нелинейных управляемых систем. Частотные критерии. Применение прямого метода Ляпунова
- 2. Интерпретация функции W(D).
- 3. Видоизмененная частотная характеристика.
- 4. Теорема В.М. Попова.
- 5. Геометрическая формулировка теоремы В.М. Попова.
- 6. О возможности при доказательстве теоремы ограничиться случаем q>0.
- 7. Лемма 1.
- 8. Лемма 2.
- 9. Доказательство теоремы В.М. Попова.
- 10. Применение прямого метода Ляпунова. Метод А. И. Лурье в теории абсолютной устойчивости нелинейных систем.
- § 7. Нелинейные системы под воздействием внешних сил
- 1. Приведение задачи к интегральным уравнениям.
- 2. Построение приближенных решений.
- § 8. Качественные методы исследования движения нелинейных систем
- 1. Нелинейные системы с одной степенью свободы.
- 2. Консервативные системы.
- 3. Диссипативные системы.
- 4. Автоколебательные системы. Метод точечных преобразований.
- § 9. Нелинейные системы под воздействием периодических внешних сил
- 1. Вынужденные колебания нелинейной системы.
- 2. Установившиеся колебания с частотой внешней силы и их устойчивость.
- Глава 3. СИСТЕМЫ С КОНЕЧНЫМ ВРЕМЕНЕМ УПРАВЛЕНИЯ
- § 10. Функции от матриц и их применение к интегрированию систем линейных дифференциальных уравнений
- 2. Теорема Гамильтона — Кэли.
- 3. Минимальный полином матрицы.
- 4. Функции от матрицы.
- 5. Интерполяционный полином Лагранжа — Сильвестра.
- 6. Построение функции.
- 7. Компоненты матрицы А.
- 8. Общие формулы, определяющие компоненты Z матрицы А.
- 9. Представление функций от матриц рядами.
- 10. Распространение на функции от матриц интегральной формулы Коши для аналитических функций.
- 11. Некоторые свойства функций от матриц.
- 12. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами при помощи функций от матриц.
- 13. Сравнение с решениями, получаемыми при помощи преобразования Лапласа.
- § 11. Управляемость и наблюдаемость линейных систем
- 1. Управляемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 2. Системы с одной управляющей силой.
- 3. Наблюдаемость систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами.
- 4. Системы с одной наблюдаемой координатой.
- 5. Принцип двойственности в теории управляемости и наблюдаемости.
- 6. Управляемость линейных нестационарных систем.
- 7. Наблюдаемость линейных нестационарных систем.
- 8. Условие управляемости линейной стационарной системы в задаче с подвижными концами.
- 9. Условие управляемости линейной нестационарной системы в задаче с подвижными концами.
- Глава 4. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- § 12. Оптимальное управление в системах с ограниченными ресурсами
- 2. Метод динамического программирования Р. Беллмана. Принцип оптимальности.
- § 13. Применение динамического программирования к дискретным системам
- 1. Рекуррентное соотношение Беллмана.
- 2. Многомерные дискретные системы.
- § 14. Применение динамического программирования к системам непрерывного действия
- 1. Задача с фиксированным временем и свободным концом траектории.
- 2. Задача с закрепленным концом траектории и свободным временем.
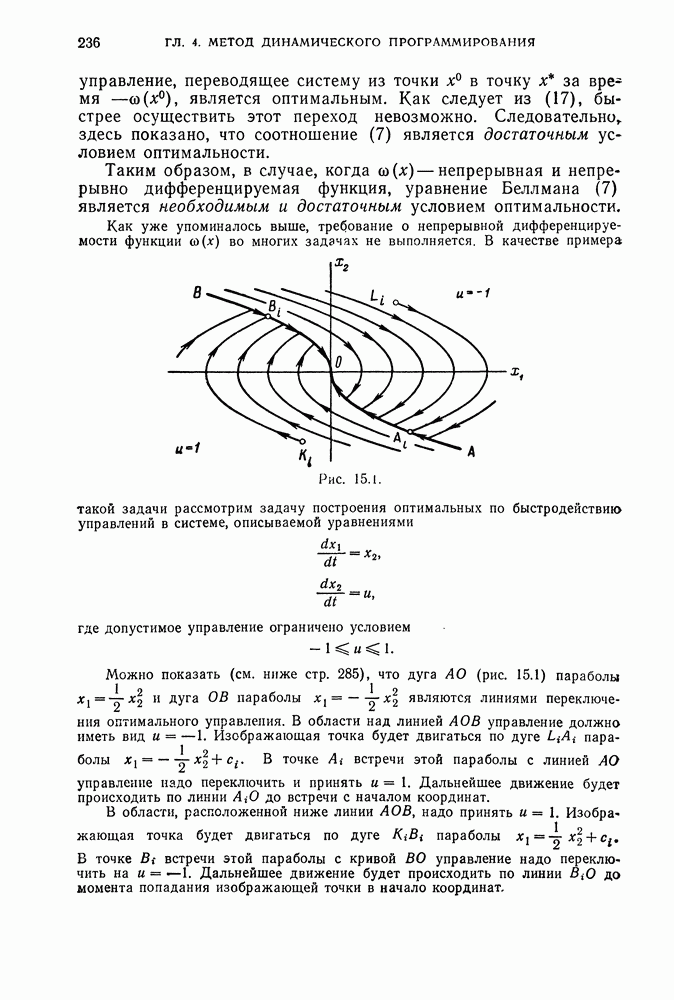
- 3. Задача о быстродействии.
- § 15. Достаточные условия оптимальности и обоснование метода динамического программирования для систем непрерывного действия. Теоремы В. Г. Болтянского
- 1. Постановка задачи. Геометрическая интерпретация уравнения Беллмана в задаче о быстродействии.
- 2. Теорема В. Г. Болтянского для задачи о быстродействии.
- 3. Теорема В. Г. Болтянского для общей задачи динамического программирования.
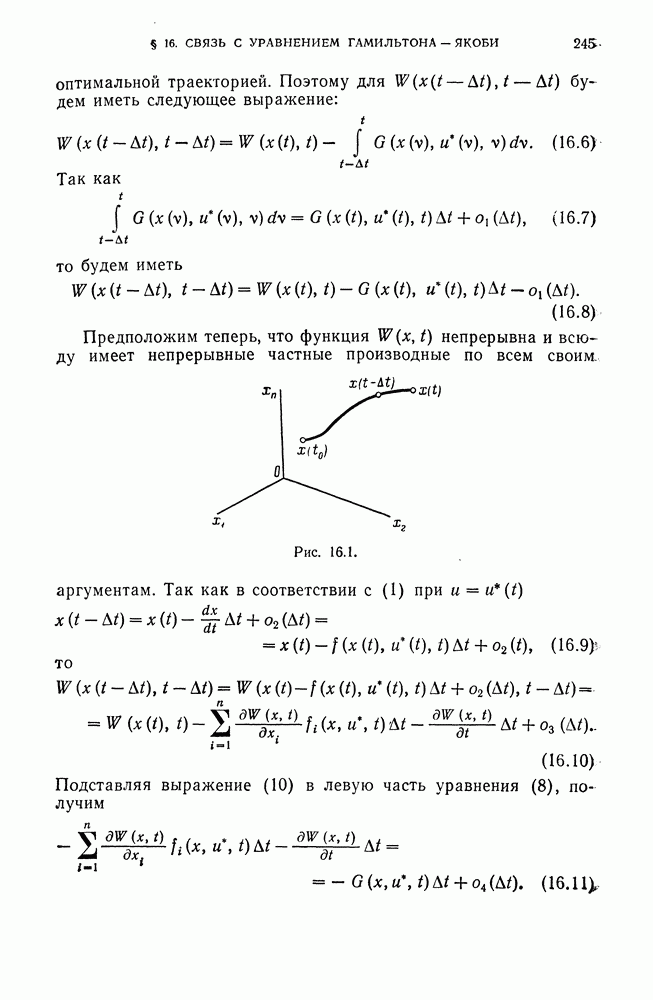
- § 16. Связь уравнения Беллмана с уравнением Гамильтона — Якоби в задачах аналитической механики
- 1. Задача о минимизации интеграла вида
- 2. Получение уравнения Гамильтона — Якоби из принципа Гамильтона.
- Глава 5. ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА В ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 17. Теорема о необходимом условии оптимальности
- 2. Принцип максимума Л. С. Понтрягина в задаче о быстродействии.
- 3. Доказательство теоремы о необходимом условии оптимальности (принципа максимума) в задаче с закрепленным временем Т и свободным концом траектории.
- § 18. Принцип максимума для неавтономных систем
- 1. Теорема о необходимом условии оптимальности для неавтономных систем.
- 2. Доказательство теоремы о необходимом условии оптимальности для неавтономной системы с линейно входящим управлением.
- 3. Линейные неавтономные системы. Приведение задачи о быстродействии к краевой задаче.
- § 19. Задача с подвижными концами. Применение принципа максимума. Условия трансверсальности
- § 20. Понятие регулярного синтеза в теории оптимальных систем
- § 21. Достаточное условие оптимальности в форме принципа максимума. Теорема В. Г. Болтянского
- § 22. Связь принципа максимума с методом динамического программирования
- § 23. Некоторые примеры применения принципа максимума
- 1. Теорема о числе переключений управления в линейной задаче о быстродействии.
- 2. Задача о максимальном отклонении.
- 3. Применение принципа максимума при отсутствии ограничений на управление.
- § 24. Оптимальные линейные системы с квадратичным критерием качества
- 1. Задача о регуляторе состояния [34].
- 2. Задача о регуляторе выхода.
- 3. Стационарные системы с бесконечным временем наблюдения.
- 4. Задача слежения [34].
- Глава 6. СТОХАСТИЧЕСКИЕ СИСТЕМЫ
- § 25. Преобразование случайных сигналов линейными системами
- § 26. Прогноз и фильтрация одномерных случайных процессов
- 1. Метод А. Н. Колмогорова и Н. Винера. Стационарные случайные процессы.
- 2. Решение интегрального уравнения, определяющего функцию веса оптимальной системы.
- 3. Нестационарные случайные процессы. Интегральное уравнение для оптимальной функции веса.
- 4. Оптимальные фильтры Калмана — Бьюси.
- § 27. Многомерные случайные процессы. Оптимальные фильтры Кальмана — Бьюси
- 1. Системы с конечным временем наблюдения.
- 2. Стационарные системы с бесконечным временем наблюдения.
- 3. Нестационарные системы с бесконечным временем наблюдения.
- 4. Оптимальная фильтрация коррелированных шумов.
- ЛИТЕРАТУРА