| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
Автор издаваемых в русском переводе лекций по теоргя спиноров Э. Картан является творцом общей теории спиноров, основы которой он опубликовал в 1913 г. в своем классическом исследовании по теории представлений простых групп. Теория спиноров — это один из наиболее интересных отделов тензорного исчисления, дающий глубокий анализ природы тензоров метрической геометрии. Книга Картана — первая в мировой литературе, излагающая общую теорию спиноров н-мерных пространств. Написана она элементарно: благодаря тому, что автор базируется в своем изложении на геометрических представлениях и пользуется при исследовании ортогональных групп методом бесконечно малых преобразований, его изложение отличается значительной простотой и наглядностью. Поэтому эта книга вполне доступна для аспирантов и студентов старших курсов физико-математических факультетов уннверснтетов. Благодаря богатству содержащихся в ней идей и методов исследовани» она значительно расширяет кругозор начинающего математика и является прекрасным введением в общую теорию линейных представлений групп Ли. В то же время она будет полезна и для физиков-теоретиков, желающих углубить свои знания в области теории спиноров.
П. Широков
ПРЕДИСЛОВИЕ АВТОРА
В квантовой механике физиками было введено понятие о спиноре. В наиболее общей математической форме спиноры были открыты автором этой книги в 1913 г. в связи с исследованием линейных представлений простых групп. Спиноры дают линейное представление группы вращений пространства и измерений, причем каждый спинор определяется при помощи 2, составляющих  или
или  Спиноры четырехмерного пространства входят в знаменитые уравнения Дирака для влек трона, причем четыре волновые функции являются не чем иным, как составляющими спинора. Было опубликовано очень много исследований по общей теории спиноров. Гериаи Вейль и Рихард Брауер недавно опубликовали прекрасный мемуар, который можно рассматривать как основной, хотя многие из полученных результатов были очень кратко указаны в упомянутом выше исследовании. О, Веблен дал очень интересное исследование спиноров с другой точки зрения в неопубликованной курсе, прочитанном в Принстонском университете. Но почти во всех работах спиноры вводятся чисто формально, без интуитивной геометрической интерпретации, и это отсутствие геометрической природы спиноров сделало столь «ложными попытки распространения на общую теорию относительности уравнений Дирака.
Спиноры четырехмерного пространства входят в знаменитые уравнения Дирака для влек трона, причем четыре волновые функции являются не чем иным, как составляющими спинора. Было опубликовано очень много исследований по общей теории спиноров. Гериаи Вейль и Рихард Брауер недавно опубликовали прекрасный мемуар, который можно рассматривать как основной, хотя многие из полученных результатов были очень кратко указаны в упомянутом выше исследовании. О, Веблен дал очень интересное исследование спиноров с другой точки зрения в неопубликованной курсе, прочитанном в Принстонском университете. Но почти во всех работах спиноры вводятся чисто формально, без интуитивной геометрической интерпретации, и это отсутствие геометрической природы спиноров сделало столь «ложными попытки распространения на общую теорию относительности уравнений Дирака.
Одной из основных целей этой книги является систематическое развитие теории спиноров на основе чисто геометрического определения этих математических объектов. Благодаря этой геометрической основе матрицы, которыми пользуются в квантовой мехаиике, возникают в ходе исследования сами
собой, и выясняется самая основа тех свойств, которыми обладают гиперкомплексные числа Клиффорда-Липшитца в теории представления вращений в пространстве любого числа измерений. Наконец, эта геометрическая основа делает очень простым введение спиноров в римановой геометрии и, в частности, применение к этим геометрическим объектам понятия параллельного переноса. Становятся понятными также и те затруднения, которые встретились в связи с последним вопросом и которые являются непреодолимыми, если пользоваться классическими приемами исследования в римановой геометрии. Эти приемы применимы к векторам и тензорам, которые помимо метрической природы имеют чисто аффинный характер, но они не могут применяться к спинорам, имеющим метрическую, но не аффинную природу.
Книга делится на две части. Первая посвящена общим вопросам теории групп вращений  -мерного пространства и линейных представлений групп, теории спиноров пространства трех измерений и исследованию линейных представлений группы - вращений этого пространства. Эти представления, как известно, играют важную роль в квантовой механике. Для их определения использован метод бесконечно малых, который требует минимума предварительных сведений для своего понимания; трансцендентный метод Г. Вейля, основанный на теории характеров, оставлен в стороне, несмотря на его большой интерес.
-мерного пространства и линейных представлений групп, теории спиноров пространства трех измерений и исследованию линейных представлений группы - вращений этого пространства. Эти представления, как известно, играют важную роль в квантовой механике. Для их определения использован метод бесконечно малых, который требует минимума предварительных сведений для своего понимания; трансцендентный метод Г. Вейля, основанный на теории характеров, оставлен в стороне, несмотря на его большой интерес.
Вторая часть посвящена теории спиноров в пространстве любого числа измерений и специально в пространстве частного принципа относительности; указаны линейные представления группы Лоренца, а также дана теория спиноров в римановой геометрии.
Эта книга, воспроизводящая с некоторыми изменениями курс, прочитанный в Сорбонне в зимнем семестре 1935/36 г., составлена по запискам, написанным А. Мерсье и использованным автором, который выражает ему свою глубокую благодарность за сотрудничество.
ЭЛИ КАРТАН.
ЧАСТЬ I. СПИНОРЫ ТРЕХМЕРНОГО ПРОСТРАНСТВА ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ
| Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ГЛАВА 1. ЭВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО; ВРАЩЕНИЯ И ОТРАЖЕНИЯ
- 2. Декартовы реперы.
- 3. Приведение квадратичной формы к сумме квадратов.
- 4. Теорема инерции.
- 6. Контравариантные и ковариантные составляющие.
- II. Вращения и отражения
- 9. Симметрии.
- 10. Разложение вращения на произведение симметрий.
- 11. Непрерывность группы вращений.
- 12. Собственные и несобственные вращения.
- 13. Пространства, у которых h = 1.
- III. Мультивекторы
- 15. Мультивекторы.
- 16. Изотропные мультивекторы.
- 17. Дополнительные мультивекторы.
- 18. Сумма p-векторов.
- IV. Бивекторы и бесконечно малые вращения
- ГЛАВА II. ТЕНЗОРЫ; ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУПП; МАТРИЦЫ
- 21. Общее определение линейных представлений группы вращений.
- 22. Эквивалентные представлений.
- 23. Понятие об эвклидовом тензоре.
- 24. Другая точка зрения.
- II. Тензорная алгебра
- III. Тензоры приводимые и неприводимые
- 33. Нахождение неприводимых тензоров, которые могут быть получены из вполне приводимого тензора.
- 35. Основная теорема.
- 36. Критерий неприводимости.
- IV. Матрицы
- 42. Характеристическое уравнение. Собственные значения.
- 43. Унитарные матрицы.
- 44. Ортогональные матрицы.
- 45. Применение к разложению вещественного вращения.
- 46. Эрмитовы матрицы.
- 47. Примечание.
- V. Неприводимость p-векторов
- ГЛАВА III. СПИНОРЫ ТРЕХМЕРНОГО ПРОСТРАНСТВА.
- II. Матрицы, соответствующие векторам
- III. Представление симметрий и вращений
- 60. Операции над спинорами.
- IV. Произведение двух спиноров и его разложение на неприводимые части
- V. Случай вещественного эвклидова пространства
- 64. Сопряженные спиноры.
- 65. Скаляр и бивектор, соответствующие двум сопряженным спинорам.
- VI. Случай псевдоэвклидова пространства
- ГЛАВА IV. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ В E1
- I. Линейные представления, выражаемые при помощи спиноров
- 71. Уравнения Дирака.
- II. Бесконечно малые вращения и определение эвклидовых тензоров
- III. Линейные представления группы комплексных вращений
- 83. Линейные представления прямого произведения двух групп.
- 84. Приложения к группе комплексных вращений.
- IV. Однозначность и двузначность
- 86. Однозначность линейных представлений унимодулярной группы двух переменных.
- 86. Линейные представления вещественной проективной группы одной переменной.
- V. Линейные представления группы вращений и отражений
- 88. Случай неприводимых представлений, индуцирующих в группе вращений неприводимое представление.
- 90. Приложения.
- 91. Случай группы вращений и отражений вещественного псевдоэвклидова пространства.
- ГЛАВА V. СПИНОРЫ ПРОСТРАНСТВА …
- I. Изотропные v-плоскости и матрицы, соответствующие векторам
- II. Представление вращений и отражений при помощи матриц порядка 2^v
- 99. Тензорный характер спинора.
- 100. Неприводимость спинора.
- III. Фундаментальная полярность в пространстве спиноров, p-векторы, определяемые парой спиноров
- IV. Простые спиноры и интерпретация их как поляризованных изотропных v-векторов
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- 117. Сопряженные спиноры.
- 118. Произведение двух сопряженных спиноров.
- 119. h-векторы, построенные на двух сопряженных спинорах.
- ГЛАВА VI. СПИНОРЫ ПРОСТРАНСТВА E2
- I. Изотропные v-плоскости и полуспиноры
- 122. Простые полуспиноры, определяемые как изотропные поляризованные v-векторы.
- 123. Условия простоты полуспинора.
- 124. Пересечение двух изотропных v-плоскостей.
- II. Матрицы, соответствующие p-векторам. Представление вращений и отражений
- 126. Применение симметрии к спинору.
- 127. Две группы вращений и отражений в применении к спинорам.
- 128. Неприводимость спинора и полуспиноров.
- 120. Матрицы порядка 2^v разложенные на суммы p-векторов.
- III. Разложение произведения двух спиноров
- 132. Разложение произведения двух полуспиноров относительно группы вращений.
- 134. Применение к группе вращеяиб для v нечетного.
- 135. Случай v четного.
- 136. Примечание.
- IV. Частные случаи
- 137. Случай v = 3.
- 188. Случай v = 4. Фундаментальная трилинейная форма.
- 139. Принцип тройственности.
- 140. Параллелизм в пространстве E2.
- 141. Формула Бриоски.
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
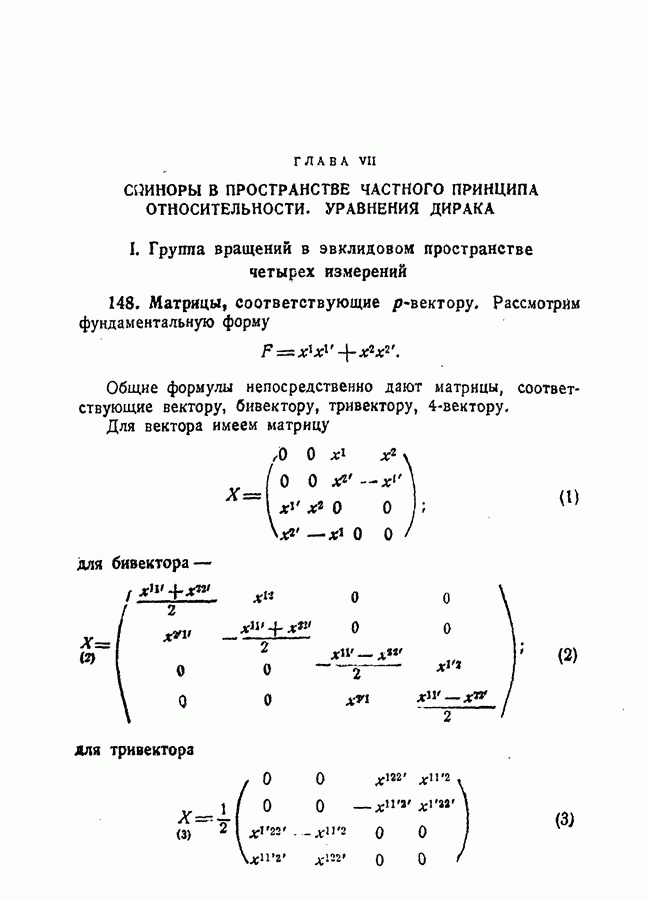
- ГЛАВА VII. СПИНОРЫ В ПРОСТРАНСТВЕ ЧАСТНОГО ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ. УРАВНЕНИЯ ДИРАКА
- II. Разложение произведения двух спиноров
- III. Сопряженные векторы и слияоры в пространстве частного принципа относительности
- IV. Уравнения Дирака
- ГЛАВА VIII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
- II. Представления группы вращений и отражений Лоренца
- III. Линейные представления группы вращений вещественного эвклидова пространства
- ГЛАВА IX. СПИНОРЫ И УРАВНЕНИЯ ДИРАКА В РИМАНОВОИ ГЕОМЕТРИИ
- II. Спинорные поля в римановой геометрии
- БИБЛИОГРАФИЯ