ГЛАВА VII. СПИНОРЫ В ПРОСТРАНСТВЕ ЧАСТНОГО ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ. УРАВНЕНИЯ ДИРАКА

I. Группа вращений в эвклидовом пространстве четырех измерений

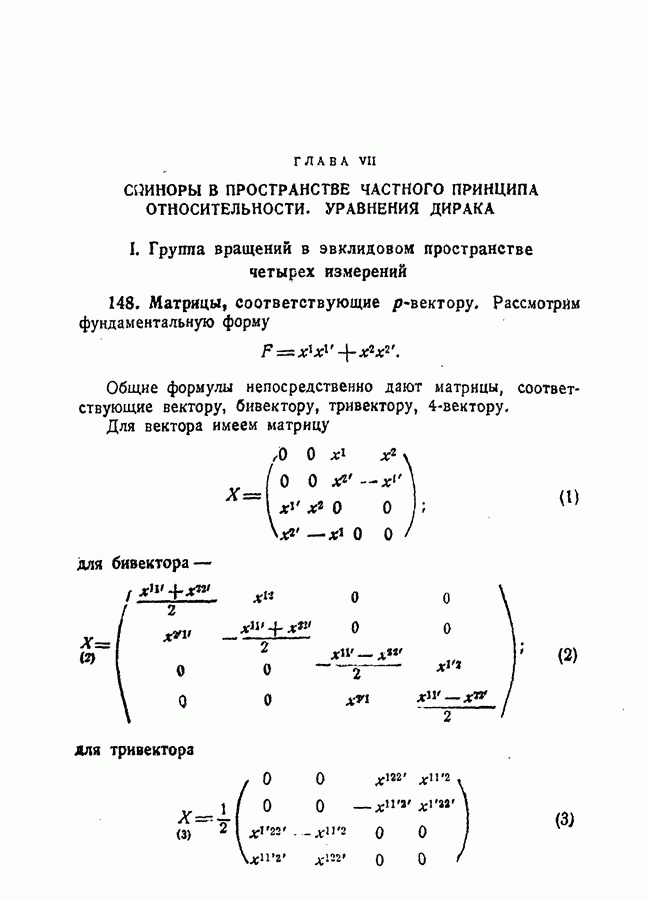
148. Матрицы, соответствующие р-вектору.

Рассмотрим фундаментальную форму

Общие формулы непосредственно дают матрицы, соответствующие вектору, бивектору, тривектору, 4-вектору.

Для вектора имеем матрицу

для бивектора —

для тривектора

наконец, для 4-вектора имеем

149. Случай прямоугольных координат.

Если взять прямоугольные координаты, заменяя через

то получим для вектора матрицу

Матрица X бивектора имеет вид (2)

где

является матрицей полубивектора первого рода с составляющими

и где

является матрицей полубивектора второго рода с составляющими

Если взять координаты, употребляемые в частном принципе относительности, с фундаментальной формой

то получим для вектора матрицу

затем матрицу

соответствующую полубивектору первого рода с составляющими

и матрицу

соответствующую полубивектору второго рода с составляю щими

ковариантные составляющие этих полубивекторов соответ. ственно имеют следующий вид:

150. Группа вращений комплексного пространства.

Каждый единичный вектор А выражается в виде

где матрица второго порядка имеет определитель, равный —1. Симметрия, соответствующая этому вектору, преобразует полуспиноры следующим образом:

а вектор по формулам

Произведение двух симметрий А, В дает соотношения

Положим

где — унимодулярные матрицы; имеем

эти формулы относятся к простому вращению. Формулы, определяющие вращение общего вида, имеют ту же самую форму. В частности, каждое вращение вектора X определяется формулой

где — унимодулярные матрицы второго порядка.

Обратно, пусть к являются любыми унимодулярными матрицами второго порядка; я утверждаю, что соотношения (15) определяют вращение четырехмерного пространства. Для этого надо доказать, что

1° если X — матрица, соответствующая вектору, то X также является матрицей, соответствующей вектору;

2° квадрат матрицы X равеи квадрату матрицы X.

Второе, предложение очевидно, так как

Что касается первого, то оно справедливо, если X является матрицей единичного вектора, то есть если определитель матрицы равен —1, а Н является матрицей, обратной , так как тогда на основании (14) определитель матрицы равен также —1 и Н является матрицей, обратной Общий случай выводится непосредственно из этого частного.

Теорема. Наиболее общее вращение комплексного эвклидова пространства 4 измерений определяется формулами

где матрица имеет вид причем и — произвольные унимодулярные комплексные матрицы.

Группа вращений является прямым произведением двух групп линейных унимодулярных подстановок двух переменных. Если мы рассмотрим, в частности, результат преобразования бивектора , то получим

Каждый из двух родов полубивекторов преобразуется группой, изоморфной группе вращений трехмерного комплексного пространства. Отметим, что согласно формулам (17) определитель каждой матрицы и Н является инвариантом группы вращений; эти инварианты определяются следующими выражениями:

они являются квадратичными формами составляющих соответствующих полубивекторов, в соответствии с найденным

выше результатом. В прямоугольных координатах имеем два инварианта

откуда вычитанием получаем инвариант равенство нулю которого выражает условие простоты бивектора. В частном принципе относительности имеем два инварианта:

В частности, мы видим, что каждый простой бивектор может быть изображен двумя векторами одинаковой длины трехмерного пространства; результат применения вращения 4-мерного пространства к бивектору эквивалентен результату применения к каждому из этих двух векторов независимых друг от друга вращений.

151. Случай вещественного эвклидова пространства. Формула (5) показывает, что матрица а, являющаяся одной из составляющих матрицы А, соответствующей вещественному единичному вектору, является унитарной с определителем, равным —1; в самом деле, матрица А — эрмитова, то есть Унимодулярные матрицы являются тогда унитарными, откуда следует

Теорема. Каждое вращение в вещественном эвкладовом пространстве 4 измерений определяется формулами (15), в которых матрицы и являются любыми унитарными унимодулярными матрицами.

В частности, составляющие полубивектора преобразуются вещественной ортогональной подстановкой с определителем, равным 1.

152. Случай пространства частного принципа относительности.

В пространстве частного принципа относительности матрица а, которая входит в матрицу Л, соответствующую вещественному единичному вектору, сопряжена с

матрицы этом случае являются унимодулярными, взаимно комплексно сопряженными.

Теорема. Всякое собственное вращение пространства частного принципа относительности определяется формулами:

где — произвольная унимодулярная комплексная матрица второго порядка, — ее сопряженная.

Таким образом, мы видим, что Лоренцева группа собственных вращений изоморфна группе комплексных унимодулярных подстановок двух переменных, то есть группе вращений эвклидова комплексного пространства 3 измерений.

Собственные отражения в применении к спинорам определяются формулами: