II. Представление вращений и отражений при помощи матриц порядка 2^v

96. Симметрия, соответствующая единичному вектору.

Как и в пространстве результат применения к вектору X симметрии относительно гиперплоскости II, перпендикулярной к единичному вектору А, выражается формулой (п. 58)

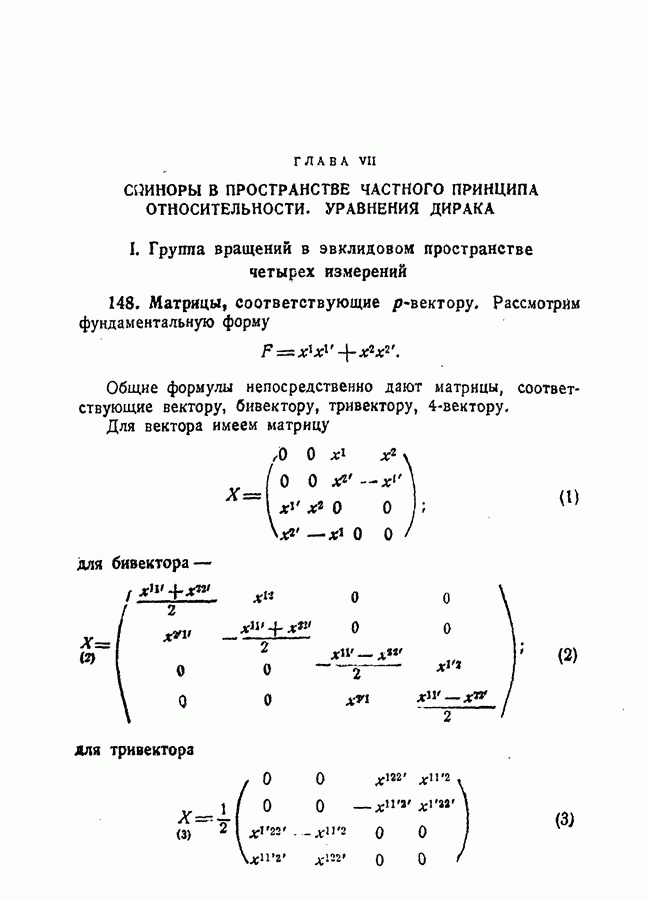
Для -вектора X имеем

Определим a priori результат применения симметрии к спинору формулой

мы расчленяем, таким образом, операцию симметрии на две, — в зависимостч от того, выбираем ли за единичный вектор, перпендикулярный к гиперплоскости II, А или — А.

Если мы исследуем, в частности, результат применения к спинору операторов базиса то получим следующее: Оператор оставляет инвариантной абсолютную величину каждой составляющей изменяя или не изменяя ее знак в зависимости от того, содержит ли составной индекс а нечетное или четное число простых индексов (относительно

составляющей следует предполагать, что она содержит четное число простых индексов, равное нулю).

Оператор обращает в нуль составляющие содержащие простой индекс и прибавляет этот индекс к тем составляющим, у которых а не содержит например, преобразует и обращает в нуль

Оператор обращает в нуль составляющие не содержащие индекса и отнимает этот индекс у тех, составной индекс а которых содержит (при условии, что индекс предварительно был переставлен на последнее место в составном индексе а); например, превращает в нуль и преобразует

97. Представление вращения.

Так как вращение является произведением четного числа симметрий то результат применения вращения к вектору или вообще -вектору определяется формулой

Преобразование спинора при вращении выражается формулой

Если положить

то предыдущие формулы примут следующий вид:

Аналогично может быть выражено отражение

причем матрица Т является произведением нечетного числа матриц, соответствующих единичным векторам.

В частности, симметрия относительно начала, которая является произведением симметрий, соответствующих а единичным взаимно перпендикулярным векторам выражается при помощи матрицы то есть матрицы, соответствующей

я-вектору единичного объема. Для вычисления этой матрицы достаточно выбрать за эти а матриц матрицы

в самом деле,

третий член этого соотношения является удвоенным скалярным произведением векторов то есть Образуя произведение, получаем с точностью до знака

Применяя правила, данные в конце п. 96, мы видим, что матрица — умножает каждую составляющую на плюс или минус единицу в зависимости от того, содержит или не содержит составной индекс а индекс 1. Следовательно, построенная выше матрица умножает каждую составляющую на Отсюда вытекает

Теорема, -вектору единичного объема соответствует скалярная матрица которая определяет симметрию относительно начала в применении к спинорам.

98. Числа Клиффорда-Липшитца.

В п. 48 была доказана неприводимость -вектора относительно группы вращений. Если мы возьмем Матрицу X, соответствующую произвольному -вектору, то элементы этой матрицы, являющиеся линейными комбинациями составляющих -вектора, при вращении преобразуются линейно между собой; отсюда следует, что или все они тождественно равны нулю (это невозможно), или линейные комбинации, которые они образуют, линейно независимы относительно составляющих -вектора. Отсюда, в частности, вытекает

Теорема. Двум различным -векторам соответствуют две различные матрицы X.

Можно пойти дальше. Рассмотрим матрицу порядка с произвольными комплексными коэффициентами элементов этой матрицы могут быть рассматриваемы как составляющие

тензора относительно группы вращений, если условиться, что вращение преобразует матрицу в Из этого тензора порядка можно выделить скаляр, вектор, бивектор, -вектор: достаточно взять матрицы, соответствующие произвольному скаляру, произвольному вектору и т. д. Мы выделим, таким образом, из полного тензора неприводимых тензоров, не эквивалентных между собой; полное число составляющих этих тензоров равно

то есть оно равно числу составляющих полного тензора. Между этими составляющими не может существовать линейных соотношений, так как в противном случае, на основании теоремы по крайней мере одни из выделенных тензоров был бы равен тождественно нулю. Таким образом, мы получили следующую теорему:

Теорема. Каждая матрица порядка может быть разложена одним и только одним способом на сумму скаляра, вектора, бивектора, -вектора.

Матрицы порядка можно рассматривать как числа гиперкомплексной системы с единицами, построенной над полем комплексных чисел; принимая за единицы этой системы матрицу 1, матрицы соответствующие единичным взаимно перпендикулярным векторам, их произведения по две, по три, по у, имеем правило умножения

Мы получаем систему гиперкомплексных чисел Клиффорда-Лип-шитца, применение которой к представлению вращений очевидно в силу сказанного выше.

Добавим, что матрица, соответствующая вектору тождественна с матрицей, соответствующей некоторому -вектору, именно: произведению Р на -вектор, дополнительный к данному -вектору. Например, учитывая, что произведение равно , имеем