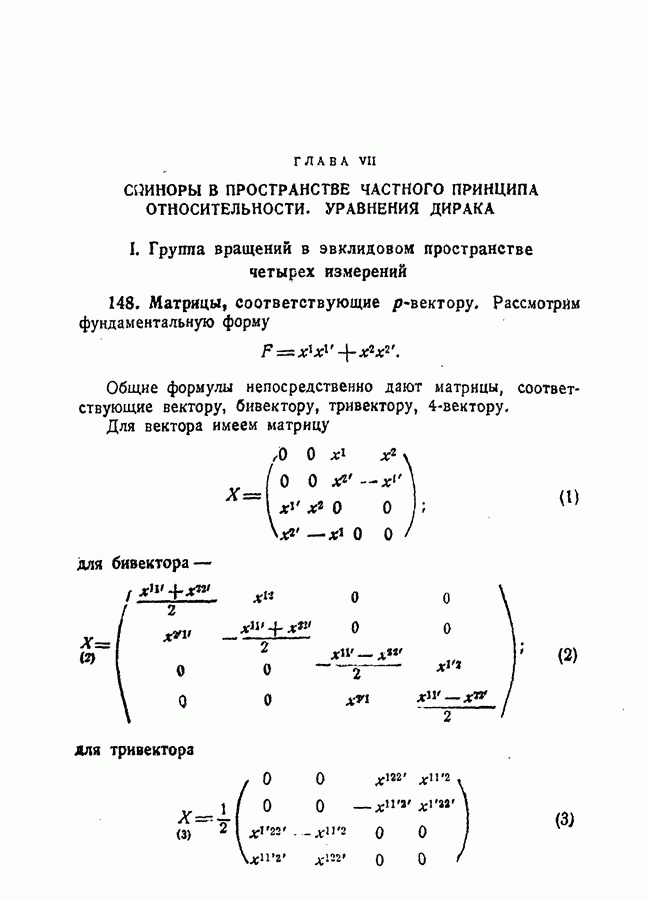
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
IV. Произведение двух спиноров и его разложение на неприводимые части
Три одночлена  образуют тензор, - эквивалентный вектору: в самом деле, они являются линейными независимыми комбинациями составляющих изотропного вектора, а изотропный вектор, рассматриваемый как тензор, эквивалентен вектору общего вида.
образуют тензор, - эквивалентный вектору: в самом деле, они являются линейными независимыми комбинациями составляющих изотропного вектора, а изотропный вектор, рассматриваемый как тензор, эквивалентен вектору общего вида.
61. Матрица С.
Рассмотрим теперь тензор 4-го порядка — произведение двух спиноров  Чтобы изучить его, введем матрицу
Чтобы изучить его, введем матрицу

она имеет. следующее замечательное свойство: каков бы ни был вектор X,

кроме того,

Тождество (9) проверяется подстановкой выражения для матрицы (п. 65); имеем:

62. Тривектор и вектор, соответствующие двум спинорам.
Рассмотрим два спинора  и
и  и форму
и форму

при применении симметрии А эта форма на основании (6) и (9) преобразуется в

то есть, только изменяет свой знак. Она определяет, таким образом, тензор, эквивалентный тривектору, который инвариантен при вращении и меняет знак при отражении. Ее явное выражение следующее:

Эта величина, действительно, при применении линейного преобразования к обоим спинорам умножается на определитель подстановки, причем определитель преобразования  равен —1, Рассмотрим теперь два спинора и произвольный вектор X и образуем форму
равен —1, Рассмотрим теперь два спинора и произвольный вектор X и образуем форму

при применении симметрии А она преобразуется на основании (2), (6) и (9) следующем образом:

то есть она инвариантна при вращениях и отражениях. Но это — билинейная форма составляющих  вектора X и произведений Отсюда следует (п. 27), что коэффициенты при
вектора X и произведений Отсюда следует (п. 27), что коэффициенты при  определяют тензор; этот тензор эквивалентен вектору, так как сумма
определяют тензор; этот тензор эквивалентен вектору, так как сумма  где
где  — составляющие некоторого вектора, инвариантна также при каждом вращении и отражении, то есть рассматриваемый тензор эквивалентен тензору ул. Определенный таким образом вектор имеет составляющие, симметричные относительно составляющих спиноров
— составляющие некоторого вектора, инвариантна также при каждом вращении и отражении, то есть рассматриваемый тензор эквивалентен тензору ул. Определенный таким образом вектор имеет составляющие, симметричные относительно составляющих спиноров  так как
так как

равенство двух первых выражений вытекает из того, что скаляр не меняется при транспонировании. Получаем следующие выражения для составляющих рассматриваемого вектора:

при  получаем изотропный вектор, соответствующий спинору при
получаем изотропный вектор, соответствующий спинору при  отметим, что скалярный Квадрат вектора равен
отметим, что скалярный Квадрат вектора равен 
Таким образом, мы получила разложение тензора  порядка
порядка  на вектор и тривектор, причем объем тривектора равен длине вектора.
на вектор и тривектор, причем объем тривектора равен длине вектора.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ГЛАВА 1. ЭВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО; ВРАЩЕНИЯ И ОТРАЖЕНИЯ
- 2. Декартовы реперы.
- 3. Приведение квадратичной формы к сумме квадратов.
- 4. Теорема инерции.
- 6. Контравариантные и ковариантные составляющие.
- II. Вращения и отражения
- 9. Симметрии.
- 10. Разложение вращения на произведение симметрий.
- 11. Непрерывность группы вращений.
- 12. Собственные и несобственные вращения.
- 13. Пространства, у которых h = 1.
- III. Мультивекторы
- 15. Мультивекторы.
- 16. Изотропные мультивекторы.
- 17. Дополнительные мультивекторы.
- 18. Сумма p-векторов.
- IV. Бивекторы и бесконечно малые вращения
- ГЛАВА II. ТЕНЗОРЫ; ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУПП; МАТРИЦЫ
- 21. Общее определение линейных представлений группы вращений.
- 22. Эквивалентные представлений.
- 23. Понятие об эвклидовом тензоре.
- 24. Другая точка зрения.
- II. Тензорная алгебра
- III. Тензоры приводимые и неприводимые
- 33. Нахождение неприводимых тензоров, которые могут быть получены из вполне приводимого тензора.
- 35. Основная теорема.
- 36. Критерий неприводимости.
- IV. Матрицы
- 42. Характеристическое уравнение. Собственные значения.
- 43. Унитарные матрицы.
- 44. Ортогональные матрицы.
- 45. Применение к разложению вещественного вращения.
- 46. Эрмитовы матрицы.
- 47. Примечание.
- V. Неприводимость p-векторов
- ГЛАВА III. СПИНОРЫ ТРЕХМЕРНОГО ПРОСТРАНСТВА.
- II. Матрицы, соответствующие векторам
- III. Представление симметрий и вращений
- 60. Операции над спинорами.
- IV. Произведение двух спиноров и его разложение на неприводимые части
- V. Случай вещественного эвклидова пространства
- 64. Сопряженные спиноры.
- 65. Скаляр и бивектор, соответствующие двум сопряженным спинорам.
- VI. Случай псевдоэвклидова пространства
- ГЛАВА IV. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ В E1
- I. Линейные представления, выражаемые при помощи спиноров
- 71. Уравнения Дирака.
- II. Бесконечно малые вращения и определение эвклидовых тензоров
- III. Линейные представления группы комплексных вращений
- 83. Линейные представления прямого произведения двух групп.
- 84. Приложения к группе комплексных вращений.
- IV. Однозначность и двузначность
- 86. Однозначность линейных представлений унимодулярной группы двух переменных.
- 86. Линейные представления вещественной проективной группы одной переменной.
- V. Линейные представления группы вращений и отражений
- 88. Случай неприводимых представлений, индуцирующих в группе вращений неприводимое представление.
- 90. Приложения.
- 91. Случай группы вращений и отражений вещественного псевдоэвклидова пространства.
- ГЛАВА V. СПИНОРЫ ПРОСТРАНСТВА …
- I. Изотропные v-плоскости и матрицы, соответствующие векторам
- II. Представление вращений и отражений при помощи матриц порядка 2^v
- 99. Тензорный характер спинора.
- 100. Неприводимость спинора.
- III. Фундаментальная полярность в пространстве спиноров, p-векторы, определяемые парой спиноров
- IV. Простые спиноры и интерпретация их как поляризованных изотропных v-векторов
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- 117. Сопряженные спиноры.
- 118. Произведение двух сопряженных спиноров.
- 119. h-векторы, построенные на двух сопряженных спинорах.
- ГЛАВА VI. СПИНОРЫ ПРОСТРАНСТВА E2
- I. Изотропные v-плоскости и полуспиноры
- 122. Простые полуспиноры, определяемые как изотропные поляризованные v-векторы.
- 123. Условия простоты полуспинора.
- 124. Пересечение двух изотропных v-плоскостей.
- II. Матрицы, соответствующие p-векторам. Представление вращений и отражений
- 126. Применение симметрии к спинору.
- 127. Две группы вращений и отражений в применении к спинорам.
- 128. Неприводимость спинора и полуспиноров.
- 120. Матрицы порядка 2^v разложенные на суммы p-векторов.
- III. Разложение произведения двух спиноров
- 132. Разложение произведения двух полуспиноров относительно группы вращений.
- 134. Применение к группе вращеяиб для v нечетного.
- 135. Случай v четного.
- 136. Примечание.
- IV. Частные случаи
- 137. Случай v = 3.
- 188. Случай v = 4. Фундаментальная трилинейная форма.
- 139. Принцип тройственности.
- 140. Параллелизм в пространстве E2.
- 141. Формула Бриоски.
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- ГЛАВА VII. СПИНОРЫ В ПРОСТРАНСТВЕ ЧАСТНОГО ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ. УРАВНЕНИЯ ДИРАКА
- II. Разложение произведения двух спиноров
- III. Сопряженные векторы и слияоры в пространстве частного принципа относительности
- IV. Уравнения Дирака
- ГЛАВА VIII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
- II. Представления группы вращений и отражений Лоренца
- III. Линейные представления группы вращений вещественного эвклидова пространства
- ГЛАВА IX. СПИНОРЫ И УРАВНЕНИЯ ДИРАКА В РИМАНОВОИ ГЕОМЕТРИИ
- II. Спинорные поля в римановой геометрии
- БИБЛИОГРАФИЯ