ГЛАВА IX. СПИНОРЫ И УРАВНЕНИЯ ДИРАКА В РИМАНОВОИ ГЕОМЕТРИИ

I. Спинорные поля в эвклидовой геометрии

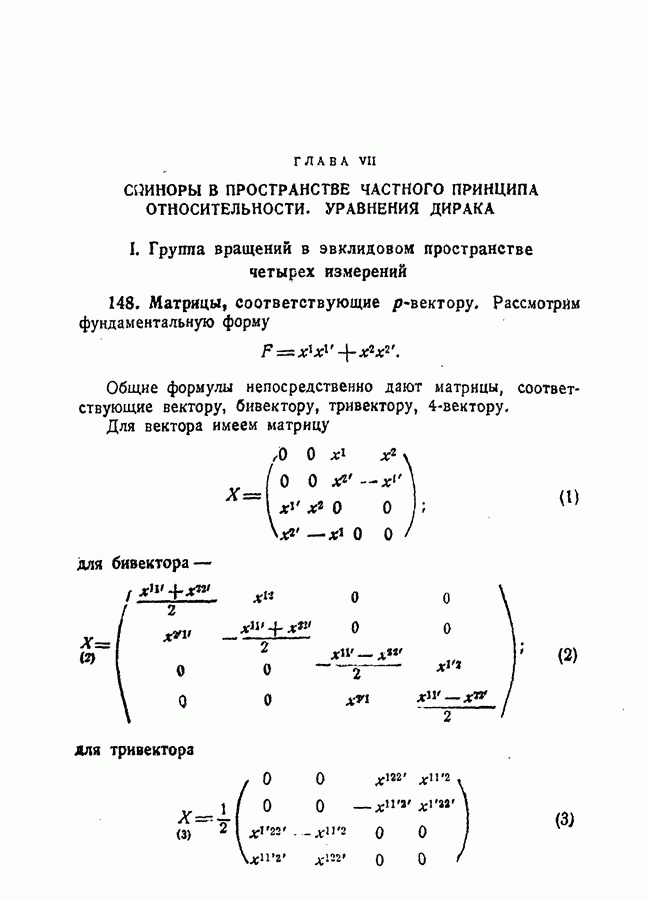
172. Бесконечно малые вращения в применении к спинорам.

В п. 19 было показано, что каждое бесконечно малое вращение эвклидова пространства определяется тензором, эквивалентным бивектору. Мы сейчас снова получим этот результат другим методом, который в то же время даст бесконечно малое вращение спиноров.

Сначала рассмотрим простое вращение на угол а, получающееся в результате применения двух симметрий, соответствующих двум единичным векторам, образующим между собой угол у.

Обозначим через первый из этих единичных векторов, через — единичный вектор, перпендикулярный к первому и лежащий в -плоскости простого вращения; тогда рассматриваемое вращение определится матрицей

Если мы предположим, что угол а — бесконечно малый, то главная часть этой матрицы равна

Применяя ее к вектору X, получим

применяя к спинору , имеем

Следовательно, обозначив через матрицу, соответствующую бивектору имеем бесконечно малое преобразование:

Если мы отнесем, например, пространство к векторам базиса причем

то бесконечно малое вращение, определяемое символом

даст в применении к вектору

Величина, стоящая в квадратных скобках, равна

Таким образом, имеем

откуда

Формула (2) дает

Например, для сохраняя обозначения главы III, можно положить

откуда, учитывая выражений для матриц (п. 55), имеем

учитывая введенные выше общие обозначения, имеем для коэффициентов следующие значения:

173. Другая интерпретация.

Полученные результаты можно интерпретировать иначе. Рассмотрим составляющие фиксированного вектора и фиксированного спинора, отнесенные последовательно к двум декартовым реперам и из которых новый получается из старого при помощи заданного бесконечно малого вращения. Если мы будем отмечать штрихом составляющие вектора или спинора в новом репере, то вектор или спинор, имеющий эти новые составляющие в старом репере, получается из данного вектора или спинора при помощи бесконечно малого вращения, обратного данному. Таким образом, имеем теорему:

Теорема. Если задан вектор X или спинор отнесенный к реперам и причем получается при помощи бесконечно малого вращения то бесконечно малые приращения составляющих этого вектора или спинора определяются формулами

Первая из них может быть записана также в виде:

В частности, формулы (4) дают

174. Абсолютное дифференцирование вектора и спинора.

Рассмотрим в пространстве векторное или спинорное поле, причем каждый вектор (или спинор) отнесен некоторой точке пространства. Представим, что каждой точке пространства отнесена декартова координатная система, относительно которой, фундаментальная форма сохраняет одни и те же коэффициенты (то есть координатные реперы в различных точках равны в смысле эвклидовой геометрии).

Обозначим через бивектор, определяющий бесконечно малое вращение, которое переводит репер с началом М в положение, параллельное реперу имеющему начало в бесконечно близкой точке М; обозначим составляющие этого бивектора через Пусть - составляющие вектора поля относительно с началом в М, в -составляющие вектора поля, отнесенные к с началом в М. Чтобы получить из первого вектора второй, можно сначала перейти от первого к вектору с началом имеющему относительно те же ставляющие при помощи вращения переводящего в затем перейти ко второму вектору, складывая

Элементарное геометрическое приращение получаемое вектором поля, определяется согласно (3) формулами

для поля спиноров имеем аналогично

обозначает относительное приращение, или — переносное приращение. и являются абсолютными дифференциалами вектора и спинора.

175. Уравнения Дирака.

Предположим, что пространственно-временной континуум частного принципа относительности отнесен к галилеевым реперам, имеющим начала в различных точках

пространства; пусть

— скалярной квадрат вектора, соединяющего точку М с бесконечно близкой точкой М; контравариантные составляющие вектора Матрица О, определяющая бесконечно малое вращение, которое переводит репер с началом в точке М в положение, параллельное реперу имеющему начало в точке имеет вид (п. 149)

причем II есть матрица

Положим

где — функция точки; если пространство отнести к реперу вектор (п. 167) должен быть заменен следующим:

причем символы имеют следующее значение: полагаем

имеем

В уравнениях (13) мы ввели ковариантные составляющие связанные с контравариантными соотношениями:

Уравнения Дирака выражаются следующим матричным соотношением:

причем матрица как и в п. 157, имеет вид где каждый элемент обозначает матрицу второго порядка.