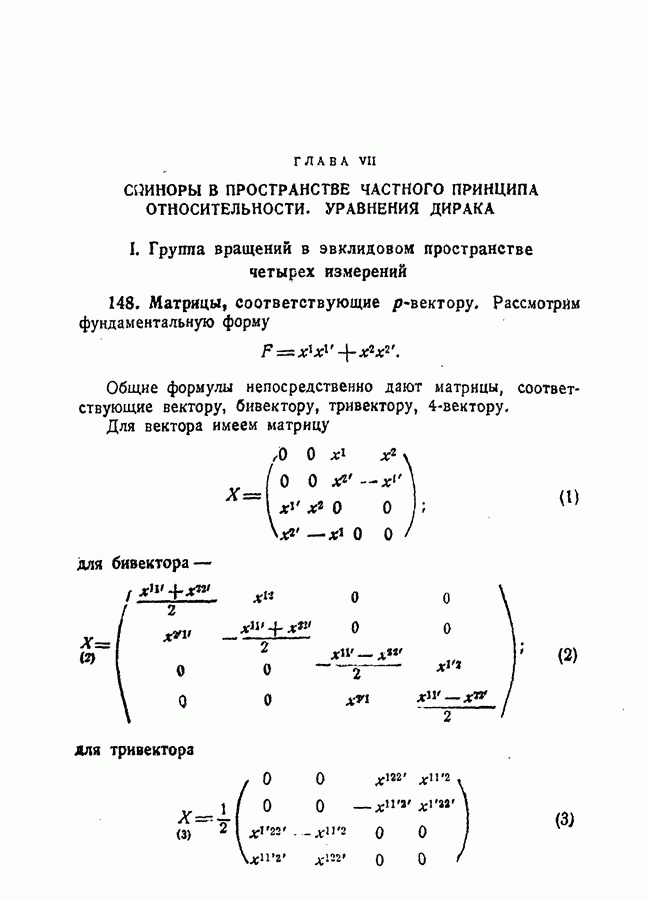
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
V. Случай вещественного эвклидова пространства
Рассмотрим группу вещественных вращений и отражений. Мы не будем менять выбранного выражения для фундаментальной формы; достаточно предполагать координату  вещественной, а
вещественной, а  комплексно сопряженными. Каждое вращение и в рассматриваемом случае есть произведение четного числа
комплексно сопряженными. Каждое вращение и в рассматриваемом случае есть произведение четного числа  симметрий, соответствующих вещественным единичным векторам А; каждое отражение есть произведение нечетного числа
симметрий, соответствующих вещественным единичным векторам А; каждое отражение есть произведение нечетного числа  таких симметрий.
таких симметрий.
112. Сопряженные векторы и p-векторы.
Из векторов базиса  первый вещественный, остальные попарно комплексно сопряженные. Отметим, что соответствующие матрицы
первый вещественный, остальные попарно комплексно сопряженные. Отметим, что соответствующие матрицы  обладают тем свойством, что две матрицы, соответствующие комплексно сопряженным векторам, являются взаимно транспонированными. Следовательно, рассматривая матрицы
обладают тем свойством, что две матрицы, соответствующие комплексно сопряженным векторам, являются взаимно транспонированными. Следовательно, рассматривая матрицы  двух
двух
комплексно сопряженных векторов, будем иметь

откуда

В частности, матрица вещественного вектора является эрмитовой

Переходя от векторов к  -векторам, получим, что
-векторам, получим, что  -вектор, сопряженный с X, есть
-вектор, сопряженный с X, есть  . Таким образом, вещественный
. Таким образом, вещественный  -вектор имеет эрмитову матрицу, если
-вектор имеет эрмитову матрицу, если  или
или  и эрмитову антисимметрическую, если
и эрмитову антисимметрическую, если  или
или 
113. Сопряженные спиноры.
Важно установить, когда два спинора должны быть рассматриваемы как сопряженные. Если эти спиноры простые, необходимо, чтобы они соответствовали двум изотропным комплексно сопряженным  -плоскостям. Но если
-плоскостям. Но если  — Простой спинор,
— Простой спинор,  -вектор изотропной
-вектор изотропной  -плоскрсти, которую этот спинор определяет, то имеем соотношение
-плоскрсти, которую этот спинор определяет, то имеем соотношение  Пусть I — один из простых спиноров, определяющих сопряженную
Пусть I — один из простых спиноров, определяющих сопряженную  -плоскость,
-плоскость,  — вектор, сопряженный с X; имеем
— вектор, сопряженный с X; имеем

откуда на основании формулы 

так  то естественно положить
то естественно положить  то есть
то есть 
Чтофы оправдать эту формулу и уточнить значение  рассмотрим изотропный у-вектор, соответствующий
рассмотрим изотропный у-вектор, соответствующий  он дается
он дается
выражением

заменим в этой формуле  -вектор X его сопряженным и
-вектор X его сопряженным и  через с; мы должны получить выражение, комплексно сопряженное первому.
через с; мы должны получить выражение, комплексно сопряженное первому.
Имеем

учитывая, что второй член равен своему транспонированному, и принимая во внимание соотношения (14), (15) (п. 101), получаем

то

Таким образом, приходим к следующему соглашению:
Спинор, сопряженный с  есть
есть 
Отметим, что спинор, сопряженный с сопряженным от  является спинором
является спинором  . Переход от спинора к его сопряженному определяет в пространстве спиноров антиинволюцию, эта антиинволюция первого рода, если
. Переход от спинора к его сопряженному определяет в пространстве спиноров антиинволюцию, эта антиинволюция первого рода, если  или —
или —  она — второго рода, если
она — второго рода, если  или
или  В первом случае в пространстве спиноров существует область вещественности, образованная спинорами, равными своим сопряженным. При
В первом случае в пространстве спиноров существует область вещественности, образованная спинорами, равными своим сопряженным. При  вещественные спиноры — те, для которых
вещественные спиноры — те, для которых  что дает уравнения
что дает уравнения

114. Тензор ...
Спинор, сопряженный с данным, при отражении не преобразуется вполне как спинор. В самом деле,
при вещественной симметрии А, преобразующей  сопряженный спинор преобразуется в
сопряженный спинор преобразуется в

Если  четкое,
четкое,  преобразуется вполне как спинор; но при
преобразуется вполне как спинор; но при  нечетном мы имеем преобразование по закону спинора только при вращении, но не при отражении.
нечетном мы имеем преобразование по закону спинора только при вращении, но не при отражении.
Мы получим разложение тензора  исходя из
исходя из  -векторов, определяемых разложением тензора в котором заменяем
-векторов, определяемых разложением тензора в котором заменяем  на спинор, сопряженный с
на спинор, сопряженный с  Рассмотрим, таким образом, выражение
Рассмотрим, таким образом, выражение

При вещественной симметрии А это выражение умножается на  (второй множитель получается потому, что спинор, сопряженный с
(второй множитель получается потому, что спинор, сопряженный с  преобразуется как спинор только в том случае, если
преобразуется как спинор только в том случае, если  четное). Следовательно, рассматриваемое выражениедает,
четное). Следовательно, рассматриваемое выражениедает,  -вектор или
-вектор или  -вектор в зависимости от четности или нечетности
-вектор в зависимости от четности или нечетности 
Тензор разлагается, таким образом, на  неприводимых тензоров, которые являются
неприводимых тензоров, которые являются  -векторами.
-векторами.
В частности, для  имеем скаляр (пренебрегаем постоянным множителем
имеем скаляр (пренебрегаем постоянным множителем 

Важно отметить, что полученные таким образом  -век-торы все вещественны.
-век-торы все вещественны.
Достаточно показать, что если  - вектор X вещественный, то выражение вещественно или чисто мнимо, так как тогда составляющие
- вектор X вещественный, то выражение вещественно или чисто мнимо, так как тогда составляющие  -вектора или
-вектора или  -вектора будут, с точностью до множителя, вещественными величинами. Но величина
-вектора будут, с точностью до множителя, вещественными величинами. Но величина
комплексно сопряженная с равна

Что и требовалось доказать.
Таким образом, чтобы иметь вещественные составляющие мультивектора, определенного двумя сопряженными спинорами, достаточно исходить из выражения

115. Пример  При
При  тензор разлагается на три неприводимых тензора:
тензор разлагается на три неприводимых тензора:
1° скаляр

2°  -вектор, определяемый формой
-вектор, определяемый формой

его контравариантные составляющие суть

3° Бивектор, определяемый формой его 10 ковариантных составляющих определяются формулами:

Мера  -вектора и бивектора с точностью до множителя равна
-вектора и бивектора с точностью до множителя равна

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ГЛАВА 1. ЭВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО; ВРАЩЕНИЯ И ОТРАЖЕНИЯ
- 2. Декартовы реперы.
- 3. Приведение квадратичной формы к сумме квадратов.
- 4. Теорема инерции.
- 6. Контравариантные и ковариантные составляющие.
- II. Вращения и отражения
- 9. Симметрии.
- 10. Разложение вращения на произведение симметрий.
- 11. Непрерывность группы вращений.
- 12. Собственные и несобственные вращения.
- 13. Пространства, у которых h = 1.
- III. Мультивекторы
- 15. Мультивекторы.
- 16. Изотропные мультивекторы.
- 17. Дополнительные мультивекторы.
- 18. Сумма p-векторов.
- IV. Бивекторы и бесконечно малые вращения
- ГЛАВА II. ТЕНЗОРЫ; ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУПП; МАТРИЦЫ
- 21. Общее определение линейных представлений группы вращений.
- 22. Эквивалентные представлений.
- 23. Понятие об эвклидовом тензоре.
- 24. Другая точка зрения.
- II. Тензорная алгебра
- III. Тензоры приводимые и неприводимые
- 33. Нахождение неприводимых тензоров, которые могут быть получены из вполне приводимого тензора.
- 35. Основная теорема.
- 36. Критерий неприводимости.
- IV. Матрицы
- 42. Характеристическое уравнение. Собственные значения.
- 43. Унитарные матрицы.
- 44. Ортогональные матрицы.
- 45. Применение к разложению вещественного вращения.
- 46. Эрмитовы матрицы.
- 47. Примечание.
- V. Неприводимость p-векторов
- ГЛАВА III. СПИНОРЫ ТРЕХМЕРНОГО ПРОСТРАНСТВА.
- II. Матрицы, соответствующие векторам
- III. Представление симметрий и вращений
- 60. Операции над спинорами.
- IV. Произведение двух спиноров и его разложение на неприводимые части
- V. Случай вещественного эвклидова пространства
- 64. Сопряженные спиноры.
- 65. Скаляр и бивектор, соответствующие двум сопряженным спинорам.
- VI. Случай псевдоэвклидова пространства
- ГЛАВА IV. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ В E1
- I. Линейные представления, выражаемые при помощи спиноров
- 71. Уравнения Дирака.
- II. Бесконечно малые вращения и определение эвклидовых тензоров
- III. Линейные представления группы комплексных вращений
- 83. Линейные представления прямого произведения двух групп.
- 84. Приложения к группе комплексных вращений.
- IV. Однозначность и двузначность
- 86. Однозначность линейных представлений унимодулярной группы двух переменных.
- 86. Линейные представления вещественной проективной группы одной переменной.
- V. Линейные представления группы вращений и отражений
- 88. Случай неприводимых представлений, индуцирующих в группе вращений неприводимое представление.
- 90. Приложения.
- 91. Случай группы вращений и отражений вещественного псевдоэвклидова пространства.
- ГЛАВА V. СПИНОРЫ ПРОСТРАНСТВА …
- I. Изотропные v-плоскости и матрицы, соответствующие векторам
- II. Представление вращений и отражений при помощи матриц порядка 2^v
- 99. Тензорный характер спинора.
- 100. Неприводимость спинора.
- III. Фундаментальная полярность в пространстве спиноров, p-векторы, определяемые парой спиноров
- IV. Простые спиноры и интерпретация их как поляризованных изотропных v-векторов
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- 117. Сопряженные спиноры.
- 118. Произведение двух сопряженных спиноров.
- 119. h-векторы, построенные на двух сопряженных спинорах.
- ГЛАВА VI. СПИНОРЫ ПРОСТРАНСТВА E2
- I. Изотропные v-плоскости и полуспиноры
- 122. Простые полуспиноры, определяемые как изотропные поляризованные v-векторы.
- 123. Условия простоты полуспинора.
- 124. Пересечение двух изотропных v-плоскостей.
- II. Матрицы, соответствующие p-векторам. Представление вращений и отражений
- 126. Применение симметрии к спинору.
- 127. Две группы вращений и отражений в применении к спинорам.
- 128. Неприводимость спинора и полуспиноров.
- 120. Матрицы порядка 2^v разложенные на суммы p-векторов.
- III. Разложение произведения двух спиноров
- 132. Разложение произведения двух полуспиноров относительно группы вращений.
- 134. Применение к группе вращеяиб для v нечетного.
- 135. Случай v четного.
- 136. Примечание.
- IV. Частные случаи
- 137. Случай v = 3.
- 188. Случай v = 4. Фундаментальная трилинейная форма.
- 139. Принцип тройственности.
- 140. Параллелизм в пространстве E2.
- 141. Формула Бриоски.
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- ГЛАВА VII. СПИНОРЫ В ПРОСТРАНСТВЕ ЧАСТНОГО ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ. УРАВНЕНИЯ ДИРАКА
- II. Разложение произведения двух спиноров
- III. Сопряженные векторы и слияоры в пространстве частного принципа относительности
- IV. Уравнения Дирака
- ГЛАВА VIII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
- II. Представления группы вращений и отражений Лоренца
- III. Линейные представления группы вращений вещественного эвклидова пространства
- ГЛАВА IX. СПИНОРЫ И УРАВНЕНИЯ ДИРАКА В РИМАНОВОИ ГЕОМЕТРИИ
- II. Спинорные поля в римановой геометрии
- БИБЛИОГРАФИЯ