III. Линейные представления группы вращений вещественного эвклидова пространства

166. Э. Картан определил все неприводимые линейные представления группы вращений вещественного эвклидова пространства измерений. С другой стороны, на основании исследот ваний Г. Вейля (п. 81, примечание 3) мы знаем, что теорема о полной приводимости имеет место для всех линейных представлений этой группы. Эти результаты распространяются непосредственно на группу собственных вращений вещественных псевдоэвклидовых пространств. Метод, примененный в пп. 82—84, позволяет получить отсюда все представления группы комплексных вращений.

Следует различать случаи нечетного и четного

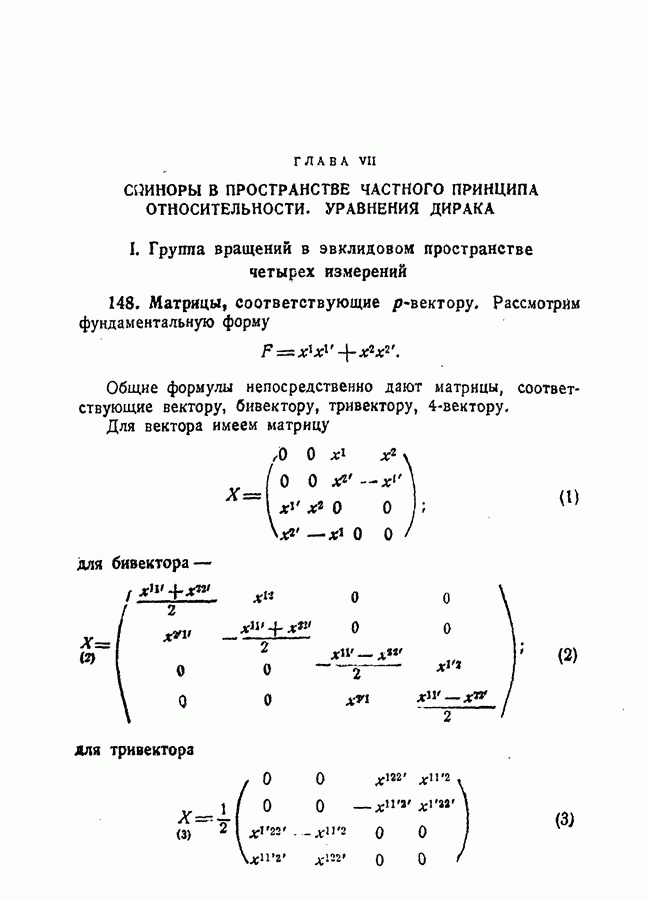
167. Случай пространства ...

За фундаментальную форму примем

Каждое неприводимое линейное представление группы вращений (собственных) получается при помощи выражения

если к нему применять различные вращения группы. Показатели являются произвольными целыми числами, положительными или равными нулю. Например, представление дает -вектор; в самом деле, -вектор, соответствующий спинору Б и определяемый выражением содержит составляющую следовательно, применяя к различные вращения, мы получим

неприводимый тензор, эквивалентный тому, который получается при применении к составляющей различных вращений, а в этом последнем случае мы получаем -вектор.

168. Случай пространства ...

Возьмем фундаментальную форму в виде

Каждое неприводимое линейное представление группы вращений получается при помощи выражения

если к нему применять различные вращения группы.

При получаем полуспинор с четиым числом индексов; при полуспинор с нечетным

числом индексов. Тензоры являются полу-У-векторами первого и второго рода; тензор является -вектором. Чтобы доказать последнее свойство, достаточно заметить, что выражение

дает -вектор, соответствующий двум полуспинорам и для этого -вектора имеем

тензор, получаемый при изменении различных вращений к произведению эквивалентен, таким образом, тензору, который получается при применении различных вращений к то есть -вектору.

169. Неприводимые линейные представления группы вращений и отражений.

В пространстве каждое отражение оставляет инвариантным каждый основных неприводимых тензоров, определяемых составляющими следовательно, если задано какое-нибудь линейное представление

группы вращений и отражений, индуцирующее для группы вращений неприводимое представление, то каждое отражение преобразует одну из неприводимых частей в другую эквивалентную. Таким образом

Каждое неприводимое представление группы вращений, а отражений (собственных) пространства индуцирует в группе вращений неприводимое представление; обратно, каждому неприводимому представлению группы вращений соответствует два неприводимых неэквивалентных представления группы вращений и отражений.

В случае пространства любое отражение оставляет инвариантным каждый неприводимых тензоров, определяемых но преобразует полуспинор в полуспинор другого рода. Таким образом,

Для группы вращений и отражений (собственных) пространства существует два рода неприводимых линейных представлений:

1° каждый неприводимый тензор, для которого дает два неприводимых неэквивалентных представления группы вращений и отражений;

2° совокупность составляющих двух тензоров при дает одно а только одно неприводимое представление группы вращений и отражений.

Отметим, что тензоры первой категории, или вернее, половина этих тензоров, получаются при применении различных вращений к выражению

так как выражение задает -вектор. Как пример неприводимого тензора второй категории достаточно привести спинор.

Следует отметить существенное различие между пространствами с четным и нечетным числом измерений.

170. Частный случай.

В случае тремя первыми основными неприводимыми представлениями группы вращений (собственных) являются полуспинор первого рода, полуспинор второго рода и вектор. Мы показали в что

к группе вращений можно присоединить пять других семейств преобразований таким образом, что преобразования из каждого семейства производят над тремя рассматриваемыми тензорами одну и ту же перестановку, причем эта перестановка меняется от одного семейства к другому. Составляющие неприводимых тензоров полной группы, составленной из шести указанных семейств, получаются тогда присоединением к составляющим тензора составляющих тензоров, получающихся при помощи применения любой перестановки к трем первым показателям Отметим, что четвертый основной тензор, именно бивектор, инвариантен при каждом преобразовании полной группы. Нетрудно проверить, например, что тензор где составляющие двух полуспиноров одного и того же рода, эквивалентен бивектору, так как в бивекторе, определяемом выражением составляющая равна — применение различных вращений к выражению дает, таким образом, тензор, эквивалентный бивектору.

171. Примечание.

Метод Г. Вейля для определения неприводимых линейных представлений замкнутых групп позволяет легко найти порядок различных указанных выше неприводимых линейных представлений. Приведем один пример, относящийся к пространству Порядок неприводимого представления равен

где

Например, порядок представления (1, 1, 1, 0) равен 350.