ГЛАВА IV. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ В E1

I. Линейные представления, выражаемые при помощи спиноров

Мы укажем простой метод построения в эвклидовом комплексном иди вещественном пространстве трех измерений неограниченной совокупности неприводимых линейных представлений группы вращений и группы вращений и отражений. В дальнейшем мы увидим, что не существует других представ лений, по крайней мере в вещественном пространстве, и что, кроме того, каждое линейное представление этих групп вполне приводимо. На основании теоремы, приводимой ниже, каждое линейное представление любой из рассматриваемых вещественных групп дает линейное представление соответствующей комплексной группы, и оба эти представления одновременно приводимы или неприводимы.

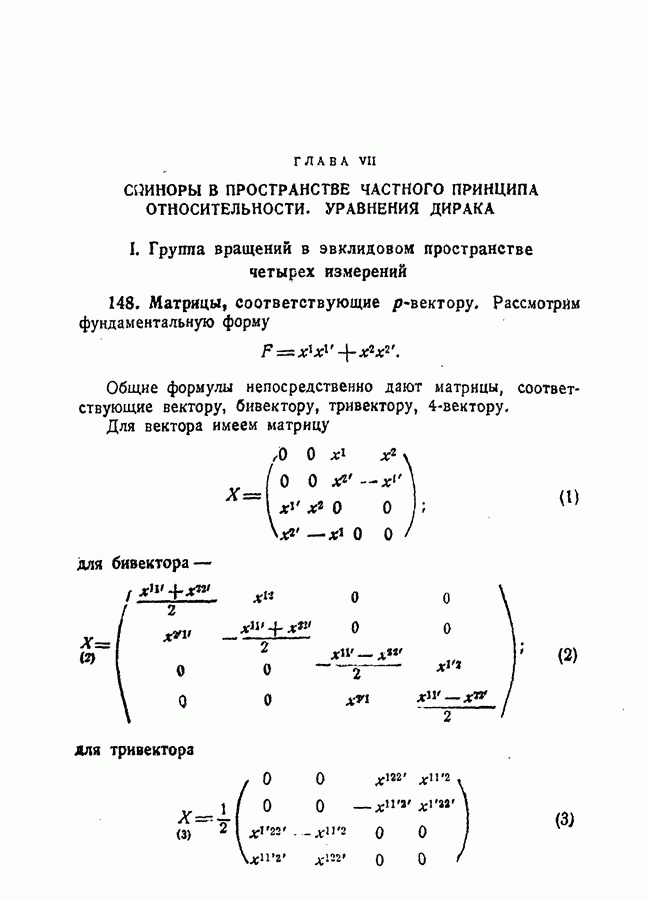
67. Представление Dp и его производящий полином.

Рассмотрим спинор Совокупность однородных полиномов степени от и образует тензор и дает линейное представление группы вращений. Можно символически представить этот тензор при помощи производящего полинома где — произвольные параметры; это надо понимать так, что коэффициенты при различных одночленах, образованных из в этом полиноме, взятом в развернутом виде, определяют составляющие тензора. Мы будем обозначать этот тензор или соответствующее линейное представление символом

Теорема. Представление неприводимо.

Достаточно доказать эту теорему для группы комплексных вращений. Рассмотрим преобразование

определяющее вращение на вещественный угол вокруг оси При этом преобразовании одночлен получает множитель Если не имеет специально подобранного частного значения, множители, соответствующие разным составляющим тензора, все различны между собой. Предположим, что представление приводимо. Тогда существовал бы тензор образованный при помощи целых полиномов порядка от пусть

— один из этих полиномов; рассматриваемое вращение преобразует его в

повторяя раз эту операцию, мы получим независимых линейных комбинаций от

Отсюда следует, что существует, по крайней мере, один одночлен входящий в состав тензора и что, следовательно, все полиномы также входят в Если предположить, что четыре 1 зстоянных не равны нулю, мы получим, что коэффициент при в соответствующем полиноме не равен нулю. Таким образом, тензор содержит то есть и следовательно, и все одночлены

При полученный тензор порядка является скаляром; при мы имеем спинор, при — вектор, в само деле, величины дают преобразование составляющих вектора, если от них взять соответствующие линейные комбинации.

Существует другое представление порядка группы вращений и отражений, оно получается при помощи тех же

составляющих, но в предположении, что при отражении эти составляющие преобразуются с помощью рассмотренной выше подстановки вместе с изменением знаков у всех составляющих. Будем обозначать это новое представление символом в отличие от предыдущего, которое условимся обозначать на основании сделанного выше соображения оно не эквивалентно первому. относится к спинору второго рода, — к бивектору, к тривектору (т. е. ). За производящий полином представления можно выбрать выражение

68. Разложение

Пусть — переменные представлений Произведения приводят к новому линейному представлению порядка которое мы будем обозначать через . В общем случае это представление приводимо, и мы разложим его на неприводимые представления.

Заметим прежде всего, что если и - два произвольных спинора, то производящие полиномы

определяют эквивалентные представления; это вытекает из того, что коэффициенты при различных одночленах в этих полиномах преобразуются одинаковым образом при каждом вращении и отражении, так как и преобразуются так же, как

На основании сделанного замечания можно выбрать за составляющие тензора полиномы от степени

относительно относительно Рассмотрим полиномы

предполагая Каждый из них определяет линейное неприводимое представление, именно

последнее имеет знак или в зависимости от четности или нечетности числа

Составляющие каждого из этих представлений являются составляющими рассматриваемого представления. Число этих составляющих равно

а это есть как раз порядок данного представления. Эти составляющие линейно независимы; в противном случае в приводимом тензоре, определяемом найденными неприводимыми тензорами, по крайней мере, один из этих тензоров имел бы все свои составляющие равными нулю а это не имеет места. Следовательно, имеем теорему:

Теорема. Произведете двух линейных неприводимых представлений вполне приводимо и разлагается на неприводимые представления:

69. Частные случаи. Гармонические полиномы.

Случай представлений для которых индекс есть целое число рассмотрим особо. Для производящий полином

может быть заменен другим, линейным относительно составляющих вектора. В самом деле, имеем

где знак обозначает, что левые части этих соотношений преобразуются, как соответствующие правые; следовательно, за производящий полином тензора можно взять

Таким образом, за производящий полином тензора можно принять

Соответствующий тензор имеет в качестве составляющих однородных полиномов порядка от это — гармонические полиномы. В самом деле, непосредственное вычисление показывает, что

Произведение то есть произведение двух векторов, разлагается на три неприводимых представления Первое дает тензор

эквивалентный тензору

определяемому гармоническими полиномами второго порядка;

второе представление дает бивектор

наконец, третье — скаляр

70. Приложения.

Рассмотрим векторное поле каждой точке пространства отнесен вектор с составляющими являющимися заданными функциями

При движении или отражении величины преобразуются, как произведения составляющих двух векторов с началом в точке О:

Определим все линейные соотношения с постоянными коэффициентами между которые остаются инвариантными при движениях. Мы должны, следовательно, выполнить разложение произведения двух векторов (символических) и приравнять нулю составляющие одного или нескольких неприводимых тензоров, дающих это разложение. Беря один из этих тензоров, мы получим одну из следующих систем:

Случай с) дает векторные соленоидальные поля (с нулевой дивергенцией); случай b) — потенциальные (безвихревые) поля; случай а) — поле скороттей движения конформно изменяемого тела.

Если бы мы рассматривали группу движений в собственном смысле (без отражений), то система

где — некоторая постоянная, была бы также инвариантной; при движении, сопровождаемом симметрией, она преобразуется в аналогичную систему, причем постоянная заменяется на . Дивергенция векторного поля, удовлетворяющего этой системе равна нулю.