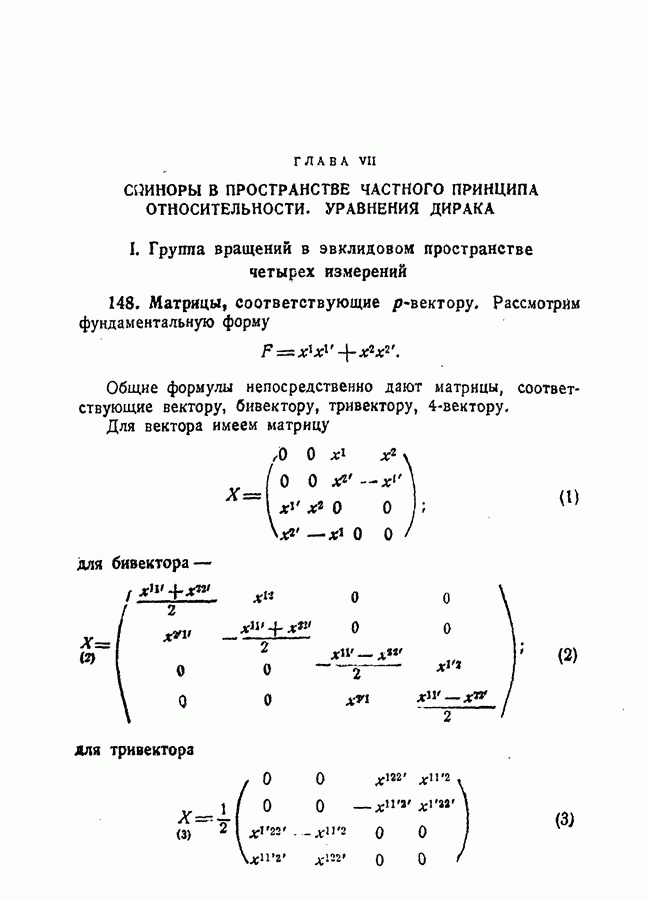
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА V. СПИНОРЫ ПРОСТРАНСТВА ...
Спиноры в эвклидовом пространстве нечетного числа измерений  мы введем при помощи рассмотрения
мы введем при помощи рассмотрения  -мерных полностью изотропных плоскостей, проходящих через начало координат О. Систему декартовых координат х мы выберем таким образом, чтобы фундаментальная форма имела следующий вид:
-мерных полностью изотропных плоскостей, проходящих через начало координат О. Систему декартовых координат х мы выберем таким образом, чтобы фундаментальная форма имела следующий вид:

Координаты х можно также рассматривать как контравариантные составляющие вектора х. В первых разделах этой главы мы будем иметь дело с комплексной областью. Плоскости, которые мы будем рассматривать, проходят все через начало.
I. Изотропные v-плоскости и матрицы, соответствующие векторам
92. 2^v уравнений изотропной у-плоскости.
Нетрудно видеть, что уравнения, определяющие изотропную плоскость (в которой все векторы изотропны), устанавливают по крайней мере одно соотношение между  в противном случае было бы невозможно обратить в нуль форму
в противном случае было бы невозможно обратить в нуль форму  принимая за
принимая за  линейные формы от
линейные формы от  Таким образом, число измерений изотропной плоскости не больше у. Мы установив сейчас вид уравнений изотропной плоскости, предполагая общий случай, когда между
Таким образом, число измерений изотропной плоскости не больше у. Мы установив сейчас вид уравнений изотропной плоскости, предполагая общий случай, когда между  не существует ни одного линейного соотношения.
не существует ни одного линейного соотношения.
Пусть

единственное соотношение между  причем коэффициент
причем коэффициент  не равен нулю. Учитывая это соотношение,
не равен нулю. Учитывая это соотношение,
приводим полином  к следующему виду:
к следующему виду:

а это позволяет положить

Уравнения (1) и (2) определяют искомую  -плоскость, К ним мы прибавим новые. Образуем комбинацию
-плоскость, К ним мы прибавим новые. Образуем комбинацию

и положим

получаем новые уравнения

причем коэффициенты. имеют характер составляющих тривектора (меняют знак при нечетной перестановке индексов). Образуем теперь комбинацию

и положим

получаем новые уравнения

причем коэффициенты  имеют характер составляющих
имеют характер составляющих  -вектора.
-вектора.
Продолжая далее, мы введем  коэффициентов
коэффициентов  обладающих тем свойством, что они сохраняют знак при четной перестановке индексов и меняют на обратный при нечетной, и
обладающих тем свойством, что они сохраняют знак при четной перестановке индексов и меняют на обратный при нечетной, и  линейных форм
линейных форм  обладающих тем же свойством. Величины где через а обозначен составной индекс:
обладающих тем же свойством. Величины где через а обозначен составной индекс:  определяются рекуррентно через
определяются рекуррентно через  Если
Если  четное, то
четное, то

если  нечетное, то
нечетное, то

Формы  определяются соотношениями:
определяются соотношениями:

Отметим еще, что каждое  с четным числом индексов
с четным числом индексов  может быть выражено с точностью до отрицательной степени
может быть выражено с точностью до отрицательной степени  при помощи суммы
при помощи суммы

в которой  суть индексы
суть индексы  расположенные в таком порядке, чтобы перестановка
расположенные в таком порядке, чтобы перестановка  была одинаковой четности с перестановкой
была одинаковой четности с перестановкой  два члена этой суммы, содержащие одинаковые множители (с точностью до знака), учитываются только один раз.
два члена этой суммы, содержащие одинаковые множители (с точностью до знака), учитываются только один раз.
2’ уравнений  параметрами определяют в случае
параметрами определяют в случае  изотропную
изотропную  -плоскость, причем
-плоскость, причем  должны удовлетворять соотношениям а) и
должны удовлетворять соотношениям а) и  . В дальнейшем (п. 106) мы увидим, что в случае
. В дальнейшем (п. 106) мы увидим, что в случае  эти уравнения также могут определять изотропную
эти уравнения также могут определять изотропную  -плоскость, если удовлетворяют соотношениям а),
-плоскость, если удовлетворяют соотношениям а),  и дополнительным, которые мы получим; мы увидим также, что таким образом может быть получена каждая изотропная
и дополнительным, которые мы получим; мы увидим также, что таким образом может быть получена каждая изотропная  -плоскость.
-плоскость.
93. Матрица, соответствующая вектору.
Мы будем называть спинором систему  произвольных величин вообще говоря не связанных соотношениями а) и
произвольных величин вообще говоря не связанных соотношениями а) и  и преобразующихся при вращениях и отражениях по законам, которые мы введем в дальнейшем (пп. 96 и 97). Мы убедимся a posteriori, что такое введение операций вращения и отражения совместимо со свойством определенного класса спиноров соответствовать изотропной
и преобразующихся при вращениях и отражениях по законам, которые мы введем в дальнейшем (пп. 96 и 97). Мы убедимся a posteriori, что такое введение операций вращения и отражения совместимо со свойством определенного класса спиноров соответствовать изотропной  -плоскости.
-плоскости.
Рассмотрим теперь  форм
форм  и в каждой из них коэффициенты при Если расположить
и в каждой из них коэффициенты при Если расположить  составных индексов в определенном порядке, то эти коэффициенты могут быть приняты за элементы матрицы порядка
составных индексов в определенном порядке, то эти коэффициенты могут быть приняты за элементы матрицы порядка  ; каждый отличный от нуля элемент равен с точностью до знака одной из координат
; каждый отличный от нуля элемент равен с точностью до знака одной из координат  которые мы будем считать за контравариантные составляющие вектора х. Мы сопоставляем такам образом каждому вектору х матрацу X порядка
которые мы будем считать за контравариантные составляющие вектора х. Мы сопоставляем такам образом каждому вектору х матрацу X порядка  ; эта матрица вполне определяется выбранным порядком в системе составных индексов. Например, если при
; эта матрица вполне определяется выбранным порядком в системе составных индексов. Например, если при  индексы расположить в следующем порядке 0,1,2,12, то получим (на основании соотношений (1), (2), (3))
индексы расположить в следующем порядке 0,1,2,12, то получим (на основании соотношений (1), (2), (3))

В этом частном случае матрицы, соответствующие векторам базиса, имеют вид 

94. Основная теорема.
Основное свойство матрицы X, соответствующей некоторому вектору, заключается в следующем:
Теорема. Квадрат матрицы X, соответствующей вектору равен скалярному квадрату этого вектора.
Для доказательства этой теоремы заметим, что единственные не равные нулю элементы  матрицы
матрицы  обозначает номер строки, Р — столбца) суть:
обозначает номер строки, Р — столбца) суть:

На основании этого элемент матрицы  , например:
, например:

где суммирование распространено на  составных индексов, может быть отличен от нуля только в том случае, если
составных индексов, может быть отличен от нуля только в том случае, если  равно
равно  или
или  Если
Если  или 1, то
или 1, то  индексов
индексов  Должны фигурировать среди индексов
Должны фигурировать среди индексов  в случае
в случае  или 1 должна иметь место обратная картина; наконец, если
или 1 должна иметь место обратная картина; наконец, если  то у обоих составных индексов
то у обоих составных индексов  должно быть по крайней мере
должно быть по крайней мере  общих индексов.
общих индексов.
Если  то даже те элементы
то даже те элементы  , которые мы отметили выше, равны нулю; в самом деле, эти элементы равны
, которые мы отметили выше, равны нулю; в самом деле, эти элементы равны

то же самое имеем, если  Тот же результат получается, еслн
Тот же результат получается, еслн  (или
(или  ), так как
), так как

Наконец, если  , то мы должны исследовать элементы
, то мы должны исследовать элементы 

Первые равны нулю: доказательство аналогично предыдущему. Вторые равны

Из этой теоремы непосредственно вытекает, что скалярное произведение двух векторов есть полусумма произведений двух соответствующих матриц.
Доказательство то же, что и для пространства  (п. 56, теорема III).
(п. 56, теорема III).
Отсюда вытекают следующие соотношения для матриц  соответствующих
соответствующих  взаимно перпендикулярным единичным векторам:
взаимно перпендикулярным единичным векторам:

96. Матрица, соответствующая p-вектору.
p-вектору, определенному векторами  можно отнести, матрицу
можно отнести, матрицу

где сумма распространена на все перестановки индексов  причем знак или — берется в зависимости от того, четной или нечетной является перестановка
причем знак или — берется в зависимости от того, четной или нечетной является перестановка  элементами этой матрицы являются линейные комбинации составляющих
элементами этой матрицы являются линейные комбинации составляющих  -вектора. Мы будем обозначать матрицу, соответствующую
-вектора. Мы будем обозначать матрицу, соответствующую  -вектору, символом X. Если
-вектору, символом X. Если  векторов взаимноперпендикулярны, то матрица, соответствующая
векторов взаимноперпендикулярны, то матрица, соответствующая  -вектору, равна
-вектору, равна
Пользуясь этим видом для матрицы, нетрудно показать, что квадрат матрицы X, соответствующей  -вектору, равен квадрату меры этого
-вектору, равен квадрату меры этого  -вектора, умноженному на
-вектора, умноженному на  например если векторы X и Y взаимно перпендикулярны, то
например если векторы X и Y взаимно перпендикулярны, то

В дальнейшем мы увидим (п. 98), что матрицы, соответствующие двум различным  -векторам, различны и что матрица, соответствующая
-векторам, различны и что матрица, соответствующая  -вектору, тождественна с матрицей, соответствующей некоторому
-вектору, тождественна с матрицей, соответствующей некоторому  -вектору.
-вектору.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ПЕРЕВОДУ
- ГЛАВА 1. ЭВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО; ВРАЩЕНИЯ И ОТРАЖЕНИЯ
- 2. Декартовы реперы.
- 3. Приведение квадратичной формы к сумме квадратов.
- 4. Теорема инерции.
- 6. Контравариантные и ковариантные составляющие.
- II. Вращения и отражения
- 9. Симметрии.
- 10. Разложение вращения на произведение симметрий.
- 11. Непрерывность группы вращений.
- 12. Собственные и несобственные вращения.
- 13. Пространства, у которых h = 1.
- III. Мультивекторы
- 15. Мультивекторы.
- 16. Изотропные мультивекторы.
- 17. Дополнительные мультивекторы.
- 18. Сумма p-векторов.
- IV. Бивекторы и бесконечно малые вращения
- ГЛАВА II. ТЕНЗОРЫ; ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУПП; МАТРИЦЫ
- 21. Общее определение линейных представлений группы вращений.
- 22. Эквивалентные представлений.
- 23. Понятие об эвклидовом тензоре.
- 24. Другая точка зрения.
- II. Тензорная алгебра
- III. Тензоры приводимые и неприводимые
- 33. Нахождение неприводимых тензоров, которые могут быть получены из вполне приводимого тензора.
- 35. Основная теорема.
- 36. Критерий неприводимости.
- IV. Матрицы
- 42. Характеристическое уравнение. Собственные значения.
- 43. Унитарные матрицы.
- 44. Ортогональные матрицы.
- 45. Применение к разложению вещественного вращения.
- 46. Эрмитовы матрицы.
- 47. Примечание.
- V. Неприводимость p-векторов
- ГЛАВА III. СПИНОРЫ ТРЕХМЕРНОГО ПРОСТРАНСТВА.
- II. Матрицы, соответствующие векторам
- III. Представление симметрий и вращений
- 60. Операции над спинорами.
- IV. Произведение двух спиноров и его разложение на неприводимые части
- V. Случай вещественного эвклидова пространства
- 64. Сопряженные спиноры.
- 65. Скаляр и бивектор, соответствующие двум сопряженным спинорам.
- VI. Случай псевдоэвклидова пространства
- ГЛАВА IV. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ В E1
- I. Линейные представления, выражаемые при помощи спиноров
- 71. Уравнения Дирака.
- II. Бесконечно малые вращения и определение эвклидовых тензоров
- III. Линейные представления группы комплексных вращений
- 83. Линейные представления прямого произведения двух групп.
- 84. Приложения к группе комплексных вращений.
- IV. Однозначность и двузначность
- 86. Однозначность линейных представлений унимодулярной группы двух переменных.
- 86. Линейные представления вещественной проективной группы одной переменной.
- V. Линейные представления группы вращений и отражений
- 88. Случай неприводимых представлений, индуцирующих в группе вращений неприводимое представление.
- 90. Приложения.
- 91. Случай группы вращений и отражений вещественного псевдоэвклидова пространства.
- ГЛАВА V. СПИНОРЫ ПРОСТРАНСТВА …
- I. Изотропные v-плоскости и матрицы, соответствующие векторам
- II. Представление вращений и отражений при помощи матриц порядка 2^v
- 99. Тензорный характер спинора.
- 100. Неприводимость спинора.
- III. Фундаментальная полярность в пространстве спиноров, p-векторы, определяемые парой спиноров
- IV. Простые спиноры и интерпретация их как поляризованных изотропных v-векторов
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- 117. Сопряженные спиноры.
- 118. Произведение двух сопряженных спиноров.
- 119. h-векторы, построенные на двух сопряженных спинорах.
- ГЛАВА VI. СПИНОРЫ ПРОСТРАНСТВА E2
- I. Изотропные v-плоскости и полуспиноры
- 122. Простые полуспиноры, определяемые как изотропные поляризованные v-векторы.
- 123. Условия простоты полуспинора.
- 124. Пересечение двух изотропных v-плоскостей.
- II. Матрицы, соответствующие p-векторам. Представление вращений и отражений
- 126. Применение симметрии к спинору.
- 127. Две группы вращений и отражений в применении к спинорам.
- 128. Неприводимость спинора и полуспиноров.
- 120. Матрицы порядка 2^v разложенные на суммы p-векторов.
- III. Разложение произведения двух спиноров
- 132. Разложение произведения двух полуспиноров относительно группы вращений.
- 134. Применение к группе вращеяиб для v нечетного.
- 135. Случай v четного.
- 136. Примечание.
- IV. Частные случаи
- 137. Случай v = 3.
- 188. Случай v = 4. Фундаментальная трилинейная форма.
- 139. Принцип тройственности.
- 140. Параллелизм в пространстве E2.
- 141. Формула Бриоски.
- V. Случай вещественного эвклидова пространства
- VI. Случай псевдоэвклидовых пространств
- ГЛАВА VII. СПИНОРЫ В ПРОСТРАНСТВЕ ЧАСТНОГО ПРИНЦИПА ОТНОСИТЕЛЬНОСТИ. УРАВНЕНИЯ ДИРАКА
- II. Разложение произведения двух спиноров
- III. Сопряженные векторы и слияоры в пространстве частного принципа относительности
- IV. Уравнения Дирака
- ГЛАВА VIII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ ЛОРЕНЦА
- II. Представления группы вращений и отражений Лоренца
- III. Линейные представления группы вращений вещественного эвклидова пространства
- ГЛАВА IX. СПИНОРЫ И УРАВНЕНИЯ ДИРАКА В РИМАНОВОИ ГЕОМЕТРИИ
- II. Спинорные поля в римановой геометрии
- БИБЛИОГРАФИЯ