| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
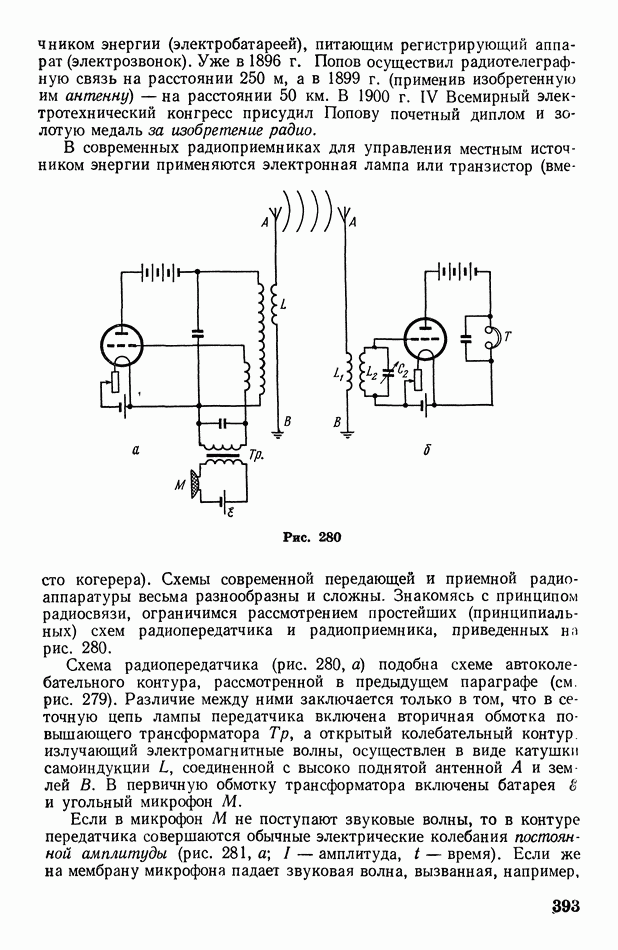
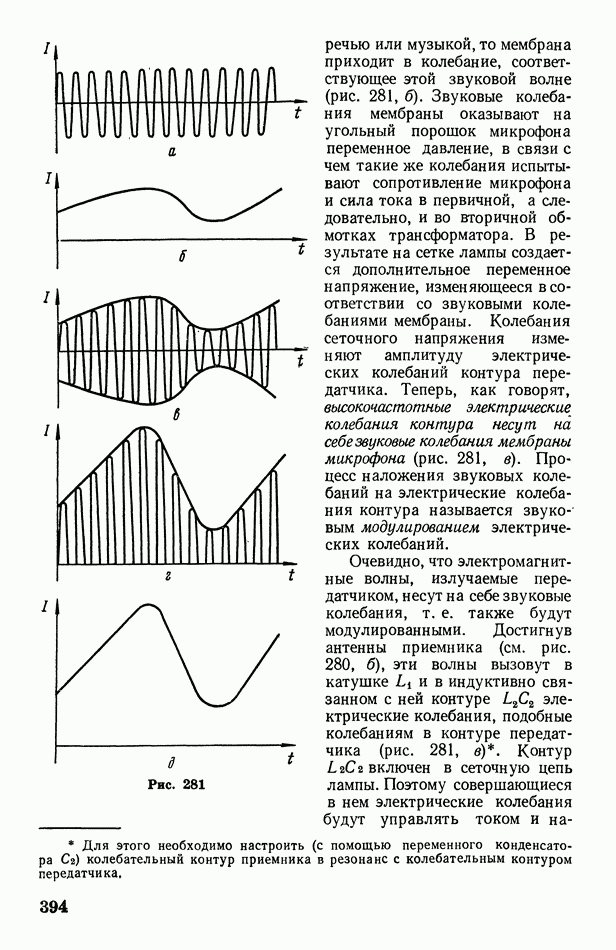
§ 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
В лабораторной практике дифракционную картину получают обычно от узких светящихся щелей. Поэтому случаи дифракции света от одной, от двух и от многих параллельных щелей мы рассмотрим более подробно.
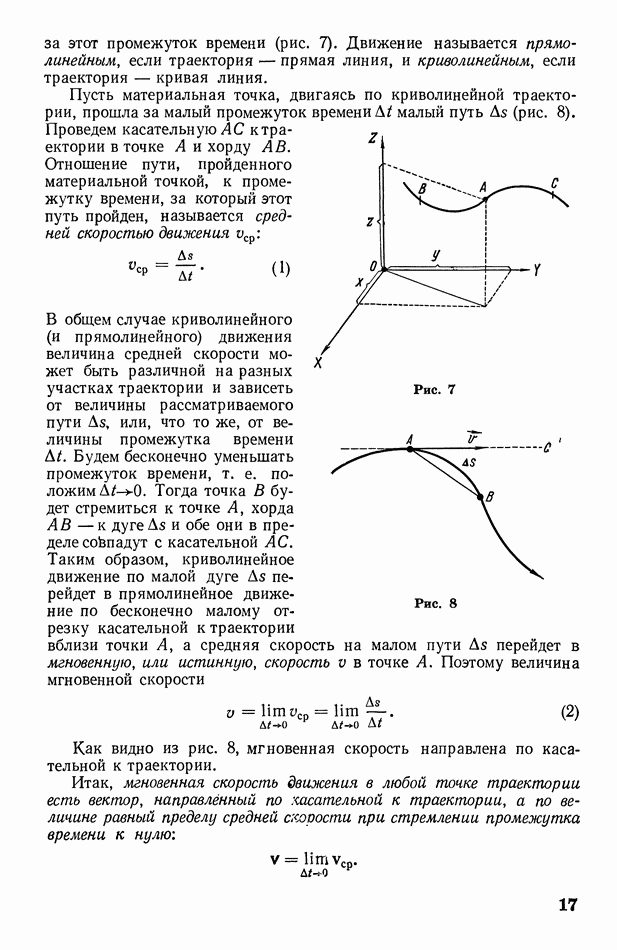
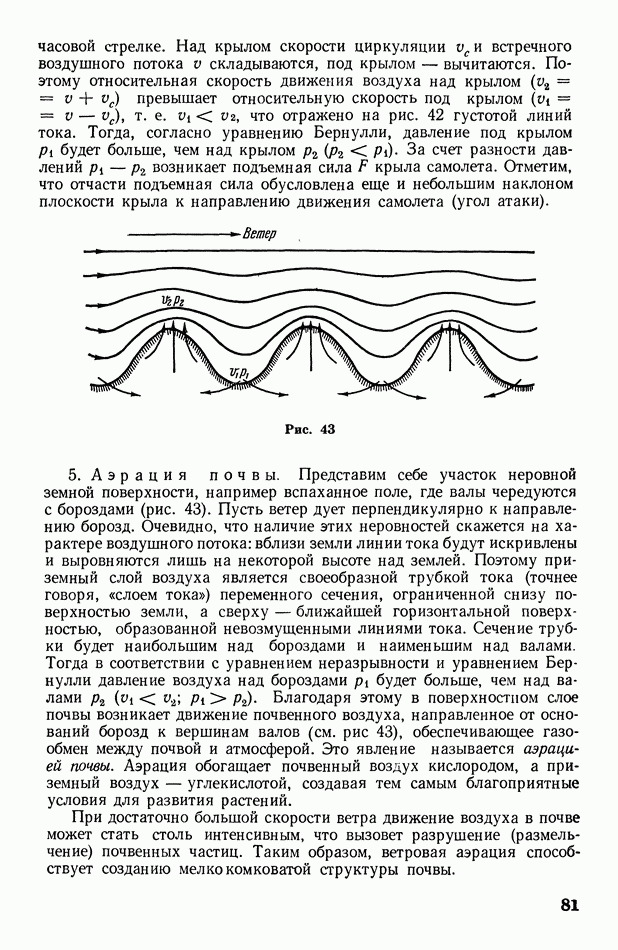
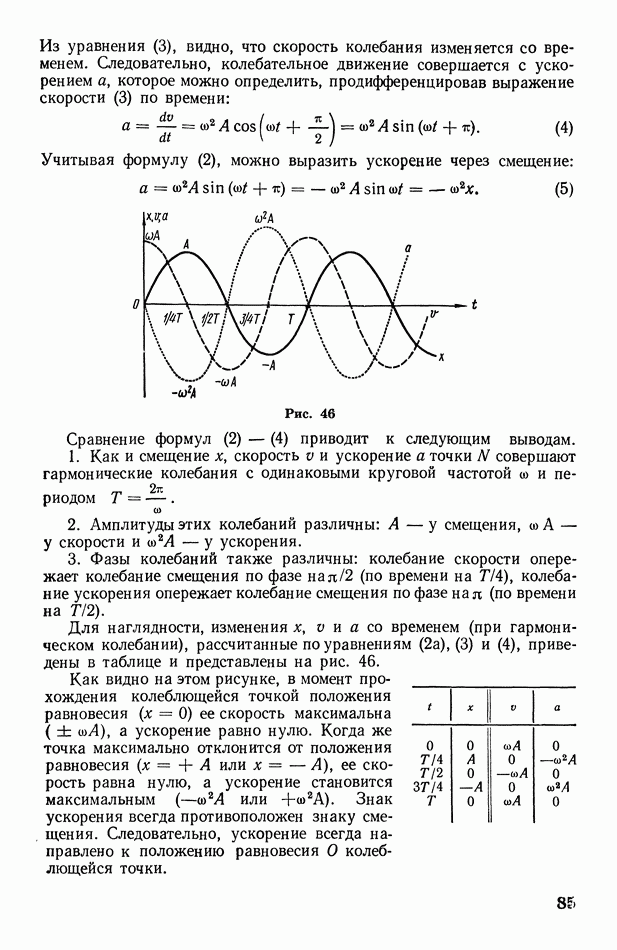
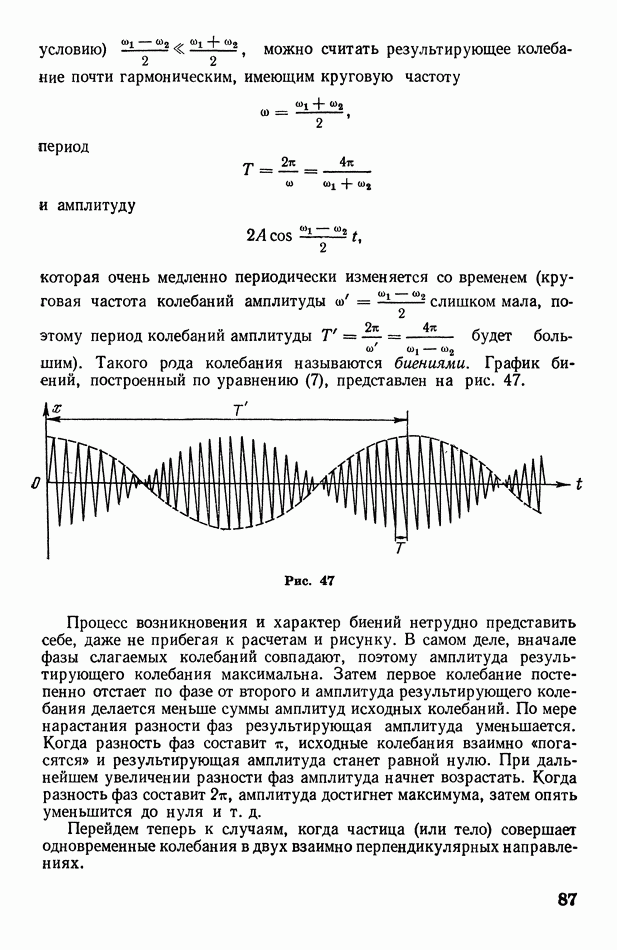
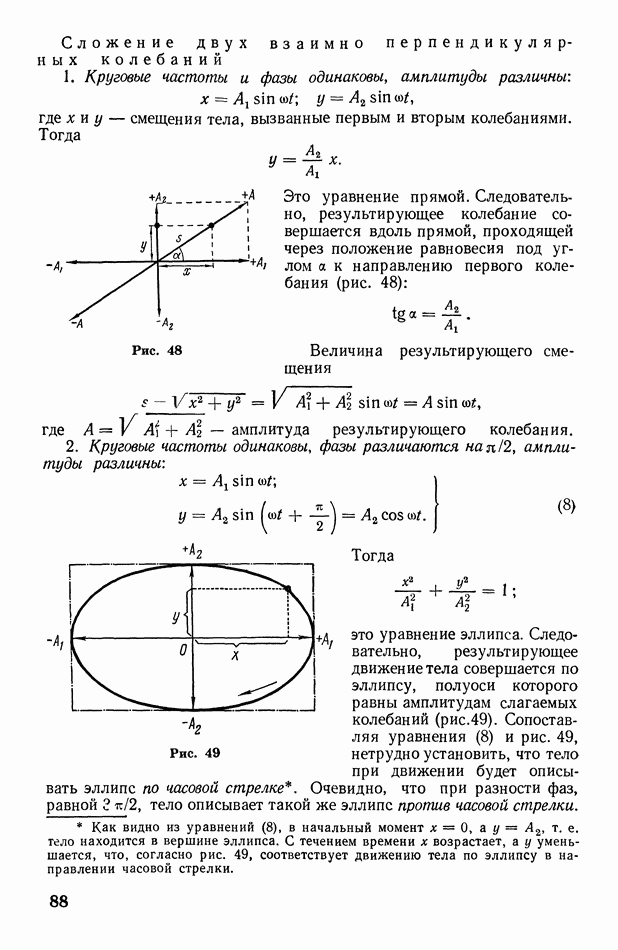
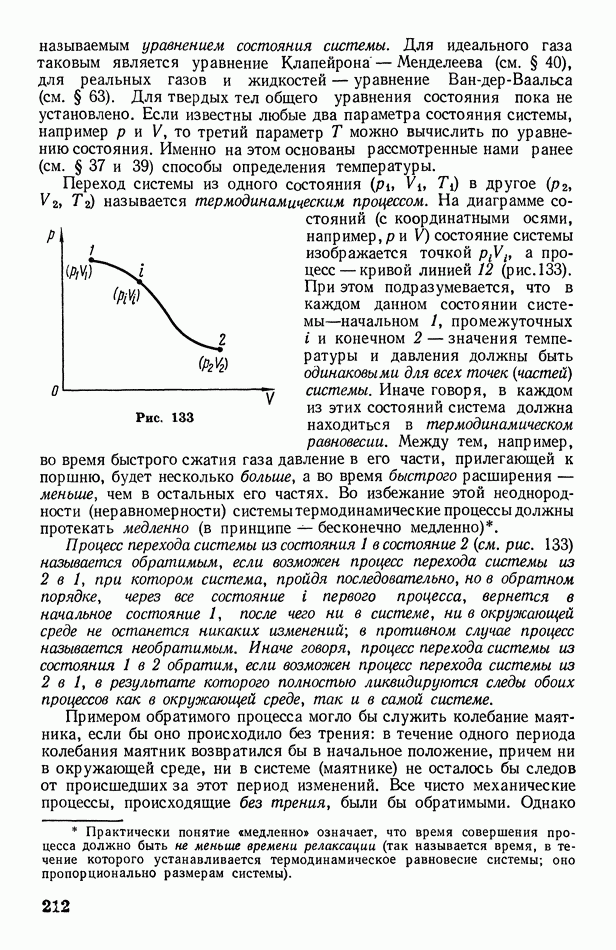
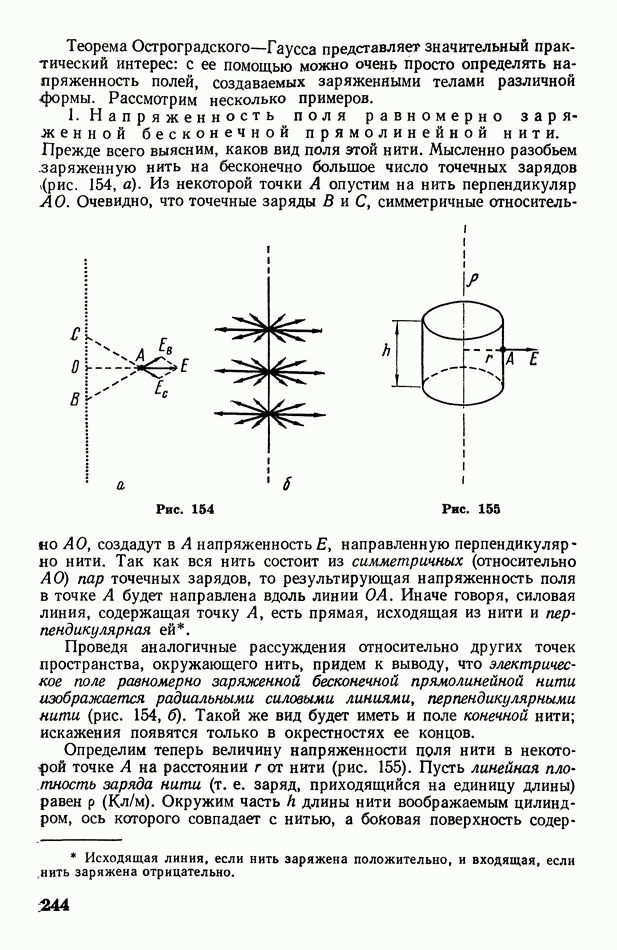
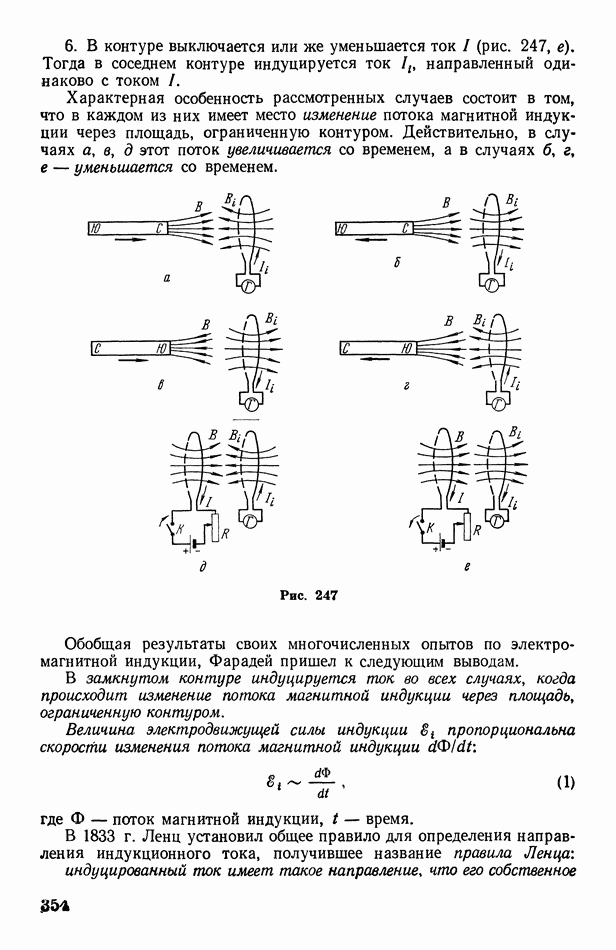
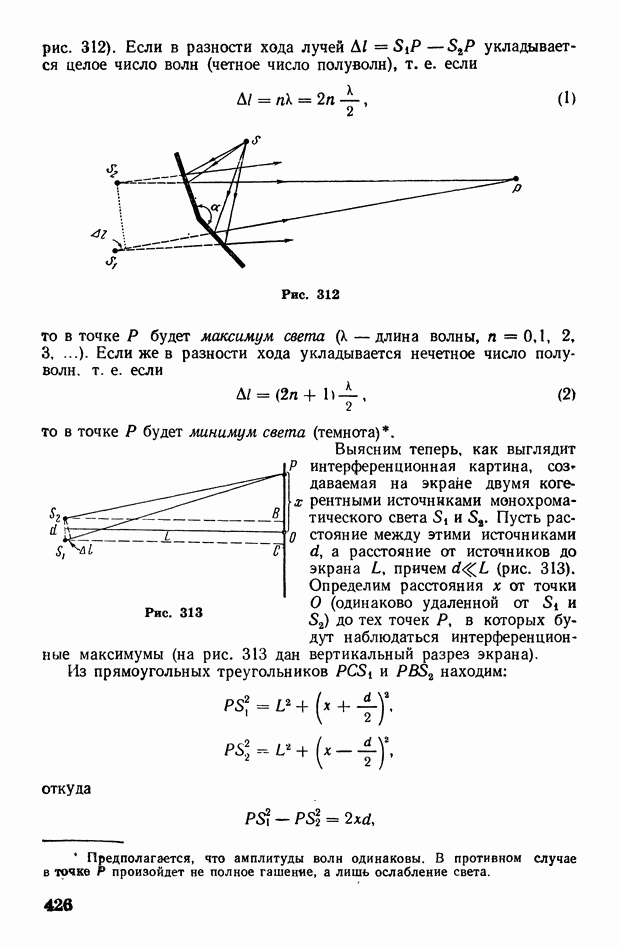
1. Дифракция от одной щели. Пусть на экран В с узкой прямоугольной щелью падает пучок параллельных монохроматических лучей нормально к экрану (рис. 325, а). Все лучи, проходящие через щель в первоначальном направлении, собираются линзой С в одну точку О экрана  расположенного в фокальной плоскости линзы (точнее говоря, лучи собираются в одну линию, проходящую через О параллельно щели). Разность хода между всеми этими лучами равна нулю, так как линза не создает разности хода лучей. Следовательно, через точку О пройдет светлая полоса (максимум освещенности), параллельная щели.
расположенного в фокальной плоскости линзы (точнее говоря, лучи собираются в одну линию, проходящую через О параллельно щели). Разность хода между всеми этими лучами равна нулю, так как линза не создает разности хода лучей. Следовательно, через точку О пройдет светлая полоса (максимум освещенности), параллельная щели.
Учтем теперь, что благодаря дифракции лучи от щели пойдут не только в первоначальном направлении, но и под различными углами  к этому направлению
к этому направлению  называется углом дифракции). Рассмотрим пучок лучей, дифрагирующих от щели под таким углом
называется углом дифракции). Рассмотрим пучок лучей, дифрагирующих от щели под таким углом  что разность
что разность

Рис. 325
хода  между крайними лучами пучка будет равна длине световой волны
между крайними лучами пучка будет равна длине световой волны  Тогда весь пучок можно разделить на такие две равные зоны
Тогда весь пучок можно разделить на такие две равные зоны  называемые зонами Френеля, для которых разность хода между каждым лучом первой зоны и соответствующим лучом второй зоны окажется равной
называемые зонами Френеля, для которых разность хода между каждым лучом первой зоны и соответствующим лучом второй зоны окажется равной  Будучи собраны линзой на линии, проходящей через точку
Будучи собраны линзой на линии, проходящей через точку  эти лучи проинтерферируют и взаимно погасятся. В результате через
эти лучи проинтерферируют и взаимно погасятся. В результате через  пройдет темная полоса — дифракционный минимум. Очевидно, что такой же дифракционный минимум пройдет через точку
пройдет темная полоса — дифракционный минимум. Очевидно, что такой же дифракционный минимум пройдет через точку  симметричную точке
симметричную точке  лучей, образующих этот минимум, на рисунке не показан).
лучей, образующих этот минимум, на рисунке не показан).
Рассмотрим другой пучок лучей, дифрагирующих под таким углом  что разность хода
что разность хода  между крайними лучами пучка равна
между крайними лучами пучка равна  (рис. 325, в). Тогда весь пучок можно разделить на три зоны Френеля:
(рис. 325, в). Тогда весь пучок можно разделить на три зоны Френеля:  и III. Понятно, что две соседние зоны (например, I и II) погасят друг друга (так как разность хода между лучами этих зон равна
и III. Понятно, что две соседние зоны (например, I и II) погасят друг друга (так как разность хода между лучами этих зон равна  а третья зона останется непогашенной и даст дифракционный максимум на линии, проходящей через точку
а третья зона останется непогашенной и даст дифракционный максимум на линии, проходящей через точку  Такой же максимум появится на линии, проходящей через точку
Такой же максимум появится на линии, проходящей через точку  симметричную
симметричную  Освещенность максимумов
Освещенность максимумов  будет значительно меньше освещенности максимума О, поскольку в О попадает весь световой пучок, проходящий через щель, тогда как в
будет значительно меньше освещенности максимума О, поскольку в О попадает весь световой пучок, проходящий через щель, тогда как в  попадает только по одной третьей части такого пучка.
попадает только по одной третьей части такого пучка.
Путем аналогичных рассуждений нетрудно показать, что, за максимумами  расположатся минимумы, создаваемые лучами, дифрагирующими под углом, при котором пучок лучей можно разделить на четыре зоны Френеля
расположатся минимумы, создаваемые лучами, дифрагирующими под углом, при котором пучок лучей можно разделить на четыре зоны Френеля  Далее расположатся максимумы, создаваемые лучами, дифрагирующими под углом, соответствующим пяти зонам Френеля
Далее расположатся максимумы, создаваемые лучами, дифрагирующими под углом, соответствующим пяти зонам Френеля  В эти максимумы попадает уже по одной пятой части всего пучка, проходящего через щель, поэтому их освещенность будет меньше освещенности максимумов
В эти максимумы попадает уже по одной пятой части всего пучка, проходящего через щель, поэтому их освещенность будет меньше освещенности максимумов 
Переходя к обобщению, можно сказать, что
пучки лучей, дифрагирующих под углами, соответствующими нечетному числу зон Френеля, создают на экране дифракционные максимумы, а пучки лучей, дифрагирующих под углами, соответствующими четному числу зон Френеля, создают дифракционные минимумы. Освещенность максимумов уменьшается при увеличении угла дифракции лучей, создающих эти максимумы.
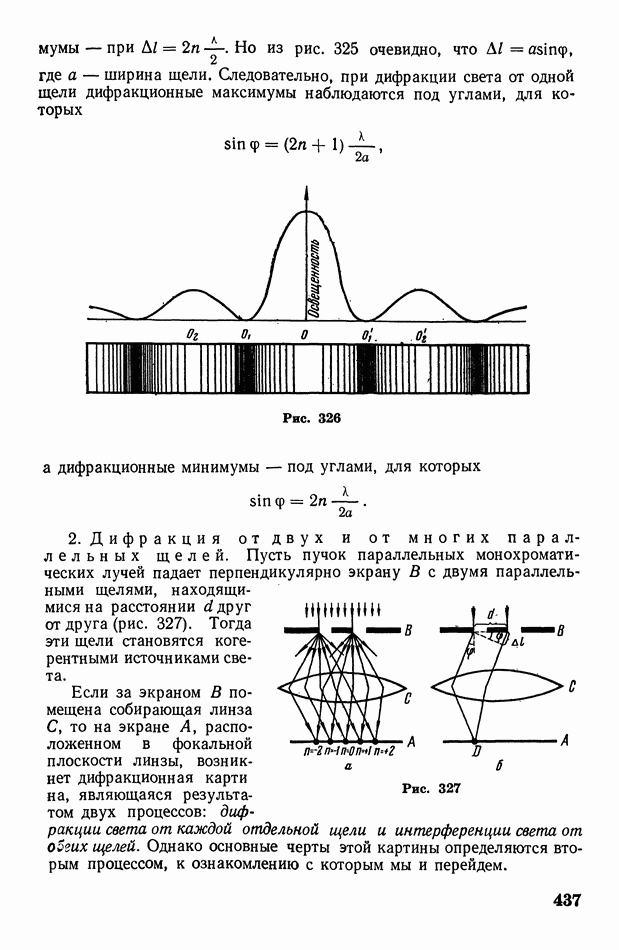
Таким образом, дифракционная картина, получаемая от одной щели, представляет собой чередование темных и светлых полос, симметрично расположенных по обе стороны от центральной светлой полосы. Освещенность светлых полос быстро убывает по мере удаления от центральной полосы. Эта дифракционная картина представлена на рис. 326 (см. также фотографию на рис. 321, б).
Как мы уже показали, дифракционные максимумы получаются при разности хода лучей  а дифракционные
а дифракционные
минимумы — при  Но из рис. 325 очевидно, что
Но из рис. 325 очевидно, что  где а — ширина щели. Следовательно, при дифракции света от одной щели дифракционные максимумы наблюдаются под углами, для которых
где а — ширина щели. Следовательно, при дифракции света от одной щели дифракционные максимумы наблюдаются под углами, для которых

а дифракционные минимумы — под углами, для которых


Рис. 326
2. Дифракция от двух и от многих параллельных щелей. Пусть пучок параллельных монохроматических лучей падает перпендикулярно экрану в с двумя параллельными щелями, находящимися на расстоянии  друг от друга (рис. 327). Тогда эти щели становятся когерентными источниками света.
друг от друга (рис. 327). Тогда эти щели становятся когерентными источниками света.

Рис. 327
Если за экраном в помещена собирающая линза С, то на экране  расположенном в фокальной плоскости линзы, возникнет дифракционная карти на, являющаяся результатом двух процессов: дифракции света от каждой отдельной щели и интерференции света от обеих щелей. Однако основные черты этой картины определяются вторым процессом, к ознакомлению с которым мы и перейдем.
расположенном в фокальной плоскости линзы, возникнет дифракционная карти на, являющаяся результатом двух процессов: дифракции света от каждой отдельной щели и интерференции света от обеих щелей. Однако основные черты этой картины определяются вторым процессом, к ознакомлению с которым мы и перейдем.
Рассмотрим лучи, падающие, например, на левые края обеих щелей. Благодаря дифракции свет от щелей будет распространяться во всевозможных направлениях (рис. 327, а). На рис. 327, б видно, что разность хода  параллельных лучей, дифрагирующих от щелей под углом
параллельных лучей, дифрагирующих от щелей под углом  равна
равна

Будучи собраны линзой С в одну линию (проходящую параллельно щелям через точку  экрана
экрана  ), эти лучи проинтерферируют; результат интерференции будет зависеть от величины разности хода
), эти лучи проинтерферируют; результат интерференции будет зависеть от величины разности хода  При разности хода, равной целому числу волн, т. е. при
При разности хода, равной целому числу волн, т. е. при

лучи дадут на экране А интерференционный максимум. При разности хода, равной нечетному числу полуволн, т. е. при

лучи дадут на экране интерференционный минимум.
Таким образом, углы дифракции, соответствующие максимумам освещенности экрана, определятся из соотношения

а углы дифракции, соответствующие минимумам освещенности, из соотношения

где  целые (положительные и отрицательные) числа натурального ряда
целые (положительные и отрицательные) числа натурального ряда 
Согласно формуле (8), по обе стороны от центрального максимума, которому соответствует значение  располагаются первые максимумы — правый
располагаются первые максимумы — правый  и левый
и левый  далее располагаются вторые максимумы
далее располагаются вторые максимумы  и т. д. Однако возможное число максимумов является ограниченным: оно не может быть больше, чем
и т. д. Однако возможное число максимумов является ограниченным: оно не может быть больше, чем  . В самом деле, согласно формуле (8),
. В самом деле, согласно формуле (8),

но  следовательно,
следовательно,

Освещенность  различных максимумов неодинакова. Сильнее всего освещен центральный максимум
различных максимумов неодинакова. Сильнее всего освещен центральный максимум  первые максимумы
первые максимумы  освещены слабее, вторые максимумы
освещены слабее, вторые максимумы  слабее и т. д. (рис. 328; по вертикали откладывается освещенность
слабее и т. д. (рис. 328; по вертикали откладывается освещенность
дифракционной картины, по горизонтали — расстояния до центрального максимума). Это обусловлено тем, что, как было выяснено при рассмотрении дифракции от одной щели, освещенность экрана, создаваемая дифрагирующими лучами, уменьшается по мере увеличения угла дифракции.
Расчеты, которых мы не будем касаться, показывают, что при дифракции света от совокупности многих параллельных щелей, расположенных близко друг к другу, создается такая же дифракционная картина, как в случае двух щелей. Только максимумы получаются более яркими и узкими, а разделяющие их минимумы — широкими и практически совершенно темными. Расстояние между соседними максимумами и их яркость возрастают по мере увеличения числа щелей.

Рис. 328
Формула (8), определяющая местоположения максимумов при дифракции от двух щелей, остается справедливой и в случае дифракции от многих щелей.
Согласно формуле (8), местоположение каждого максимума зависит от длины волны света Чем больше X, тем больше  т. е. тем под большим углом дифракции
т. е. тем под большим углом дифракции  получается максимум для этой волны. Отсюда следует, что при использовании белого света каждый максимум (кроме центрального) приобретает радужную окраску, причем внутренний его край (по отношению к центральному максимуму) станет фиолетовым, а наружный — красным, так как фиолетовому цвету соответствуют наиболее короткие волны, а красному — наиболее длинные; между фиолетовым и красным краями максимума расположатся остальные спектральные цвета (рис. 329). В этой связи дифракционные максимумы принято называть дифракционными
получается максимум для этой волны. Отсюда следует, что при использовании белого света каждый максимум (кроме центрального) приобретает радужную окраску, причем внутренний его край (по отношению к центральному максимуму) станет фиолетовым, а наружный — красным, так как фиолетовому цвету соответствуют наиболее короткие волны, а красному — наиболее длинные; между фиолетовым и красным краями максимума расположатся остальные спектральные цвета (рис. 329). В этой связи дифракционные максимумы принято называть дифракционными

Рис. 329
спектрами, а число  порядком спектра. Спектр нулевого порядка остается белым, так как, согласно формуле (8), при
порядком спектра. Спектр нулевого порядка остается белым, так как, согласно формуле (8), при  угол дифракции
угол дифракции  для всех длин волн
для всех длин волн 
Следует отметить, что дифракционные спектры высоких порядков начинают налагаться друг на друга. Так, в случае использования белого света спектры второго и третьего порядков уже частично перекрываются длинноволновый участок спектра 2-го порядка налагается на коротковолновый участок спектра 3-го порядка).

Рис. 330
Совокупность большого числа узких параллельных щелей, расположенных близко друг от друга, называется дифракционной решеткой, а расстояние  между соседними щелями — периодом решетки (рис. 330, схема). Решетку, имеющую постоянный период и одинаковую ширину всех щелей, называют регулярной.
между соседними щелями — периодом решетки (рис. 330, схема). Решетку, имеющую постоянный период и одинаковую ширину всех щелей, называют регулярной.
Дифракционные решетки изготавливают путем нанесения тонких штрихов (царапин) на поверхности стеклянной пластинки (прозрачная решетка) или металлического зеркала (отражательная решетка). Очевидно, что в таких решетках роль щелей играют промежутки между штрихами. Штрихи наносятся алмазным резцом с помощью делительной машины. Лучшие дифракционные решетки имеют до 1200—1500 штрихов на миллиметр, что соответствует периоду 

Рис. 331
Посредством дифракционной решетки проводятся очень точные измерения длины световых волн. Для этого пользуются дифракционным спектроскопом, схема которого изображена на рис. 331. Дифракционная решетка 1 установлена на неподвижном круге 2, имеющем угловые деления. Свет от источника  проходит через узкую щель коллиматора 3 и падает на решетку. Поворачивая зрительную трубу 4, набодят ее визир на исследуемую линию дифракционного спектра. Отсчет угла дифракции
проходит через узкую щель коллиматора 3 и падает на решетку. Поворачивая зрительную трубу 4, набодят ее визир на исследуемую линию дифракционного спектра. Отсчет угла дифракции  соответствующего этой линии, производят с помощью нониуса 5, связанного со зрительной трубой. Затем в формулу
соответствующего этой линии, производят с помощью нониуса 5, связанного со зрительной трубой. Затем в формулу

полученную из формулы (8), подставляют измеренное значение угла  и порядок спектра
и порядок спектра  , в котором наблюдалась линия, и вычисляют длину волны
, в котором наблюдалась линия, и вычисляют длину волны 
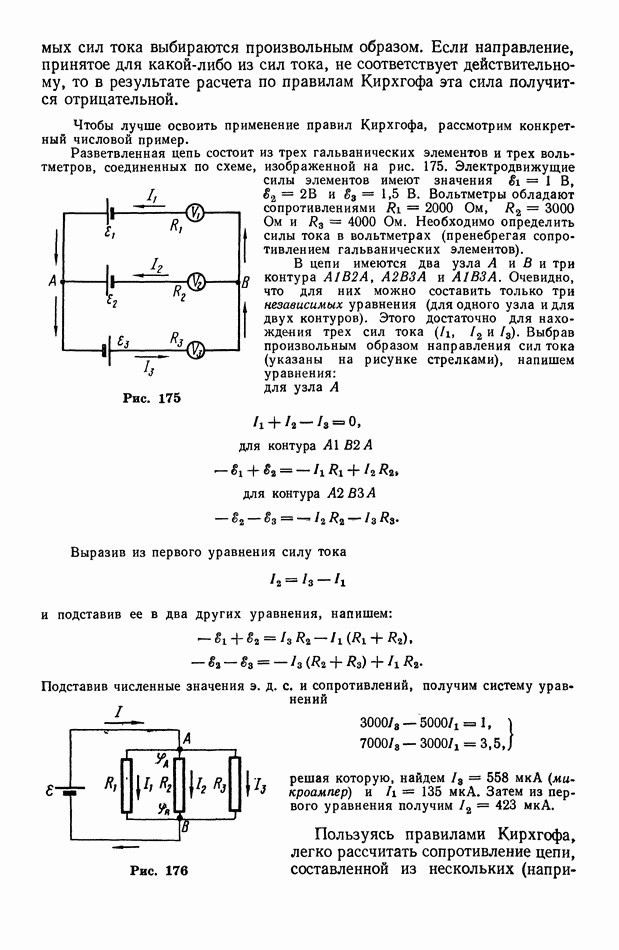
Вообще говоря, дифракционной решеткой может служить не только совокупность щелей, но и совокупность большого числа любых неоднородностей (отверстий и преград) на плоскости или в объеме; в последнем случае решетка называется пространственной. Пространственной (нерегулярной) решеткой является, например, так называемая мутная среда, т. е. среда, в которой взвешено множество очень мелких частиц какого-нибудь инородного вещества. К мутным средам относятся коллоидные растворы, задымленные газы и т. п.
Проходя через мутную среду, свет дифрагирует от ее беспорядочно (нерегулярно) расположенных микронеоднородностей и распространяется во всевозможных направлениях, т. е., как говорят, рассеивается (не создавая какой-либо определенной дифракционной картины). Поэтому дифракцию света в мутных средах обычно называют рассеянием света. Такое рассеяние наблюдается, например, в запыленном воздухе, пронизываемом солнечными лучами: благодаря рассеянию света на пылинках лучи становятся видимыми со стороны.
Особый интерес представляет так называемое молекулярное рассеяние света, происходящее в жидкостях и газах, совершенно очищенных от посторонних частиц. В данном случае свет дифрагирует (рассеивается) от мельчайших уплотнений среды (флуктуаций плотности), обусловленных случайными скоплениями значительного числа молекул в отдельных местах объема жидкости (или газа); эти скопления создаются при беспорядочном тепловом движении молекул.
Интенсивность рассеянного света при молекулярном рассеянии очень мала; она становится заметной лишь в случаях, когда свет проходит через большую толщу рассеивающей среды.
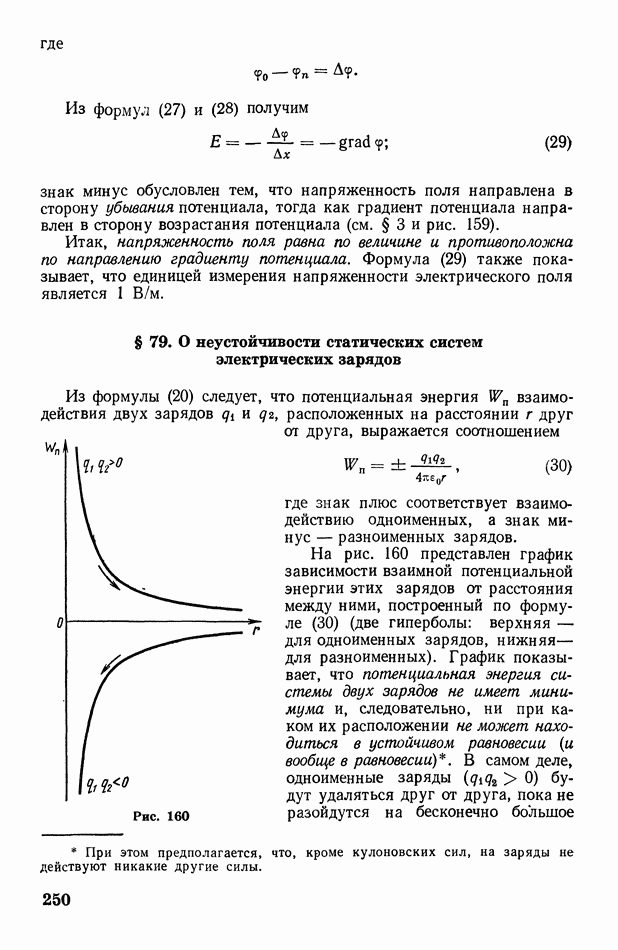
В заключение отметим, что молекулярным рассеянием света в атмосфере объясняются голубой цвет неба и желтоватый оттенок солнечного диска. Согласно закону Рэлея,
интенсивность  рассеянного света обратно пропорциональна четвертой степени длины волны
рассеянного света обратно пропорциональна четвертой степени длины волны

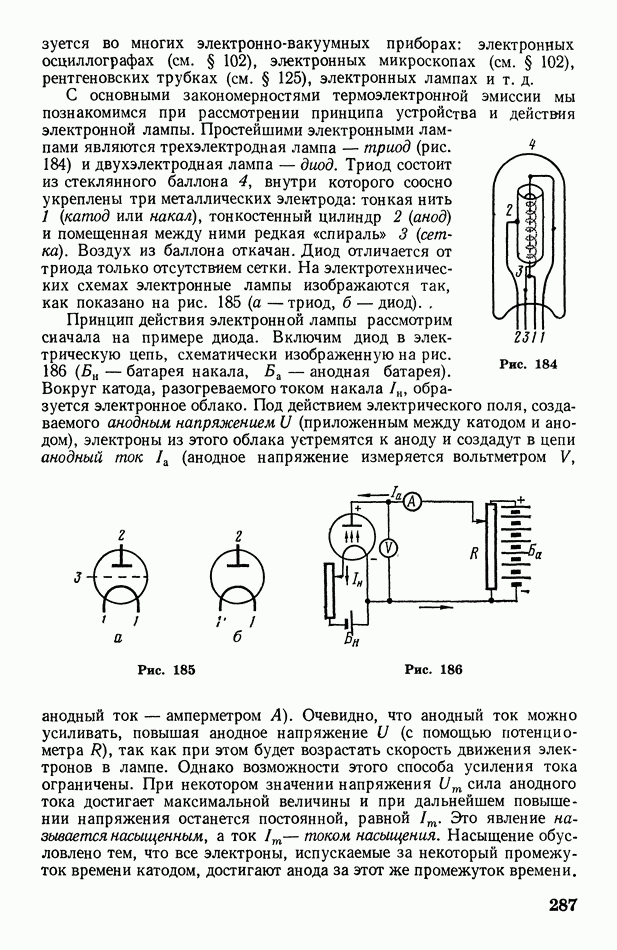
Следовательно, из белого (солнечного) света, проходящего через атмосферу, рассеиваются преимущественно короткие волны, соответствующие синему и голубому цвету. В связи с этим свет, прошедший через атмосферу, состоит преимущественно из длинных волн, придающих ему и солнечному диску оранжево-желтый оттенок.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
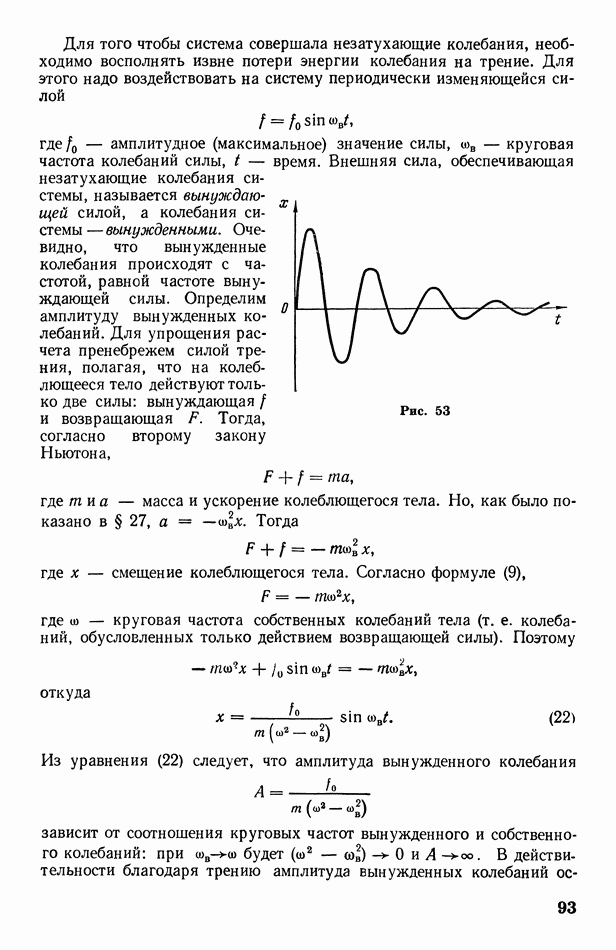
- § 30. О затухающих и вынужденных колебаниях
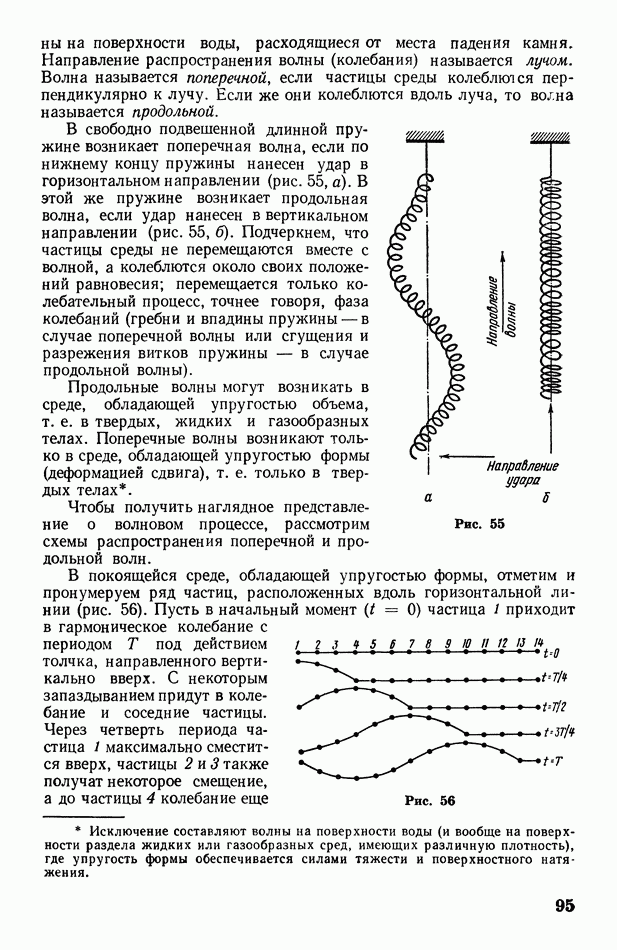
- § 31. Волновой процесс
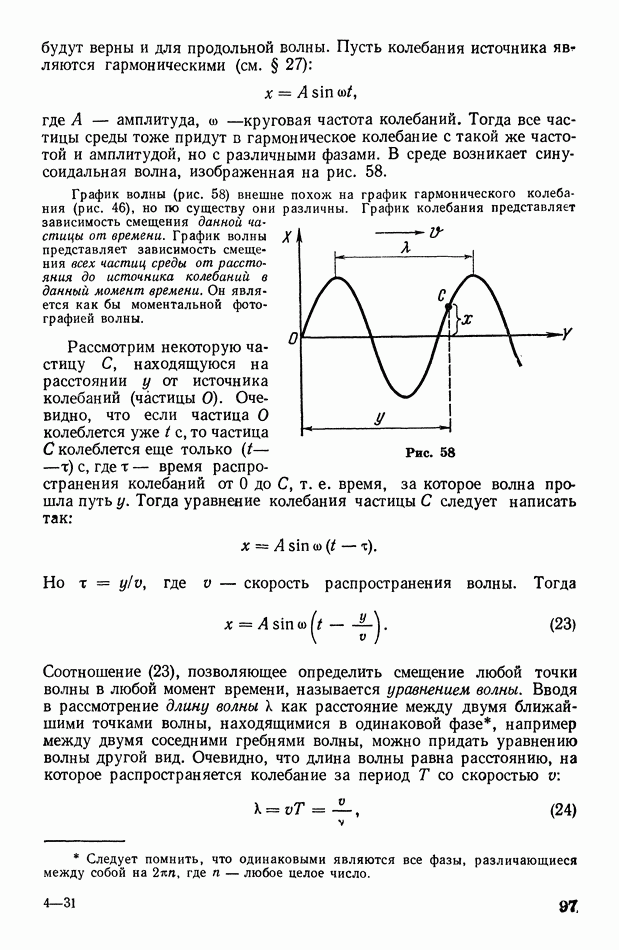
- § 32. Уравнение волны. Интенсивность волны
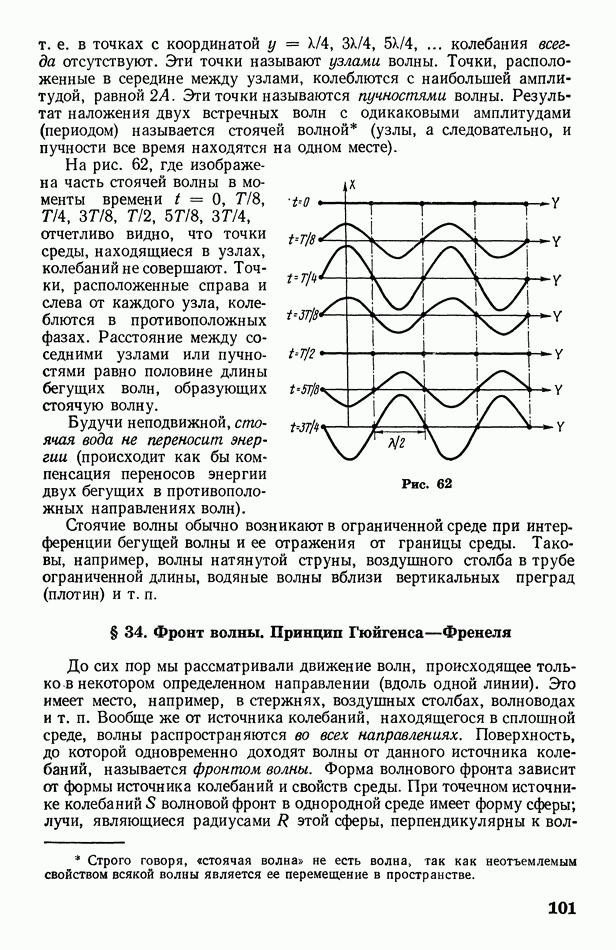
- § 33. Интерференция волн. Стоячие волны
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
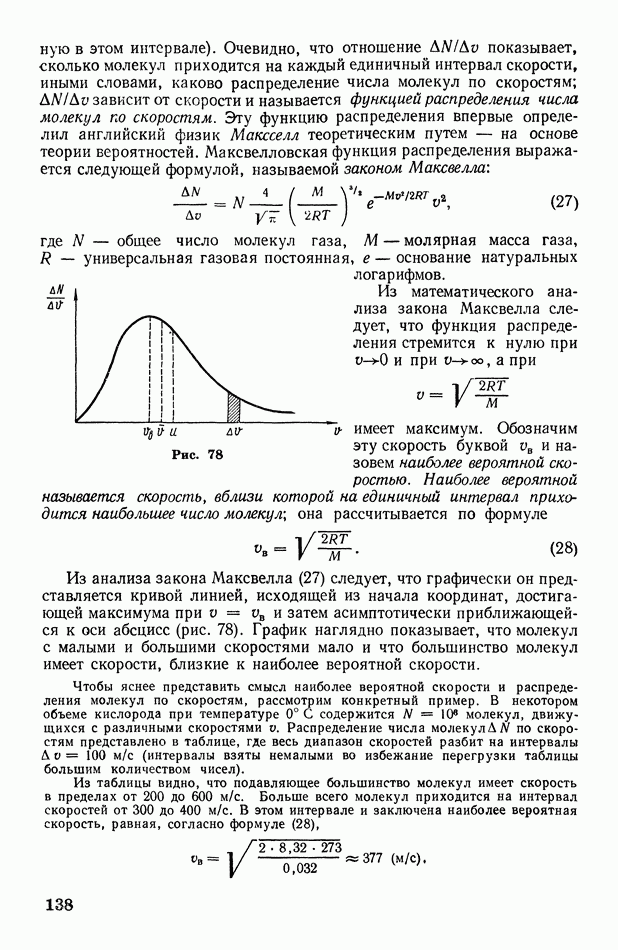
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
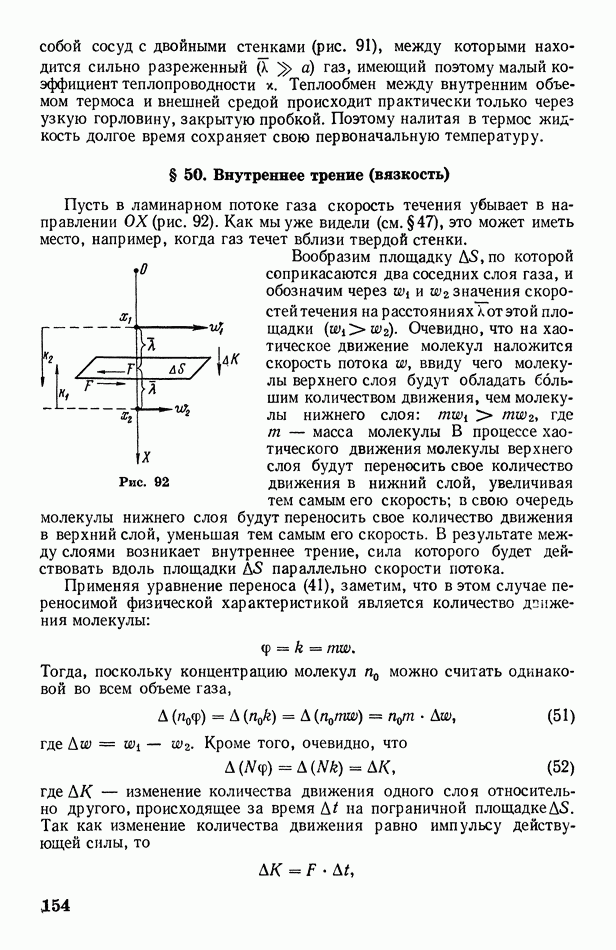
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
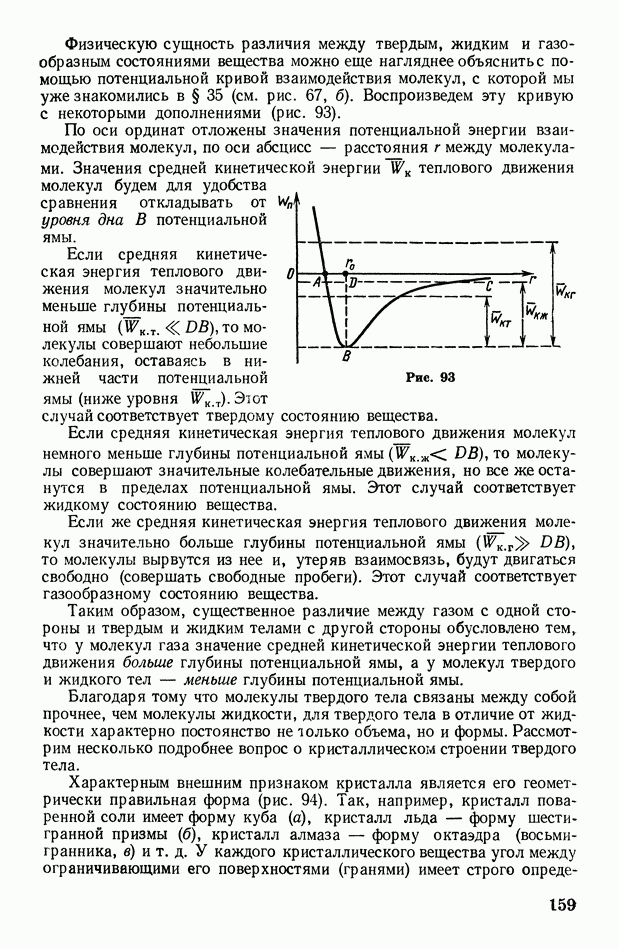
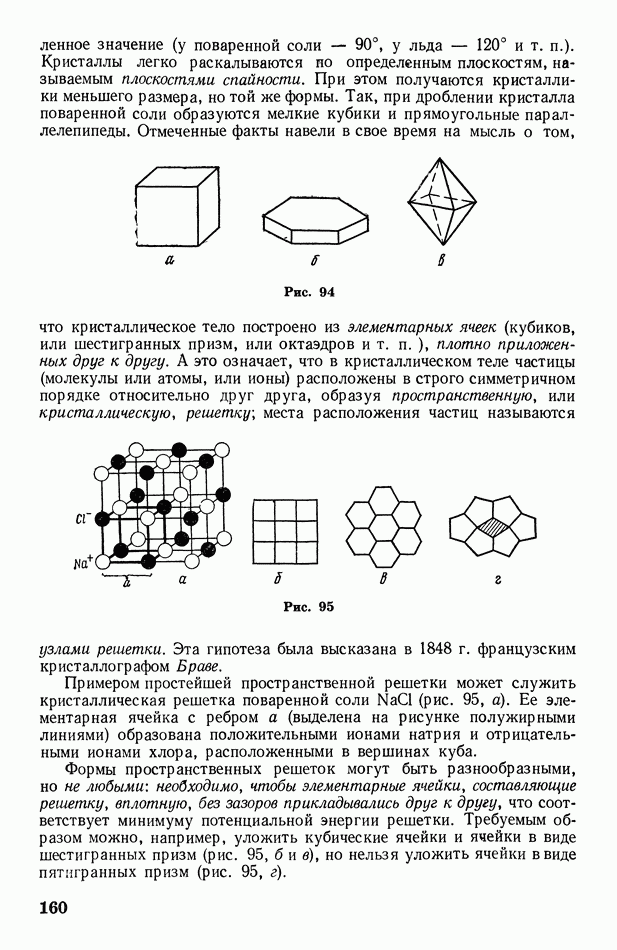
- § 51. Особенности строения жидкостей и твердых тел
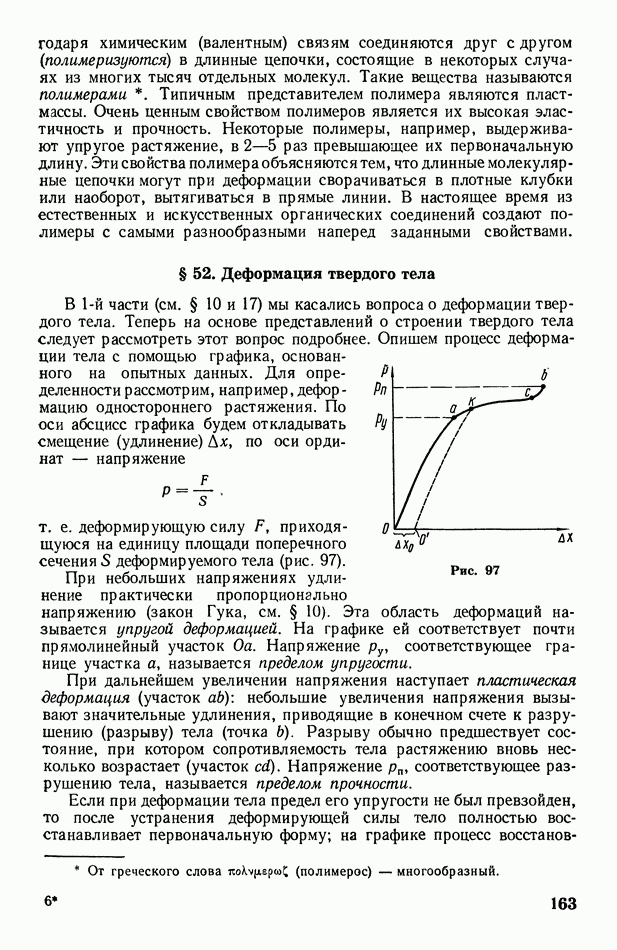
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
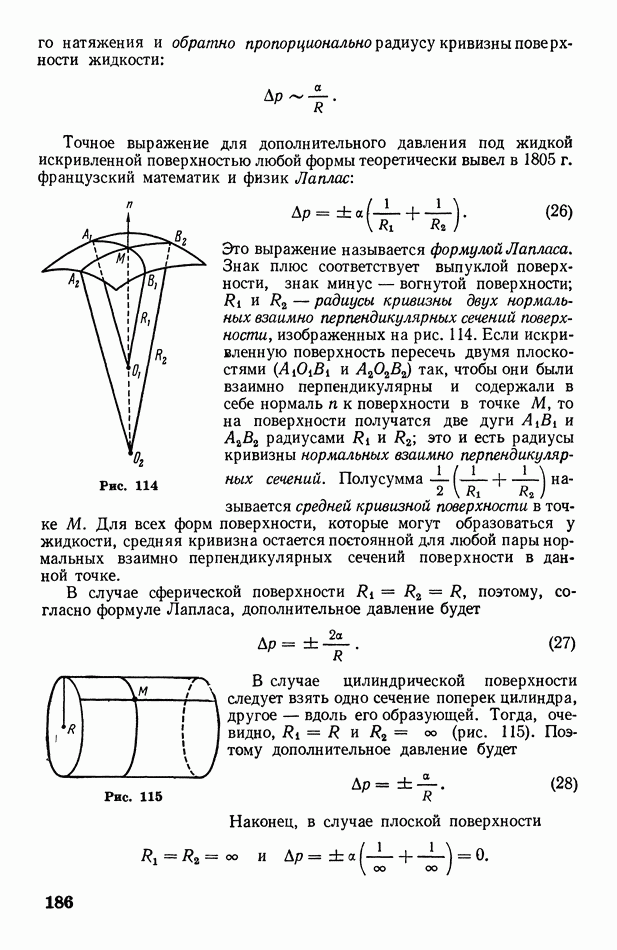
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
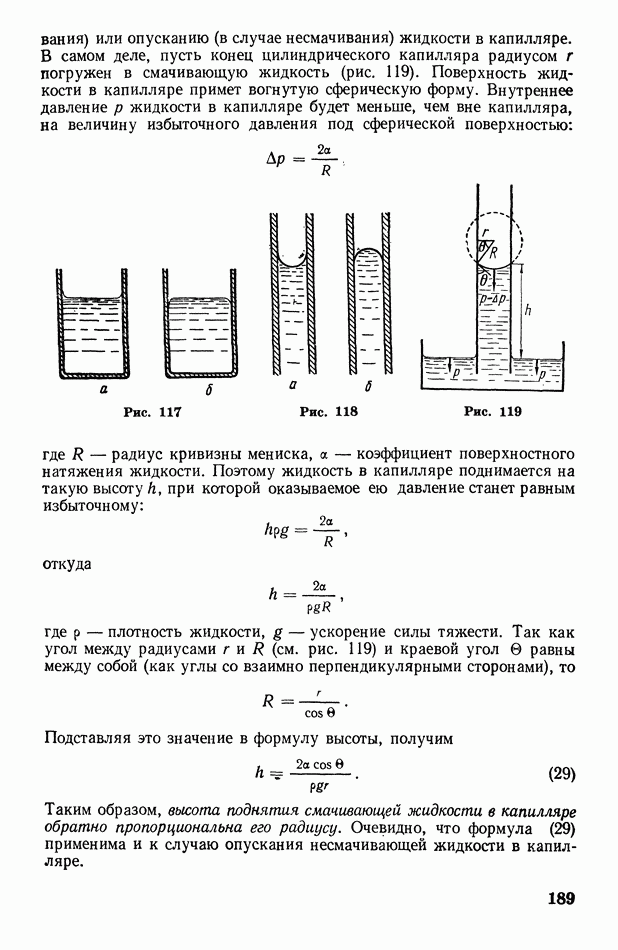
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
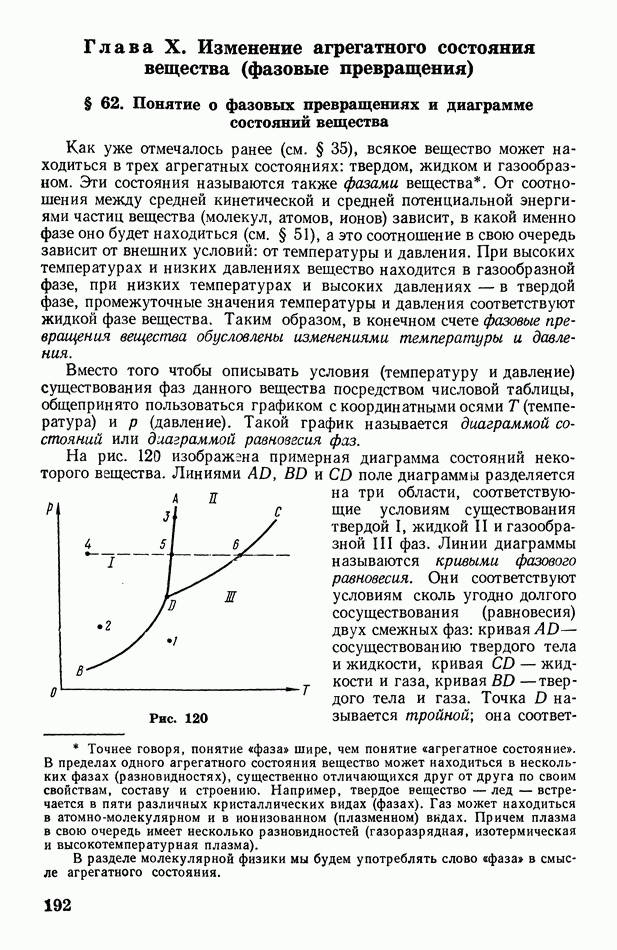
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
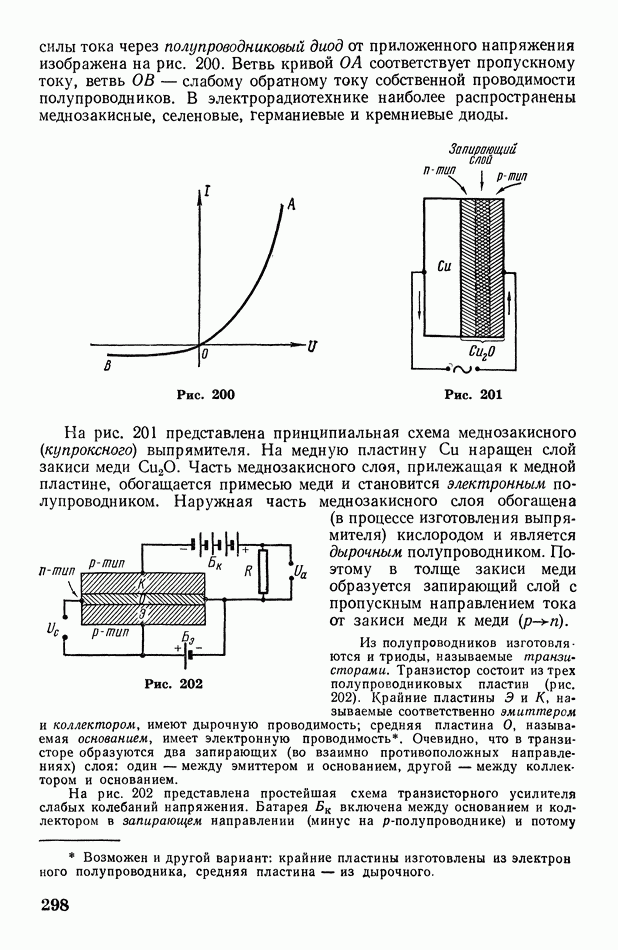
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
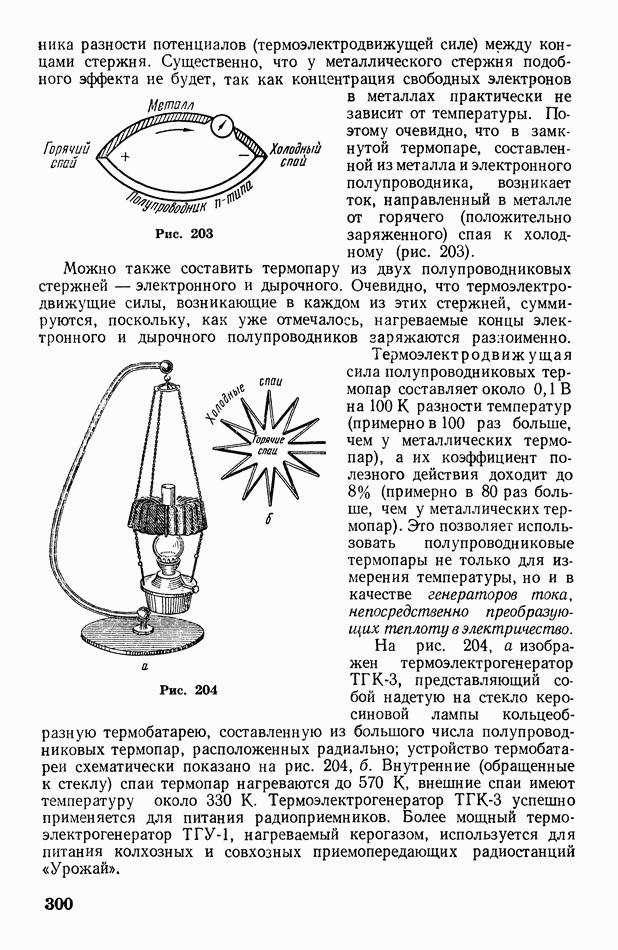
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
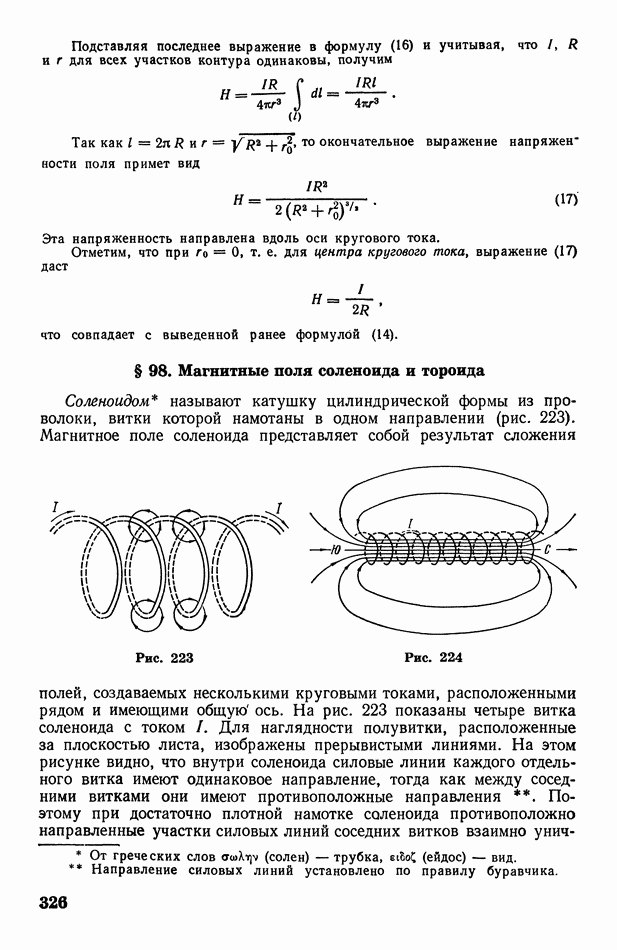
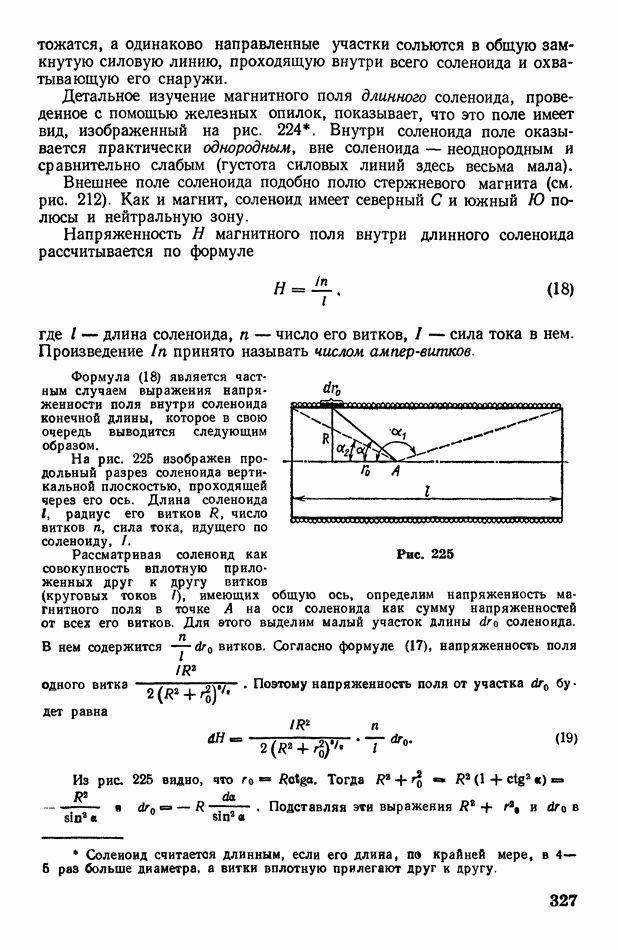
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
- § 117. Тонкие линзы. Микроскоп
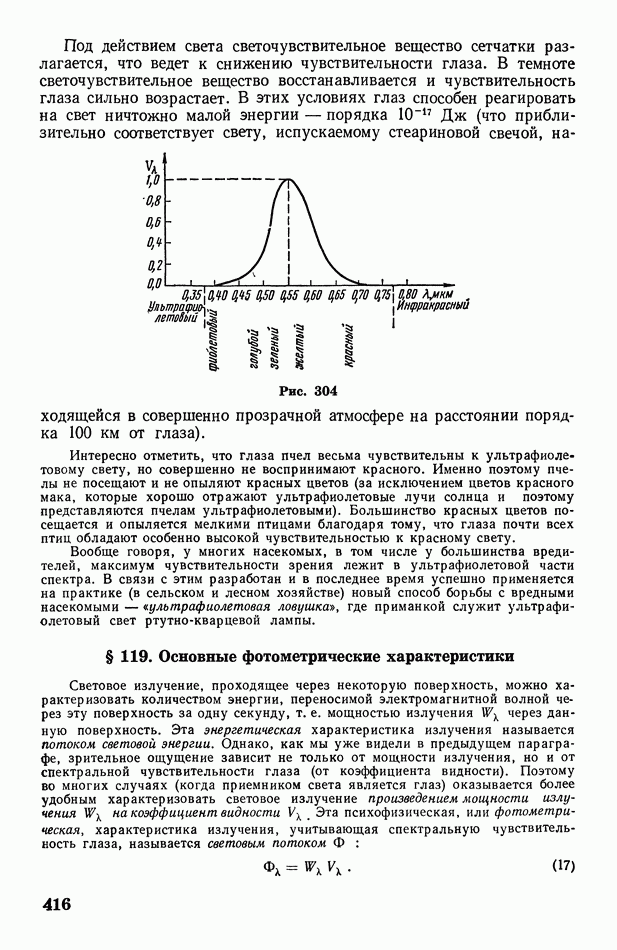
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
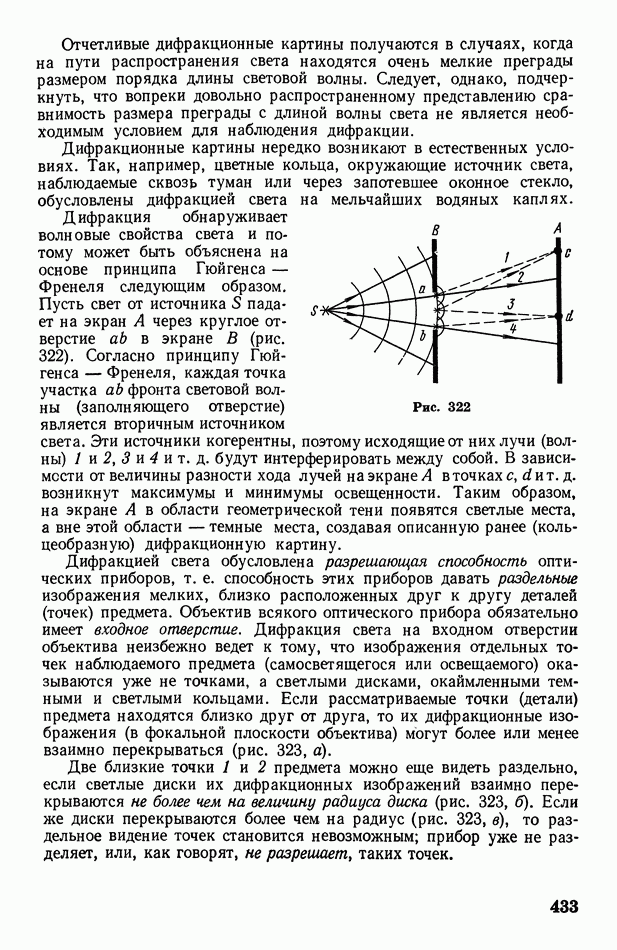
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии