| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
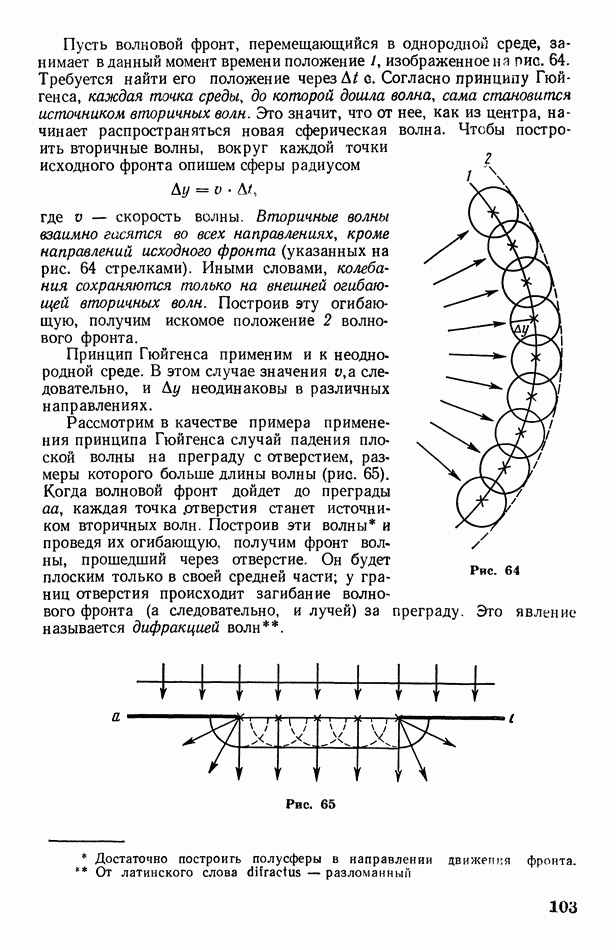
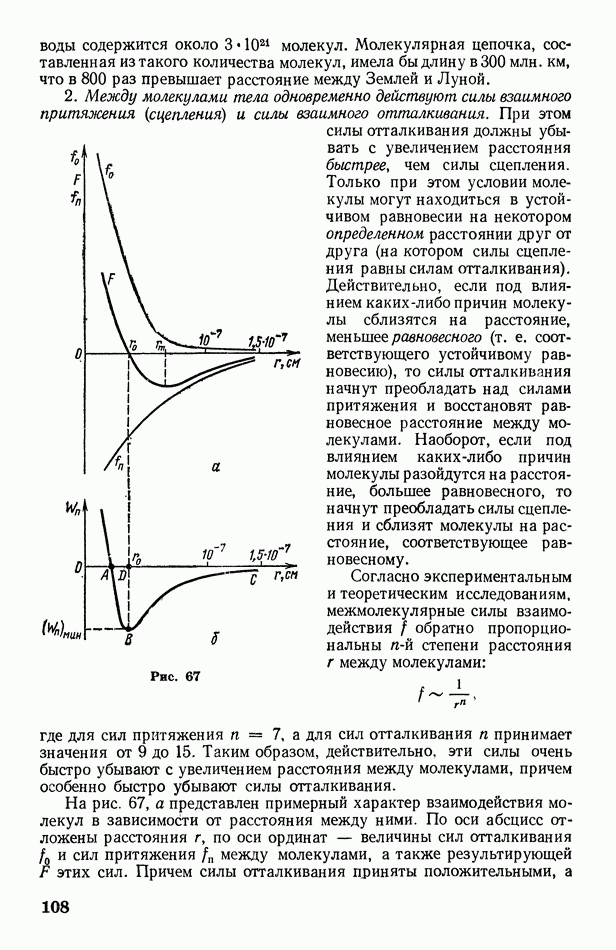
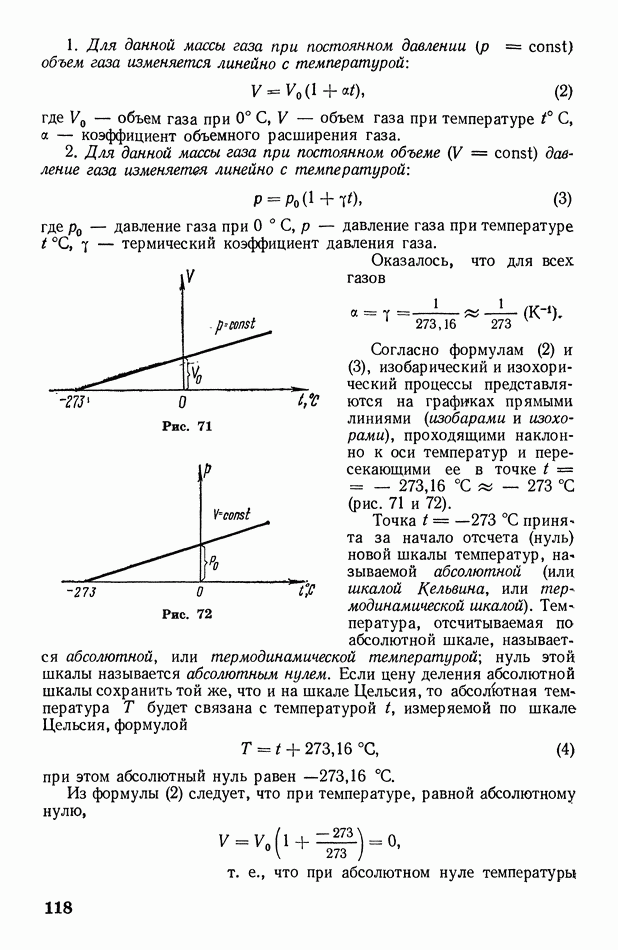
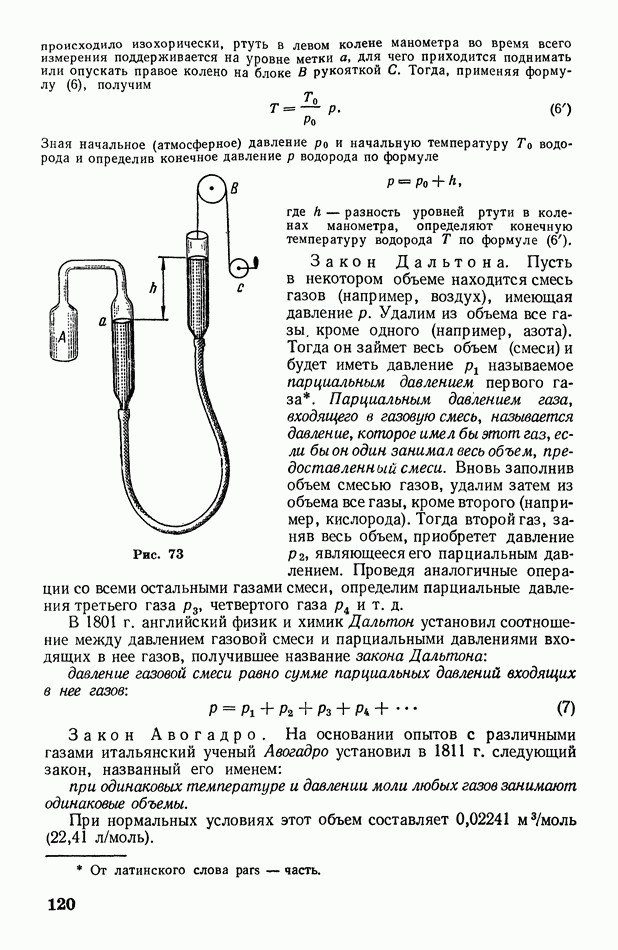
§ 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
Для нахождения средней квадратичной скорости поступательного движения газовых молекул напишем полученные ранее (см § 42) выражения средней кинетической энергии поступательного движения молекул:

Приравняв правые части этих выражений, получим

откуда

но  (молярной массе газа), поэтому
(молярной массе газа), поэтому

т. е. для данного газа средняя квадратичная скорость молекул пропорциональна корню квадратному из абсолютной температуры и зависисит только от нее. Формула (26) выражает среднюю квадратичную скорость молекул через легко измеряемую макроскопическую характеристику газа — температуру. Подсчитаем, например, среднюю квадратичную скорость молекул кислорода при температуре  Так как
Так как  то
то

Таким образом, при комнатной температуре молекулы газа движутся со скоростями, близкими к скорости полета снаряда.
Средняя квадратичная скорость — лишь статистическая характеристика движения молекул, полученная путем усреднения различных значений скорости множества молекул В действительности же молекулы движутся с различными скоростями  даже при некоторой заданной температуре
даже при некоторой заданной температуре  Разобьем весь диапазон этих скоростей на малые интервалы, равные
Разобьем весь диапазон этих скоростей на малые интервалы, равные  Тогда на каждый интервал скорости будет приходиться некоторое число молекул
Тогда на каждый интервал скорости будет приходиться некоторое число молекул  (имеющих скорость,
(имеющих скорость,
заключенную в этом интервале). Очевидно, что отношение  показывает, сколько молекул приходится на каждый единичный интервал скорости, иными словами, каково распределение числа молекул по скоростям;
показывает, сколько молекул приходится на каждый единичный интервал скорости, иными словами, каково распределение числа молекул по скоростям;  зависит от скорости и называется функцией распределения числа молекул по скоростям. Эту функцию распределения впервые определил английский физик Максселл теоретическим путем — на основе теории вероятностей. Максвелловская функция распределения выражается следующей формулой, называемой законом Максвелла:
зависит от скорости и называется функцией распределения числа молекул по скоростям. Эту функцию распределения впервые определил английский физик Максселл теоретическим путем — на основе теории вероятностей. Максвелловская функция распределения выражается следующей формулой, называемой законом Максвелла:

где  общее число молекул газа,
общее число молекул газа,  молярная масса газа,
молярная масса газа,  универсальная газовая постоянная,
универсальная газовая постоянная,  основание натуральных логарифмов.
основание натуральных логарифмов.

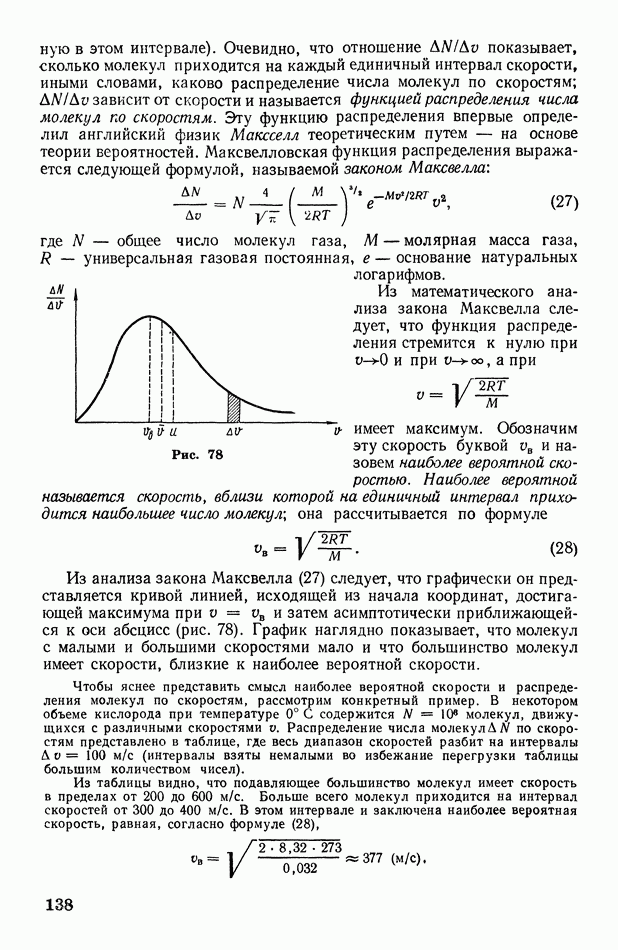
Рис. 78
Из математического анализа закона Максвелла следует, что функция распределения стремится к нулю при и при  а при
а при

имеет максимум. Обозначим эту скорость буквой  и назовем наиболее вероятной скоростью. Наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул; она рассчитывается по формуле
и назовем наиболее вероятной скоростью. Наиболее вероятной называется скорость, вблизи которой на единичный интервал приходится наибольшее число молекул; она рассчитывается по формуле

Из анализа закона Максвелла (27) следует, что графически он представляется кривой линией, исходящей из начала координат, достигающей максимума при  затем асимптотически приближающейся к оси абсцисс (рис. 78). График наглядно показывает, что молекул с малыми и большими скоростями мало и что большинство молекул имеет скорости, близкие к наиболее вероятной скорости.
затем асимптотически приближающейся к оси абсцисс (рис. 78). График наглядно показывает, что молекул с малыми и большими скоростями мало и что большинство молекул имеет скорости, близкие к наиболее вероятной скорости.
Чтобы яснее представить смысл наиболее вероятной скорости и распределения молекул по скоростям, рассмотрим конкретный пример. В некотором объеме кислорода при температуре 0° С содержится  молекул, движущихся с различными скоростями
молекул, движущихся с различными скоростями  Распределение числа молекул
Распределение числа молекул  по скоростям представлено в таблице, где весь диапазон скоростей разбит на интервалы
по скоростям представлено в таблице, где весь диапазон скоростей разбит на интервалы  (интервалы взяты немалыми во избежание перегрузки таблицы большим количеством чисел).
(интервалы взяты немалыми во избежание перегрузки таблицы большим количеством чисел).
Из таблицы видно, что подавляющее большинство молекул имеет скорость в пределах от 200 до 600 м/с. Больше всего молекул приходится на интервал скоростей от 300 до 400 м/с. В этом интервале и заключена наиболее вероятная скорость, равная, согласно формуле (28),

Из закона Максвелла можно получить выражение для средней арифметической скорости 

Формулы (26), (28) и (29) показывают, что скорости  различаются между собой только численными коэффициентами и
различаются между собой только численными коэффициентами и  Количественное соотношение между ними таково:
Количественное соотношение между ними таково:

В нашем примере с кислородом при температуре  оказалось, что
оказалось, что  Тогда по формулам (30) получим
Тогда по формулам (30) получим 
(см. скан)
Отметив в соответствии с формулами (30) значения  и на рис. 78, увидим, что средней арифметической скоростью обладает несколько меньшее число молекул, чем наиболее вероятной скоростью, а средней квадратичной скоростью обладает еще меньшее число молекул.
и на рис. 78, увидим, что средней арифметической скоростью обладает несколько меньшее число молекул, чем наиболее вероятной скоростью, а средней квадратичной скоростью обладает еще меньшее число молекул.
Отметим на оси абцисс (см. рис. 78) один интервал скоростей  и проведем ординаты его границ. Площадь очень узкого (заштрихованного) прямоугольника равна
и проведем ординаты его границ. Площадь очень узкого (заштрихованного) прямоугольника равна  т. е. числу молекул, имеющих скорость в интервале
т. е. числу молекул, имеющих скорость в интервале  Следовательно, площадь, заключенная между всей кривой распределения и осью абцисс, равна общему числу молекул газа
Следовательно, площадь, заключенная между всей кривой распределения и осью абцисс, равна общему числу молекул газа 
При изменении температуры газа изменяются скорости движения всех молекул, а следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться вправо (при повышении температуры) или влево (при понижении температуры) Однако площадь, ограниченная кривой, останется неизменной, так как общее число молекул газа не зависит от температуры. В связи с этим при повышении температуры кривая распределения будет растягиваться и понижаться, а при понижении температуры, наоборот, — сужаться и повышаться, как это показано на рис. 79.

Рис. 79
Для экспериментальной проверки закона Максвелла немецкий физик Штерн в 1920 г. поставил специальный опыт. Прибор Штерна состоял из двух жестко скрепленных друг с другом цилиндрических сосудов, вдоль общей оси которых была натянута платиновая посеребренная проволочка (рис. 80). Основания обоих цилиндров были герметично закрыты и воздух из цилиндров откачан. В узком внутреннем цилиндре имелась очень узенькая вертикальная щель. При нагревании проволочки током до температуры порядка 1000 °С серебро начинало испаряться и внутренний цилиндр наполнялся атомами серебра. Таким образом, Штерн экспериментировал с одноатомным серебряным газом. Те атомы, которые летели от проволочки по радиусу к щели, вылетали во внешний цилиндр (радиусом  ) и оседали на его стенке, образуя узенькую серебряную полоску а — проекцию щели (рис. 80 и 81).
) и оседали на его стенке, образуя узенькую серебряную полоску а — проекцию щели (рис. 80 и 81).

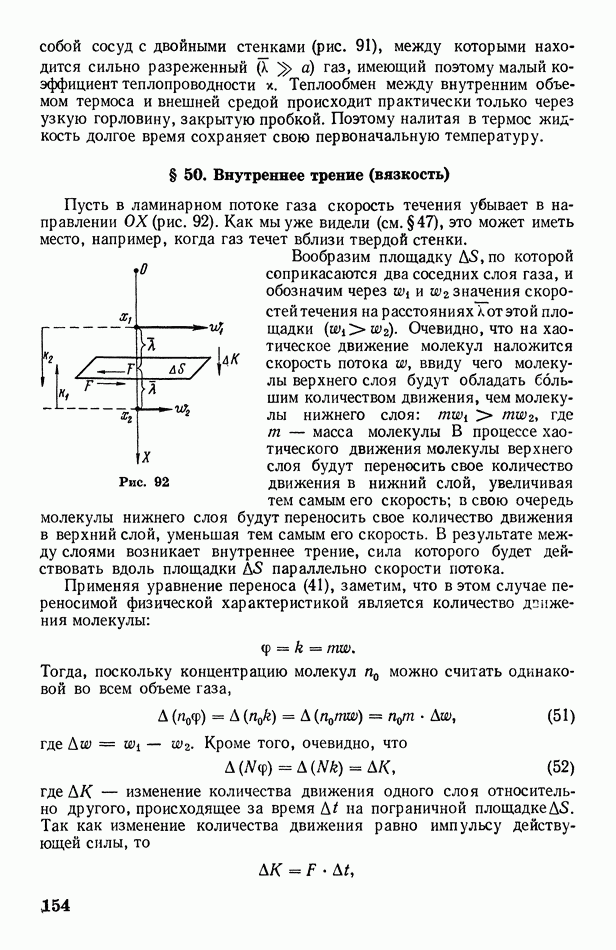
Рис. 80

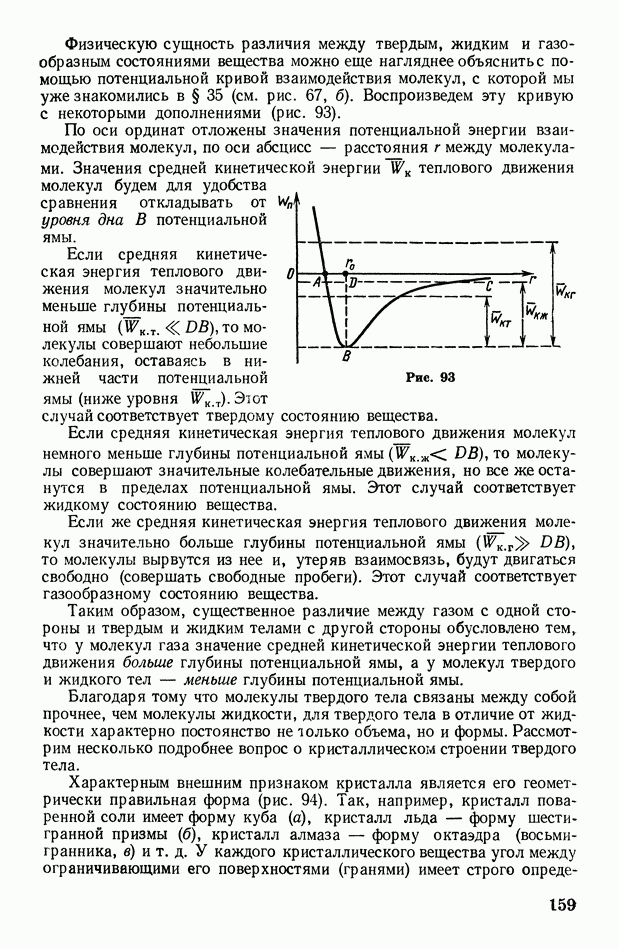
Рис. 81
Такая картина получилась бы при неподвижном приборе. Но Штерн приводил прибор во вращение с угловой скоростью со вокруг общей оси цилиндров (см. рис. 81). Поэтому атомы серебра оседали не против щели, а смещались на некоторое расстояние. В итоге на поверхности внешнего цилиндра образовывалась не узенькая серебряная полоска, а широкая полоса  не одинаковой толщины, показанная в разрезе на рис. 81. Полоса получилась широкой потому, что разные атомы имели различные скорости: более быстрые оседали ближе к началу полосы а, более медленные — ближе к его концу
не одинаковой толщины, показанная в разрезе на рис. 81. Полоса получилась широкой потому, что разные атомы имели различные скорости: более быстрые оседали ближе к началу полосы а, более медленные — ближе к его концу  Неодинаковость толщины полосы обусловлена тем, что на разные скорости движения атомов приходится различное число атомов: тем местам полосы, где она тоньше, соответствуют, очевидно, скорости, которыми обладает меньшее число атомов.
Неодинаковость толщины полосы обусловлена тем, что на разные скорости движения атомов приходится различное число атомов: тем местам полосы, где она тоньше, соответствуют, очевидно, скорости, которыми обладает меньшее число атомов.
Таким образом, каждое место (например,  на разрезе полосы соответствует определенной скорости и определенному числу осевших атомов, а вид поперечного разреза полосы (см. рис. 81) характеризует распределение числа атомов по скоростям. В этой связи следует обратить внимание на большое сходство видов максвелловского графика (см. рис. 78) и разреза серебряной полосы (см. рис. 81), что уже является качественным подтверждением правильности закона Максвелла.
на разрезе полосы соответствует определенной скорости и определенному числу осевших атомов, а вид поперечного разреза полосы (см. рис. 81) характеризует распределение числа атомов по скоростям. В этой связи следует обратить внимание на большое сходство видов максвелловского графика (см. рис. 78) и разреза серебряной полосы (см. рис. 81), что уже является качественным подтверждением правильности закона Максвелла.
Для того чтобы количественно оценить это распределение, надо найти скорости  для ряда мест поперечного разреза полосы и число атомов
для ряда мест поперечного разреза полосы и число атомов  осевших на каждом из этих мест. Число атомов
осевших на каждом из этих мест. Число атомов  в любом месте
в любом месте  полосы Штерн определял по толщине полосы, а соответствующую скорость
полосы Штерн определял по толщине полосы, а соответствующую скорость  по расстоянию
по расстоянию  от начала полосы а до
от начала полосы а до 
Формула для подсчета  выводится из следующих соображений. За время
выводится из следующих соображений. За время  точки поверхности внешнего цилиндра пройдут путь
точки поверхности внешнего цилиндра пройдут путь  с линейной скоростью, равной
с линейной скоростью, равной  а атомы серебра пролетят путь
а атомы серебра пролетят путь  со скоростью
со скоростью  Поэтому
Поэтому

Поделив второе равенство на первое, получим

откуда

Значения со и  известны как характеристики прибора Штерна, значения
известны как характеристики прибора Штерна, значения  определяются непосредственными измерениями на серебряной полосе.
определяются непосредственными измерениями на серебряной полосе.
Наиболее точные эксперименты, выполненные впоследствии с помощью усовершенствованного прибора Штерна, показали, что распределение числа атомов по скоростям, даваемое опытом, находится в соответствии с теоретическим законом Максвелла.
Задача 24. Чему равна энергия  теплового движения молекул, содержащихся в
теплового движения молекул, содержащихся в  кислорода при температуре
кислорода при температуре  Какая часть этой энергии приходится на долю поступательного движения молекул и какая часть — на долю их вращательного движения? Решение. Согласно формуле
Какая часть этой энергии приходится на долю поступательного движения молекул и какая часть — на долю их вращательного движения? Решение. Согласно формуле  ,
,

где  молярная масса кислорода,
молярная масса кислорода,  число степеней свободы его молекул. Поэтому
число степеней свободы его молекул. Поэтому

Так как у двухатомной молекулы на поступательное движение приходится три степени свободы, а на вращательное две (см. § 43), то искомые части энергии  находятся в отношении
находятся в отношении  Следовательно, на долю поступательного движения приходится энергия
Следовательно, на долю поступательного движения приходится энергия

а на долю вращательного движения приходится энергия

Задача 25. Для нагревания некоторого количества газа на  при постоянном давлении необходимо затратить
при постоянном давлении необходимо затратить  Если это же количество газа охладить
Если это же количество газа охладить  при постоянном объеме, то выделится
при постоянном объеме, то выделится  Какое число
Какое число  степеней свободы имеют молекулы этого газа?
степеней свободы имеют молекулы этого газа?
Решение. Энергия, затрачиваемая на нагревание газа при постоянном давлении,

а энергия, выделяемая при охлаждении этого газа при постоянном объеме,

где  масса газа,
масса газа,  молярная масса газа,
молярная масса газа,  молярные теплоемко
молярные теплоемко  газа при постоянном давлении и постоянном объеме. Поделив почленно первое равенство на второе, получим
газа при постоянном давлении и постоянном объеме. Поделив почленно первое равенство на второе, получим

или, учитывая формулы (20) и (20),

Тогда  откуда
откуда 
Задача 26. В момент взрыва водородной бомбы развивается температура, равная примерно  Считая, что при такой температуре все молекулы полностью диссоциированы, а все атомы ионизованы, найти среднюю квадратичную скорость и ионов водорода. Решение. Согласно формуле (26),
Считая, что при такой температуре все молекулы полностью диссоциированы, а все атомы ионизованы, найти среднюю квадратичную скорость и ионов водорода. Решение. Согласно формуле (26),

где  молярная масса водорода. Поэтому
молярная масса водорода. Поэтому

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
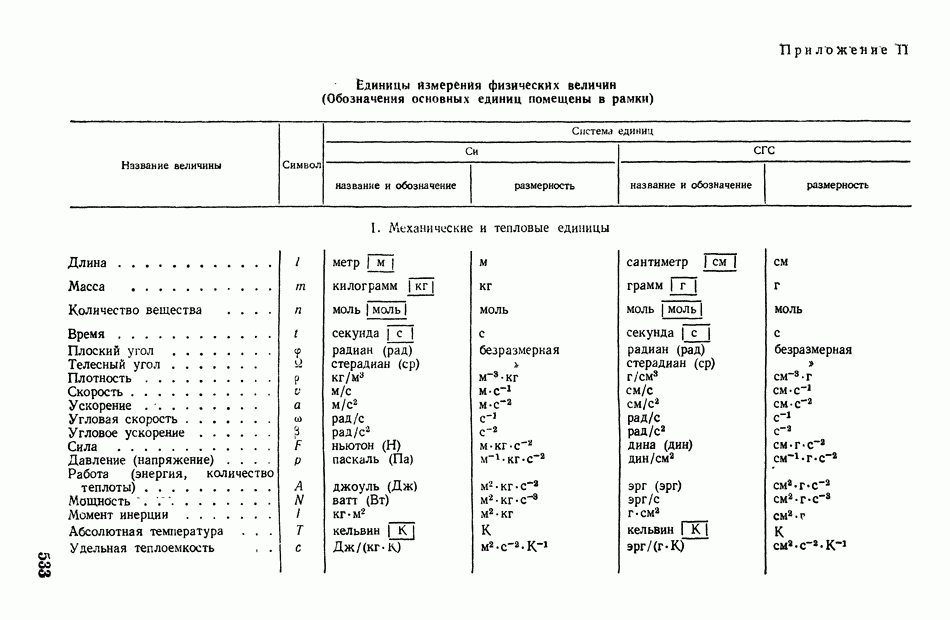
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
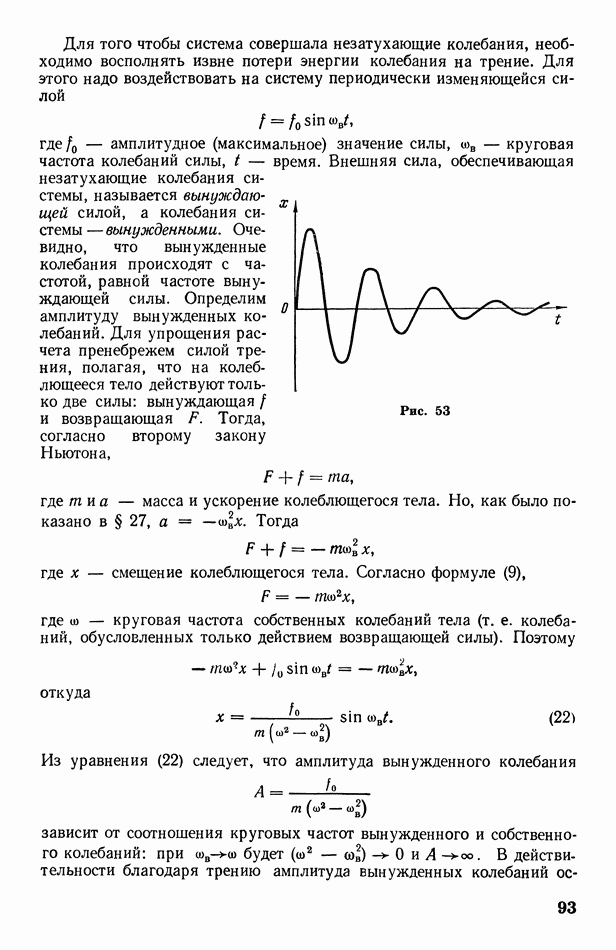
- § 30. О затухающих и вынужденных колебаниях
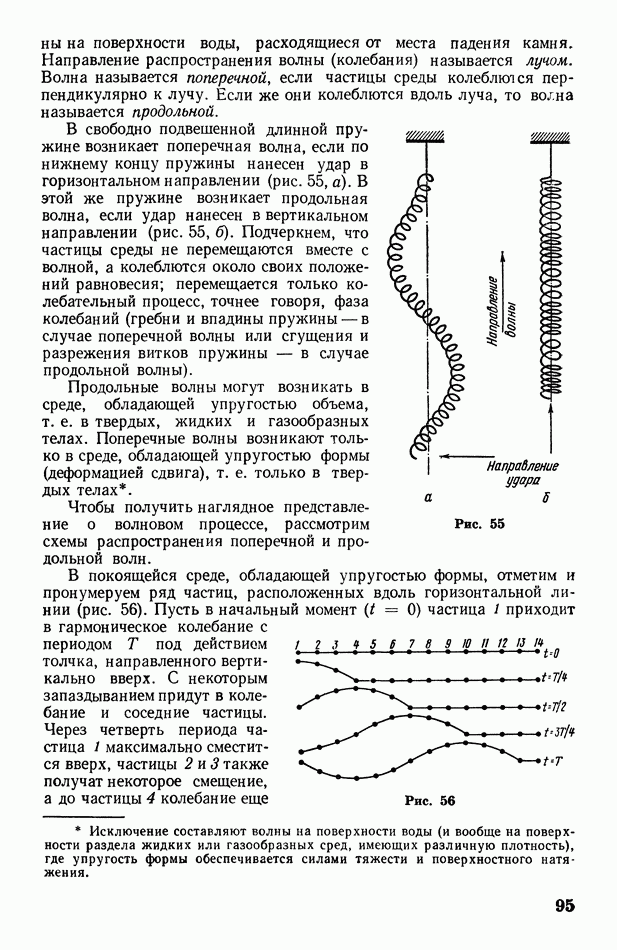
- § 31. Волновой процесс
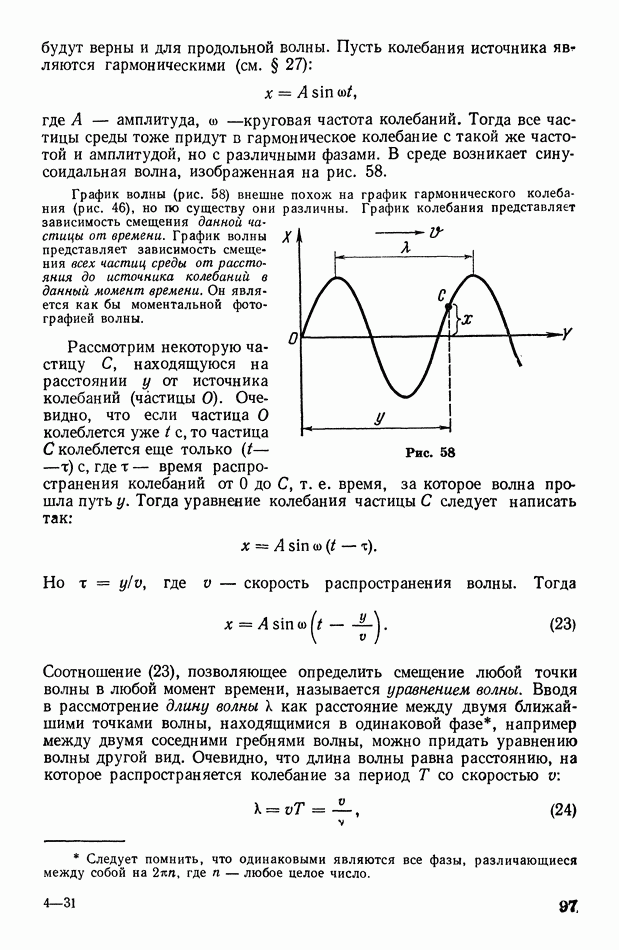
- § 32. Уравнение волны. Интенсивность волны
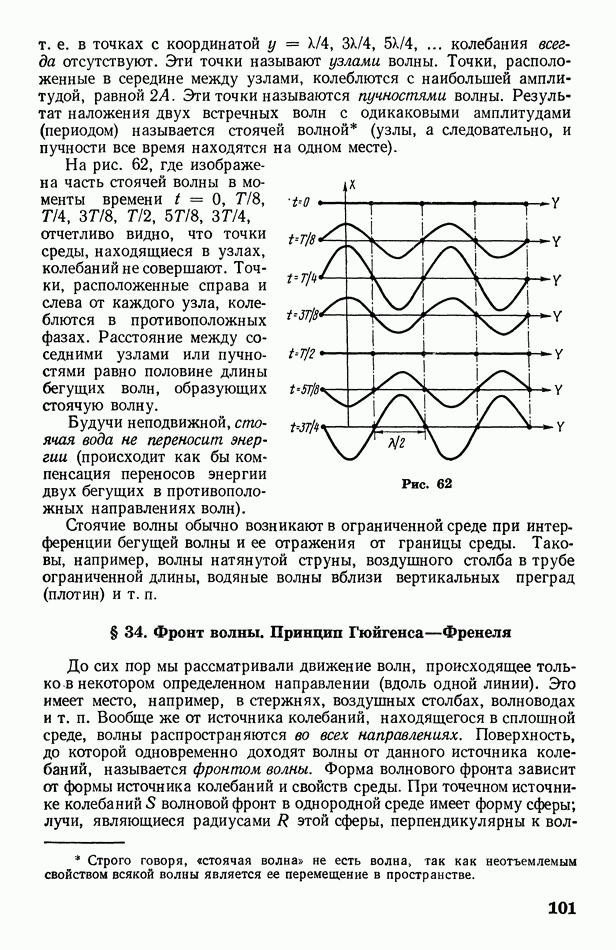
- § 33. Интерференция волн. Стоячие волны
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
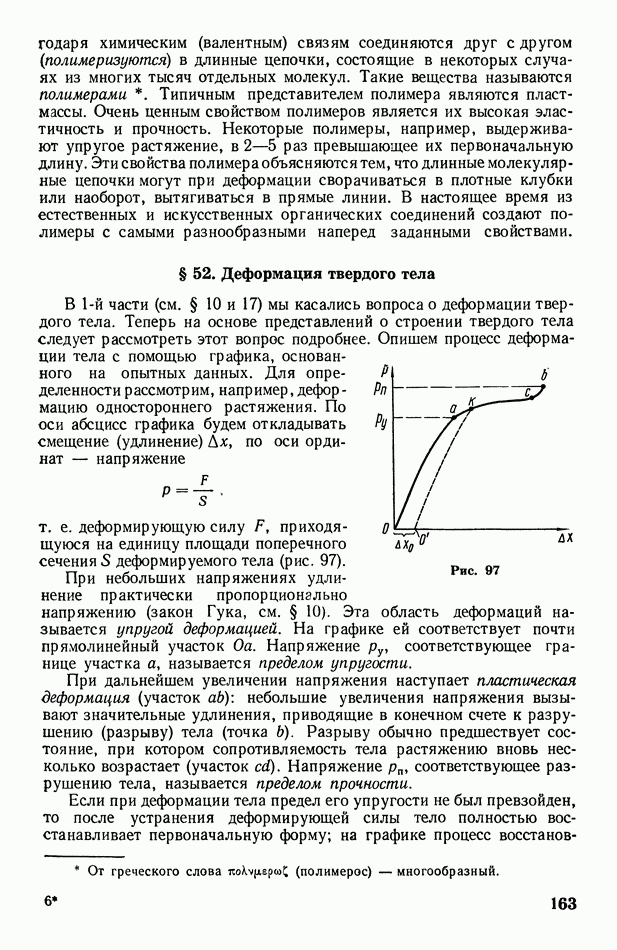
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
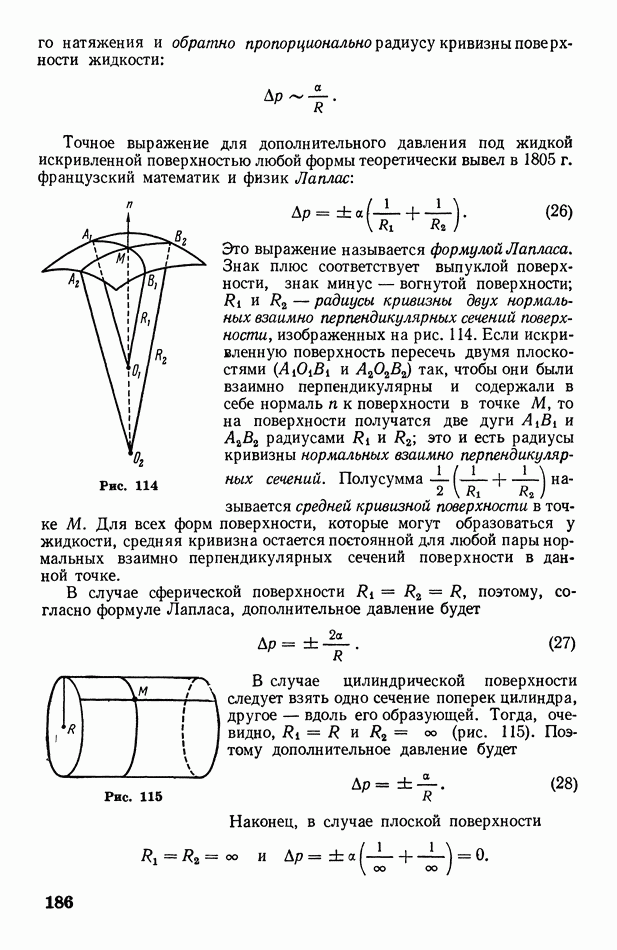
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
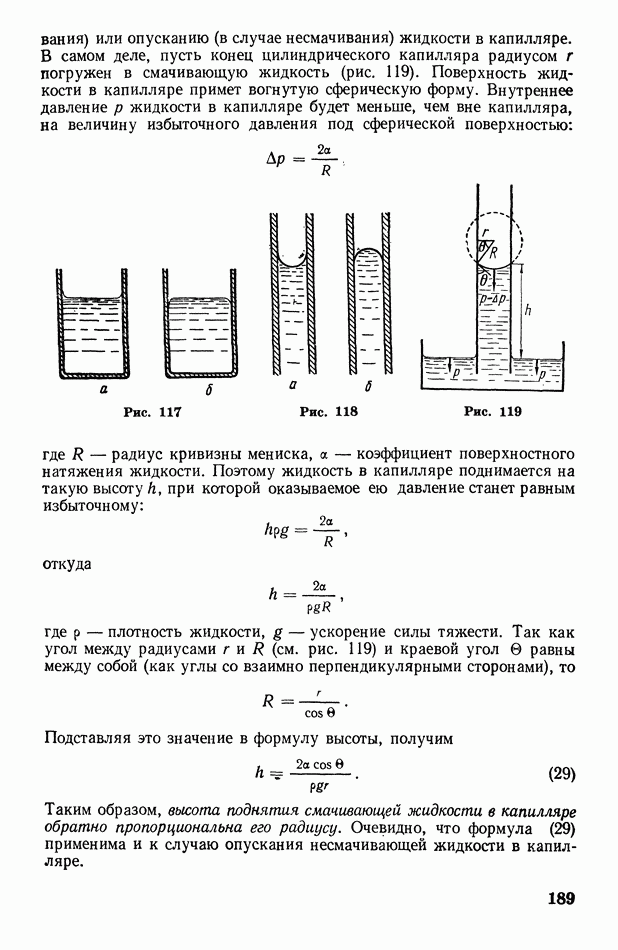
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
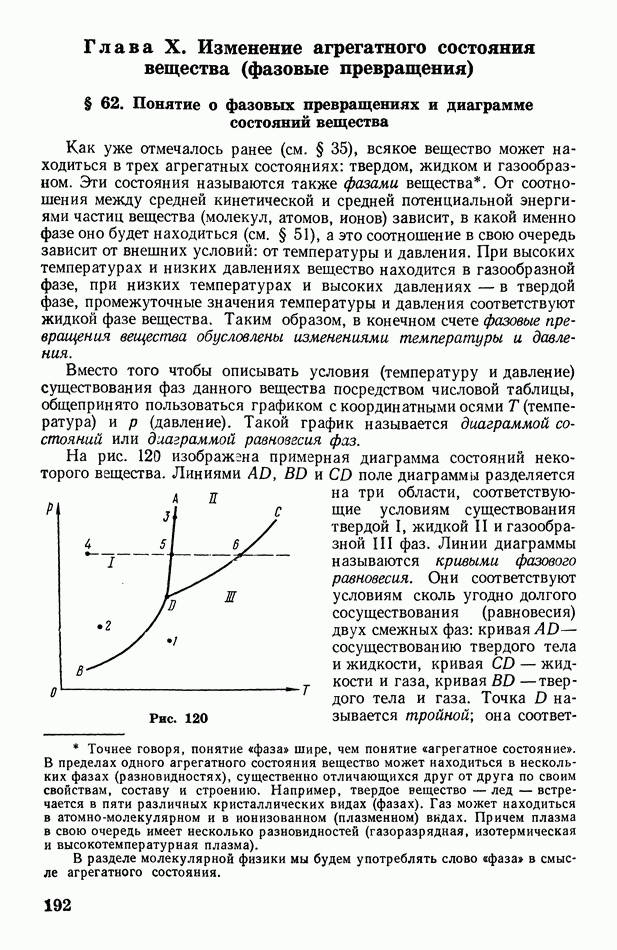
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
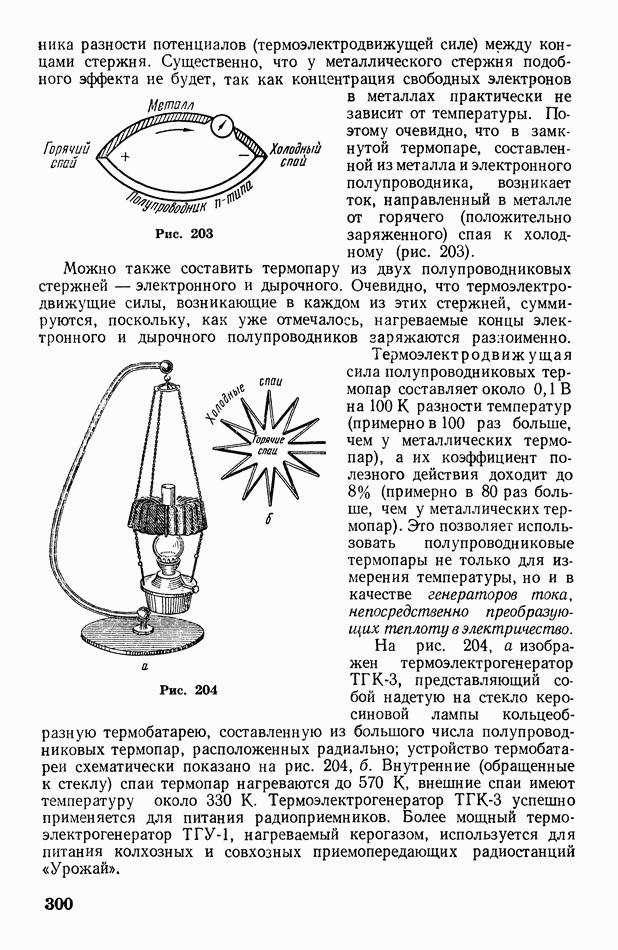
- § 87. Контактная разность потенциалов. Термоэлектрические явления
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
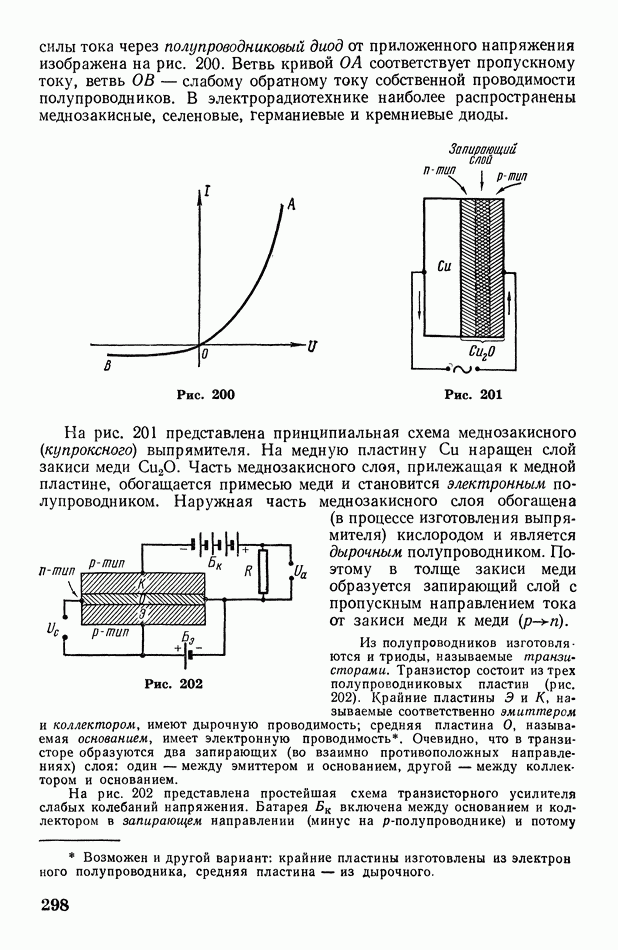
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
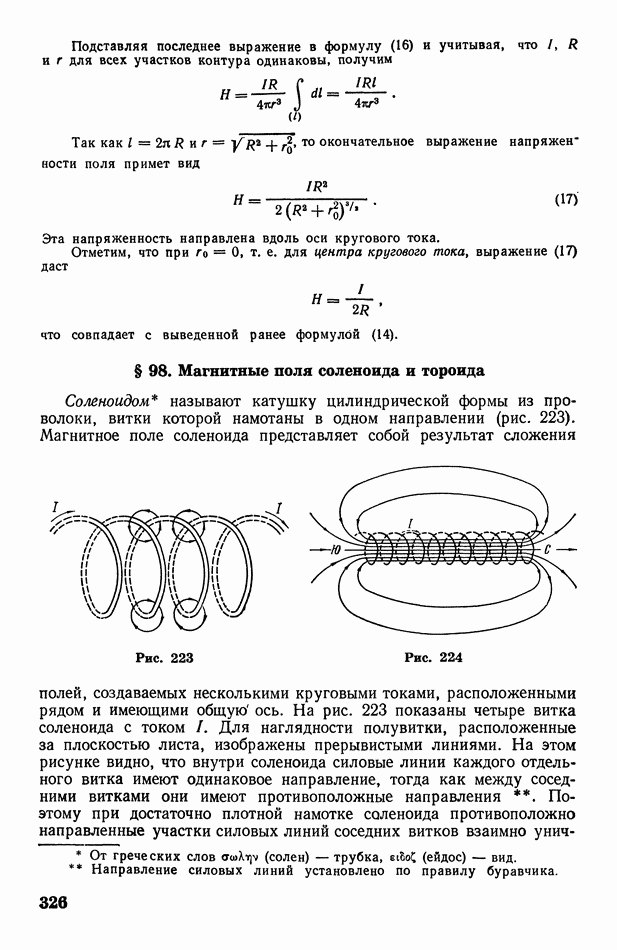
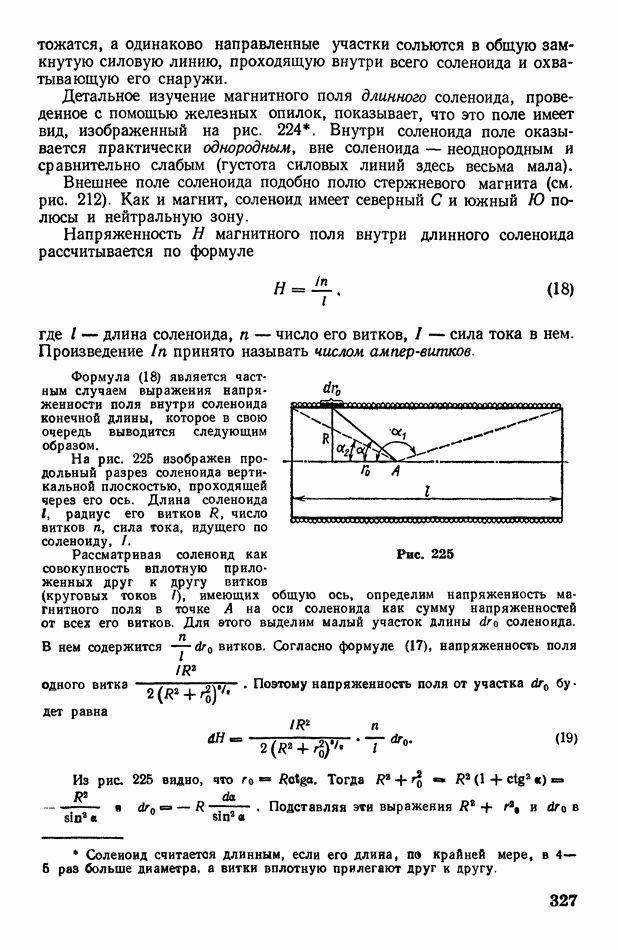
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
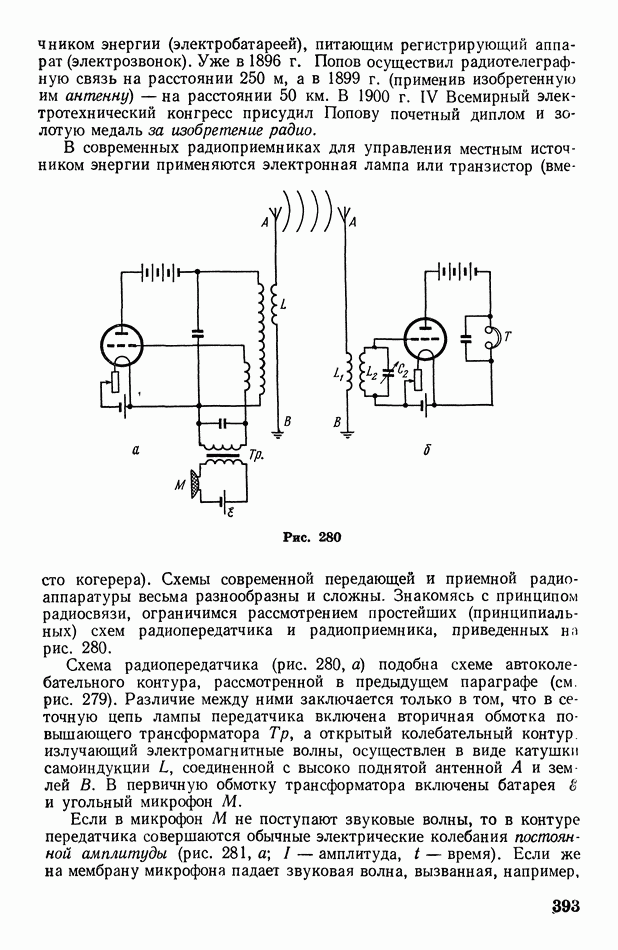
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
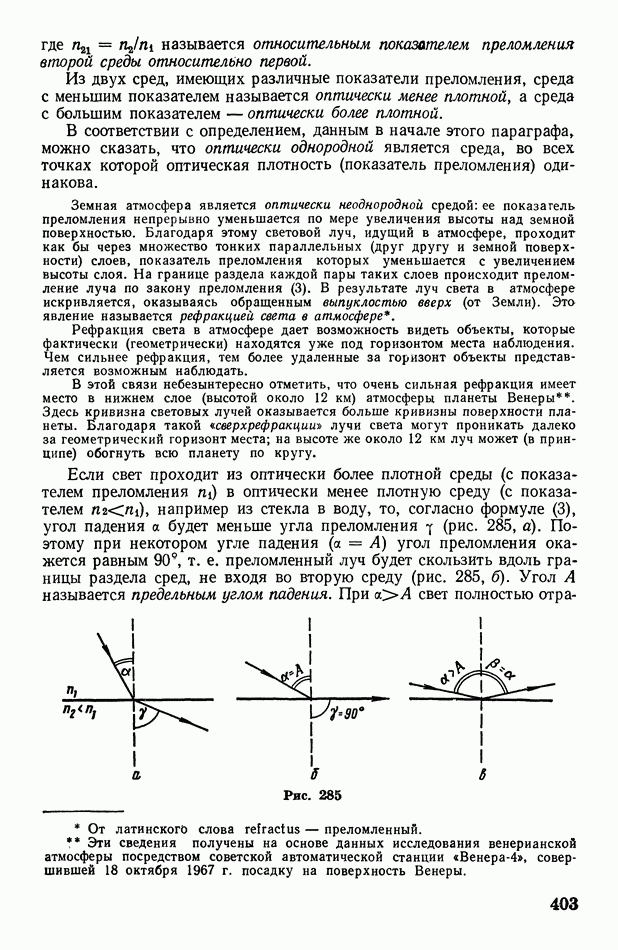
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
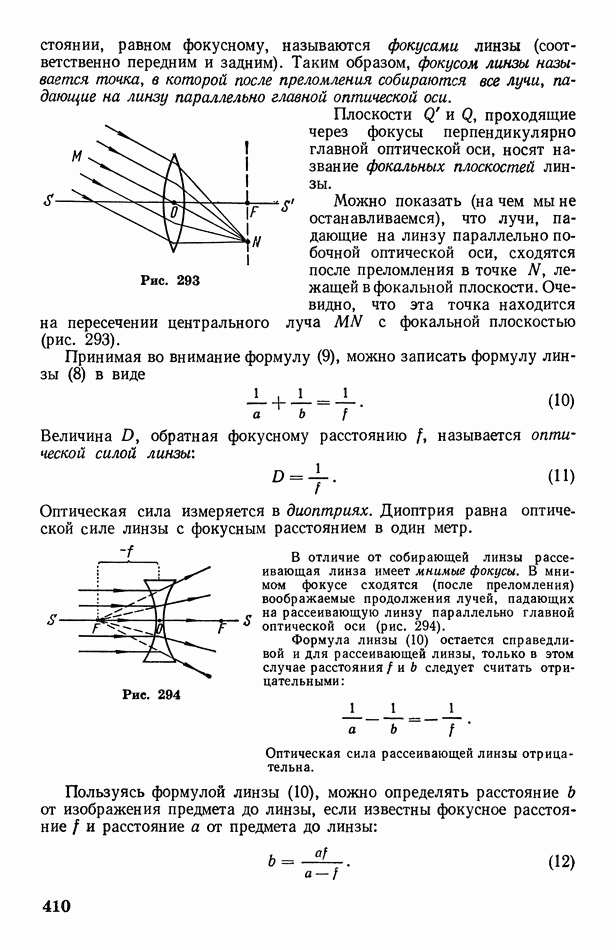
- § 117. Тонкие линзы. Микроскоп
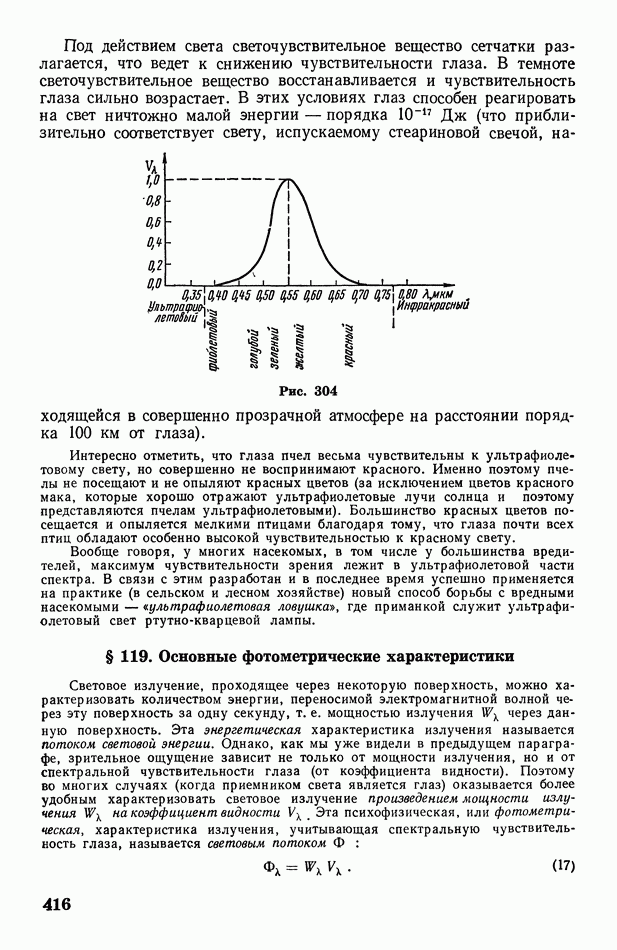
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
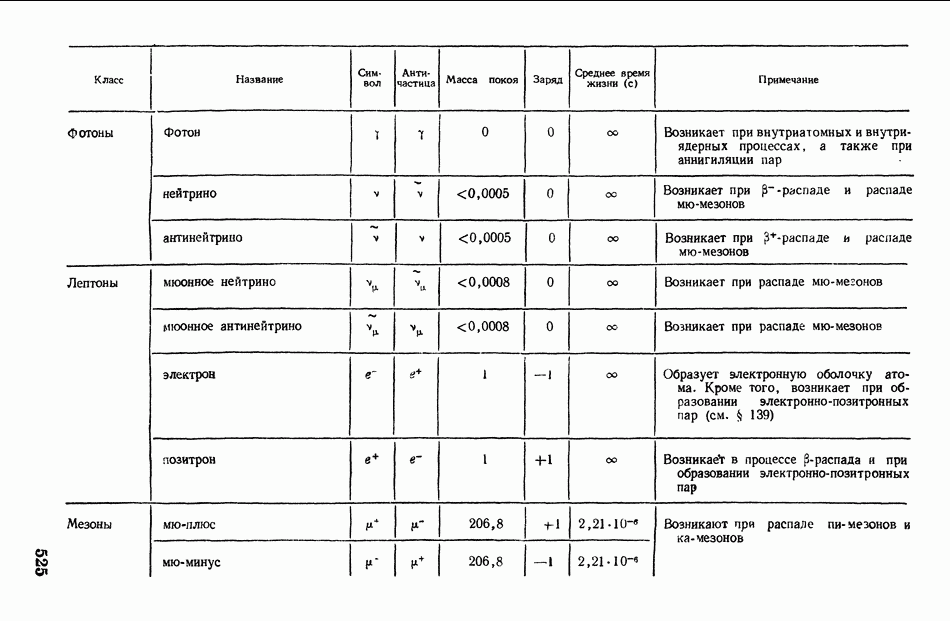
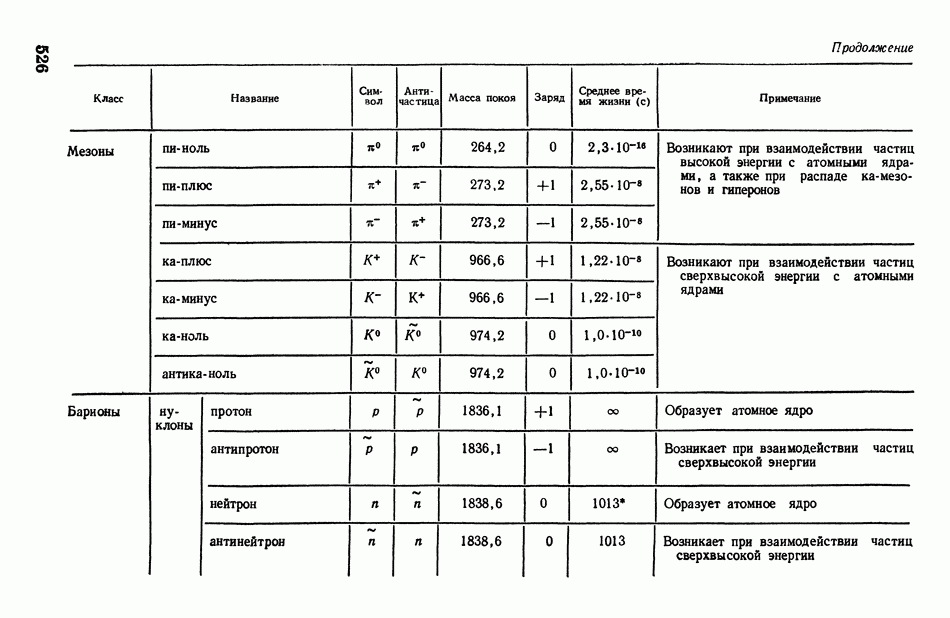
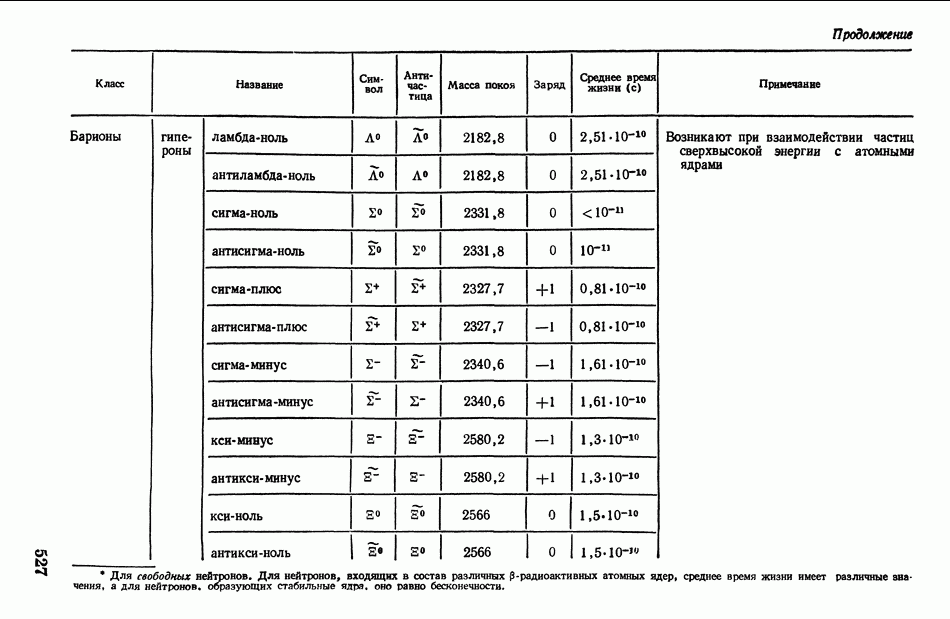
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии