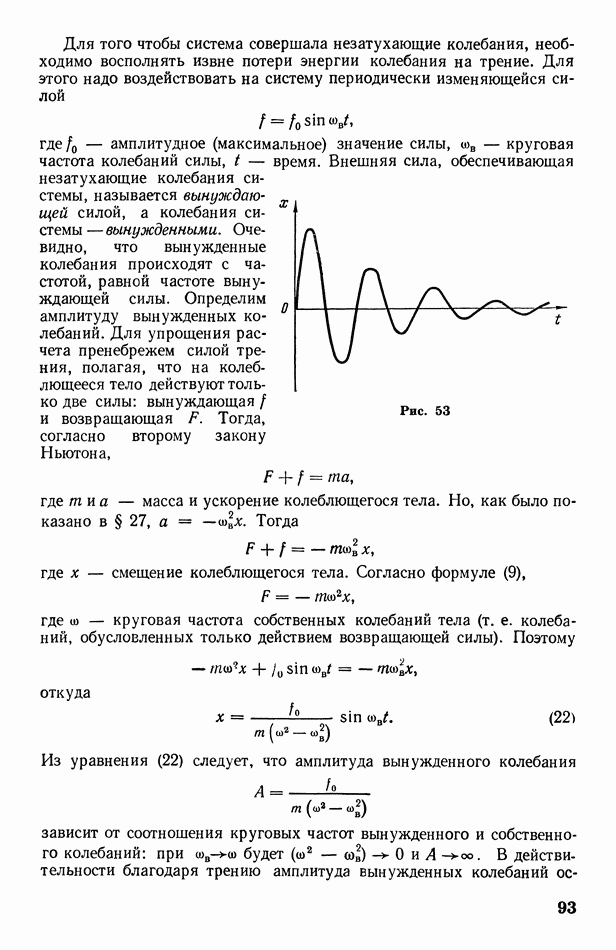
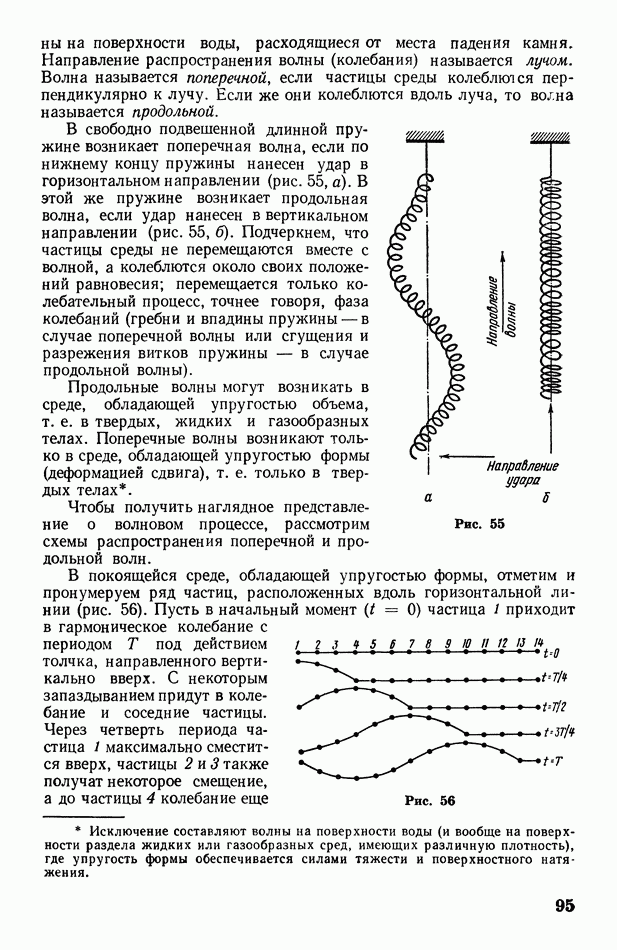
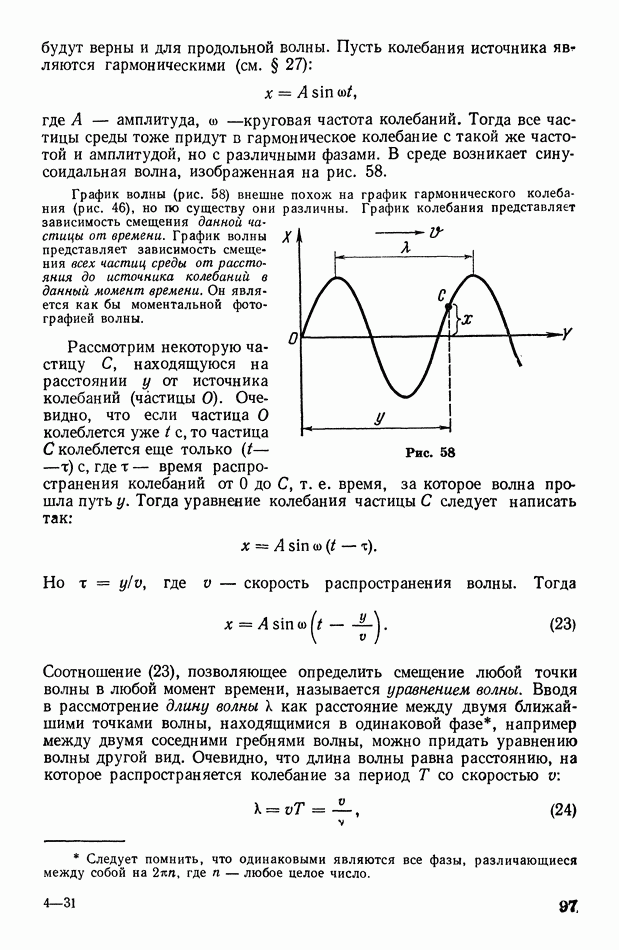
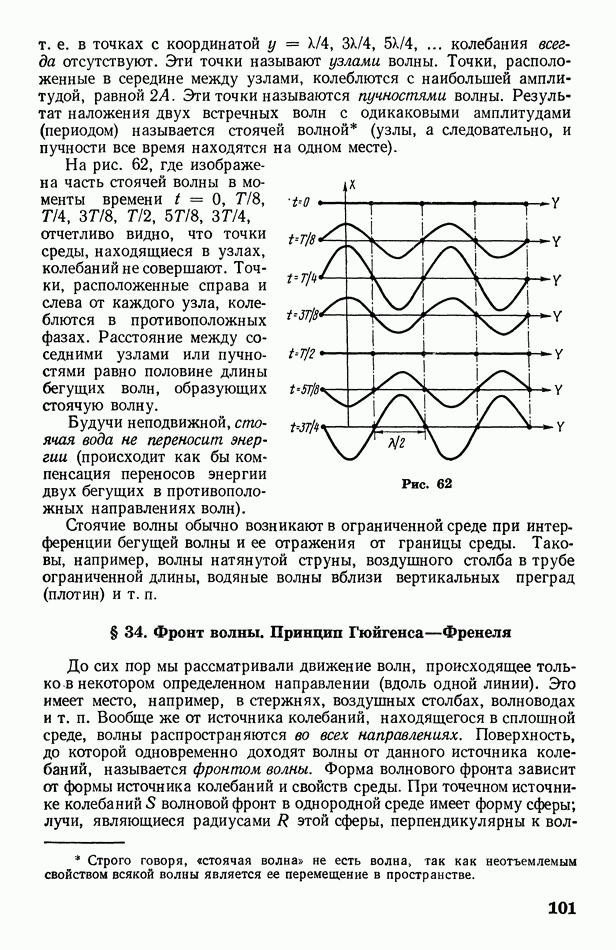
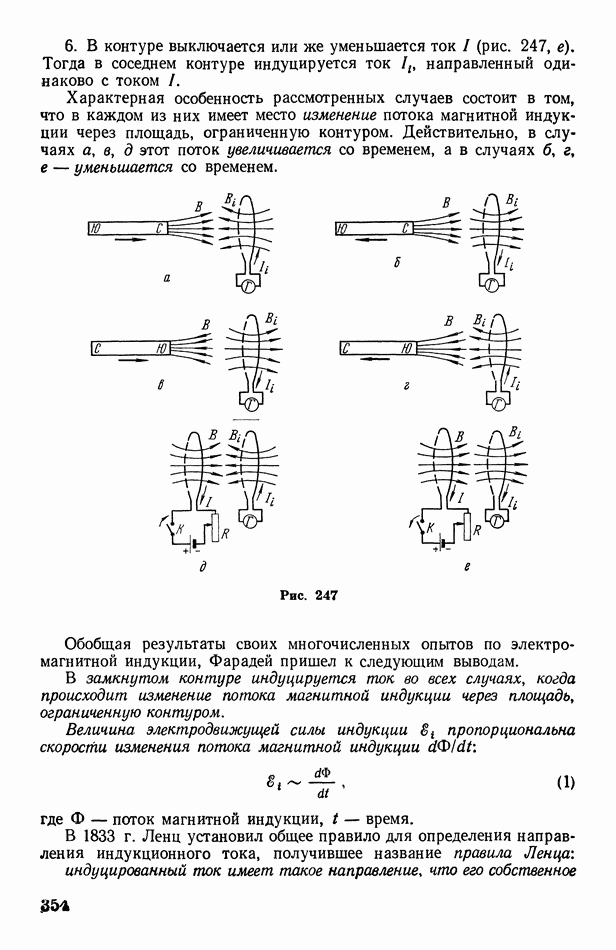
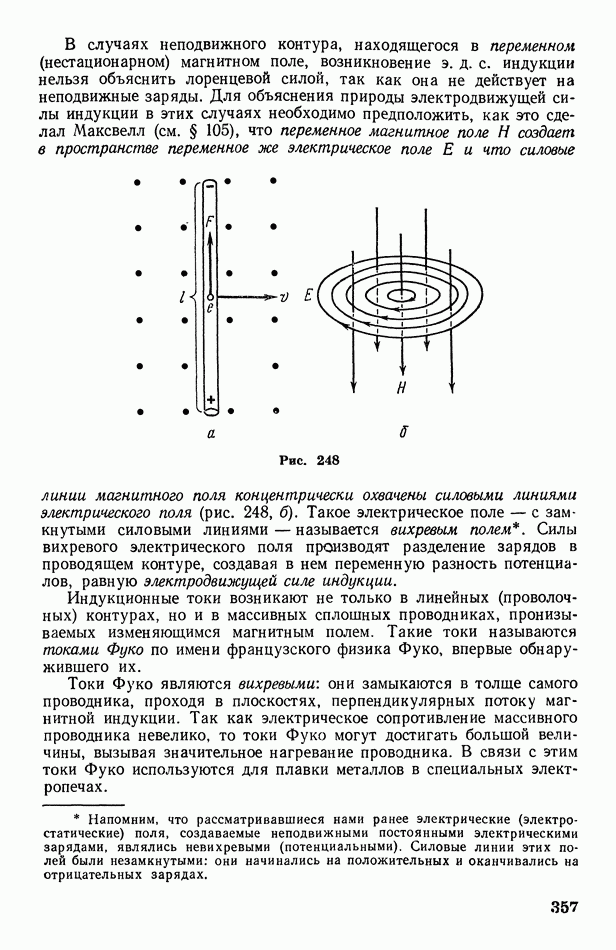
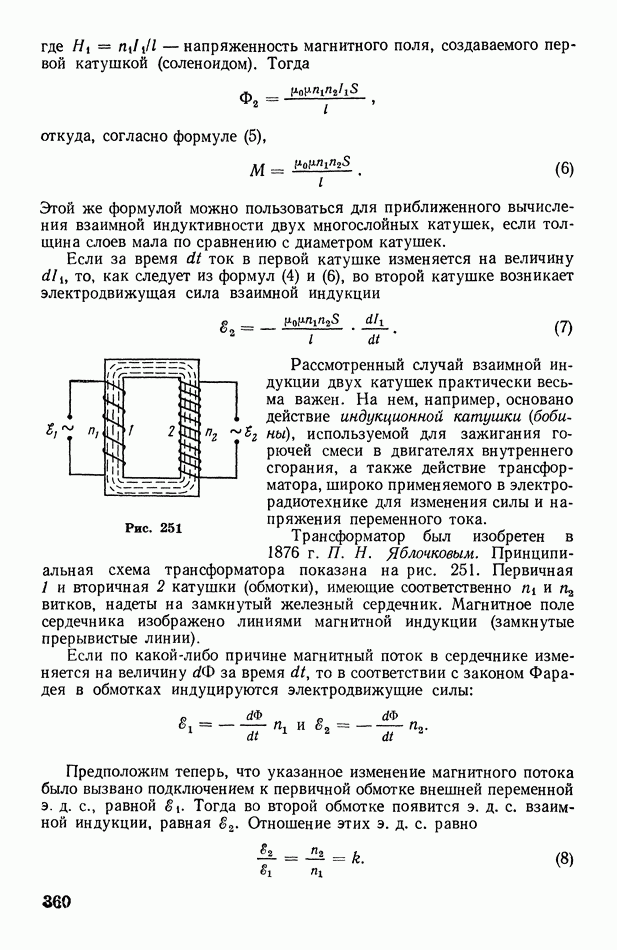
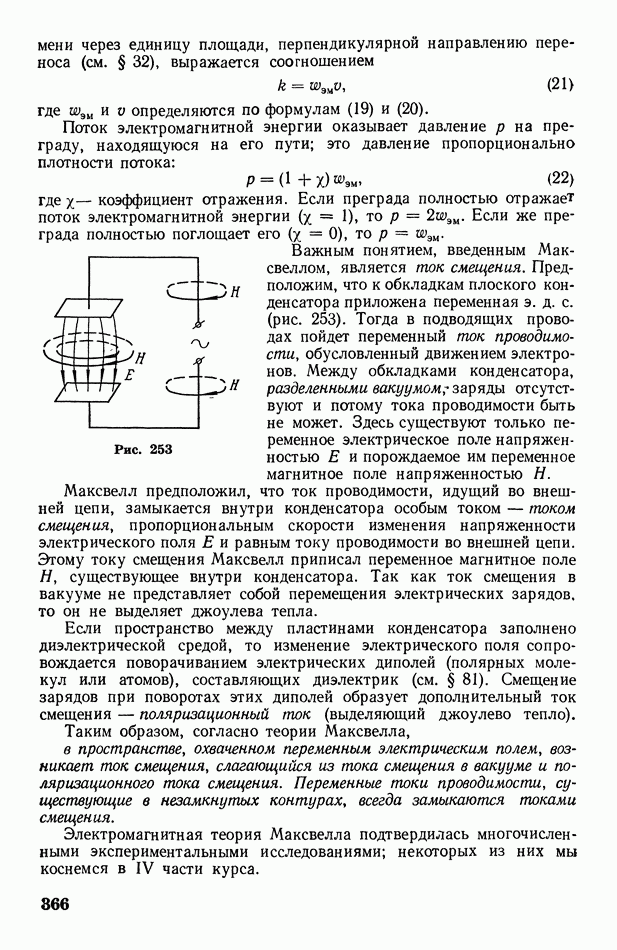
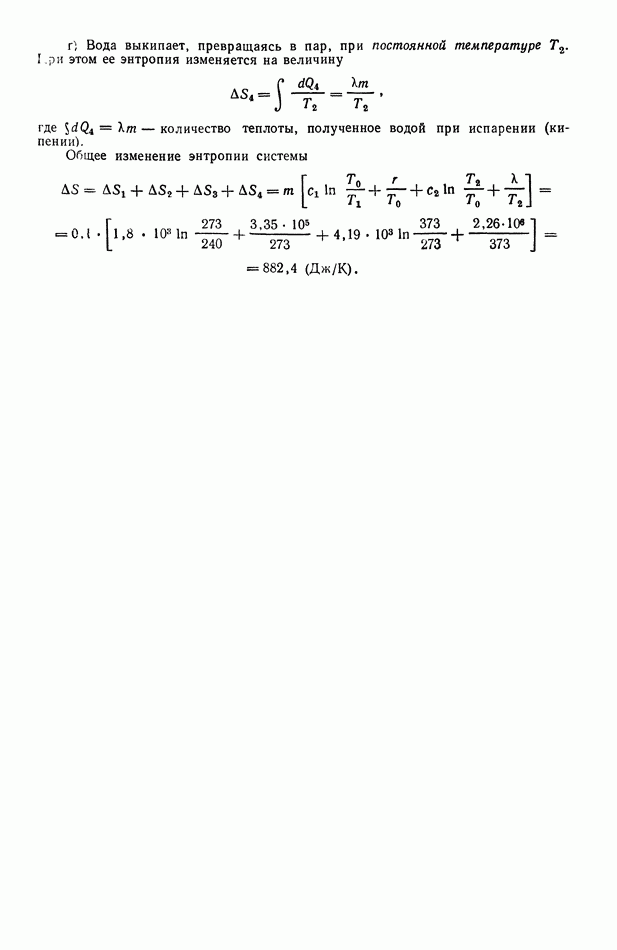| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. О некоторых математических понятиях и символах
С самого начала и на протяжении всего курса мы будем широко пользоваться некоторыми математическими символами и понятиями, не встречавшимися (или редко применявшимися) в школьном курсе физики. Дадим необходимые в этой связи пояснения.
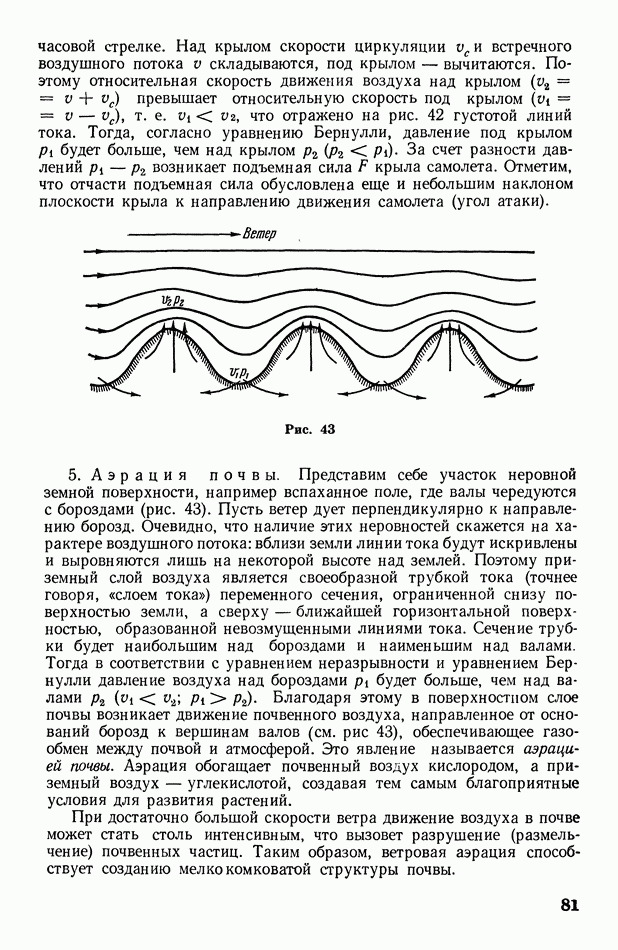
1. О знаках малости, неравенства и приближенного равенства
Для обозначения малых величин (или малых изменений величин) принято ставить перед этими величинами знак  (буква греческого алфавита «дельта»). Например,
(буква греческого алфавита «дельта»). Например,  малая масса,
малая масса,  — малый промежуток времени и т. д.
— малый промежуток времени и т. д.
Помимо общеизвестных знаков неравенства  употребляются знаки
употребляются знаки  (не равно),
(не равно),  (гораздо больше) и (гораздо меньше).
(гораздо больше) и (гораздо меньше).
Для обозначения приближенного равенства применяется знак  . Например, радиус Земли
. Например, радиус Земли 
2. О натуральных логарифмах
Наряду с десятичными логарифмами  применяются натуральные логарифмы
применяются натуральные логарифмы  основанием которых служит иррациональное число
основанием которых служит иррациональное число  Переход от десятичного логарифма к натуральному совершается по формуле
Переход от десятичного логарифма к натуральному совершается по формуле 
3. Об абсолютном значении и порядке величины
Абсолютным значением величины называется ее значение, взятое с положительным знаком; условно обозначается посредством заключения величины в прямые скобки. Если, например, ускорение  , то абсолютное значение ускорения
, то абсолютное значение ускорения  .
.
Порядком величины называется ближайшее к ее значению число, которое может быть выражено в виде  Например, ускорение силы тяжести
Например, ускорение силы тяжести  имеет порядок
имеет порядок  , длина световой волны
, длина световой волны  см имеет порядок
см имеет порядок  см и т. п.
см и т. п.
4. О кратных и дольных единицах измерения
Наряду с основными  и производными) единицами измерения физическихвеличин применяются кратные и дольные единицы, образующиеся путем умножения первых на
и производными) единицами измерения физическихвеличин применяются кратные и дольные единицы, образующиеся путем умножения первых на  При этом к названиям исходных единиц добавляются следующие приставки:
При этом к названиям исходных единиц добавляются следующие приставки:
(см. скан)
Примеры образования кратных и дольных единиц: 1 миллиметр  метра, 1 пикофарада
метра, 1 пикофарада  фарады, 1 мегаом
фарады, 1 мегаом  ом.
ом.
5. О символической записи суммы Сумму большого числа однородных величин

принято записывать сокращенно с помощью знака 2 (буква греческого алфавита «сигма») следующим образом:

Стоящие при знаке суммы числа  (пределы суммирования) показывают, что надо складывать все величины
(пределы суммирования) показывают, что надо складывать все величины  подряд, начиная с
подряд, начиная с  и кончая
и кончая 
6. О способах усреднения величин Существует ряд способов вычисления среднего значения величины по нескольким  отдельным ее значениям
отдельным ее значениям  Мы будем пользоваться следующими тремя из них:
Мы будем пользоваться следующими тремя из них:
а) средним арифметическим значением х величины называется сумма отдельных значений величины, деленная на их число:

б) средним геометрическим значением х величины называется корень  степени из произведения
степени из произведения  отдельных ее значений:
отдельных ее значений:

в) средним квадратичным значением х величины называется квадратный корень из суммы квадратов отдельных значений величины, деленной на их число:

Результаты усреднения, полученные этими способами, обычно мало отличаются друг от друга (но все же 
7. Линейные операции над векторами
Все физические величины подразделяются на две группы: на скалярные величины (скаляры) к векторные величины (векторы).
Скалярная величина полностью определяется численным значением. Скалярами являются, например, время, площадь, масса, работа. Действия над скалярами производятся по правилам алгебры и дифференциального и интегрального исчислений.

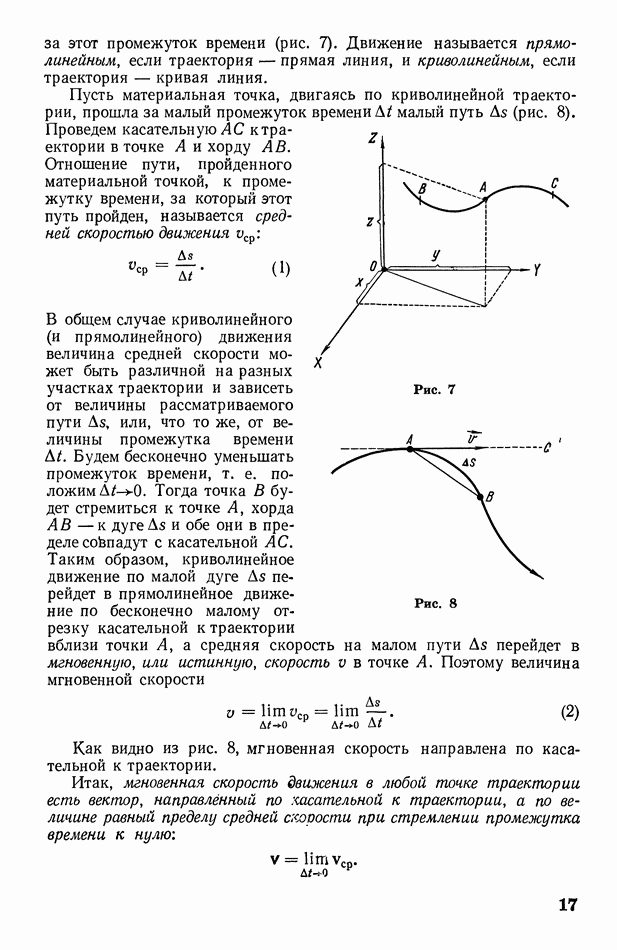
Рис. 1
Векторная величина полностью определяется численным значением и направлением. Векторами являются, например, скорость, ускорение, сила. В отличие от скаляров векторы обозначаются полужирными буквами или буквами со стрелкой сверху. Например,  вектор скорости,
вектор скорости,  вектор силы и т. п. Графически вектор изображают отрезком со стрелкой на конце. Длина отрезка соответствует (в произвольном масштабе) численному значению вектора; стрелка указывает направление вектора. На рис. 1 изображен вектор силы тяжести
вектор силы и т. п. Графически вектор изображают отрезком со стрелкой на конце. Длина отрезка соответствует (в произвольном масштабе) численному значению вектора; стрелка указывает направление вектора. На рис. 1 изображен вектор силы тяжести  численное значение которого равно
численное значение которого равно  (ньютон).
(ньютон).
Векторы, имеющие одинаковые численные значения и направления, равны между собой. Отсюда следует, что при параллельном переносе вектор не изменяется.
Два численно равных, но противоположно направленных вектора  называются противоположными векторами. Для них имеет место равенство
называются противоположными векторами. Для них имеет место равенство

Действия над векторами производятся по правилам векторного исчисления. Познакомимся с некоторыми из них.
а) Сложение векторов. Сложение векторов производится по правилу параллелограмма. Чтобы сложить два вектора  (рис. 2, а), необходимо путем параллельного переноса совместить их начала и построить на векторах параллелограмм (рис. 2, б). Вектор
(рис. 2, а), необходимо путем параллельного переноса совместить их начала и построить на векторах параллелограмм (рис. 2, б). Вектор  являющийся диагональю параллелограмма, представляет собой искомую сумму:
являющийся диагональю параллелограмма, представляет собой искомую сумму:

Из рис. 2, б следует, что данные векторы можно сложить и другим способом, совмещая начало второго вектора с концом первого. Вектор С, соединяющий начало первого вектора с концом второго, также представляет искомую сумму (рис. 2, в).

Рис. 2
Этот способ, называемый правилом треугольника, особенно удобен при сложении нескольких векторов, например четырех:  (рис. 3, а). В этом случае начало второго вектора совмещают с концом первого, начало третьего — с концом второго и т. д. (рис. 3,б). Вектор
(рис. 3, а). В этом случае начало второго вектора совмещают с концом первого, начало третьего — с концом второго и т. д. (рис. 3,б). Вектор  соединяющий начало первого вектора с концом последнего, является суммой данных векторов:
соединяющий начало первого вектора с концом последнего, является суммой данных векторов:


Рис. 3
Он не зависит от последовательности, в которой производилось сложение векторов, в чем легко убедиться путем соответствующих построений.
б) Вычитание векторов. Вычитание вектора В из вектора А можно заменить сложением А с вектором  противоположным В (рис. 4, а):
противоположным В (рис. 4, а):


Рис. 4
Тогда, применяя правило треугольника, получим вектор разности С (рис. 4, б).
в) Умножение и деление вектора на скаляр. При умножении вектора А на скаляр  получается вектор, совпадающий по направлению с А и равный по величине
получается вектор, совпадающий по направлению с А и равный по величине  Скаляр
Скаляр  может иметь любые значения (целые и дробные, положительные и отрицательные). Поэтому данное правило умножения является вместе с тем и правилом деления вектора на скаляр. Примером умножения вектора на скаляр может служить определение перемещения
может иметь любые значения (целые и дробные, положительные и отрицательные). Поэтому данное правило умножения является вместе с тем и правилом деления вектора на скаляр. Примером умножения вектора на скаляр может служить определение перемещения  по скорости
по скорости  и времени
и времени  (при равномерном прямолинейном движении):
(при равномерном прямолинейном движении):

Примером деления вектора на скаляр является определение ускорения а по силе  действующей на тело, и массе
действующей на тело, и массе  тела:
тела:

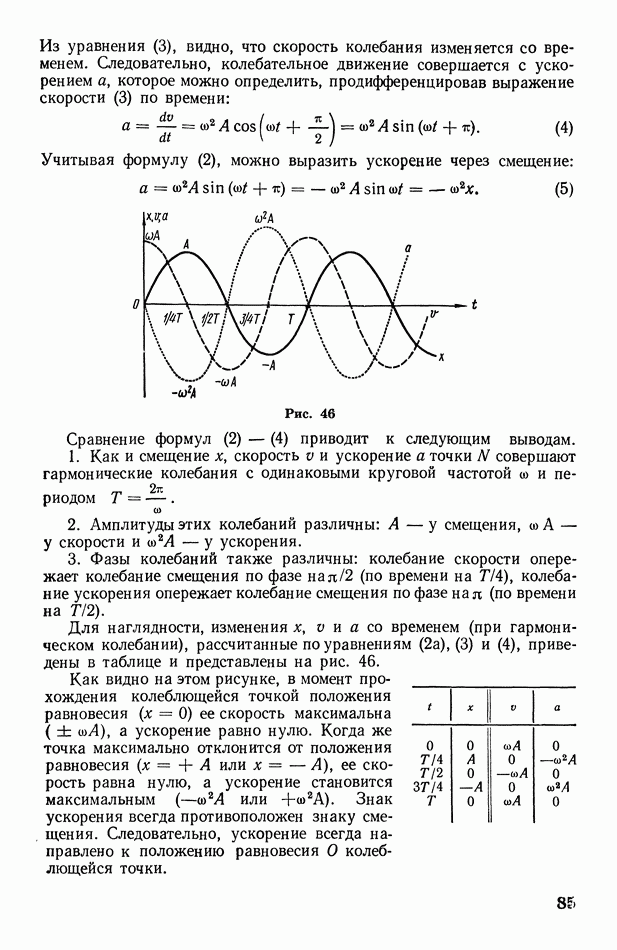
8. О градиенте физической величины

Рис. 5
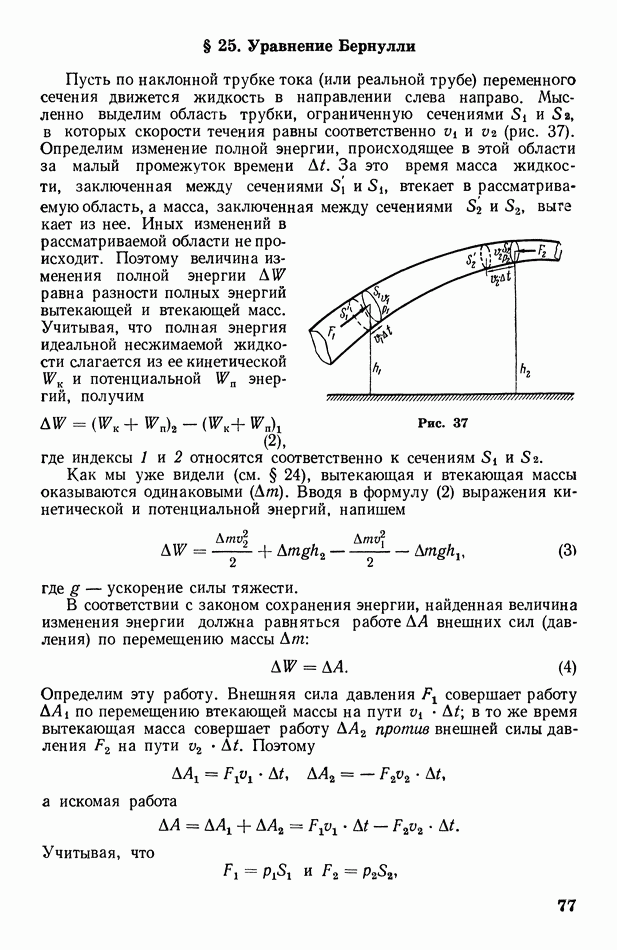
Если некоторая физическая величина имеет в каждой точке пространства определенное (иное, чем в других точках) значение, то говорят, что эта величина распределена в пространстве. Пространственно распределенным является, например, атмосферное давление: в различных точках атмосферы его значения различны.
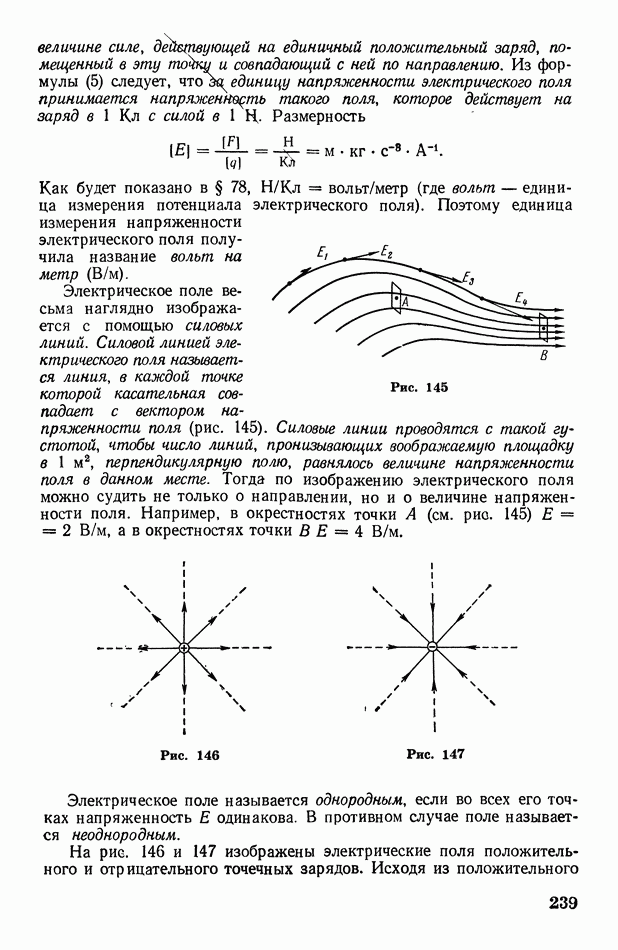
Если пространственно распределенная физическая величина  возрастает в некотором направлении
возрастает в некотором направлении  то «пространственную быстроту» ее возрастания удобно характеризовать отношением изменения величины
то «пространственную быстроту» ее возрастания удобно характеризовать отношением изменения величины  к расстоянию
к расстоянию  на котором это изменение происходит (рис. 5). Ось
на котором это изменение происходит (рис. 5). Ось  располагают в направлении максимального возрастания величины
располагают в направлении максимального возрастания величины  расстояние
расстояние  следует брать возможно меньшим. Отношение
следует брать возможно меньшим. Отношение

называется градиентом физической величины  и обозначается так:
и обозначается так:

Таким образом, градиентом физической величины называется ее изменение, приходящееся на единицу расстояния в направлении наибольшего возрастания. Следовательно, градиент есть вектор, направленный в сторону наибольшего возрастания физической величины.
Понятие градиента применимо к любой физической величине (скорости, плотности, температуре, давлению и т. д.), если только она имеет пространственное распределение. Размерность градиента равна размерности физической величины, деленной на размерность длины. Например, размерность градиента скорости

размерность градиента температуры

Известно, что средний градиент температуры земной коры (геотермический градиент) направлен к центру Земли и составляет около 

Рис. 6
Это означает, что температура земной коры возрастает в среднем на 3° С на каждые  глубины.
глубины.
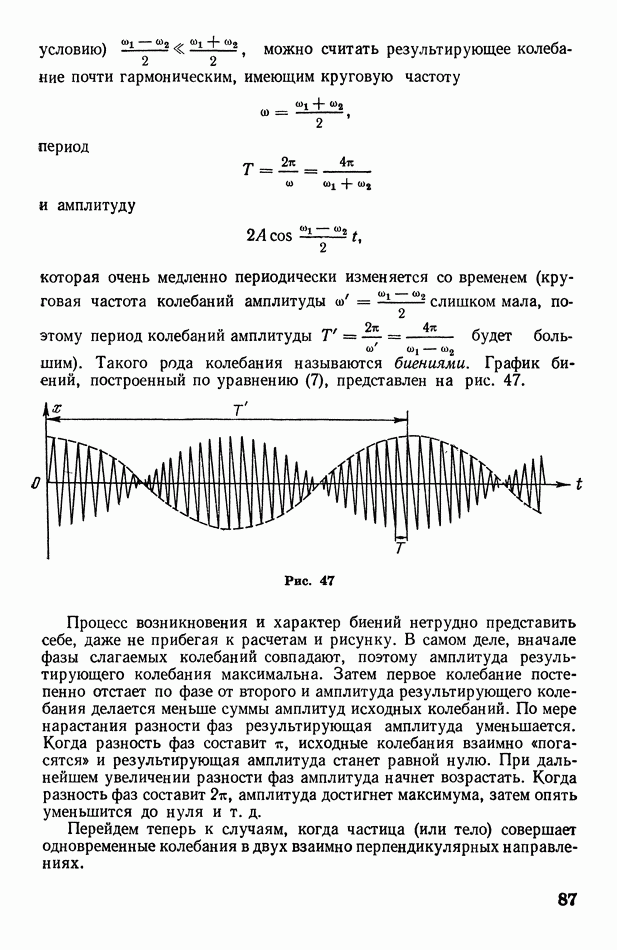
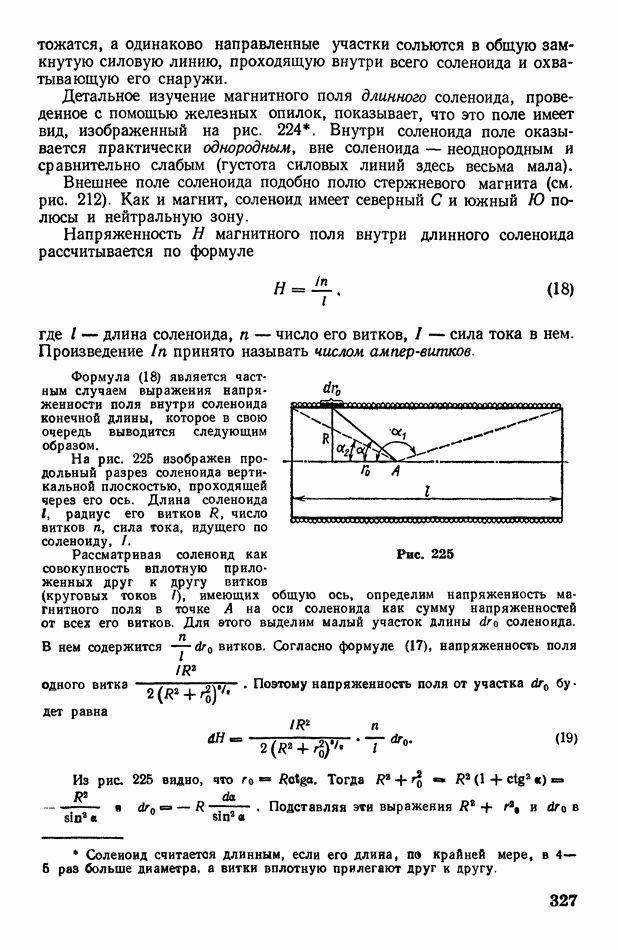
9. О кривизне и радиусе кривизны кривой
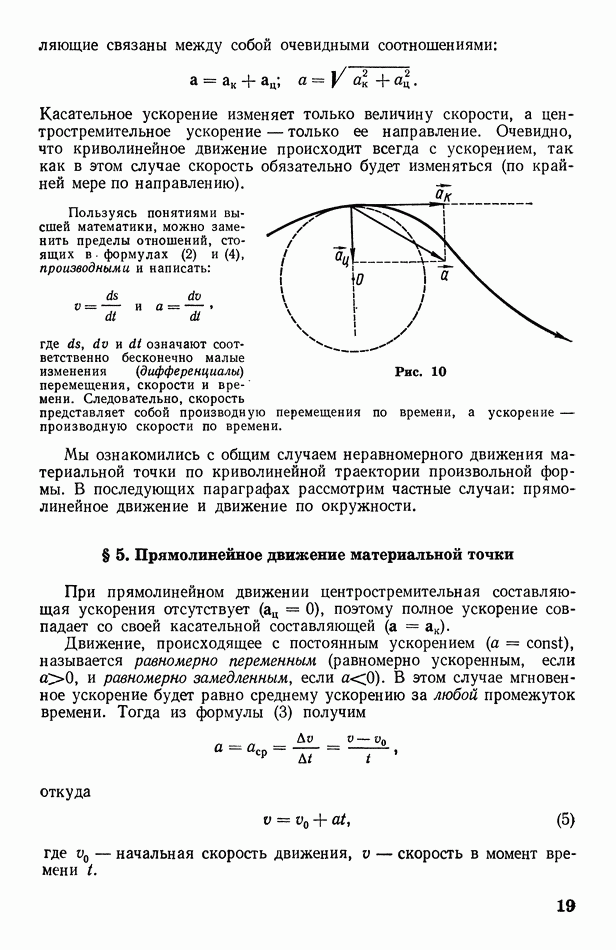
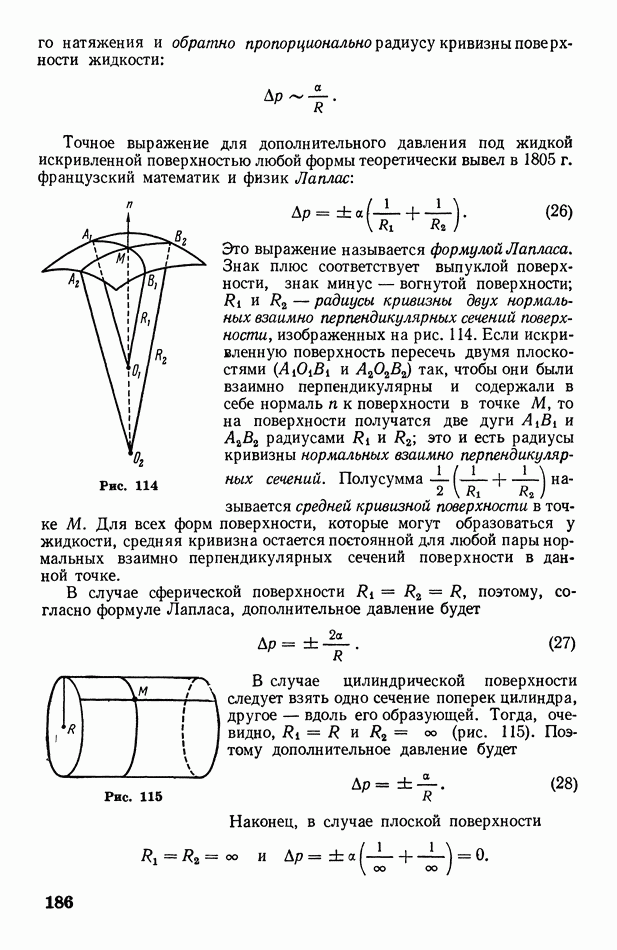
На различных участках кривой линии ее кривизна может быть различной. Для оценки кривизны линий введены понятия кривизны и радиуса кривизны.
Малые участки и  кривой линии
кривой линии  всегда можно совместить с некоторой окружностью (рис. 6). Радиусы
всегда можно совместить с некоторой окружностью (рис. 6). Радиусы  этих окружностей называются радиусами кривизны кривой линии на данных участках. Если вообще участок кривой бесконечно мал
этих окружностей называются радиусами кривизны кривой линии на данных участках. Если вообще участок кривой бесконечно мал  то можно говорить о радиусе кривизны
то можно говорить о радиусе кривизны  кривой в данной точке.
кривой в данной точке.
Величина, обратная радиусу кривизны, называется кривизной кривой линии:

Отметим, что у прямой линии 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
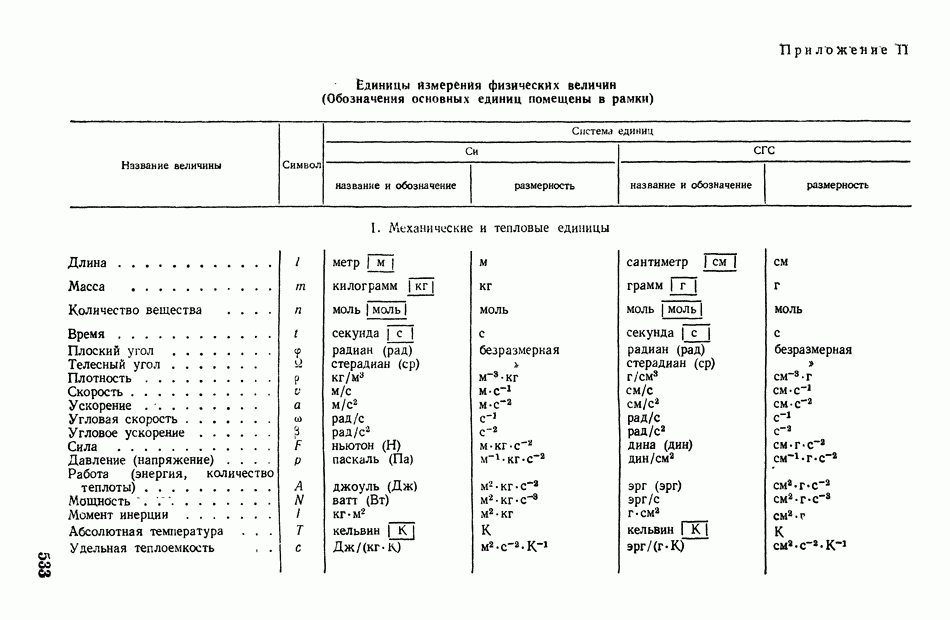
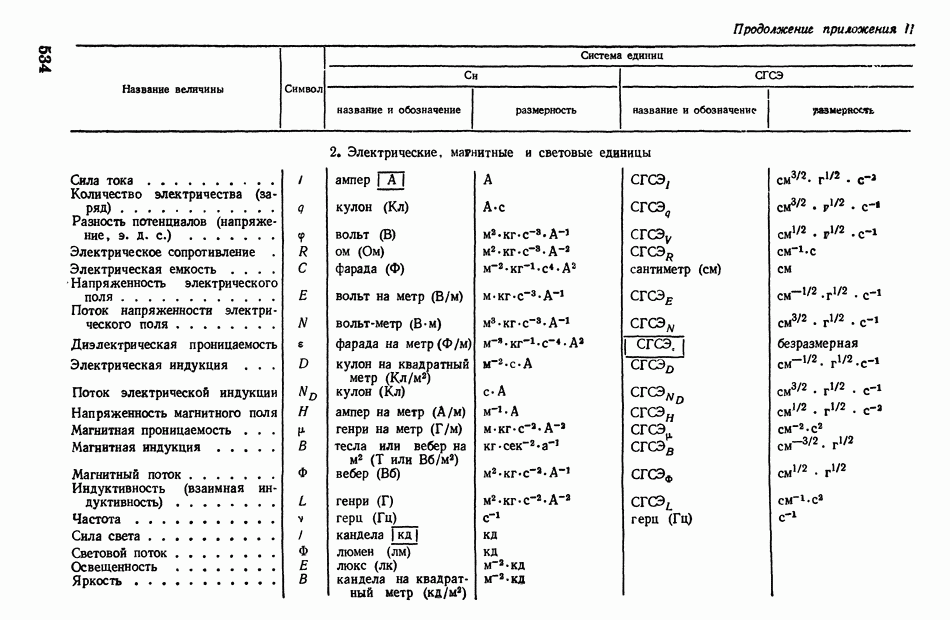
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
- § 30. О затухающих и вынужденных колебаниях
- § 31. Волновой процесс
- § 32. Уравнение волны. Интенсивность волны
- § 33. Интерференция волн. Стоячие волны
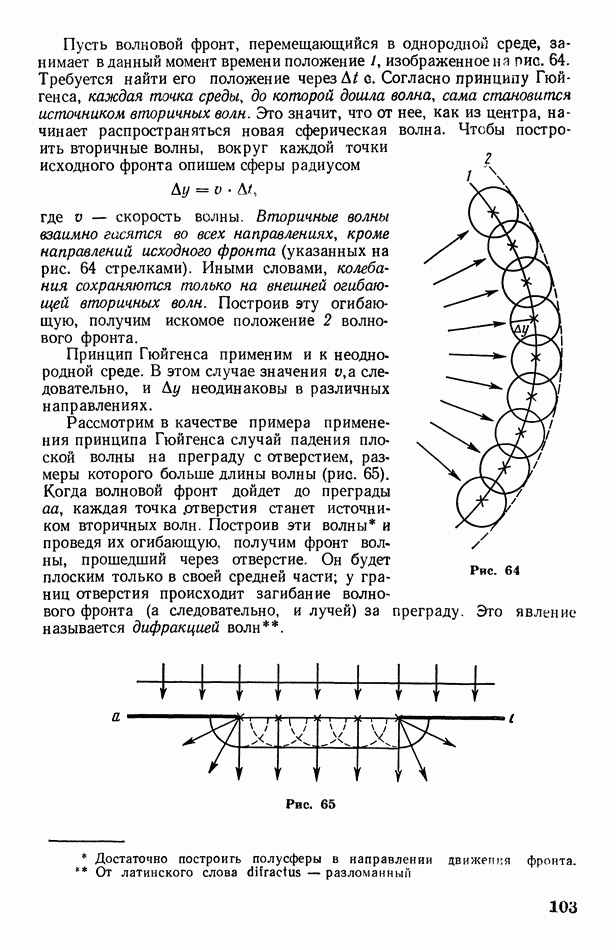
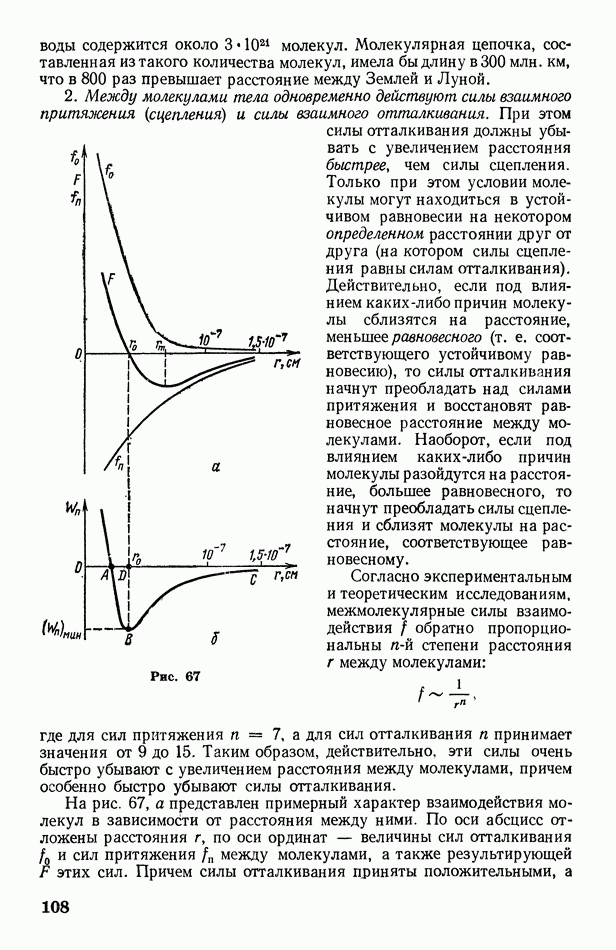
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
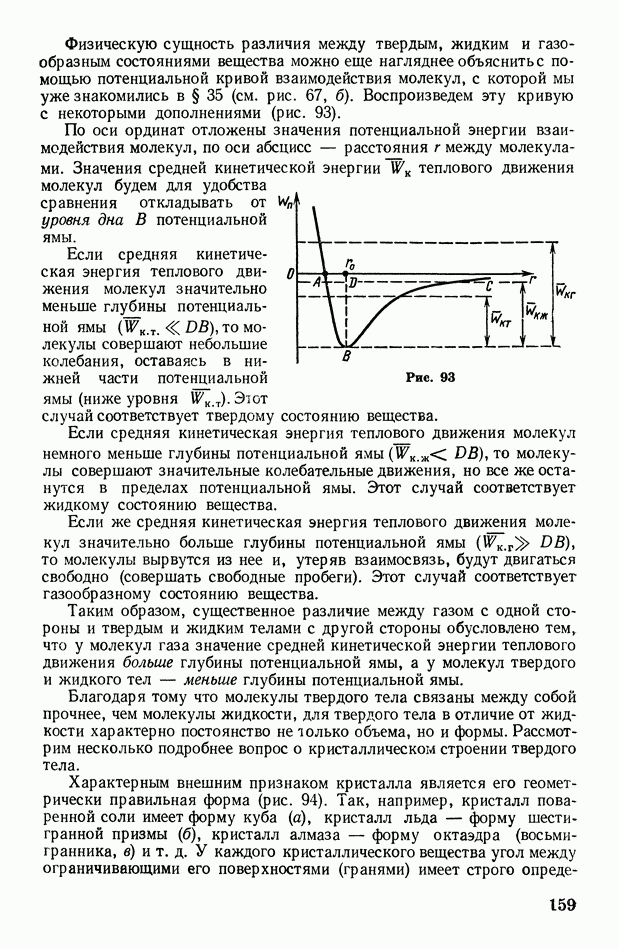
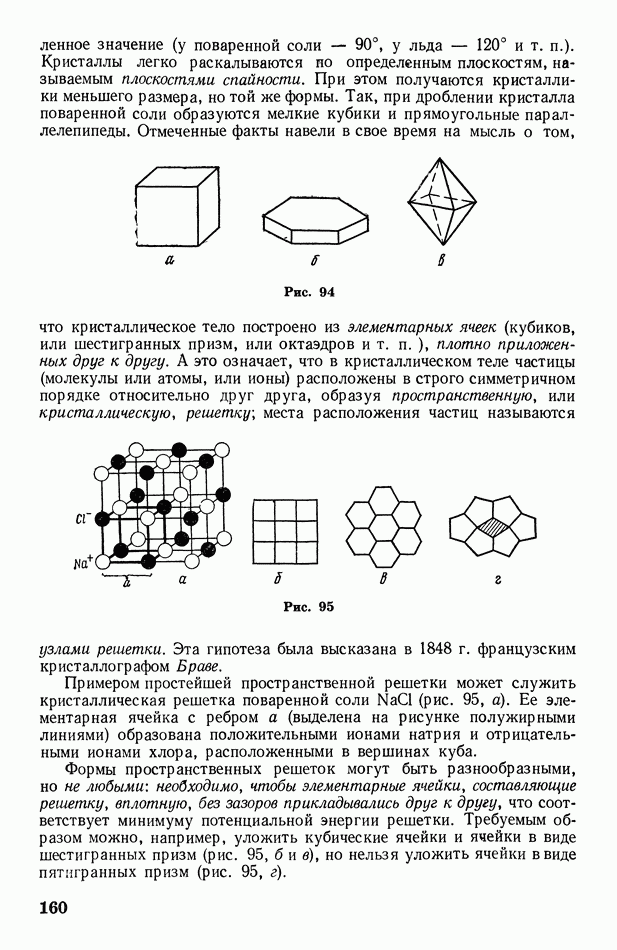
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
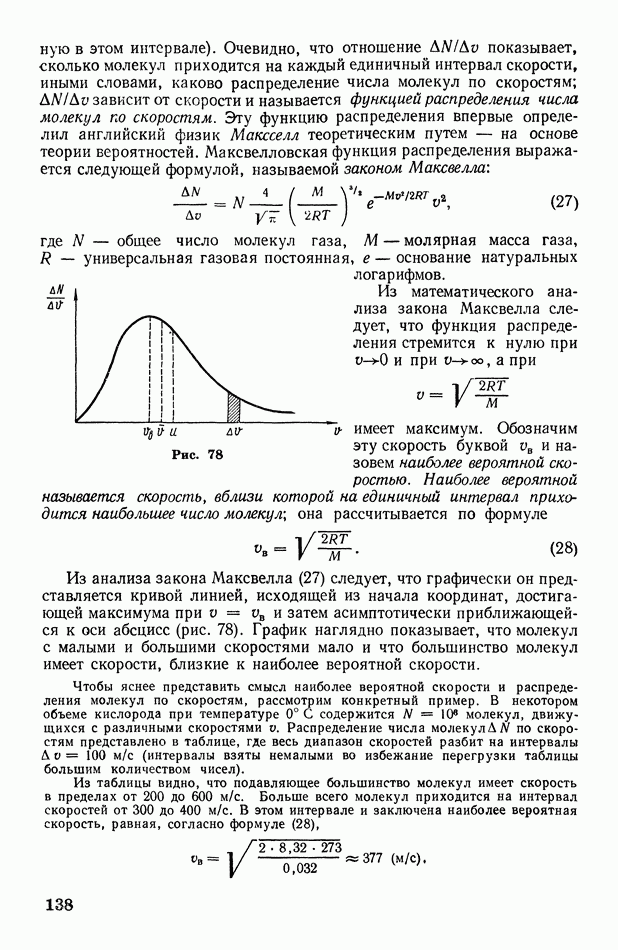
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
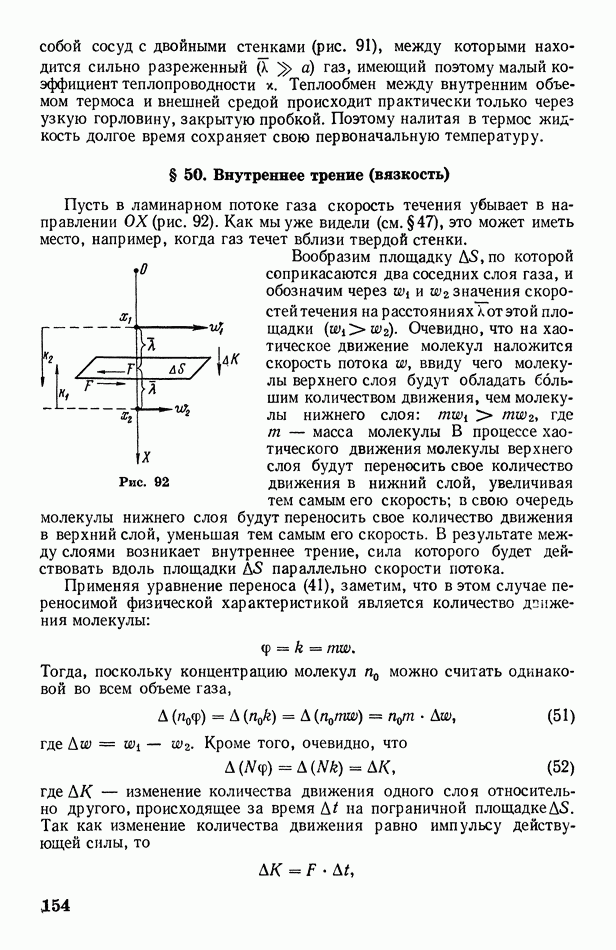
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
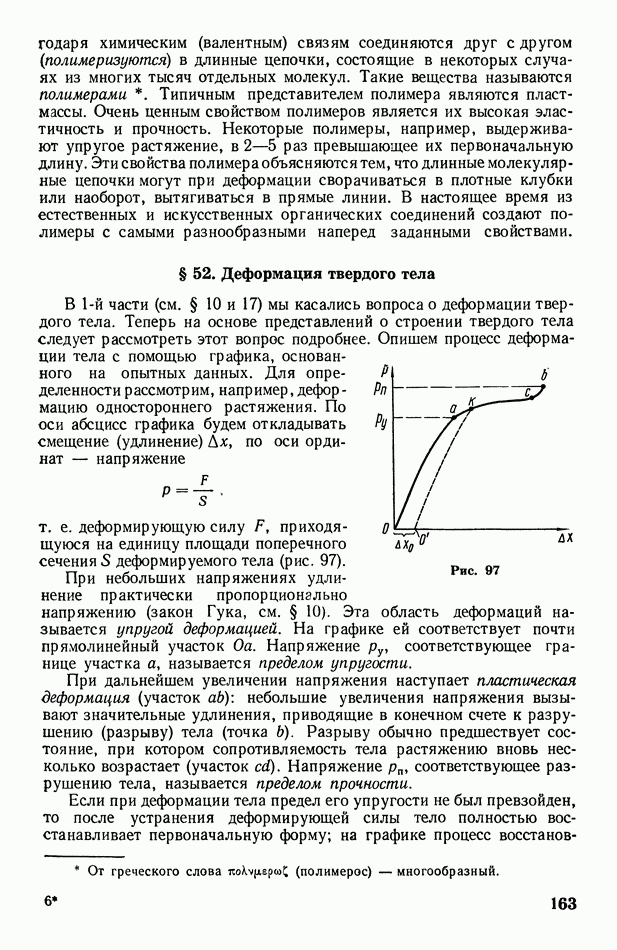
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
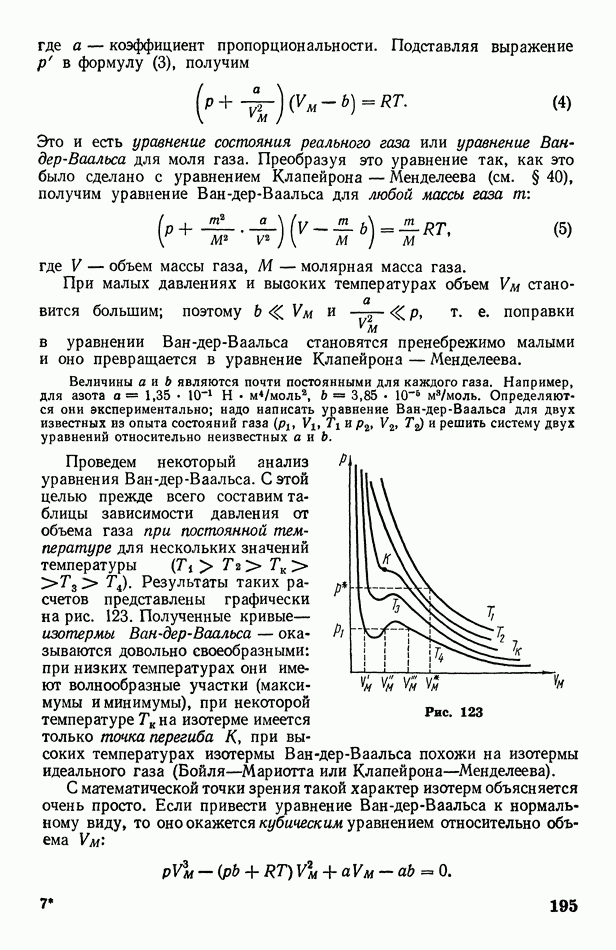
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
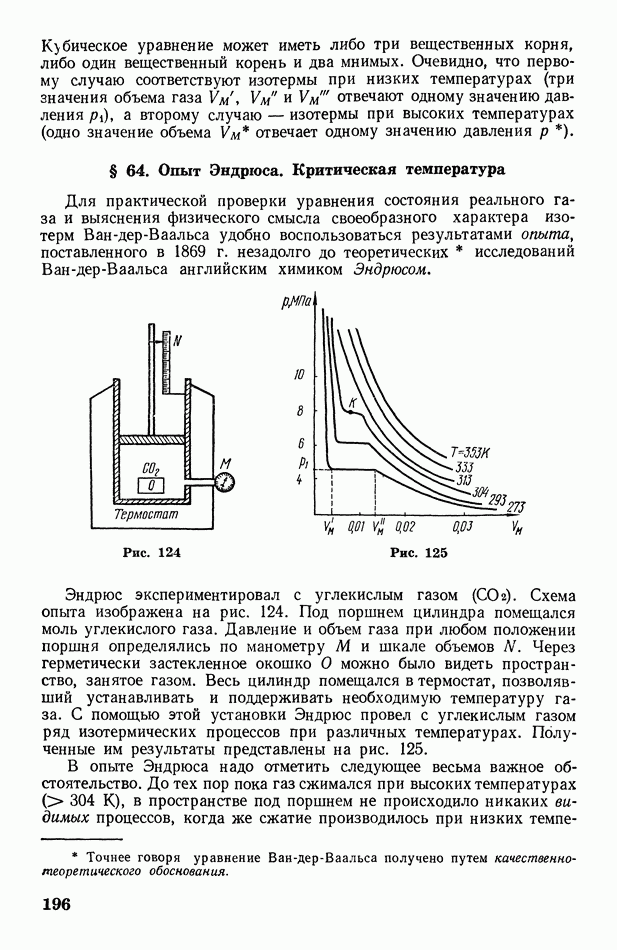
- § 64. Опыт Эндрюса. Критическая температура
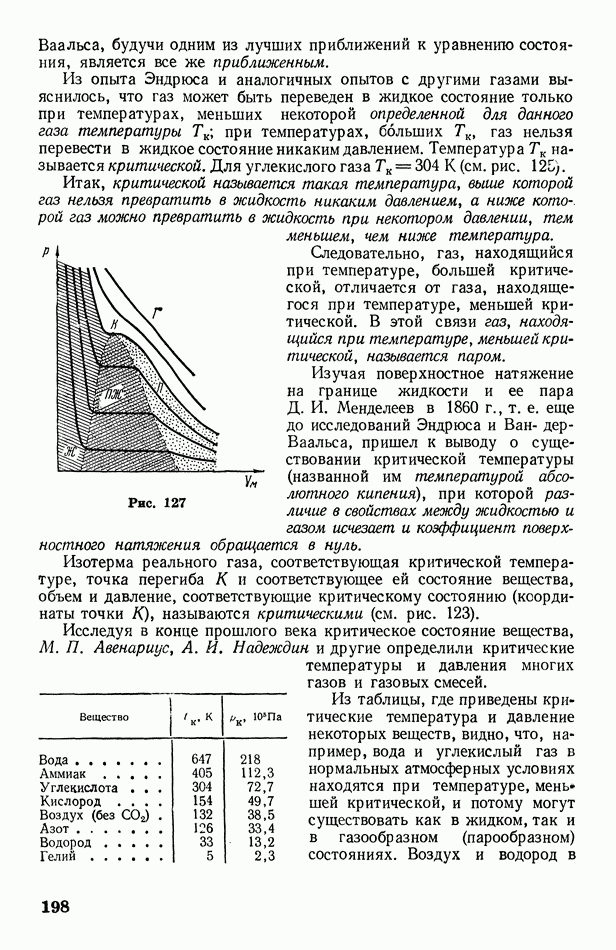
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
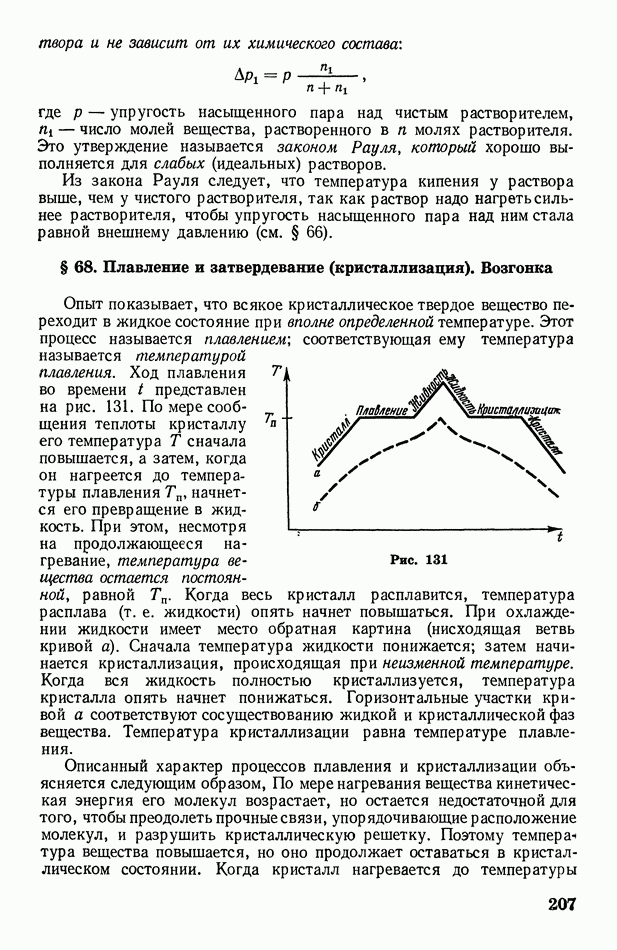
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
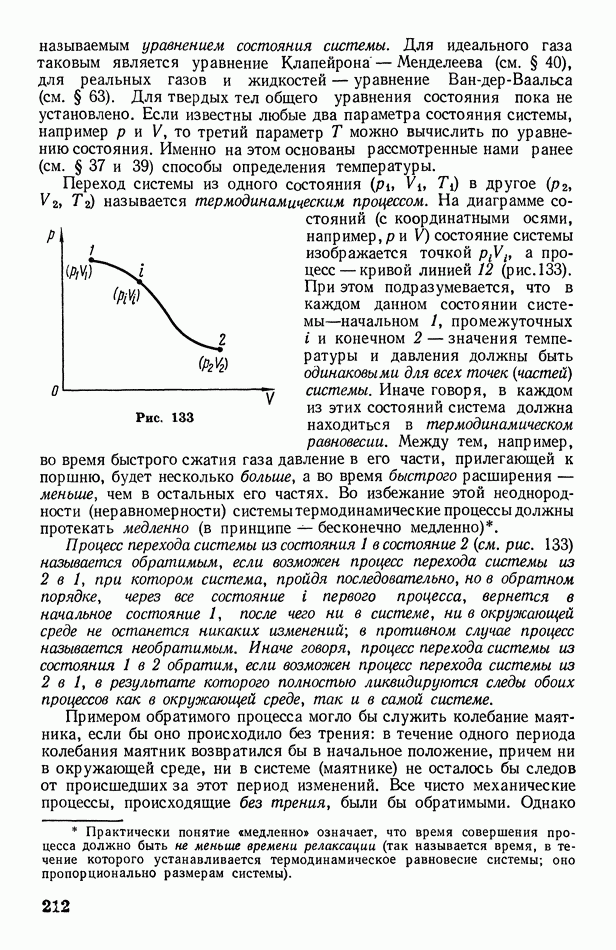
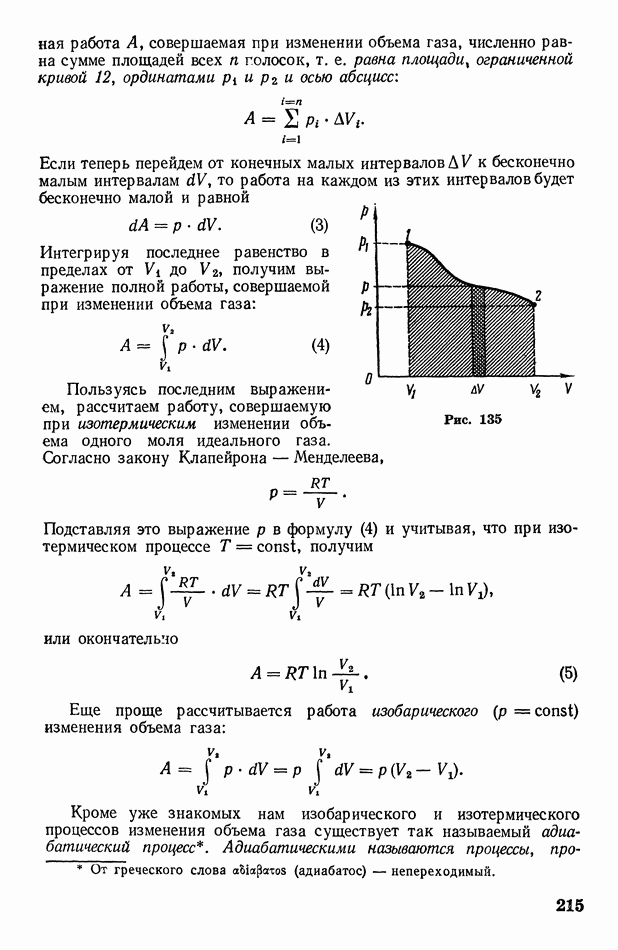
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
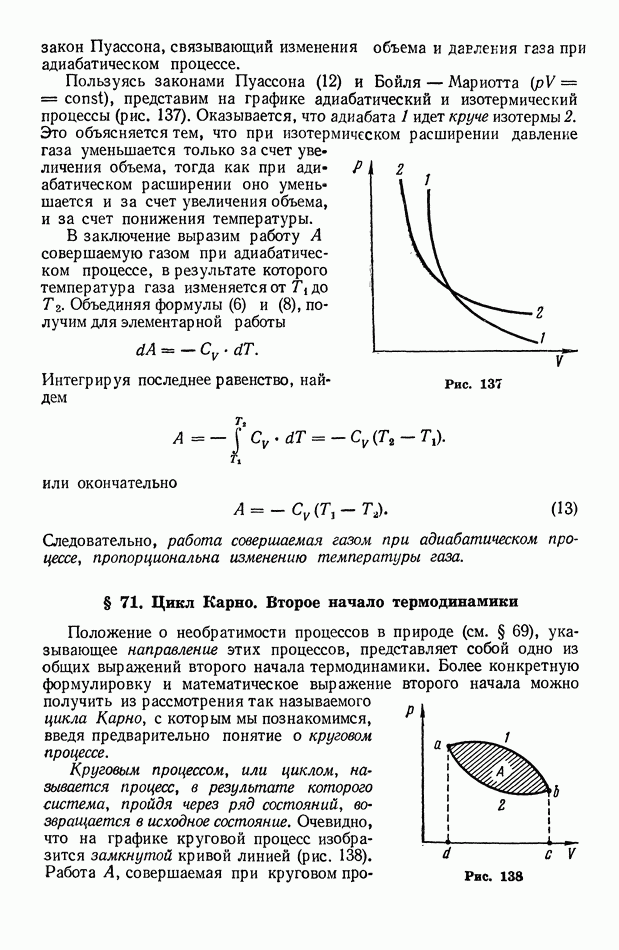
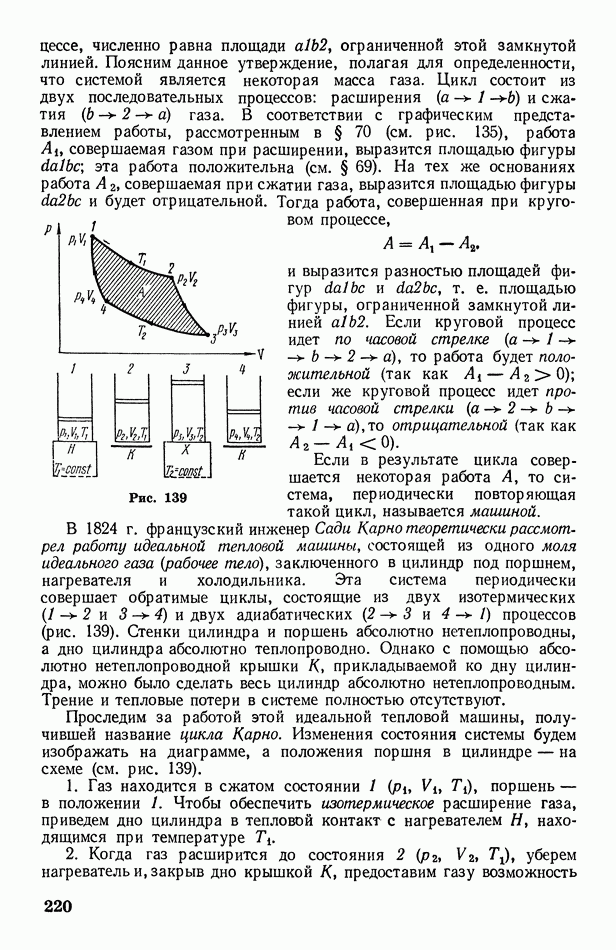
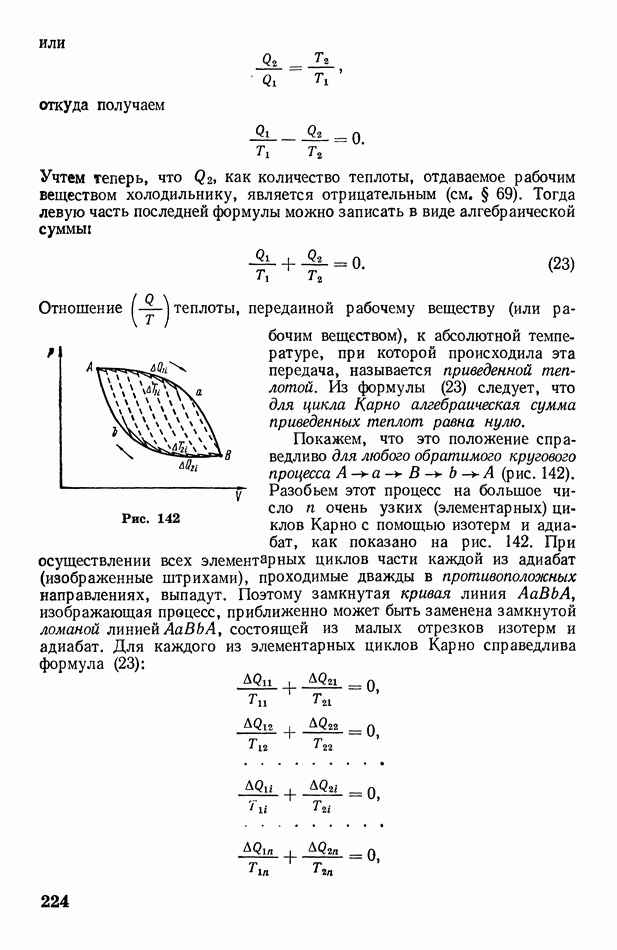
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
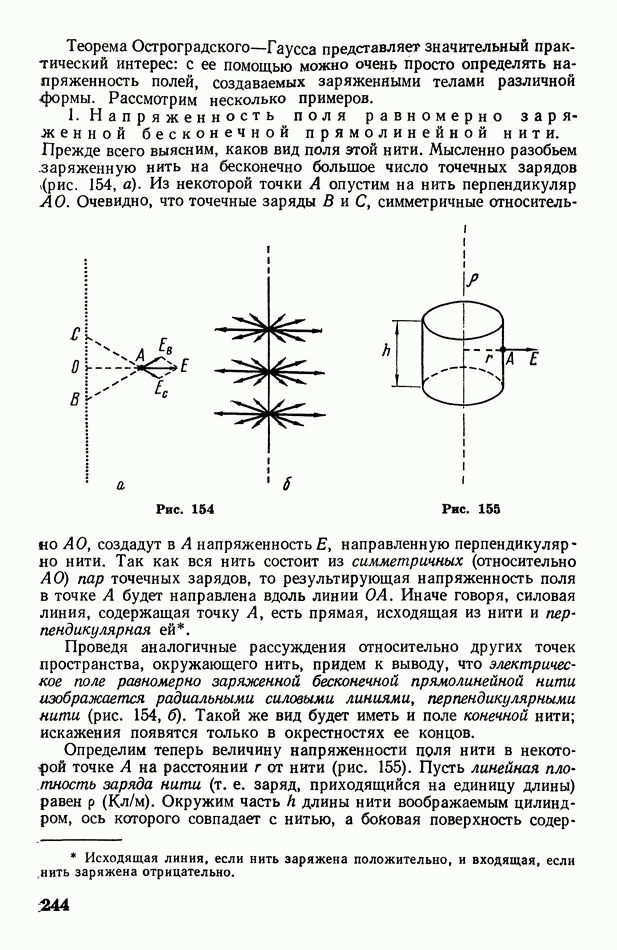
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
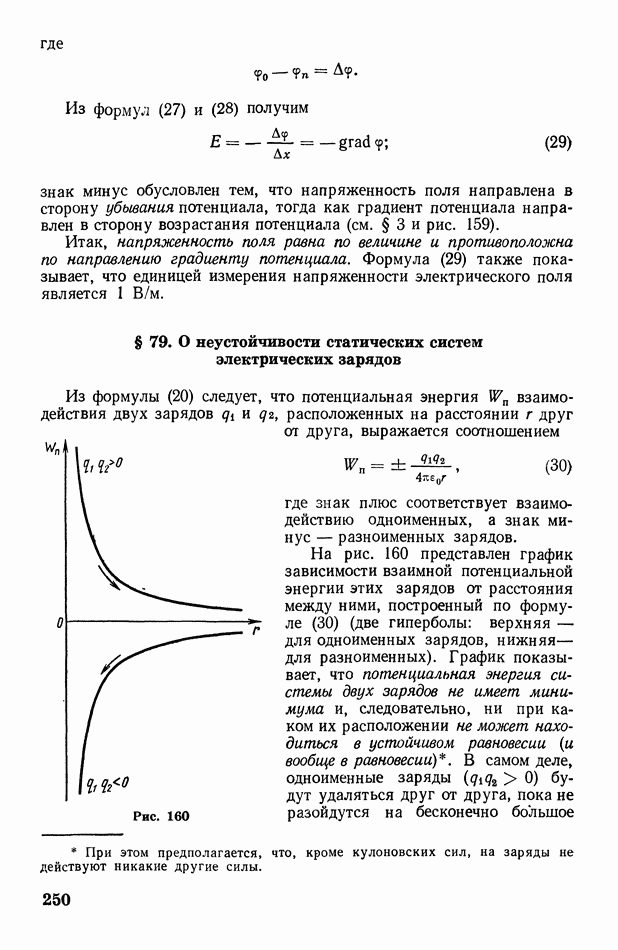
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
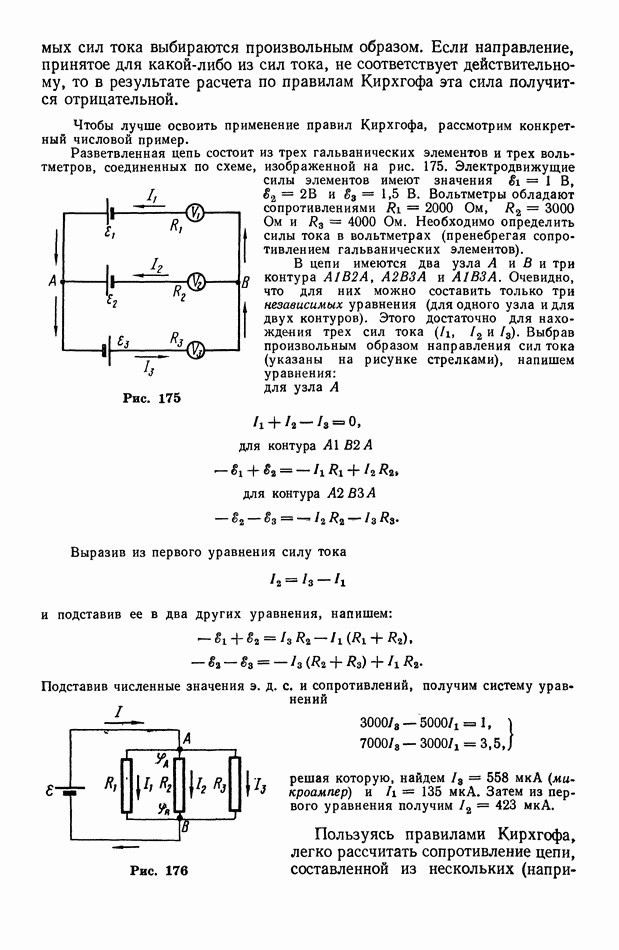
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
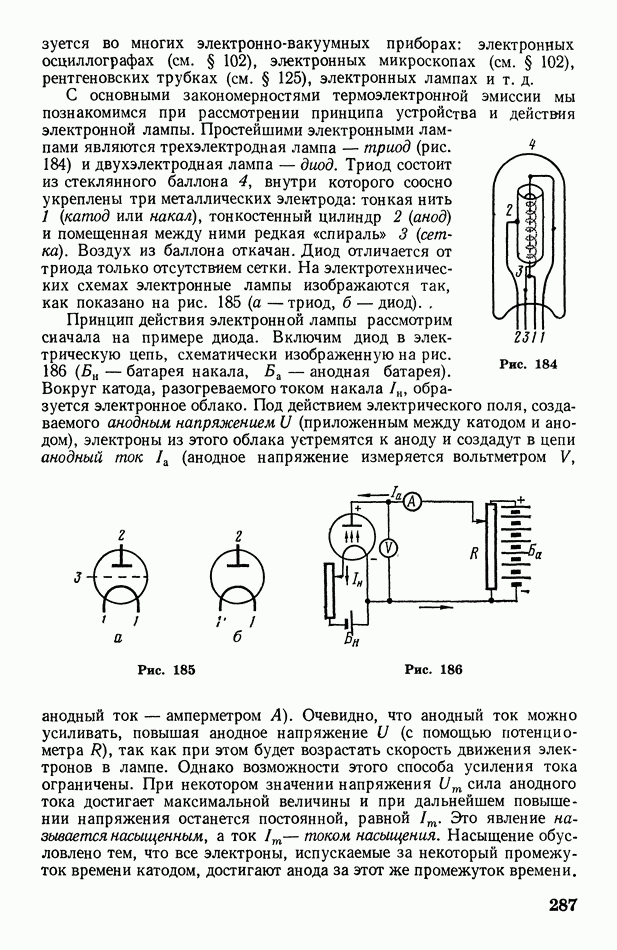
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
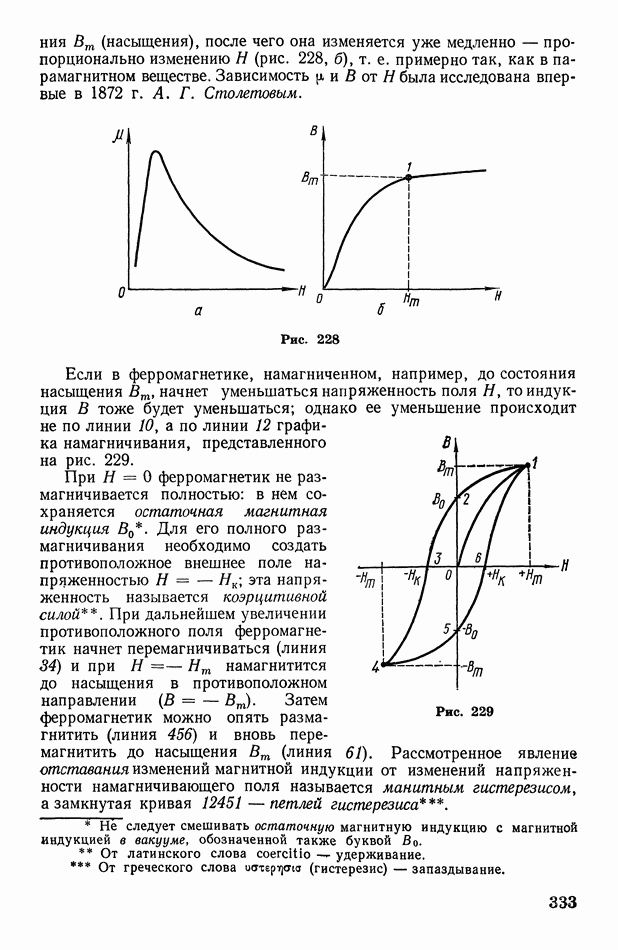
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
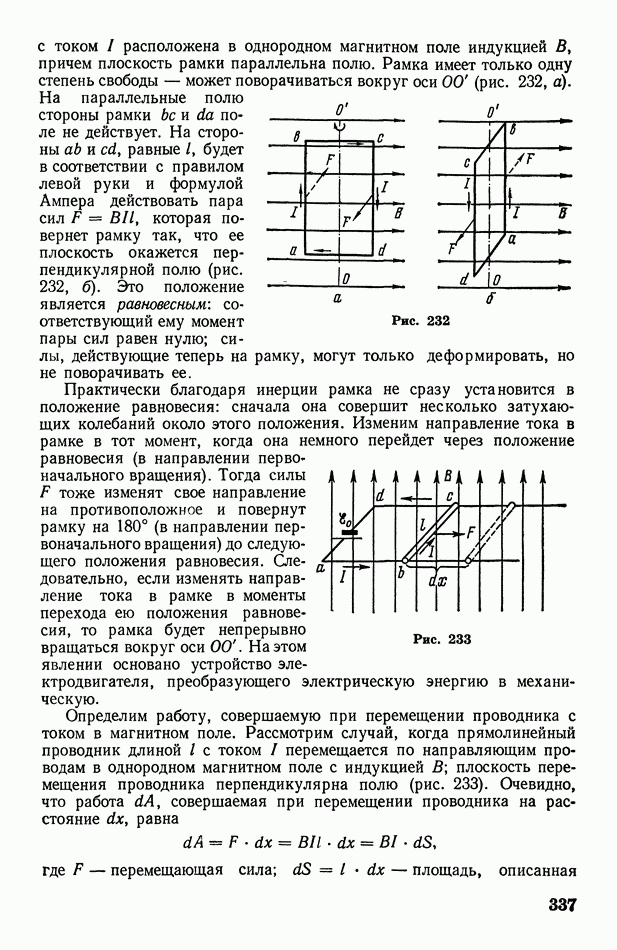
- § 100. Действие магнитного поля на проводник с током. Определение ампера
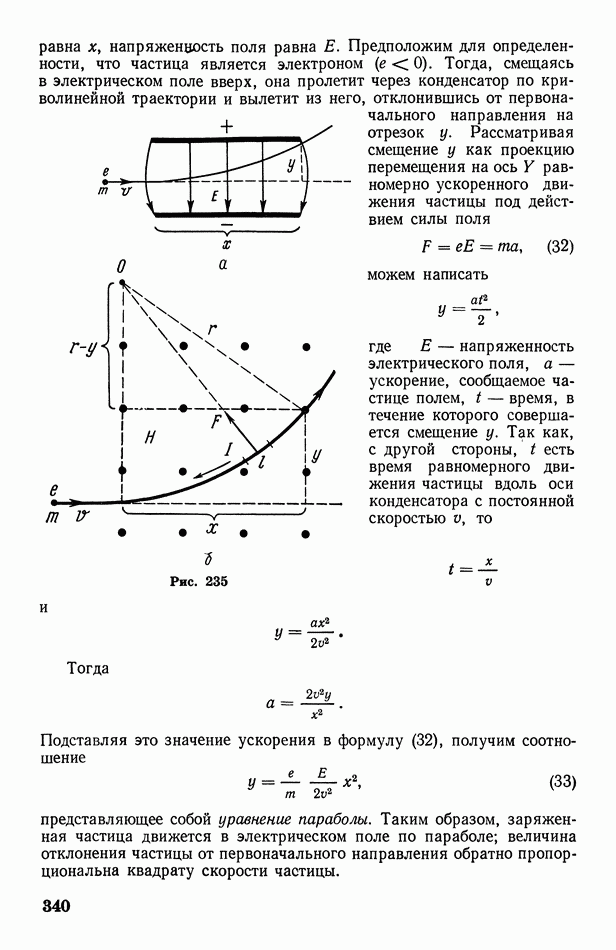
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
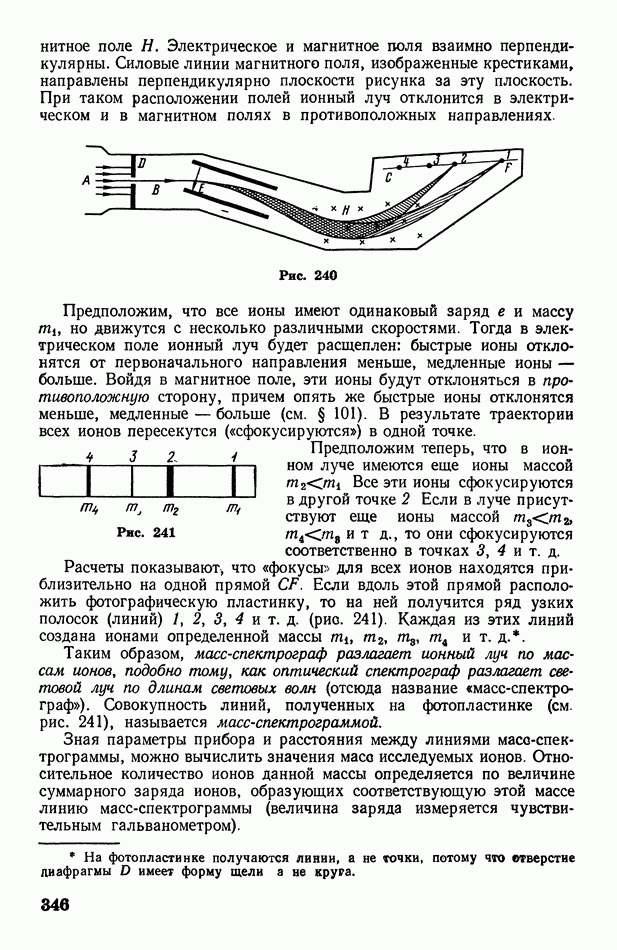
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
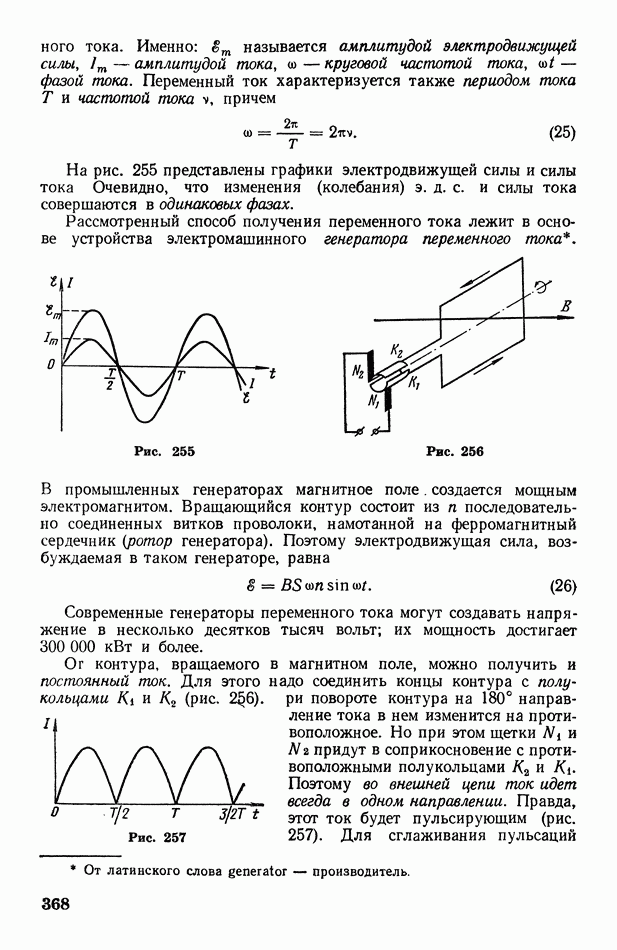
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
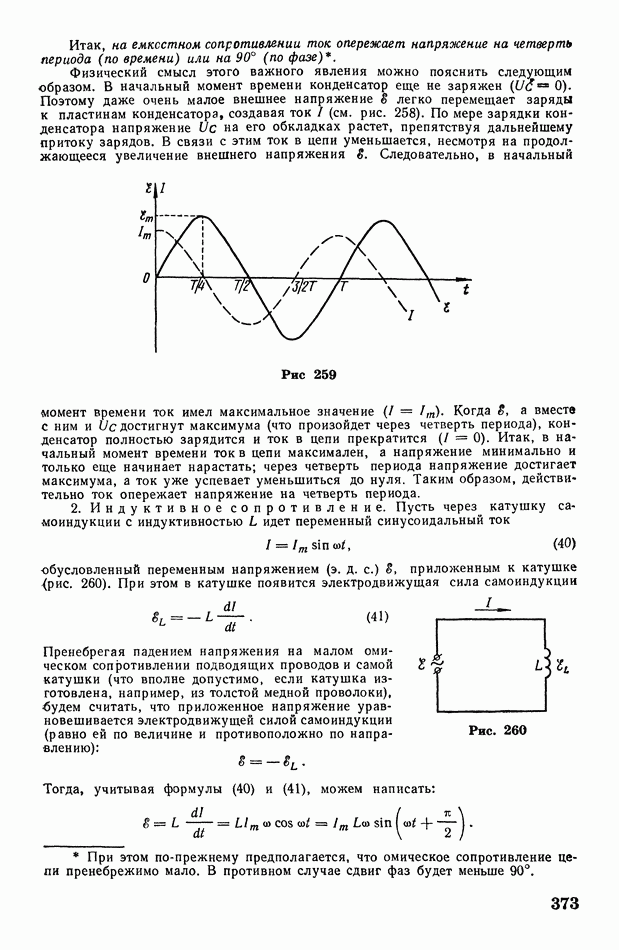
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
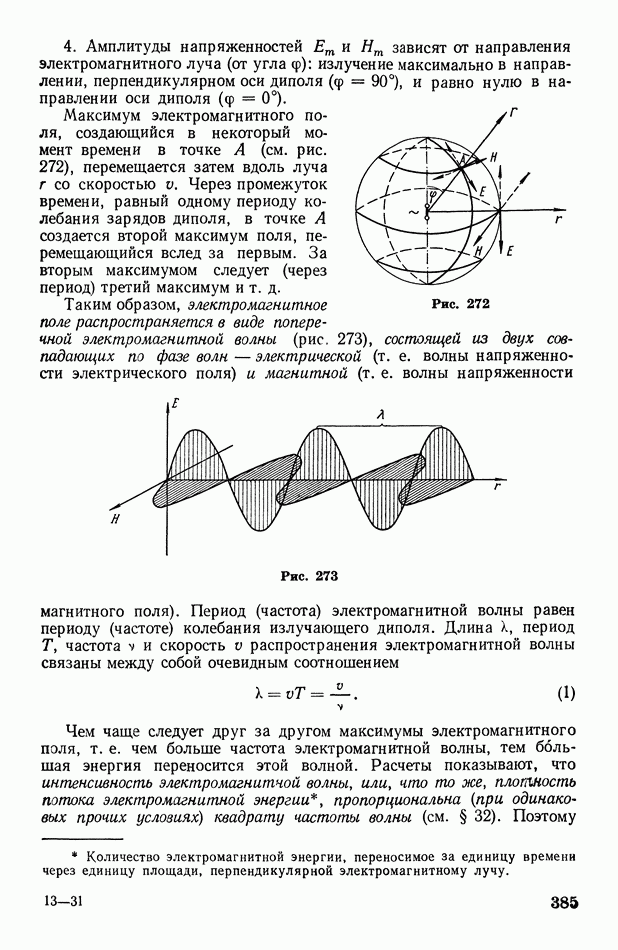
- § 111. Закрытый колебательный контур
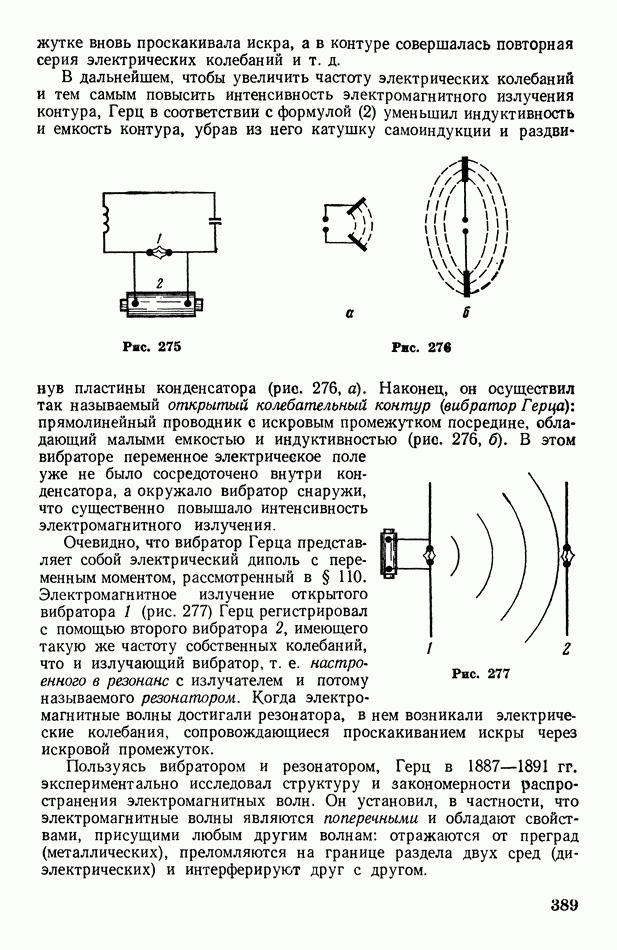
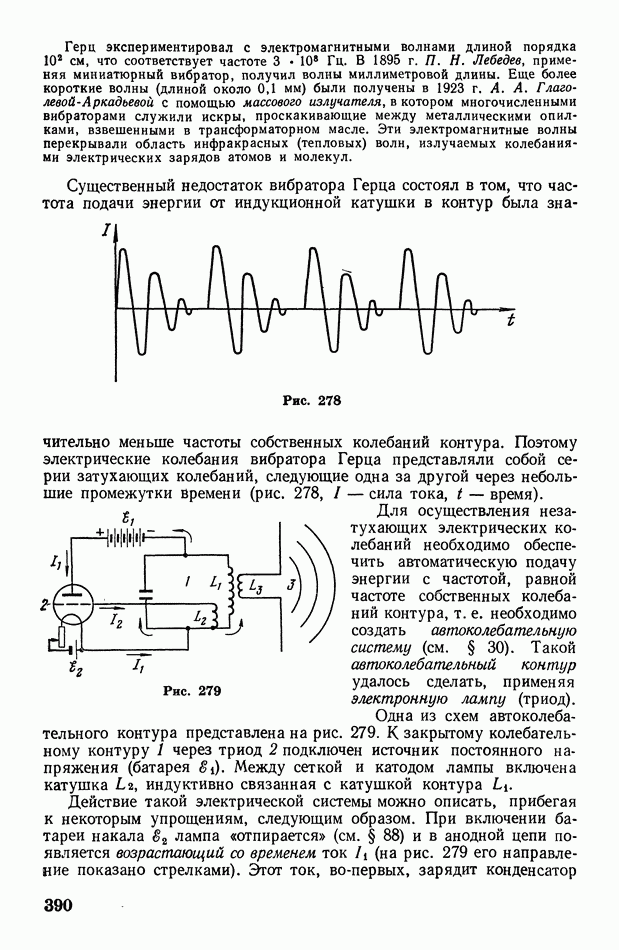
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
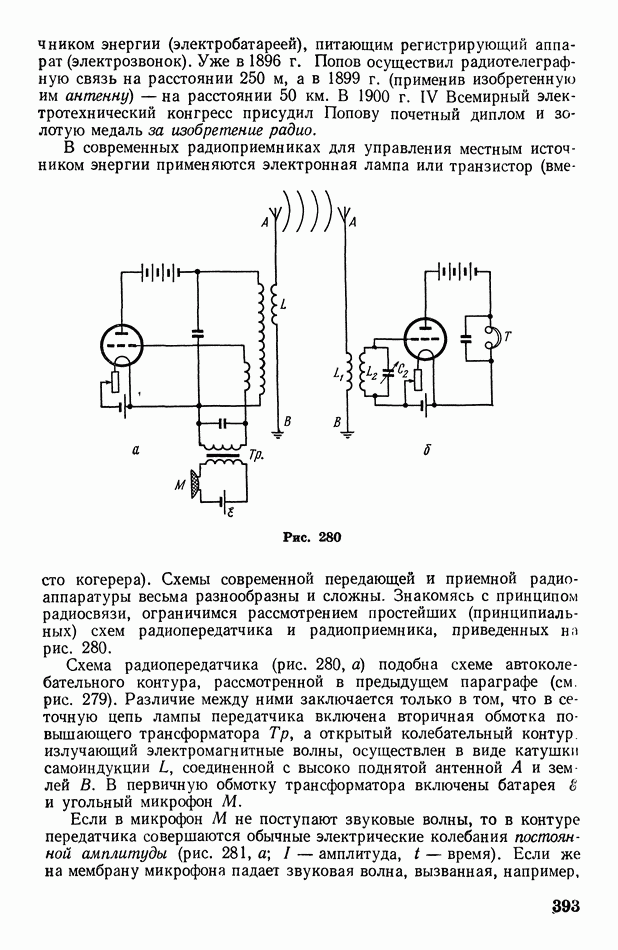
- § 113. Радиосвязь
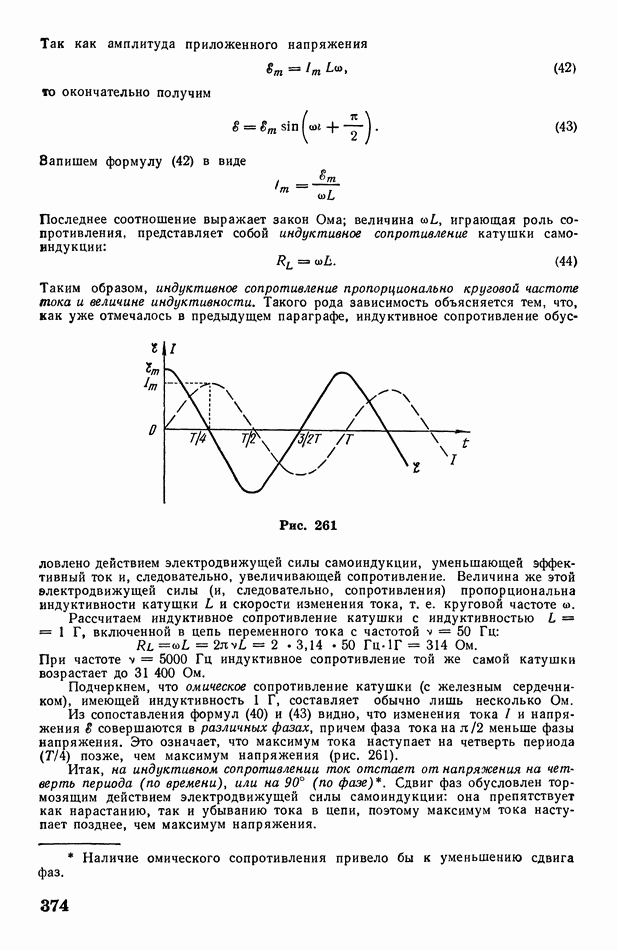
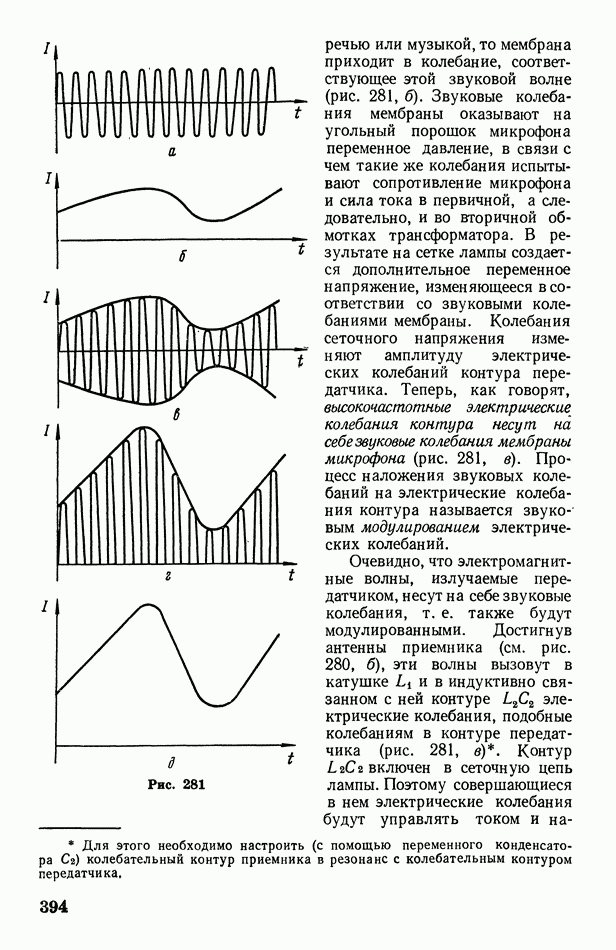
- 4. Оптика и атомная физика
- § 114. Природа света
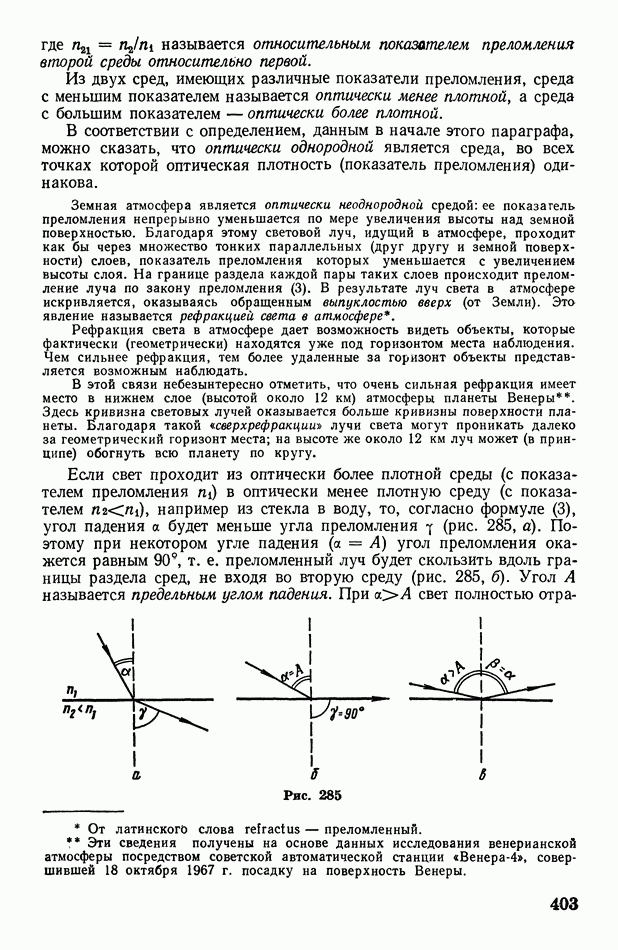
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
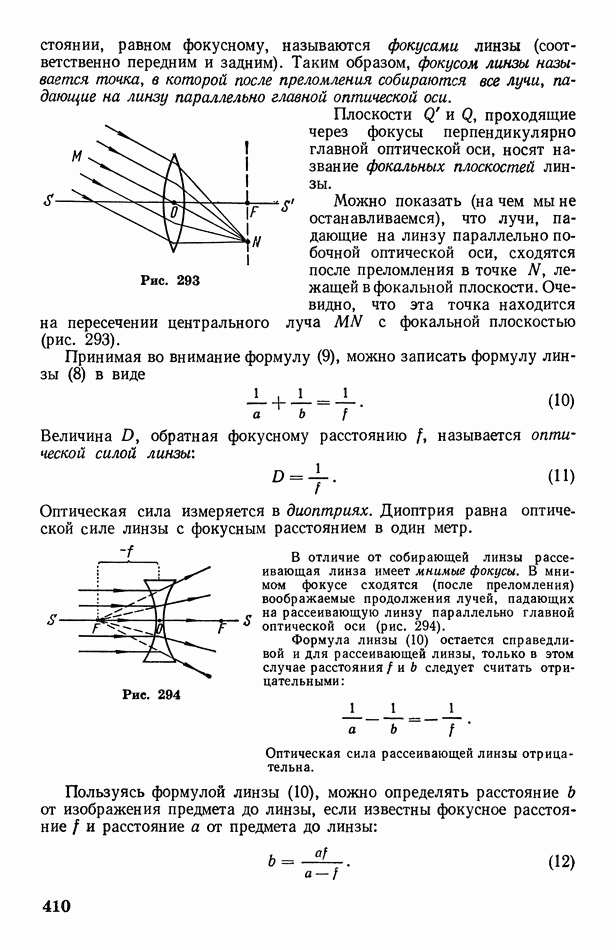
- § 117. Тонкие линзы. Микроскоп
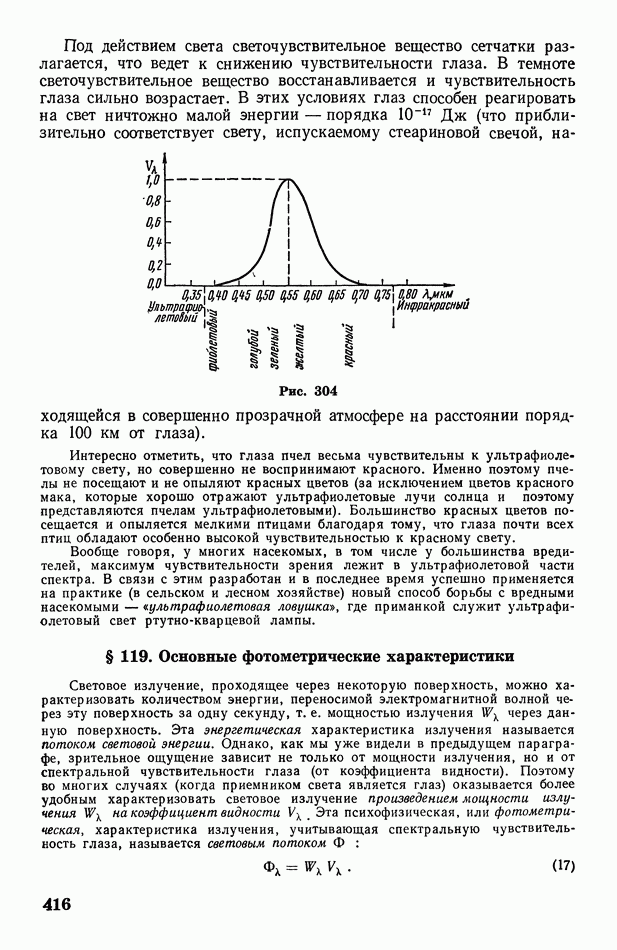
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
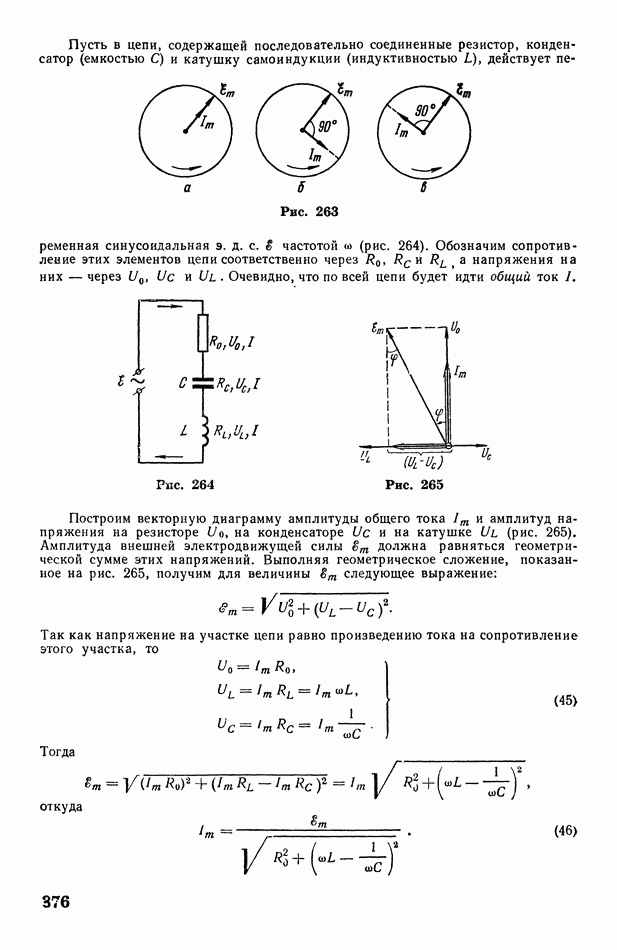
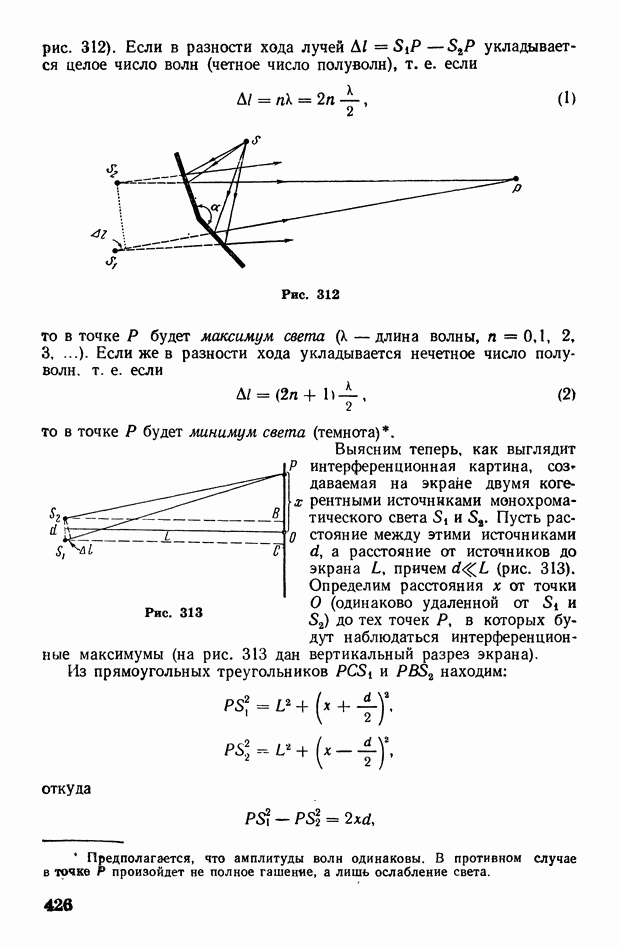
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
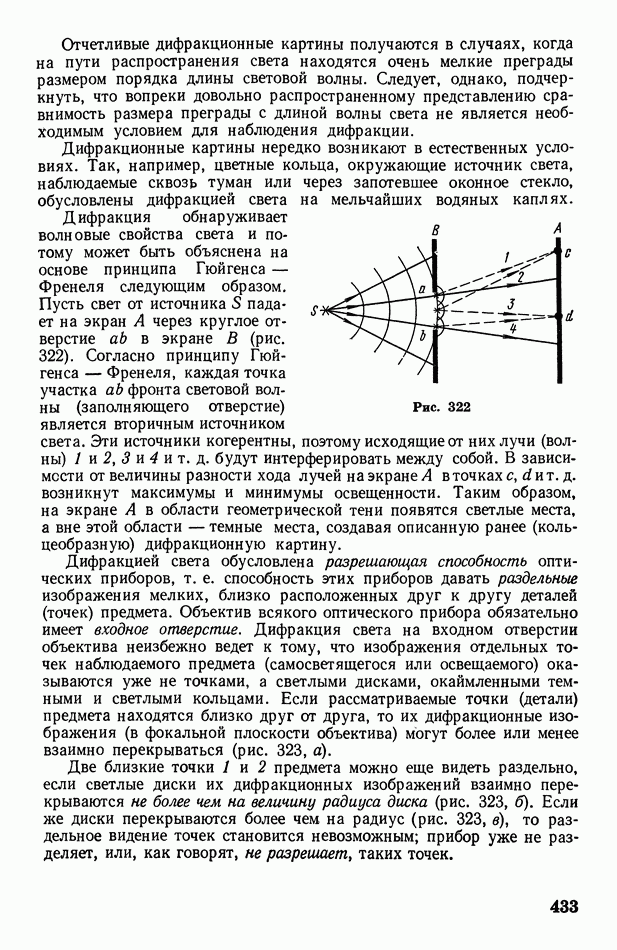
- § 123. Дифракция света. Разрешающая способность оптических приборов
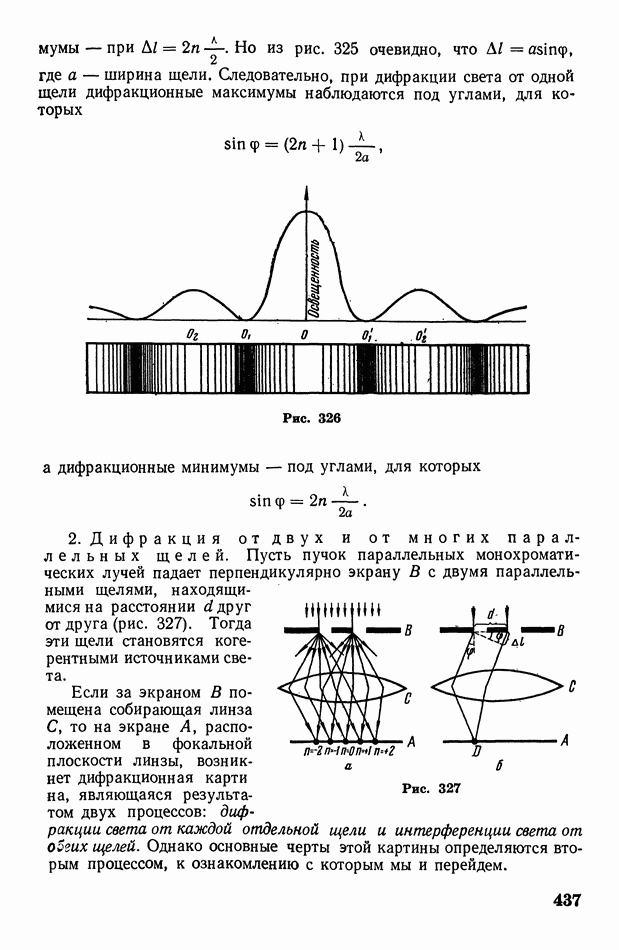
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
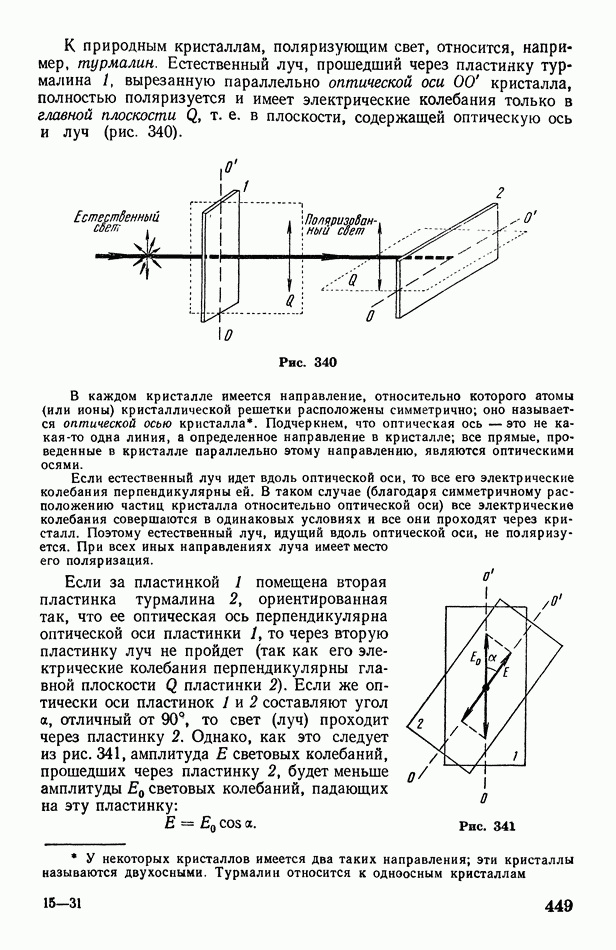
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
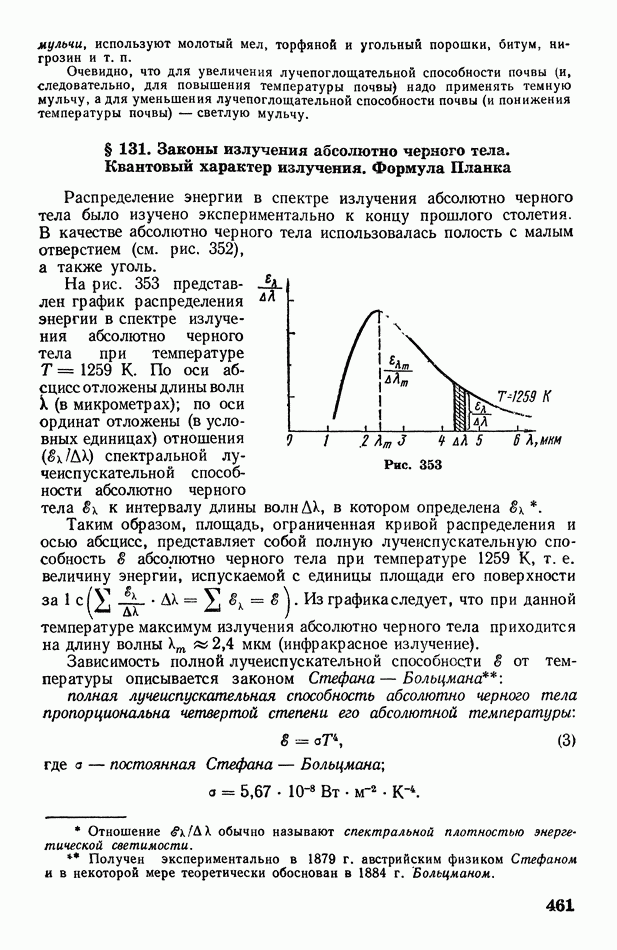
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
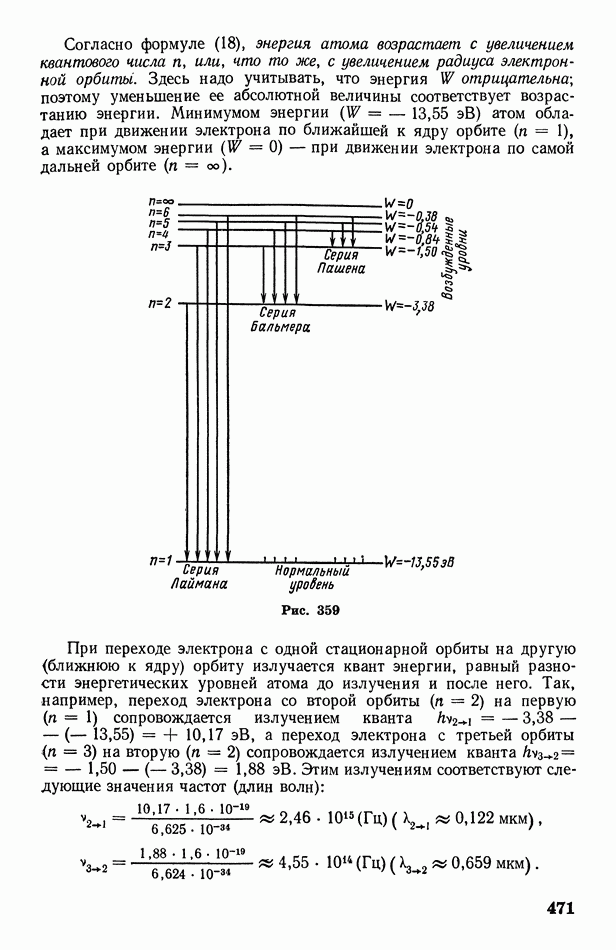
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
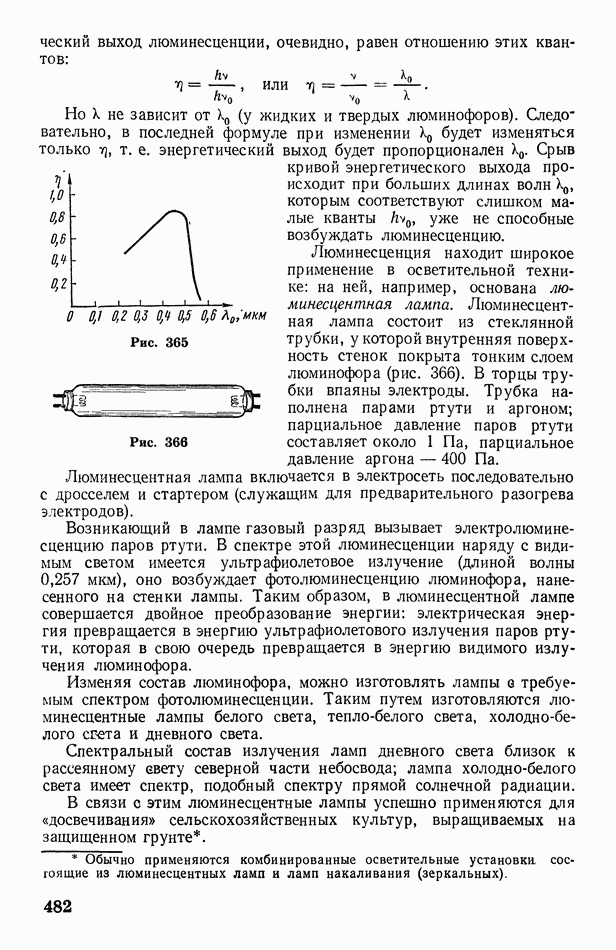
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
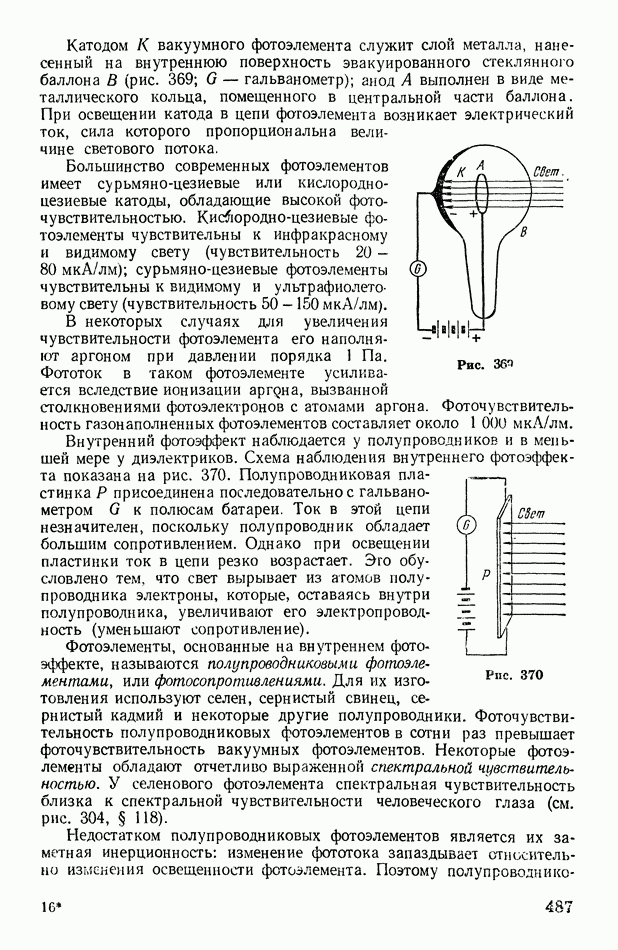
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
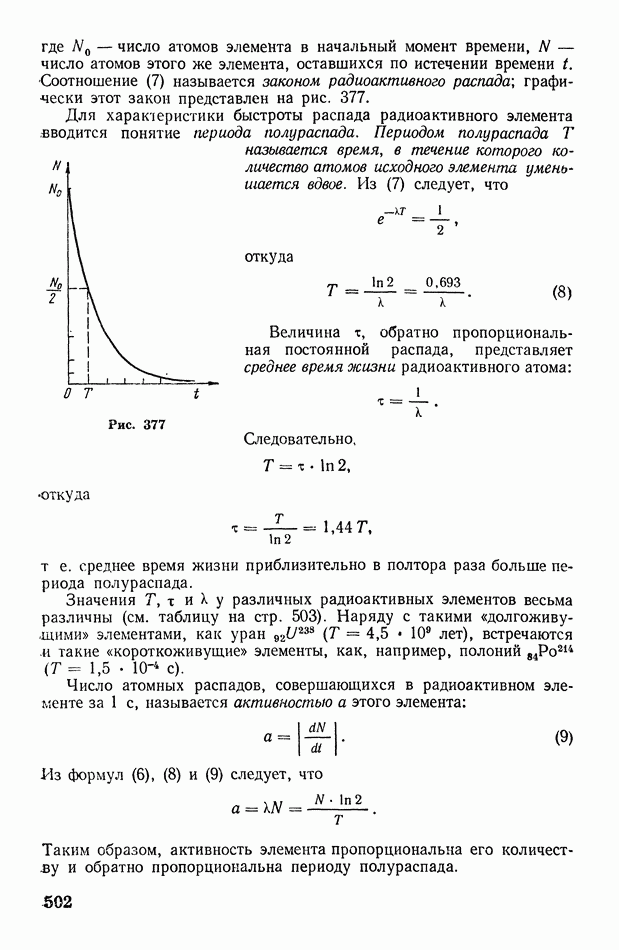
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
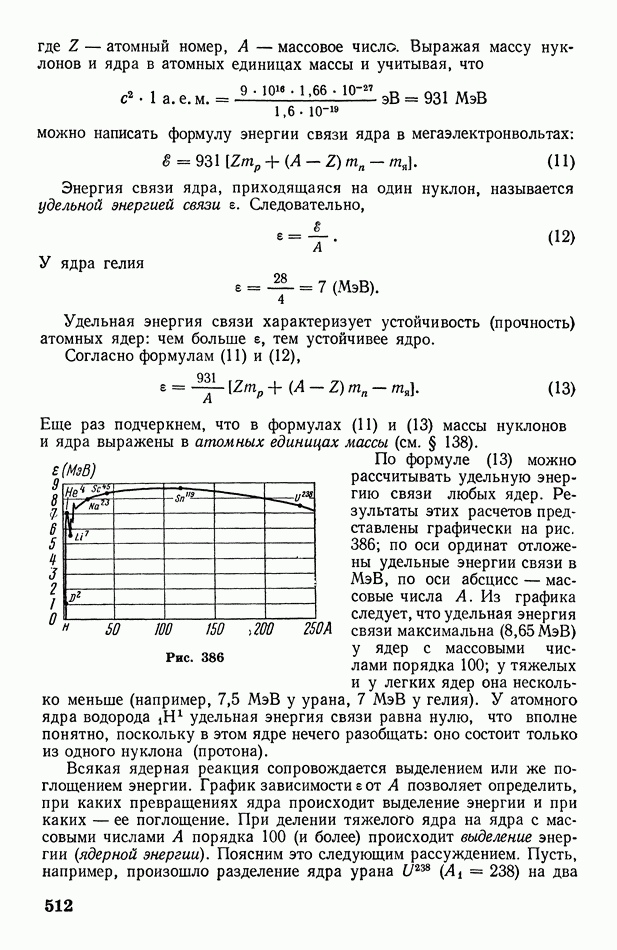
- § 142. Энергия связи и дефект массы атомного ядра
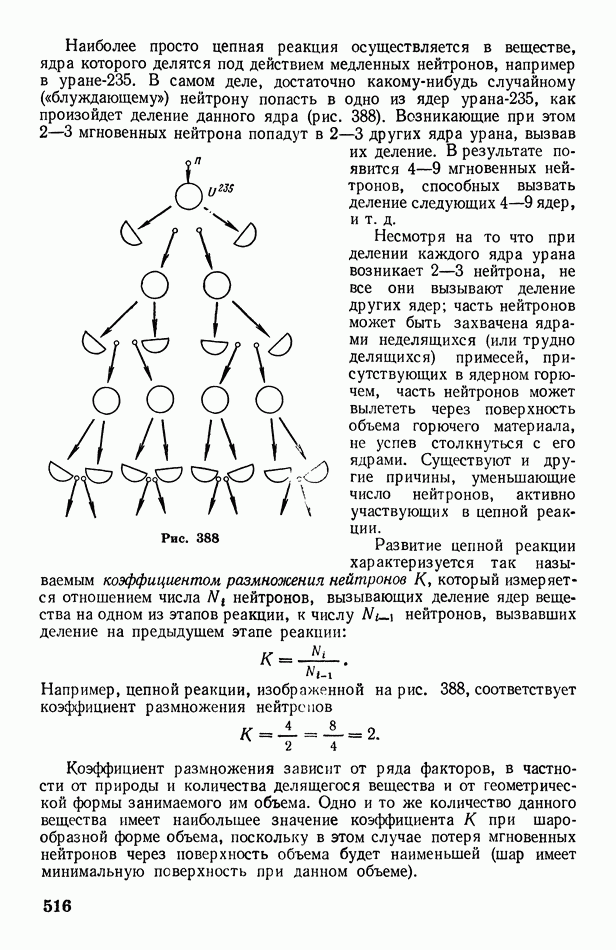
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
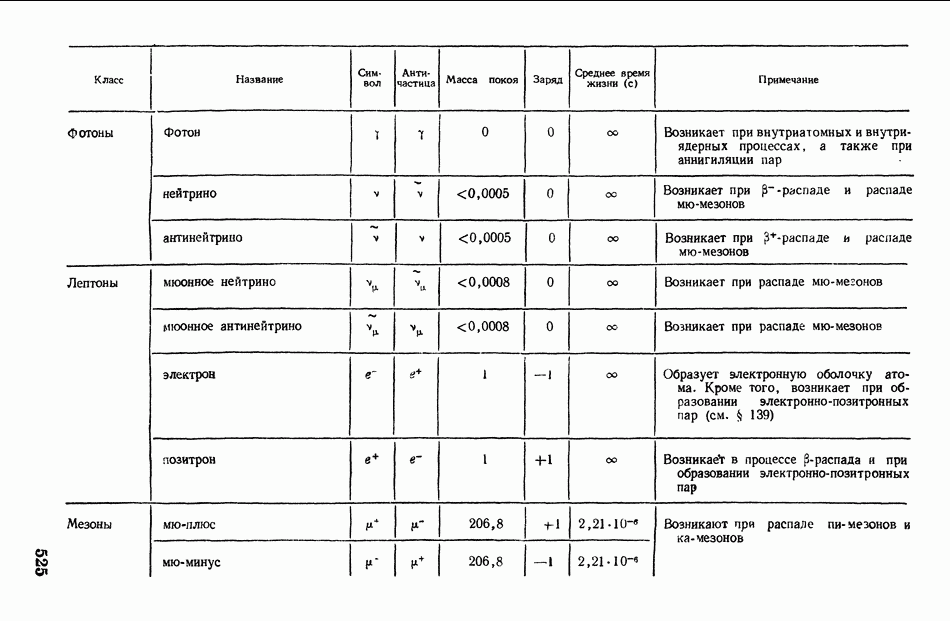
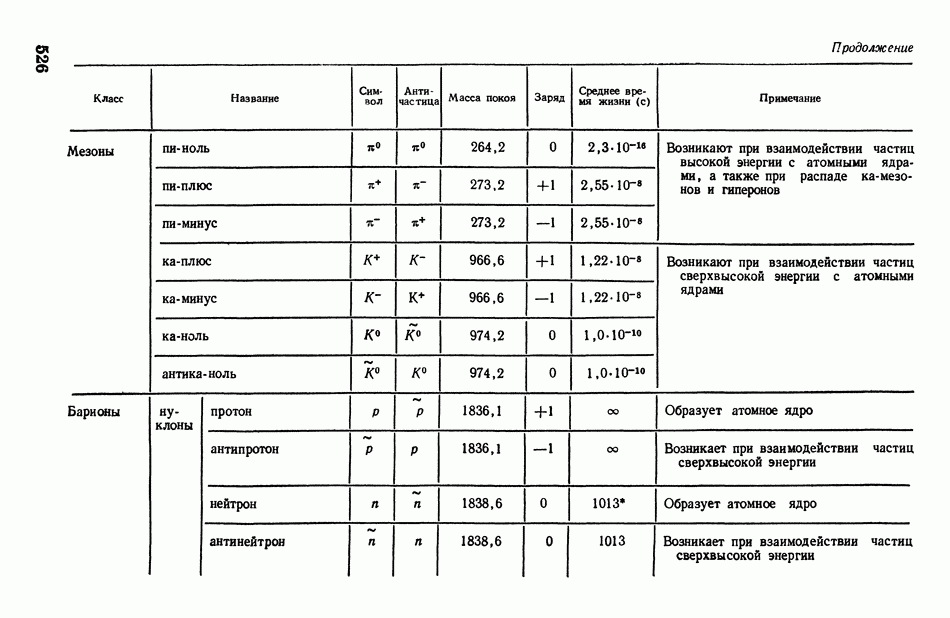
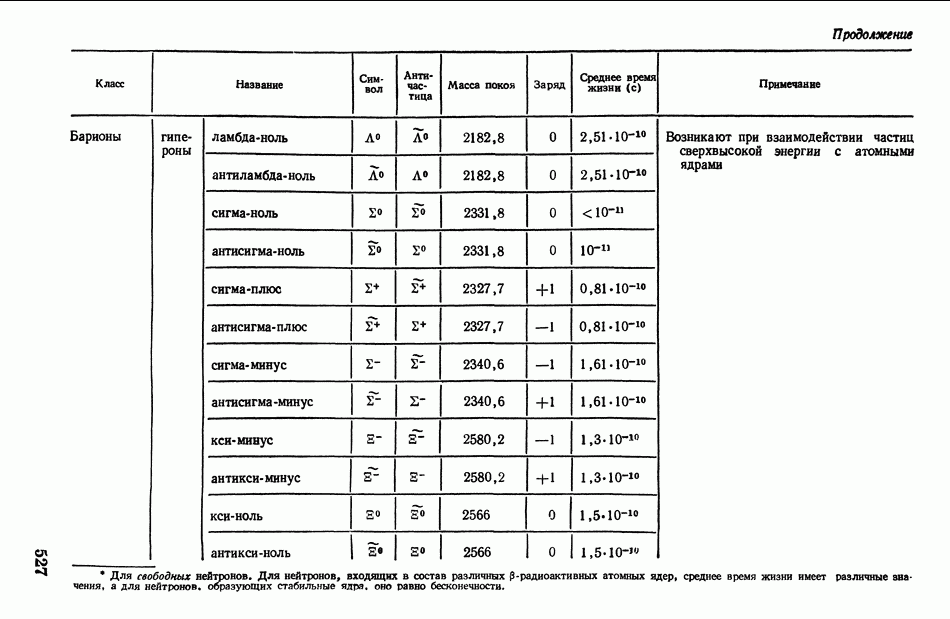
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии