| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
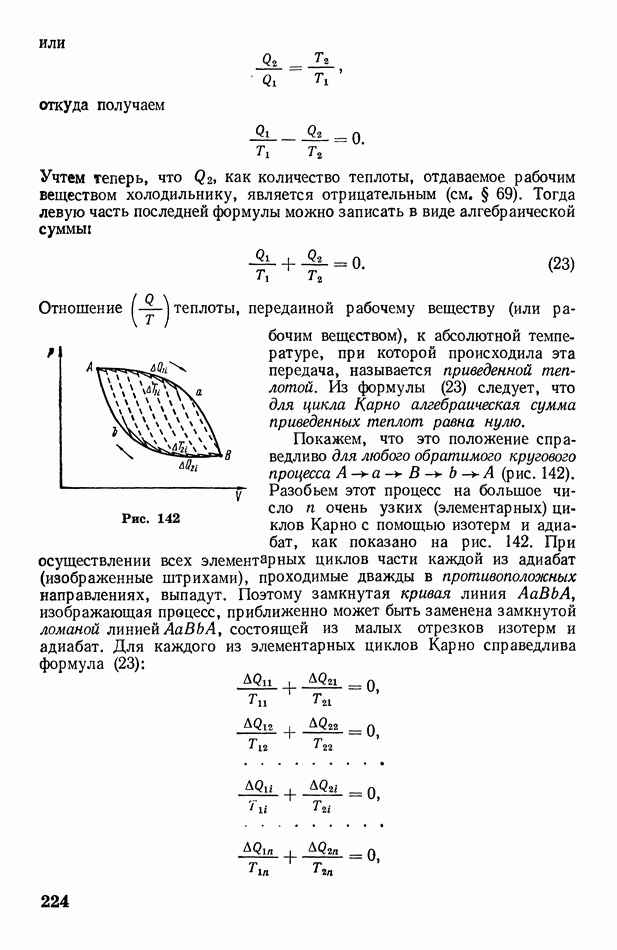
142
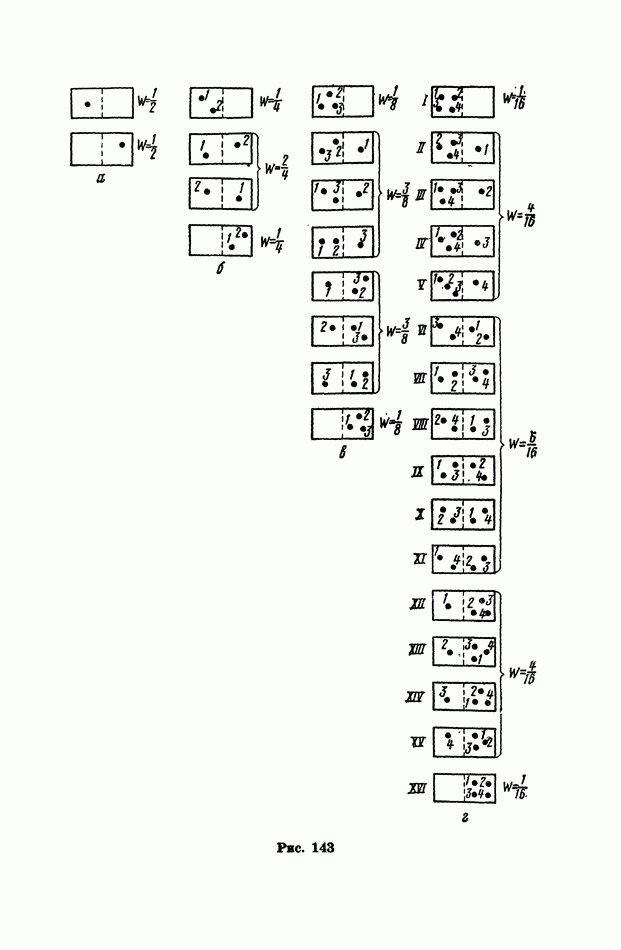
143
144
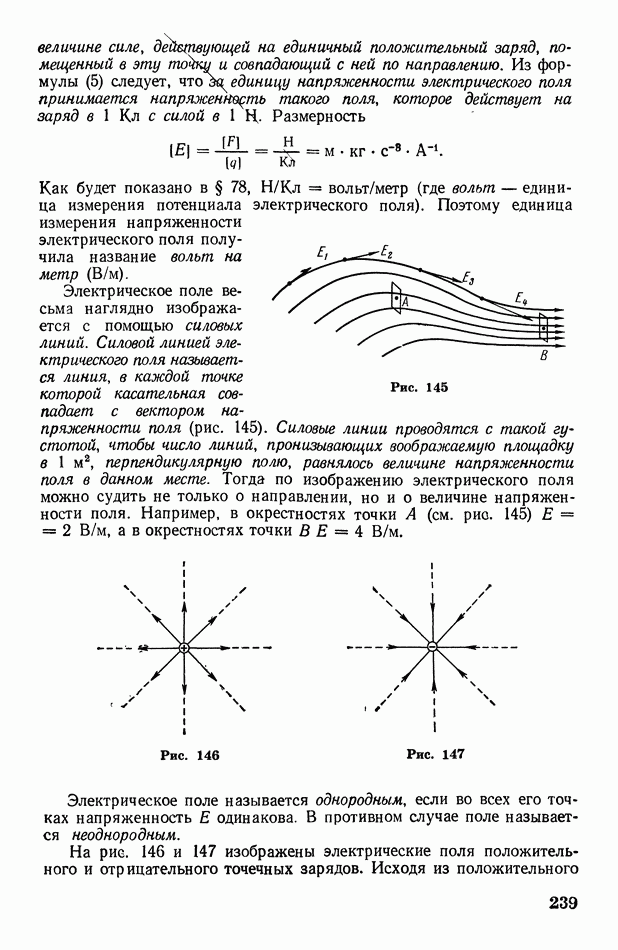
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
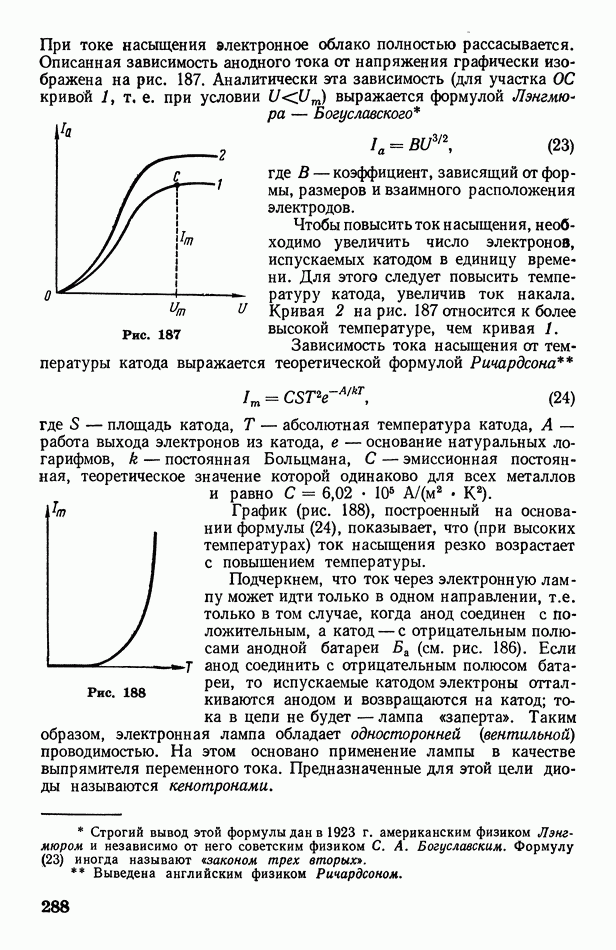
187
188
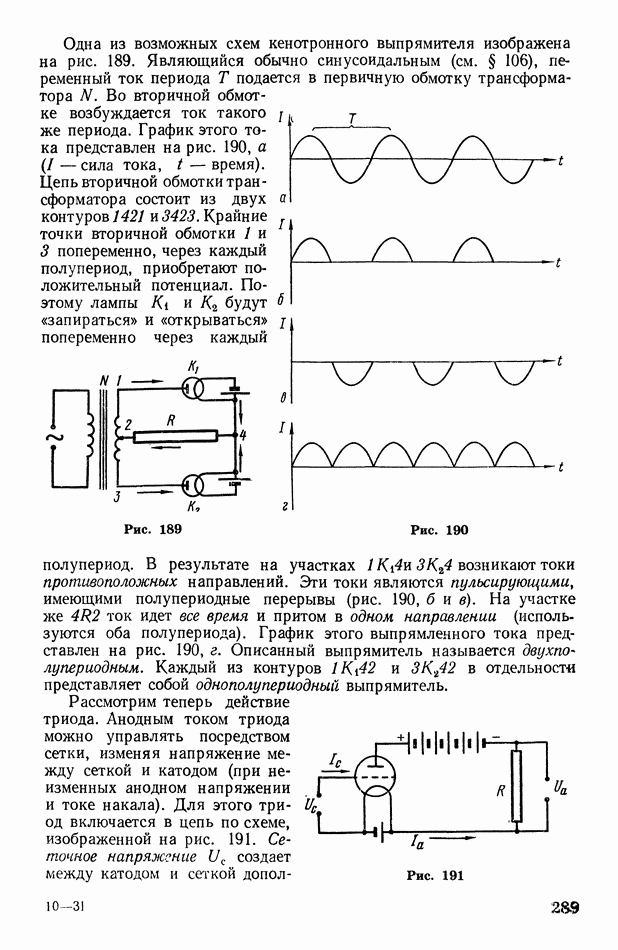
189
190
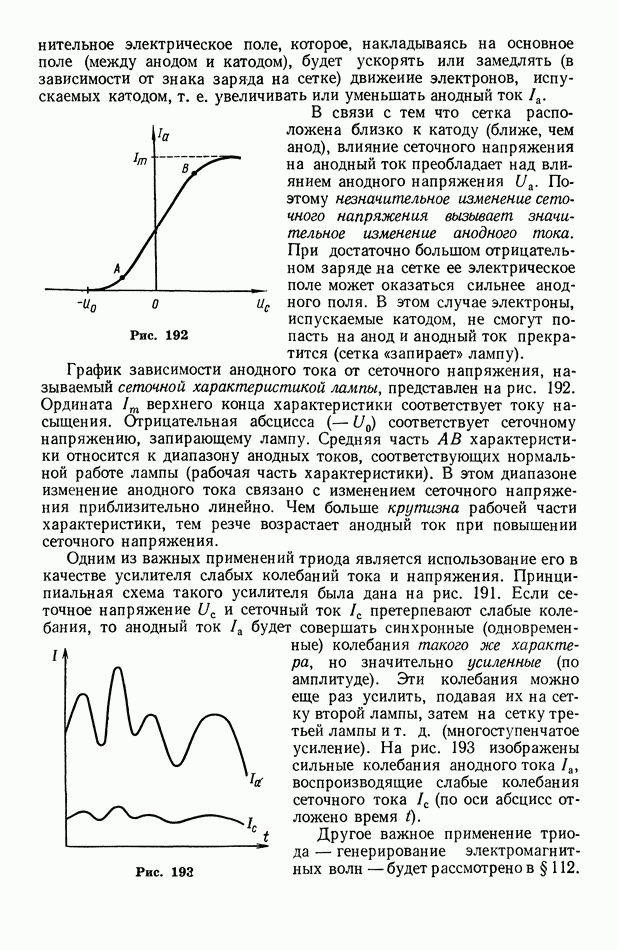
191
192
193
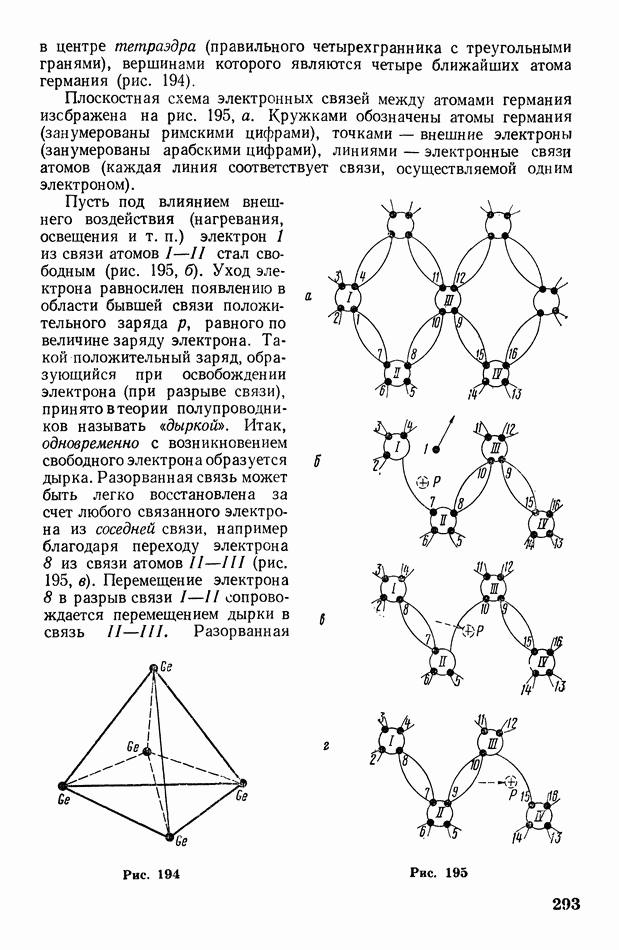
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
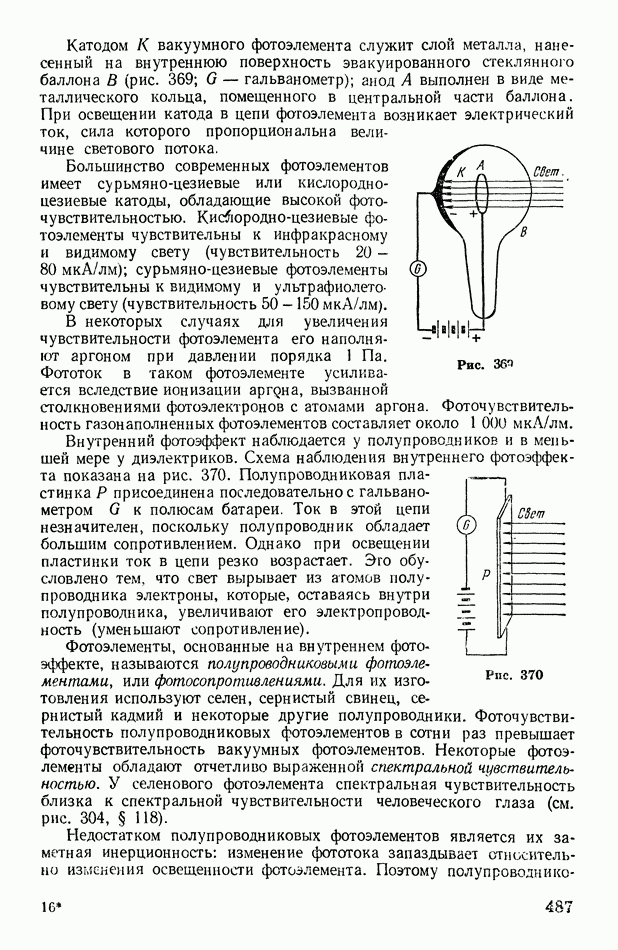
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
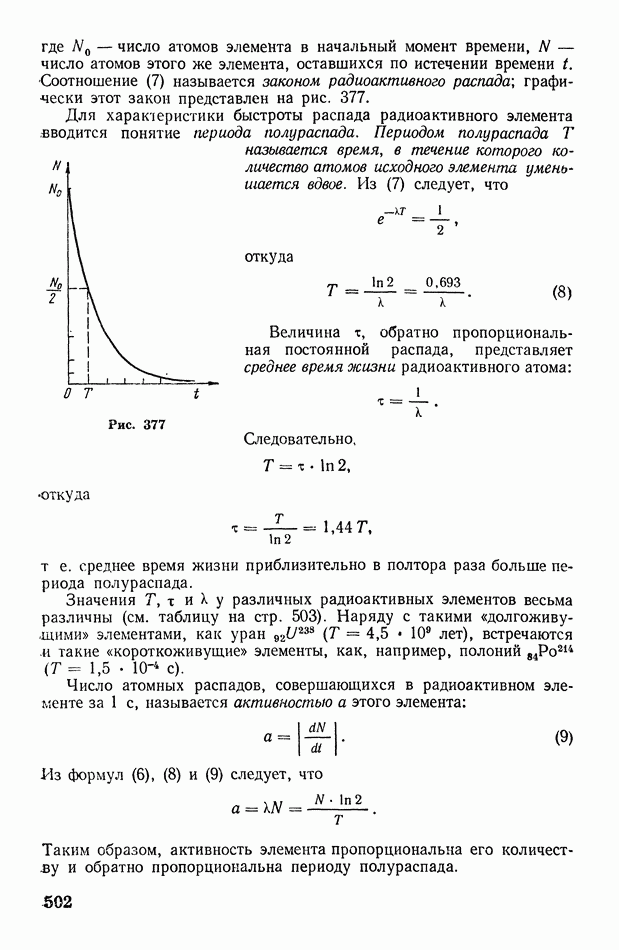
502
503
504
505
506
507
508
509
510
511
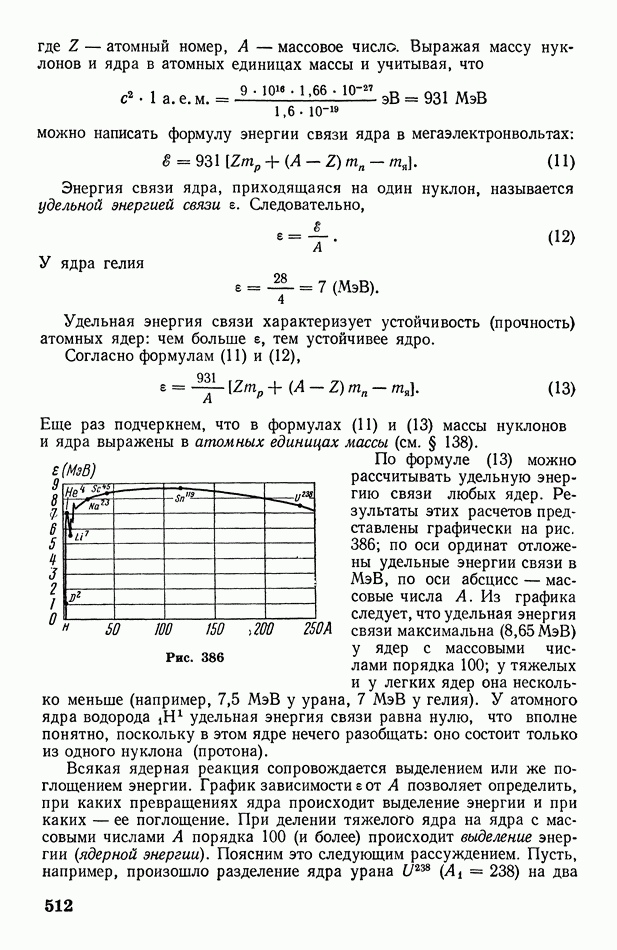
512
513
514
515
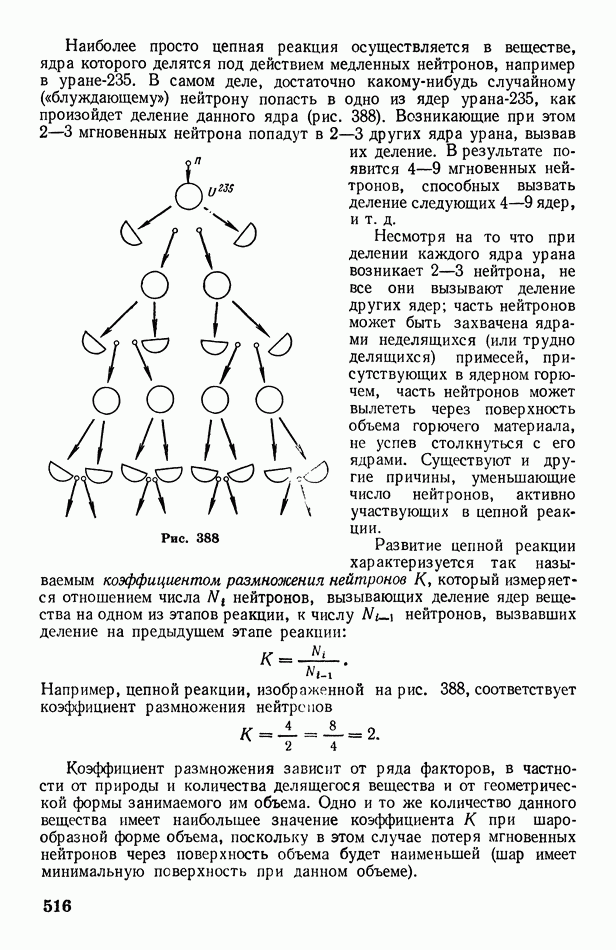
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 28. Сложение гармонических колебаний
Независимые гармонические колебания могут складываться друг с другом. Например, в точке разветвления проводов трехфазной сети переменного тока (соединенных «звездой») складываются различные синусоидальные переменные токи (см. § 109). В результате возникает более сложное колебание, характер которого зависит от соотношения фаз, частот, амплитуд и направлений слагаемых колебаний. Рассмотрим несколько наиболее простых случаев сложения гармонических колебаний.
Сложение двух колебаний одного направления
1. Круговые частоты а фазы колебаний одинаковы, амплитуды различны:

Тогда

т. е. возникает гармоническое колебание такой же частоты с амплитудой, равной сумме амплитуд слагаемых колебаний.
2. Круговые частоты и амплитуды одинаковы, фазы различны:

где  — разность фаз. Тогда, применяя формулу сложения синусов, получим
— разность фаз. Тогда, применяя формулу сложения синусов, получим

Возникает гармоническое колебание такой же частоты, но отличающееся по фазе от первичных колебаний на половину разности фаз этих колебаний. Амплитуда  вообще говоря, меньше суммы амплитуд первичных колебаний. Только при разности фаз, кратной
вообще говоря, меньше суммы амплитуд первичных колебаний. Только при разности фаз, кратной  При разности фаз, равной
При разности фаз, равной  и слагаемые колебания взаимно «гасятся».
и слагаемые колебания взаимно «гасятся».
3. Амплитуды одинаковы, круговые частоты мало отличаются друг от друга:

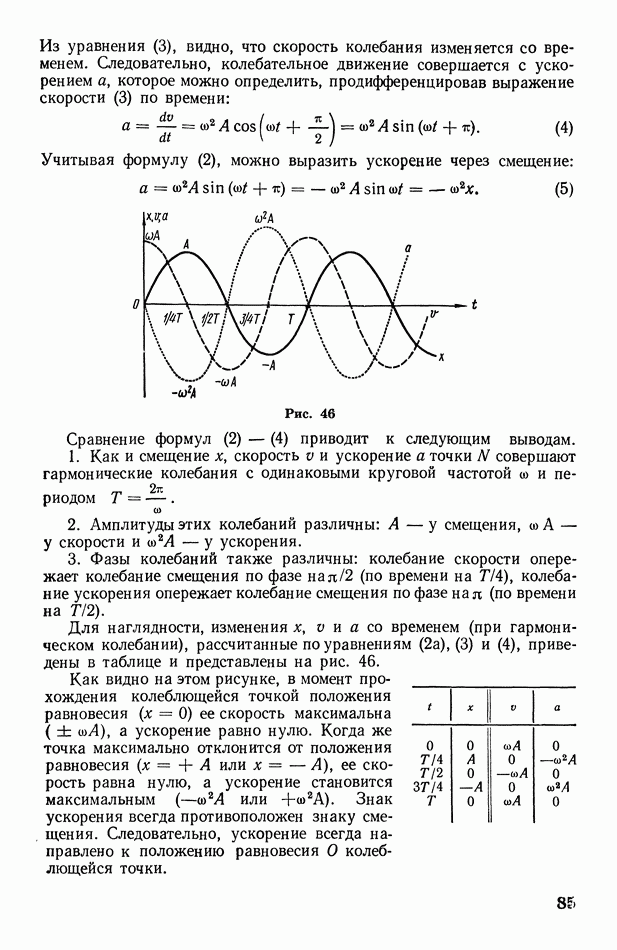
Тогда

Результирующее колебание оказывается не гармоническим, так как оно не соответствует уравнению (2). Однако учитывая, что (согласно
условию)  можно считать результирующее колебание почти гармоническим, имеющим круговую частоту
можно считать результирующее колебание почти гармоническим, имеющим круговую частоту

период

и амплитуду

которая очень медленно периодически изменяется со временем (круговая частота колебаний амплитуды  слишком мала, поэтому период колебаний амплитуды
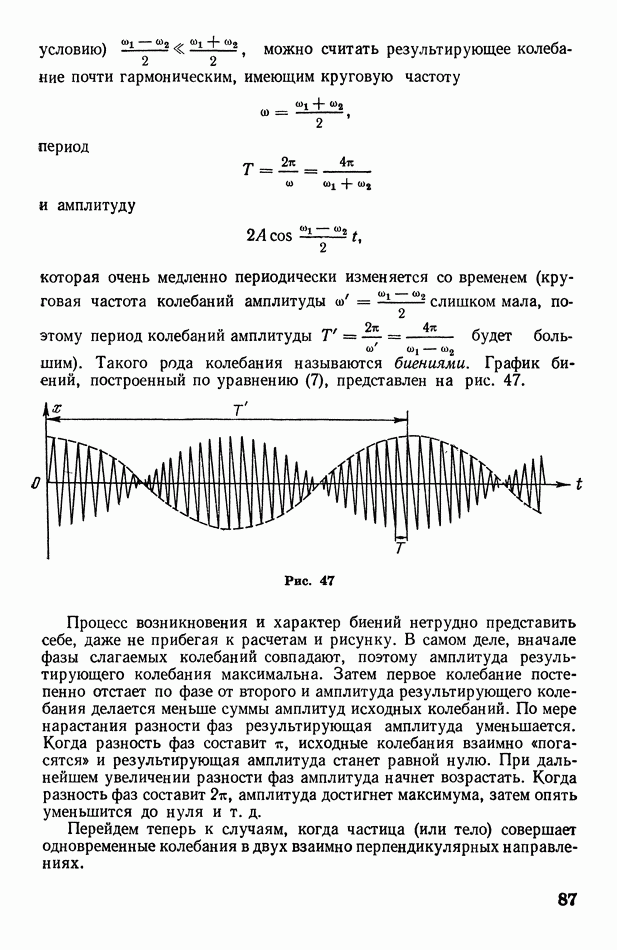
слишком мала, поэтому период колебаний амплитуды  будет большим). Такого рода колебания называются биениями. График биений, построенный по уравнению (7), представлен на рис. 47.
будет большим). Такого рода колебания называются биениями. График биений, построенный по уравнению (7), представлен на рис. 47.

Рис. 47
Процесс возникновения и характер биений нетрудно представить себе, даже не прибегая к расчетам и рисунку. В самом деле, вначале фазы слагаемых колебаний совпадают, поэтому амплитуда результирующего колебания максимальна. Затем первое колебание постепенно отстает по фазе от второго и амплитуда результирующего колебания делается меньше суммы амплитуд исходных колебаний. По мере нарастания разности фаз результирующая амплитуда уменьшается. Когда разность фаз составит  исходные колебания взаимно «пога-сятся» и результирующая амплитуда станет равной нулю. При дальнейшем увеличении разности фаз амплитуда начнет возрастать. Когда разность фаз составит
исходные колебания взаимно «пога-сятся» и результирующая амплитуда станет равной нулю. При дальнейшем увеличении разности фаз амплитуда начнет возрастать. Когда разность фаз составит  амплитуда достигнет максимума, затем опять уменьшится до нуля и т. д.
амплитуда достигнет максимума, затем опять уменьшится до нуля и т. д.
Перейдем теперь к случаям, когда частица (или тело) совершает одновременные колебания в двух взаимно перпендикулярных направлениях.
Сложение двух взаимно перпендикулярных колебаний
1. Круговые частоты и фазы одинаковы, амплитуды различны:

где х и у — смещения тела, вызванные первым и вторым колебаниями. Тогда

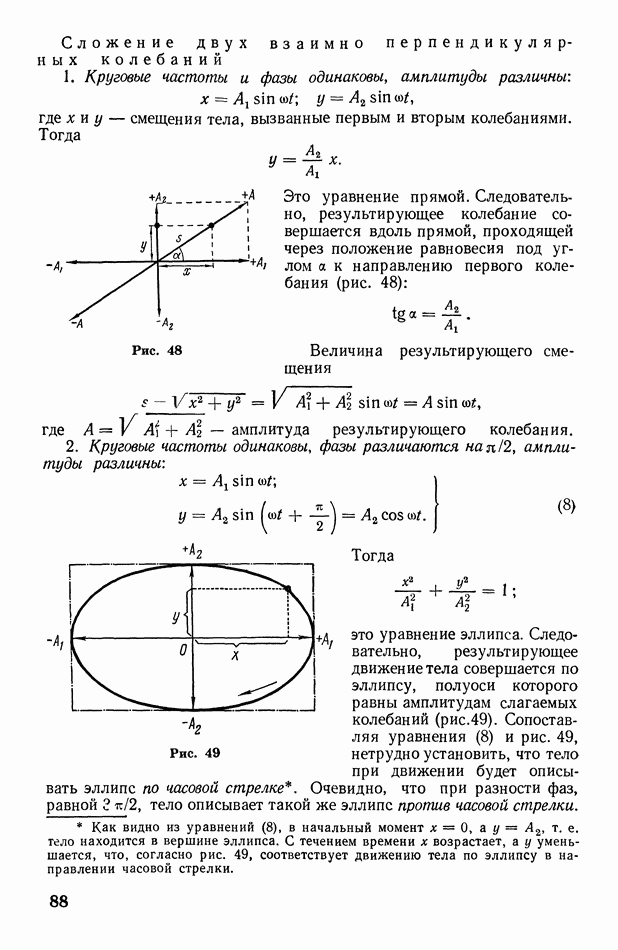
Это уравнение прямой. Следовательно, результирующее колебание совершается вдоль прямой, проходящей через положение равновесия под углом а к направлению первого колебания (рис. 48):


Рис. 48
Величина результирующего смещения

где  амплитуда результирующего колебания.
амплитуда результирующего колебания.
2. Круговые частоты одинаковы, фазы различаются  амплитуды различны:
амплитуды различны:

Тогда

это уравнение эллипса. Следовательно, результирующее движение тела совершается по эллипсу, полуоси которого равны амплитудам слагаемых колебаний (рис. 49). Сопоставляя уравнения (8) и рис. 49, нетрудно установить, что тело при движении будет описывать эллипс по часовой стрелке. Очевидно, что при разности фаз, равной  тело описывает такой же эллипс против часовой стрелки.
тело описывает такой же эллипс против часовой стрелки.

Рис. 49
Если  то уравнение эллипса переходит в уравнение окружности
то уравнение эллипса переходит в уравнение окружности  и тело будет описывать окружность.
и тело будет описывать окружность.
Не останавливаясь на анализе более сложных случаев сложения колебаний отметим только, что форма и расположение эллипса зависят от величины разности фаз 8. По мере изменения разности фаз эллипс  поворачиваться в плоскости слагаемых колебаний вокруг положения равновесия О. Кроме того, он будет деформироваться, оставаясь при этом вписанным в прямоугольник со сторонами, равными удвоенным амплитудам слагаемых колебаний (прямоугольник изображен на рис. 49 пунктиром). При
поворачиваться в плоскости слагаемых колебаний вокруг положения равновесия О. Кроме того, он будет деформироваться, оставаясь при этом вписанным в прямоугольник со сторонами, равными удвоенным амплитудам слагаемых колебаний (прямоугольник изображен на рис. 49 пунктиром). При  эллипс вырождается в прямую линию. На рис. 50 представлены траектории колеблющегося тела при некоторых значениях разности фаз. Стрелками указаны направления движения тела по траектории.
эллипс вырождается в прямую линию. На рис. 50 представлены траектории колеблющегося тела при некоторых значениях разности фаз. Стрелками указаны направления движения тела по траектории.

Рис. 50
Если слагаемые колебания имеют различную частоту, то траектории результирующего движения тела будут весьма сложными и разнообразными по форме (фигуры Лиссажу).
Описанные формы траекторий можно непосредственно наблюдать на экране электронного осциллографа (см. § 102), если сообщить электронному лучу одновременные колебания в двух взаимно перпендикулярных направлениях.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
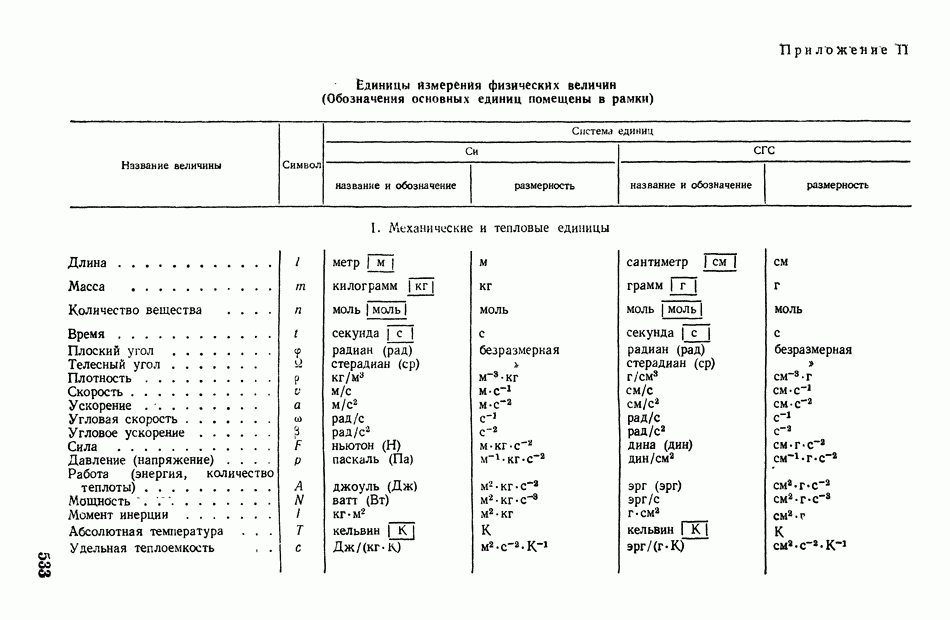
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
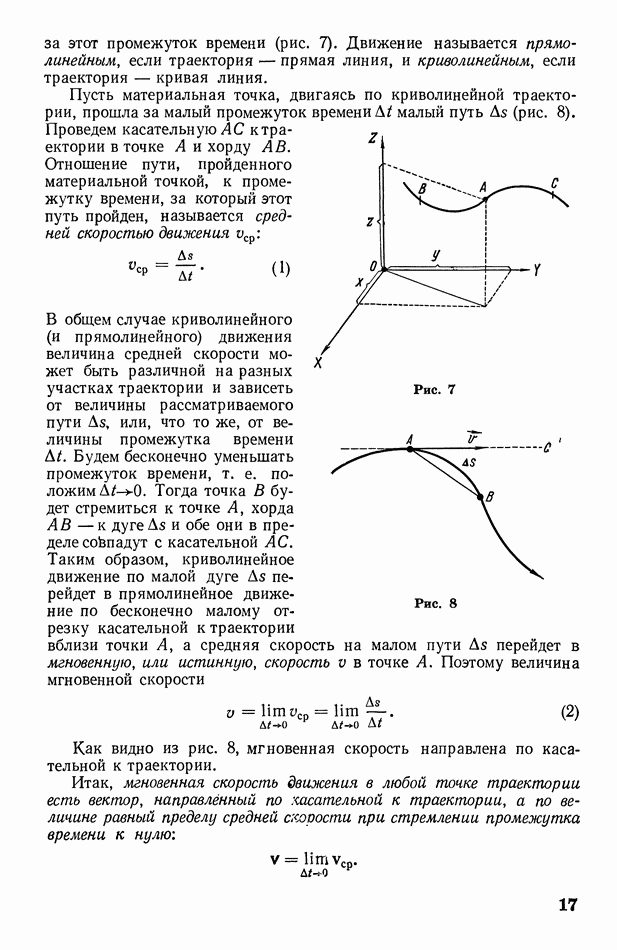
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
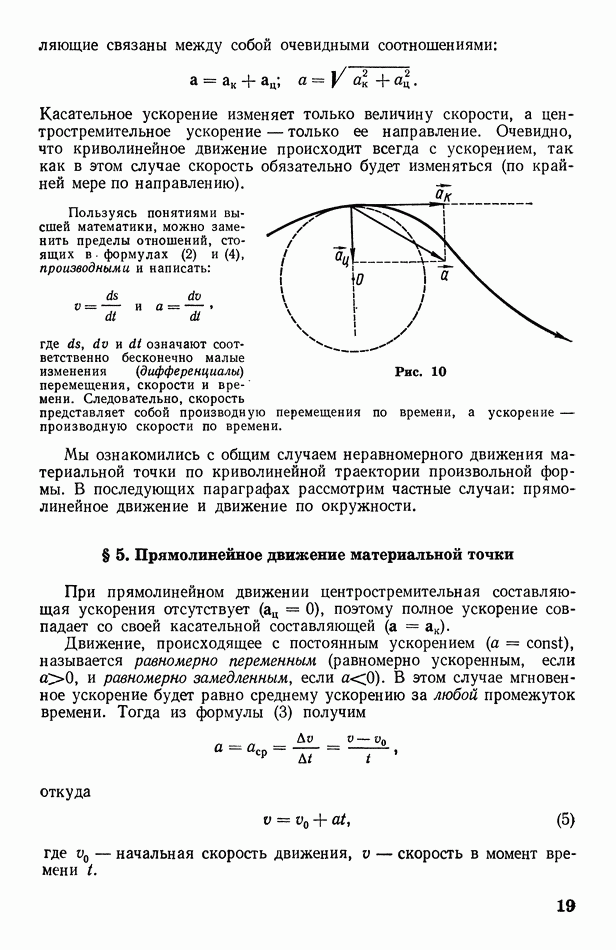
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
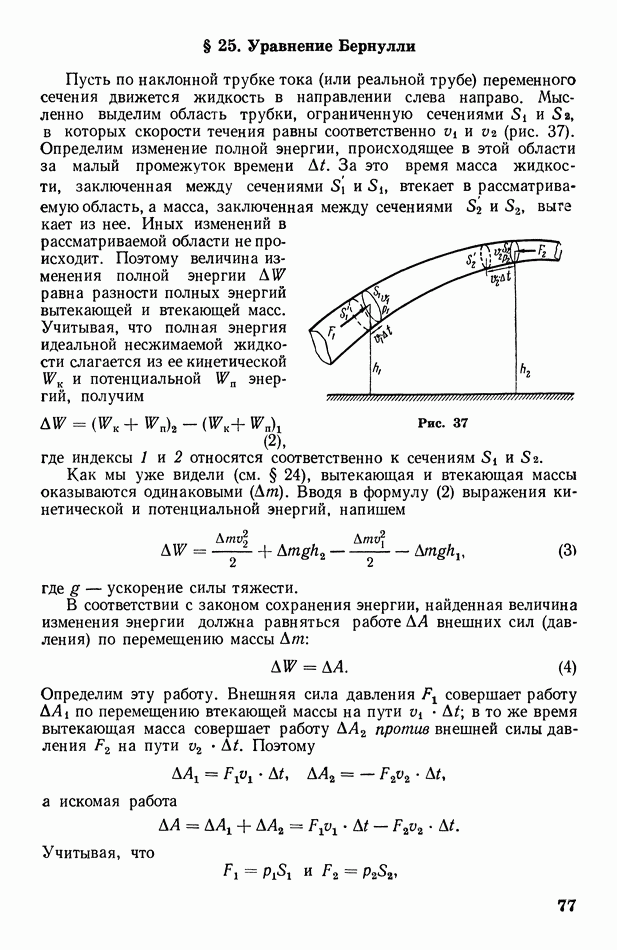
- § 25. Уравнение Бернулли
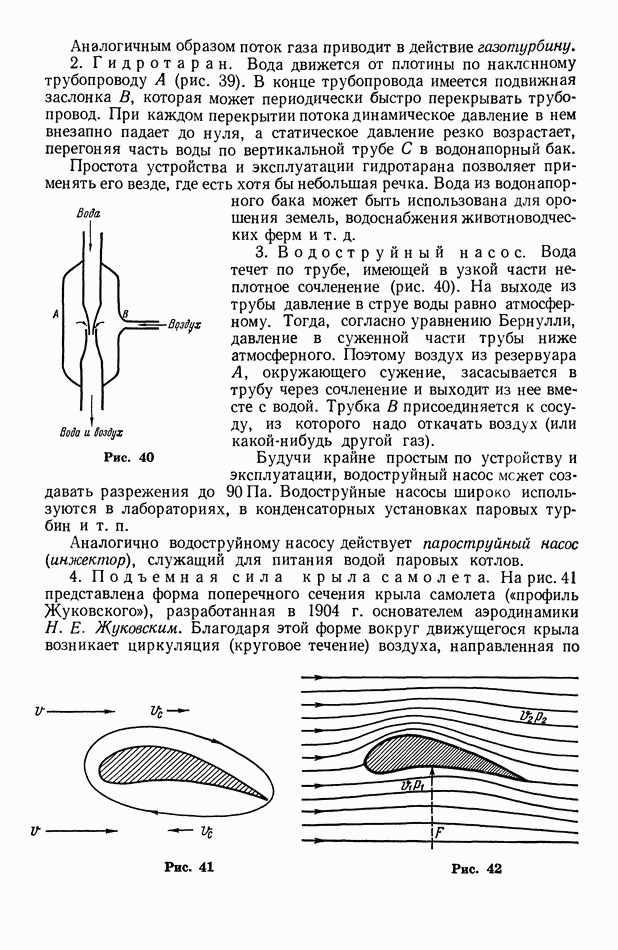
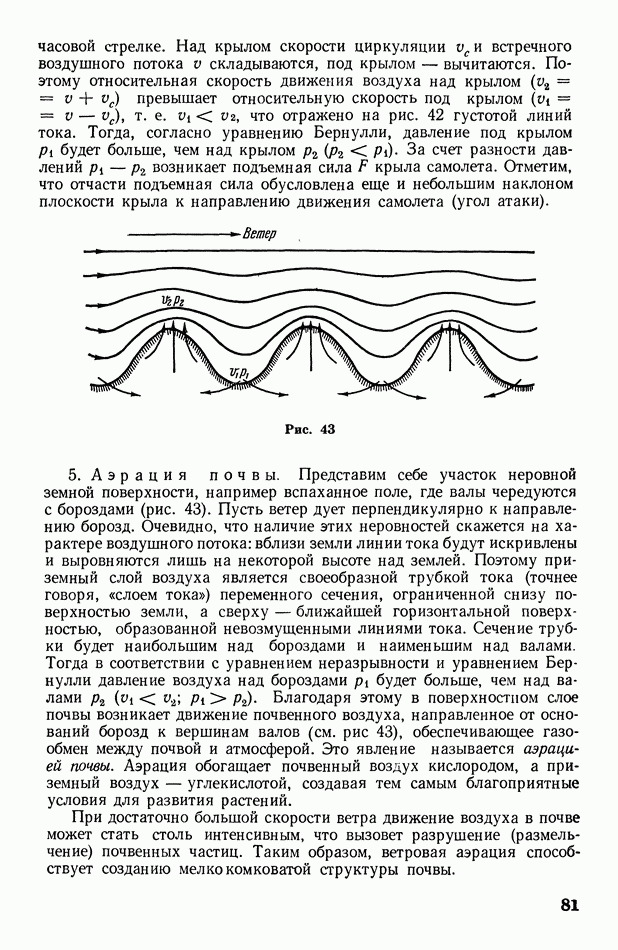
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
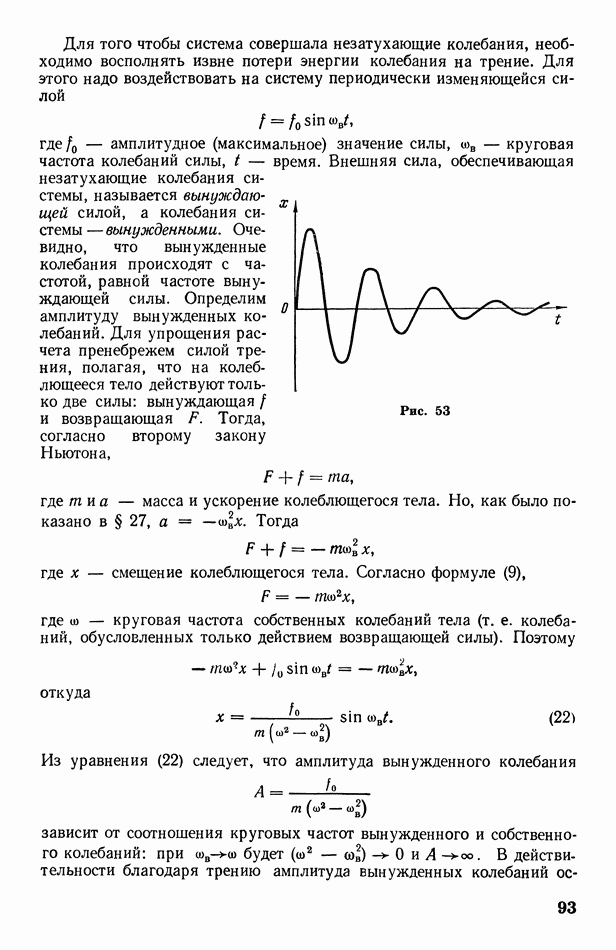
- § 30. О затухающих и вынужденных колебаниях
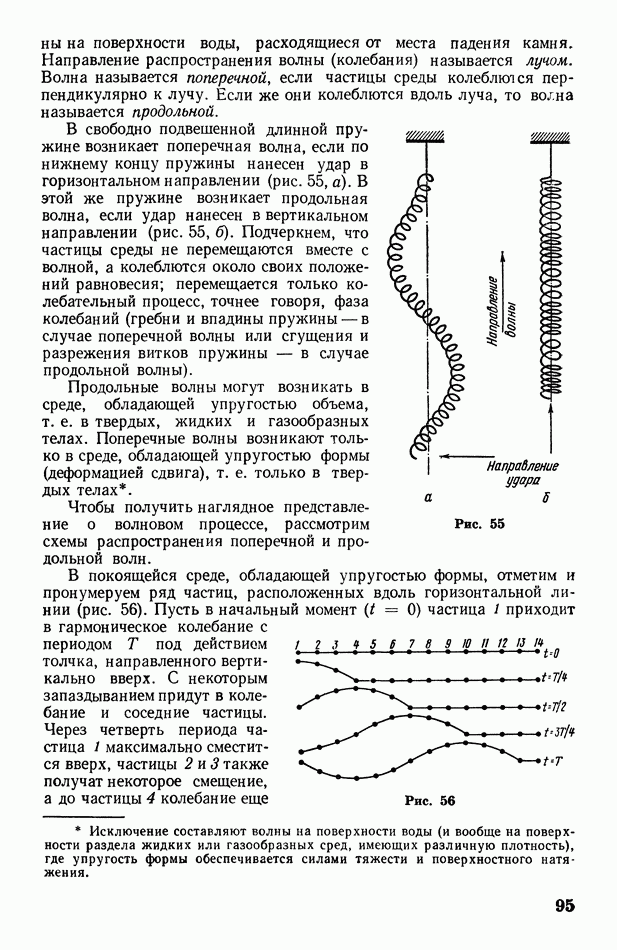
- § 31. Волновой процесс
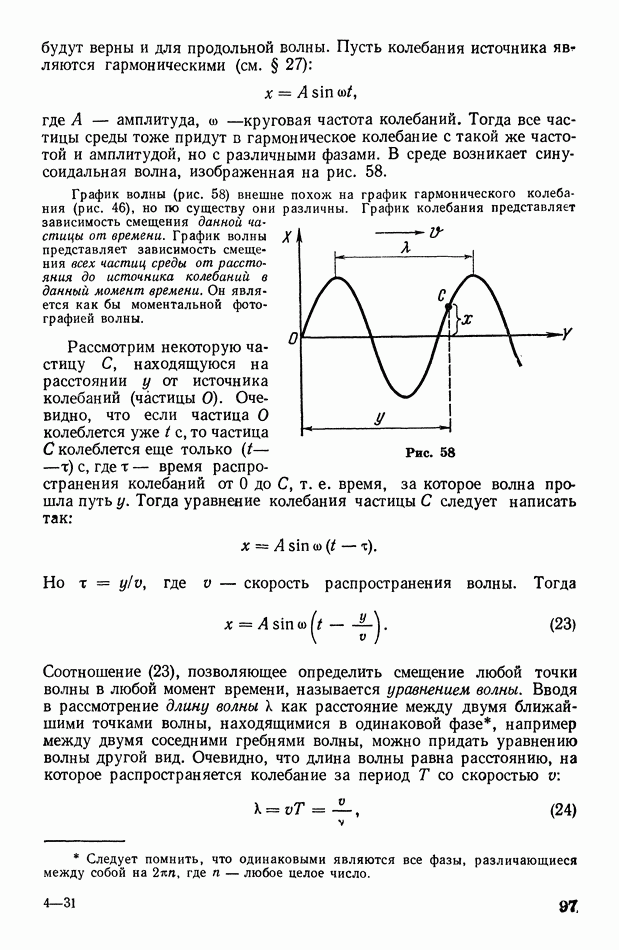
- § 32. Уравнение волны. Интенсивность волны
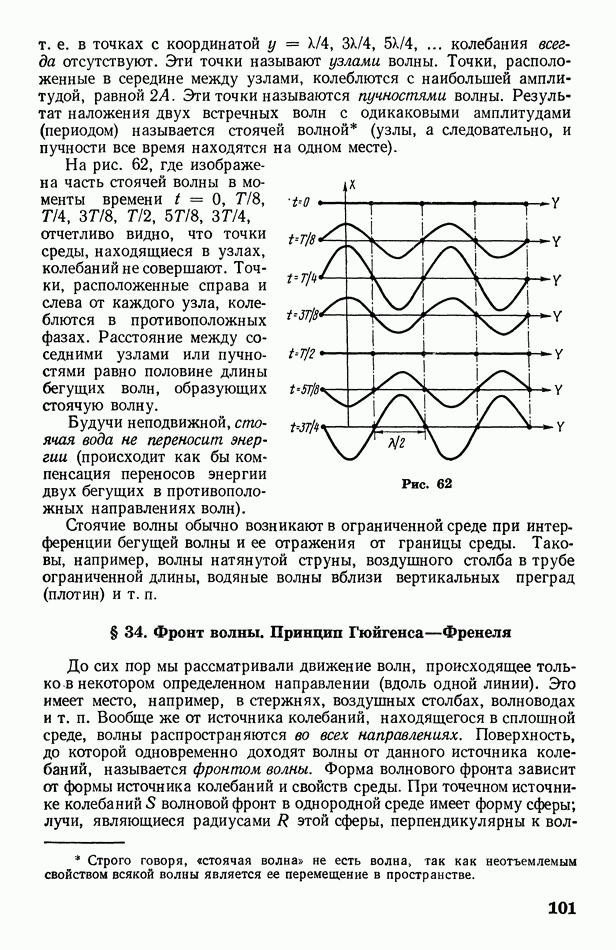
- § 33. Интерференция волн. Стоячие волны
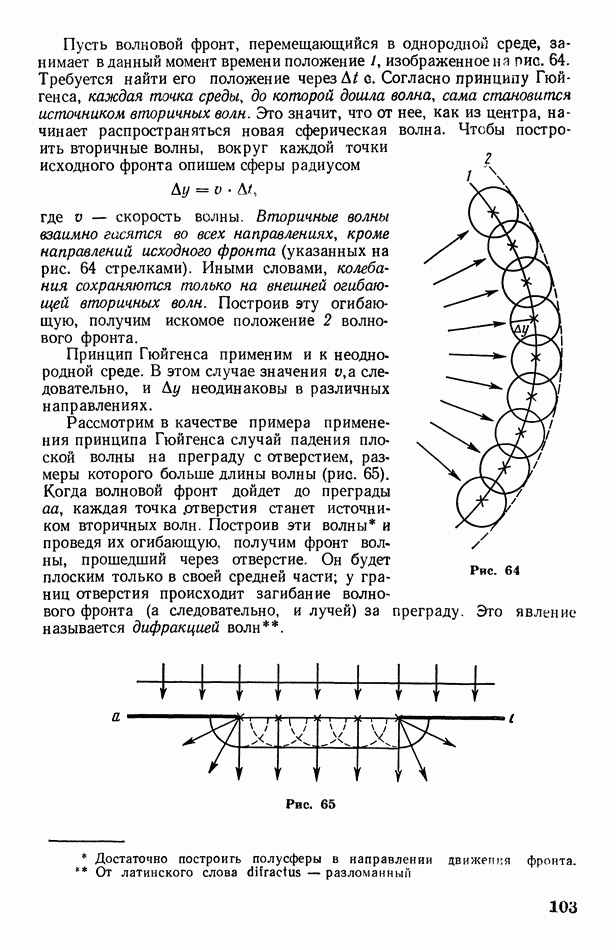
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
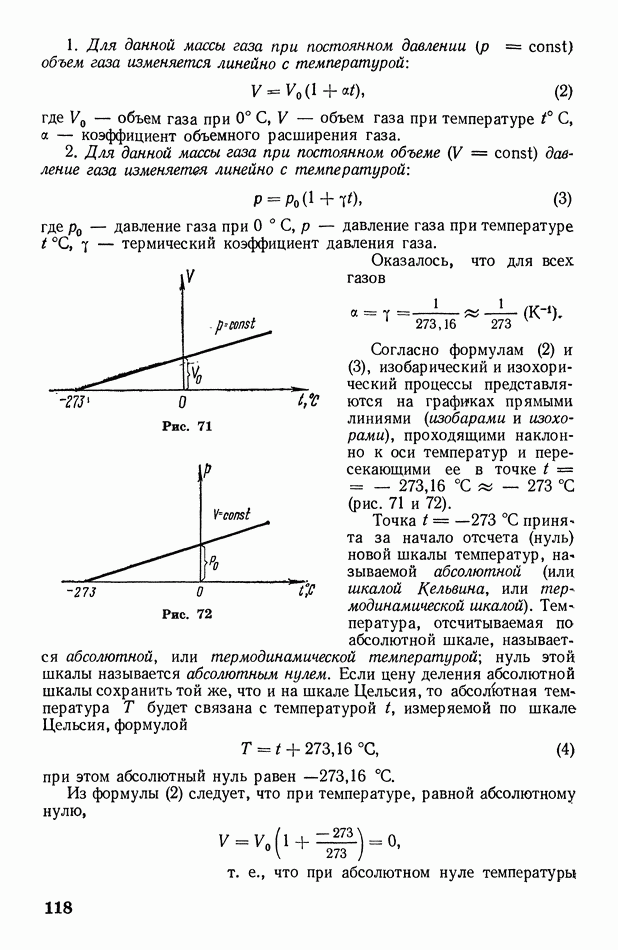
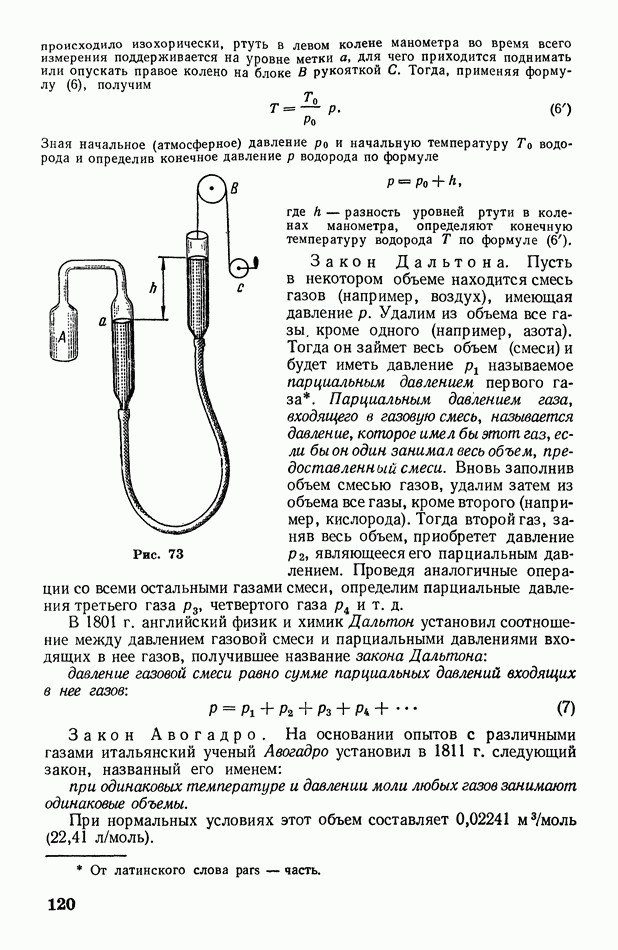
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
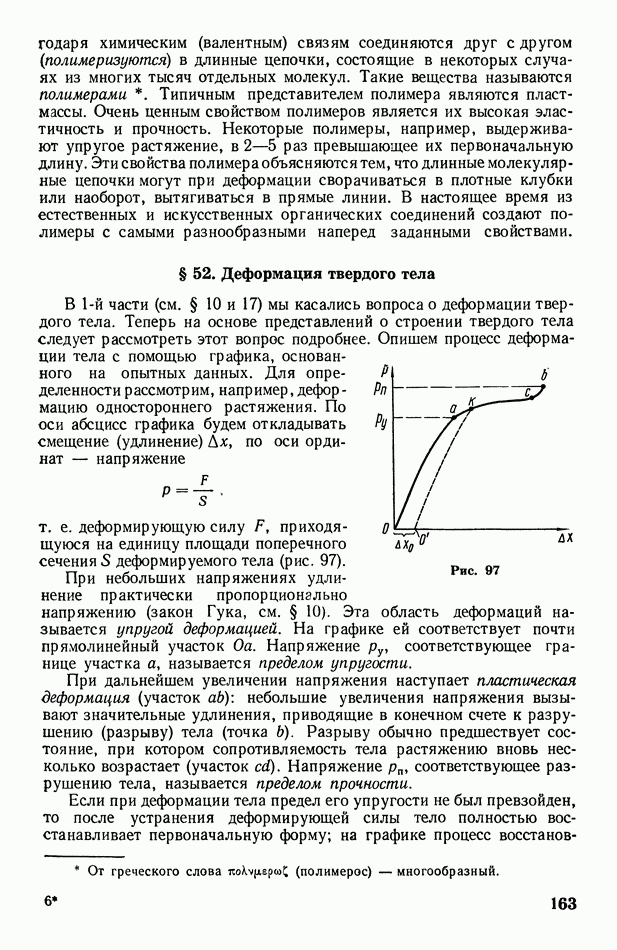
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
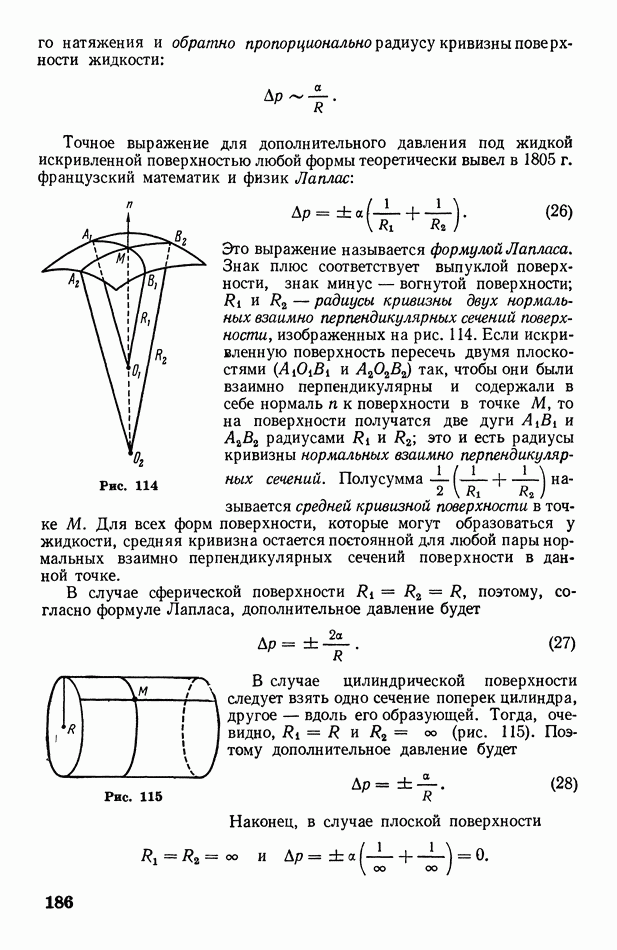
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
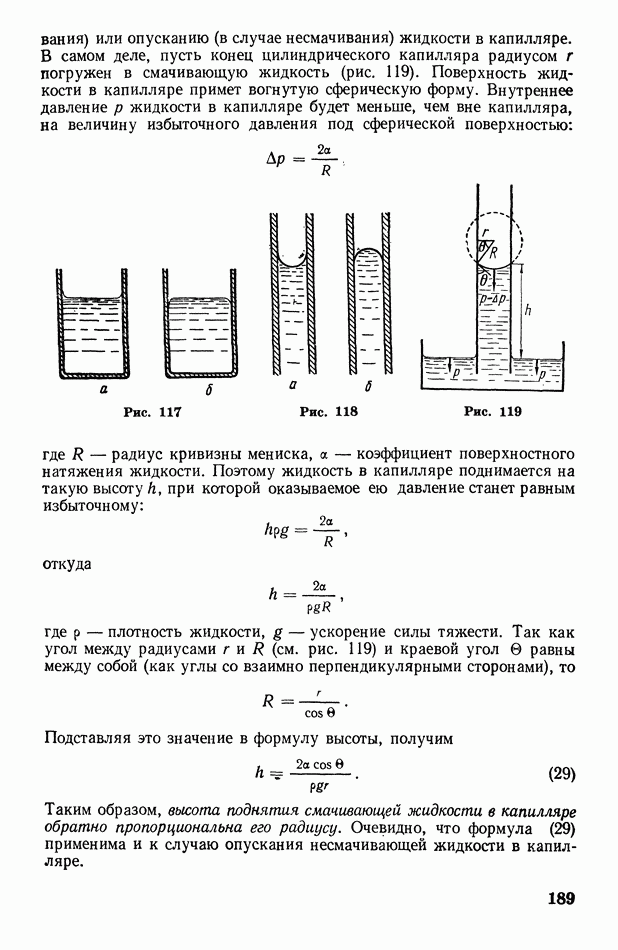
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
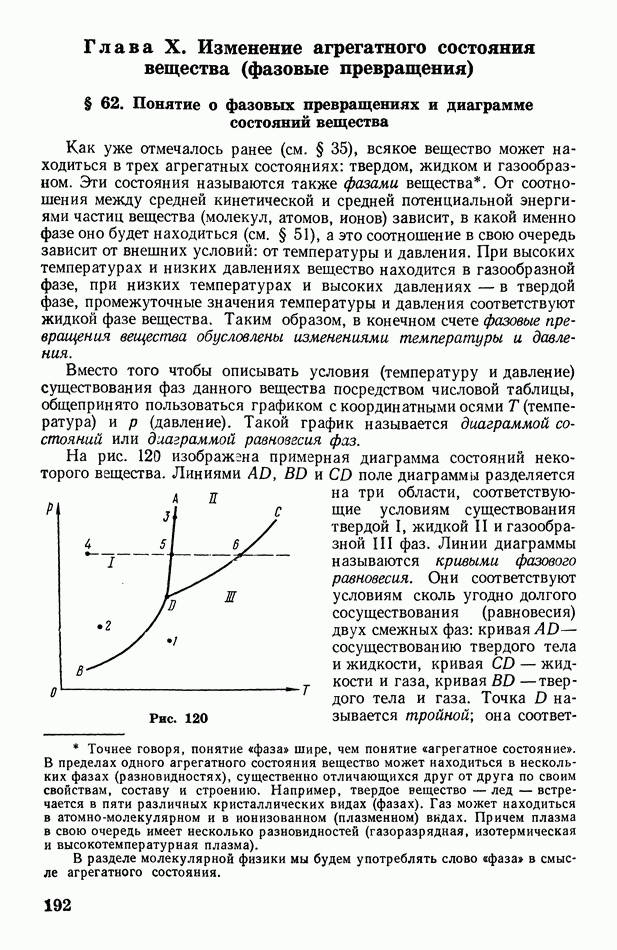
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
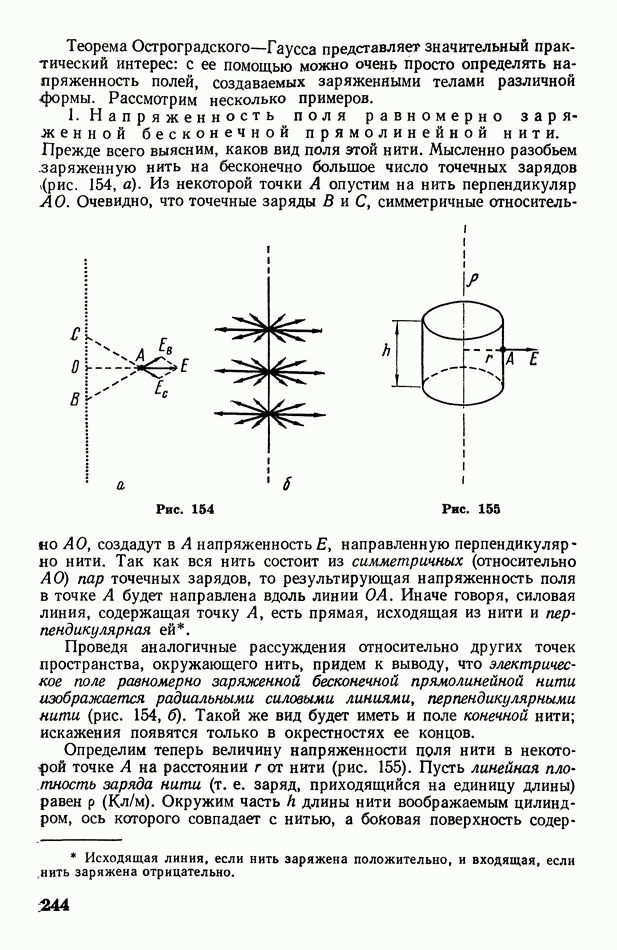
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
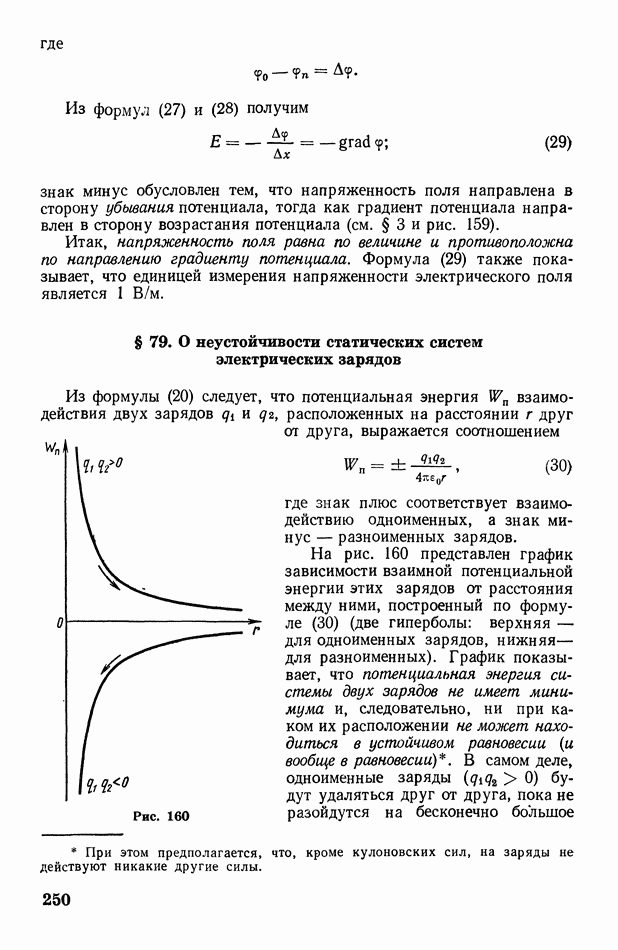
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
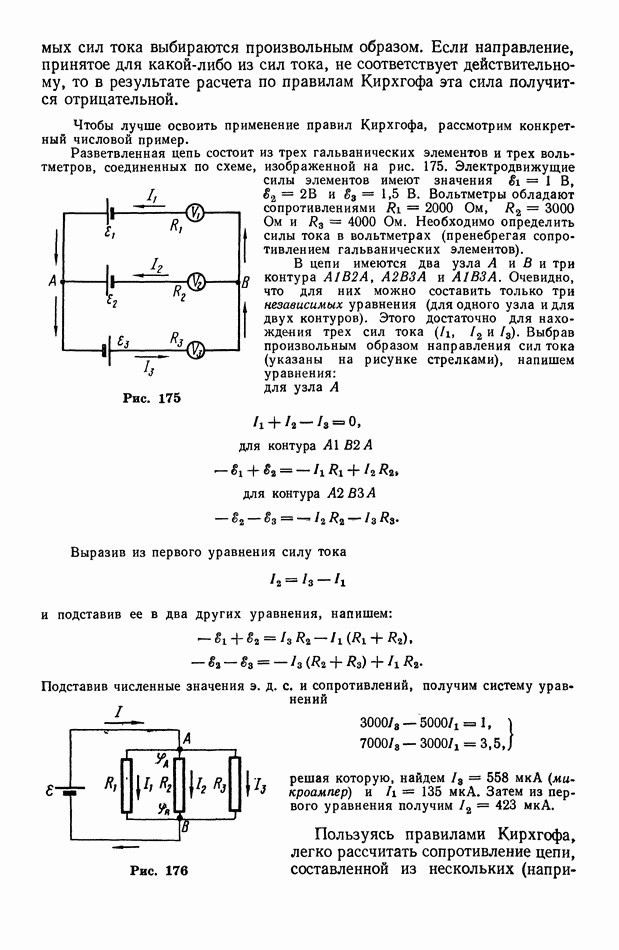
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
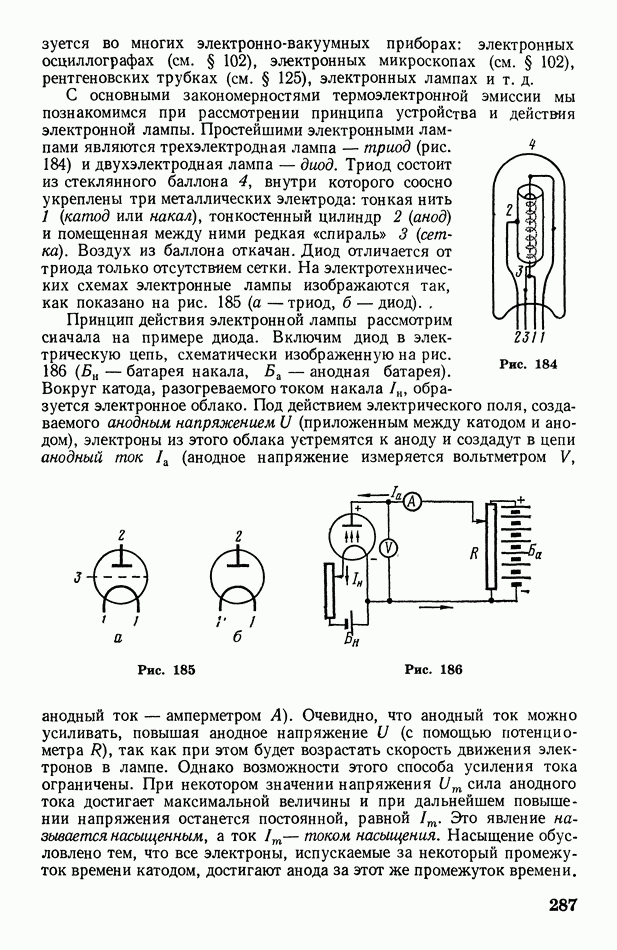
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
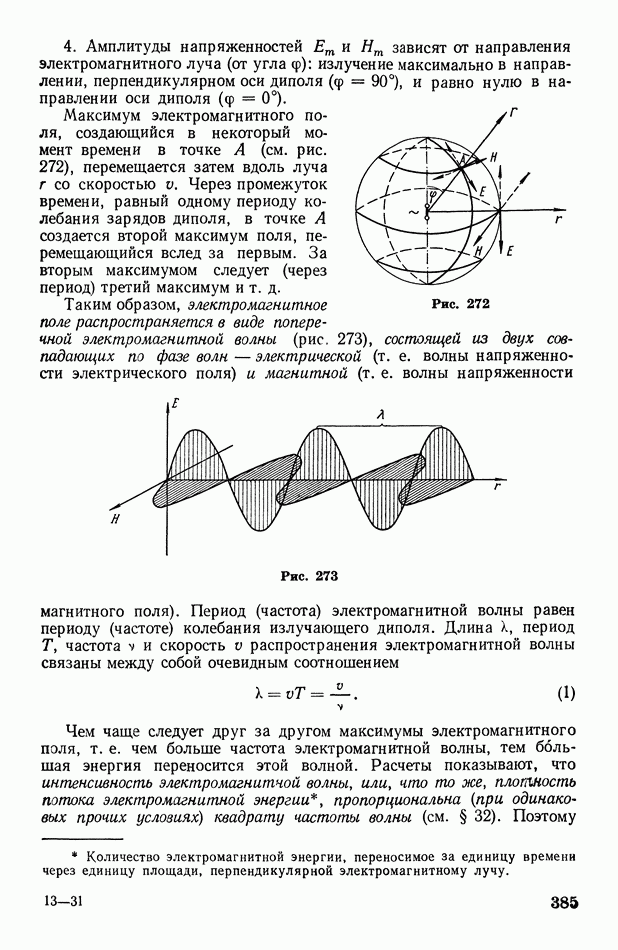
- § 110. Электромагнитные волны
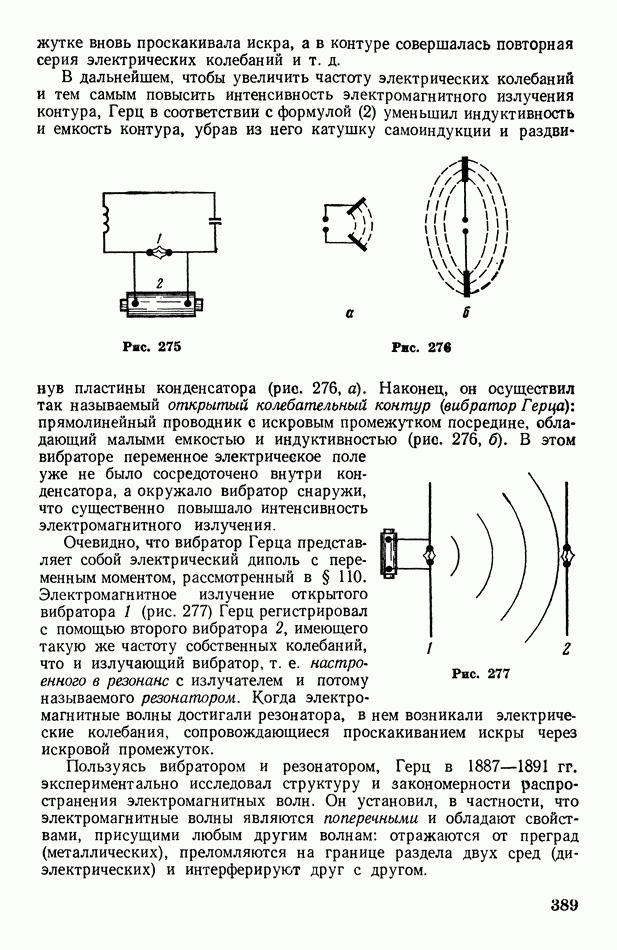
- § 111. Закрытый колебательный контур
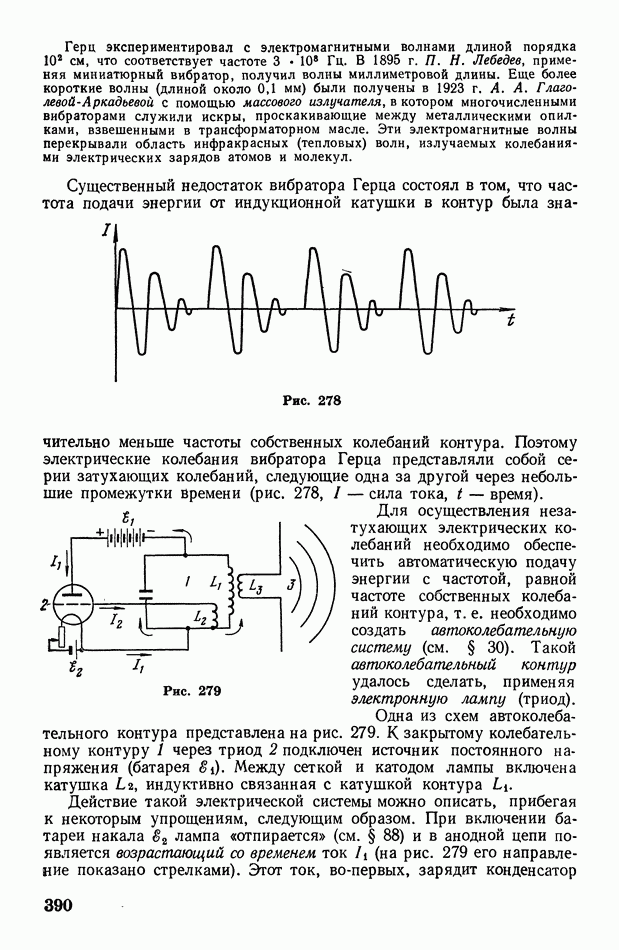
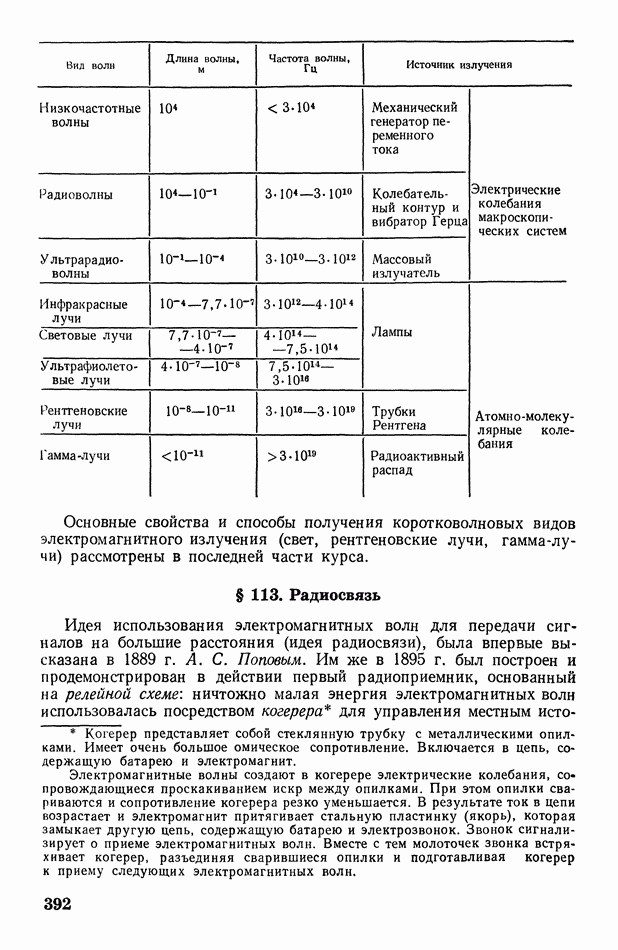
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
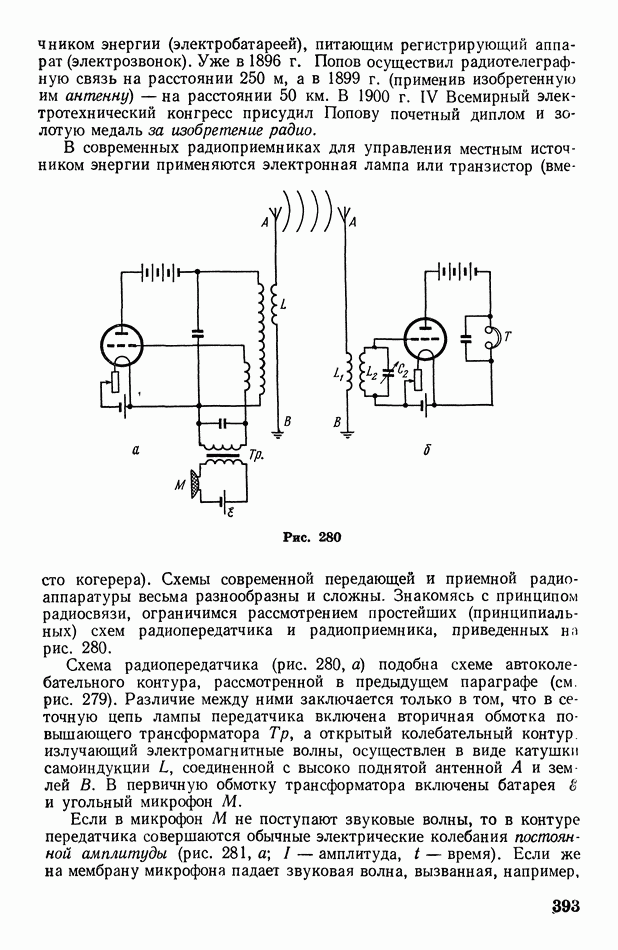
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
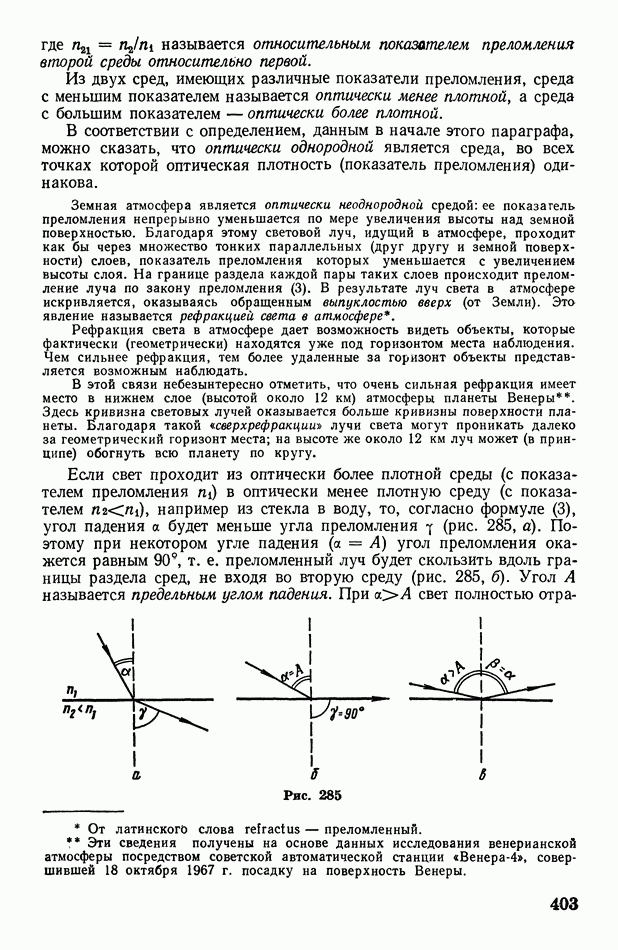
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
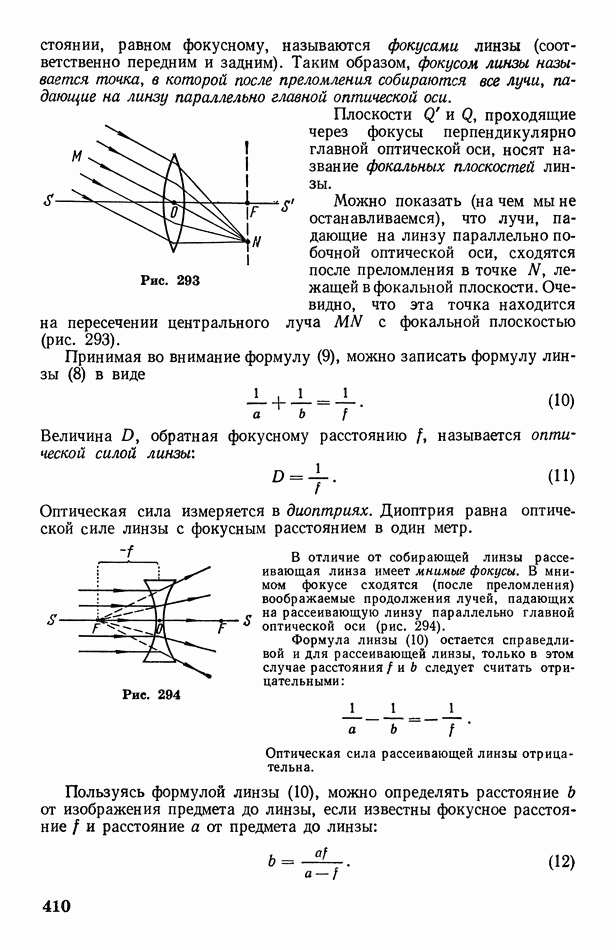
- § 117. Тонкие линзы. Микроскоп
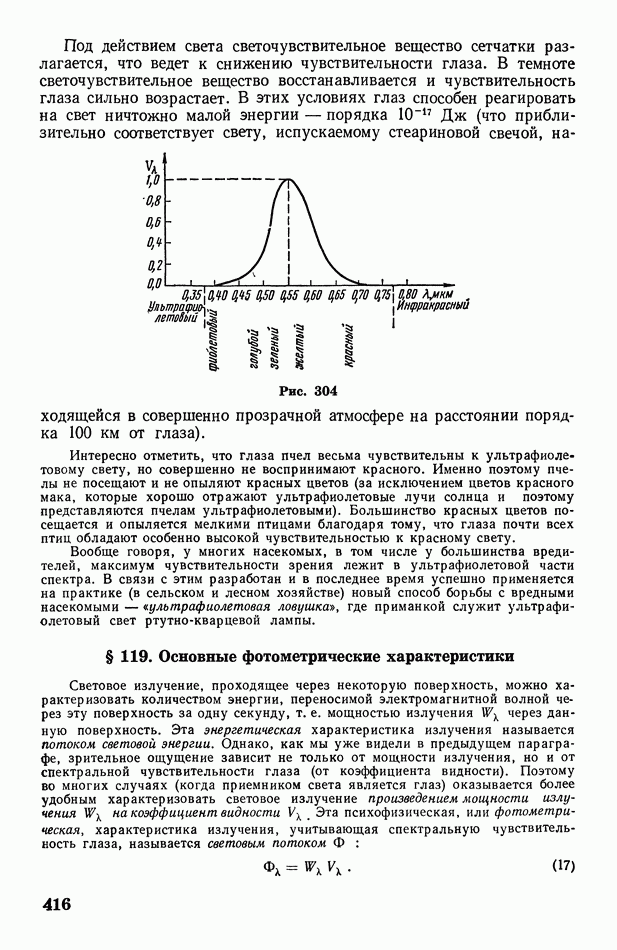
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
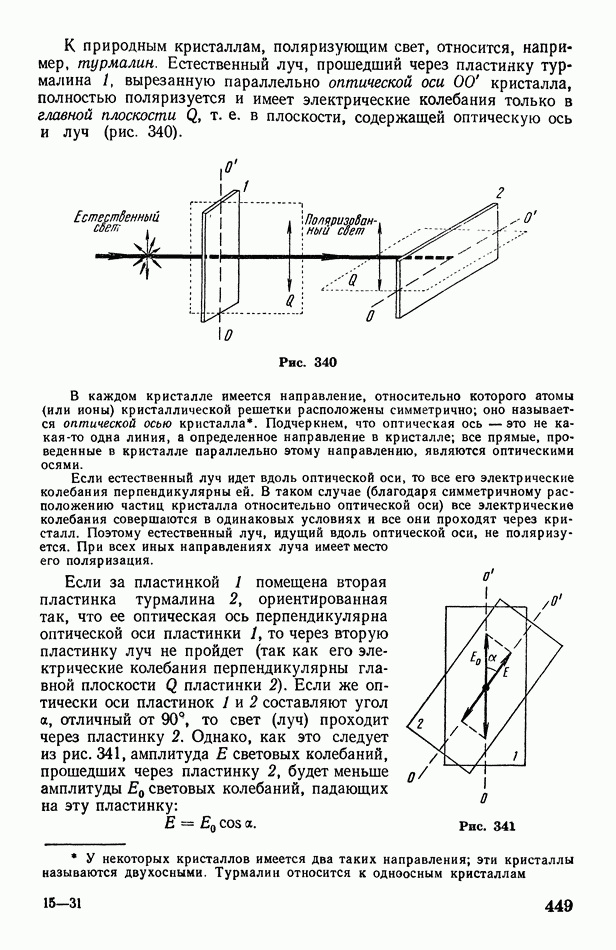
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
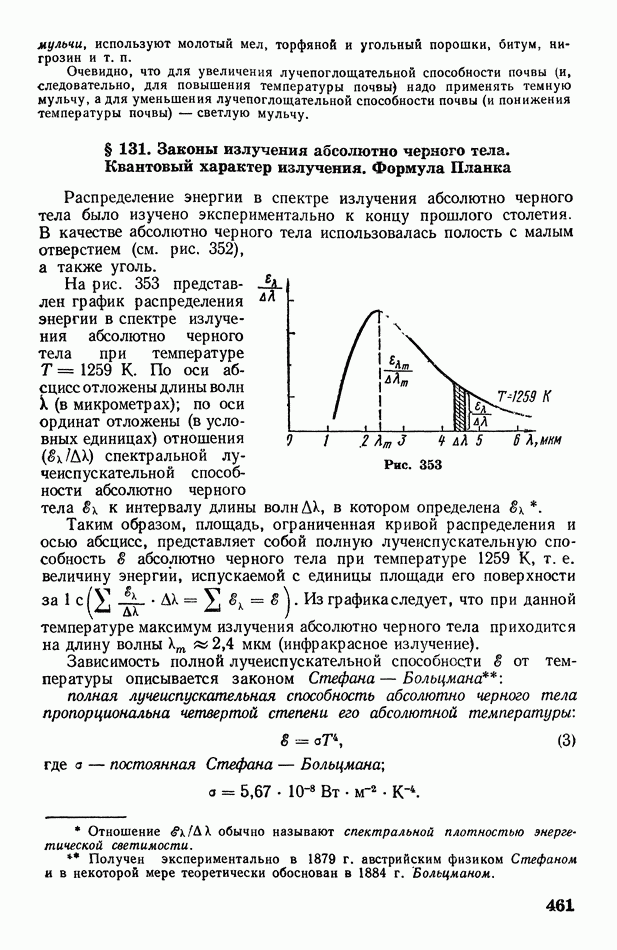
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
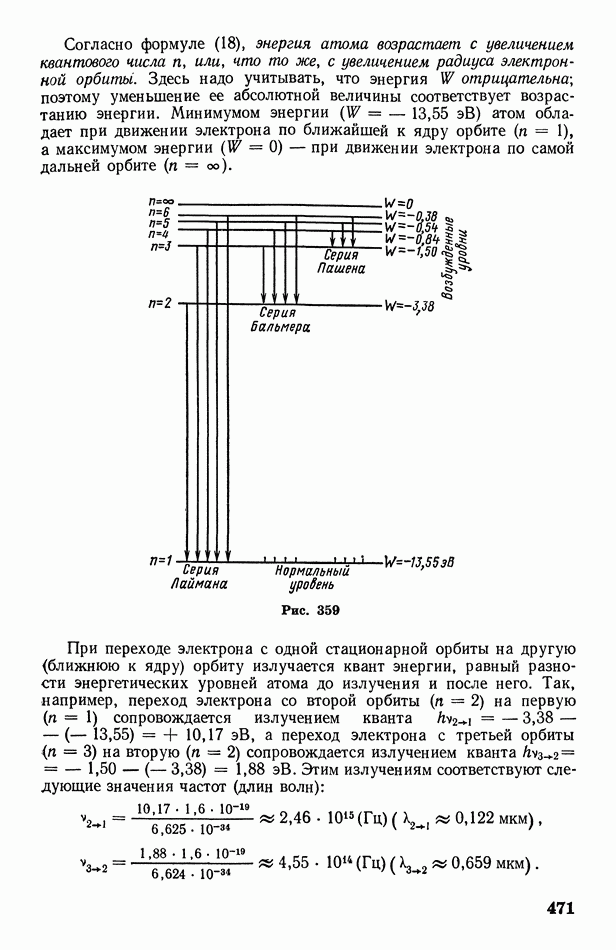
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
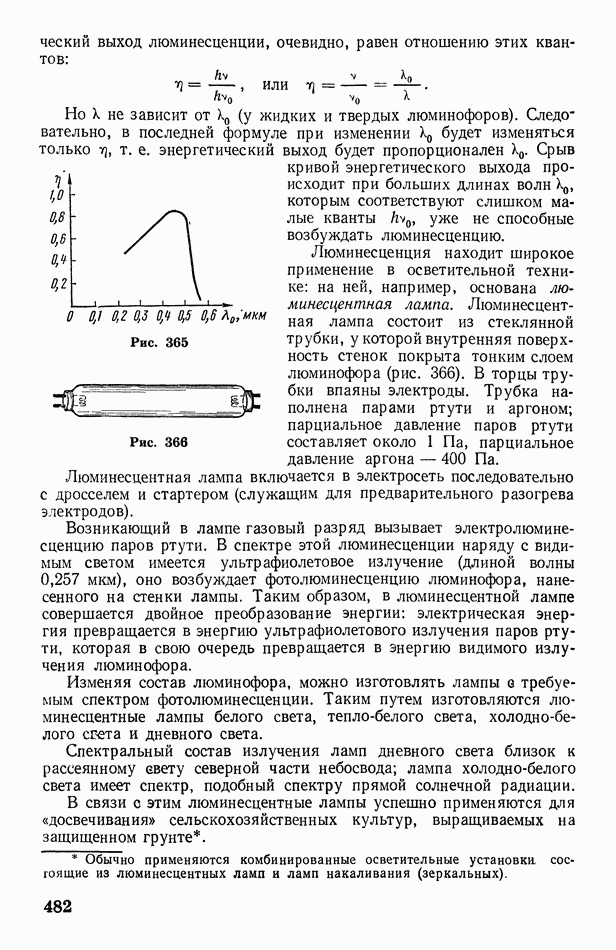
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
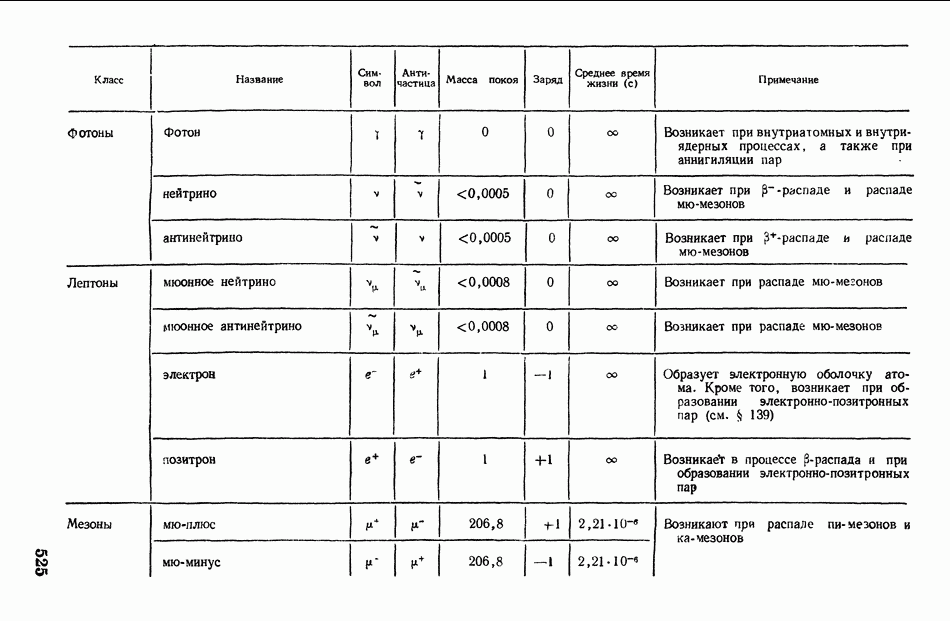
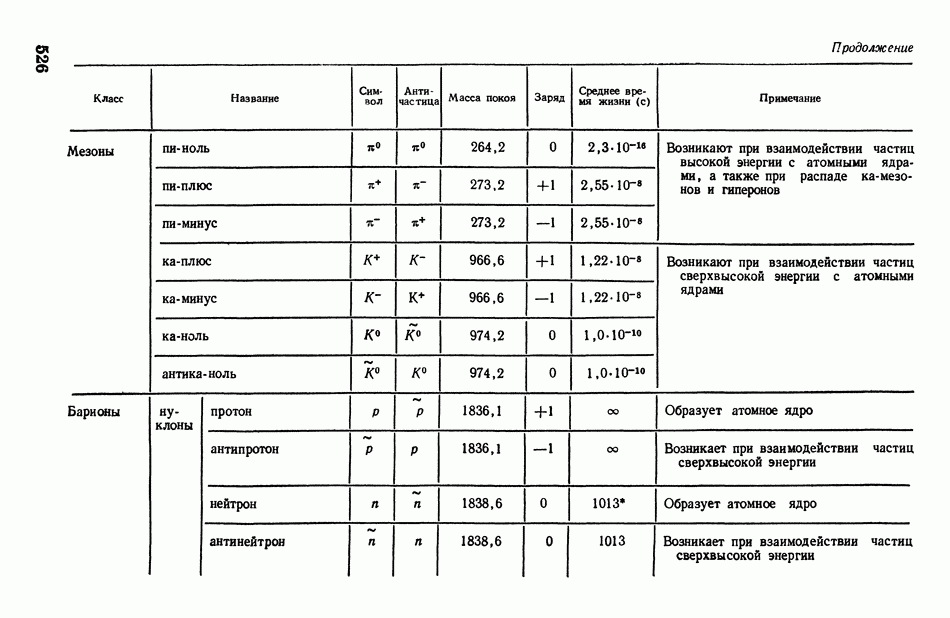
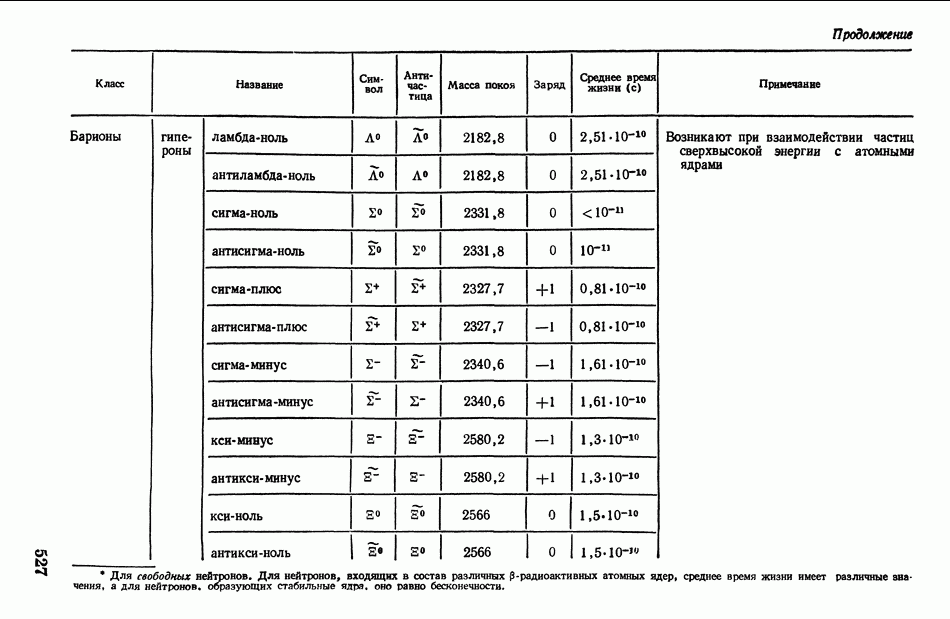
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии