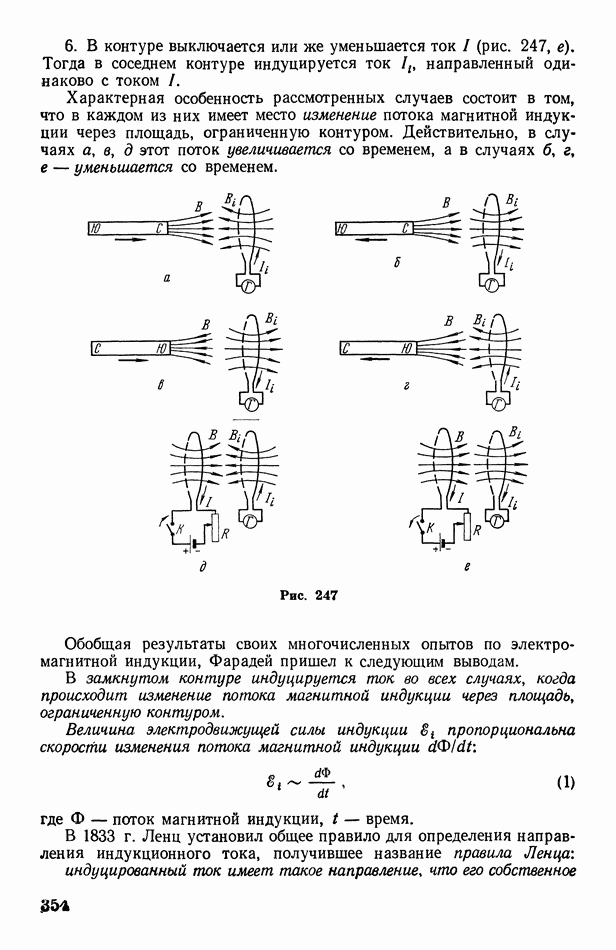
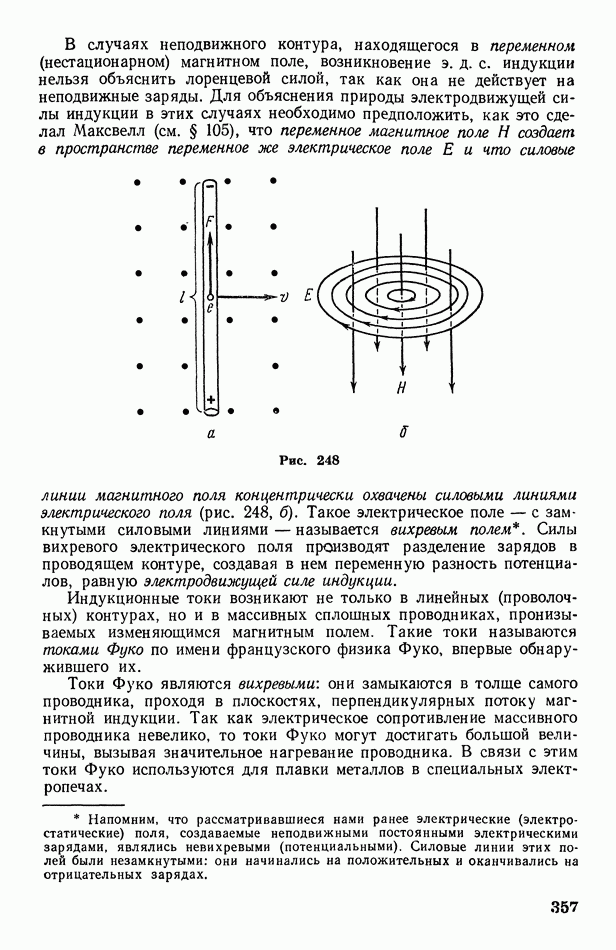
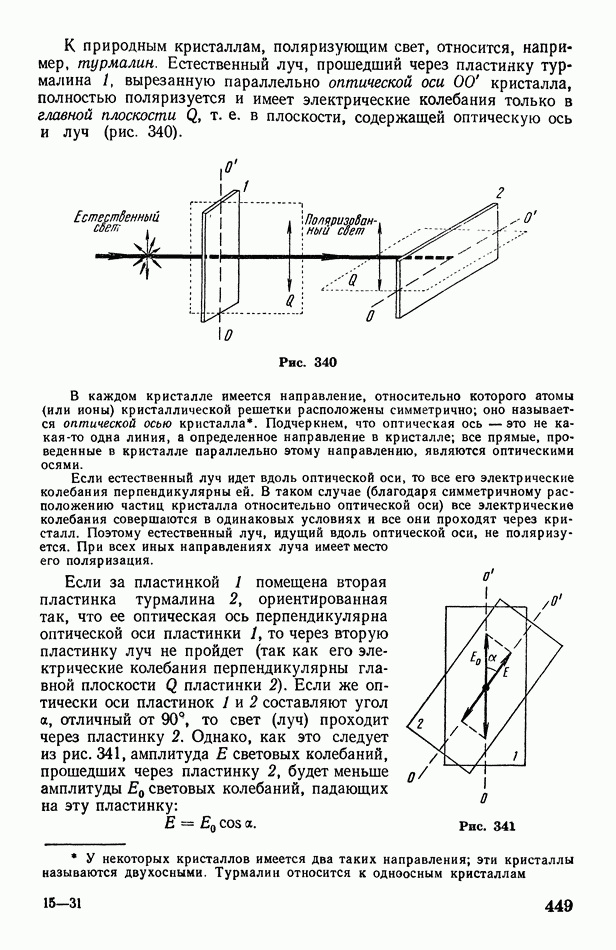
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
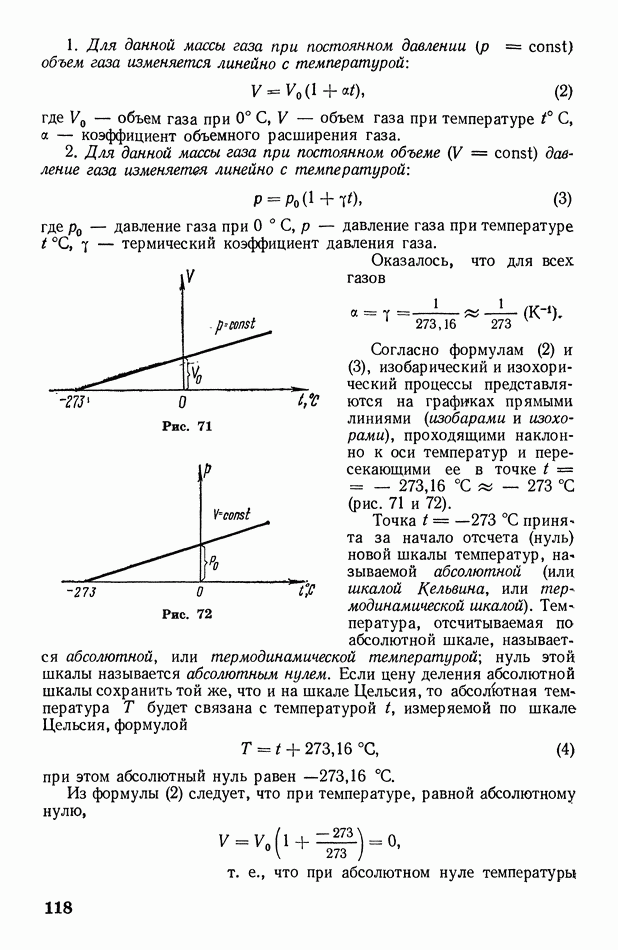
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 34. Фронт волны. Принцип Гюйгенса-Френеля
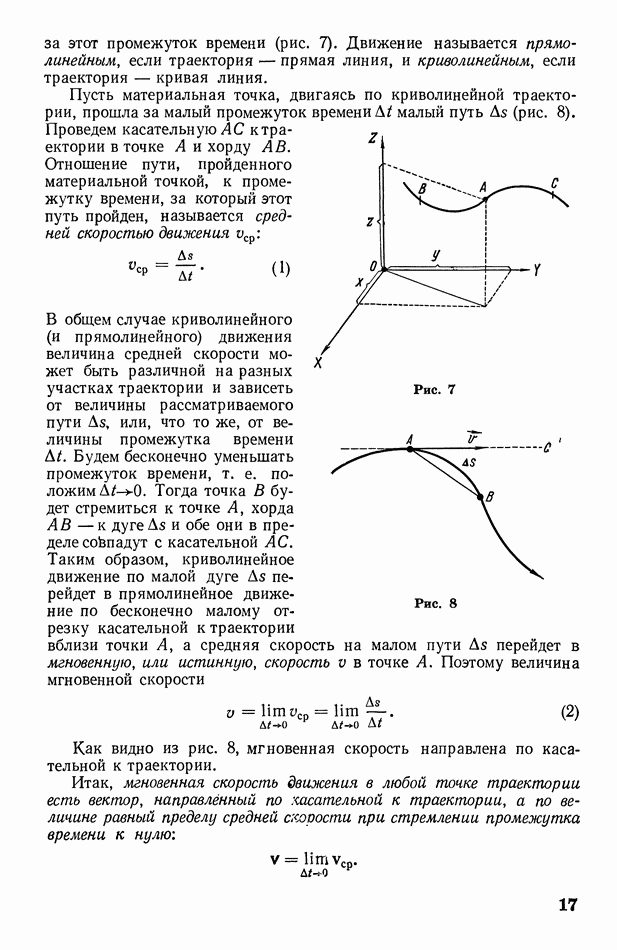
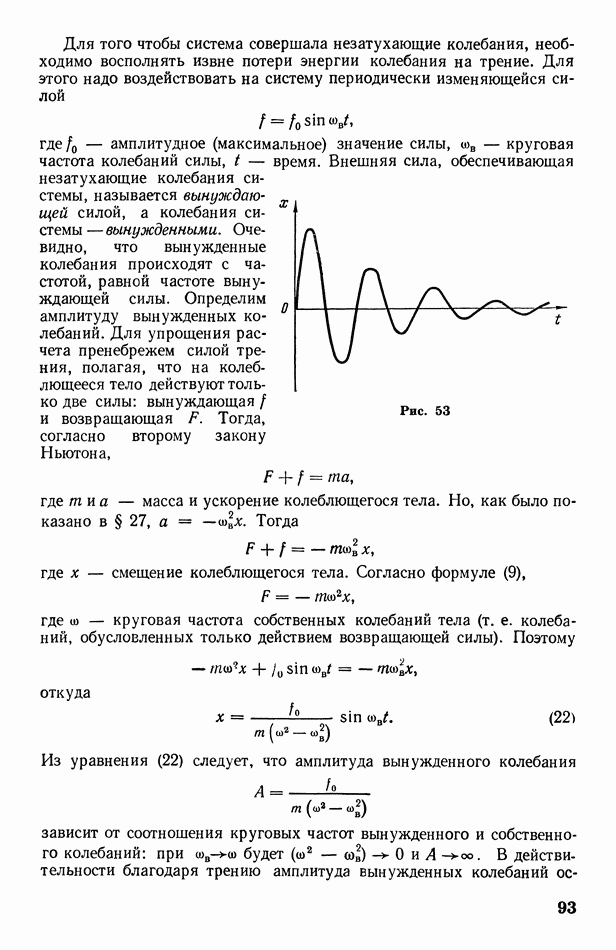
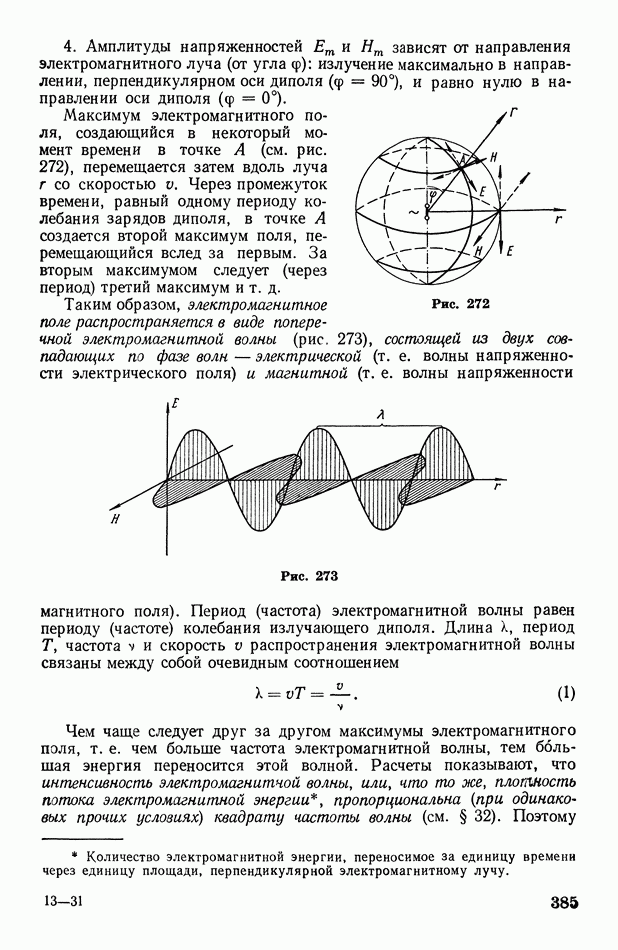
До сих пор мы рассматривали движение волн, происходящее только в некотором определенном направлении (вдоль одной линии). Это имеет место, например, в стержнях, воздушных столбах, волноводах и т. п. Вообще же от источника колебаний, находящегося в сплошной среде, волны распространяются во всех направлениях. Поверхность, до которой одновременно доходят волны от данного источника колебаний, называется фронтом волны. Форма волнового фронта зависит от формы источника колебаний и свойств среды. При точечном источнике колебаний  волновой фронт в однородной среде имеет форму сферы; лучи, являющиеся радиусами
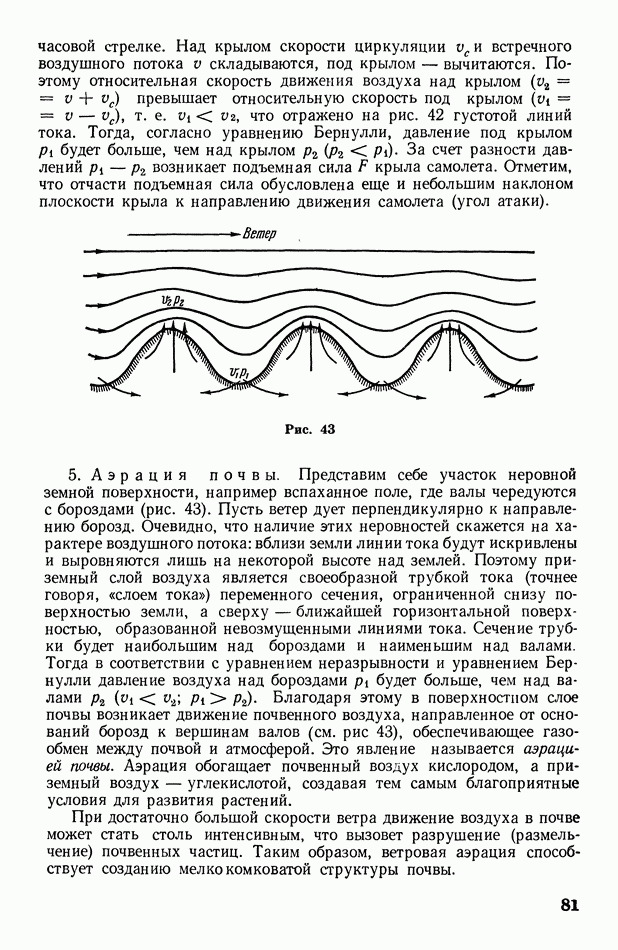
волновой фронт в однородной среде имеет форму сферы; лучи, являющиеся радиусами  этой сферы, перпендикулярны к
этой сферы, перпендикулярны к
волновому фронту (рис. 63, а). Очевидно, что

где  скорость волны,
скорость волны,  время ее распространения. Волны, образующие сферический фронт, называются сферическими. Сферический волновой фронт является (в изотропной среде) вместе с тем фазовой, или волновой поверхностью, т. е. поверхностью, все точки которой колеблются в одинаковой фазе.
время ее распространения. Волны, образующие сферический фронт, называются сферическими. Сферический волновой фронт является (в изотропной среде) вместе с тем фазовой, или волновой поверхностью, т. е. поверхностью, все точки которой колеблются в одинаковой фазе.
Если фронт волны представляет собой плоскость, то волна называется плоской. В этом случае лучи параллельны между собой (рис.
63, б). Небольшой участок сферического волнового фронта, находящегося на достаточном удалении от источника колебаний, можно практически считать плоским (пренебрегая кривизной фронта).

Рис. 63
В неоднородной среде, где скорость волны неодинакова в различных направлениях, волновой фронт может иметь весьма сложную форму.
Если не учитывать затухания, то интенсивность плоской волны не будет изменяться по мере удаления волнового фронта от источника колебаний, так как площадь фронта остается в этом случае постоянной.
Иначе обстоит дело с интенсивностью сферической волны. Энергия колебания  переносимая в единицу времени через всю площадь
переносимая в единицу времени через всю площадь  волнового фронта, остается, согласно закону сохранения энергии, постоянной. Но
волнового фронта, остается, согласно закону сохранения энергии, постоянной. Но  возрастает по мере удаления фронта от источника колебаний пропорционально квадрату расстояния у, так как
возрастает по мере удаления фронта от источника колебаний пропорционально квадрату расстояния у, так как  Поэтому
Поэтому

т. е. интенсивность сферической волны изменяется обратно пропорционально квадрату расстояния фронта от источника колебаний. Так как, согласно формуле (26), интенсивность волны пропорциональна квадрату амплитуды  то
то  т. е. амплитуда сферической волны обратно пропорциональна расстоянию волнового фронта от источника колебаний. Тогда, заменяя в формуле (25) А на
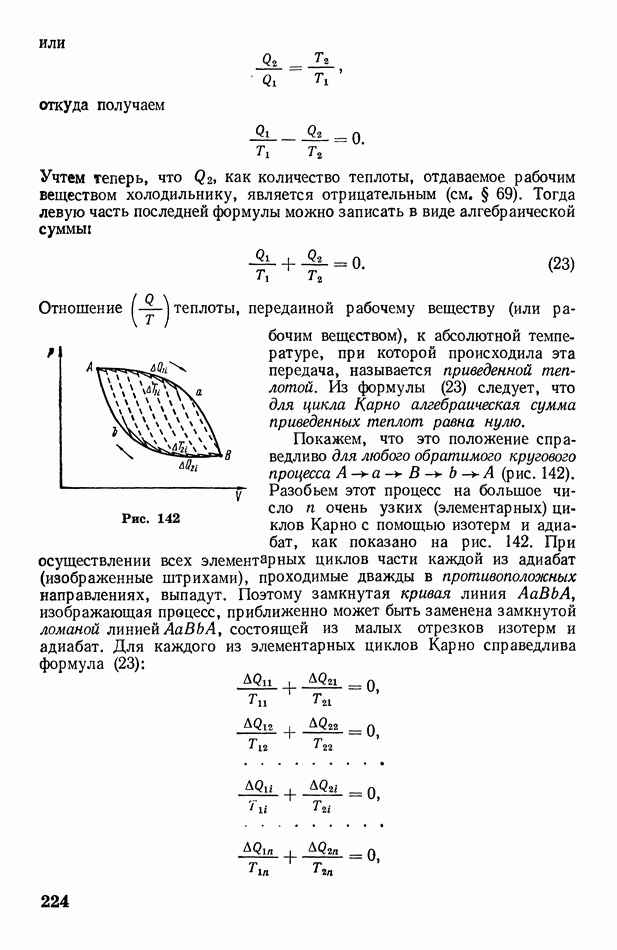
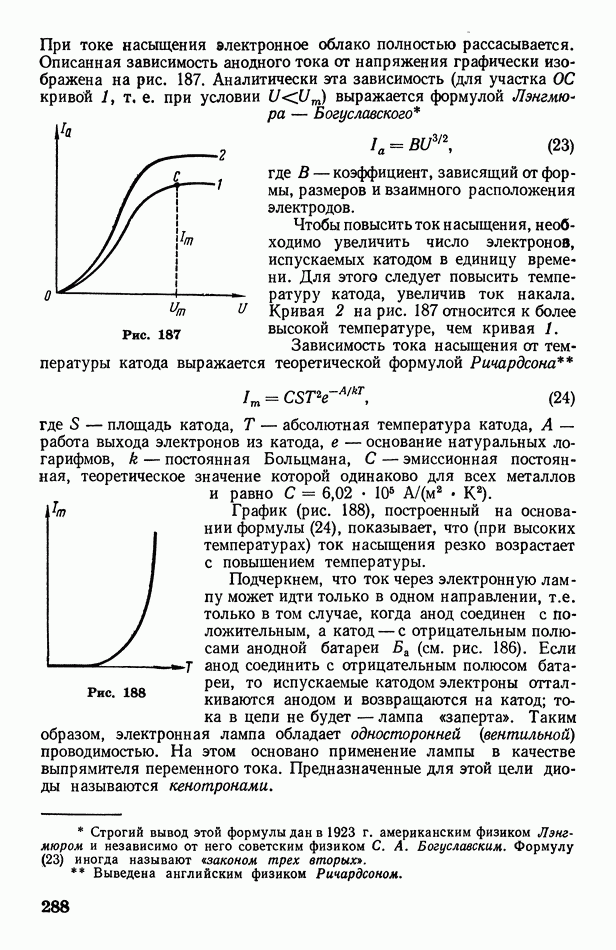
т. е. амплитуда сферической волны обратно пропорциональна расстоянию волнового фронта от источника колебаний. Тогда, заменяя в формуле (25) А на  получим следующее уравнение сферической волны:
получим следующее уравнение сферической волны:

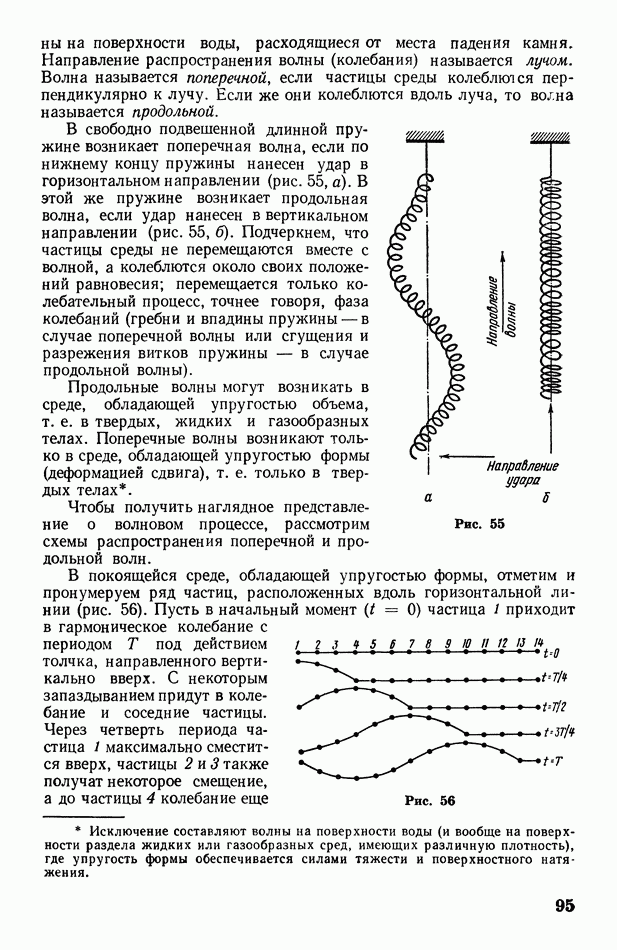
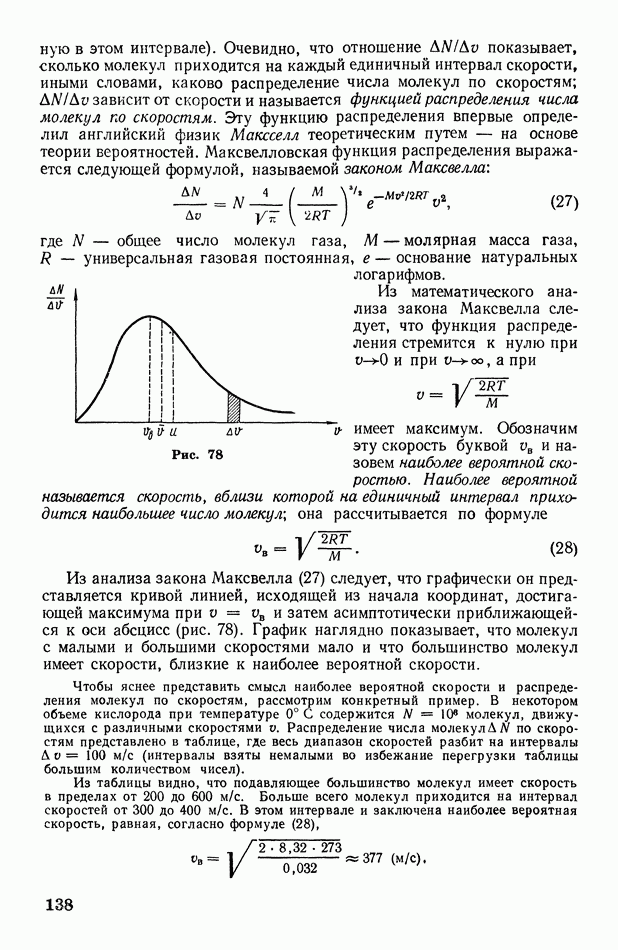
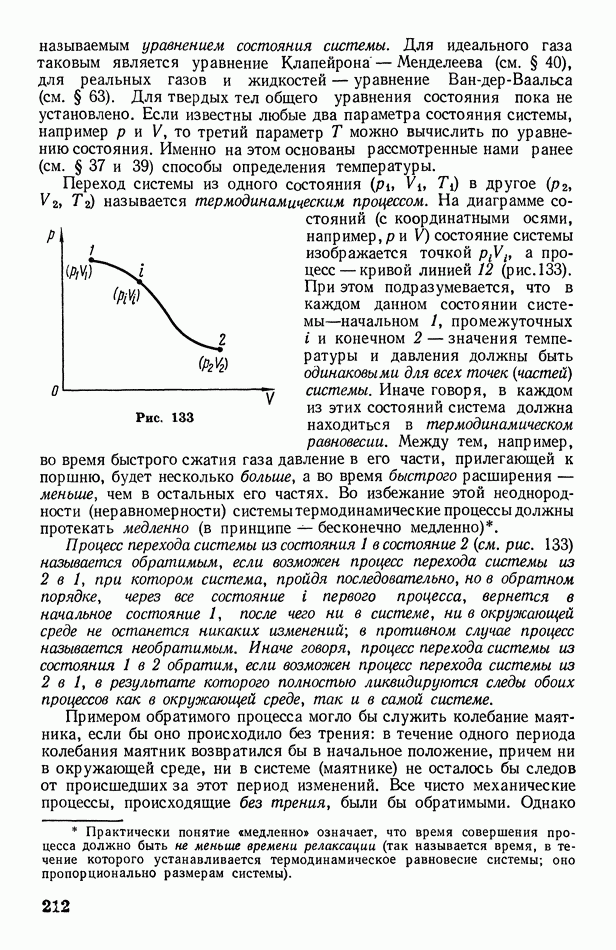
При решении задач о распространении волн зачастую бывает необходимо построить волновой фронт для некоторого момента времени по волновому фронту, заданному для начального момента времени. Это можно сделать с помощью метода, называемого принципом Гюйгенса, сущность которого состоит в следующем.
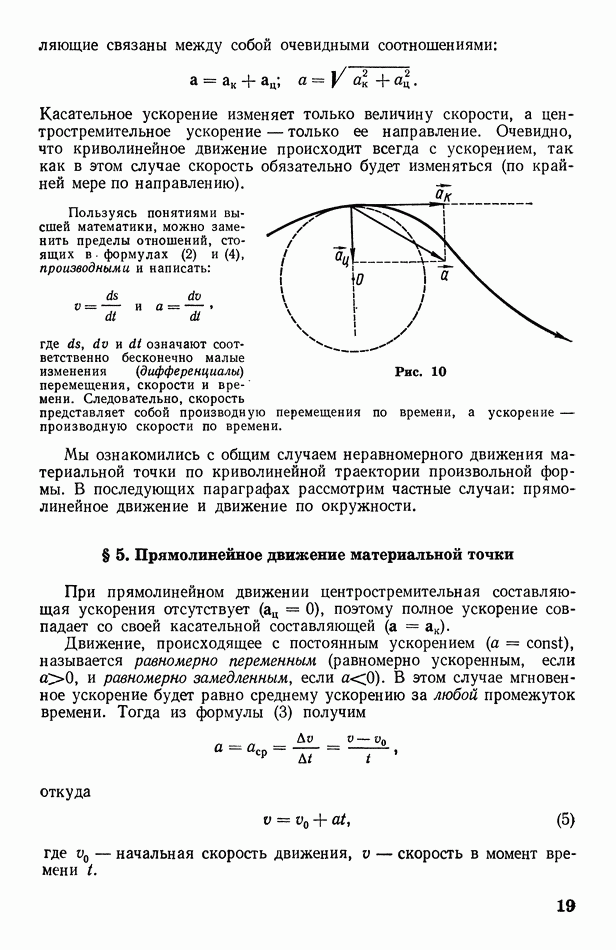
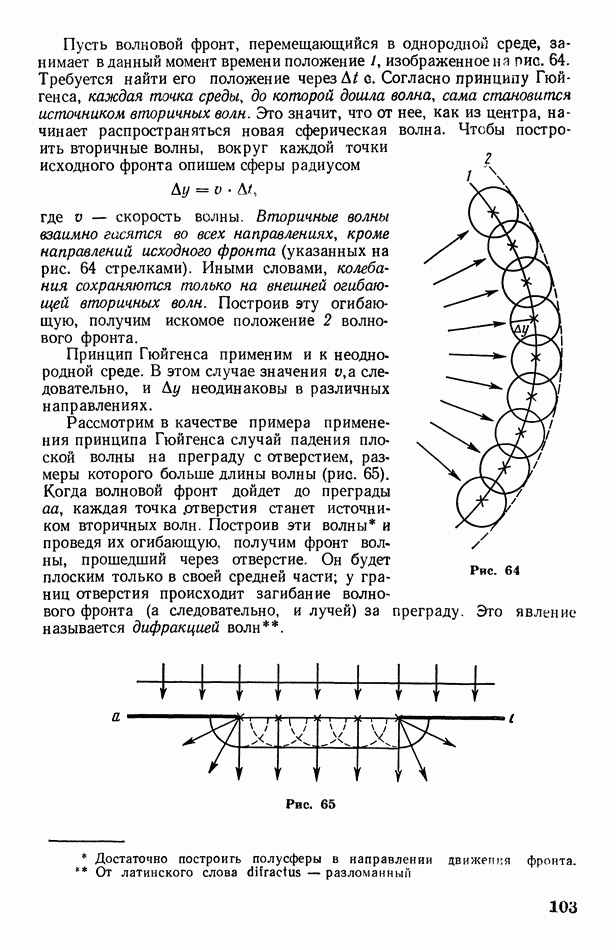
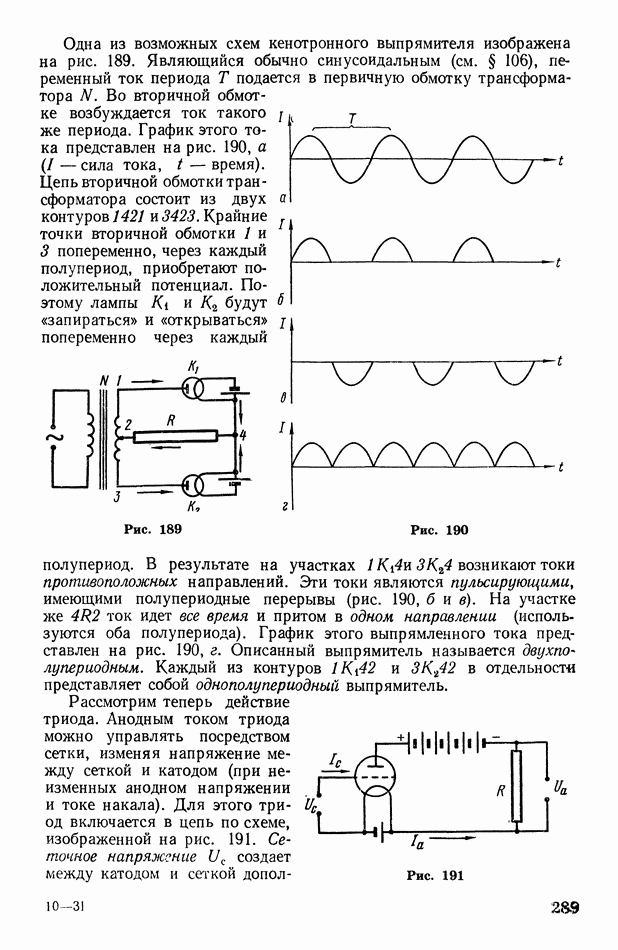
Пусть волновой фронт, перемещающийся в однородной среде, занимает в данный момент времени положение У, изображенное на рис. 64. Требуется найти его положение через  Согласно принципу Гюйгенса, каждая точка среды, до которой дошла волна, сама становится источником вторичных волн. Это значит, что от нее, как из центра, начинает распространяться новая сферическая волна. Чтобы построить вторичные волны, вокруг каждой точки исходного фронта опишем сферы радиусом
Согласно принципу Гюйгенса, каждая точка среды, до которой дошла волна, сама становится источником вторичных волн. Это значит, что от нее, как из центра, начинает распространяться новая сферическая волна. Чтобы построить вторичные волны, вокруг каждой точки исходного фронта опишем сферы радиусом

где  скорость волны. Вторичные волны взаимно гасятся во всех направлениях, кроме направлений исходного фронта (указанных на рис. 64 стрелками). Иными словами, колебания сохраняются только на внешней огибающей вторичных волн. Построив эту огибающую, получим искомое положение 2 волнового фронта.
скорость волны. Вторичные волны взаимно гасятся во всех направлениях, кроме направлений исходного фронта (указанных на рис. 64 стрелками). Иными словами, колебания сохраняются только на внешней огибающей вторичных волн. Построив эту огибающую, получим искомое положение 2 волнового фронта.
Принцип Гюйгенса применим и к неоднородной среде. В этом случае значения  а следовательно, и
а следовательно, и  неодинаковы в различных направлениях.
неодинаковы в различных направлениях.
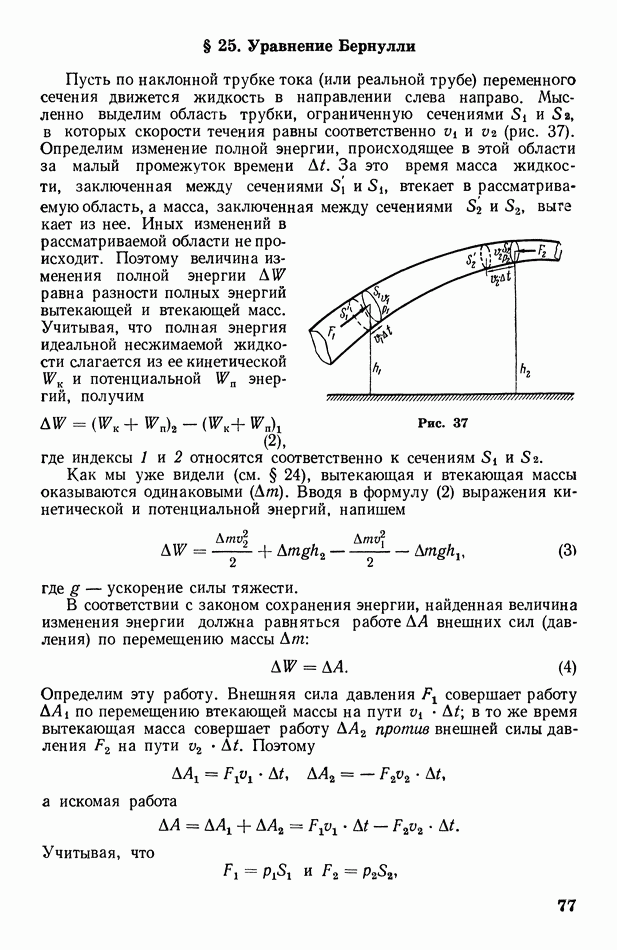
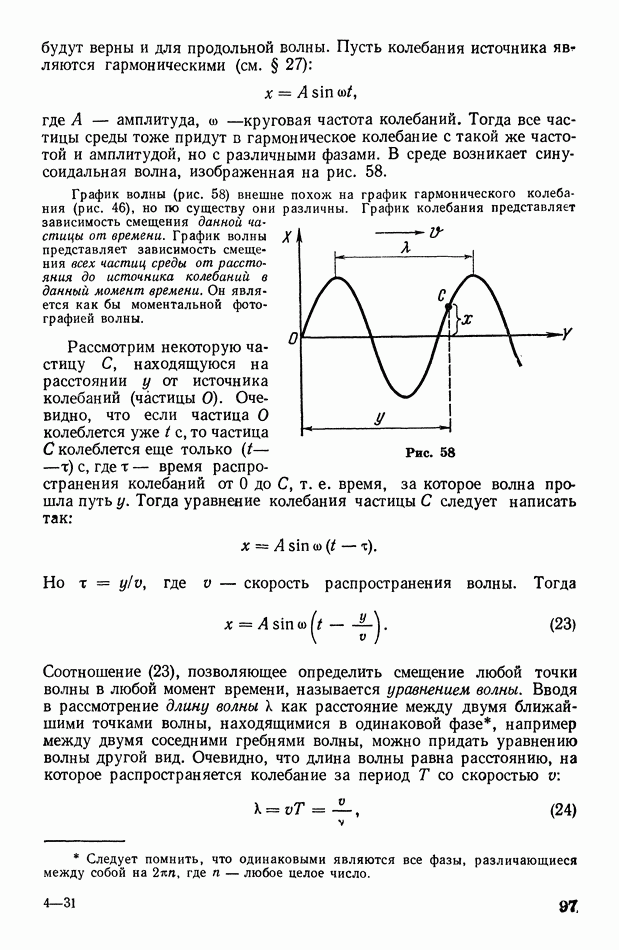
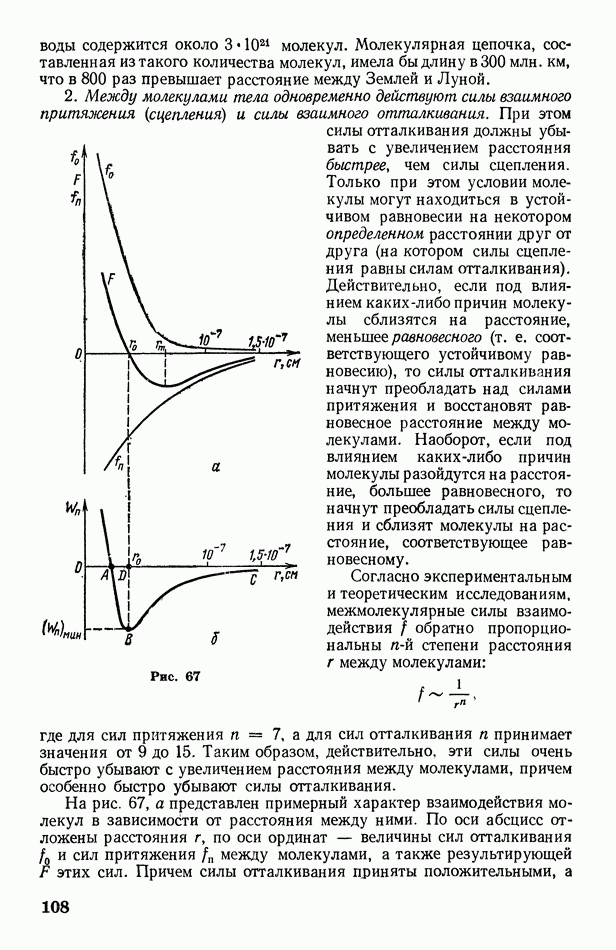
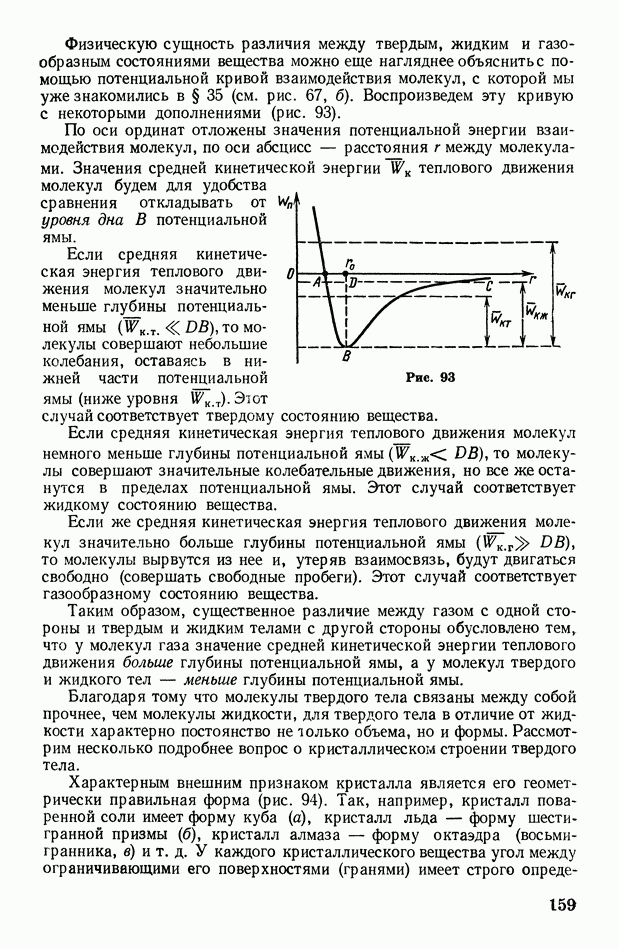
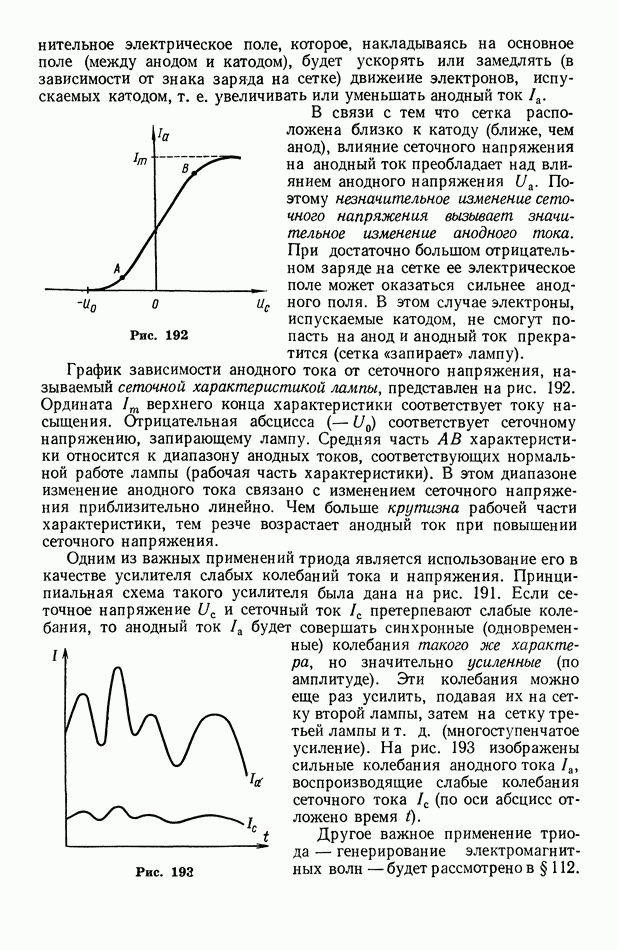
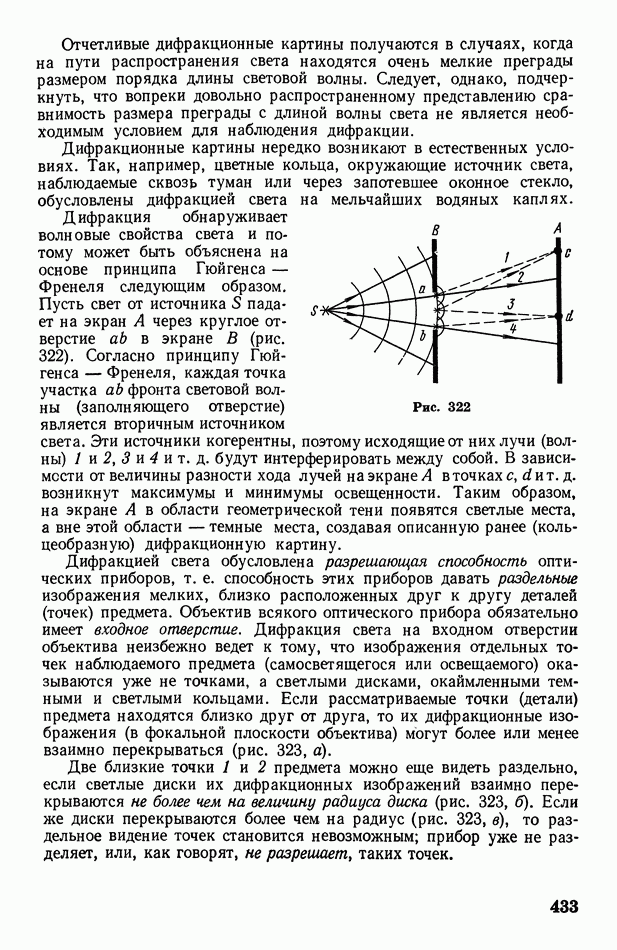
Рассмотрим в качестве примера применения принципа Гюйгенса случай падения плоской волны на преграду с отверстием, размеры которого больше длины волны (рис. 65). Когда волновой фронт дойдет до преграды  каждая точка отверстия станет источником вторичных волн. Построив эти волны и проведя их огибающую, получим фронт волны, прошедший через отверстие. Он будет плоским только в своей средней части; у границ отверстия происходит загибание волнового фронта (а следовательно, и лучей) за преграду. Это явление называется дифракцией волн.
каждая точка отверстия станет источником вторичных волн. Построив эти волны и проведя их огибающую, получим фронт волны, прошедший через отверстие. Он будет плоским только в своей средней части; у границ отверстия происходит загибание волнового фронта (а следовательно, и лучей) за преграду. Это явление называется дифракцией волн.

Рис. 64

Рис. 65
Однако объяснение дифракции волн, даваемое принципом Гюйгенса, является неполным, так как он ничего не говорит об амплитудах волн, распространяющихся в различных направлениях, и, следовательно оставляет открытым вопрос о распределении интенсивности вдоль волнового фронта. Отмеченный недостаток принципа Гюйгенса устранил в 1815 г. французский физик Френель, дополнив этот принцип положением об интерференции вторичных волн.
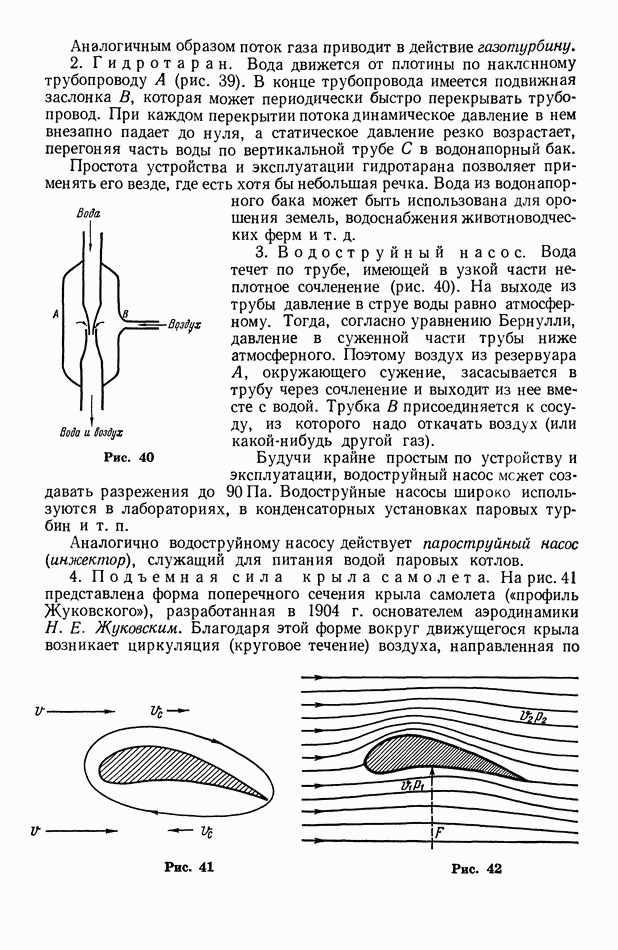
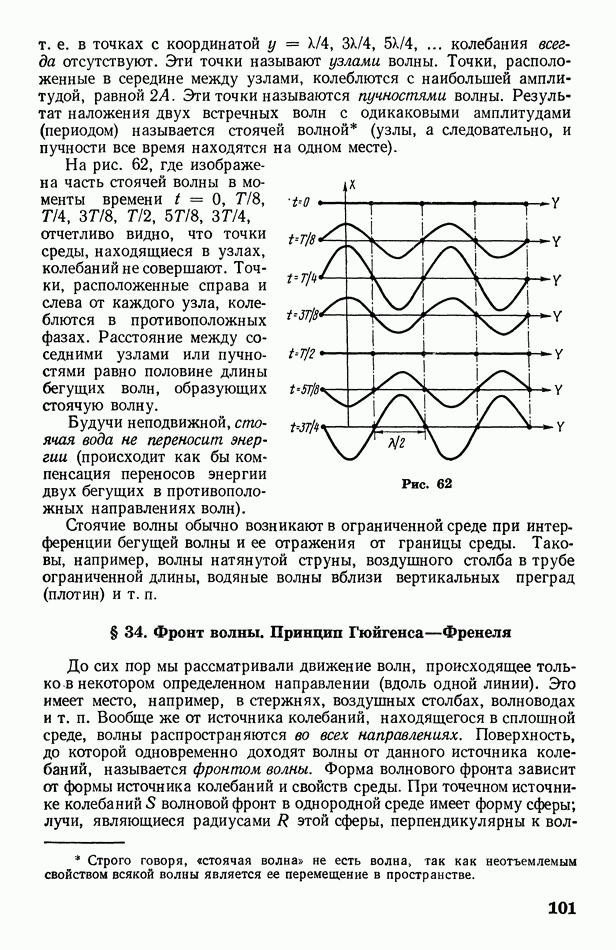
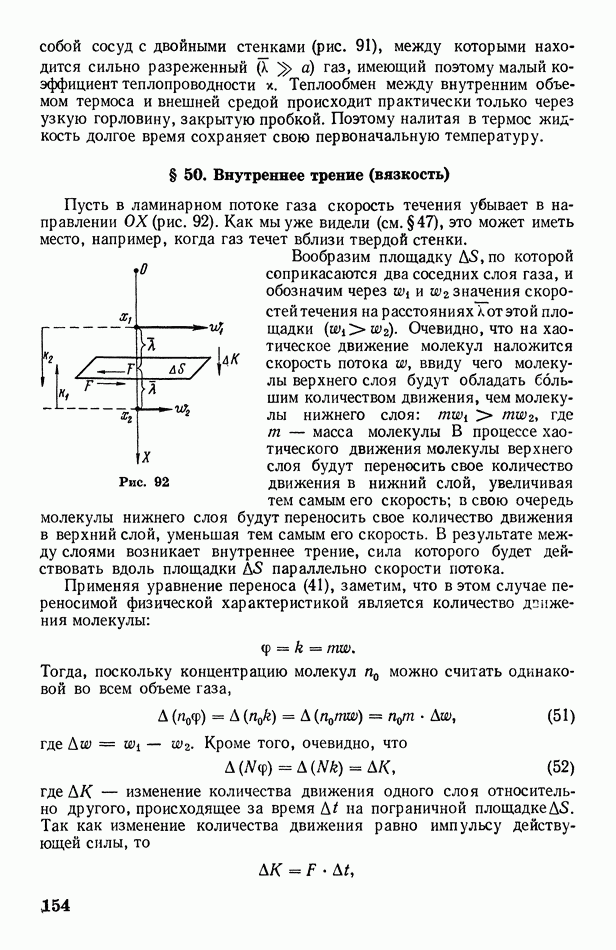
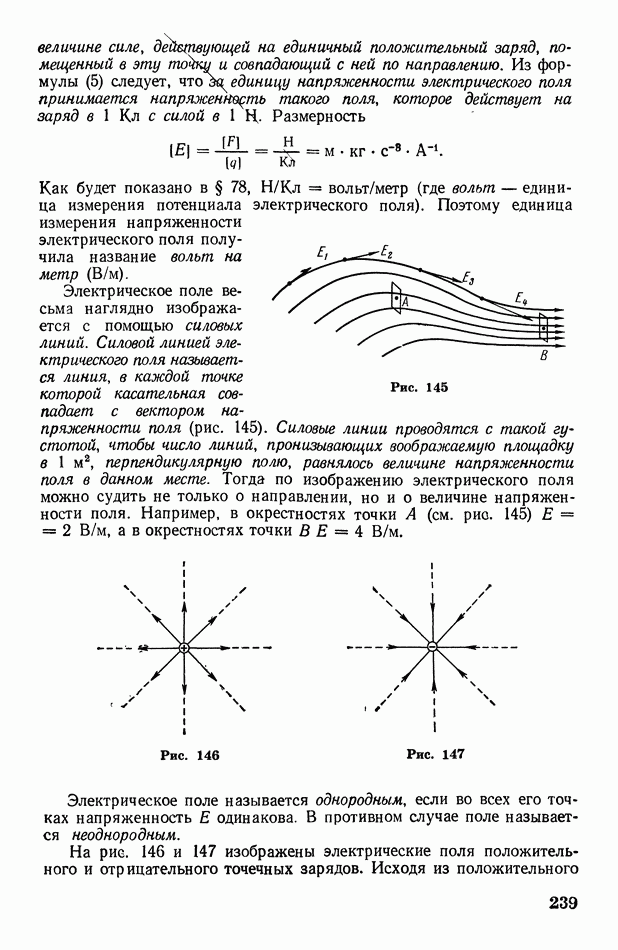
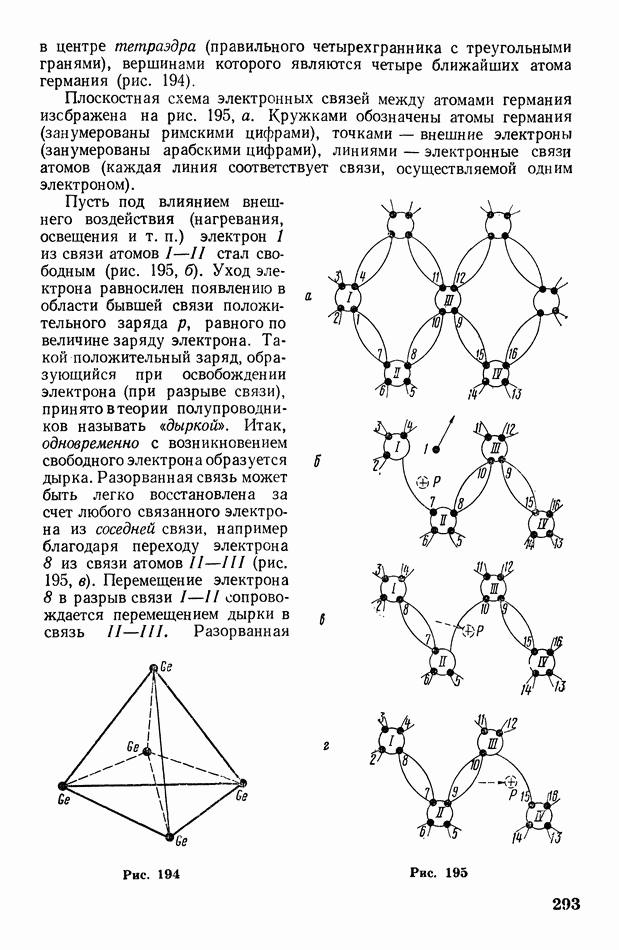
Согласно Френелю, волну, приходящую в любую точку  от первичного источника
от первичного источника  можно рассматривать как результат интерференции вторичных волн, приходящих в эту точку от множества элементарных вторичных источников
можно рассматривать как результат интерференции вторичных волн, приходящих в эту точку от множества элементарных вторичных источников  некоторого волнового фронта
некоторого волнового фронта  (рис. 66). Тогда интенсивность волны в точке
(рис. 66). Тогда интенсивность волны в точке  определится путем суммирования всех вторичных волн (с учетом размера
определится путем суммирования всех вторичных волн (с учетом размера  вторичных источников, их расстояния
вторичных источников, их расстояния  до
до  и угла
и угла  между направлениями
между направлениями  и нормали
и нормали 

Рис. 66
Принцип Гюйгенса с дополнением Френеля получил название принципа Гюйгенса-Френеля и оказался весьма плодотворным для решения многих вопросов о распространении волн. С конкретными применениями принципа Гюйгенса — Френеля к электромагнитным (световым) волнам мы встретимся в последней части курса (см. гл. XVII и XVIII).
Задача 17. Уравнение колебания материальной точки массой  имеет вид —
имеет вид —  Найти: а) максимальные значения скорости
Найти: а) максимальные значения скорости  и ускорения
и ускорения  движения точки; б) значение максимальной силы
движения точки; б) значение максимальной силы  действующей на точку; в) полную энергию
действующей на точку; в) полную энергию  колеблющейся точки.
колеблющейся точки.
Решение. Сравнивая уравнение колебаний данной точки с уравнением гармонического колебания (2а), видим, что амплитуда колебания точки  начальная фаза
начальная фаза  и круговая частота
и круговая частота  где
где  — период колебания точки.
— период колебания точки.
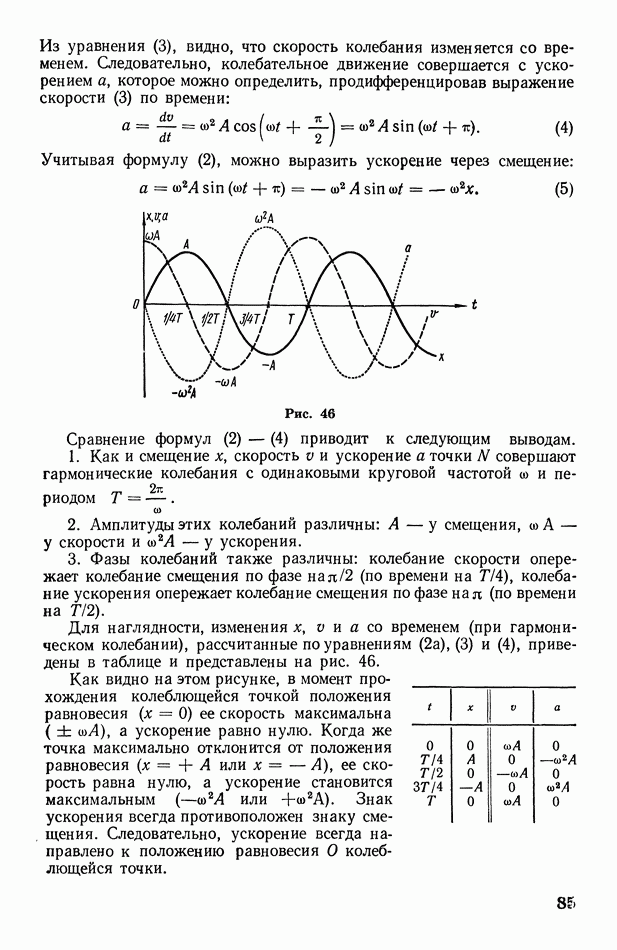
а) Из формул (3) и (4) следует, что скорость и ускорение гармонического колебания точки имеют максимальные значения соответственно при

Поэтому


б) Очевидно, что при максимальном значении ускорения будет иметь место и максимальное значение силы, действующей на точку. Поэтому, согласно второму закону Ньютона,

в) Полную энергию колеблющейся точки найдем по формуле 

Задача 18. Найти амплитуду В и начальную фазу  гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями:
гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями:

Решение. Амплитуды и начальные фазы слагаемых колебаний соответственно равны: 
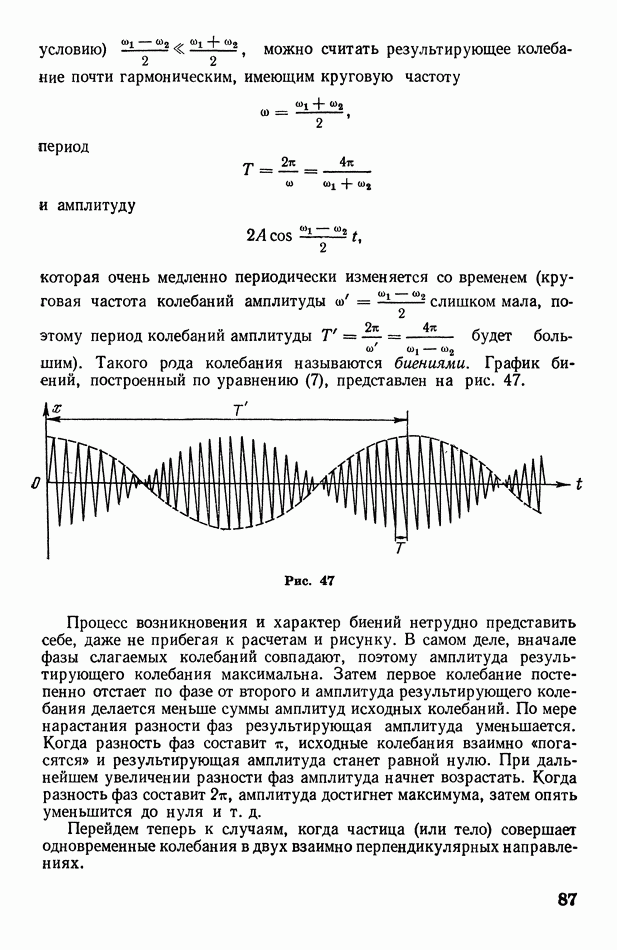
Условия задачи соответствуют случаю сложения колебаний одного направления, имеющих одинаковые круговые частоты и амплитуды, но различные фазы (см. § 28). Поэтому начальная фаза результирующего колебания должна отличаться от начальных фаз слагаемых колебаний на половину разности последних, т. е.

Тогда амплитуда результирующего колебания

Задача 19. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, заданных уравнениями

Определить траекторию движения точки.
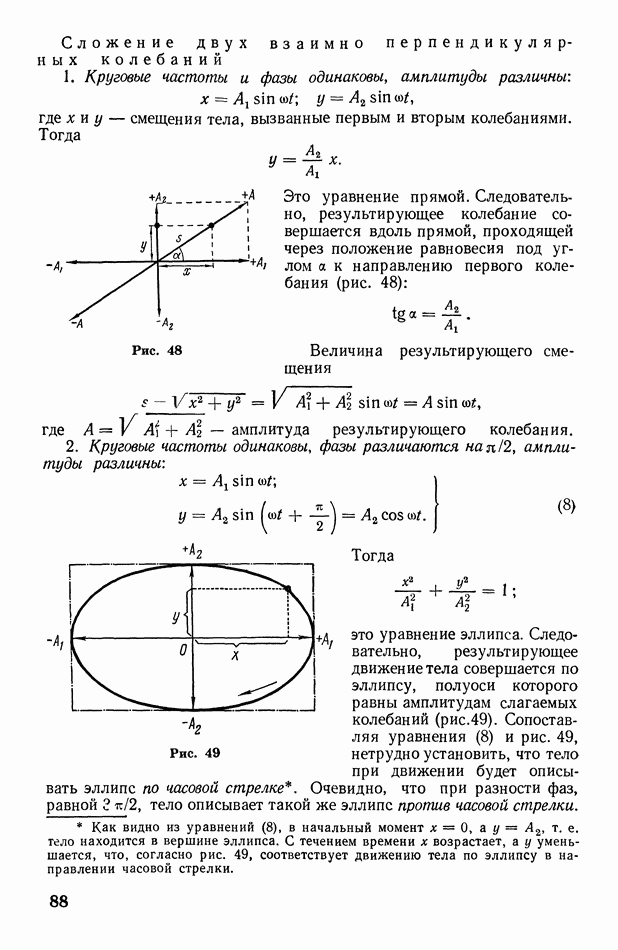
Решение. Уравнение второго колебания перепишем в виде  Тогда станет очевидным, что условия задачи соответствуют случаю сложения двух взаимно перпендикулярных колебаний, имеющих одинаковые круговые частоты, различные амплитуды
Тогда станет очевидным, что условия задачи соответствуют случаю сложения двух взаимно перпендикулярных колебаний, имеющих одинаковые круговые частоты, различные амплитуды  и различающиеся на
и различающиеся на  начальные фазы (см. § 28). Поэтому в соответствии с формулами (8) точка движется по эллипсу, определяемому уравнением
начальные фазы (см. § 28). Поэтому в соответствии с формулами (8) точка движется по эллипсу, определяемому уравнением

(см. также рис. 49). Полуоси эллипса равны амплитудам слагаемых колебаний, т. е. 
Задача 20. Вдоль упругого шнура распространяется поперечная волна со скоростью  Период колебаний точек шнура
Период колебаний точек шнура  с, амплитуда колебаний
с, амплитуда колебаний  Определить: а) длину волны X и б) фазу
Определить: а) длину волны X и б) фазу  и
и
смещение х точки, отстоящей на расстоянии  от источника волн в момент времени
от источника волн в момент времени 
Решение, а) По формуле (24) находим длину волны:

б) Фазу и смещение заданной точки определим из уравнения волны (25):

Так как фаза определяется выражением, находящимся под знаком синуса в уравнении волны, то

Тогда

Знак минус показывает, что в заданный момент времени точка шнура отклонялась книзу от положения равновесия (см. рис. 58).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
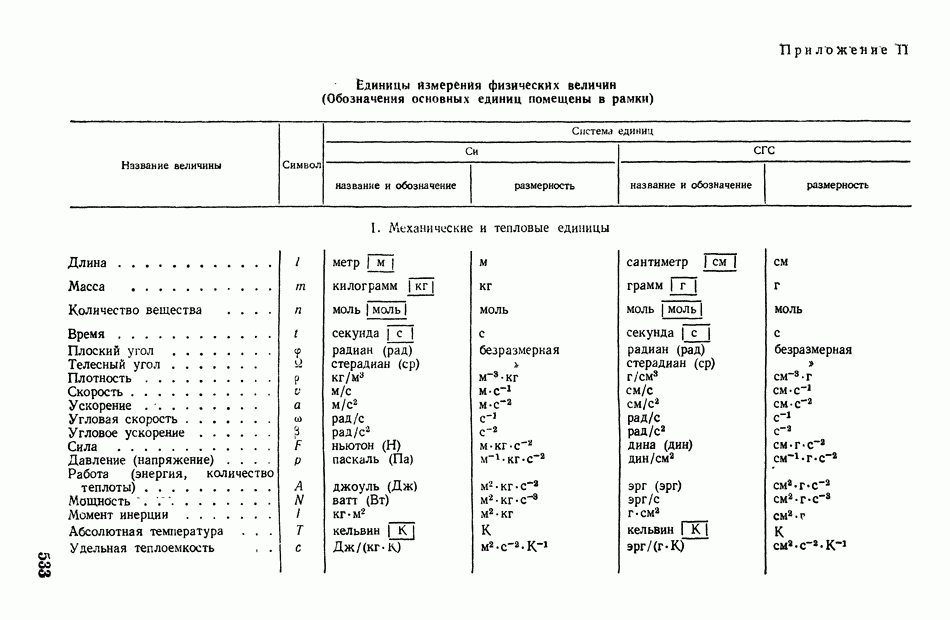
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
- § 30. О затухающих и вынужденных колебаниях
- § 31. Волновой процесс
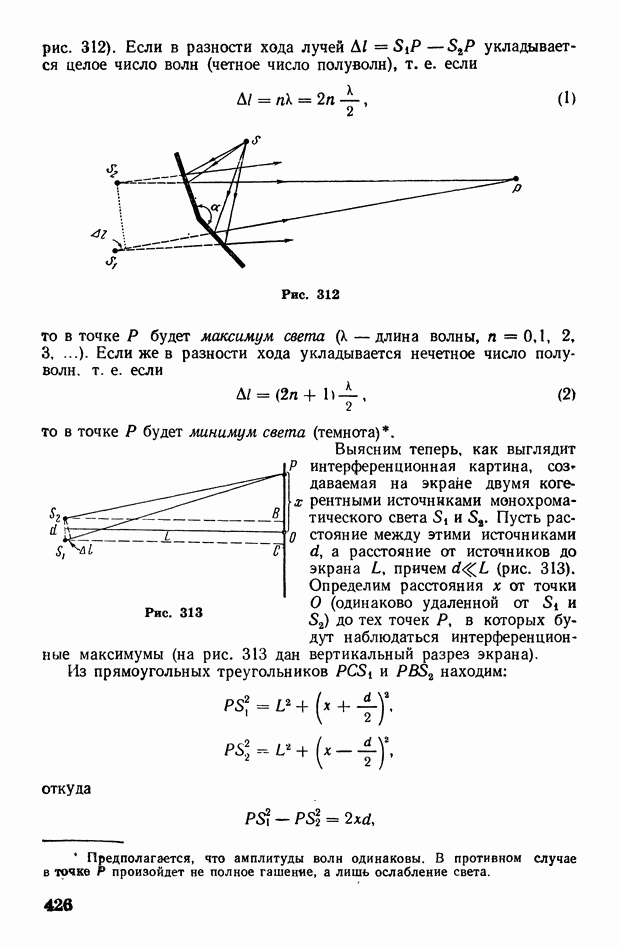
- § 32. Уравнение волны. Интенсивность волны
- § 33. Интерференция волн. Стоячие волны
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
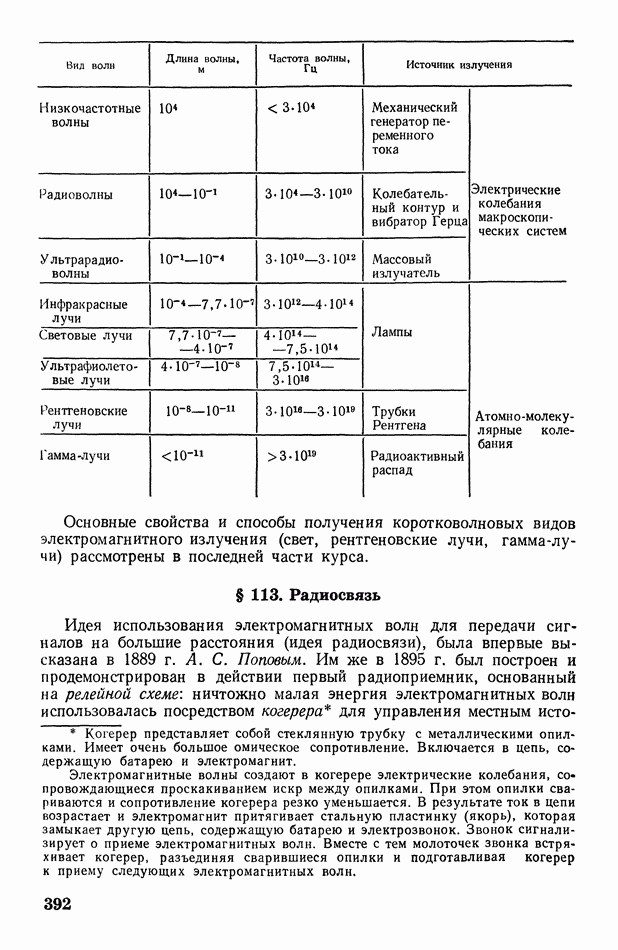
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
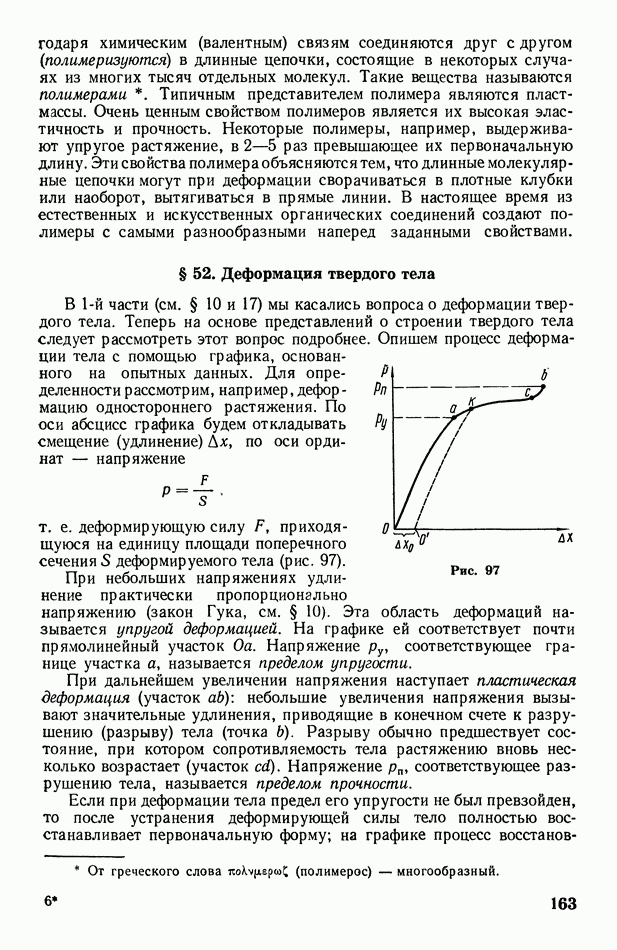
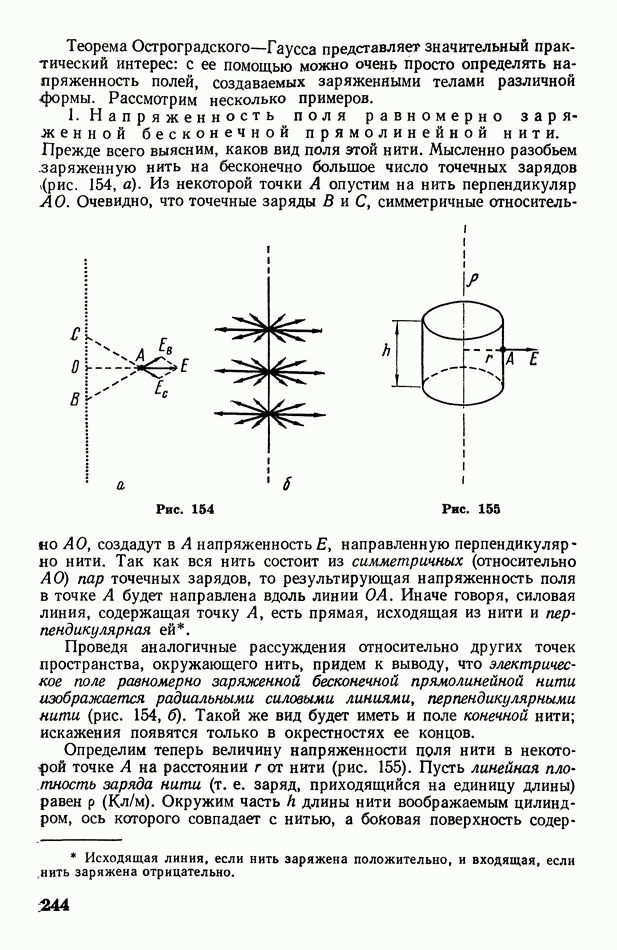
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
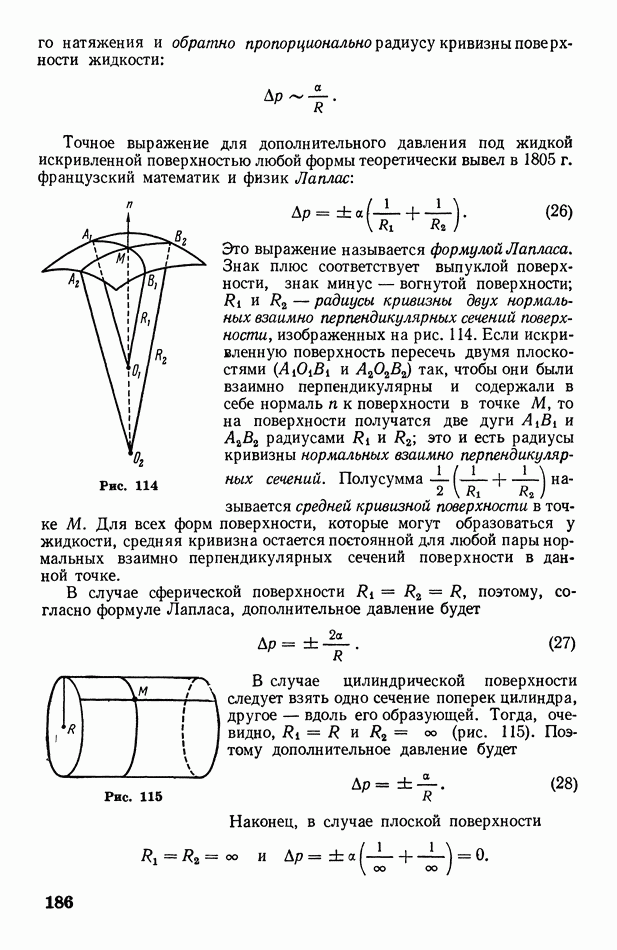
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
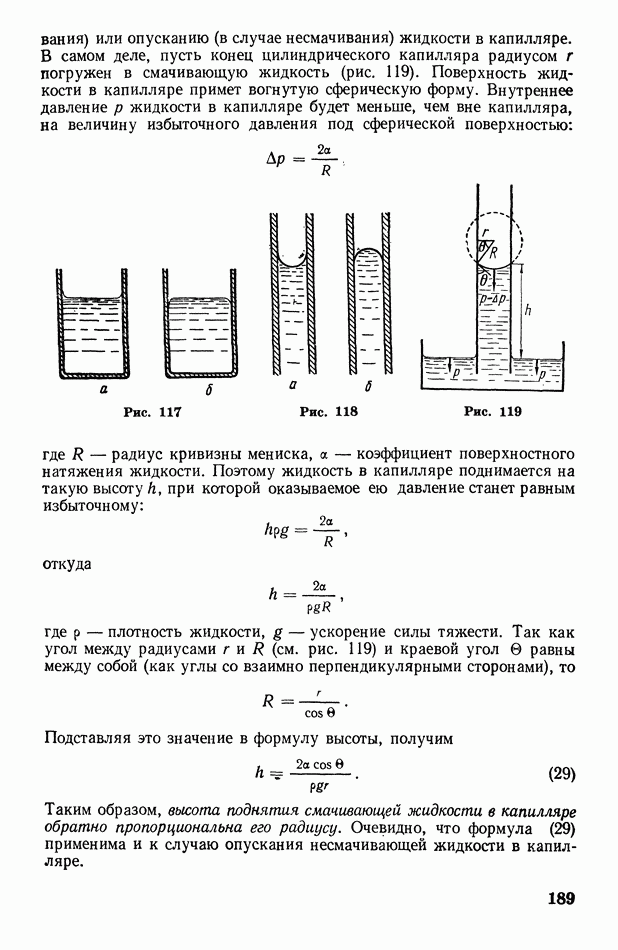
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
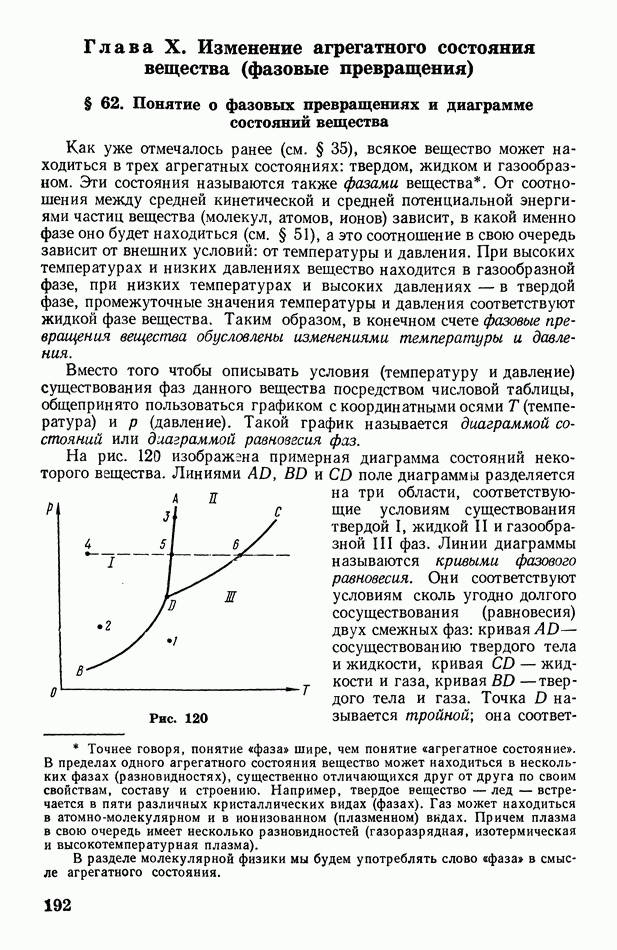
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
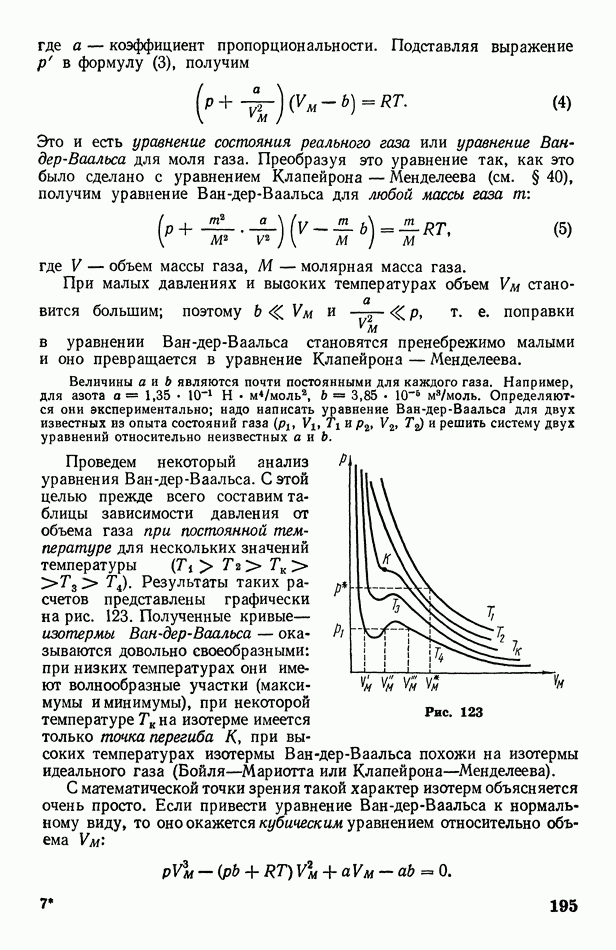
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
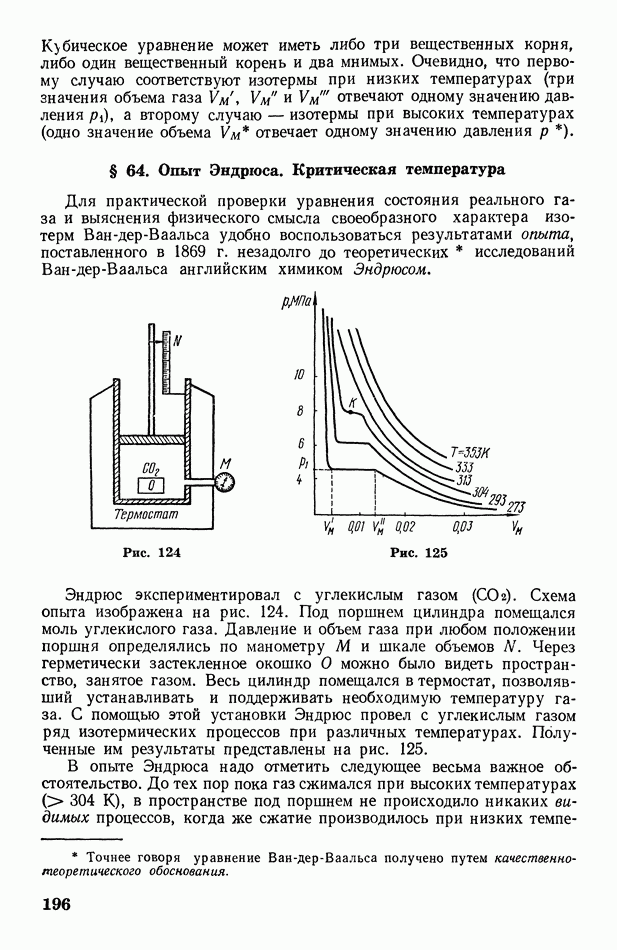
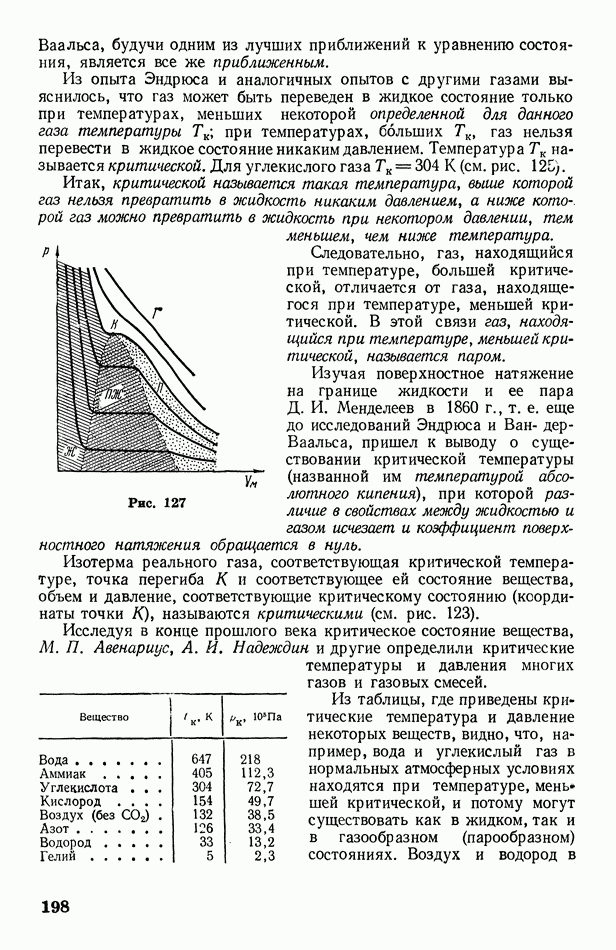
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
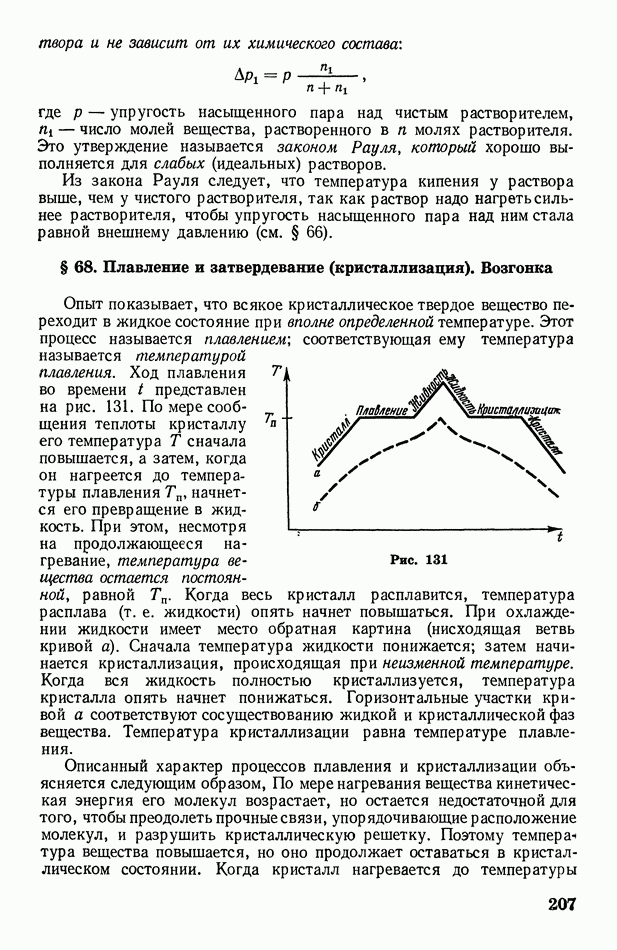
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
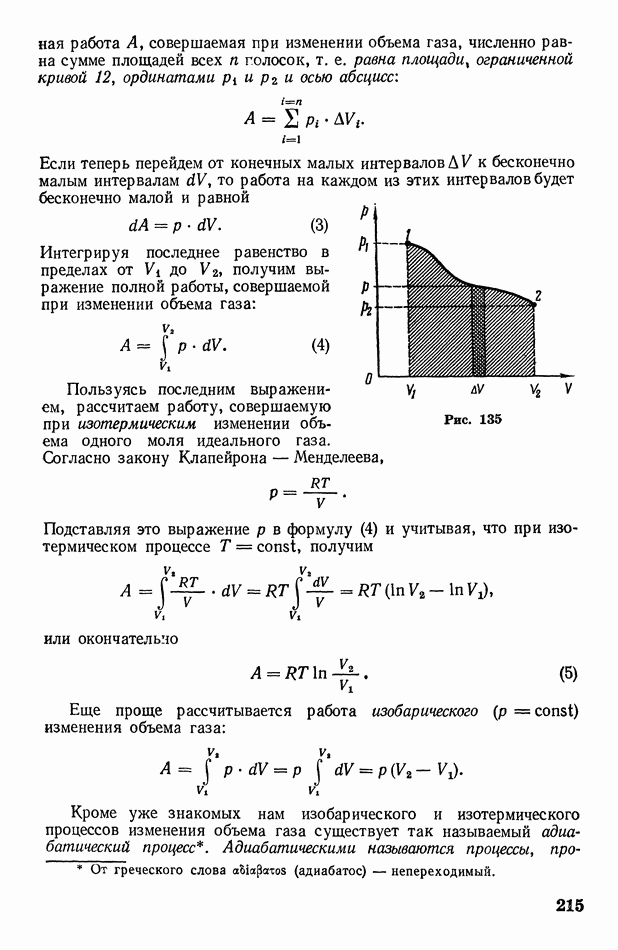
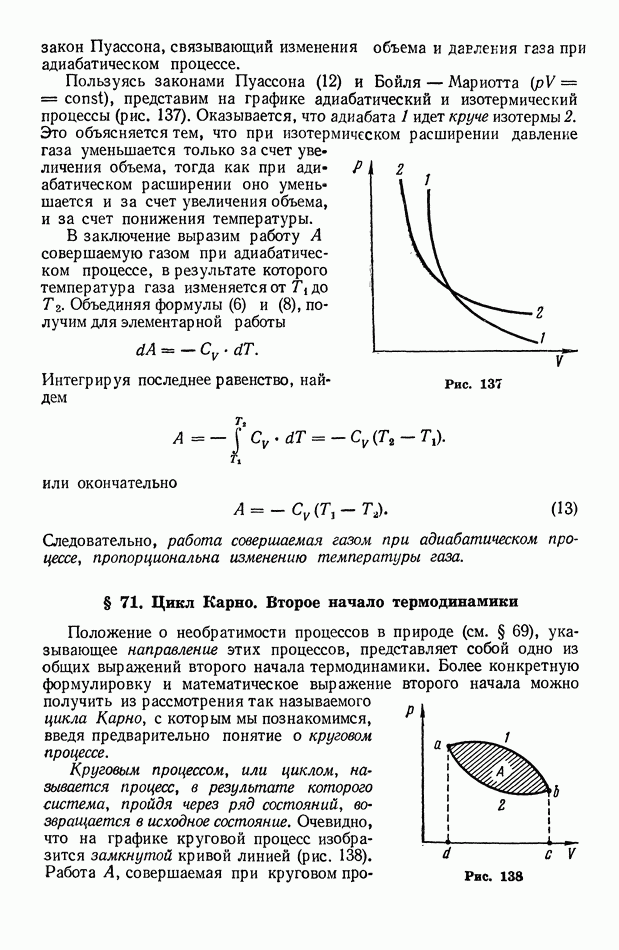
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
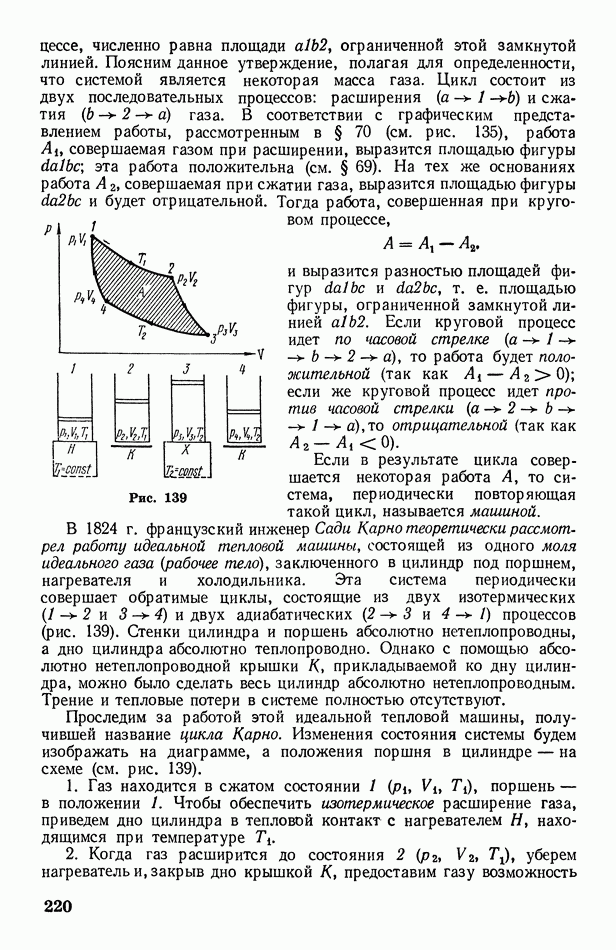
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
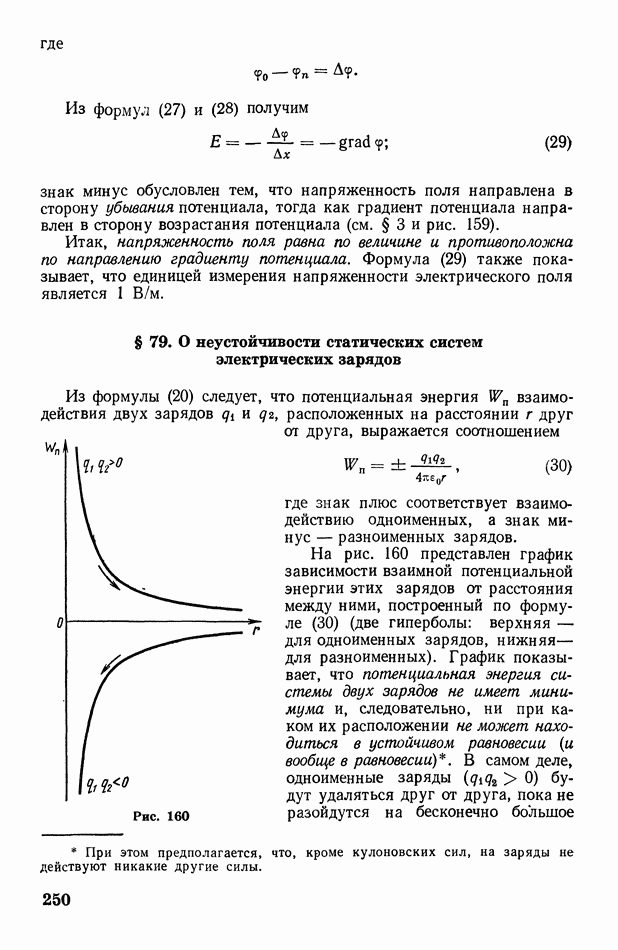
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
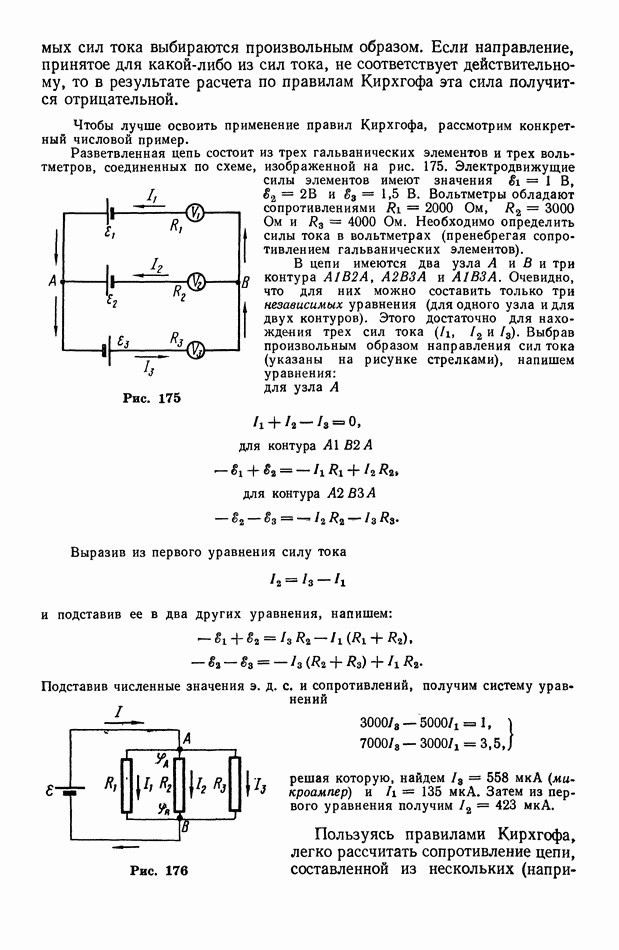
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
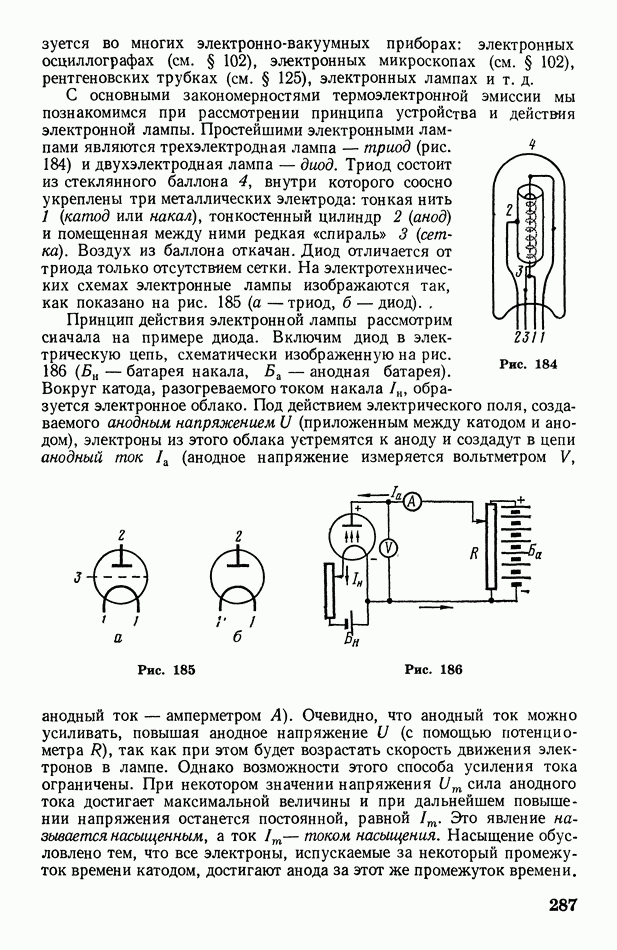
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
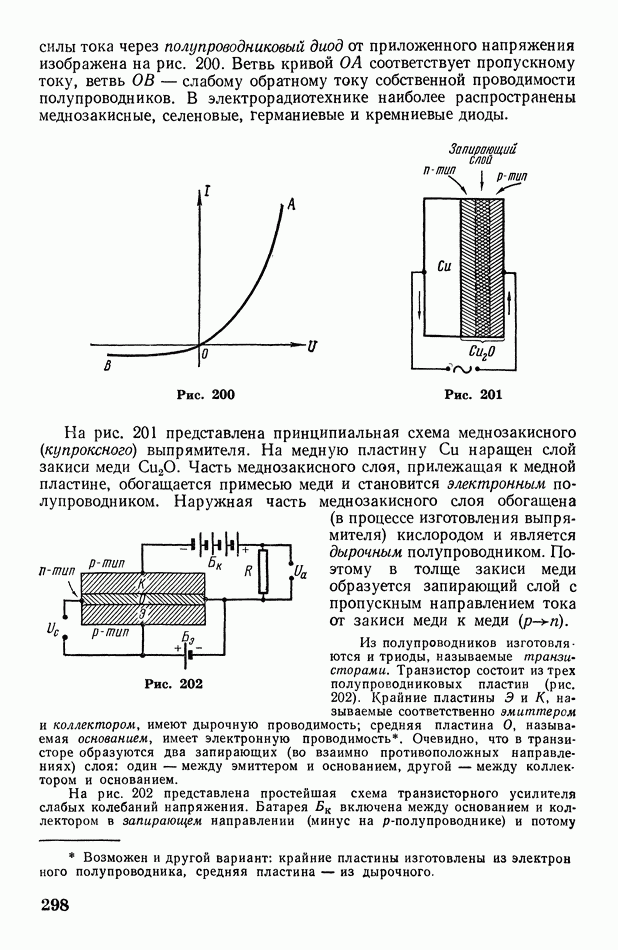
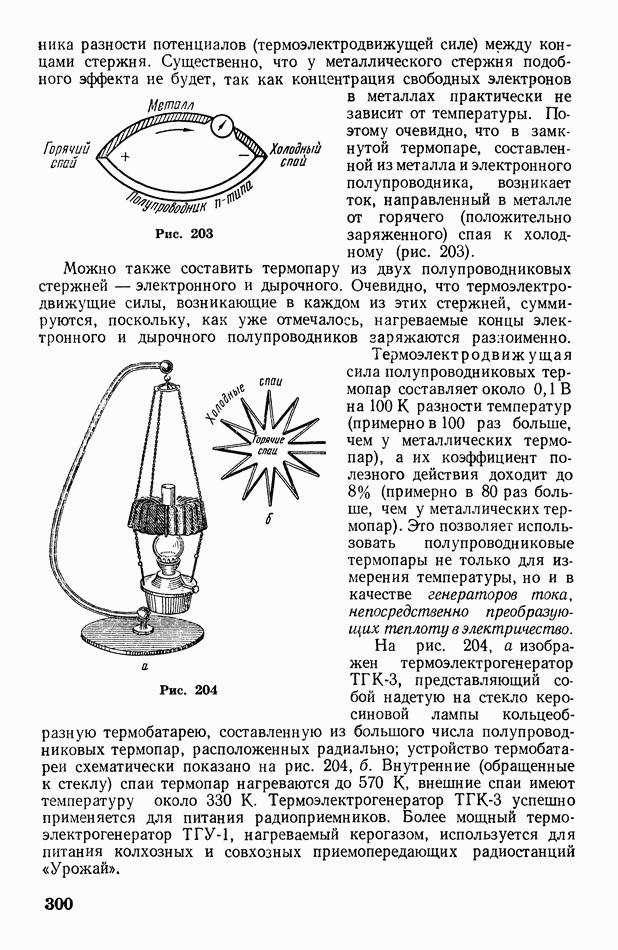
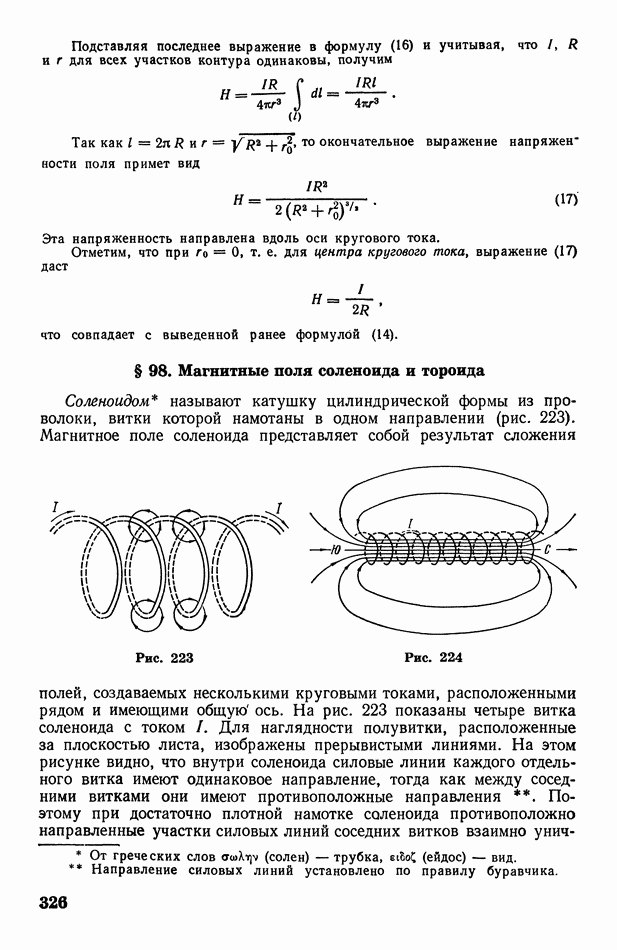
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
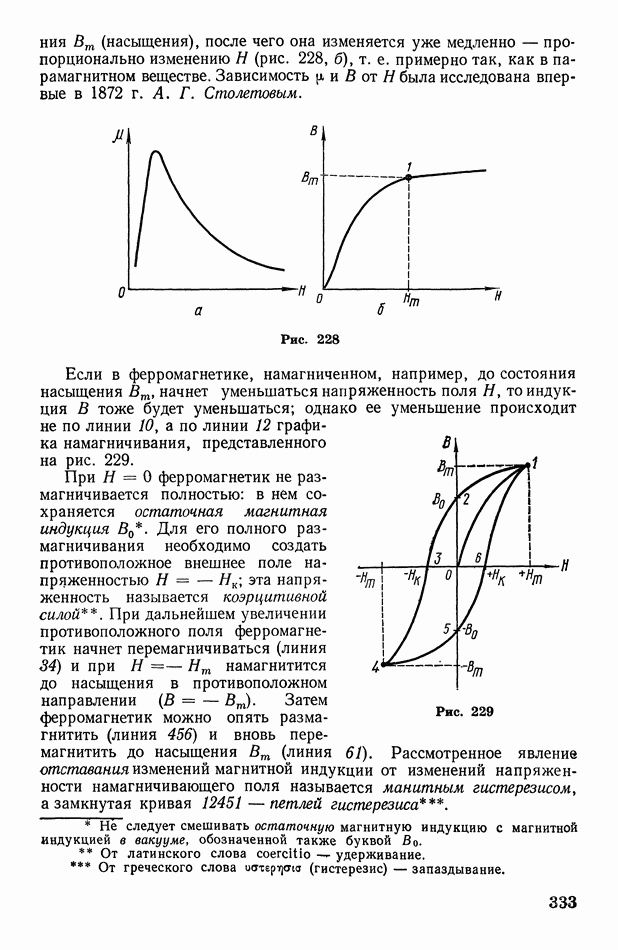
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
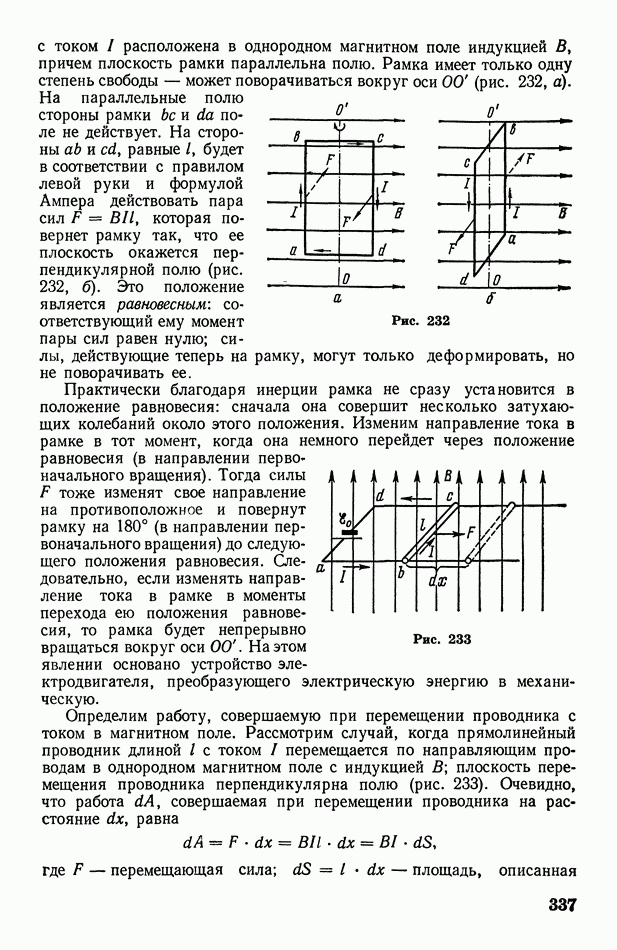
- § 100. Действие магнитного поля на проводник с током. Определение ампера
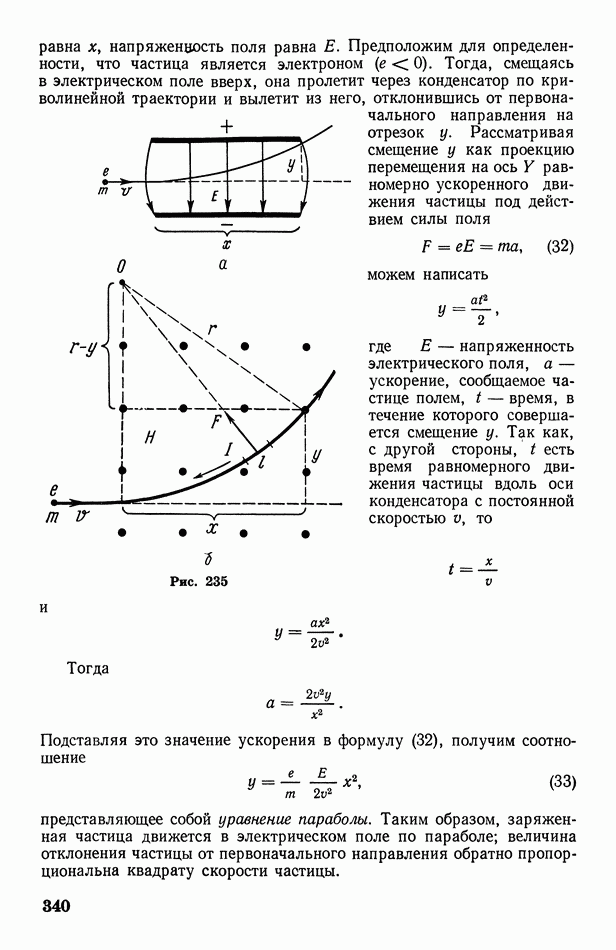
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
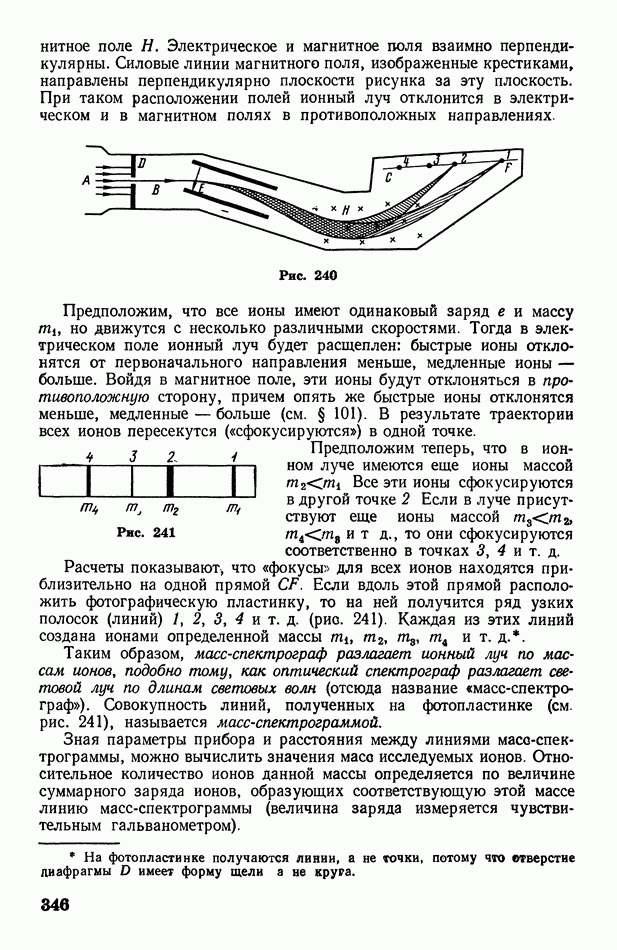
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
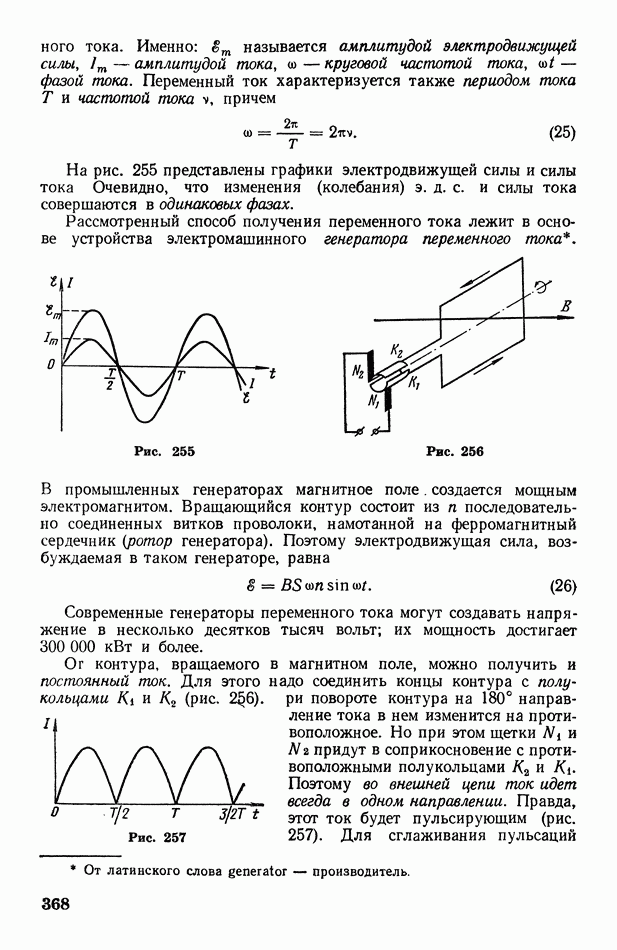
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
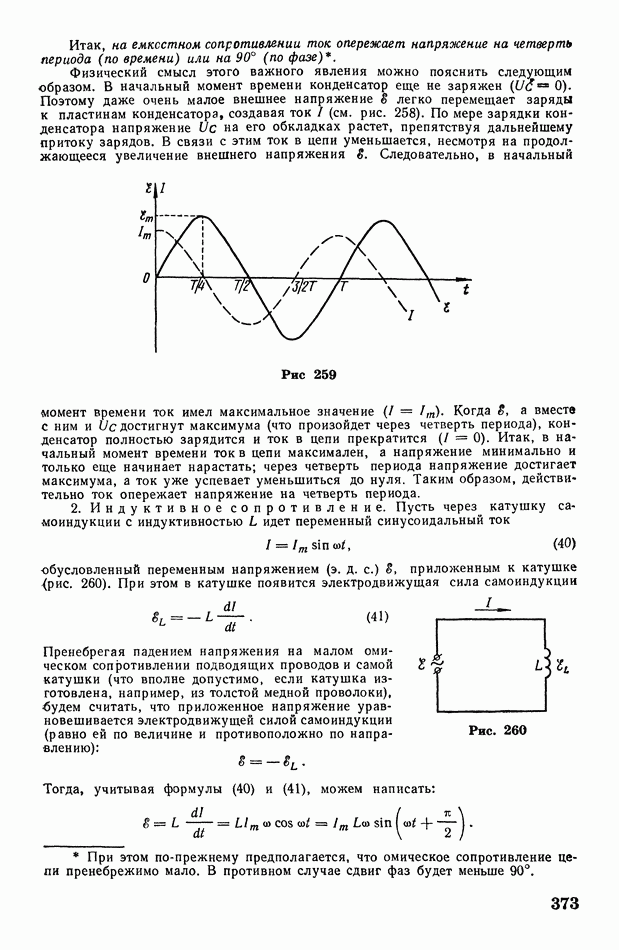
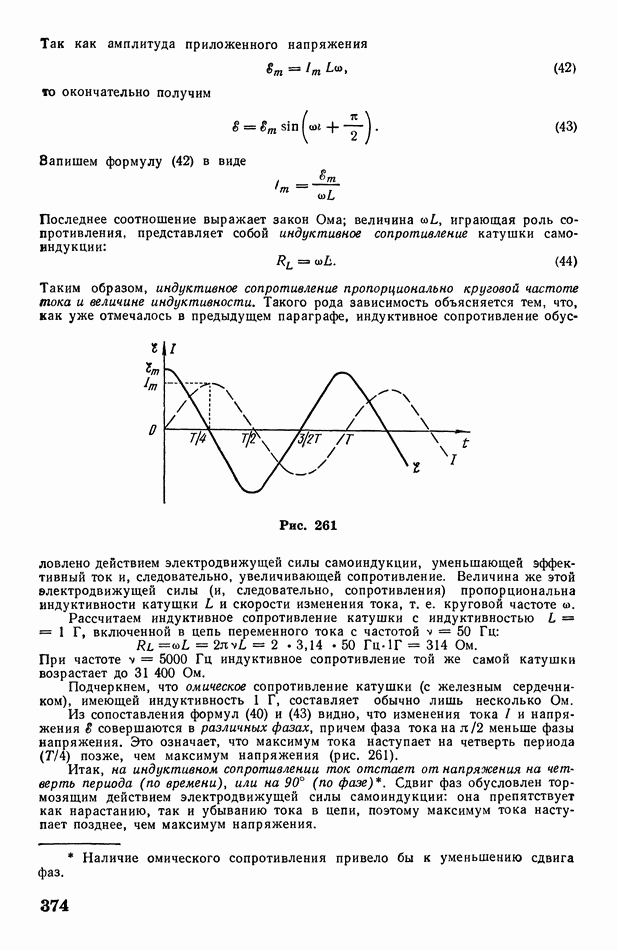
- § 107. Емкостное и индуктивное сопротивления
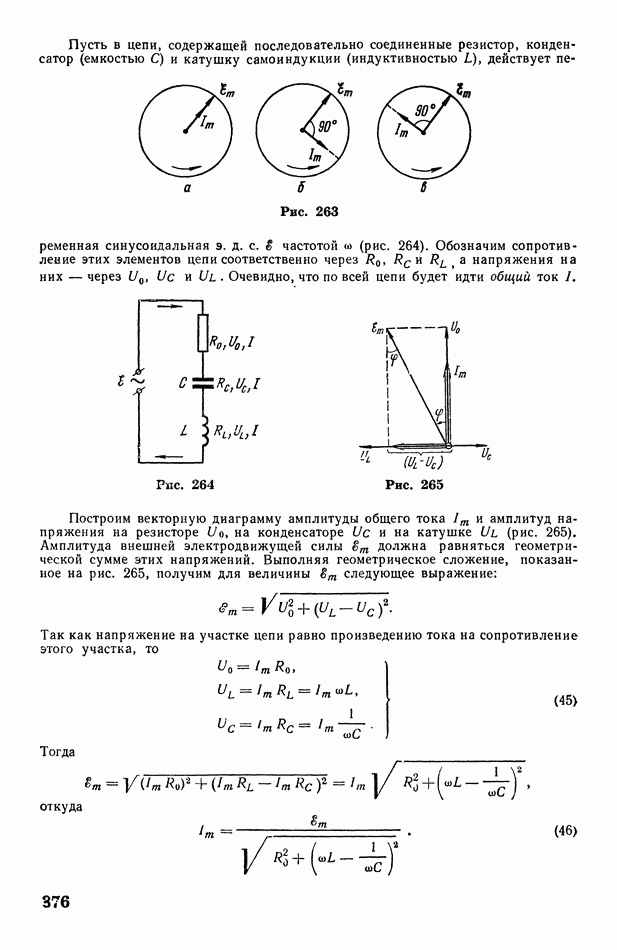
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
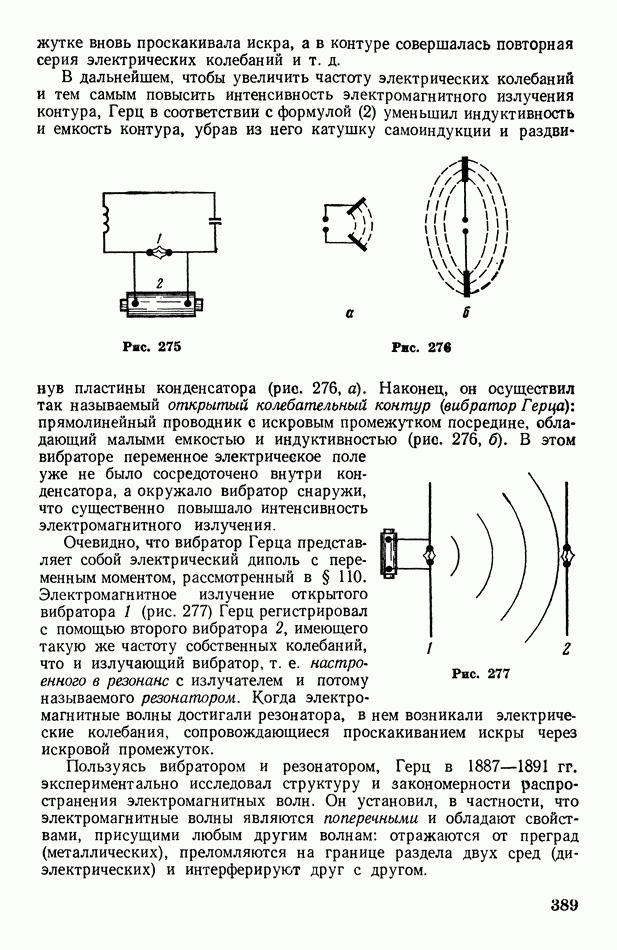
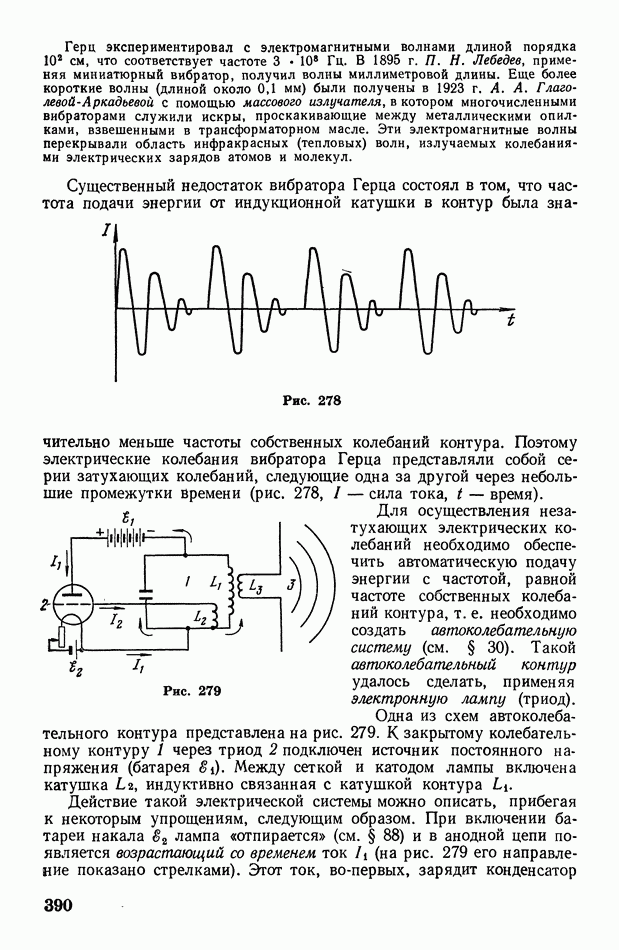
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
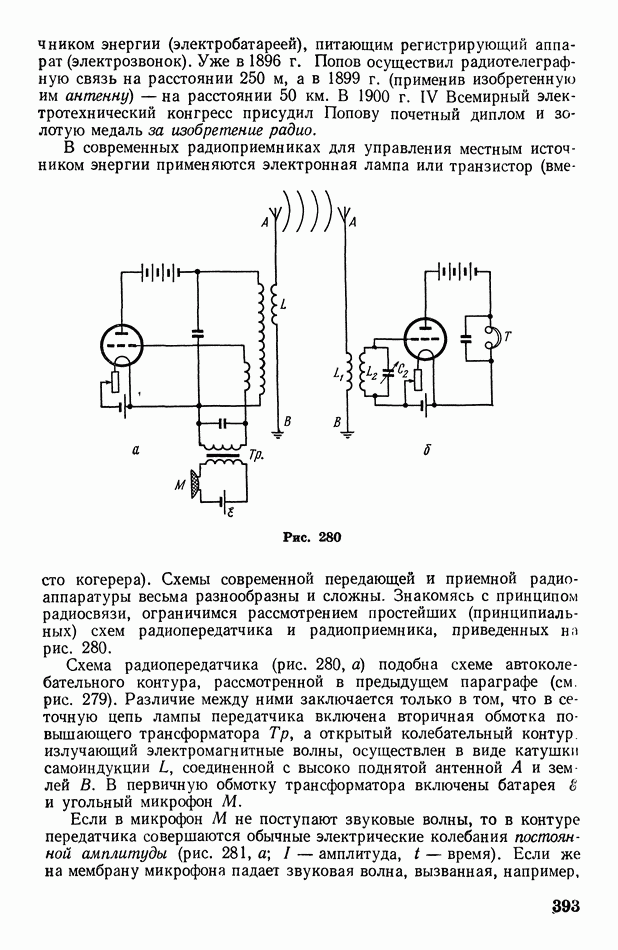
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
- § 117. Тонкие линзы. Микроскоп
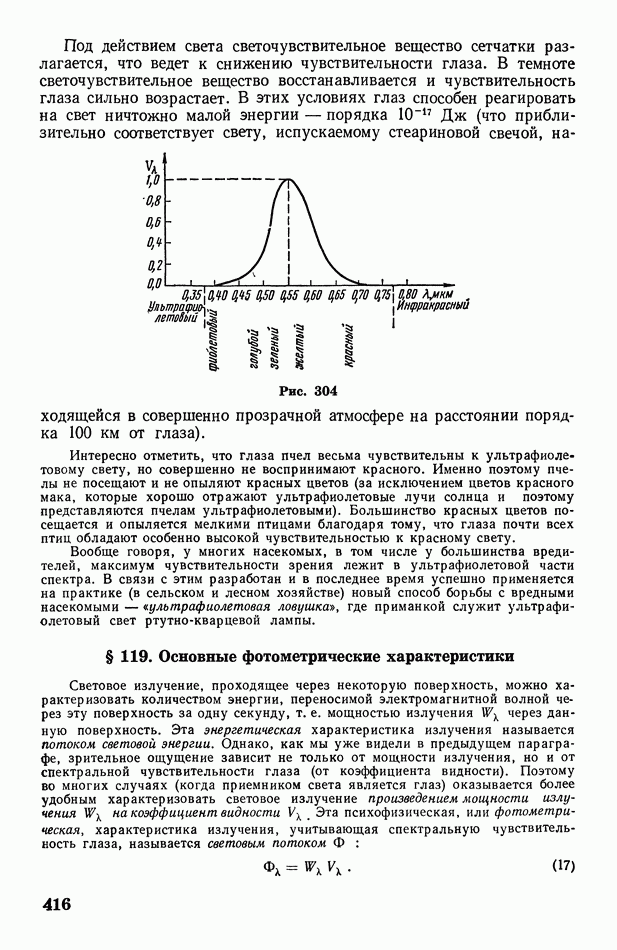
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
- § 123. Дифракция света. Разрешающая способность оптических приборов
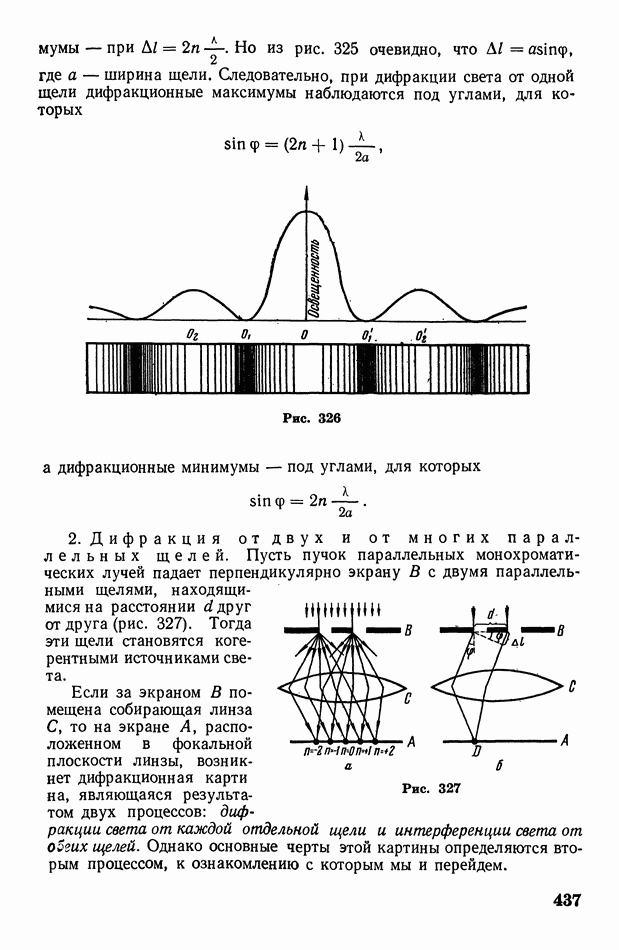
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
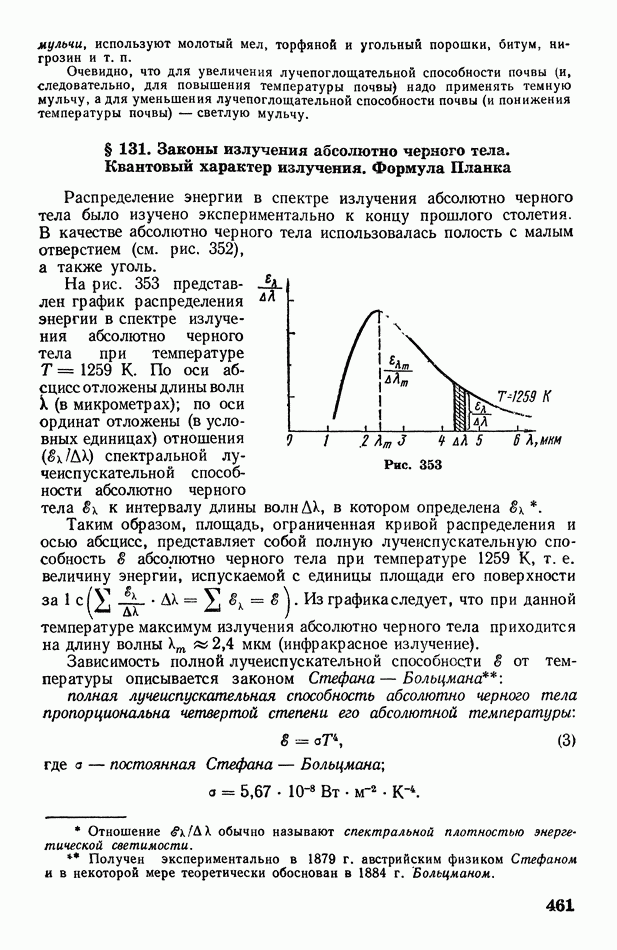
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
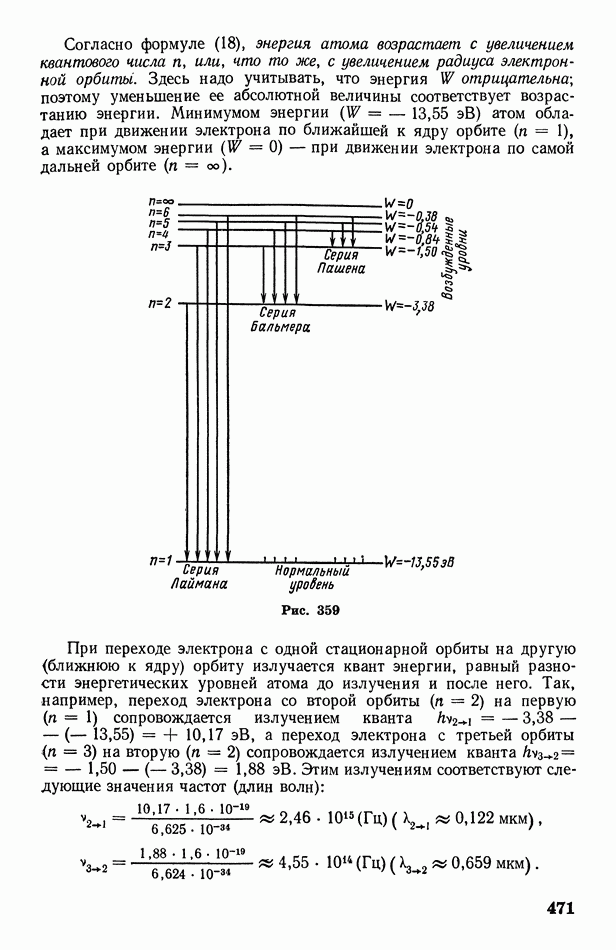
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
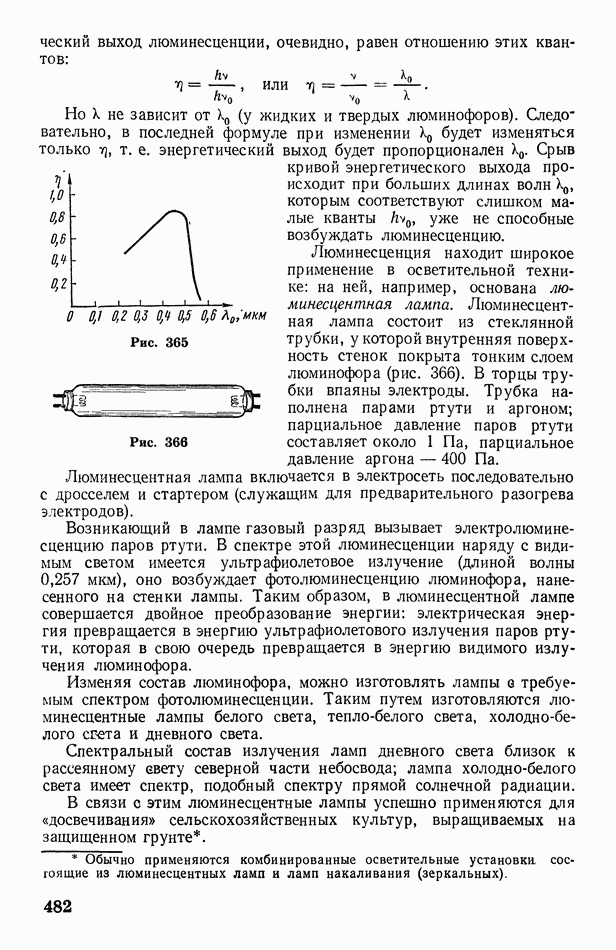
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
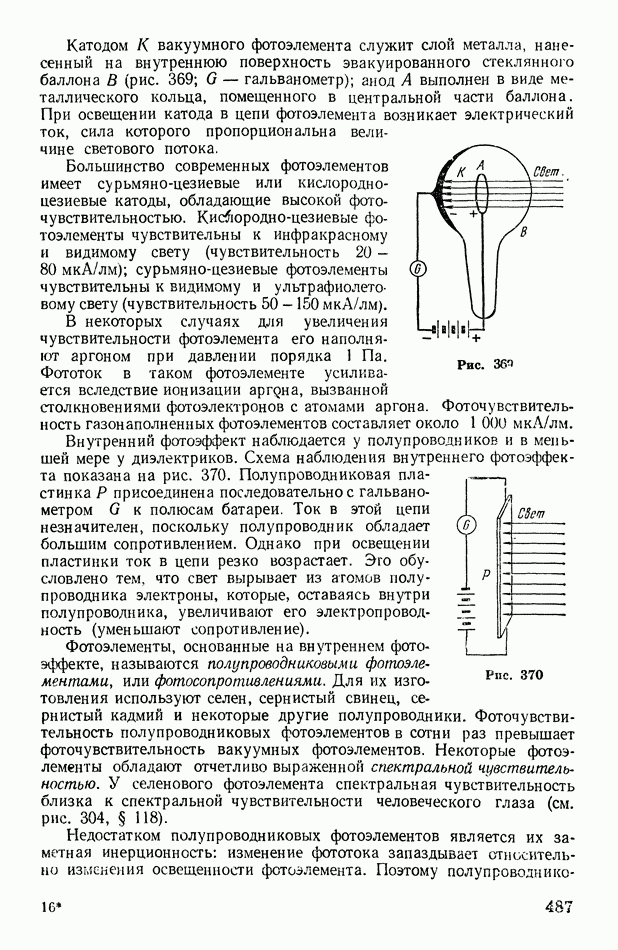
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
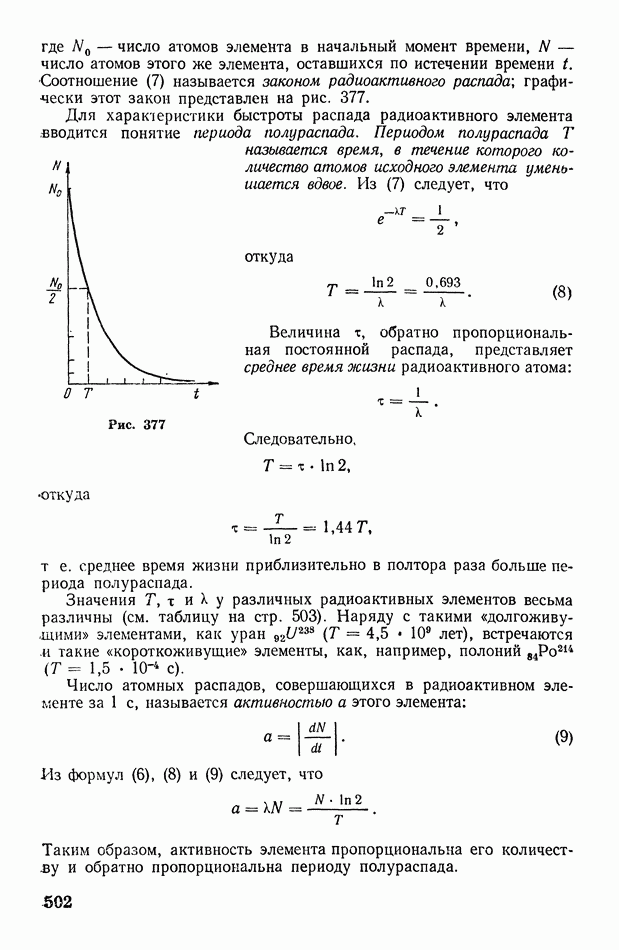
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
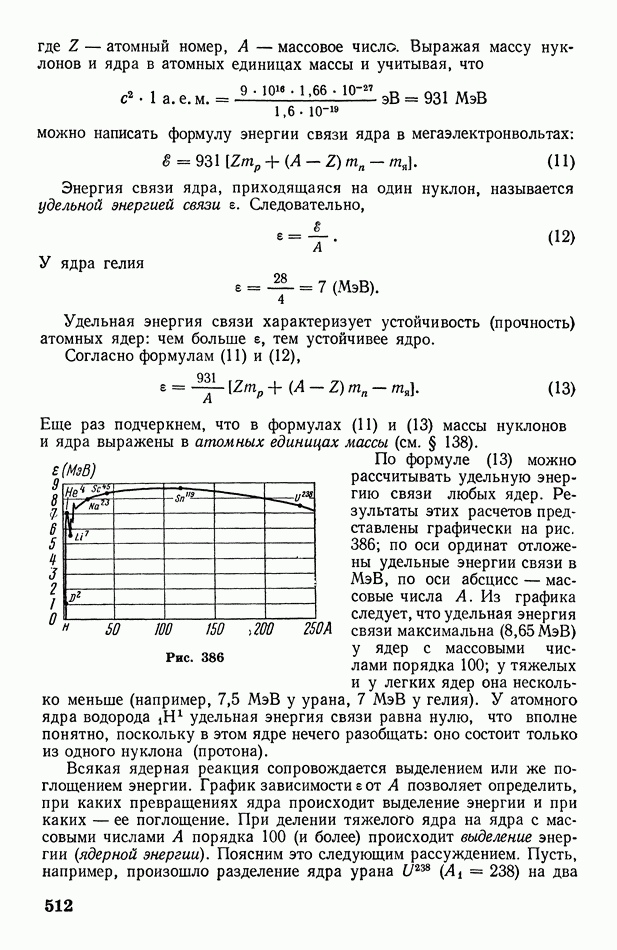
- § 142. Энергия связи и дефект массы атомного ядра
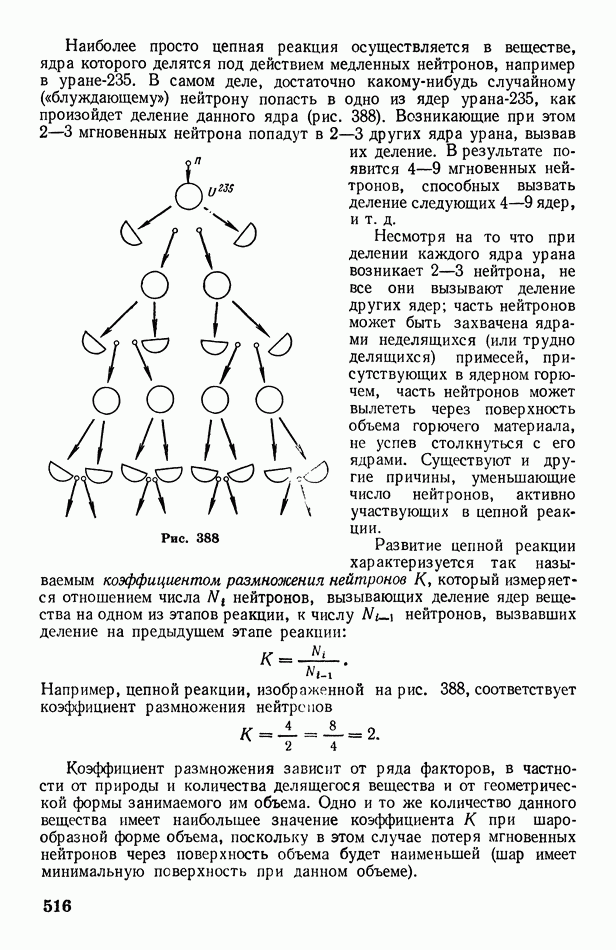
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
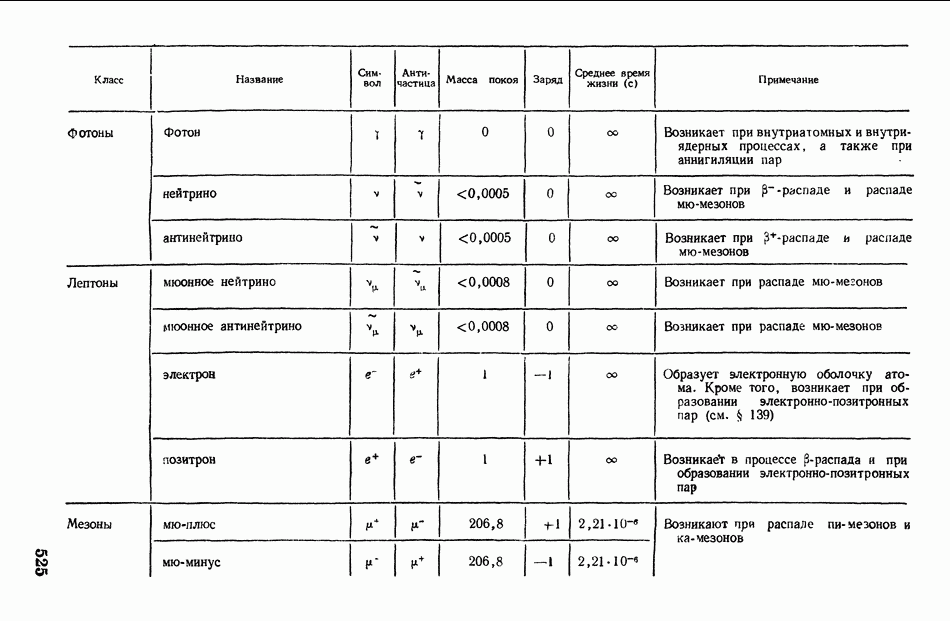
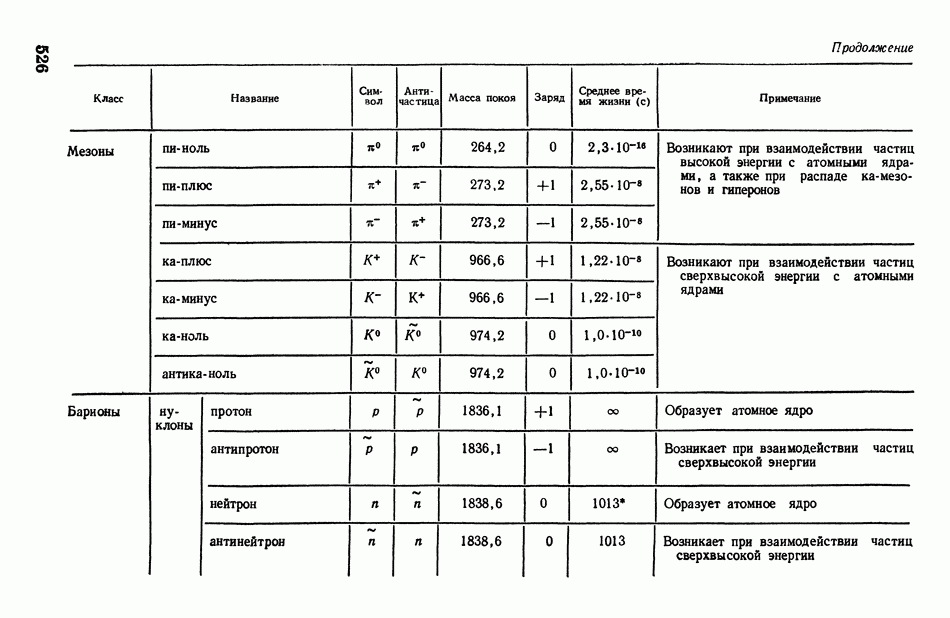
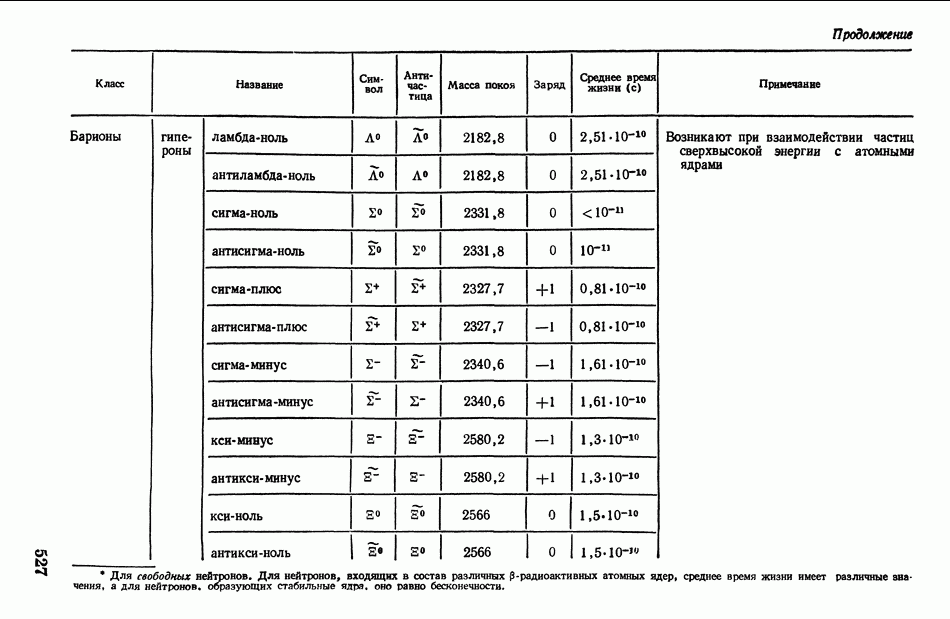
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии