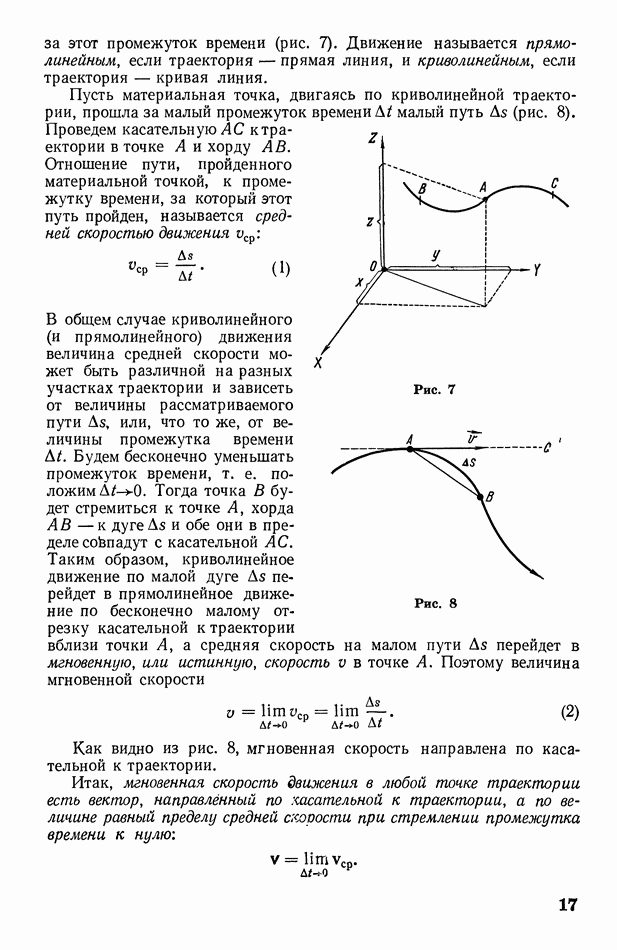
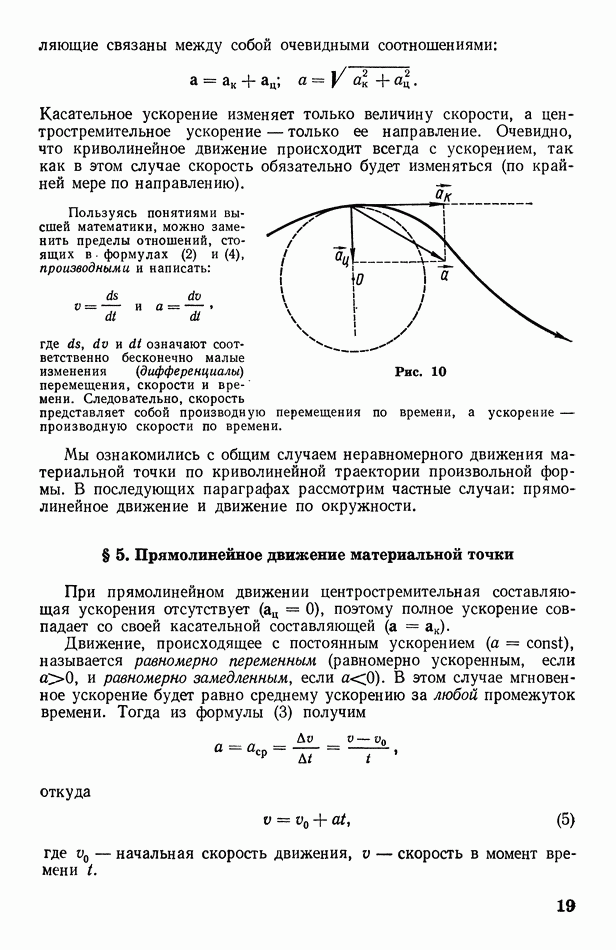
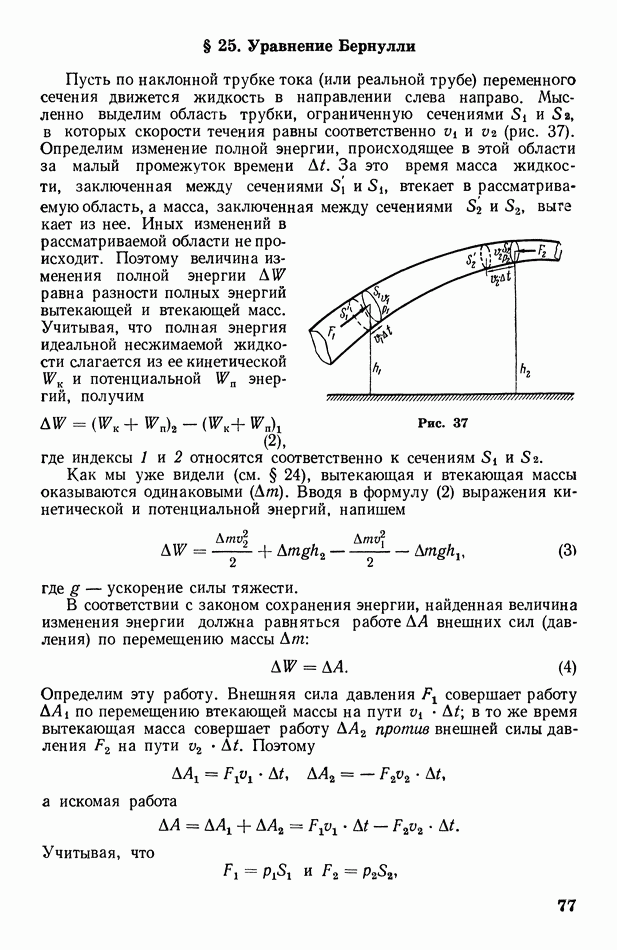
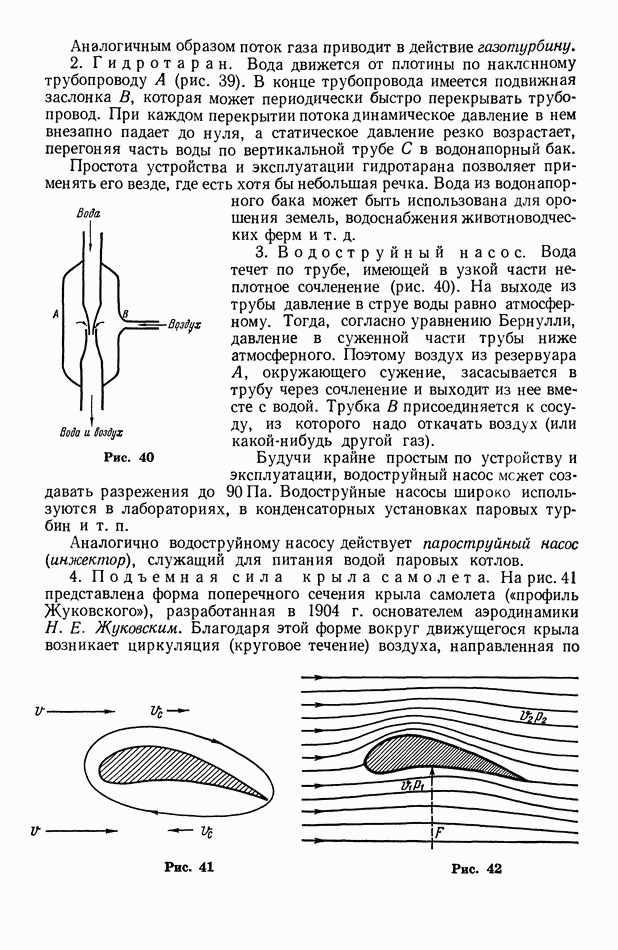
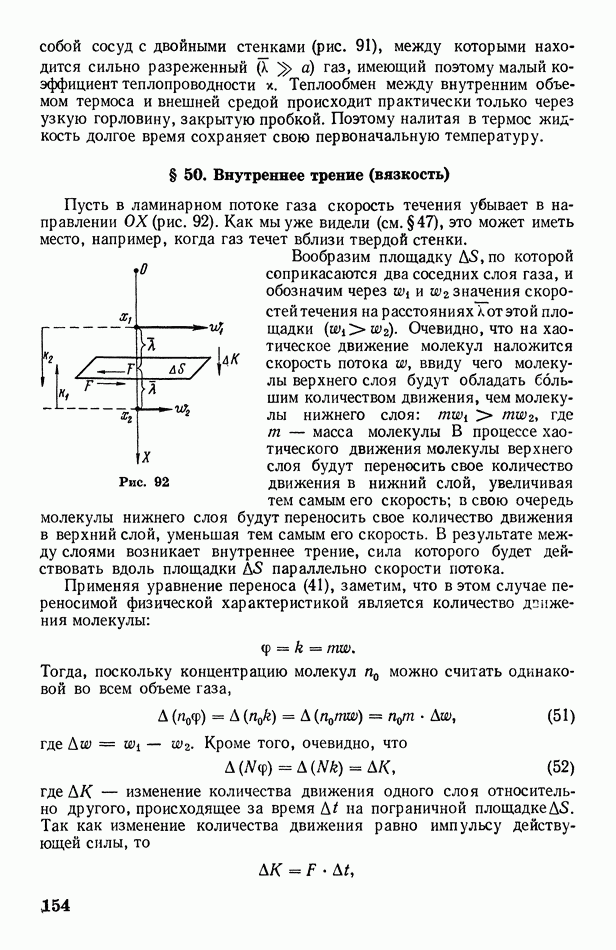
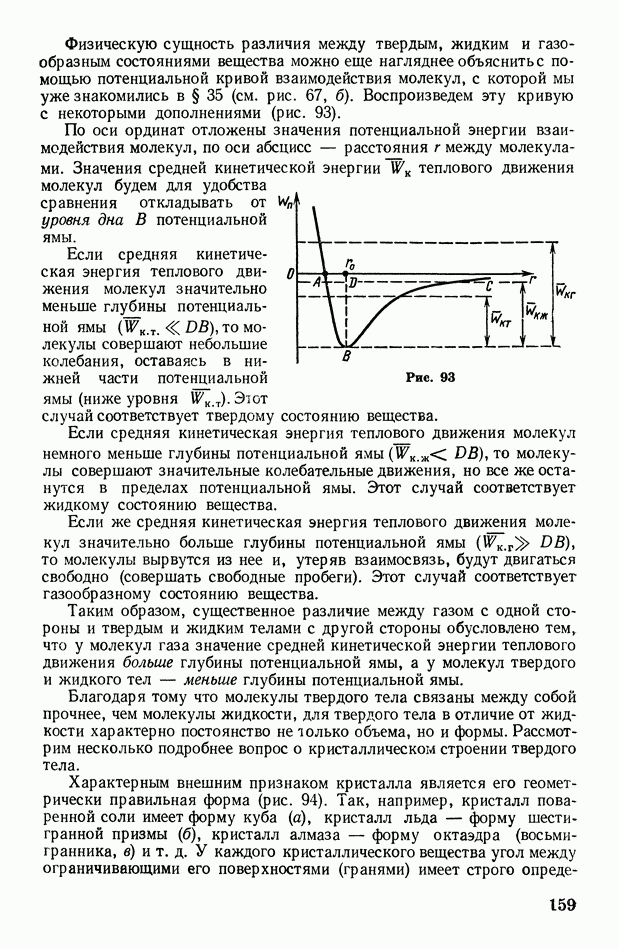
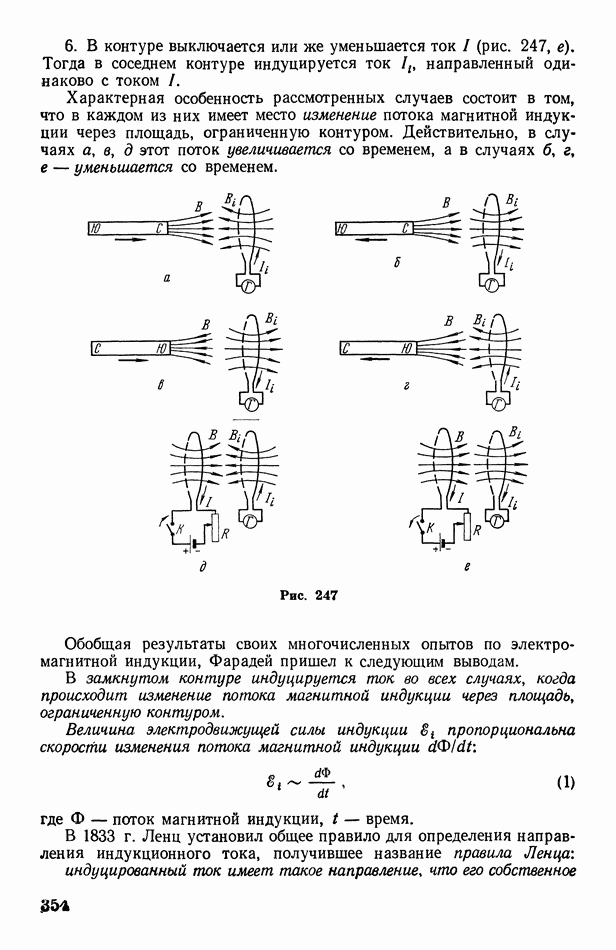
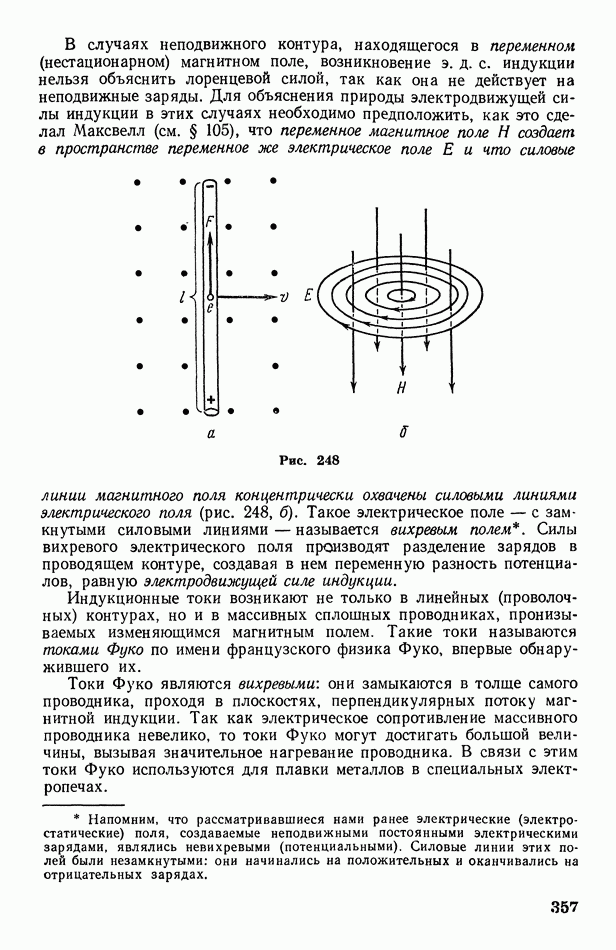
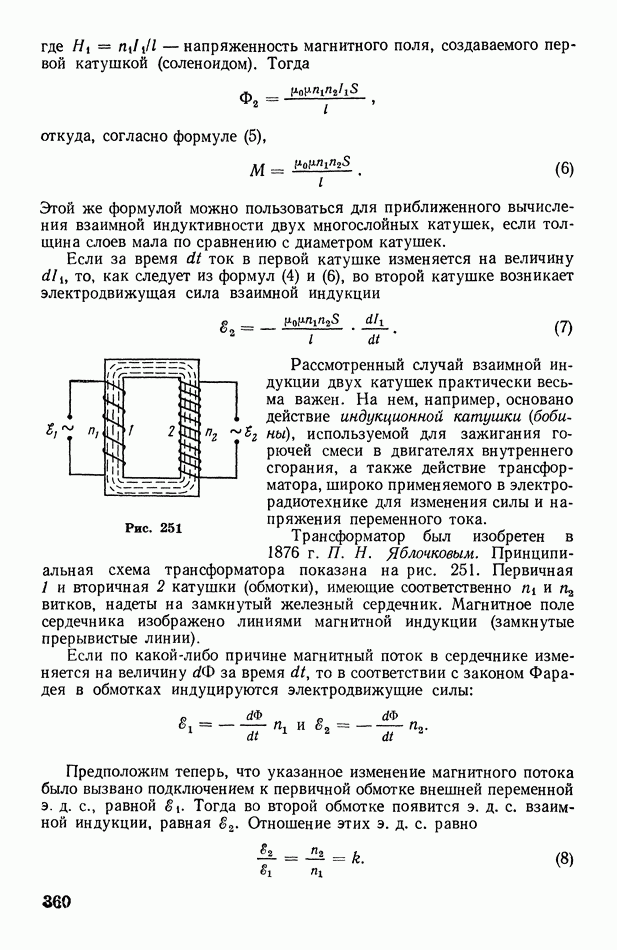
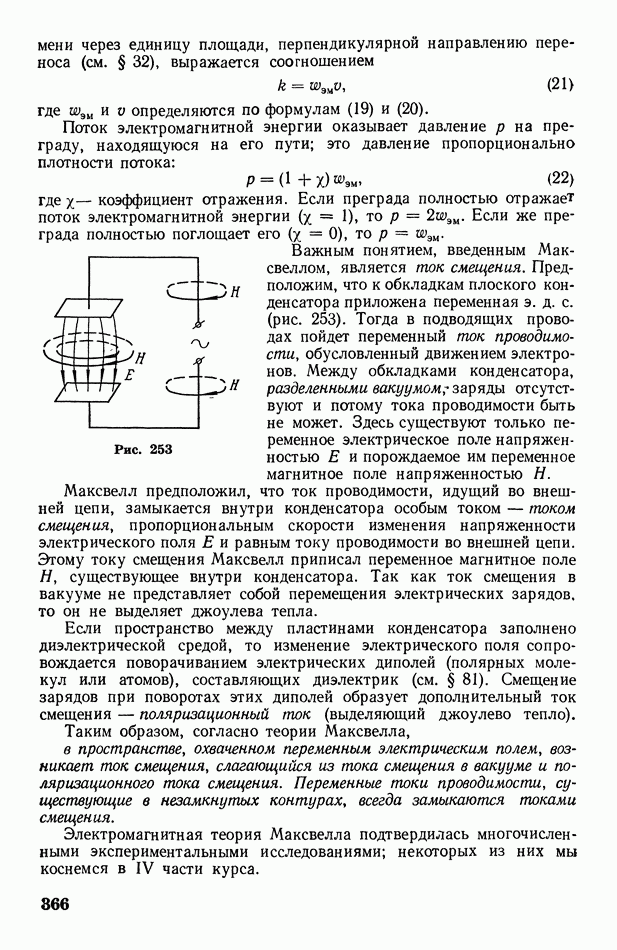
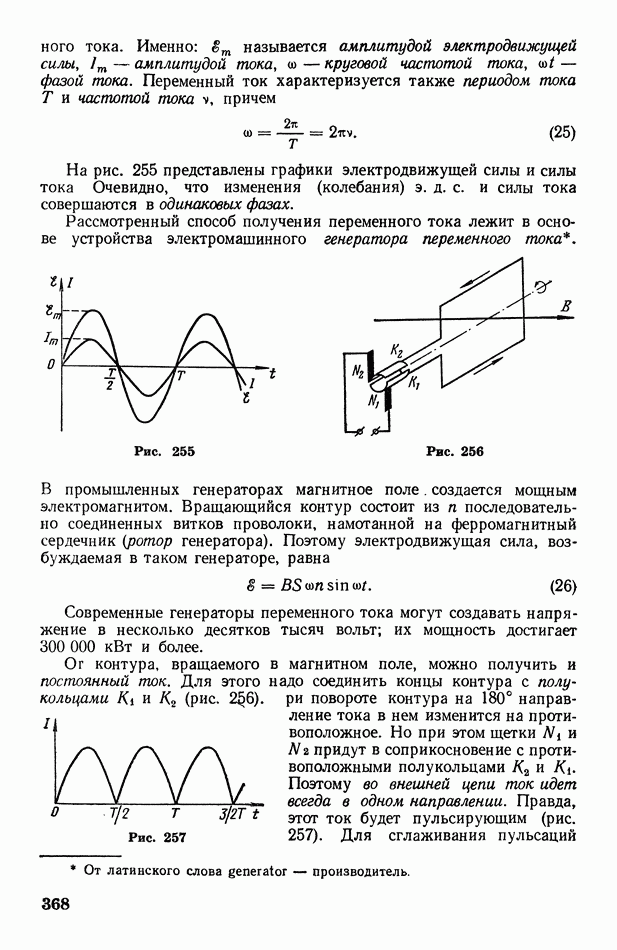
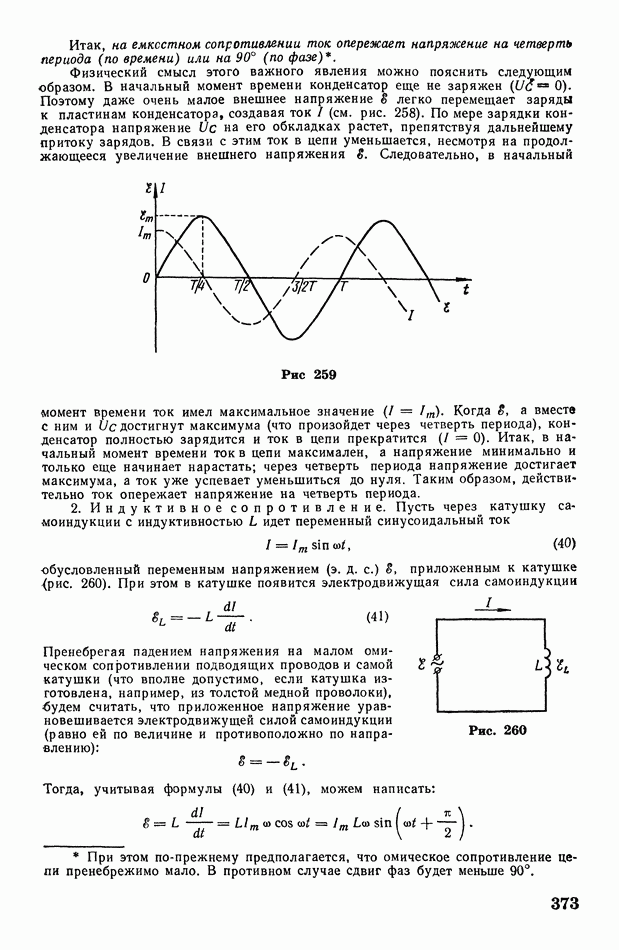
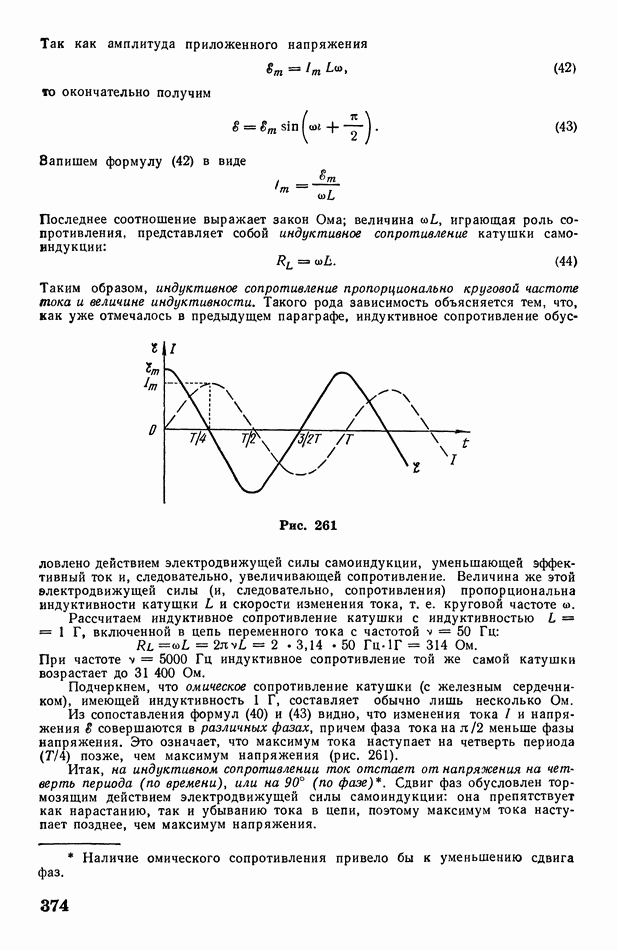
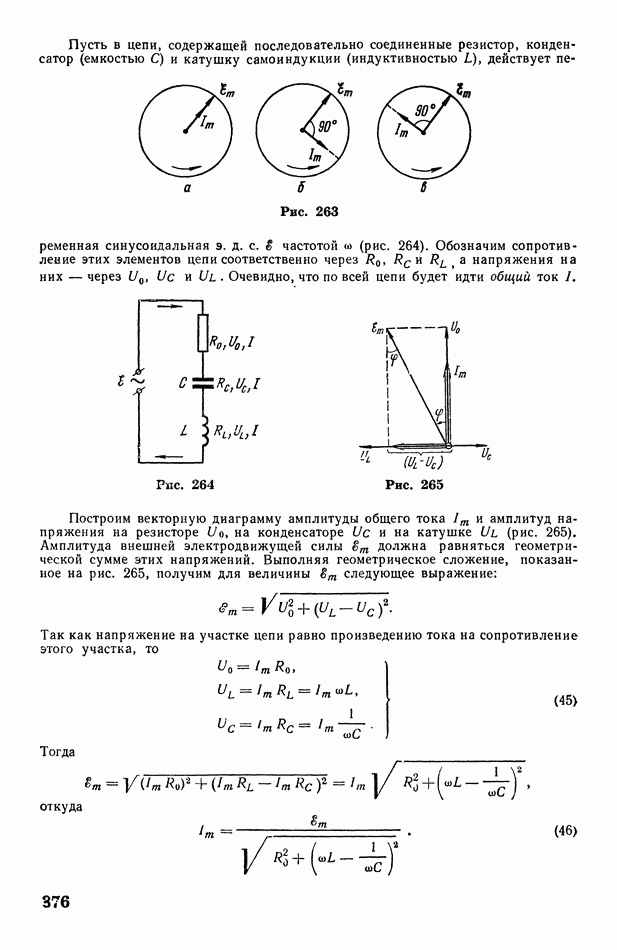
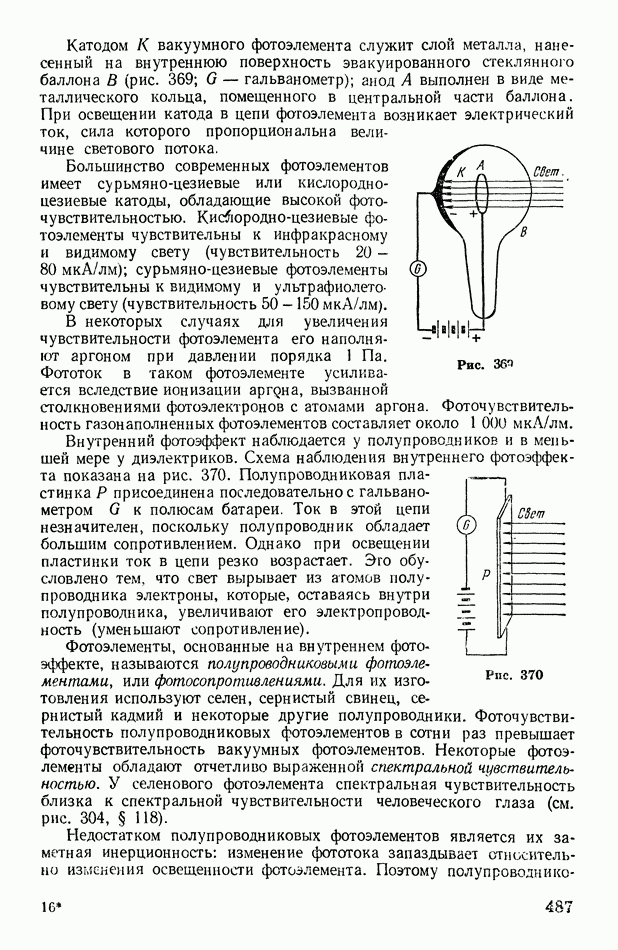
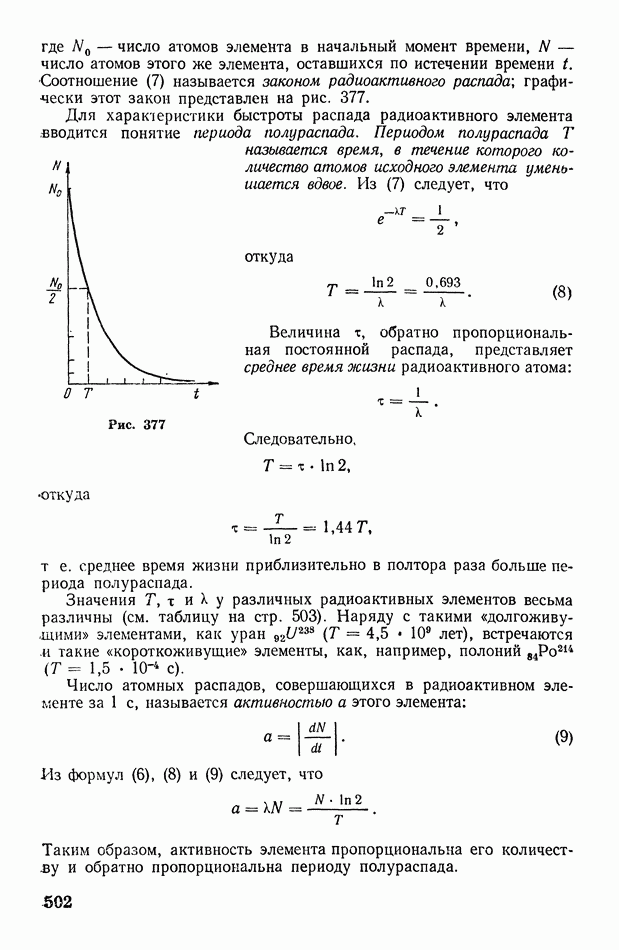
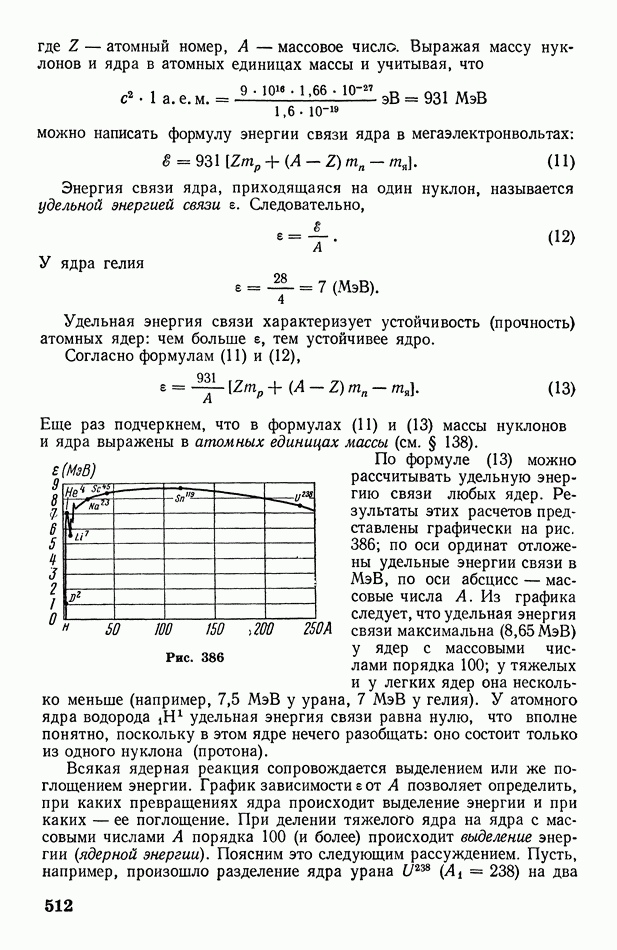
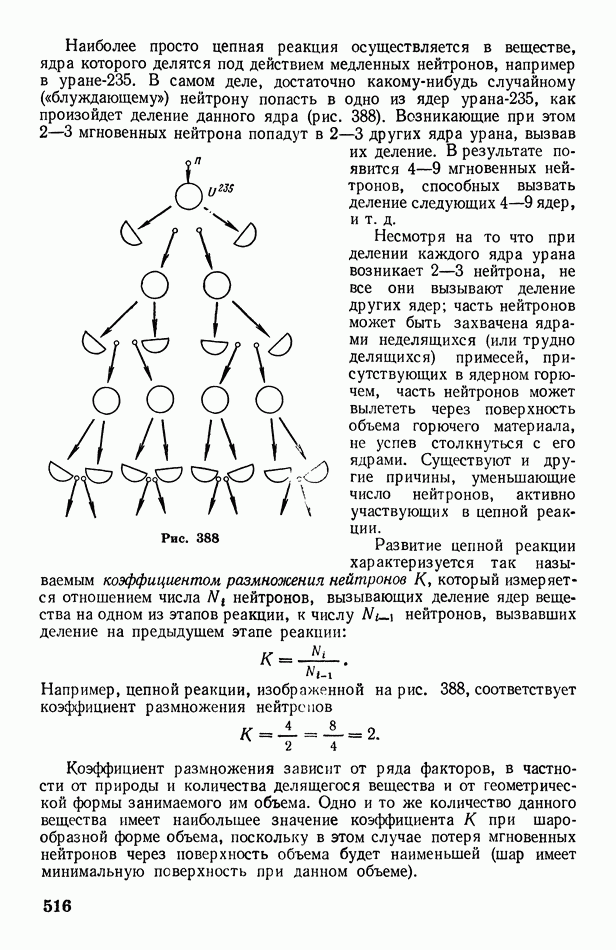
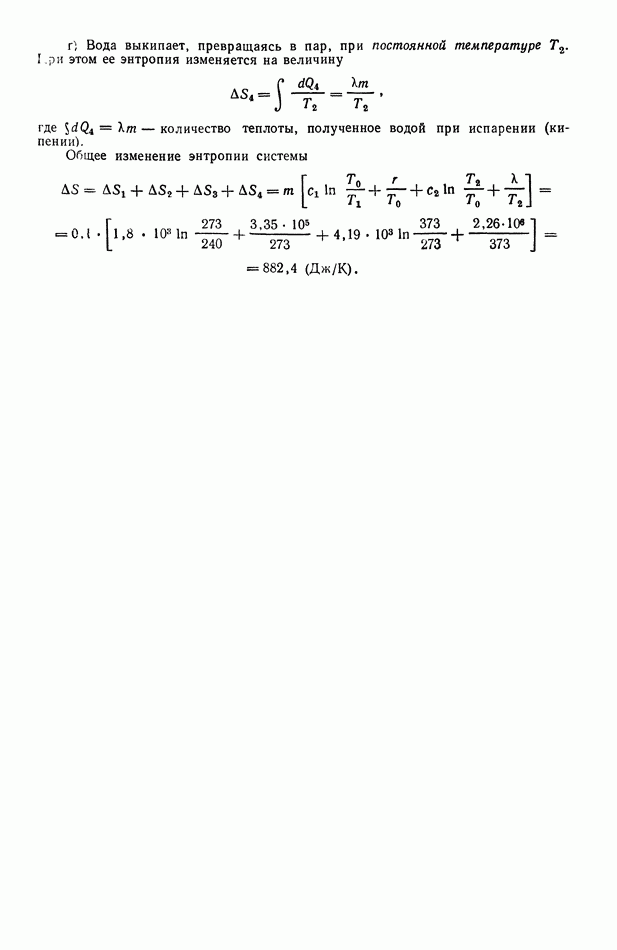| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 73. О статистическом смысле энтропии и второго начала термодинамики
Из несколько формального математического определения, посредством которого Клаузиус ввел понятие энтропии  трудно уяснить ее физический смысл. Физическая сущность энтропии была выяснена позднее благодаря статистическим исследованиям Больцмана. Для ознакомления с результатами этих исследований необходимо иметь представление о так называемой вероятности состояния системы
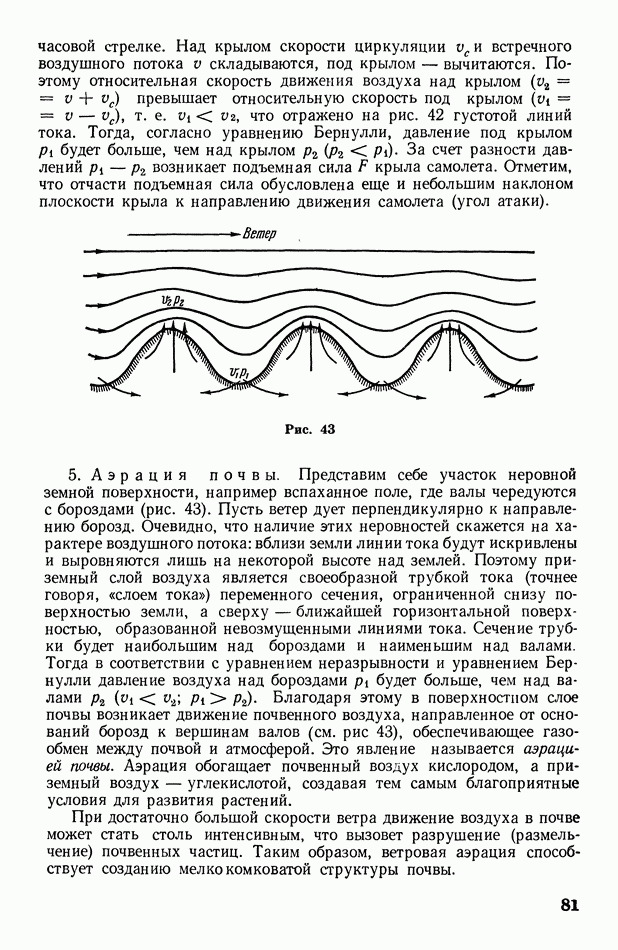
трудно уяснить ее физический смысл. Физическая сущность энтропии была выяснена позднее благодаря статистическим исследованиям Больцмана. Для ознакомления с результатами этих исследований необходимо иметь представление о так называемой вероятности состояния системы 
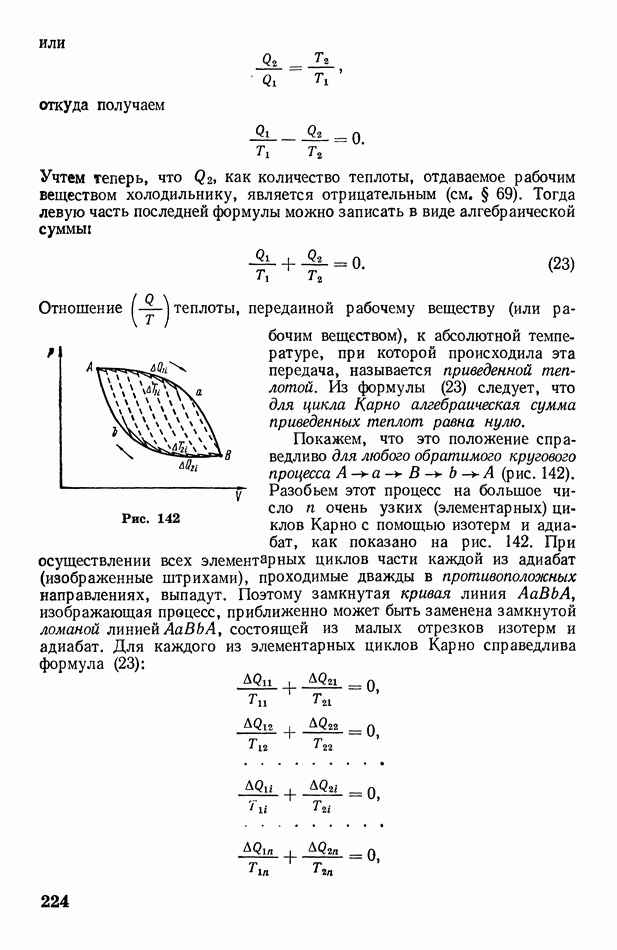
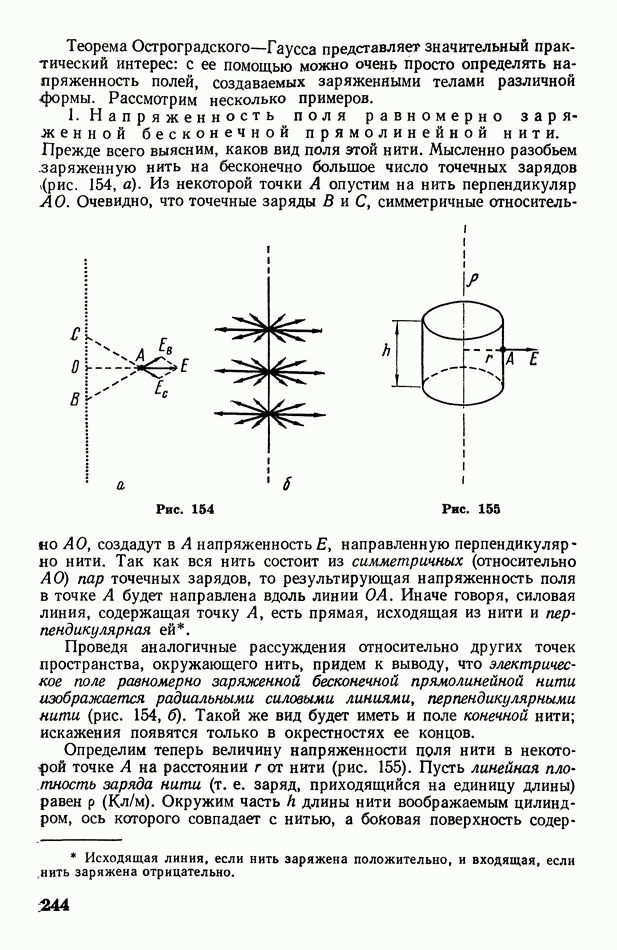
Рассмотрим сосуд, мысленно разделив его на две равные части (рис. 143, а). Пусть в нем находится только одна молекула. Двигаясь хаотически, она может оказаться как в левой, так и в правой части сосуда, причем оба случая одинаково возможны, или, как говорят, равновероятны.
Вероятность события характеризуется отношением числа случаев осуществляющих данное событие, к числу всех возможных случаев.

(кликните для просмотра скана)
Очевидно, что вероятности случая, когда правая часть сосуда оказывается пустой, и случая, когда в ней находится молекула, одинаковы и равны 1/2.
Поместим теперь в сосуд две молекулы, предварительно пронумеровав их (рис. 143, б). Тогда число возможных случаев размещения молекул по частям сосуда станет равным  а вероятность случая
а вероятность случая 
Если в сосуде будут находиться три пронумерованных молекулы (рис. 143, в), то число случаев размещения возрастет до  а вероятность каждого случая уменьшится до
а вероятность каждого случая уменьшится до 
При наличии в сосуде четырех молекул (рис. 143, г) число случаев окажется равным  а вероятность каждого случая
а вероятность каждого случая 
Нетрудно сообразить, что при наличии в сосуде  молекул число случаев размещения этих молекул станет равным 2, а вероятность каждого случая 1/2
молекул число случаев размещения этих молекул станет равным 2, а вероятность каждого случая 1/2
Таким образом, по мере увеличения числа молекул вероятность каждого случая индивидуального размещения молекул уменьшается.
Учтем теперь, что молекулы пронумерованы совершенно условно. В действительности же невозможно отличить молекулы друг от друга: макроскопическое состояние системы не изменится от того, что, например, молекула 2, находящаяся в левой части сосуда, поменяется местом с молекулой 4, находящейся в правой его части. С этой точки зрения случаи VI — XI (см. рис. 143, г) совершенно тождественны: все они соответствуют одному состоянию системы (газа) — равномерному распределению молекул по объему сосуда. Вероятность этого состояния  так как оно может осуществляться шестью способами. Точно так же случаи II—V являются тождественными и соответствуют другому состоянию системы, вероятность которого
так как оно может осуществляться шестью способами. Точно так же случаи II—V являются тождественными и соответствуют другому состоянию системы, вероятность которого  так как оно может осуществляться четырьмя способами. Тождественные случаи XII—XV соответствуют третьему состоянию системы, вероятность которого
так как оно может осуществляться четырьмя способами. Тождественные случаи XII—XV соответствуют третьему состоянию системы, вероятность которого  Четвертое состояние (случай I) осуществляется только одним единственным способом; его вероятность
Четвертое состояние (случай I) осуществляется только одним единственным способом; его вероятность  Такова же вероятность пятого состояния (случай XVI).
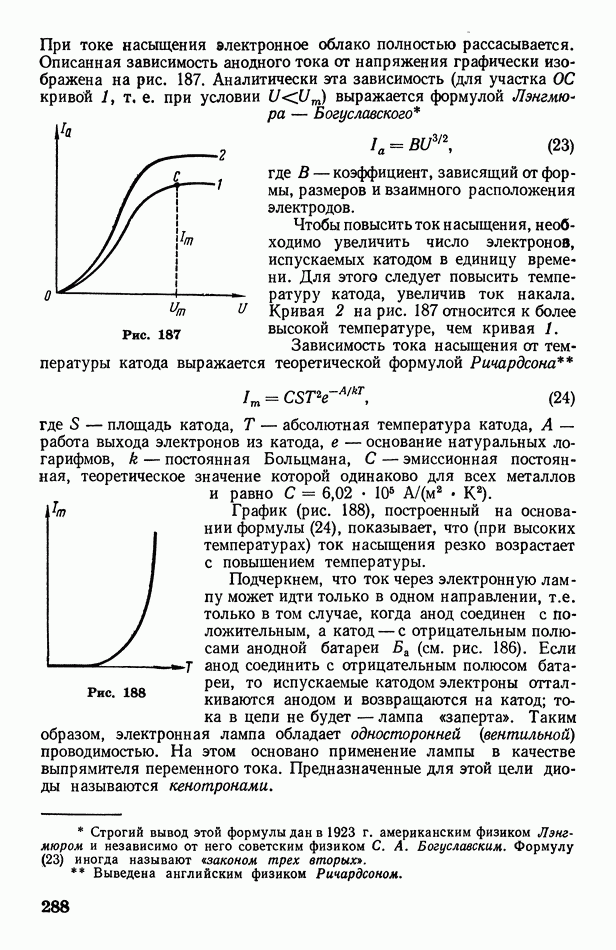
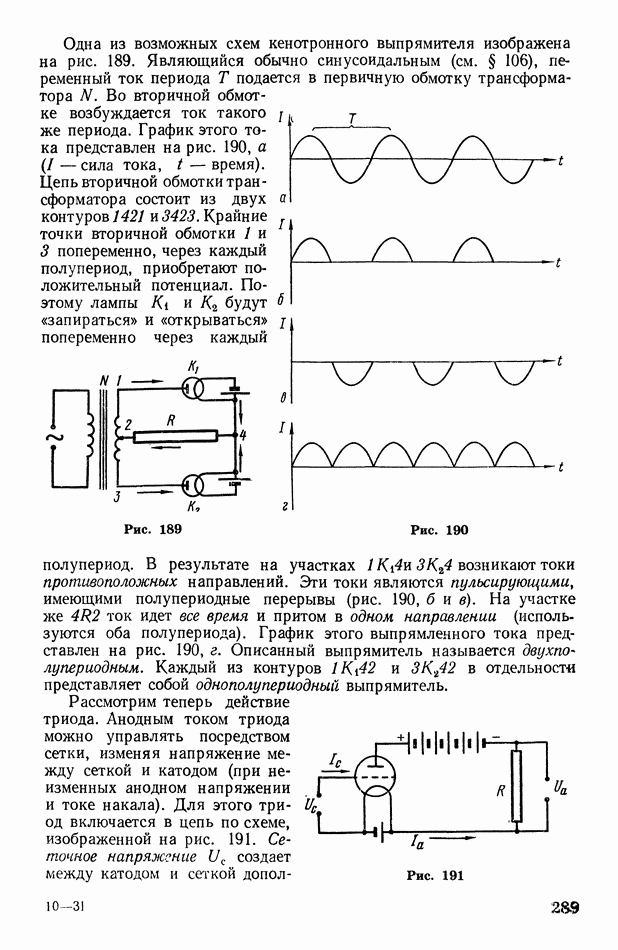
Такова же вероятность пятого состояния (случай XVI).
Таким образом, система из четырех молекул может находиться в пяти различных состояниях, причем из всех этих состояний наиболее вероятным является равномерное распределение молекул по объему сосуда. Назовем такое состояние равновесным.
С увеличением числа молекул вероятность равновесного состояния будет все более и более возрастать по сравнению с вероятностью любого неравновесного состояния. Например, в двухмолекулярной системе (см. рис. 143, в) вероятность равновесного состояния в два раза больше, а в четырехмолекулярной системе (см. рис. 143, г) — в шесть раз больше вероятности состояния, при котором все молекулы собираются в левой части сосуда. Как показывают статистические расчеты, при очень большом числе молекул  вероятность равновесного состояния приблизительно в
вероятность равновесного состояния приблизительно в  раз больше вероятности состояния
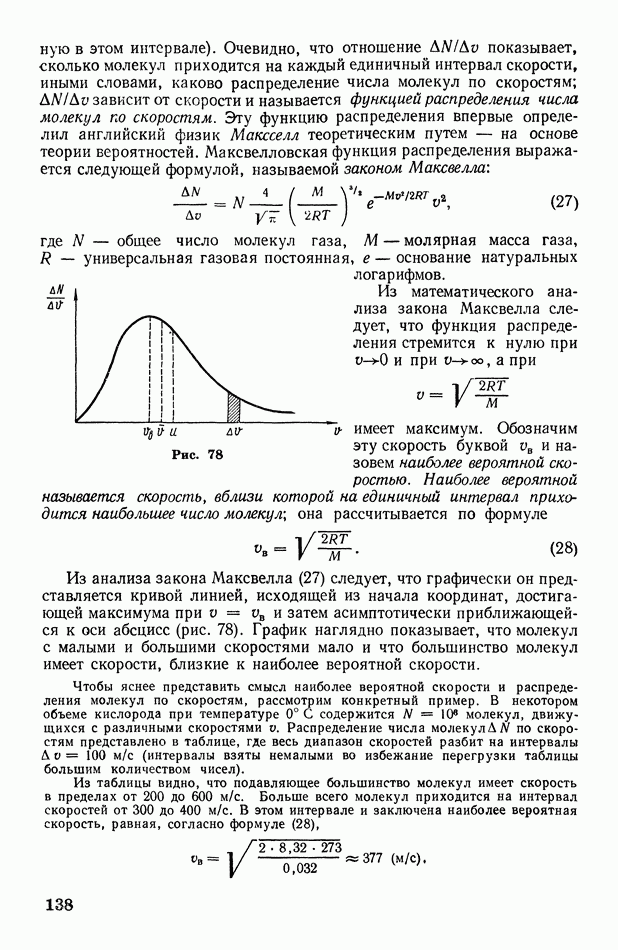
раз больше вероятности состояния  при котором все молекулы оказываются в левой части сосуда (рис. 144).
при котором все молекулы оказываются в левой части сосуда (рис. 144).
Подчеркнем, что равномерное распределение молекул по объему является вместе с тем и наиболее беспорядочным их распределением. Поэтому наиболее вероятное состояние системы является вместе с тем и наиболее беспорядочным ее состоянием. В этом смысле можно сказать, что вероятность состояния есть мера беспорядка состояния системы.
Очевидно, что предоставленная самой себе изолированная система должна перейти в наиболее вероятное, т. е. равновесное состояние. Всякое отклонение от равновесного состояния влечет за собой уменьшение вероятности состояния; очень неравновесные состояния являются практически неосуществимыми, хотя в принципе они возможны.

Рис. 144
Вернемся теперь к необратимым процессам и рассмотрим их в связи с вероятностью состояния системы. Почему, например, необратим процесс расширения газа в пустоту? Потому что расширяющийся газ, занимая весь объем сосуда, переходит в наиболее вероятное состояние равномерного распределения молекул по объему. Самопроизвольное сжатие газа означало бы скопление всех молекул в одной части сосуда, т. е. переход системы в наименее вероятное состояние  которое практически неосуществимо. Почему необратим процесс теплообмена между двумя соприкасающимися телами различной температуры? Потому что переходу теплоты от горячего тела к холодному соответствует наиболее беспорядочное (равномерное) распределение «быстрых» и «медленных» молекул по всей системе (телам), т. е. наиболее вероятное состояние системы. Передача теплоты от холодного тела к горячему означала бы увеличение порядка в распределении молекул (скопление «быстрых» молекул в одном теле, а «медленных» — в другом), т. е. самопроизвольный переход системы в менее вероятное состояние.
которое практически неосуществимо. Почему необратим процесс теплообмена между двумя соприкасающимися телами различной температуры? Потому что переходу теплоты от горячего тела к холодному соответствует наиболее беспорядочное (равномерное) распределение «быстрых» и «медленных» молекул по всей системе (телам), т. е. наиболее вероятное состояние системы. Передача теплоты от холодного тела к горячему означала бы увеличение порядка в распределении молекул (скопление «быстрых» молекул в одном теле, а «медленных» — в другом), т. е. самопроизвольный переход системы в менее вероятное состояние.
Анализ любого необратимого процесса, происходящего в конечной изолированной системе, привел бы к одному и тому же выводу: необратимые процессы необратимы потому, что они сопровождаются возрастанием вероятности состояния системы.
Вспомним о том, что (как было показано в предыдущем параграфе) необратимые процессы сопровождаются возрастанием энтропии системы.
Таким образом оказывается, что существуют две физические величины — энтропия  и вероятность состояния
и вероятность состояния  которые возрастают при необратимых процессах в изолированной системе. Поэтому естественно предположить, что между энтропией и вероятностью состояния должна существовать связь. Согласно исследованиям Больцмана, эта связь выражается формулой:
которые возрастают при необратимых процессах в изолированной системе. Поэтому естественно предположить, что между энтропией и вероятностью состояния должна существовать связь. Согласно исследованиям Больцмана, эта связь выражается формулой:

где  постоянная Больцмана (см. § 42).
постоянная Больцмана (см. § 42).
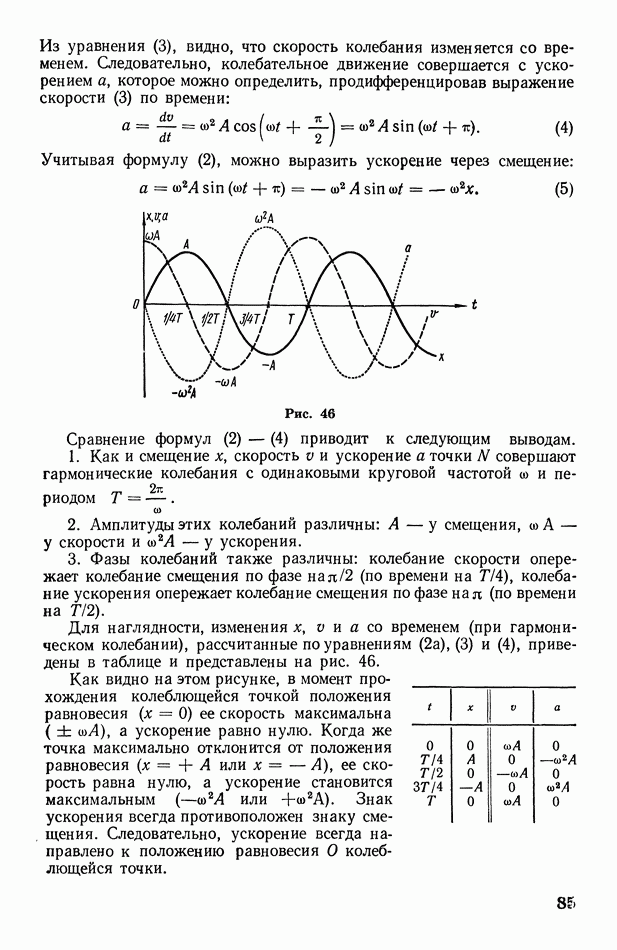
Итак, энтропия пропорциональна натуральному логарифму вероятности состояния. Следовательно, как и вероятность, энтропия является мерой беспорядка состояния системы. К такому же заключению мы пришли ранее (см. § 72) из несколько иных соображений.
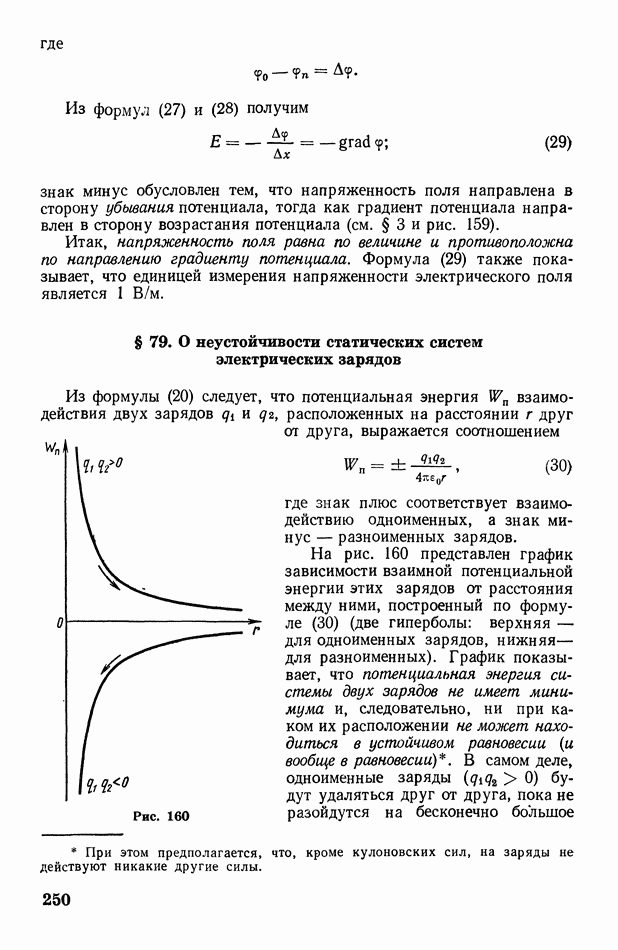
Сопоставляя неравенство Клаузиуса (28) с формулой (29), можно дать еще одну формулировку второго начала термодинамики, отражающую его статистический характер:
при необратимых процессах, протекающих в конечной изолированной системе, вероятность состояния системы возрастает, при обратимых процессах — остается неизменной.
Необходимо подчеркнуть, что второе начало термодинамики (принцип возрастания энтропии) не столь универсально, как первое начало (закон сохранения энергии). В самом деле, случаи уменьшения энтропии (и вероятности состояния) не исключены: они принципиально возможны, хотя мало вероятны. Наглядным примером этому служит броуновское движение (см. § 36). Под влиянием нескомпенсированных ударов молекул броуновская частица может, например, переместиться вверх, против действия силы тяжести. В этом случае некоторое количество теплоты системы самопроизвольно (без воздействия внешних сил) переходит в механическую энергию, т. е. теплота превращается в работу. Иначе говоря, беспорядочное движение молекул самопроизвольно переходит в упорядоченное движение броуновской частицы. При этом энтропия и вероятность состояния системы уменьшаются, что противоречит принципу возрастания энтропии.
Как объяснить это противоречие? Дело в том, что принцип возрастания энтропии применим только к конечным изолированным системам, т. е. к системам, состоящим из достаточно большого, конечного числа молекул. К бесконечным системам и системам, состоящим из малого числа молекул, этот принцип неприменим. Это нетрудно понять. В системе из малого числа молекул вероятность равновесного состояния незначительно превосходит вероятность неравновесного состояния. Например, в случае системы из двух молекул (см. рис. 143, б) вероятность равновесного состояния всего лишь вдвое больше вероятности
любого из неравновесных состояний. Переход такой системы в неравновесное  тояние и уменьшение ее энтропии весьма вероятны и часто имеют место.
тояние и уменьшение ее энтропии весьма вероятны и часто имеют место.
Что касается бесконечной системы  то в этом случае число состояний становится бесконечно большим. Кроме того, становится бесконечно большим число способов, которыми может осуществиться любое из этих состояний, как равновесие, так и неравновесие. Очевидно, что в этих условиях бессмысленно говорить о наиболее вероятном (равновесном) состоянии системы, ибо все ее состояния равновероятны. Поэтому вероятность состояния и энтропия бесконечной системы остаются неизменными. Следовательно, принцип возрастания энтропии неприменим к бесконечной системе.
то в этом случае число состояний становится бесконечно большим. Кроме того, становится бесконечно большим число способов, которыми может осуществиться любое из этих состояний, как равновесие, так и неравновесие. Очевидно, что в этих условиях бессмысленно говорить о наиболее вероятном (равновесном) состоянии системы, ибо все ее состояния равновероятны. Поэтому вероятность состояния и энтропия бесконечной системы остаются неизменными. Следовательно, принцип возрастания энтропии неприменим к бесконечной системе.
В середине XIX в. в связи с открытием второго начала термодинамики возникла так называемая проблема тепловой смерти Вселенной. Суть ее сводилась к следующему. Энтропия Вселенной как изолированной системы все время возрастает, стремясь к некоторому максимуму. В связи с этим различные виды энергии все в большей и большей степени обесцениваются, превращаясь в теплоту. Теплота переходит от горячих тел к холодным. Наконец, температура всех частей и тел Вселенной уравнивается. Устанавливается полное тепловое равновесие: все процессы во Вселенной прекращаются, наступает тепловая смерть Вселенной.
Этот реакционный вывод ведет к другому, не менее реакционному выводу: раз будет конец Вселенной, значит, было ее начало, когда возникло неравновесное состояние, из которого Вселенная переходит постепенно к равновесию. Религия не преминула воспользоваться этим выводом для «научного обоснования» актов сотворения и конца мира.
Ошибочность вывода о тепловой смерти заключается в неправомерном применении принципа возрастания энтропии к бесконечной системе (Вселенной). На несостоятельность этого вывода указал в свое время Энгельс, исходя из общефилософских соображений о бесконечности Вселенной во времени. Он отметил также, что тепловая смерть Вселенной, означая потерю энергией способности к превращениям, противоречит закону сохранения энергии. Способность к превращениям является неотъемлемым свойством энергии. Не подлежит сомнению, что наряду с процессами обесценивания энергии, распространенными в земных условиях, в иных частях космоса столь же распространены пока мало известные нам процессы саморазвития Вселенной, ведущие к концентрации теплоты и превращению ее в другие виды энергии.
Вселенная в целом не находится в равновесии и не стремится к какому-либо пределу. Она развивается, и возможности ее развития неисчерпаемы и неограниченны.
В заключение коснемся тепловой теоремы Нернста, согласно которой энтропия равна нулю при абсолютном нуле температуры.

Это утверждение следует из соотношения (29). В самом дзле, при абсолютном нуле состоянию термодинамической системы соответствует минимальный беспорядок (наибольший порядок): все атомы находятся в определенных местах (узлах кристаллической решетки твердого тела), а все электроны располагаются на самых низких энергетических уровнях. Такое состояние, являясь при абсолютном нуле единственно возможным (достоверным), обладает вероятностью, равной единице. Следовательно,  Отметим, что немецкий физик Нернст пришел к соотношению (30) иным путем — изучая изменения теплоемкости тел при низких температурах.
Отметим, что немецкий физик Нернст пришел к соотношению (30) иным путем — изучая изменения теплоемкости тел при низких температурах.
Рассмотренные в этой главе два начала термодинамики и тепловая теорема Нернста (называемая иногда третьим началом термодинамики) лежат в основе теплотехники, позволяя анализировать всевозможные термодинамические процессы и рассчитывать различные тепловые машины (двигатели внутреннего сгорания, паровые и реактивные двигатели).
Задача 38. Кислород массой  находящийся при нормальных условиях, сжимают до объема
находящийся при нормальных условиях, сжимают до объема  Найти давление
Найти давление  и температуру
и температуру  кислорода после сжатия и работу А сжатия, если кислород сжимают: а) изотермически; б) адиабатически.
кислорода после сжатия и работу А сжатия, если кислород сжимают: а) изотермически; б) адиабатически.
Решение, а) Применяя уравнения Клапейрона — Менделеева [(см. § 40, формула (11)] к начальному состоянию газа, выразим объем кислорода до сжатия:

где, по условию,  Тогда
Тогда

При изотермическом процессе  Из закона Бойля — Мариотта [см. § 39, формула (1)] следует, что
Из закона Бойля — Мариотта [см. § 39, формула (1)] следует, что

Работу сжатия определим по формуле (5), учитывая, что сжатию подвергнуто  молей кислорода:
молей кислорода:

б) Применяя законы Пуассона [см. (12) и (11)] и учитывая, что для кислорода отношение теплоемкостей  (см. § 44), получим
(см. § 44), получим

и

Работу сжатия газа определим по формуле (13), учитывая, что сжатию подвергнуто  молей кислорода и что его молярная теплоемкость при постоянном объеме
молей кислорода и что его молярная теплоемкость при постоянном объеме  (число степеней свободы молекулы кислорода
(число степеней свободы молекулы кислорода 

Итак, работа изотермического сжатия кислорода оказывается меньше работы его адиабатического сжатия.
В обоих случаях работа сжатия отрицательна, так как ее совершают внешние силы (см. § 69).
Задача 39. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу  Температура нагревателя
Температура нагревателя  температура холодильника
температура холодильника  Найти коэффициент полезного действия машины
Найти коэффициент полезного действия машины  количество теплоты
количество теплоты  получаемое машиной за один цикл от нагревателя, и количество теплоты
получаемое машиной за один цикл от нагревателя, и количество теплоты  отдаваемое за один цикл холодильнику.
отдаваемое за один цикл холодильнику.
Решение. По формуле (20) найдем

Согласно формуле (16), работа, совершаемая идеальной тепловой машиной за один цикл, равна

Но, по формуле (18),

Поэтому

Тогда

Задача 40. Кусок льда массой  имевший температуру
имевший температуру  превращен в пар при температуре
превращен в пар при температуре  Определить изменение энтропии
Определить изменение энтропии  полагая, что давление
полагая, что давление  Па оставалось неизменным. Удельная теплоемкость льда
Па оставалось неизменным. Удельная теплоемкость льда  удельная теплоемкость воды
удельная теплоемкость воды  удельная теплота плавления льда
удельная теплота плавления льда  удельная теплота кипения воды
удельная теплота кипения воды 
Решение. Согласно формуле (27), изменение энтропии системы

где  количество теплоты, получаемое (или отдаваемое) системой при температуре
количество теплоты, получаемое (или отдаваемое) системой при температуре  характеристики начального и конечного состояний системы (см. § 72).
характеристики начального и конечного состояний системы (см. § 72).
В рассматриваемом случае система, переходя из начального состояния (лед) в конечное (пар), подвергается следующим изменениям!
а) Лед нагревается от температуры  до температуры плавления
до температуры плавления  При этом, согласно формуле (27), его энтропия изменяется на величину
При этом, согласно формуле (27), его энтропия изменяется на величину

где  количество теплоты, получаемое льдом при изменении температуры на величину
количество теплоты, получаемое льдом при изменении температуры на величину 
б) Лед плавится, превращаясь в воду, при постоянной температуре Т. При этом его энтропия изменяется на величину

где  количество теплоты, полученное льдом при плавлении.
количество теплоты, полученное льдом при плавлении.
в) Вода нагревается от температуры То до температуры кипения  При этом ее энтропия изменяется на величину
При этом ее энтропия изменяется на величину

где  количество теплоты, получаемой водой при изменении температуры на величину
количество теплоты, получаемой водой при изменении температуры на величину 
г) Вода выкипает, превращаясь в пар, при постоянной температуре  этом ее энтропия изменяется на величину
этом ее энтропия изменяется на величину

где  количество теплоты, полученное водой при испарении (кипении).
количество теплоты, полученное водой при испарении (кипении).
Общее изменение энтропии системы

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
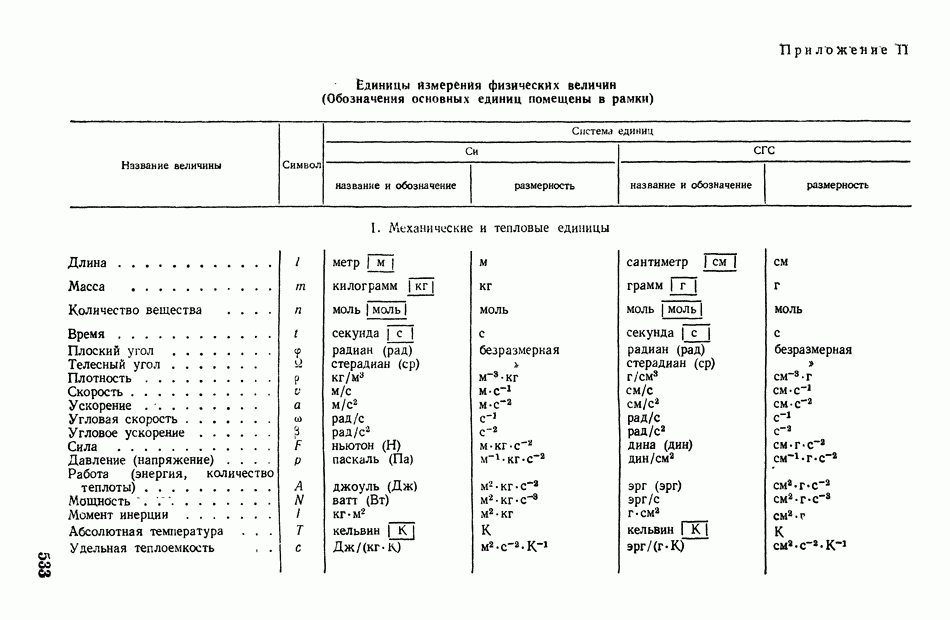
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
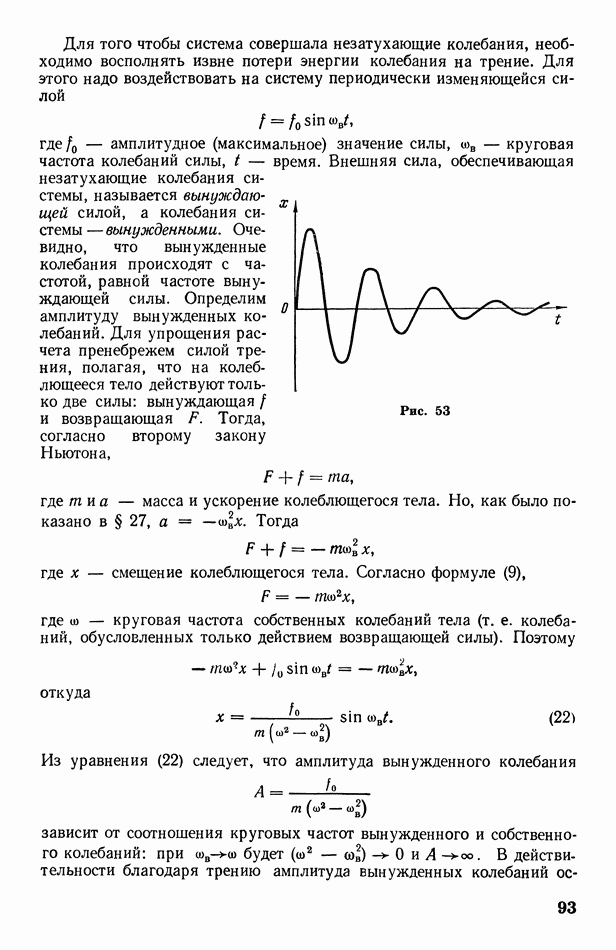
- § 30. О затухающих и вынужденных колебаниях
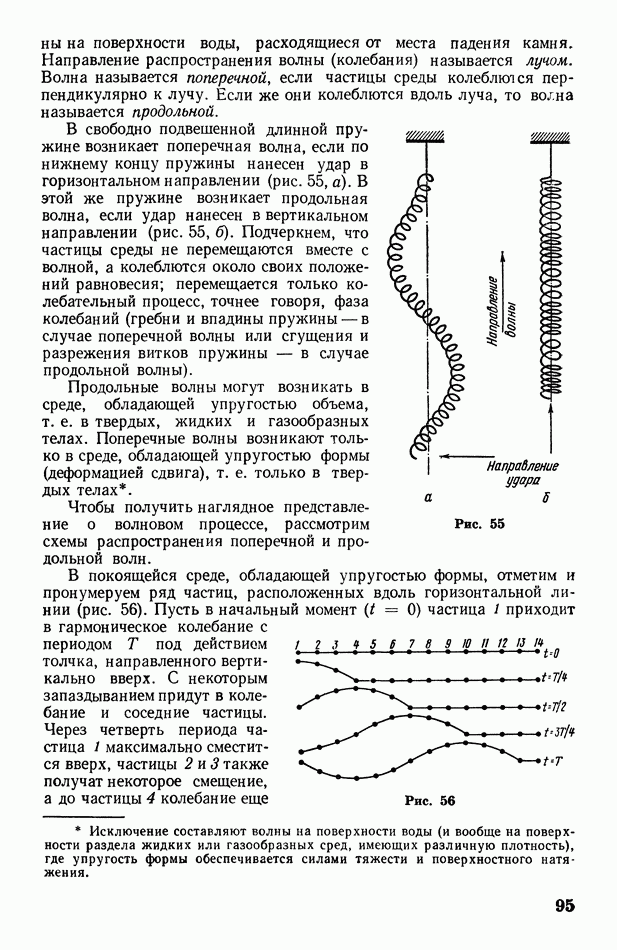
- § 31. Волновой процесс
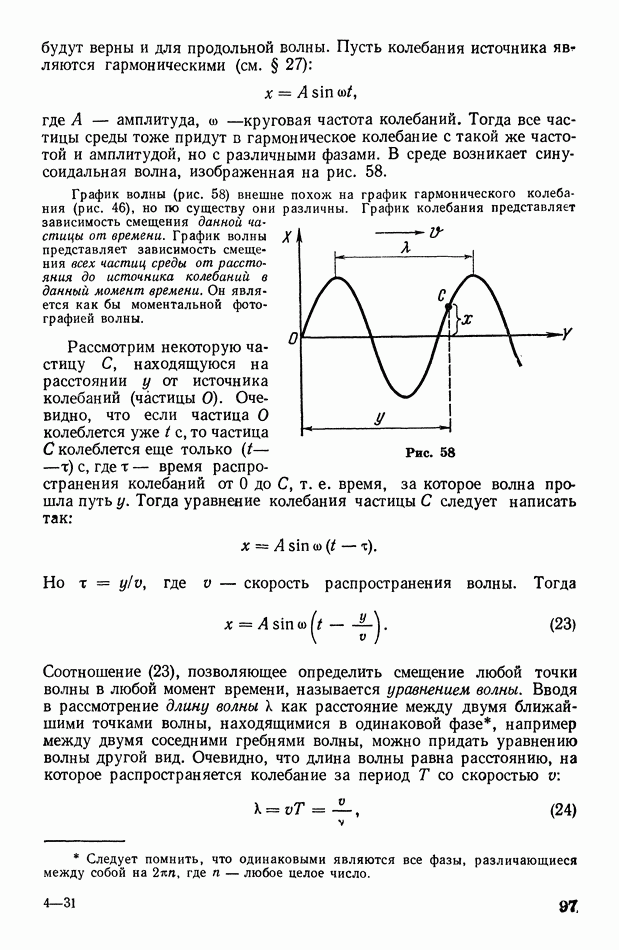
- § 32. Уравнение волны. Интенсивность волны
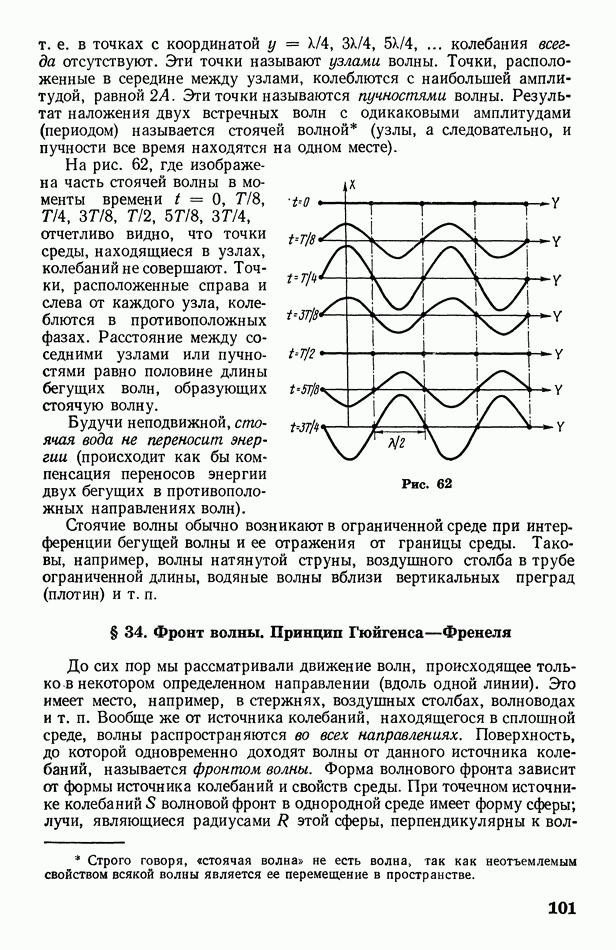
- § 33. Интерференция волн. Стоячие волны
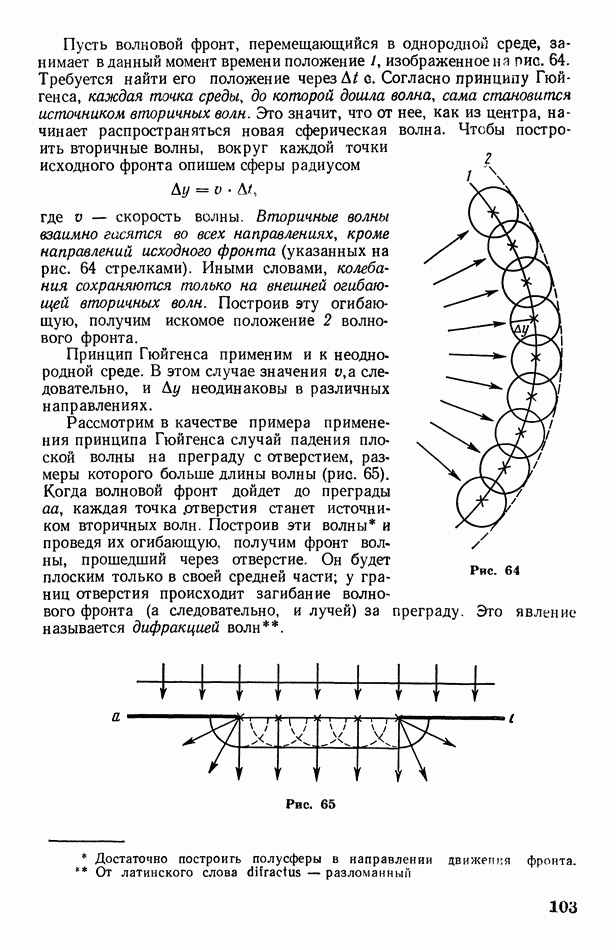
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
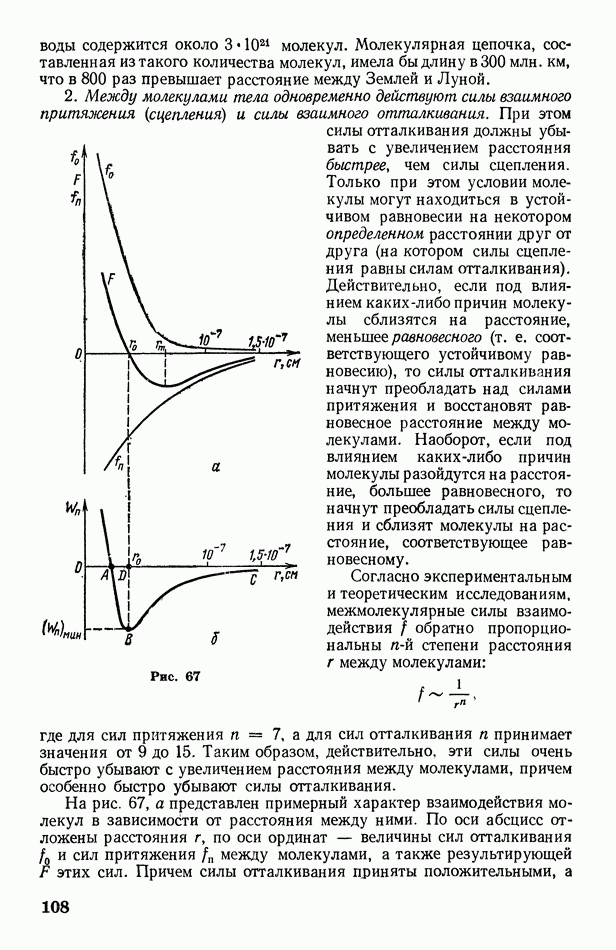
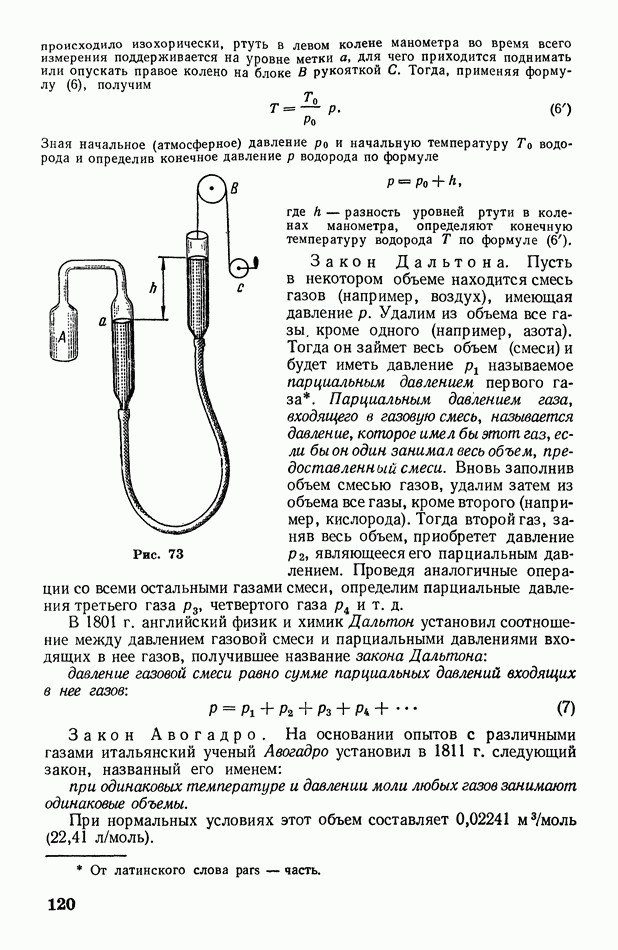
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
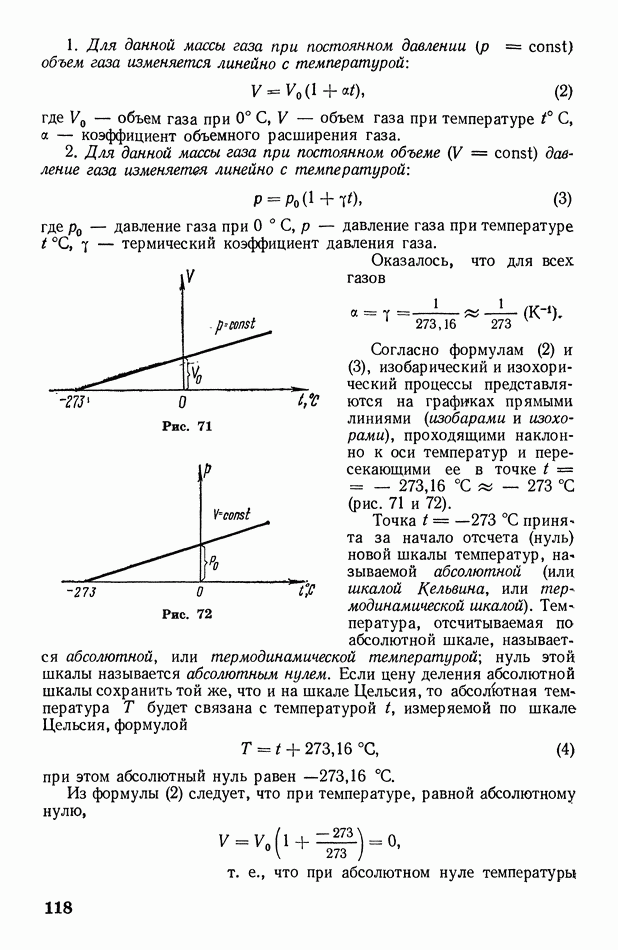
- § 51. Особенности строения жидкостей и твердых тел
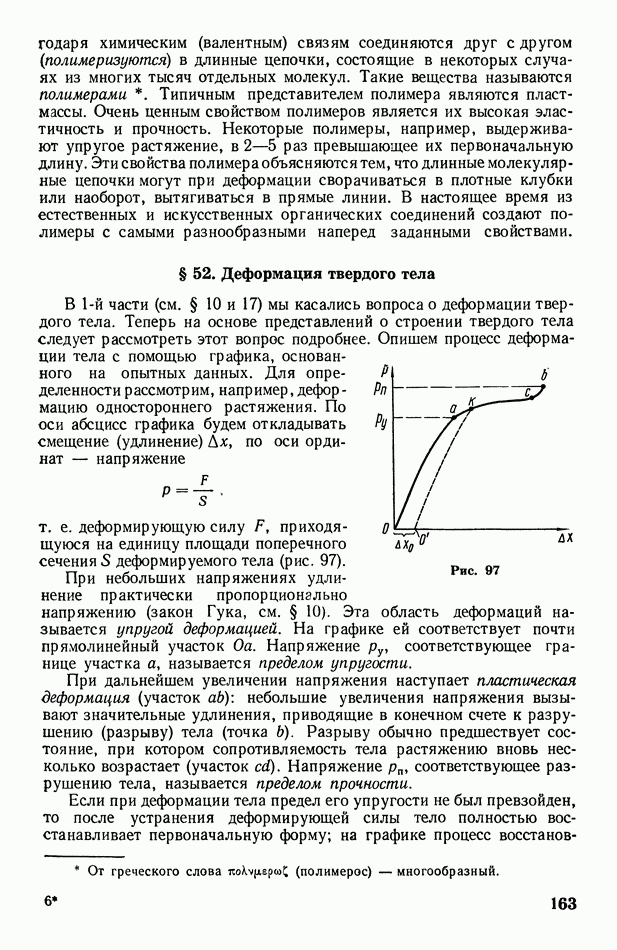
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
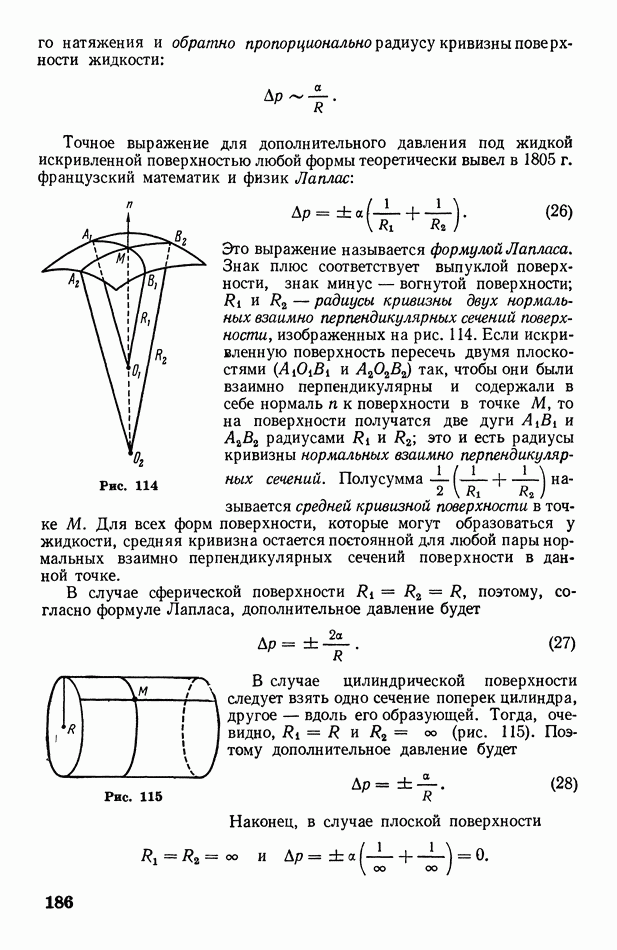
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
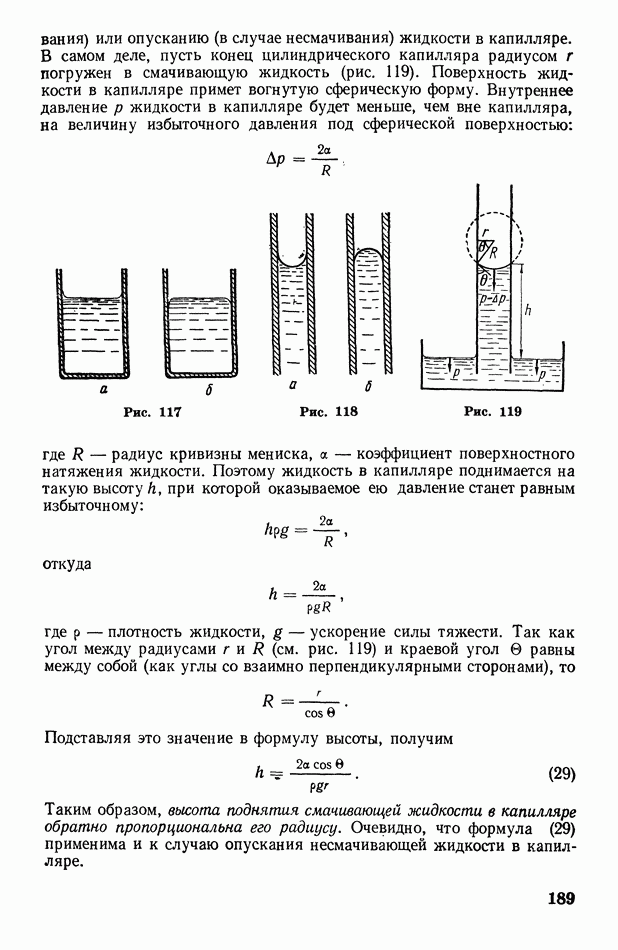
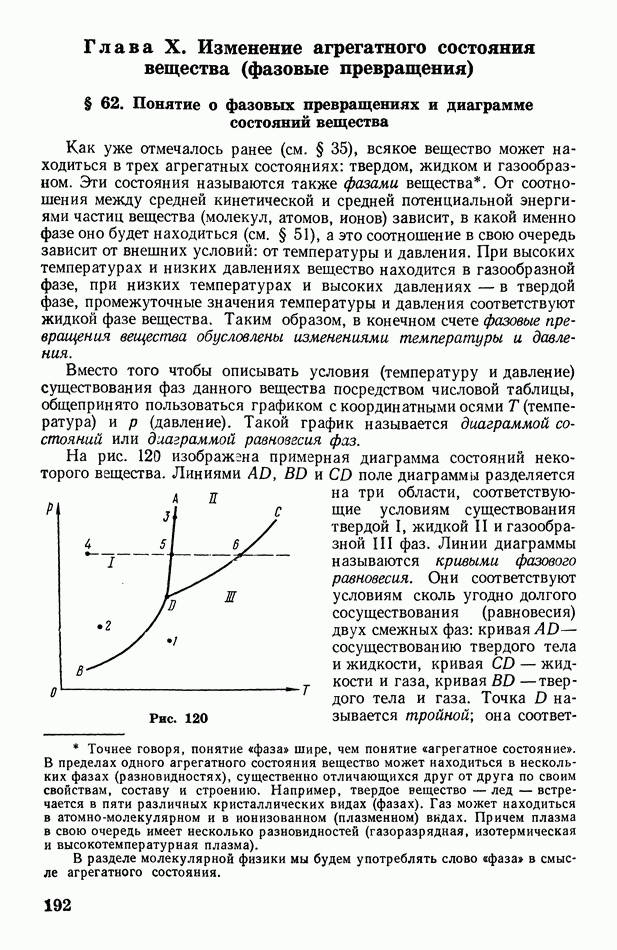
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
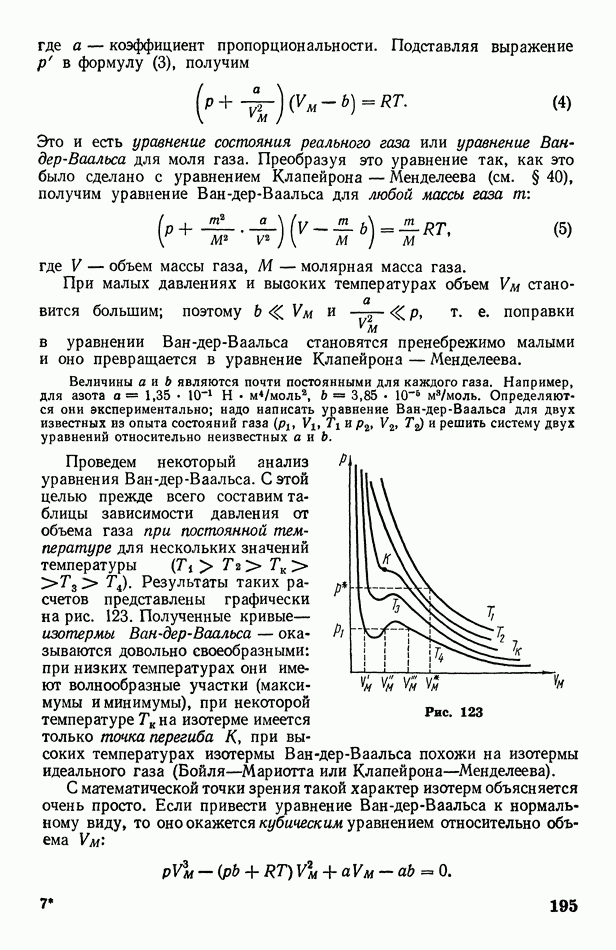
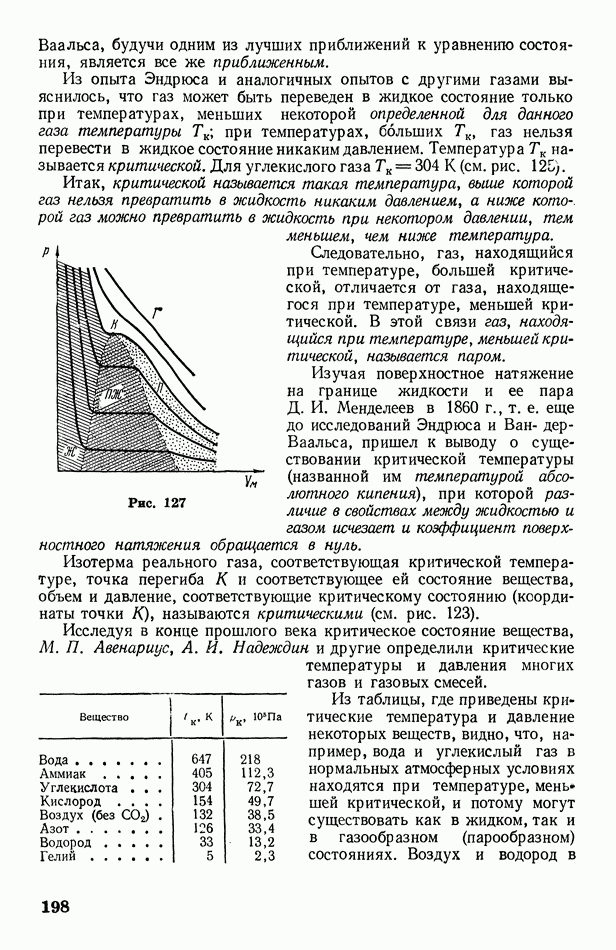
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
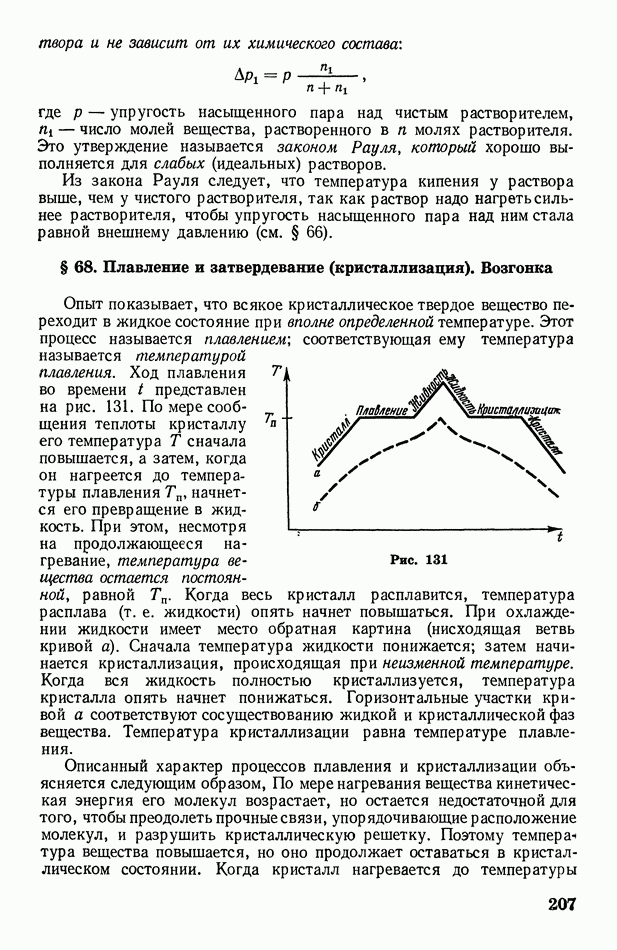
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
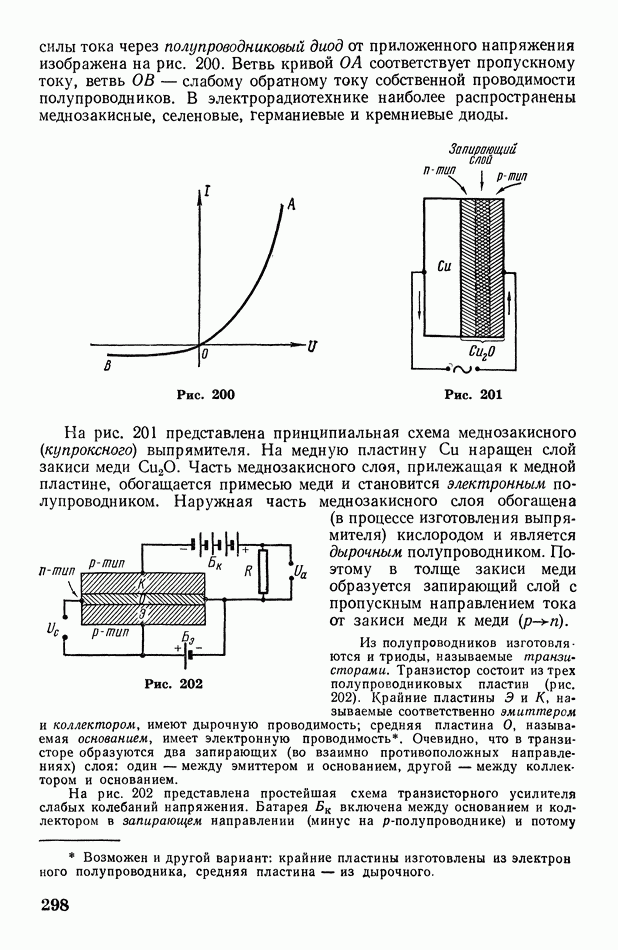
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
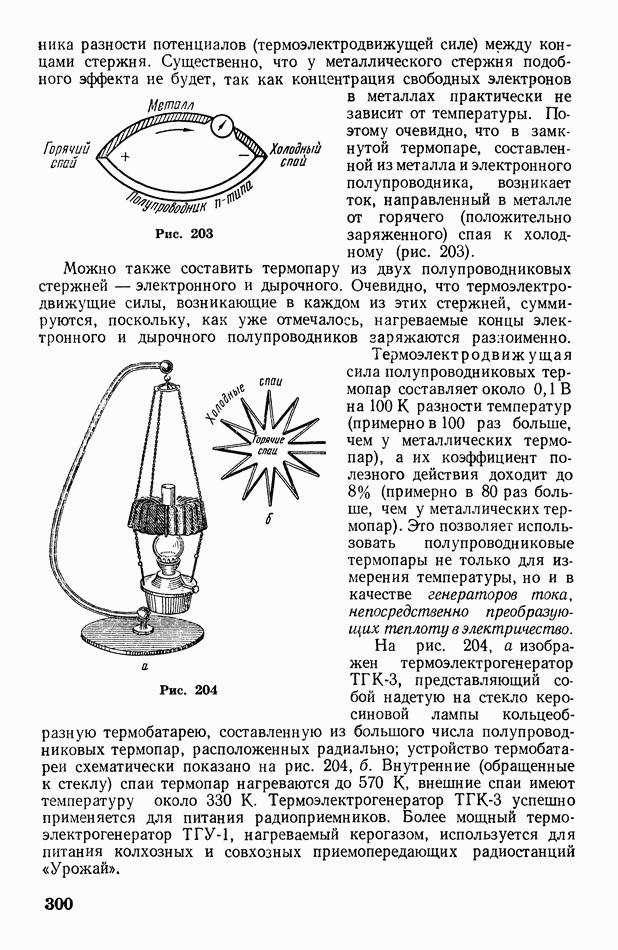
- Глава XI. Основы термодинамики
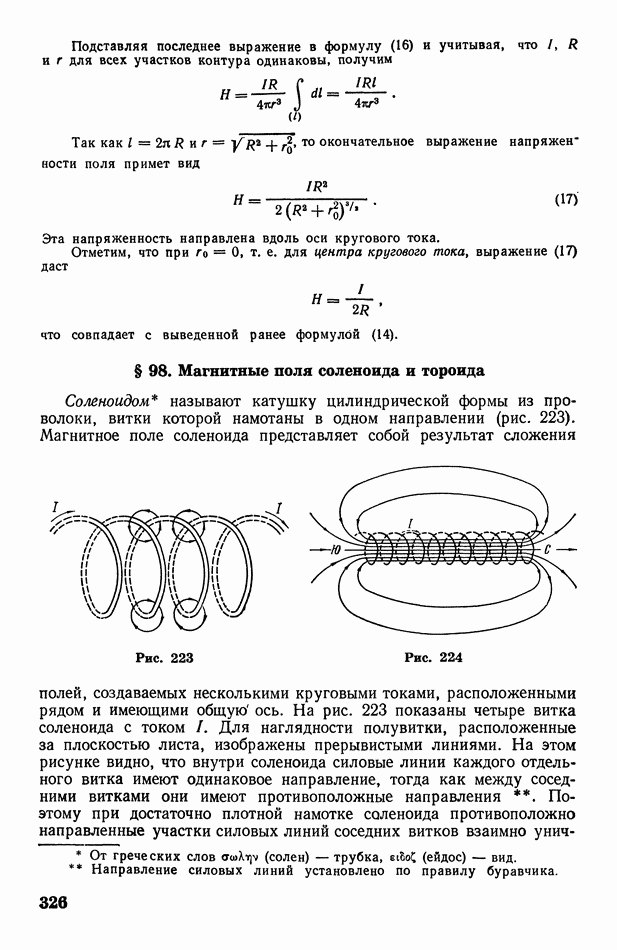
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
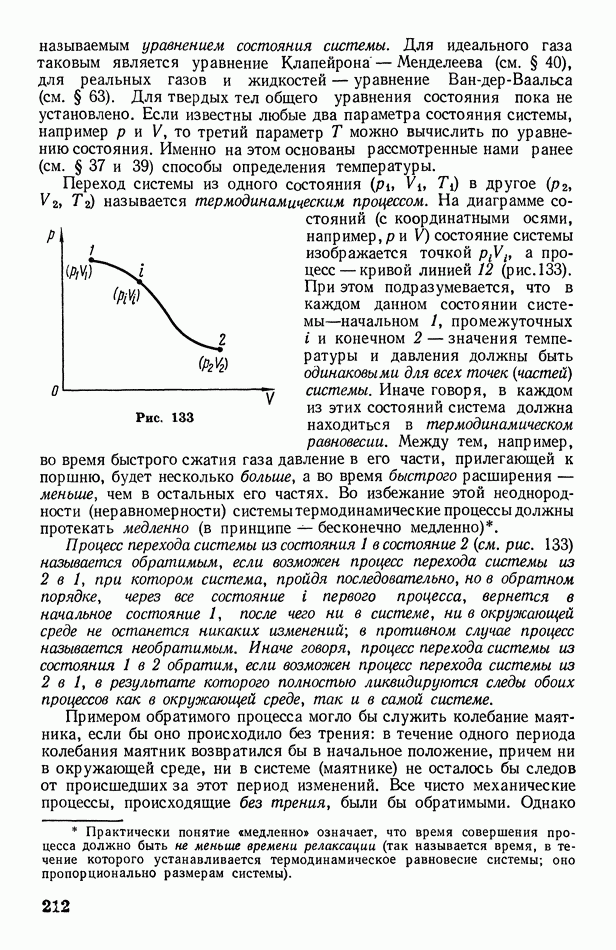
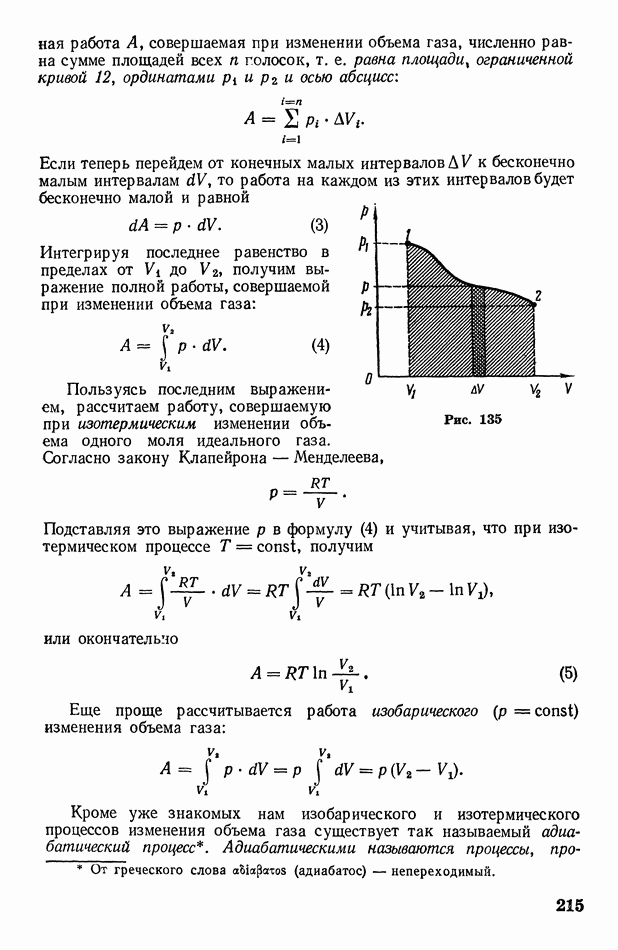
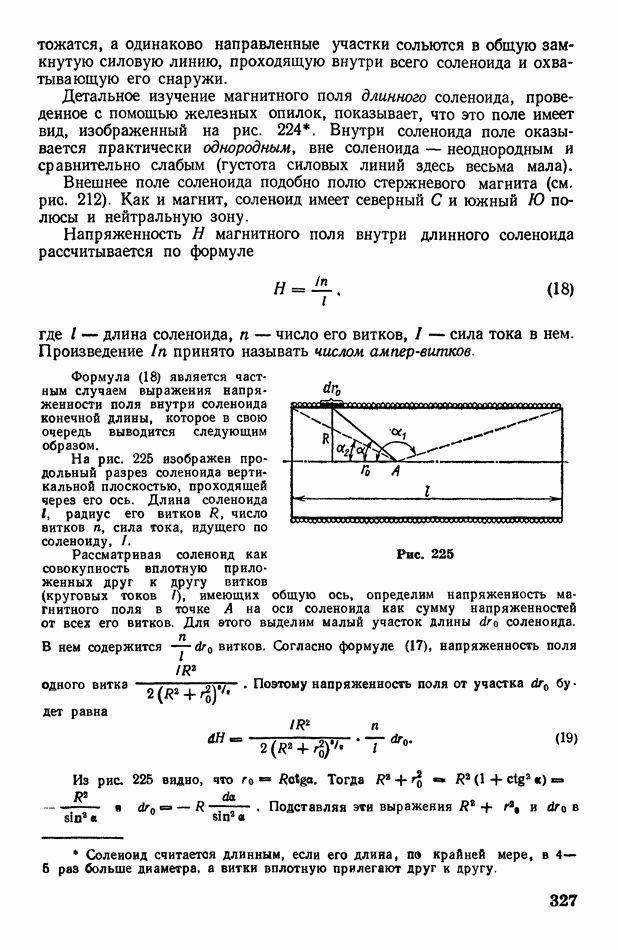
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
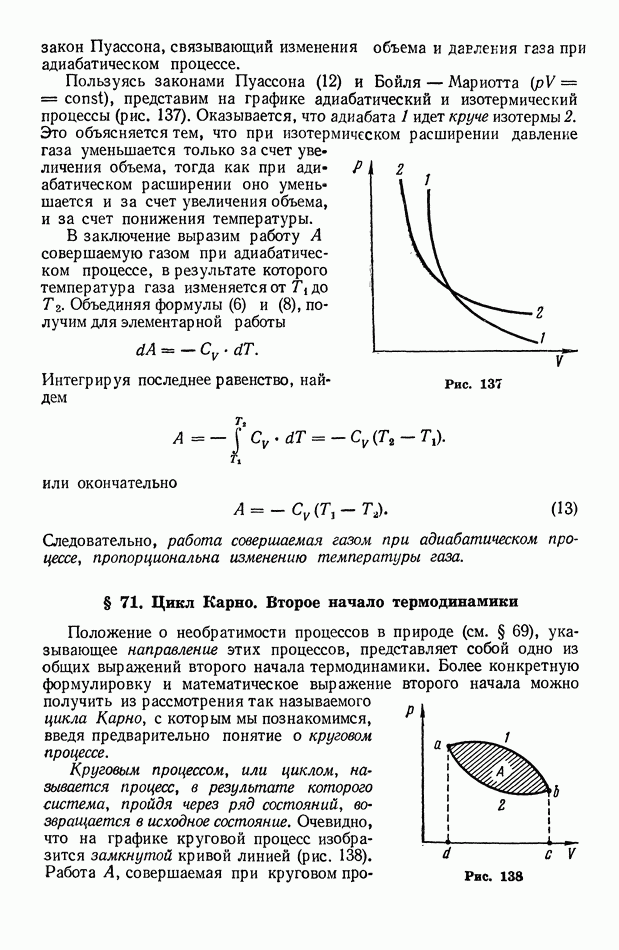
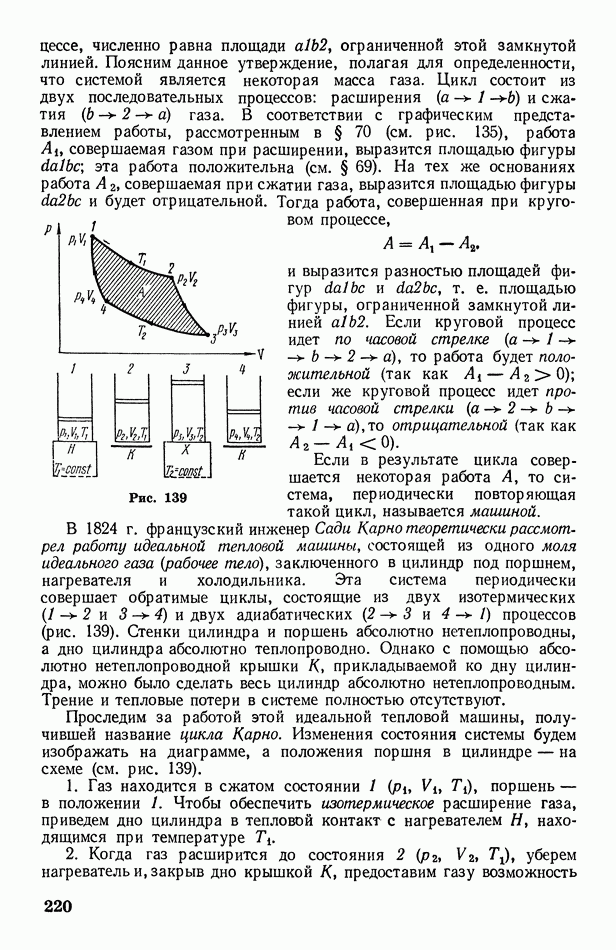
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
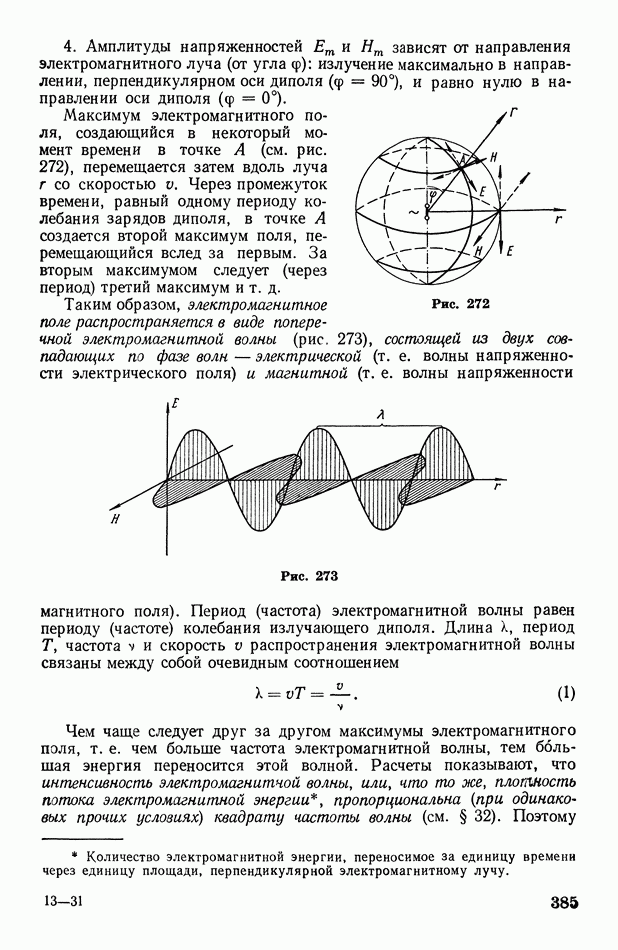
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
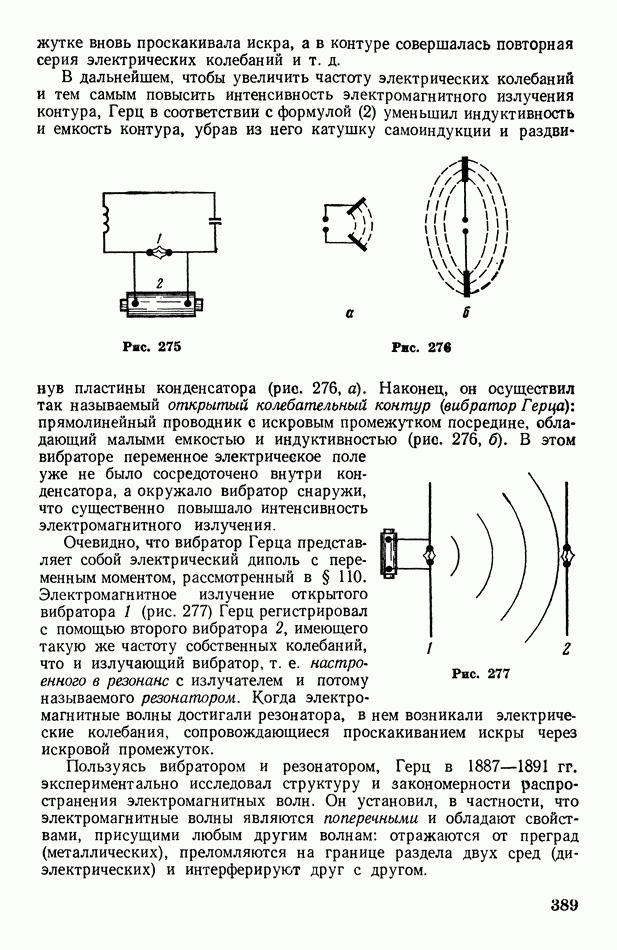
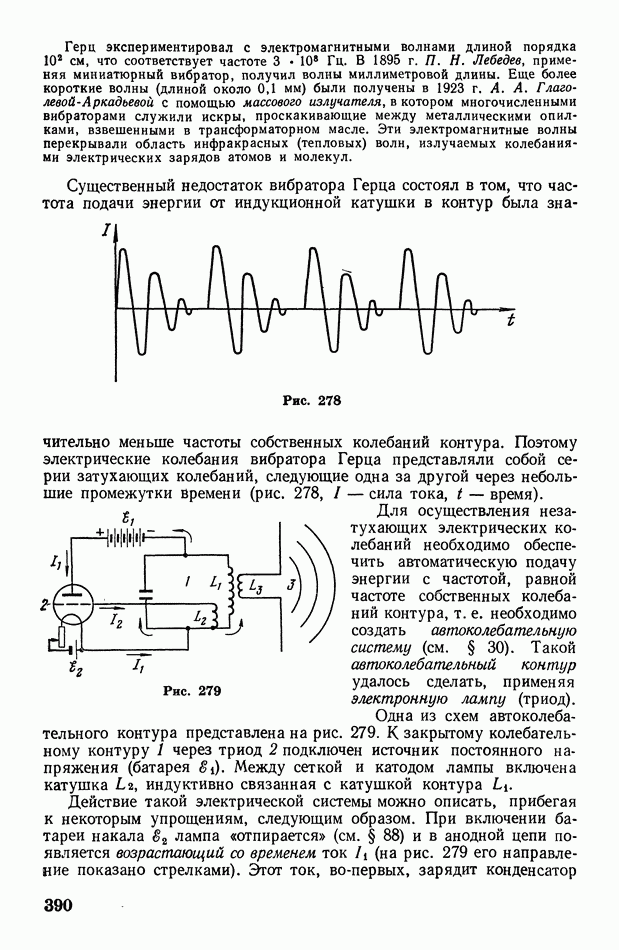
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
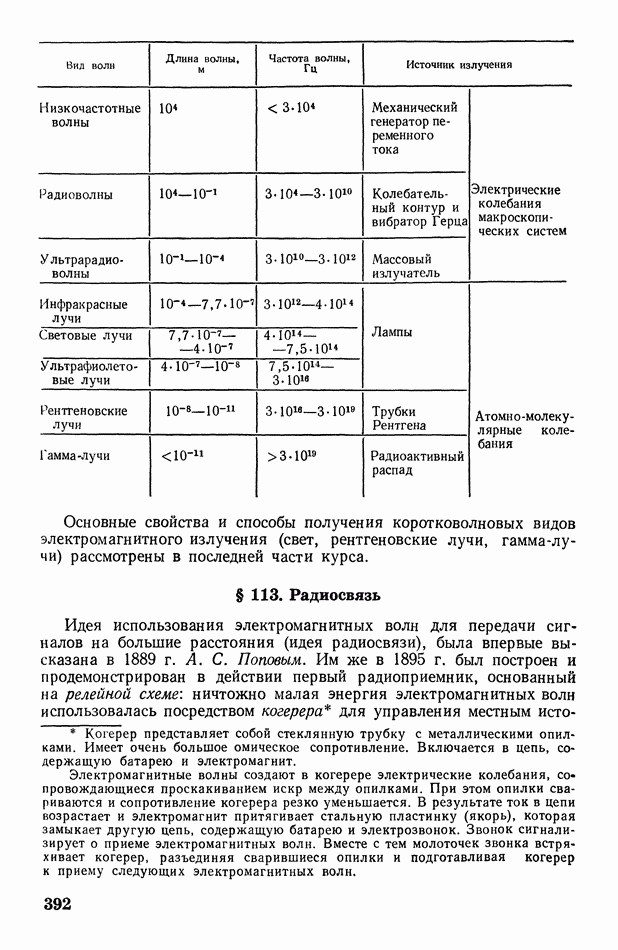
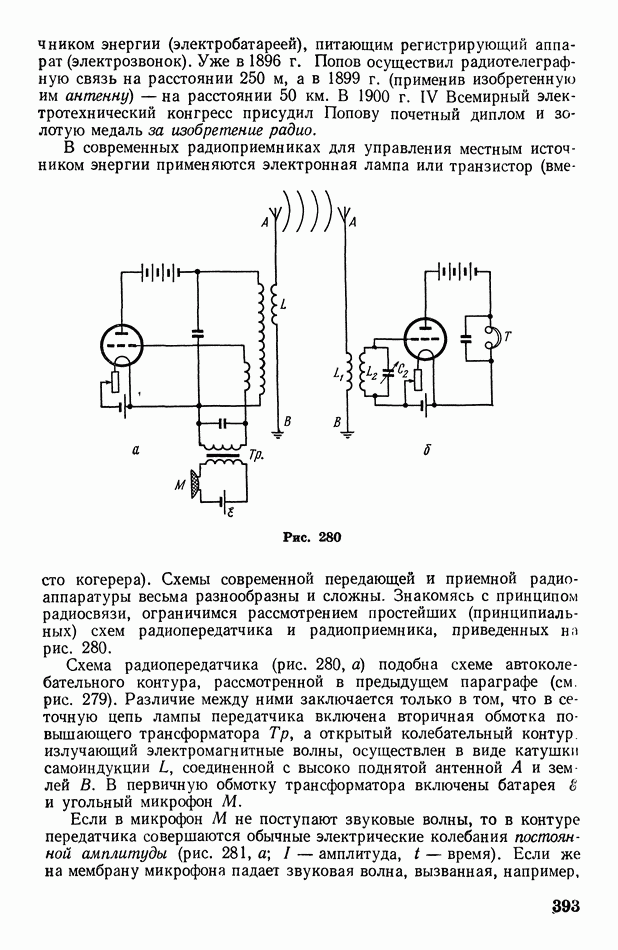
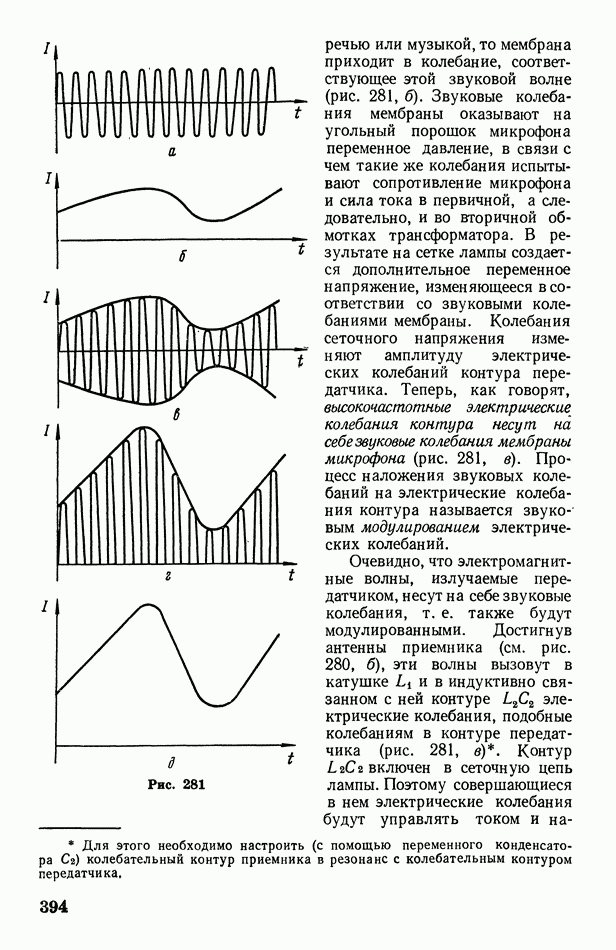
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
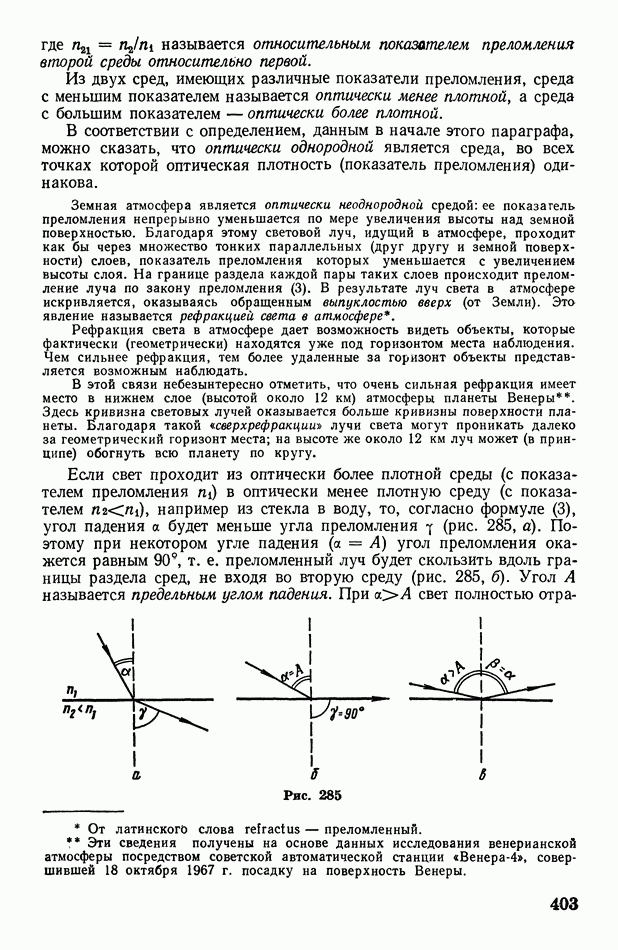
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
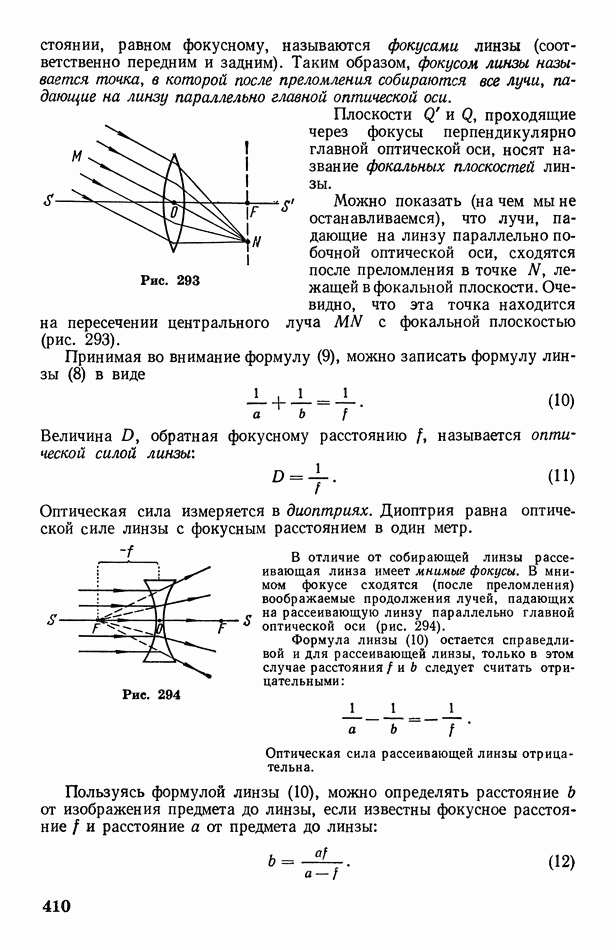
- § 117. Тонкие линзы. Микроскоп
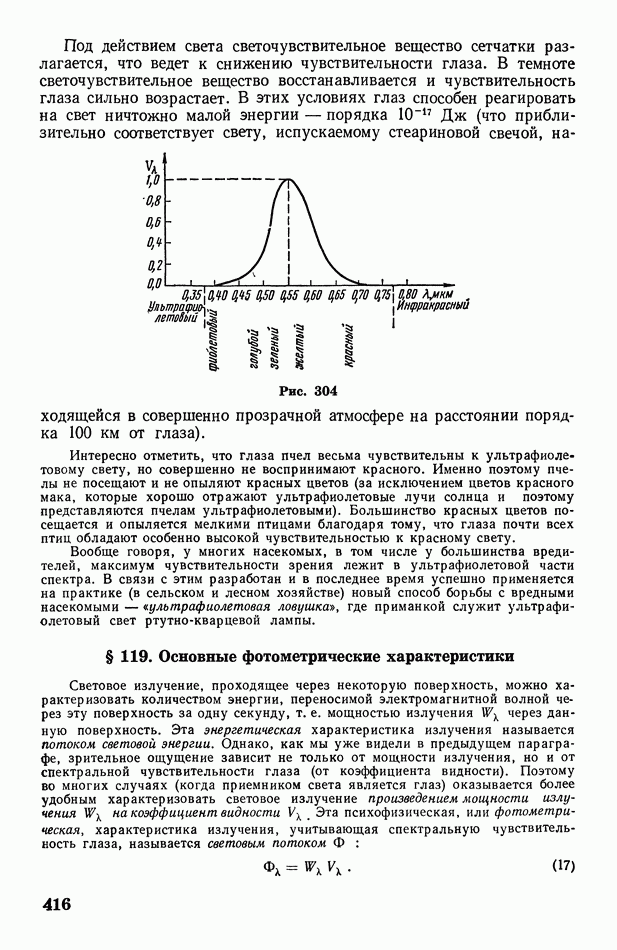
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
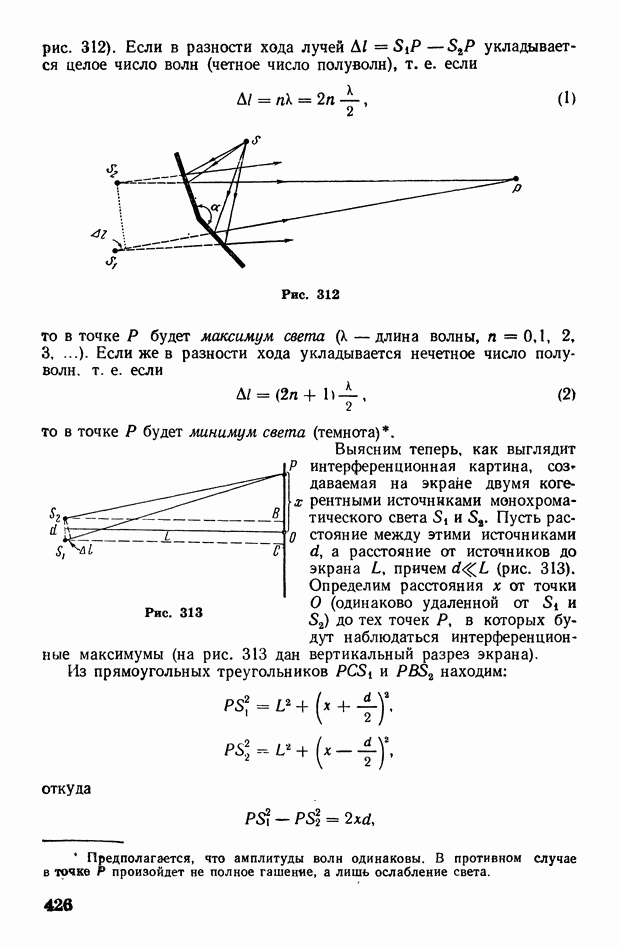
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
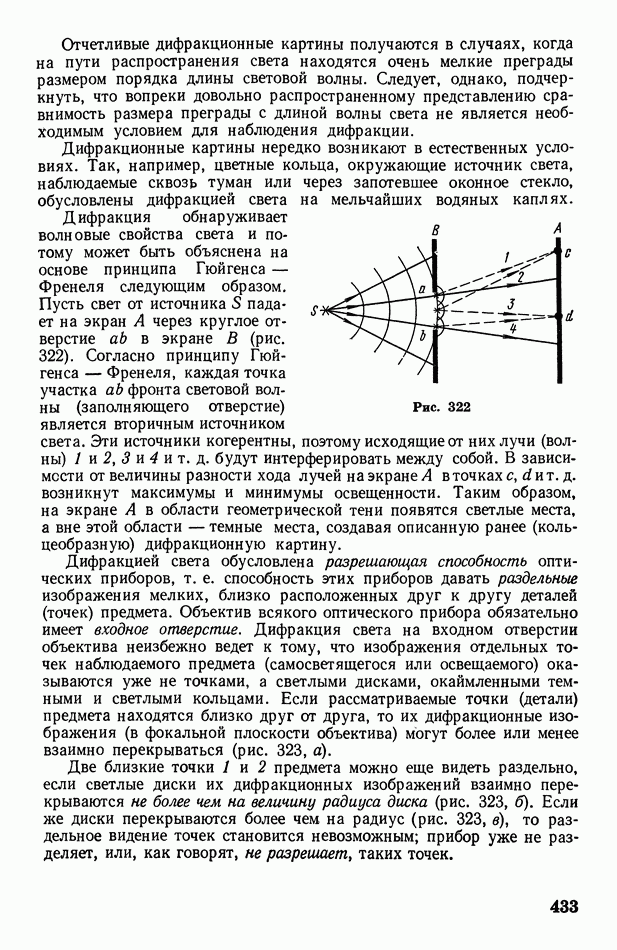
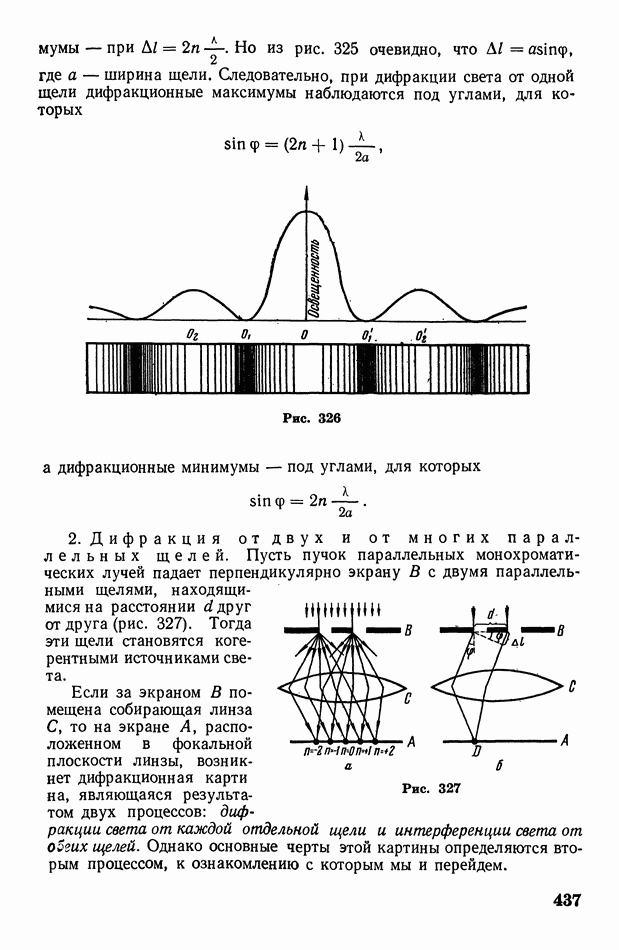
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
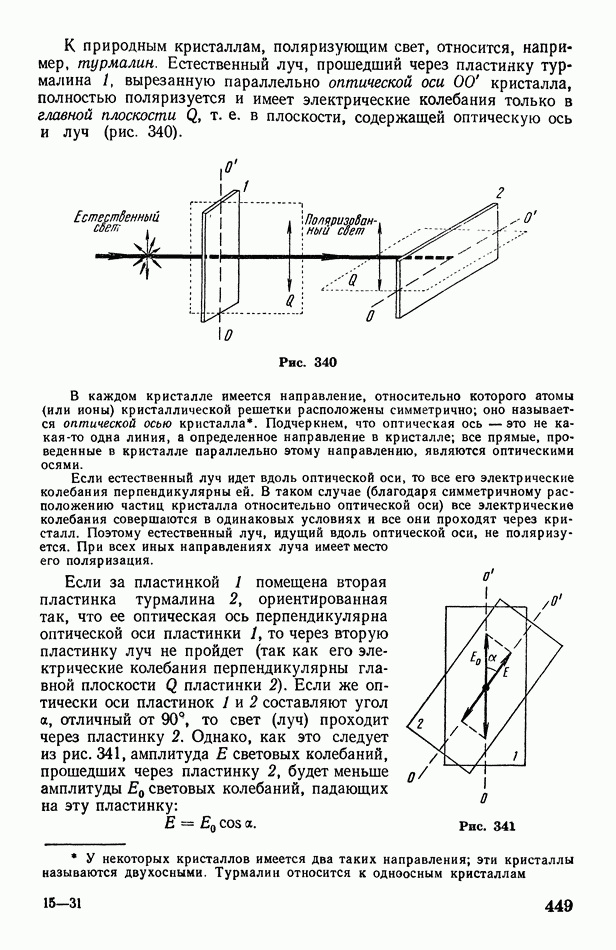
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
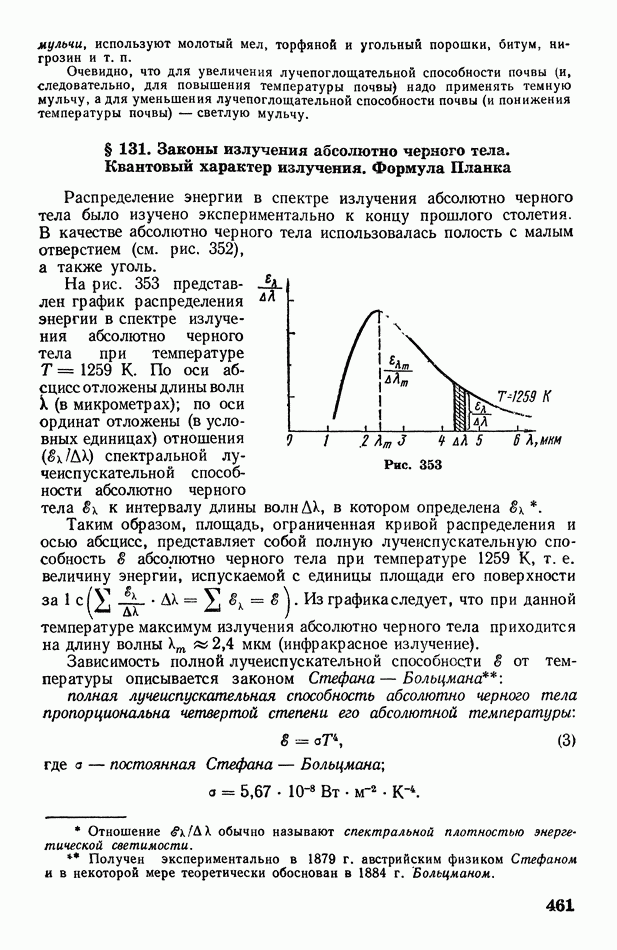
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
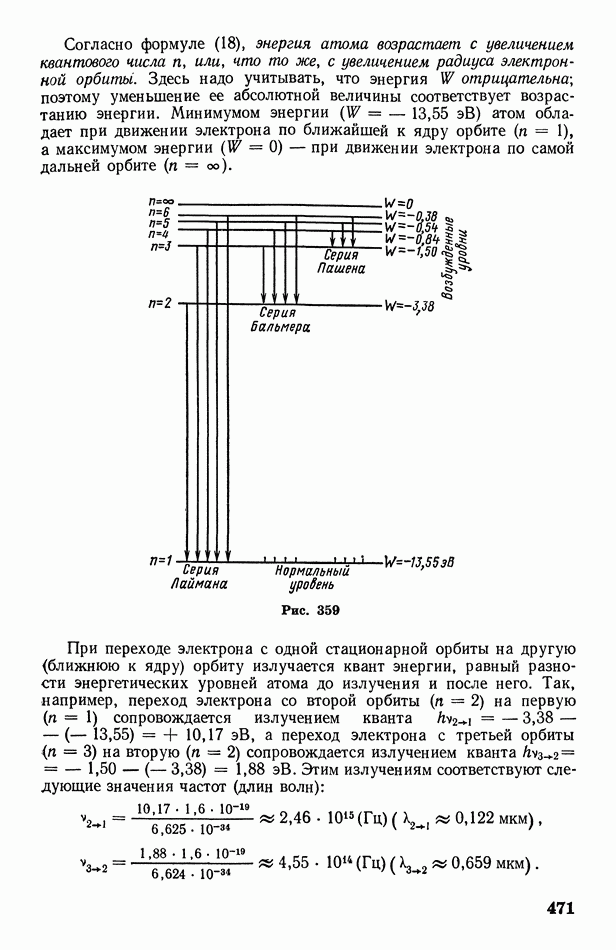
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
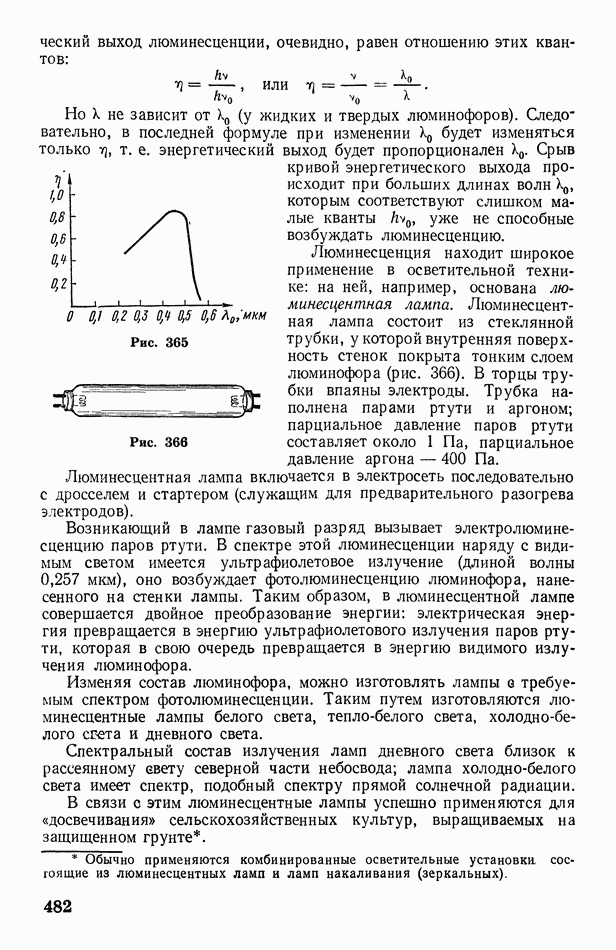
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
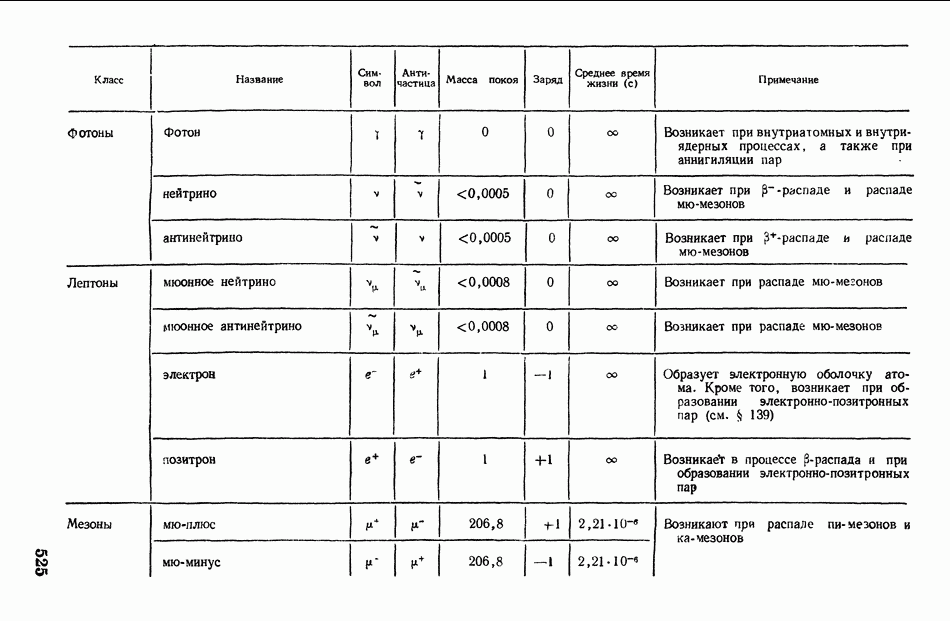
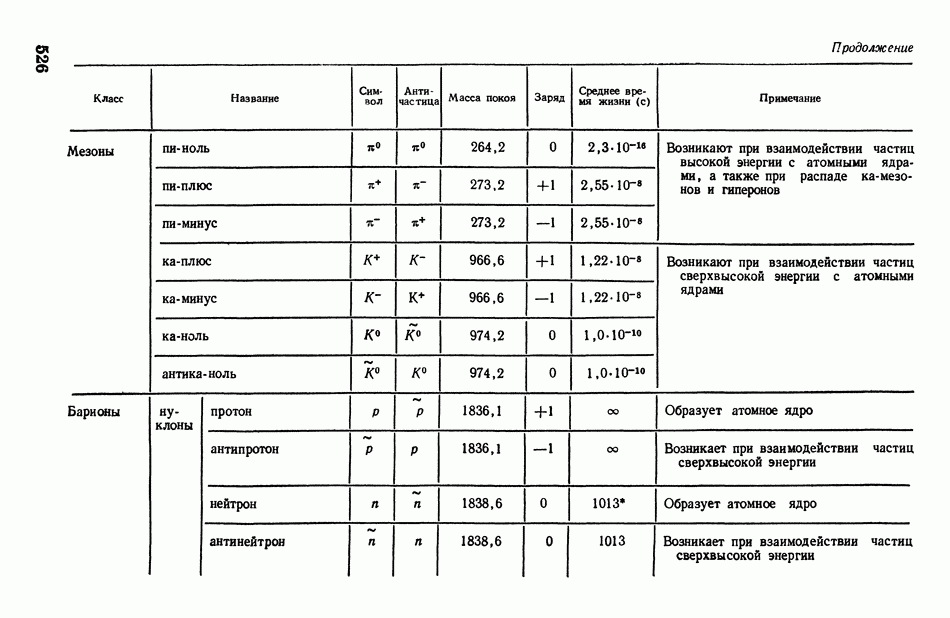
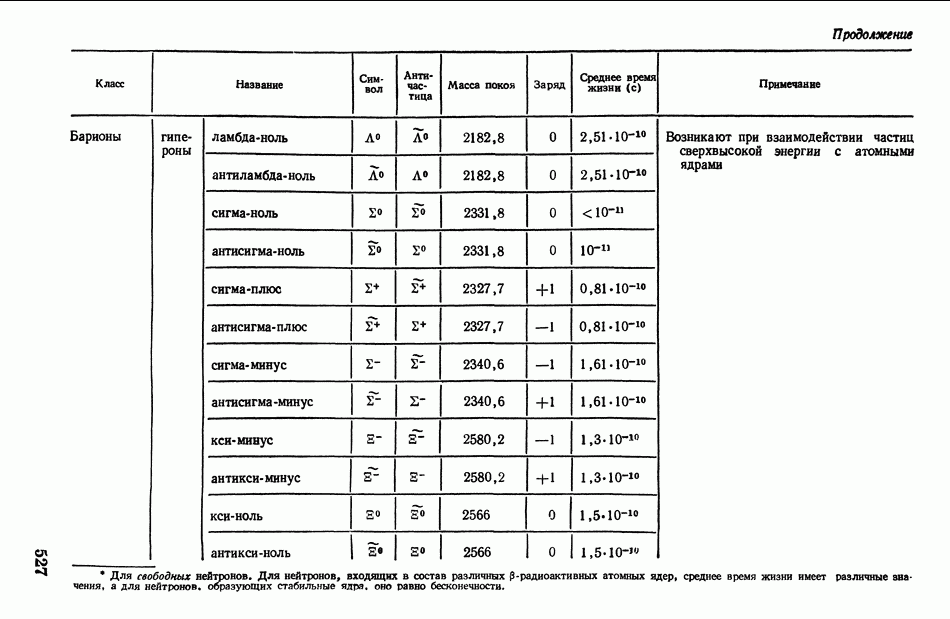
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии