| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 117. Тонкие линзы. Микроскоп
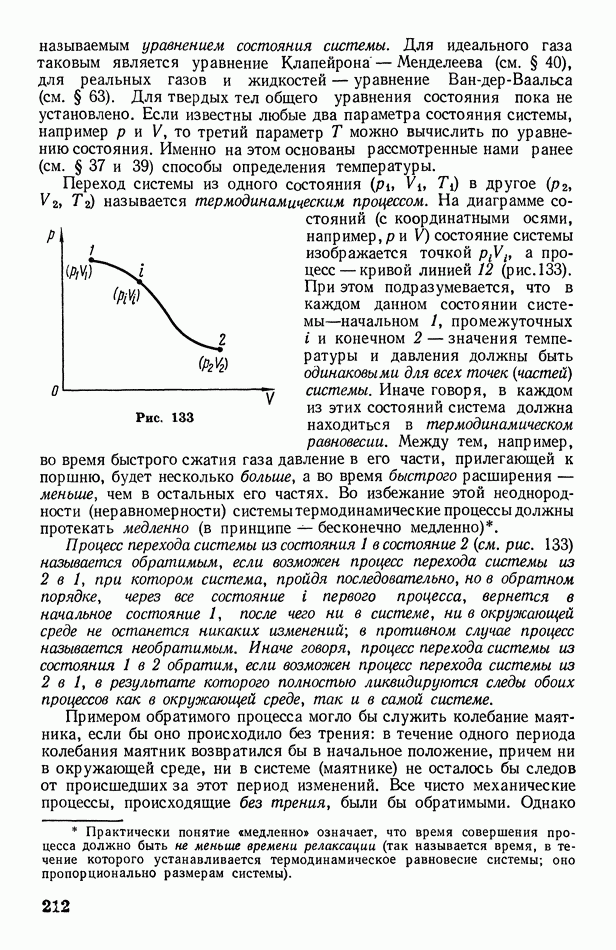
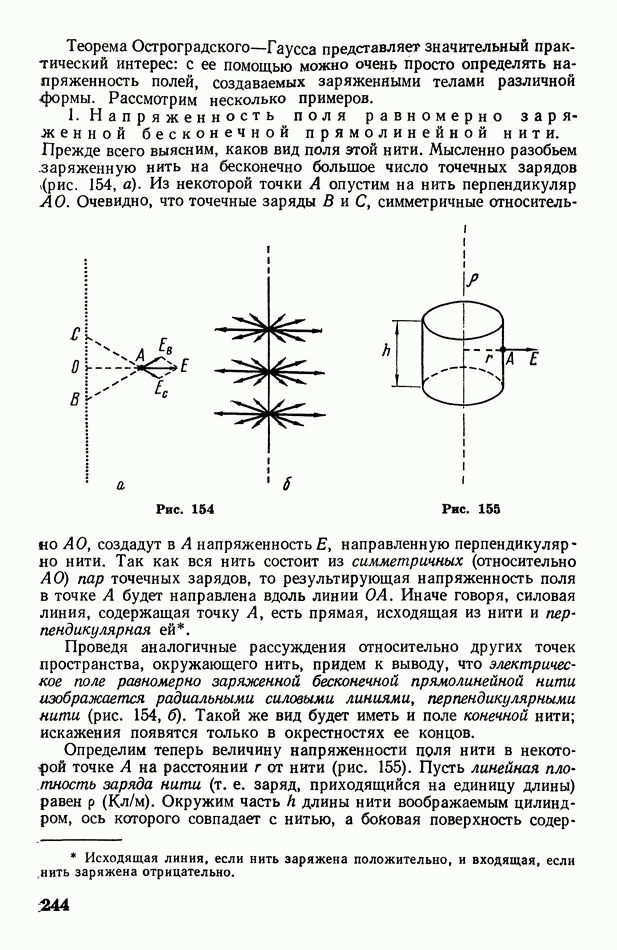
Для изменения направления световых лучей в оптических приборах широко используются линзы. Линзой называется прозрачное (чаще всего стеклянное) тело, ограниченное двумя криволинейными (обычно сферическими) поверхностями или одной криволинейной и одной плоской поверхностью. На рис. 288 изображены поперечные сечения двояковыпуклой (а) и двояковогнутой (б) сферических линз  радиусы сфер). Прямая
радиусы сфер). Прямая  проходящая через центры кривизны поверхностей, образующих линзу, называется главной оптической осью (или просто осью) линзы.
проходящая через центры кривизны поверхностей, образующих линзу, называется главной оптической осью (или просто осью) линзы.
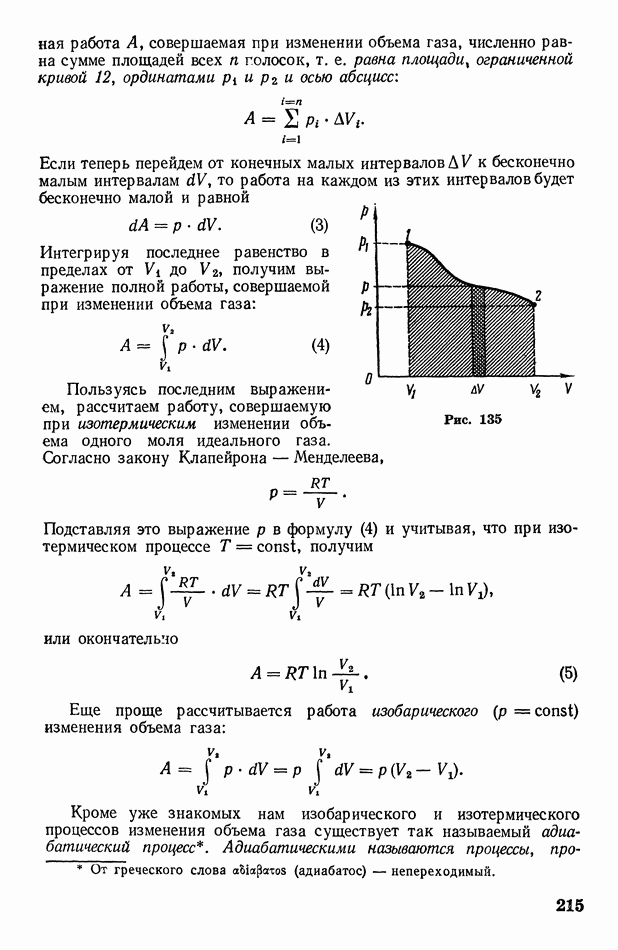
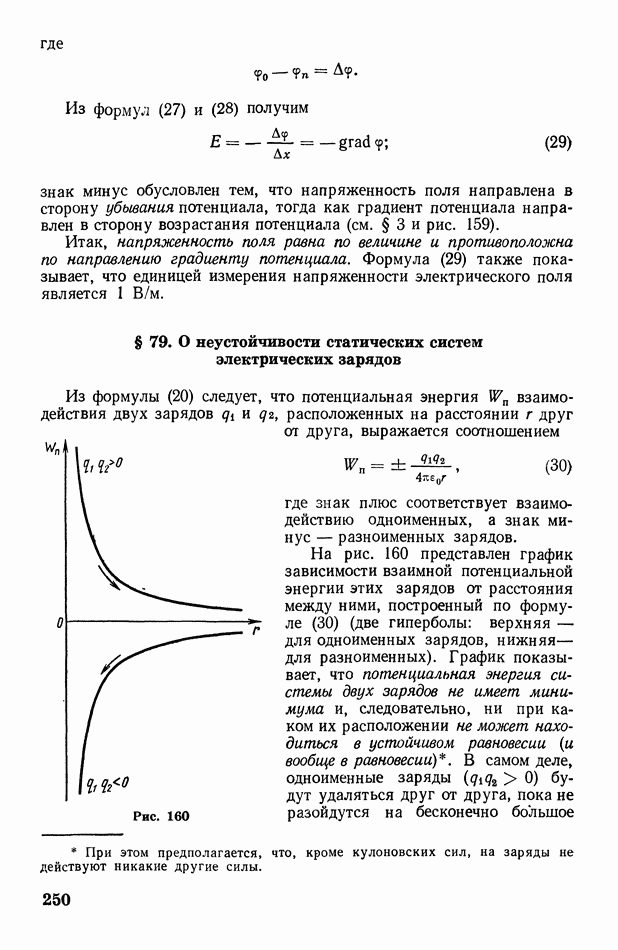
Мы будем рассматривать только тонкие линзы, толщина  которых пренебрежимо мала по сравнению с радиусами кривизны линзы (рис. 289). У тонкой линзы имеется точка О, обладающая тем свойством, что проходящие через нее лучи практически не преломляются линзой. Эту
которых пренебрежимо мала по сравнению с радиусами кривизны линзы (рис. 289). У тонкой линзы имеется точка О, обладающая тем свойством, что проходящие через нее лучи практически не преломляются линзой. Эту

Рис. 287

Рис. 288
точку называют оптическим центром линзы; она лежит на пересечении главной оптической оси со средним сечением  линзы. Любая прямая
линзы. Любая прямая  проходящая под углом к главной оптической оси через оптический центр линзы, называется побочной оптической осью. Луч, идущий вдоль оптической оси (главной или побочной), носит название центрального луча.
проходящая под углом к главной оптической оси через оптический центр линзы, называется побочной оптической осью. Луч, идущий вдоль оптической оси (главной или побочной), носит название центрального луча.
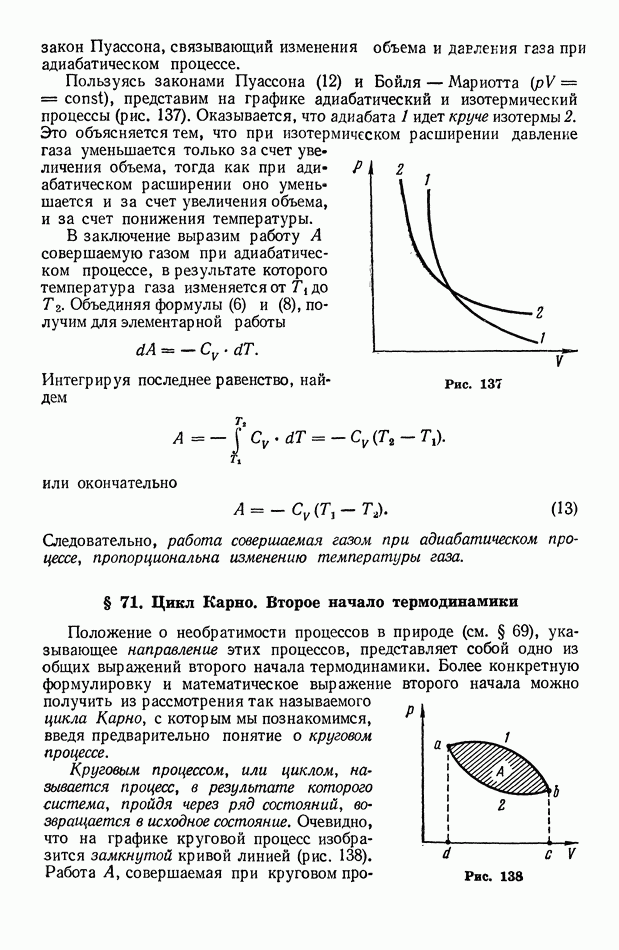
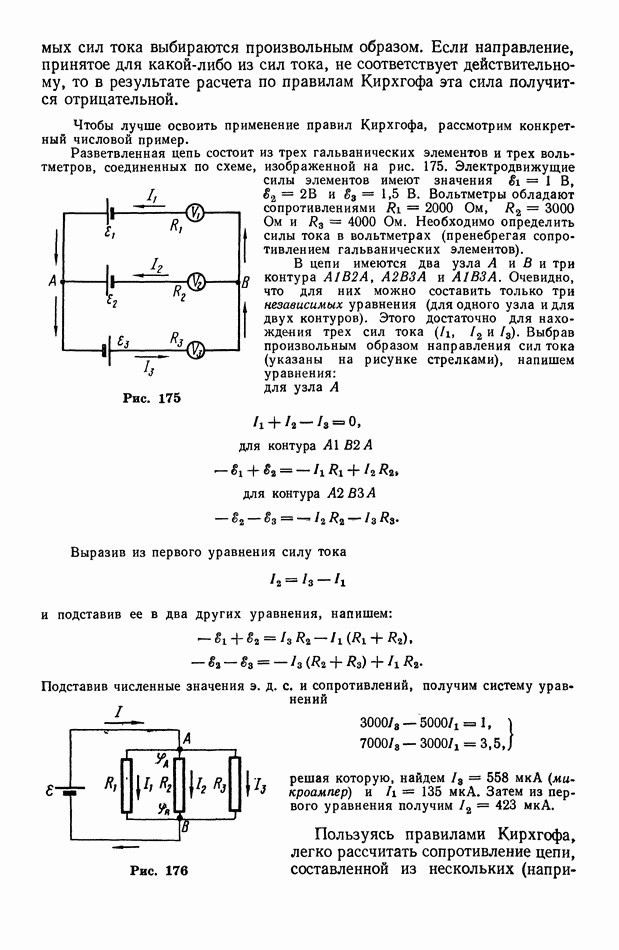
Линзу можно представить как совокупность множества призм (рис. 290). Тогда становится очевидным, что выпуклая линза отклоняет лучи к оптической оси, а вогнутая — от оптической оси. Поэтому выпуклая линза называется собирающей, а вогнутая — рассеивающей.

Рис. 290
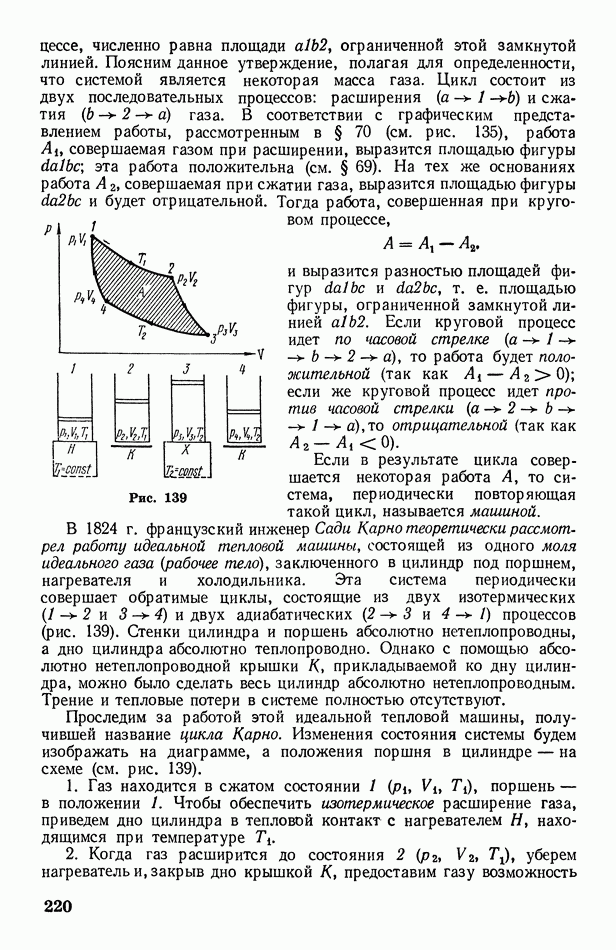
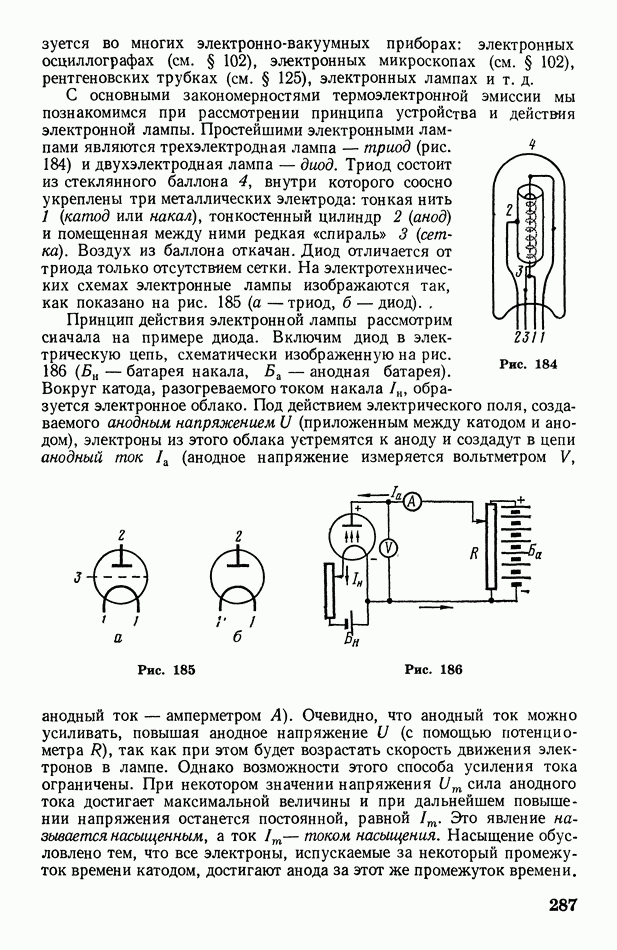
Покажем, что лучи, исходящие из некоторой точки  лежащей на оптической оси, под небольшими углами а к этой оси, собираются линзой в одну точку А и расположенную также на оптической оси и называемую изображением точки А (рис. 291).
лежащей на оптической оси, под небольшими углами а к этой оси, собираются линзой в одну точку А и расположенную также на оптической оси и называемую изображением точки А (рис. 291).
Построим плоскости, касательные к поверхностям линзы в точках  (т. е. в местах падения луча на линзу и выхода его из линзы), и проведем в эти точки радиусы
(т. е. в местах падения луча на линзу и выхода его из линзы), и проведем в эти точки радиусы  кривизны линзы.
кривизны линзы.

Рис. 291
Тогда луч  можно будет рассматривать как луч, преломленный в тонкой призме с преломляющим углом
можно будет рассматривать как луч, преломленный в тонкой призме с преломляющим углом  Учитывая малость углов
Учитывая малость углов  и толщины линзы, можно написать следующие приближенные
и толщины линзы, можно написать следующие приближенные
равенства:

где  высота (над оптической осью) точки
высота (над оптической осью) точки  падения луча на линзу,
падения луча на линзу,  высота точки
высота точки  выхода луча из линзы, a и b — соответственно расстояния от источника света
выхода луча из линзы, a и b — соответственно расстояния от источника света  и от его изображения до оптического центра линзы. Из треугольников
и от его изображения до оптического центра линзы. Из треугольников  и
и 

 Тогда, принимая во внимание формулы (7), получим
Тогда, принимая во внимание формулы (7), получим

Но, согласно формуле (6),

где  абсолютный показатель преломления линзы. Поэтому
абсолютный показатель преломления линзы. Поэтому

Последнее соотношение называется формулой линзы. В формулу не входит высота  Это означает, что расстояние
Это означает, что расстояние  не зависит от местоположения точки
не зависит от местоположения точки  т. е. что все лучи, исходящие из точки А у соберутся после преломления различными частями линзы в одной точке
т. е. что все лучи, исходящие из точки А у соберутся после преломления различными частями линзы в одной точке 

Рис. 292
Если точка А находится бесконечно далеко от линзы  т. е. если лучи падают на линзу параллельно главной оптической оси (рис. 292), то, согласно формуле (8),
т. е. если лучи падают на линзу параллельно главной оптической оси (рис. 292), то, согласно формуле (8),

Соответствующее этому случаю расстояние  называется фокусным расстоянием линзы:
называется фокусным расстоянием линзы:

Оно зависит только от показателя преломления и радиусов кривизны линзы. Точки  лежащие по обе стороны от линзы на
лежащие по обе стороны от линзы на
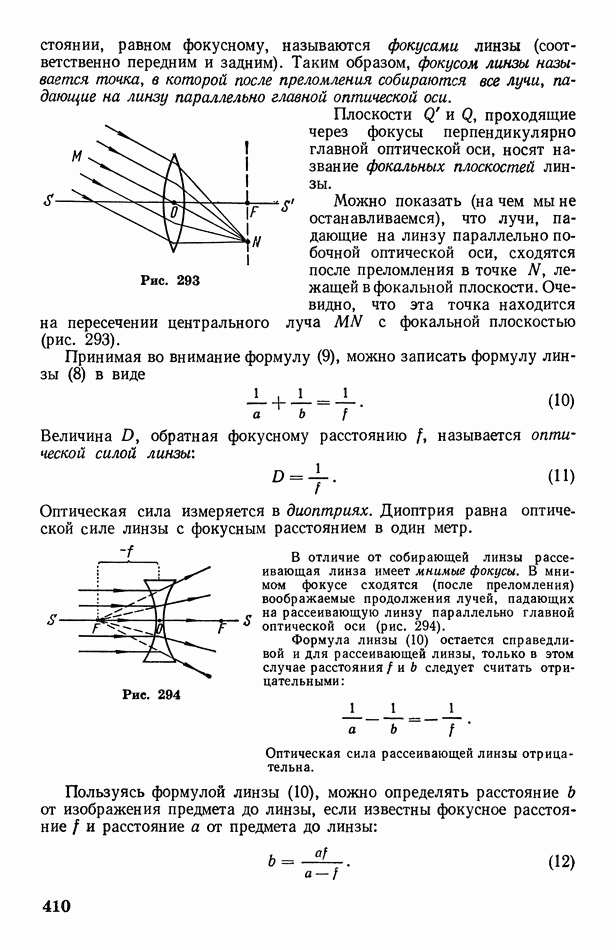
расстоянии, равном фокусному, называются фокусами линзы (соответственно передним и задним). Таким образом, фокусом линзы называется точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси.
Плоскости  проходящие через фокусы перпендикулярно главной оптической оси, носят название фокальных плоскостей линзы.
проходящие через фокусы перпендикулярно главной оптической оси, носят название фокальных плоскостей линзы.

Рис. 293
Можно показать (на чем мы не останавливаемся), что лучи, падающие на линзу параллельно побочной оптической оси, сходятся после преломления в точке  лежащей в фокальной плоскости. Очевидно, что эта точка находится на пересечении центрального луча
лежащей в фокальной плоскости. Очевидно, что эта точка находится на пересечении центрального луча  с фокальной плоскостью (рис. 293).
с фокальной плоскостью (рис. 293).
Принимая во внимание формулу (9), можно записать формулу линзы (8) в виде

Величина  обратная фокусному расстоянию называется оптической силой линзы:
обратная фокусному расстоянию называется оптической силой линзы:

Оптическая сила измеряется в диоптриях. Диоптрия равна оптической силе линзы с фокусным расстоянием в один метр.
В отличие от собирающей линзы рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся (после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси (рис. 294).

Рис. 294
Формула линзы (10) остается справедливой и для рассеивающей линзы, только в этом случае расстояния  следует считать отрицательными:
следует считать отрицательными:

Оптическая сила рассеивающей линзы отрицательна.
Пользуясь формулой линзы (10), можно определять расстояние  от изображения предмета до линзы, если известны фокусное расстояние
от изображения предмета до линзы, если известны фокусное расстояние  и расстояние а от предмета до линзы:
и расстояние а от предмета до линзы:

Линейный размер изображения  определяется по линейному размеру предмета
определяется по линейному размеру предмета  из очевидного соотношения (рис. 295)
из очевидного соотношения (рис. 295)

Отношение

называется линейным увеличением линзы.

Рис. 295
Изображение предмета, даваемое линзой, можно получить непосредственным геометрическим построением, не прибегая к расчету по формулам (12) и (13). Для этого достаточно провести от каждой из крайних точек предмета по два луча. Один луч должен быть параллельным оптической оси (проходит через фокус после преломления в линзе), другой — центральным (не преломляется линзой). Пересечение двух таких лучей дает изображение крайней точки предмета. Примеры построения изображений приведены на рис. 296, 297.
Если предмет помещен между фокусом и двойным фокусом линзы, то изображение получается действительным, увеличенным, перевернутым и находящимся за двойным фокусом линзы (рис. 296).

Рис. 296

Рис. 297
Если предмет помещен между фокусом и линзой, то изображение оказывается мнимым, увеличенным и прямым (рис. 297). Этот случай соответствует применению линзы в качестве лупы (предмет помещается вблизи переднего фокуса, глаз — в заднем фокусе).
Как было показано при выводе формулы линзы, лучи, исходящие под малыми углами к оптической оси из некоторой точки  лежащей на этой оси, собираются линзой в одну точку
лежащей на этой оси, собираются линзой в одну точку  Однако при большом диаметре линзы часть лучей падает на нее под большими углами к оптической оси (рис. 298). Такие лучи собираются уже в другой точке
Однако при большом диаметре линзы часть лучей падает на нее под большими углами к оптической оси (рис. 298). Такие лучи собираются уже в другой точке  В результате изображение точки А приобретает вид размытого пятна. Этот недостаток линзы называется
В результате изображение точки А приобретает вид размытого пятна. Этот недостаток линзы называется

Рис. 298
сферической аберрацией. У выпуклой линзы лучи, падающие на ее края, собираются ближе, чем лучи, падающие на ее центральную часть  вогнутой линзы имеет место обратное явление. Благодаря этому можно создать оптическую систему из соответствующим образом подобранных собирающей и рассеивающей линз, у которой сферическая аберрация почти полностью отсутствует. В некоторых случаях сферическую аберрацию ослабляют путем диафрагмирования краевых лучей.
вогнутой линзы имеет место обратное явление. Благодаря этому можно создать оптическую систему из соответствующим образом подобранных собирающей и рассеивающей линз, у которой сферическая аберрация почти полностью отсутствует. В некоторых случаях сферическую аберрацию ослабляют путем диафрагмирования краевых лучей.
В связи с дисперсией фокусное расстояние линзы для лучей различного цвета оказывается различным (рис. 299). Поэтому при использовании белого или иного немонохроматического света изображение предмета, даваемое линзой, имеет окрашенные края. Этот недостаток линзы называется хроматической аберрацией.

Рис. 299

Рис. 300
Собирающая линза приближает к оптической оси сильнее фиолетовые лучи, чем красные (см. рис. 299;  фокус для красного луча,
фокус для красного луча,  фокус для фиолетового луча), а рассеивающая линза, наоборот, приближает к оптической оси сильнее красные лучи (рис. 300). Благодаря этому можно создать оптическую систему, не имеющую хроматической аберрации. Такая система {ахроматическая линза) состоит из склеенных между собой собирающей и рассеивающей линз, обладающих различной дисперсией.
фокус для фиолетового луча), а рассеивающая линза, наоборот, приближает к оптической оси сильнее красные лучи (рис. 300). Благодаря этому можно создать оптическую систему, не имеющую хроматической аберрации. Такая система {ахроматическая линза) состоит из склеенных между собой собирающей и рассеивающей линз, обладающих различной дисперсией.
В 1941 г. Д. Д. Максутовым была создана безаберрационная оптическая система (менисковый телеобъектив), состоящая из вогнутого сферического зеркала и выпукло-вогнутой сферической линзы (мениска). Зеркало и мениск в отдельности обладают большими аберрациями (сферическими), имеющими противоположные знаки; в менисковом телеобъективе эти аберрации полностью компенсируются.
Менисковые оптические системы с большим успехом применяются в телескопах (менисковый телескоп Максутова), фотоаппаратах и других оптических приборах.
Для значительного увеличения малых объектов применяется микроскоп — оптическая система, состоящая в простейшем случае из короткофокусной собирающей линзы (объектива)  с фокусным расстоянием
с фокусным расстоянием  и длиннофокусной собирающей линзы (окуляра)
и длиннофокусной собирающей линзы (окуляра)  с фокусным расстоянием
с фокусным расстоянием  (рис. 301). Предмет А В помещается на расстоянии, немного большем
(рис. 301). Предмет А В помещается на расстоянии, немного большем  от объектива. Действительное, увеличенное и перевернутое изображение
от объектива. Действительное, увеличенное и перевернутое изображение  оказывается на расстоянии, немного меньшем
оказывается на расстоянии, немного меньшем  от окуляра; оно рассматривается в окуляр,
от окуляра; оно рассматривается в окуляр,
как в лупу. В результате получается мнимое, увеличенное и перевернутое (относительно предмета) изображение  находящееся от окуляра на расстоянии
находящееся от окуляра на расстоянии  называемом расстоянием ясного зрения (для нормального глаза
называемом расстоянием ясного зрения (для нормального глаза  см). Расстояние
см). Расстояние  между «внутренними» фокусами объектива и окуляра называется оптической длиной тубуса микроскопа (обычно
между «внутренними» фокусами объектива и окуляра называется оптической длиной тубуса микроскопа (обычно  см).
см).

Рис. 301
На рисунке сильно преувеличены расстояния от предмета  до фокуса объектива и от изображения
до фокуса объектива и от изображения  до фокуса окуляра. Кроме того, не соблюдено соотношение расстояний
до фокуса окуляра. Кроме того, не соблюдено соотношение расстояний  в действительности
в действительности  гораздо меньше
гораздо меньше  (по этим причинам изображение
(по этим причинам изображение  предмета оказалось расположенным между объективом и окуляром, хотя обычно оно располагается по одну сторону с предметом АВ от объектива). Учитывая это, получим на основании формулы (14) следующие приближенные выражения увеличений объектива
предмета оказалось расположенным между объективом и окуляром, хотя обычно оно располагается по одну сторону с предметом АВ от объектива). Учитывая это, получим на основании формулы (14) следующие приближенные выражения увеличений объектива  и окуляра
и окуляра 

Общее увеличение микроскопа  равно произведению увеличений объектива и окуляра:
равно произведению увеличений объектива и окуляра:

Практически увеличение микроскопа не может превышать 2500—3000. Это связано с ограниченной разрешающей способностью микроскопа, обусловленной дифракционными явлениями (см. § 123).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
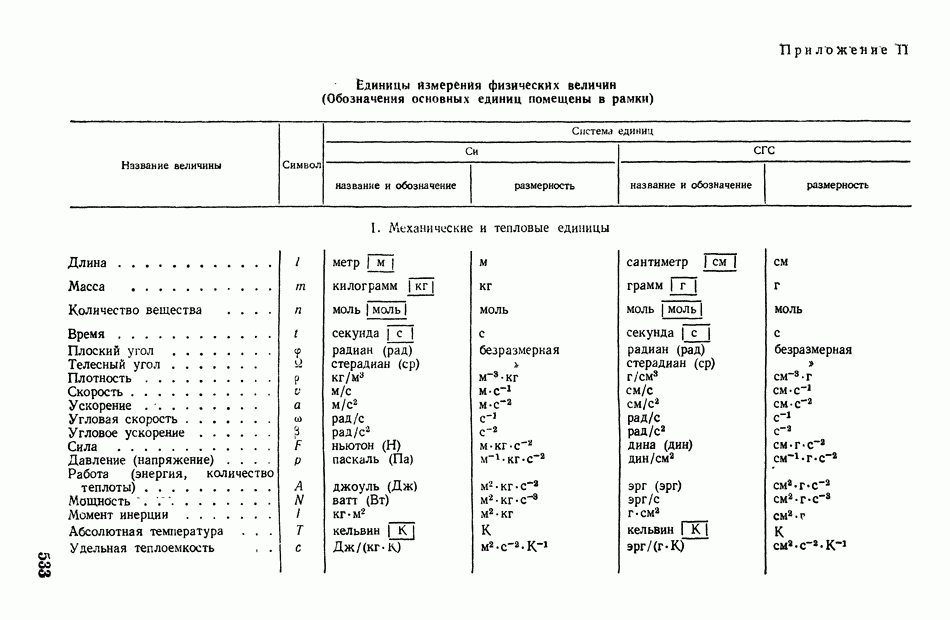
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
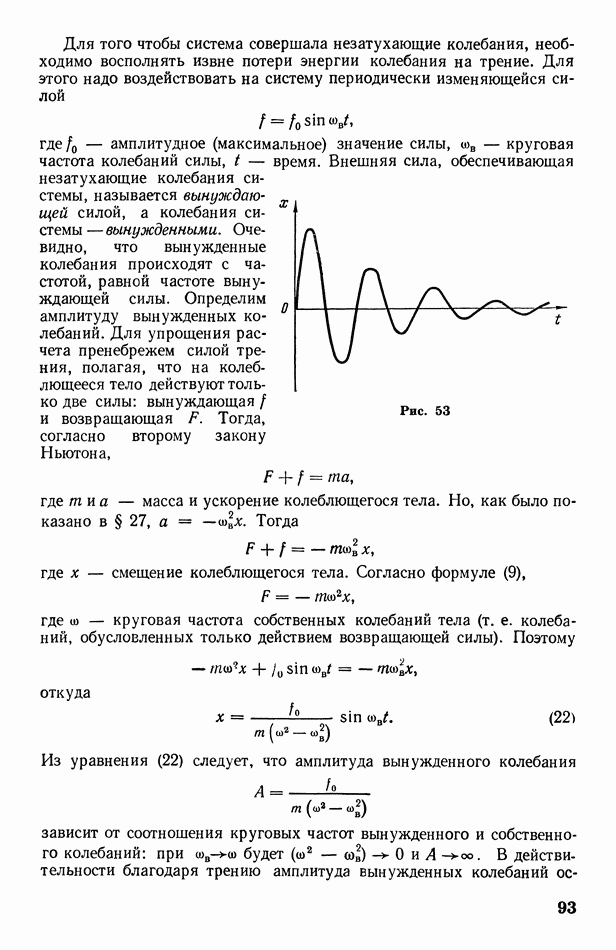
- § 30. О затухающих и вынужденных колебаниях
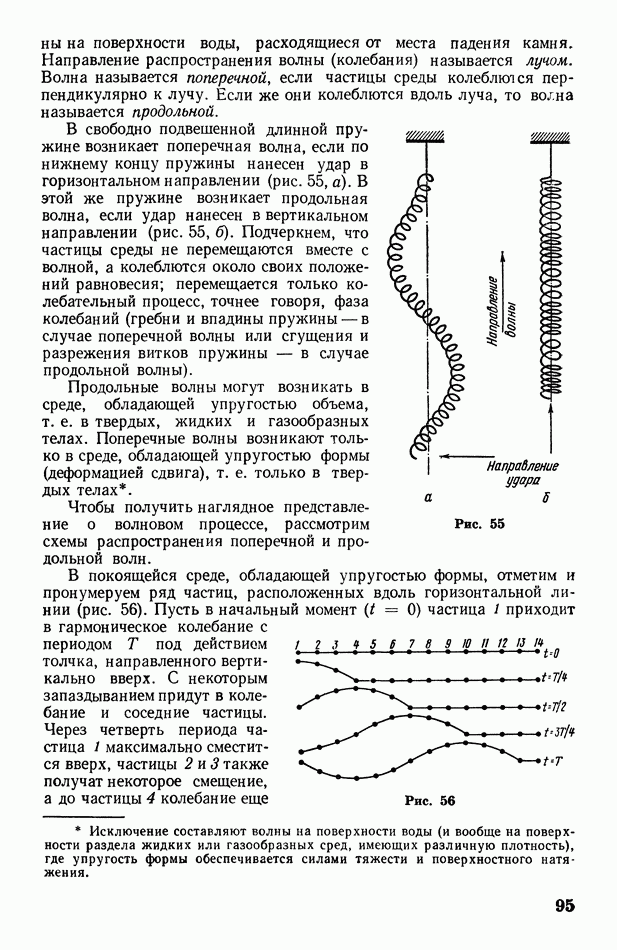
- § 31. Волновой процесс
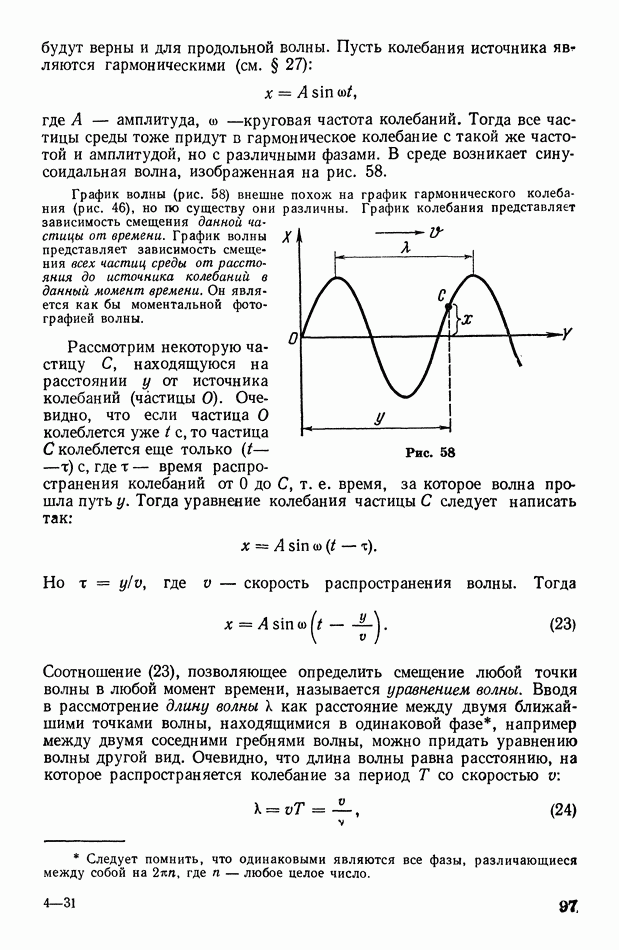
- § 32. Уравнение волны. Интенсивность волны
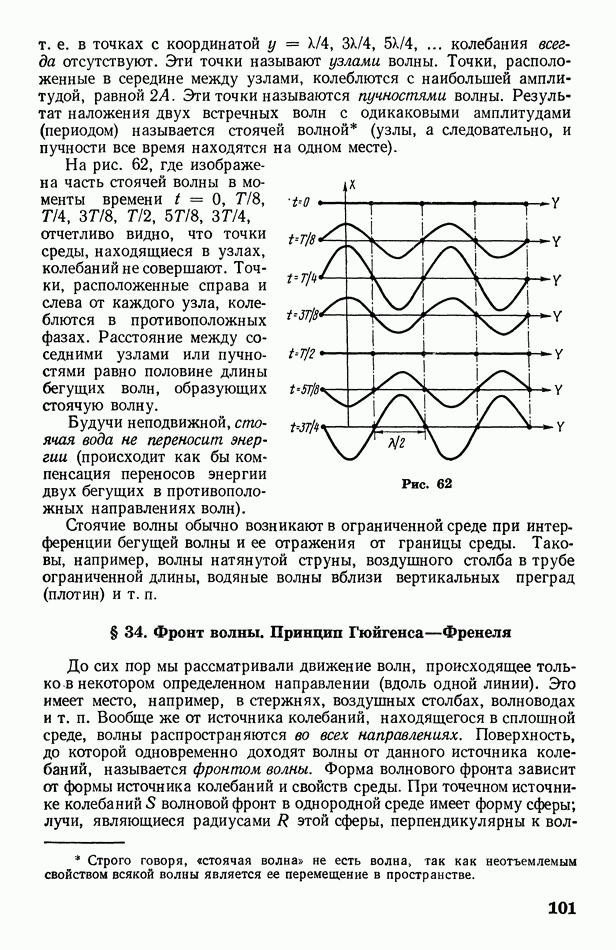
- § 33. Интерференция волн. Стоячие волны
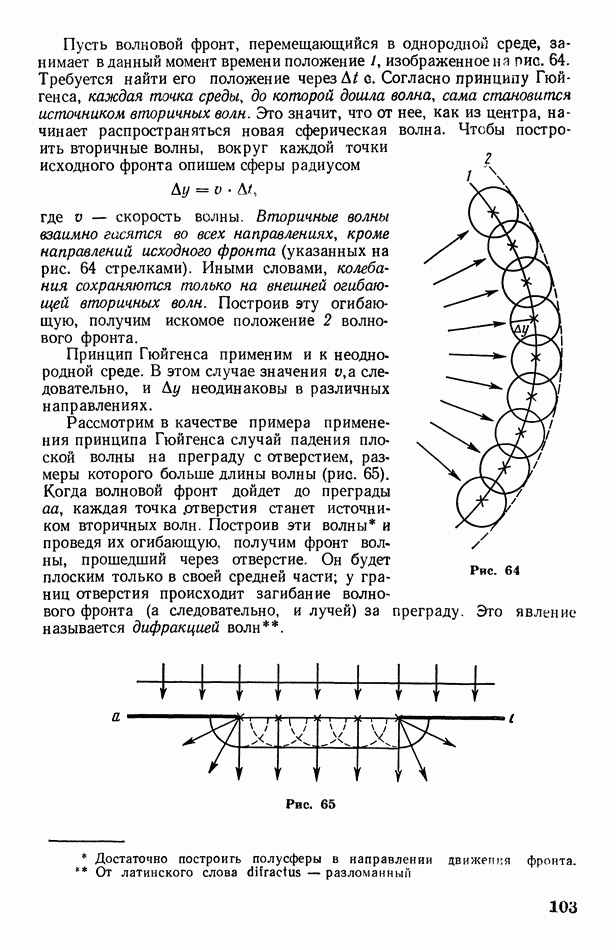
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
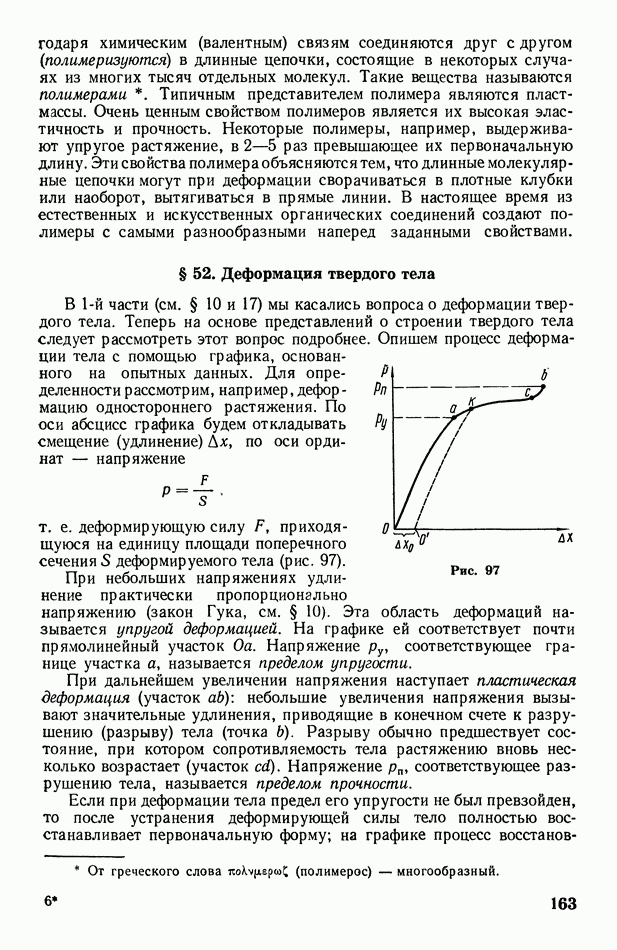
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
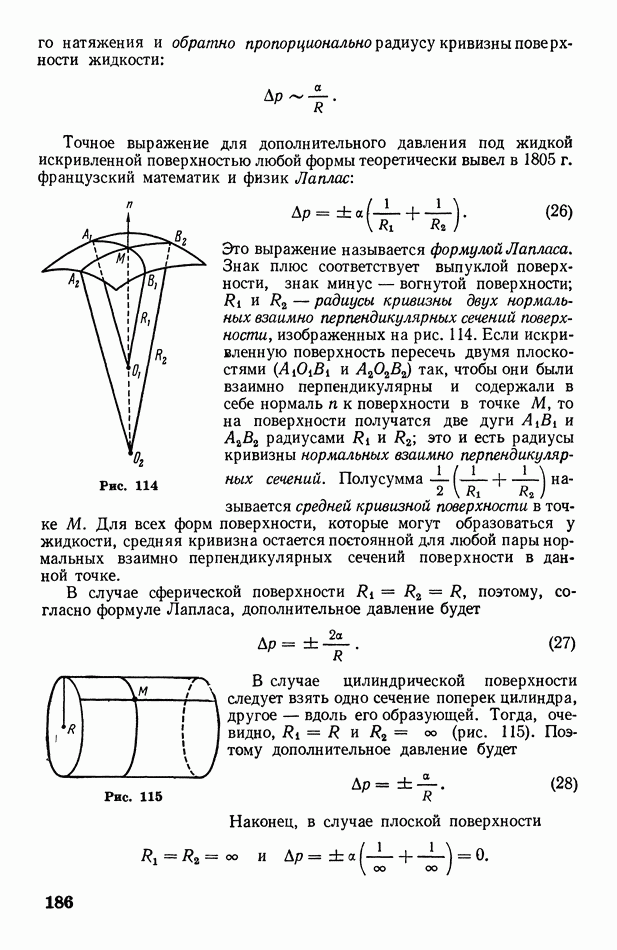
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
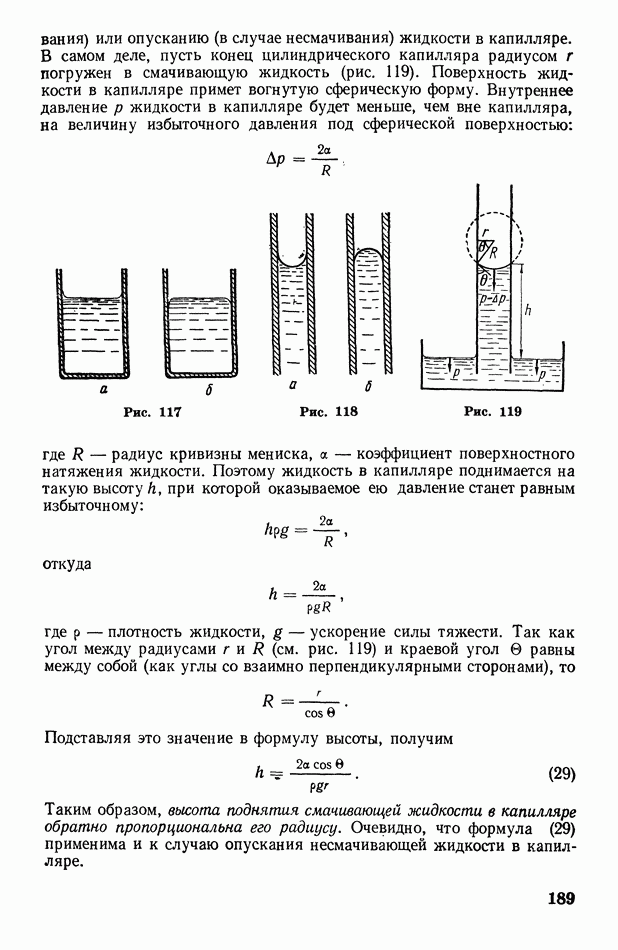
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
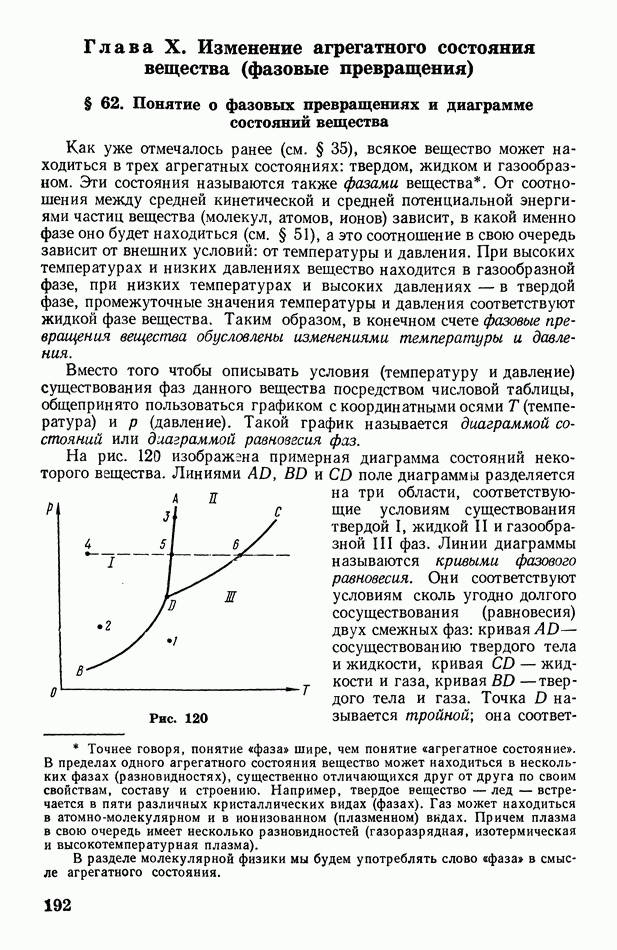
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
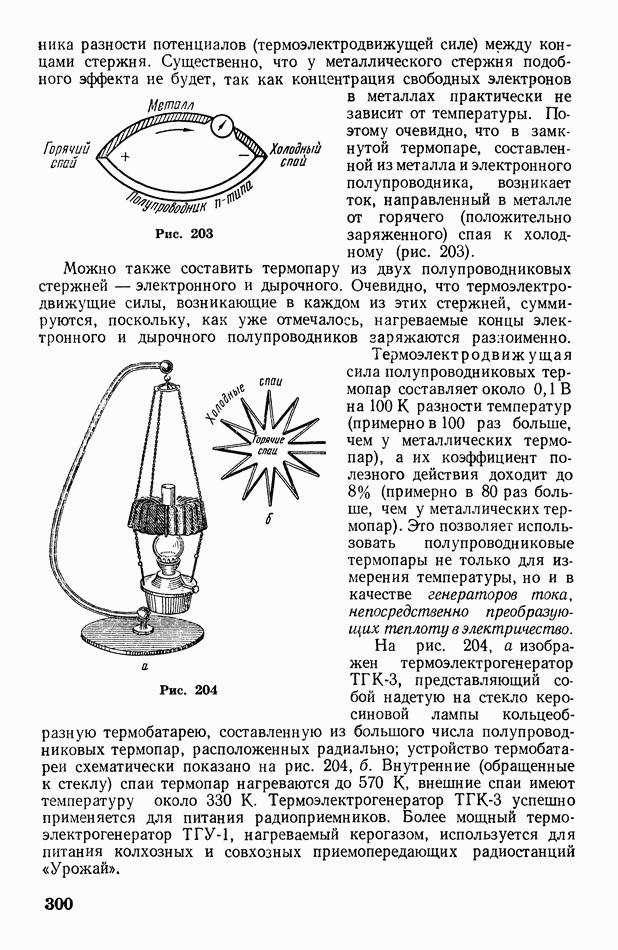
- § 87. Контактная разность потенциалов. Термоэлектрические явления
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
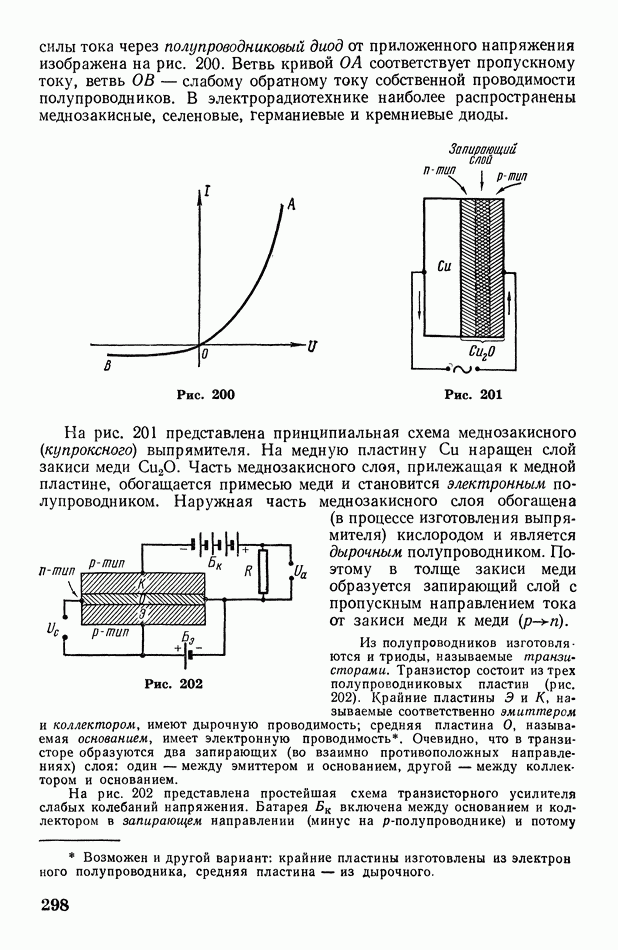
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
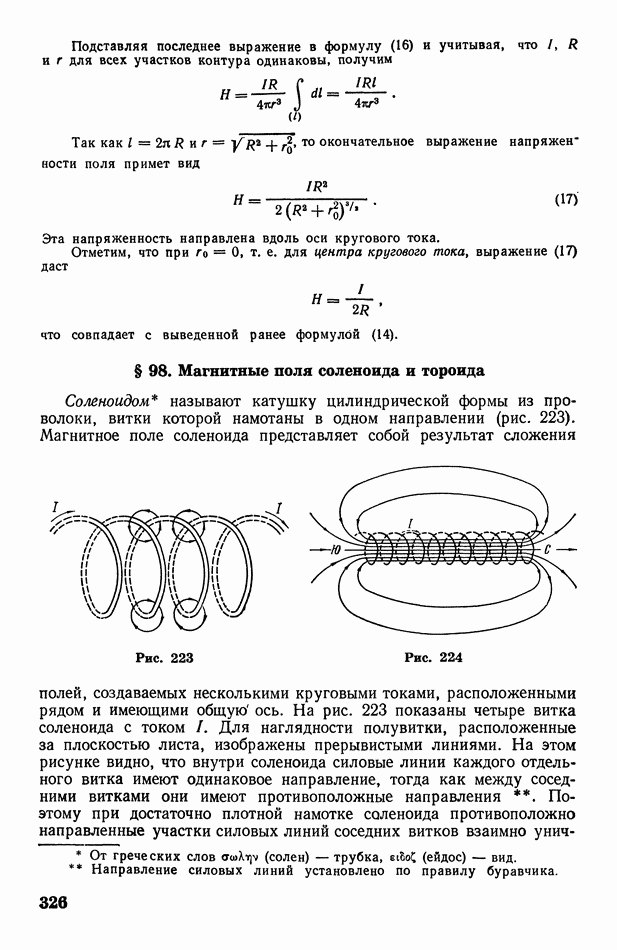
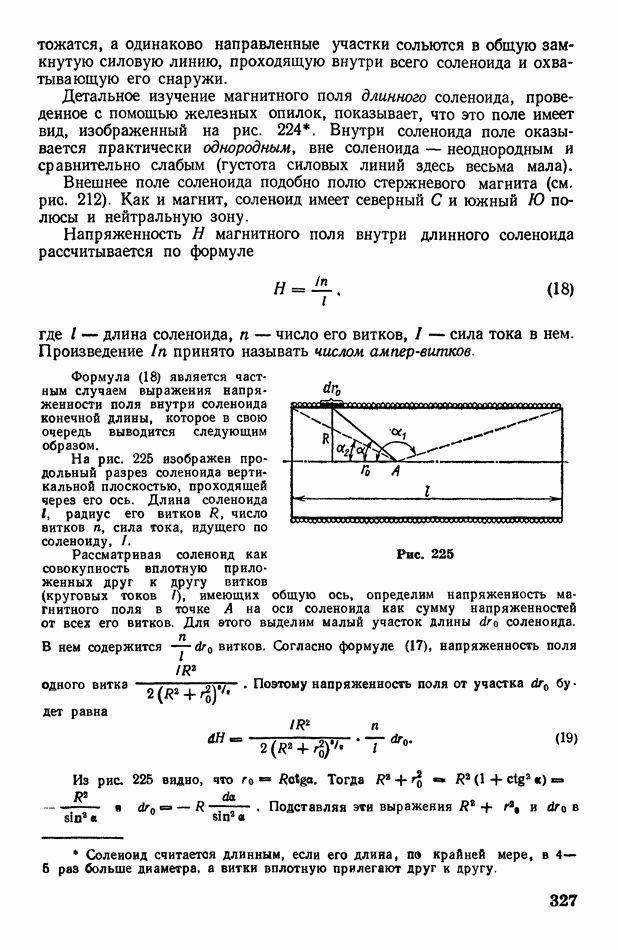
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
- § 117. Тонкие линзы. Микроскоп
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
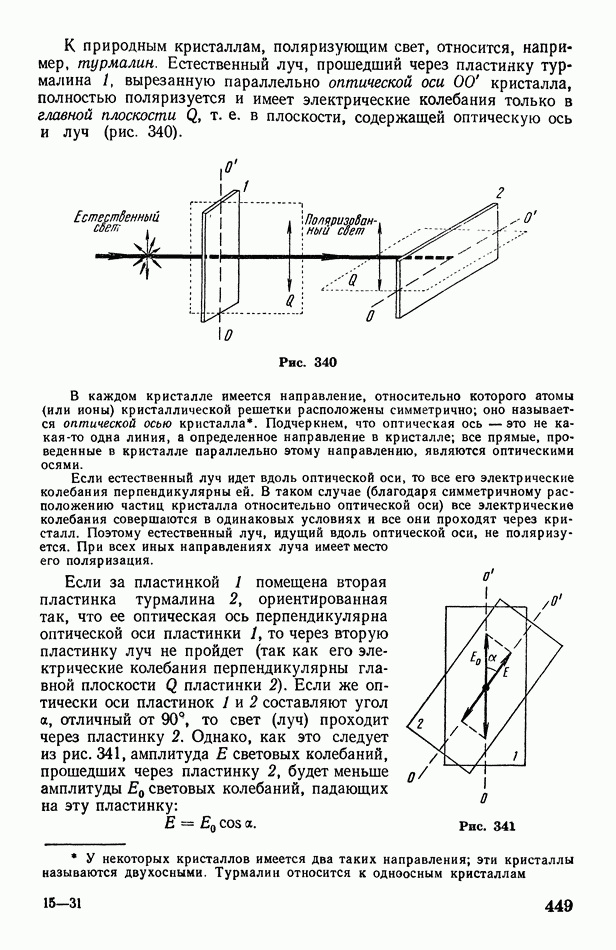
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
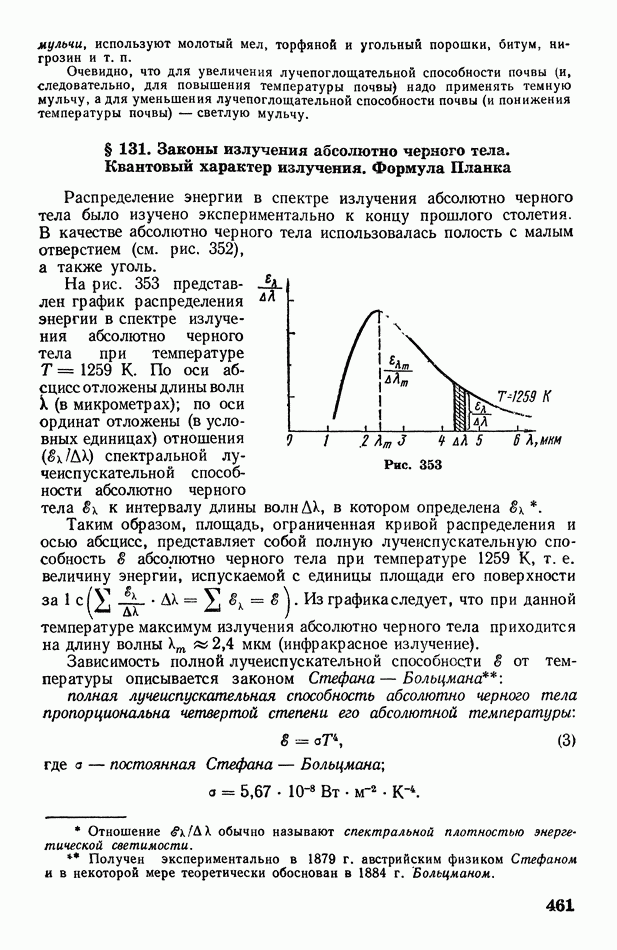
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
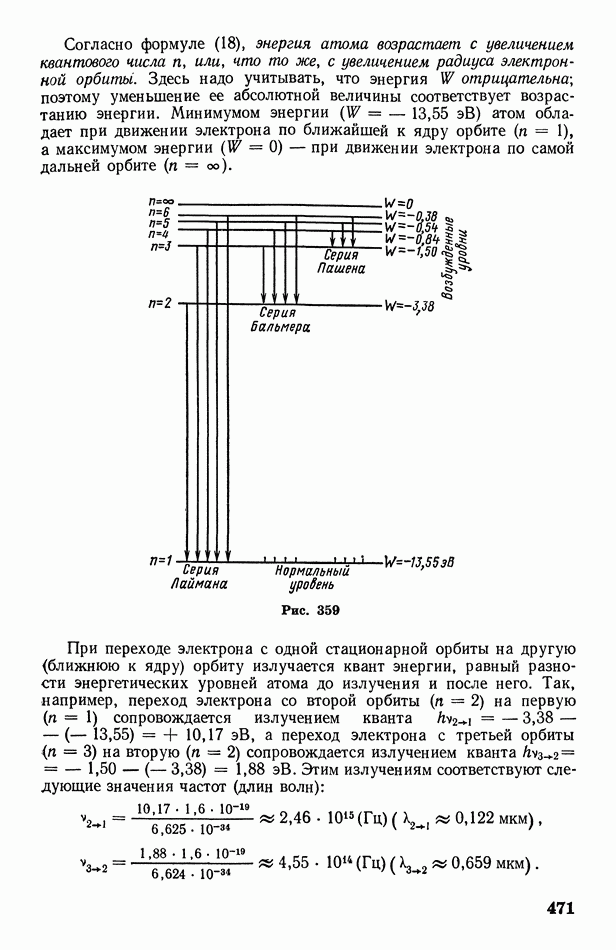
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
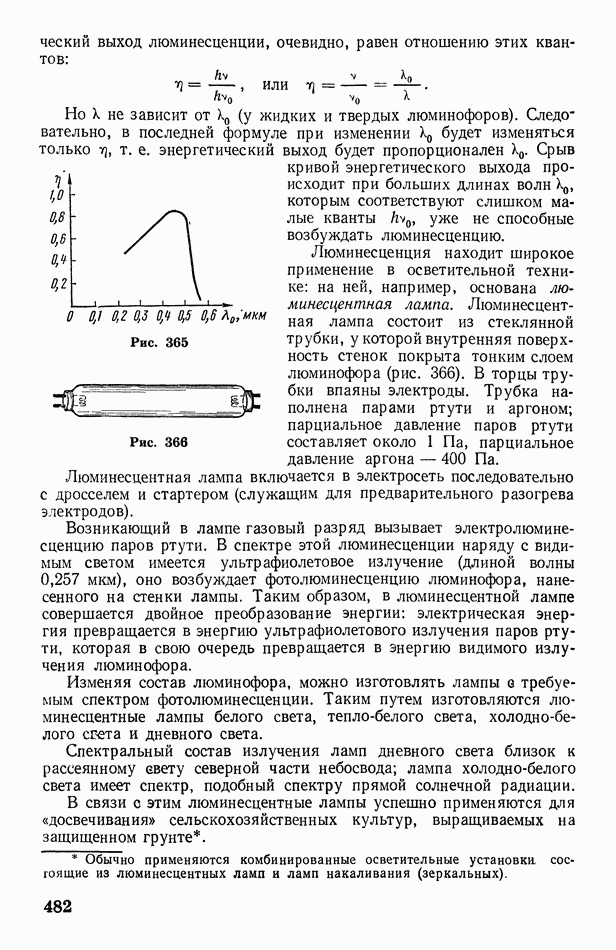
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
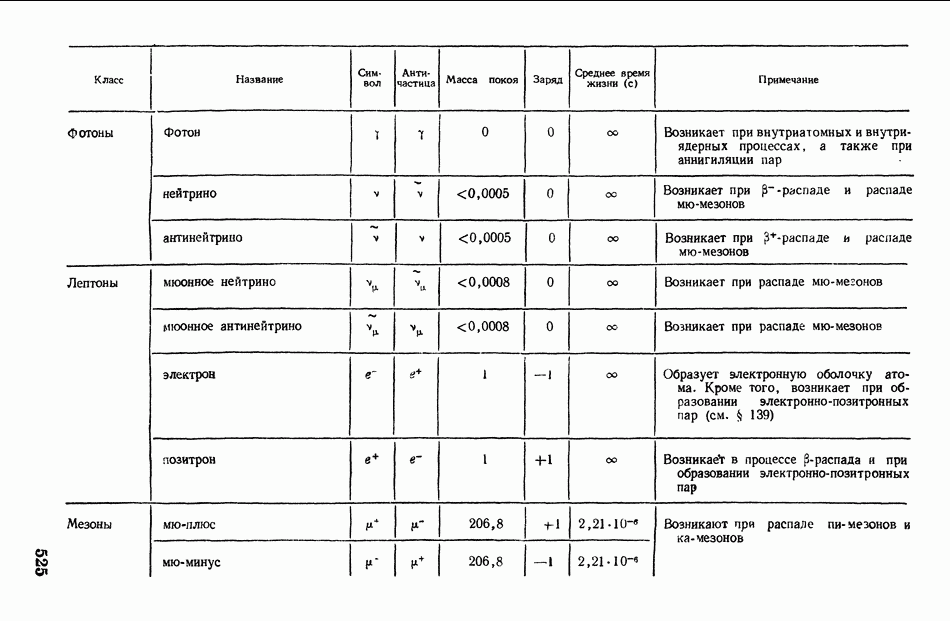
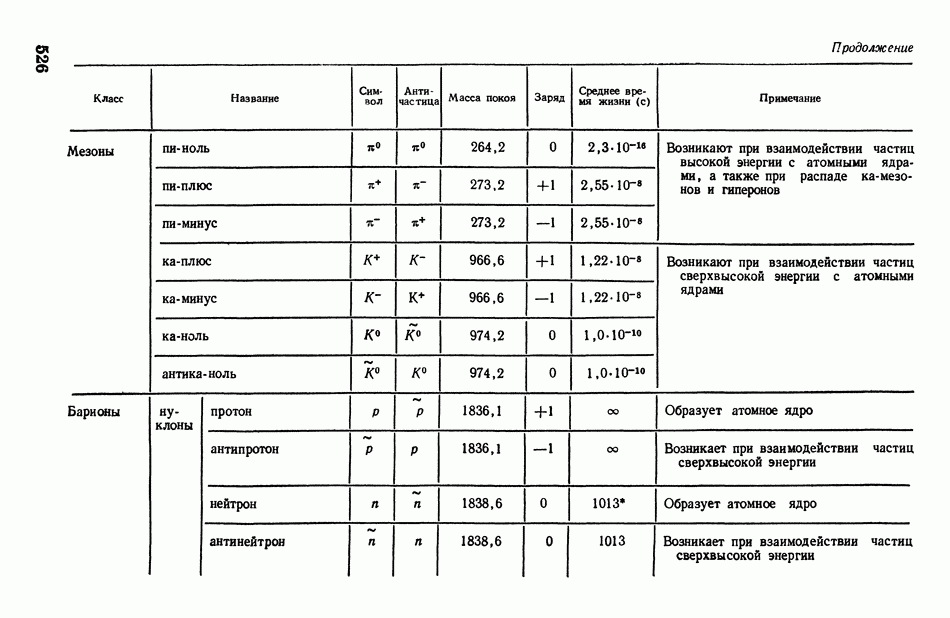
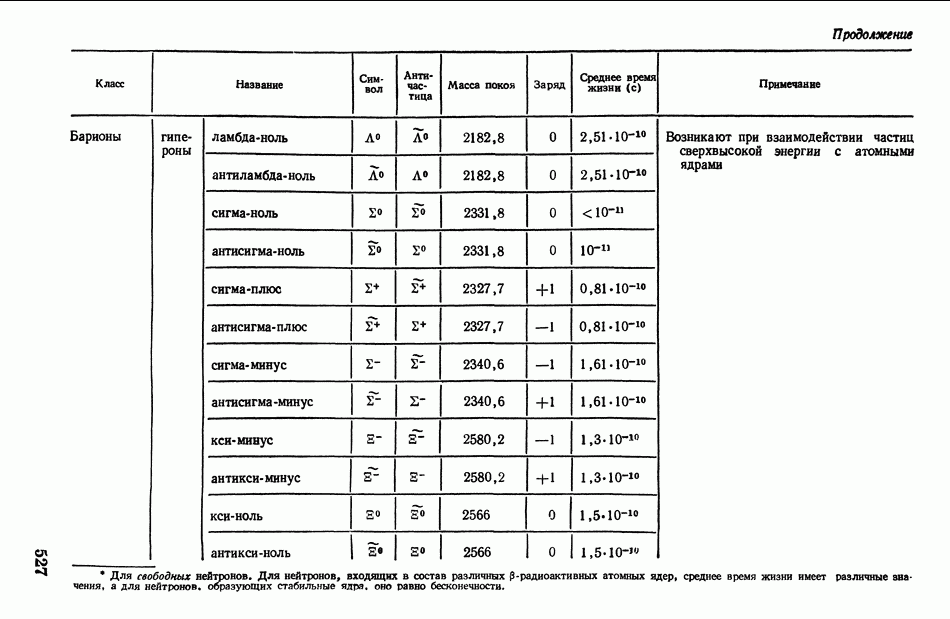
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии