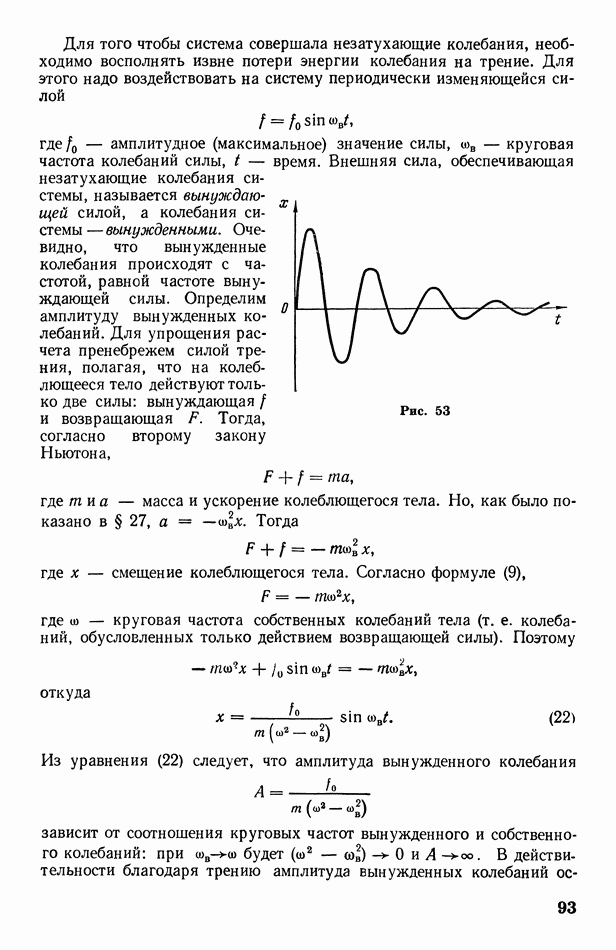
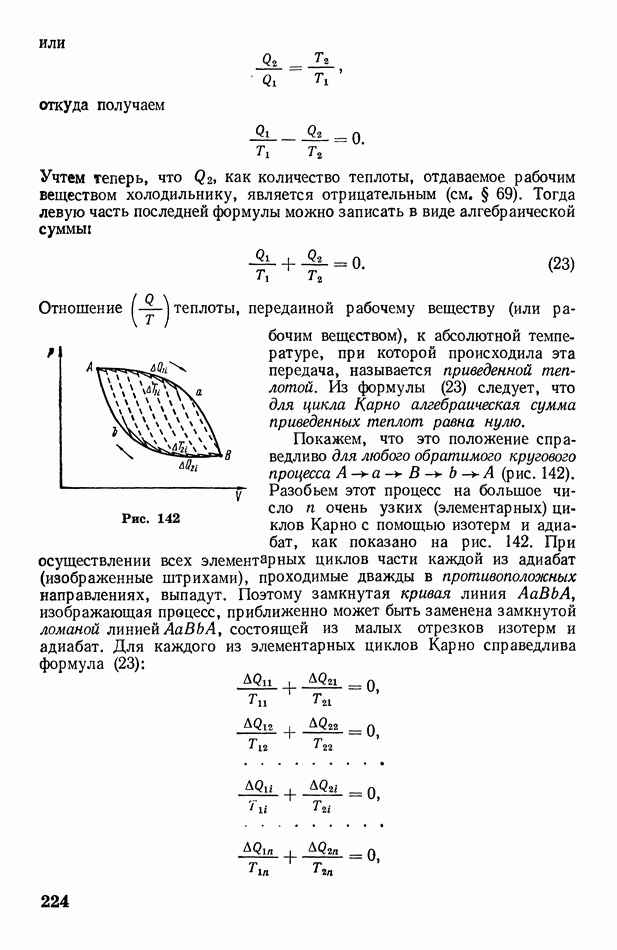
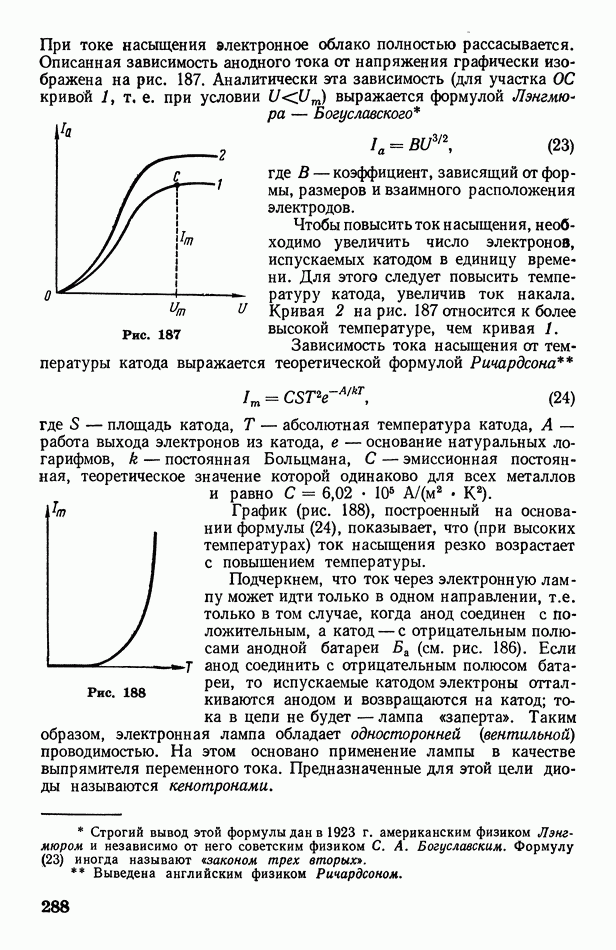
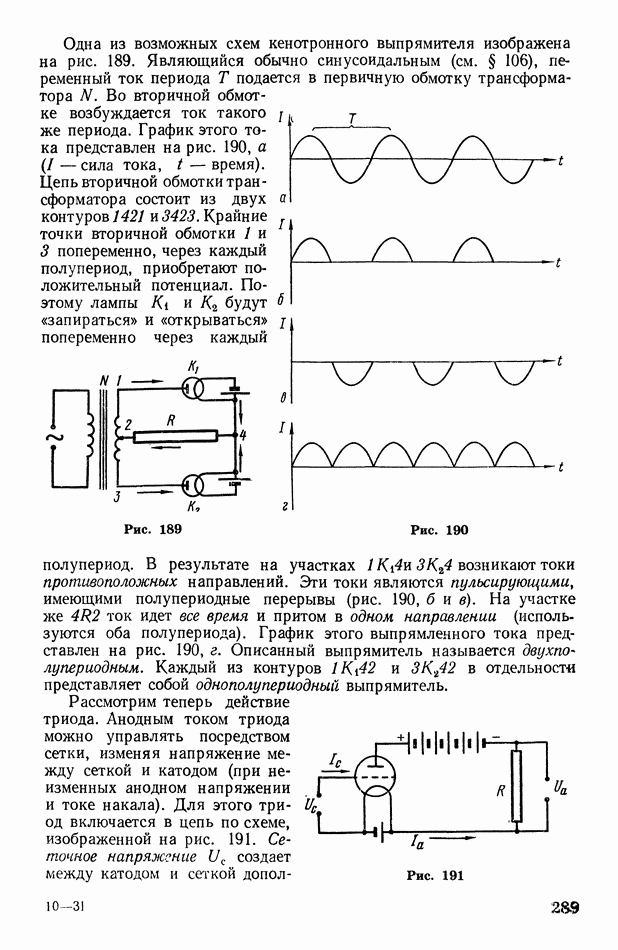
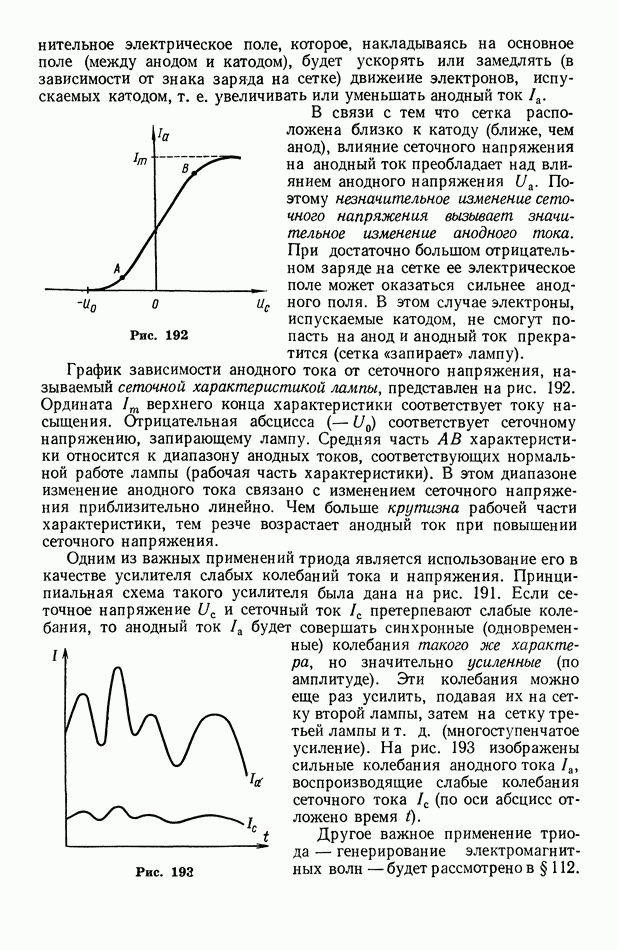
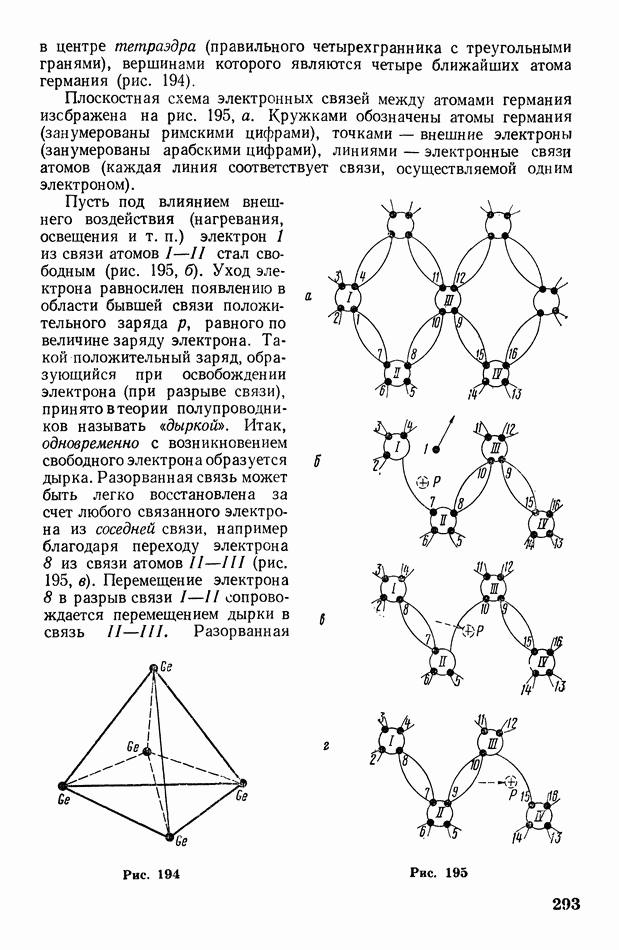
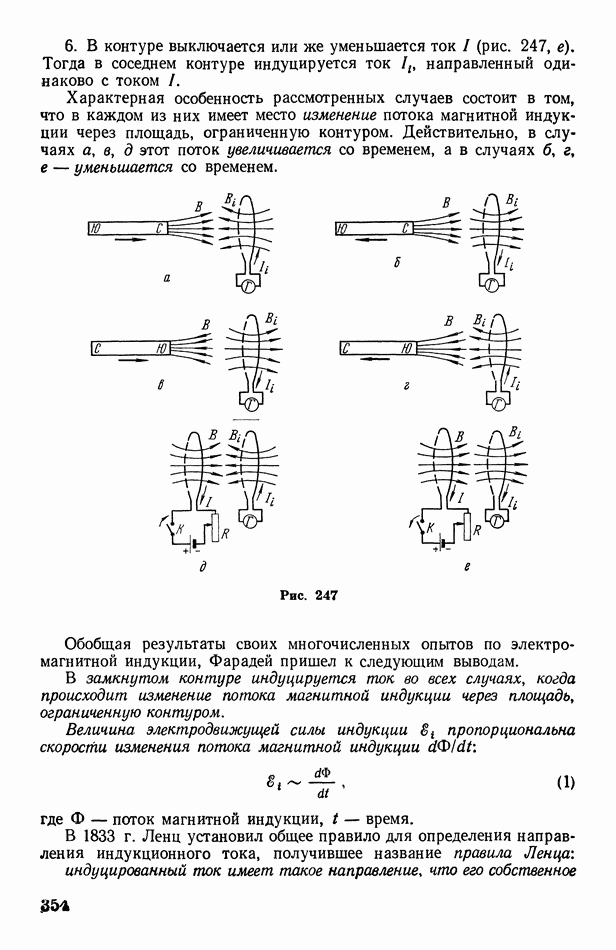
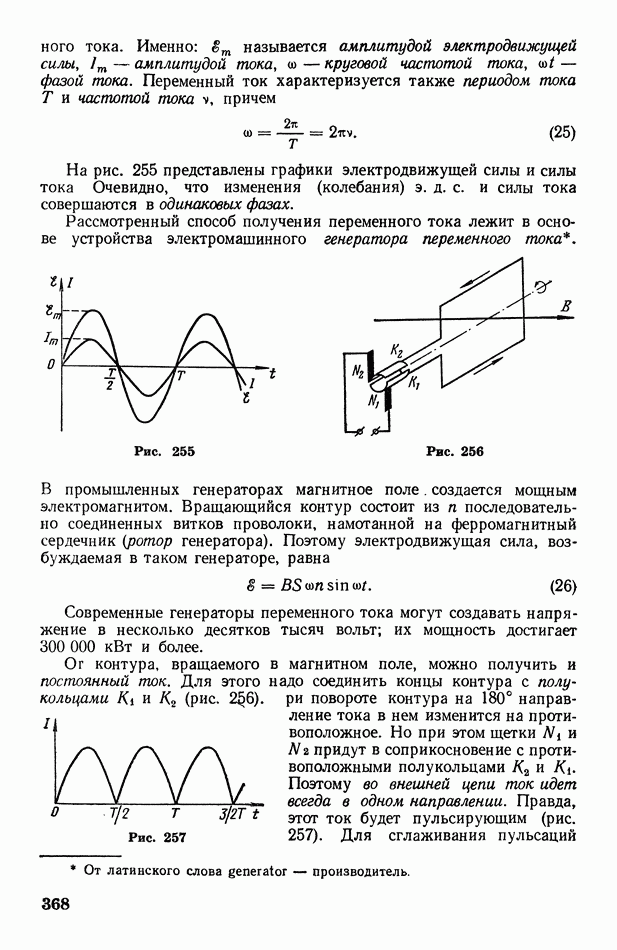
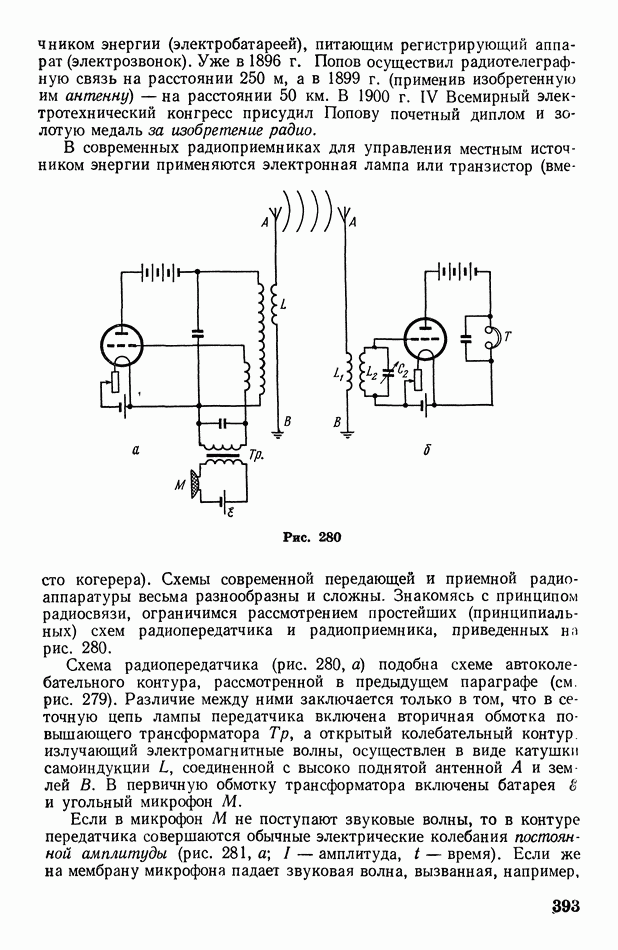
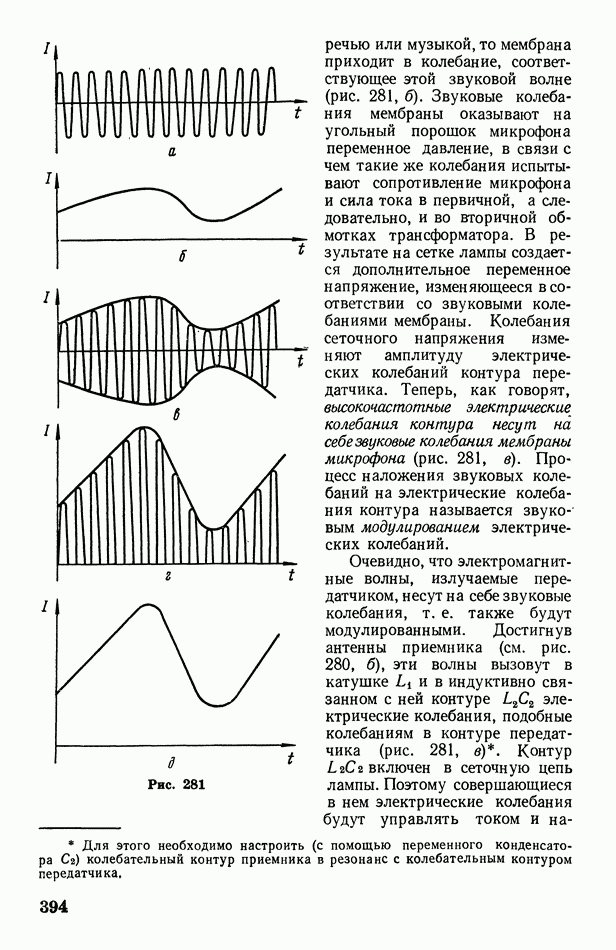
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
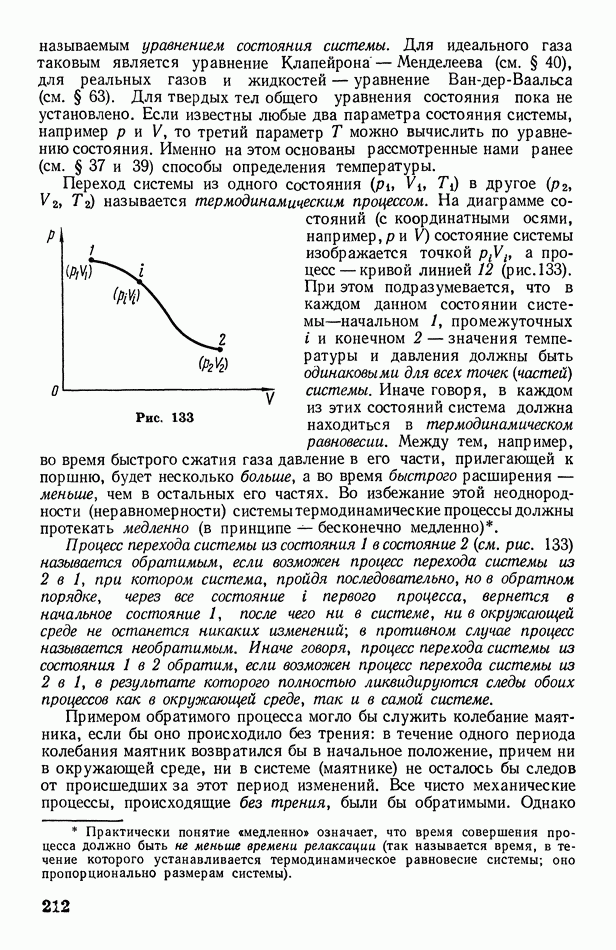
§ 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
Представим себе газ, расширяющийся в цилиндре под поршнем от объема  при давлении
при давлении  до объема
до объема  при давлении
при давлении 
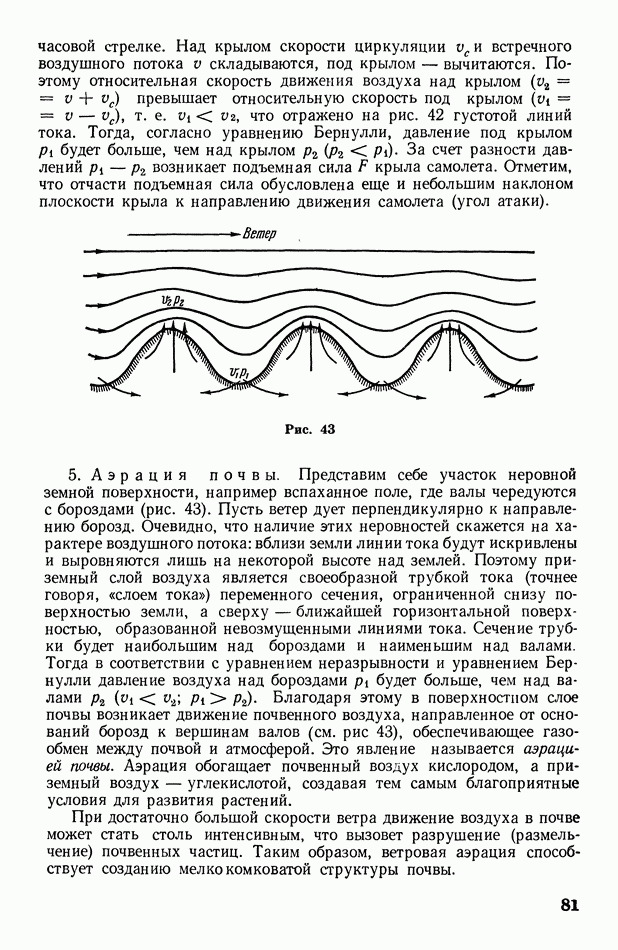
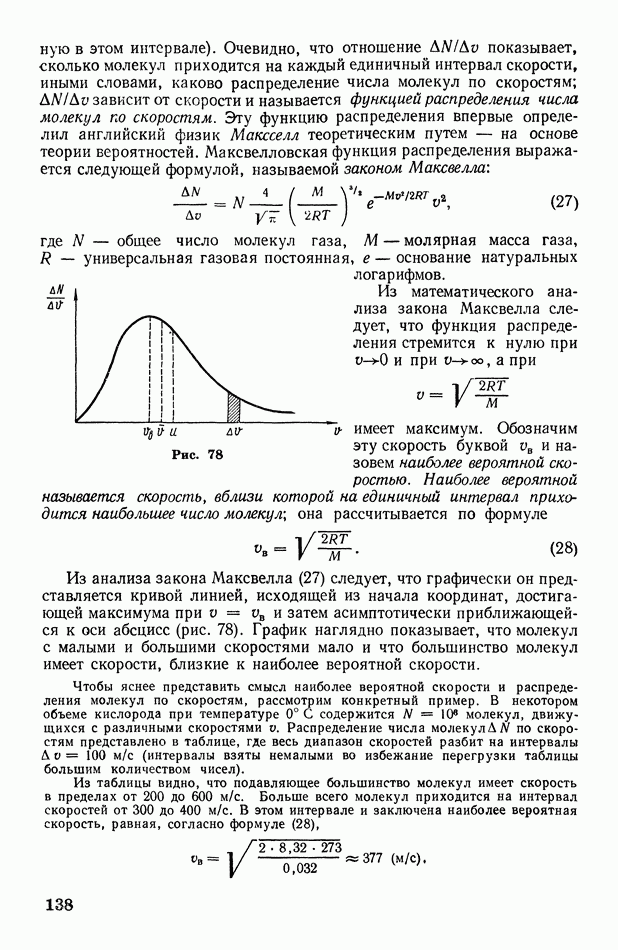
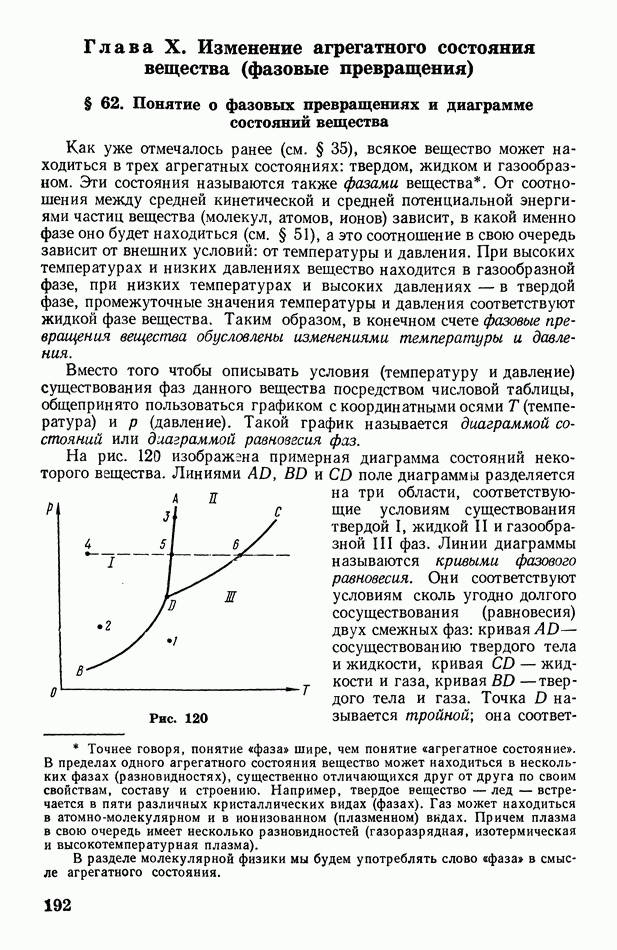
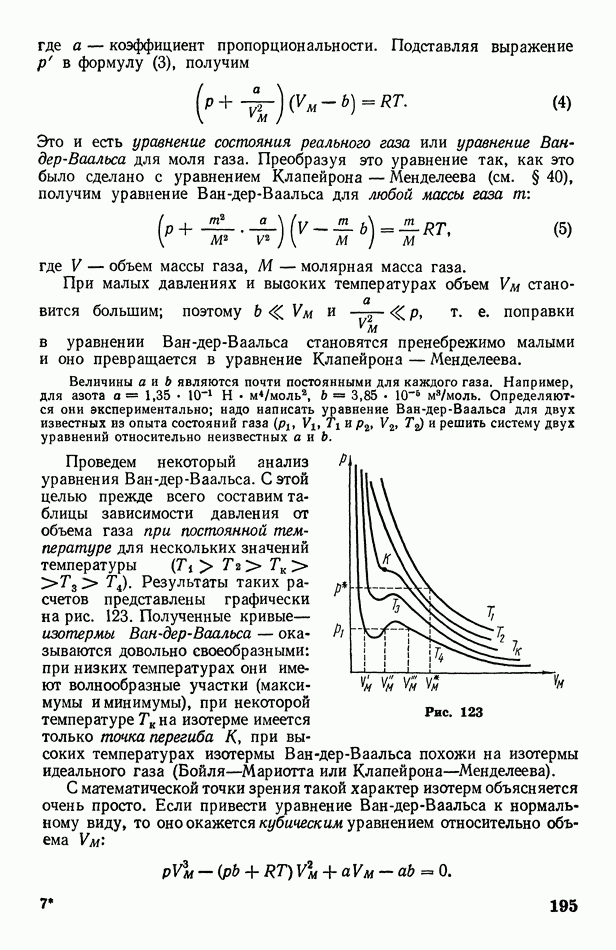
На графике этот процесс изобразится кривой линией 1—2 (рис. 135). Рассмотрим маленький интервал расширения  для которого давление можно считать приблизительно постоянным и равным
для которого давление можно считать приблизительно постоянным и равным  Как было показано в § 44 [см. рис. 77 и формулу
Как было показано в § 44 [см. рис. 77 и формулу  работа, совершаемая газом при малом расширении, равна произведению
работа, совершаемая газом при малом расширении, равна произведению  На графике видно, что эта работа численно равна площади узкой полоски шириной
На графике видно, что эта работа численно равна площади узкой полоски шириной  Разбивая полное изменение объема от
Разбивая полное изменение объема от  до
до  на
на  малых интервалов:
малых интервалов:  получим, очевидно, что
получим, очевидно, что
полная работа А, совершаемая при изменении объема газа, численно равна сумме площадей всех  полосок, т. е. равна площадих ограниченной кривой 12, ординатами
полосок, т. е. равна площадих ограниченной кривой 12, ординатами  и осью абсцисс:
и осью абсцисс:

Если теперь перейдем от конечных малых интервалов  к бесконечно малым интервалам
к бесконечно малым интервалам  то работа на каждом из этих интервалов будет бесконечно малой и равной
то работа на каждом из этих интервалов будет бесконечно малой и равной

Интегрируя последнее равенство в пределах от  до
до  получим выражение полной работы, совершаемой при изменении объема газа:
получим выражение полной работы, совершаемой при изменении объема газа:


Рис. 135
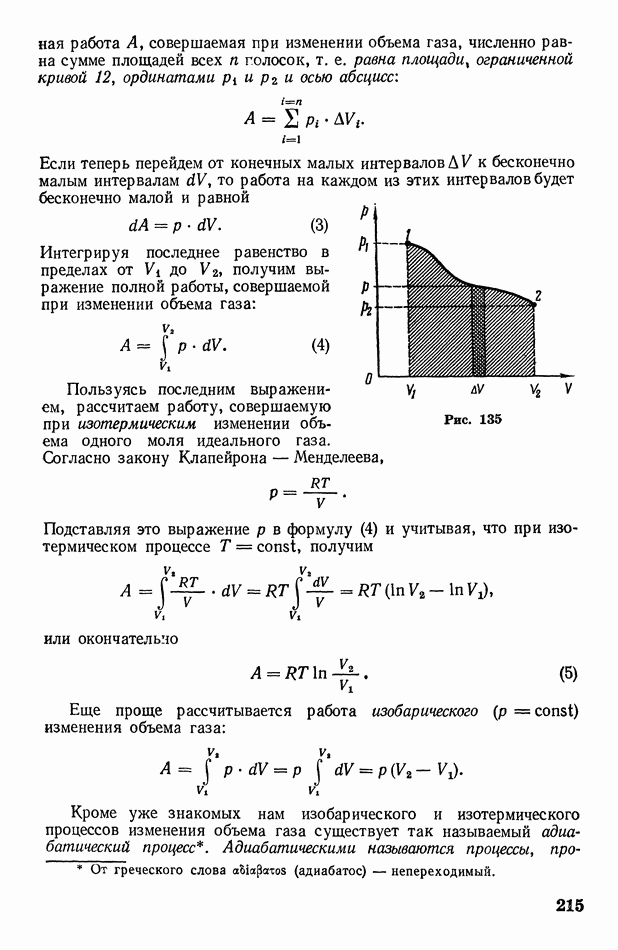
Пользуясь последним выражением, рассчитаем работу, совершаемую при изотермическим изменении объема одного моля идеального газа. Согласно закону Клапейрона — Менделеева,

Подставляя это выражение  в формулу (4) и учитывая, что при изотермическом процессе
в формулу (4) и учитывая, что при изотермическом процессе  получим
получим

или окончательно

Еще проще рассчитывается работа изобарического  изменения объема газа:
изменения объема газа:

Кроме уже знакомых нам изобарического и изотермического процессов изменения объема газа существует так называемый адиабатический процесс. Адиабатическими называются процессы,
происходящие при отсутствии теплообмена между системой и окружающей средой. В этом случае  и формула (2) первого начала термодинамики принимает вид
и формула (2) первого начала термодинамики принимает вид

Знак минус показывает, что при адиабатическом расширении внутренняя энергия системы уменьшается: система совершает работу за счет своей внутренней энергии. В случае адиабатического сжатия внутренняя энергия системы увеличивается за счет работы, совершаемой внешними силами. Поэтому  будет положительно, но зато
будет положительно, но зато  примет отрицательное значение (см. § 69) и равенство (6) остается справедливым.
примет отрицательное значение (см. § 69) и равенство (6) остается справедливым.
Рассмотрим адиабатический процесс в системе, состоящей из одного моля идеального газа, помещенного в цилиндр, стенки и поршень которого абсолютно нетеплопрсводны. Как известно [см. § 44, формула (20)], внутренняя энергия моля идеального газа равна

где  молярная теплоемкость при постоянном объеме,
молярная теплоемкость при постоянном объеме,  температура. Так как
температура. Так как  постоянная величина, то, дифференцируя равенство (7), получим
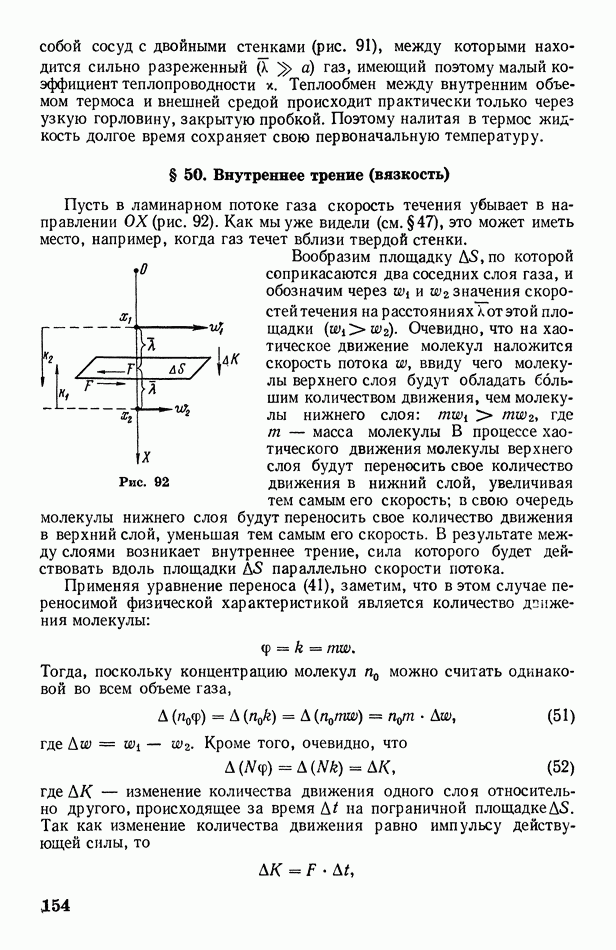
постоянная величина, то, дифференцируя равенство (7), получим

Подставляя в формулу (6) выражения  из формулы (3) и
из формулы (3) и  из формулы (8), получим
из формулы (8), получим

Используя закон Клапейрона — Менделеева, заменим  на
на 

Из последнего равенства следует, что адиабатическое изменение объема газа сопровождается изменением его температуры. Интегрируя это равенство в пределах от до  и соответственно от
и соответственно от  до
до  получим
получим

откуда

или

Потенцируя последнее равенство и учитывая [см. § 44, формулы (23) и  что
что

получим

и

или окончательно

Формула (11) выражает закон Пуассона, описывающий адиабатические процессы в идеальном газе. Из закона Пуассона следует, что при адиабатическом расширении газа его температура понижается, а при сжатии — повышается.
Для осуществления адиабатических процессов необходима абсолютная теплоизоляция системы от окружающей среды. Наоборот, для осуществления изотермических процессов необходимо обеспечить абсолютную теплопроводность между системой и средой. Однако в природе нет ни абсолютных теплоизоляторов, ни абсолютных теплопроводников. Поэтому реальные процессы изменения объема газа могут быть только близкими к адиабатическим (если теплообмен между системой и средой незначителен) или к изотермическим (если теплообмен между системой и средой хороший).
Для практического осуществления процессов, близких к адиабатическим, возможны два пути: 1) очень быстрое изменение объема газа и 2) изменение объема очень большой массы газа. В обоих случаях не успевает произойти значительного теплообмена между системой (газом) и окружающей средой, что равносильно наличию хорошей теплоизоляции между ними.
Примером адиабатического процесса, осуществляемого первым путем, может служить быстрое накачивание велокамеры насосом. Значительное количество теплоты, выделяющееся при многократном частом сжатии воздуха, не успевает переходить в окружающую среду, в результате чего насос, как известно, заметно нагревается.
Адиабатическими можно считать такие процессы, как расширение и сжатие горючей смеси в цилиндрах двигателя внутреннего сгорания. Особенно отчетливо выражен адиабатический характер процесса сжатия в дизеле. Дизель не имеет зажигания: адиабатическое нагревание смеси при сжатии приводит к ее самовоспламенению.
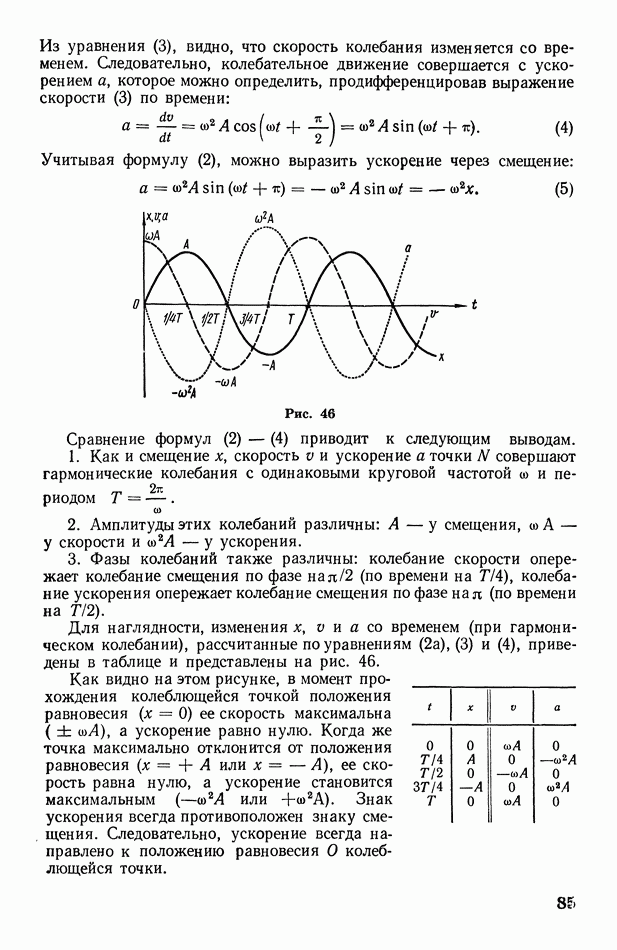
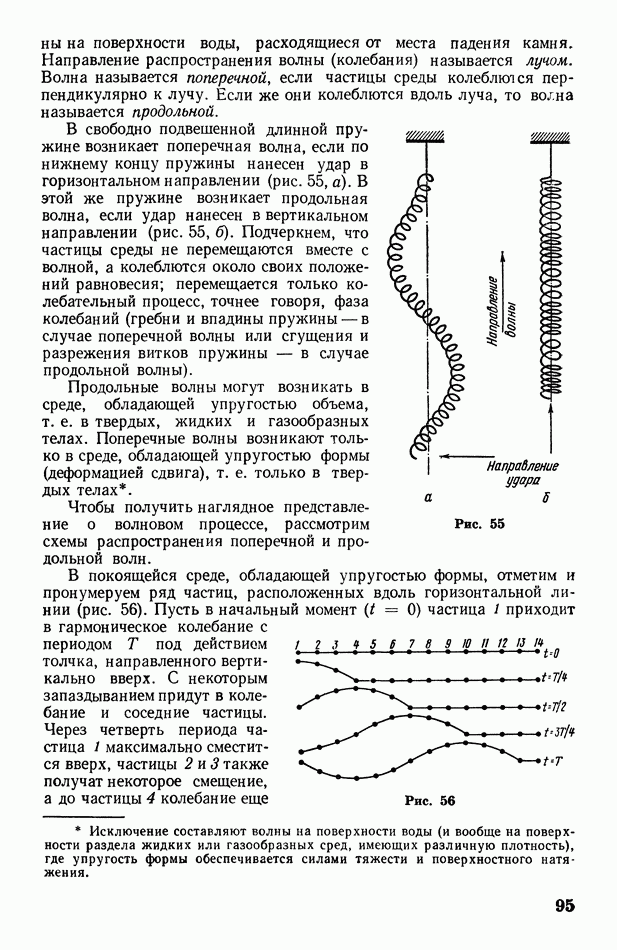
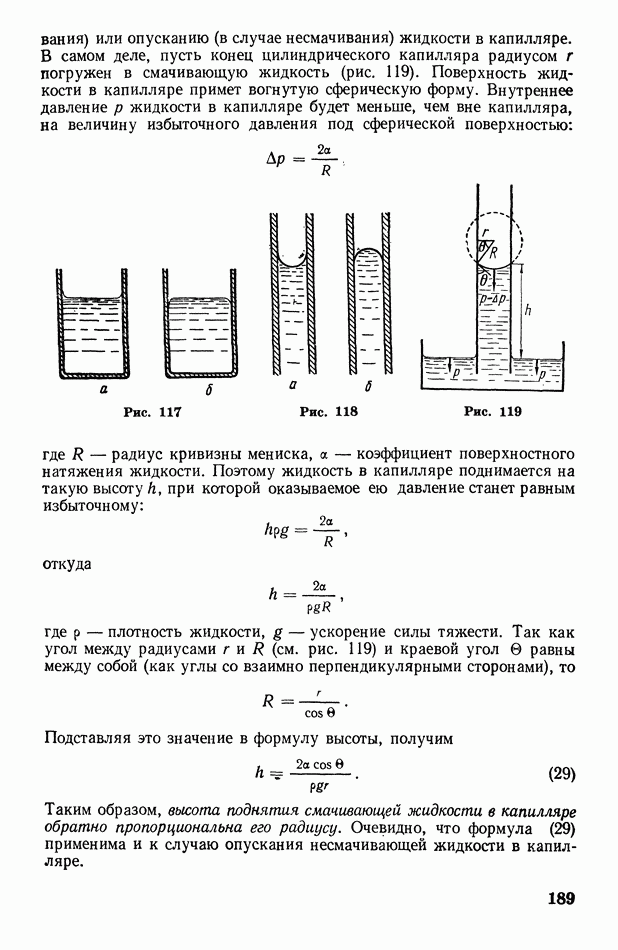
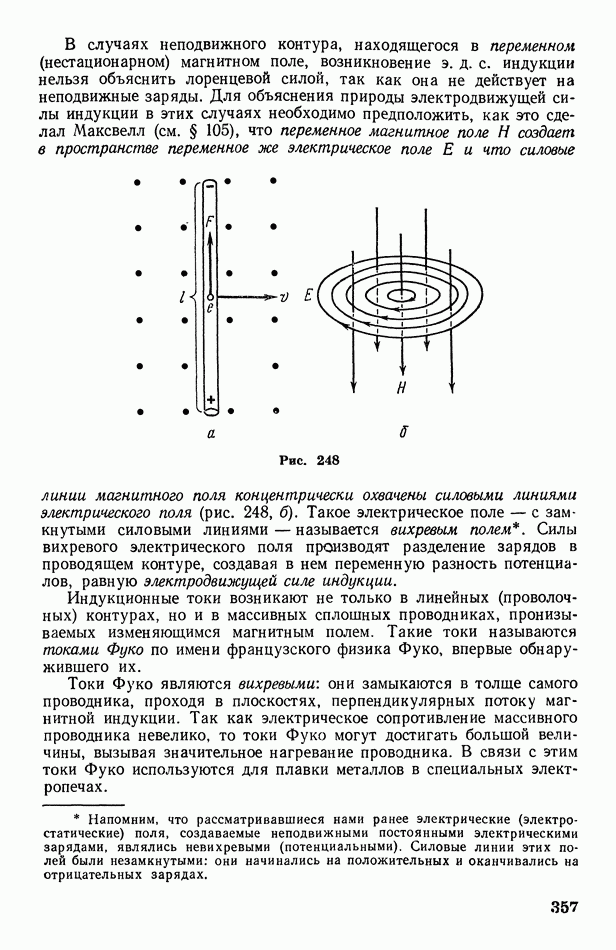
Что касается адиабатических процессов в больших массах газа, то они весьма распространены в природе. Если, например, большой участок вспаханного поля а граничит с водным бассейном  и лесным массивом с, то в ясный летний день полевой участок нагреется солнцем сильнее соседних участков (рис. 136). Расположенная над этим участком воздушная масса А также нагреется сильнее соседних масс
и лесным массивом с, то в ясный летний день полевой участок нагреется солнцем сильнее соседних участков (рис. 136). Расположенная над этим участком воздушная масса А также нагреется сильнее соседних масс  сделавшись более легкой, начнет подниматься (конвекция).
сделавшись более легкой, начнет подниматься (конвекция).

Рис. 136
Так как давление в атмосфере убывает с высотой, то по мере подъема воздушная масса будет расширяться и, следовательно, адиабатически охлаждаться. Когда ее температура понизится до точки росы, водяной пар, находящийся в воздушной массе, начнет конденсироваться на ядрах конденсации. Образуются кучевые облака О, типичные для полуденного времени жаркого дня и потому называемые также «облаками хорошей погоды».
Возвратимся к закону Пуассона и придадим формуле (11) несколько иной вид, выразив температуру через давление. Так как, согласно уравнению Клапейрона — Менделеева,

то, подставляя это выражение температуры в формулу (11), получим

(поскольку  ). Формула (12) представляет собой
). Формула (12) представляет собой
закон Пуассона, связывающий изменения объема и давления газа при адиабатическом процессе.
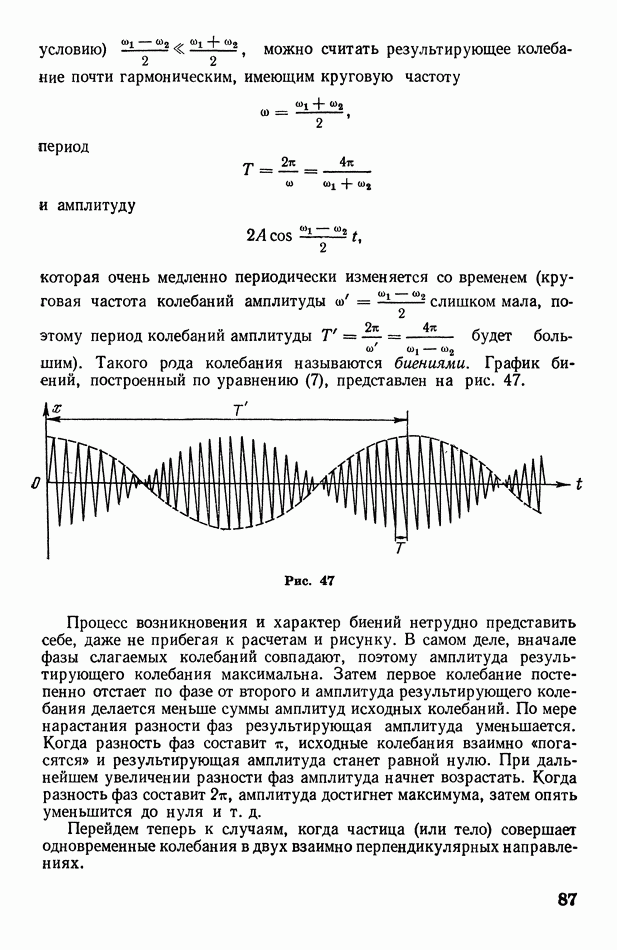
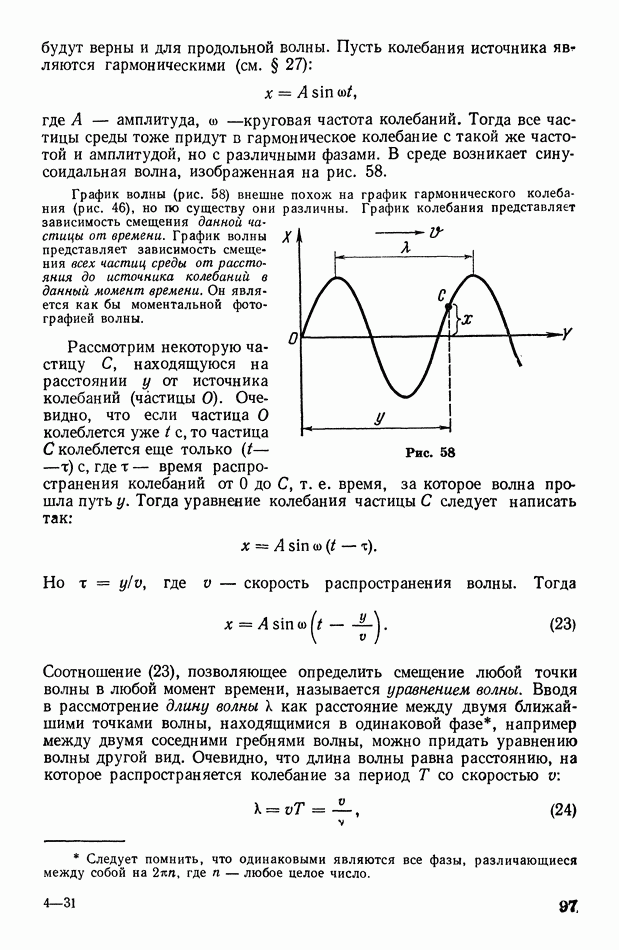
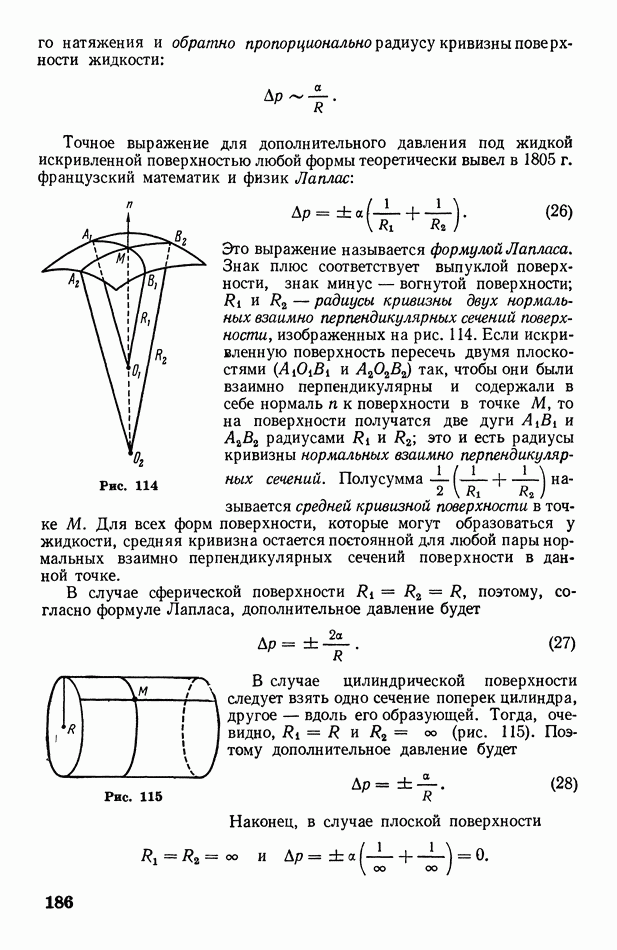
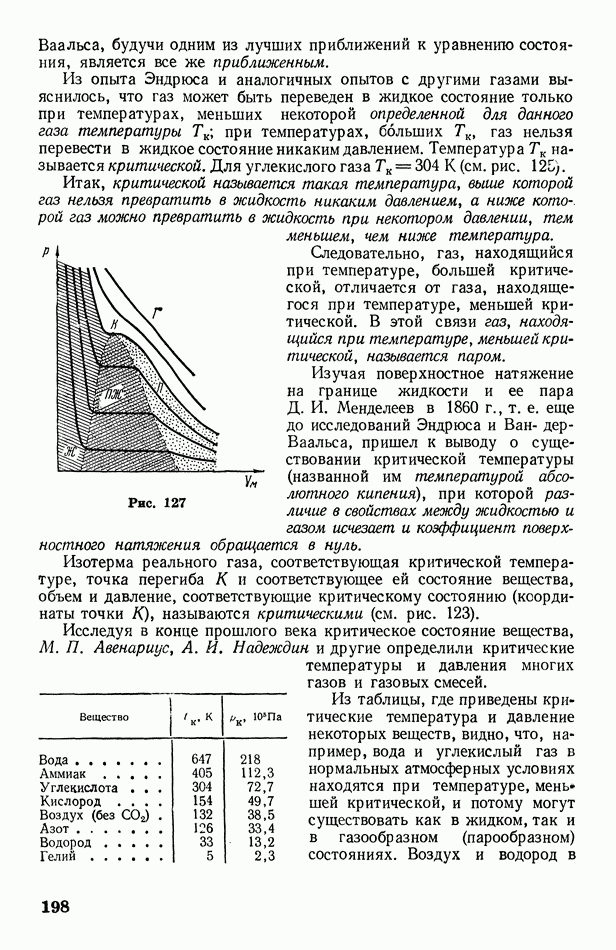
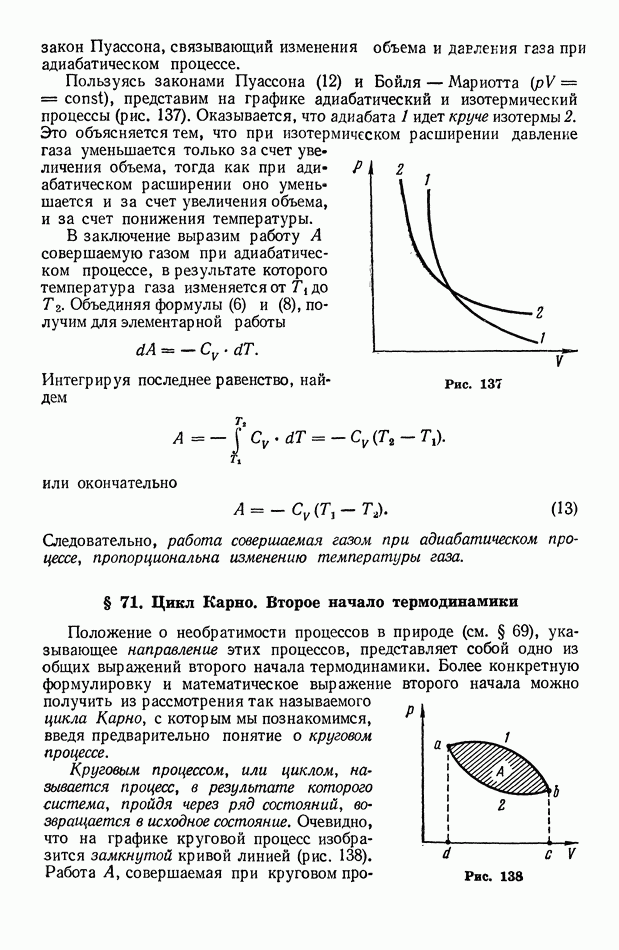
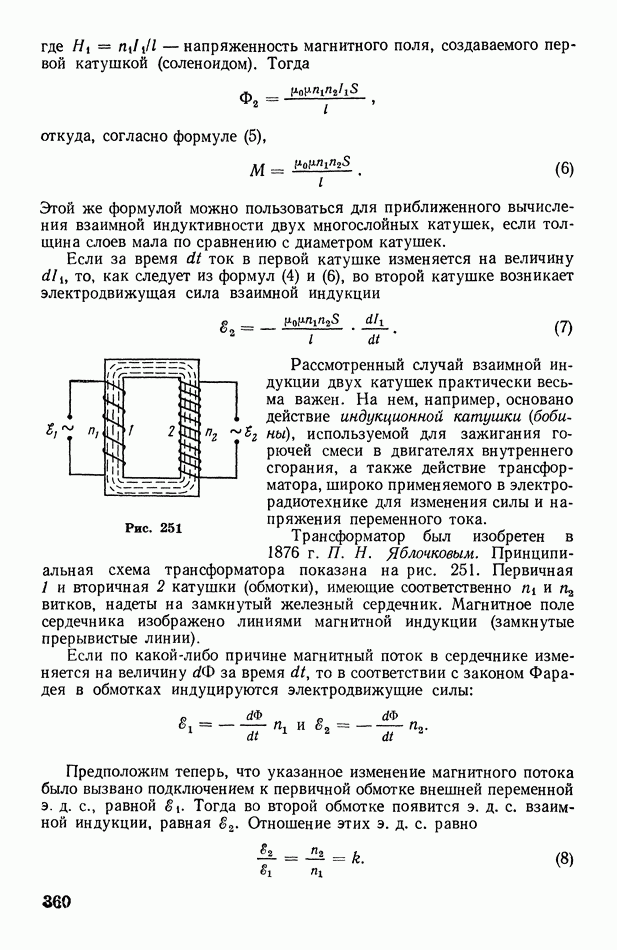
Пользуясь законами Пуассона (12) и Бойля — Мариотта  представим на графике адиабатический и изотермический процессы (рис. 137). Оказывается, что адиабата 1 идет круче изотермы Это объясняется тем, что при изотермическом расширении давление газа уменьшается только за счет увеличения объема, тогда как при адиабатическом расширении оно уменьшается и за счет увеличения объема, и за счет понижения температуры.
представим на графике адиабатический и изотермический процессы (рис. 137). Оказывается, что адиабата 1 идет круче изотермы Это объясняется тем, что при изотермическом расширении давление газа уменьшается только за счет увеличения объема, тогда как при адиабатическом расширении оно уменьшается и за счет увеличения объема, и за счет понижения температуры.
В заключение выразим работу А совершаемую газом при адиабатическом процессе, в результате которого температура газа изменяется от  до
до  Объединяя формулы (6) и (8), получим для элементарной работы
Объединяя формулы (6) и (8), получим для элементарной работы


Рис. 137
Интегрируя последнее равенство, найдем

или окончательно

Следовательно, работа совершаемая газом при адиабатическом процессе, пропорциональна изменению температуры газа.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
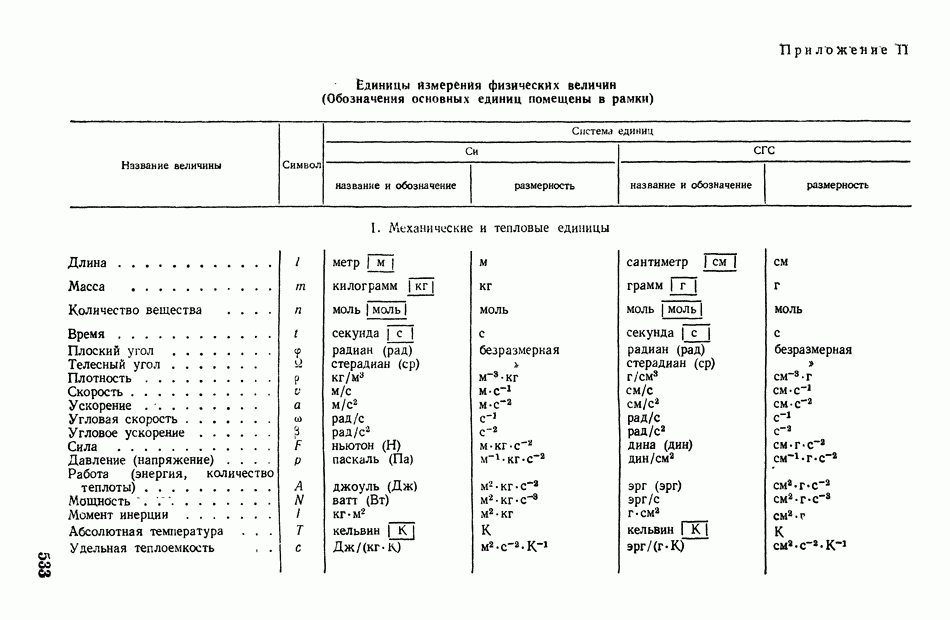
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
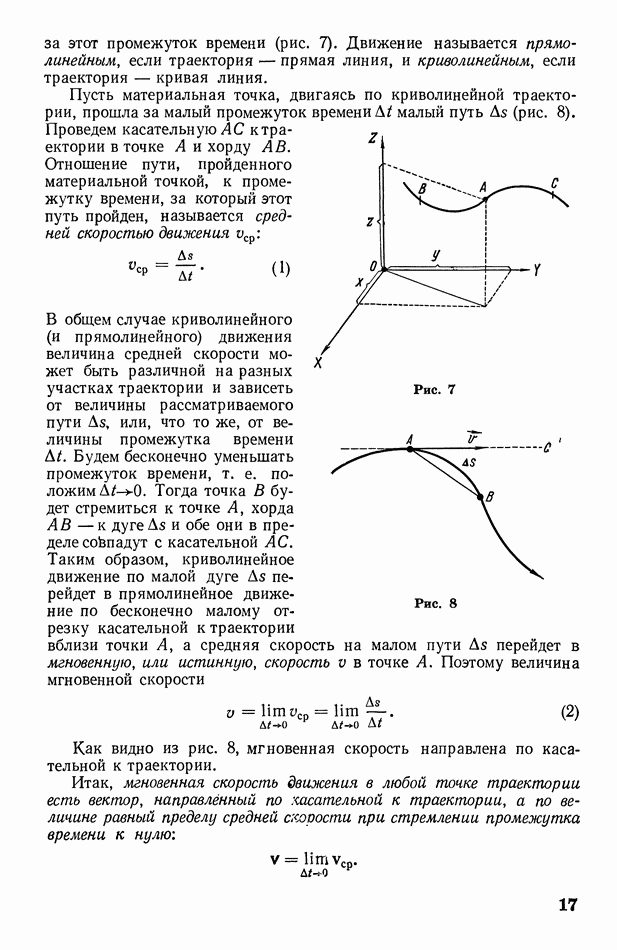
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
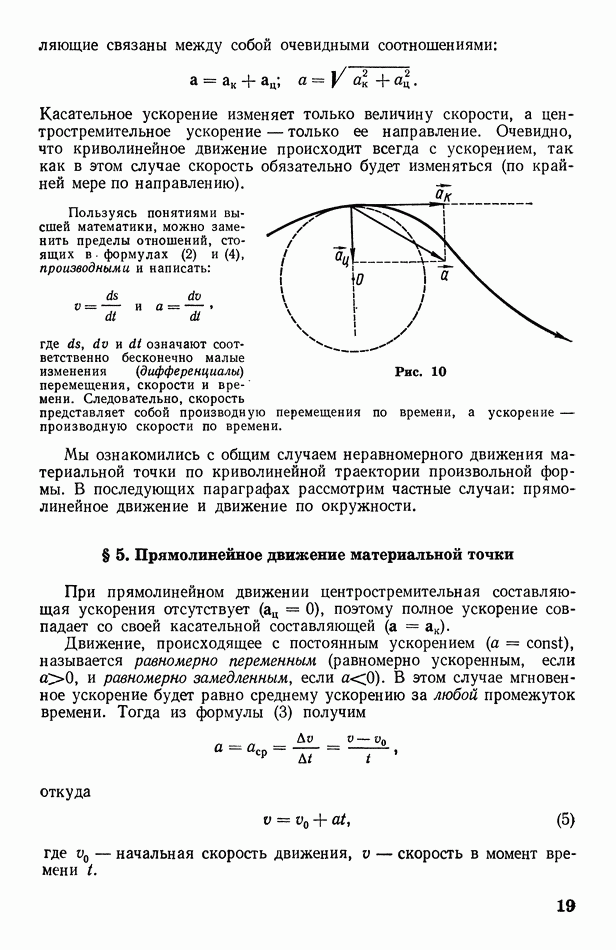
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
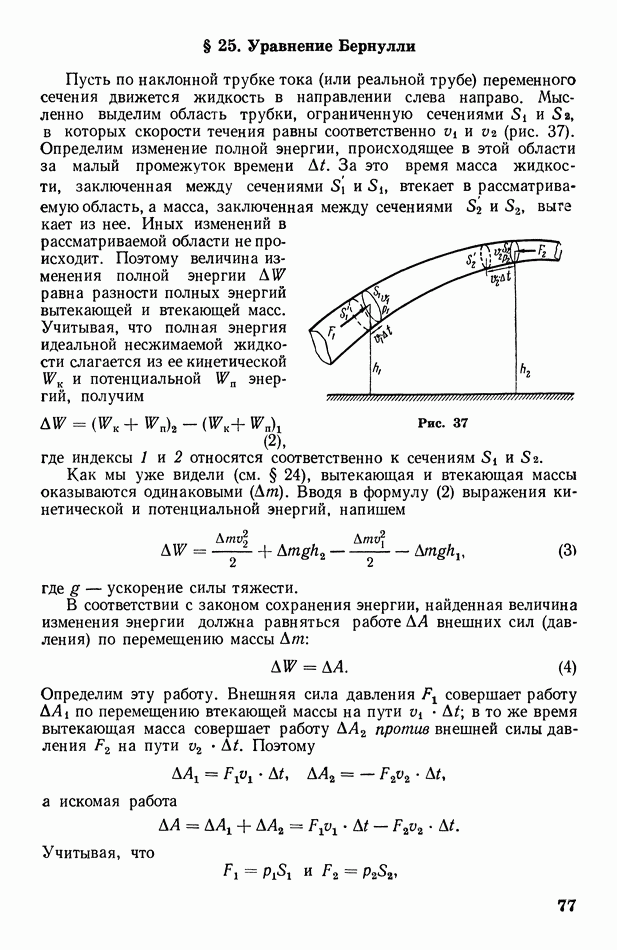
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
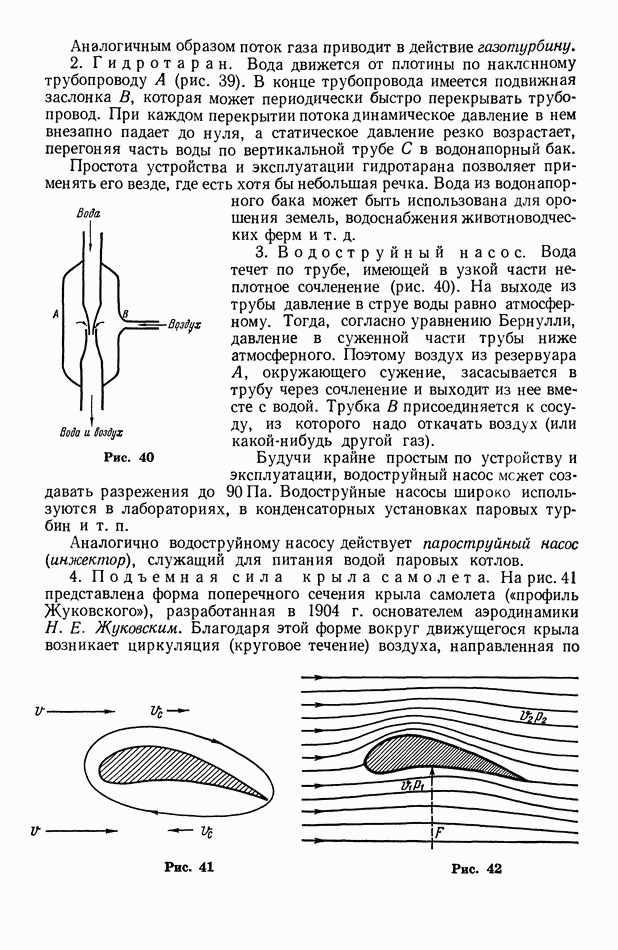
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
- § 30. О затухающих и вынужденных колебаниях
- § 31. Волновой процесс
- § 32. Уравнение волны. Интенсивность волны
- § 33. Интерференция волн. Стоячие волны
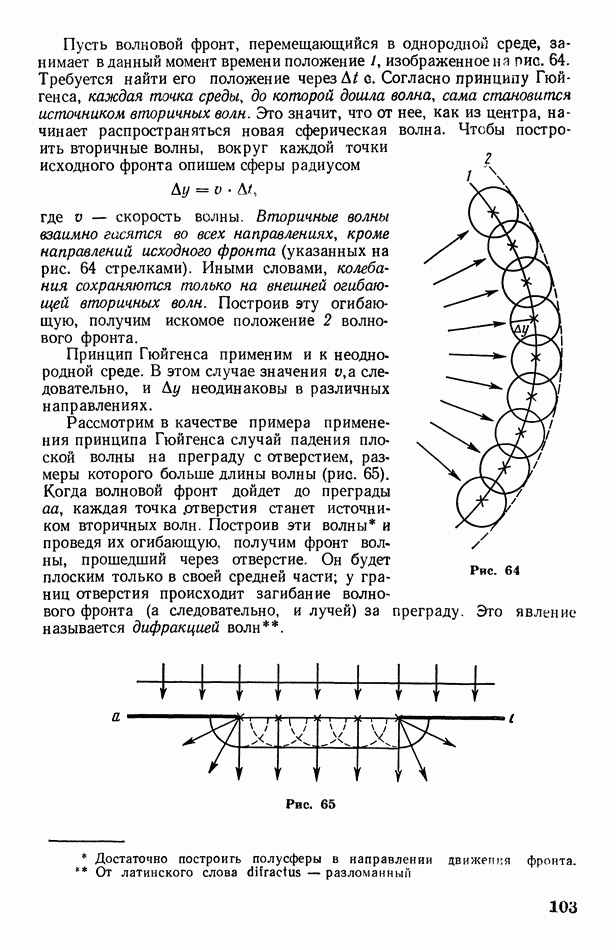
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
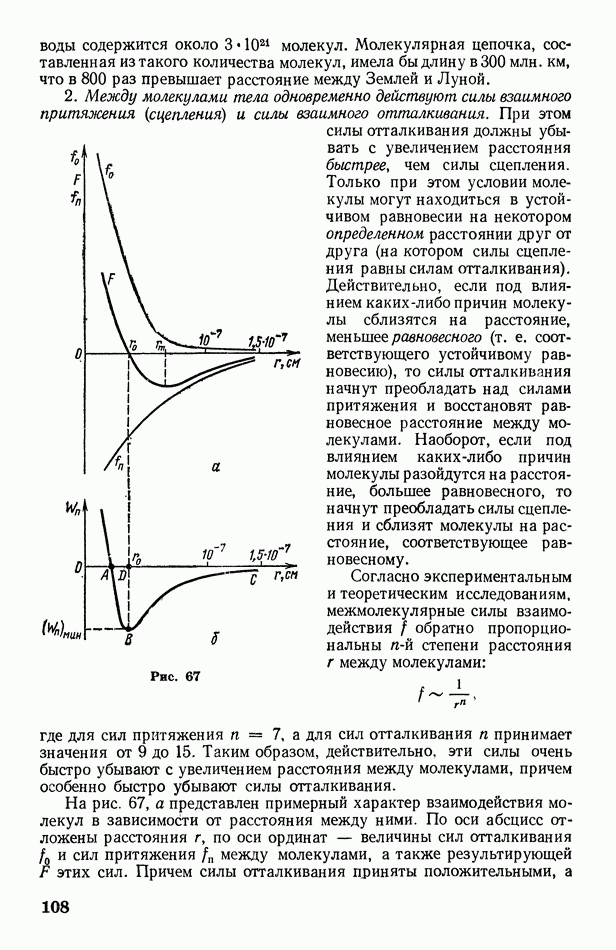
- 2. Молекулярная физика и термодинамика
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
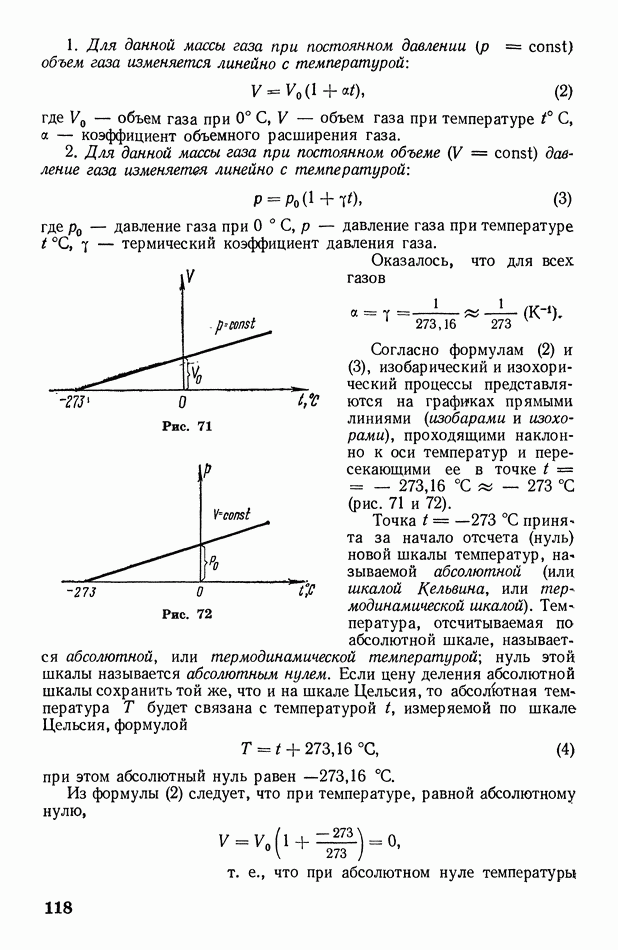
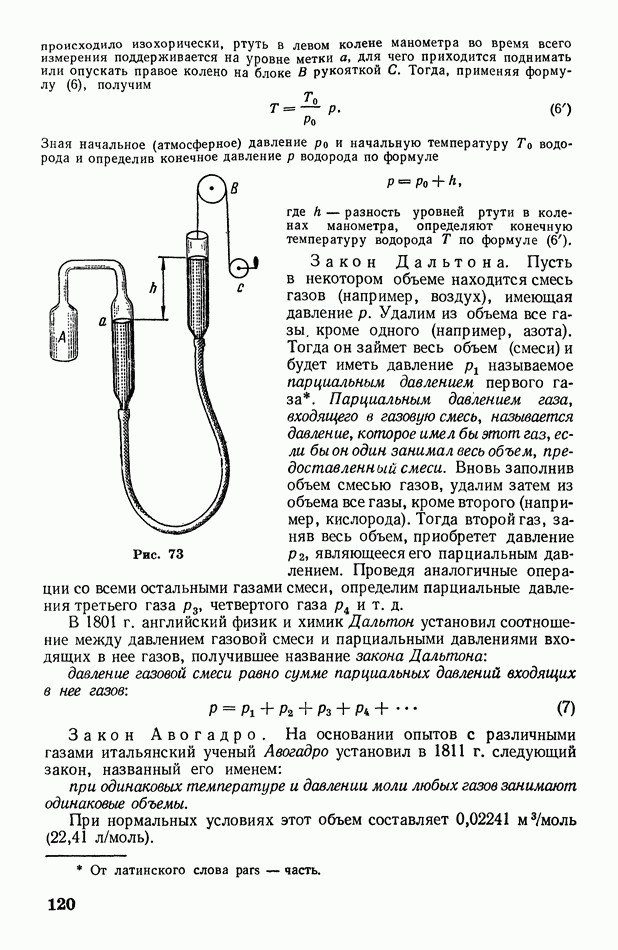
- Глава VIII. Газы
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
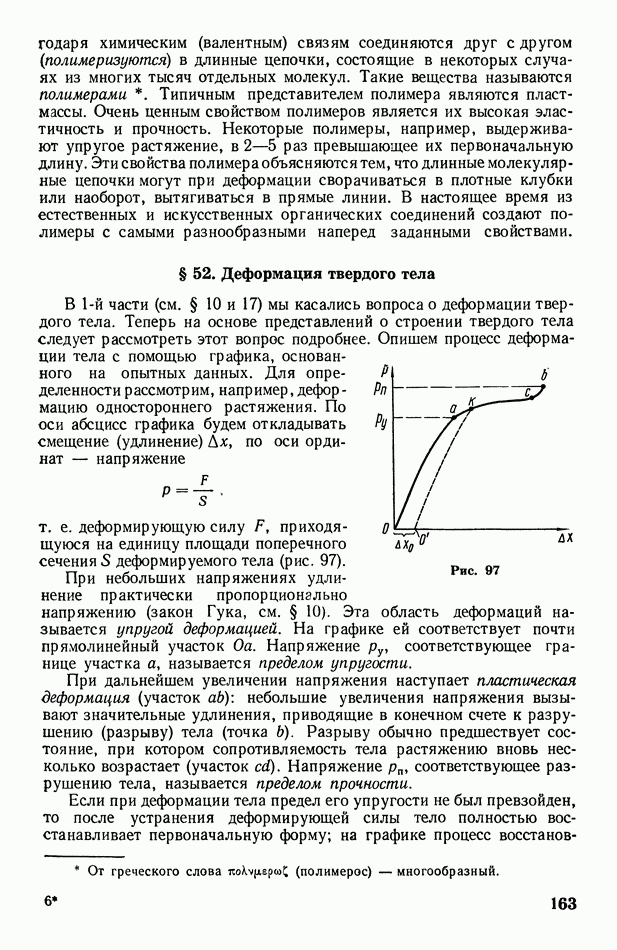
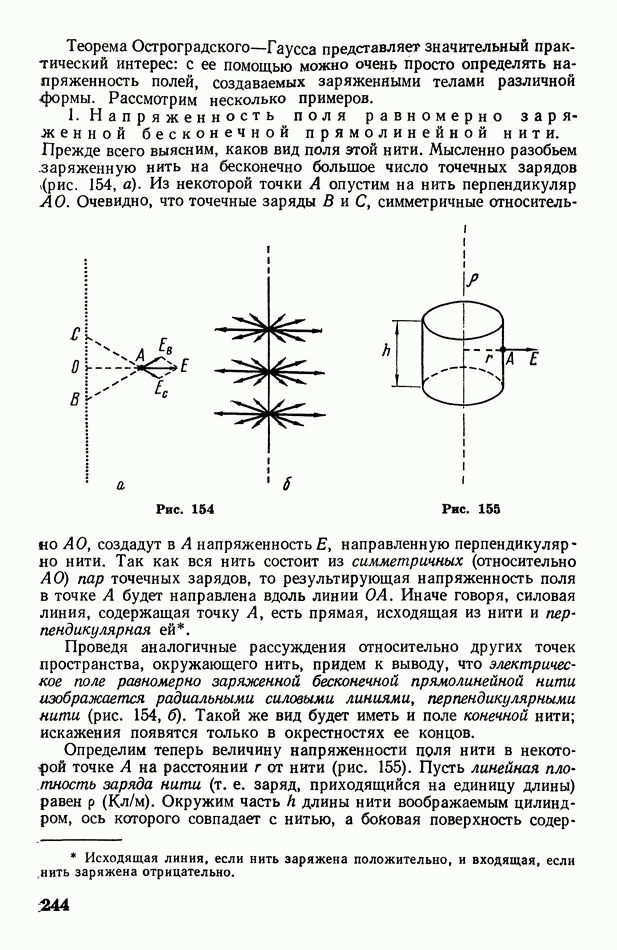
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
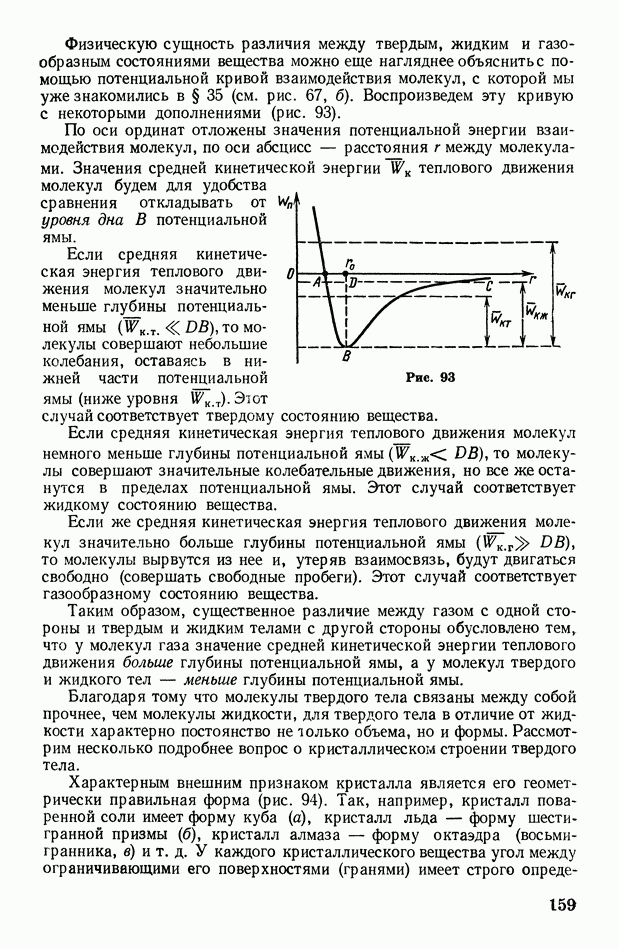
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
- § 61. Капиллярные явления; формула Жюрена
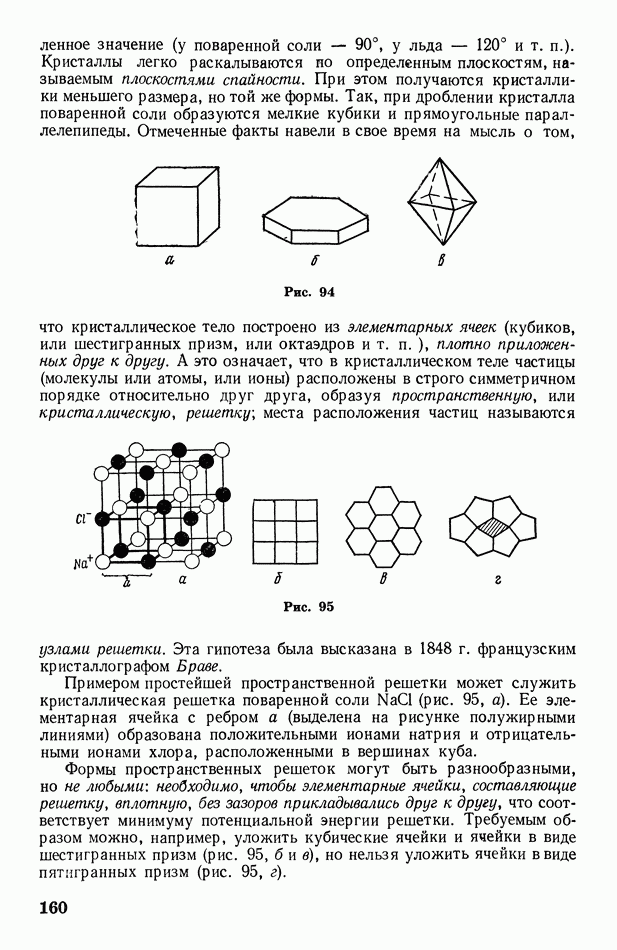
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
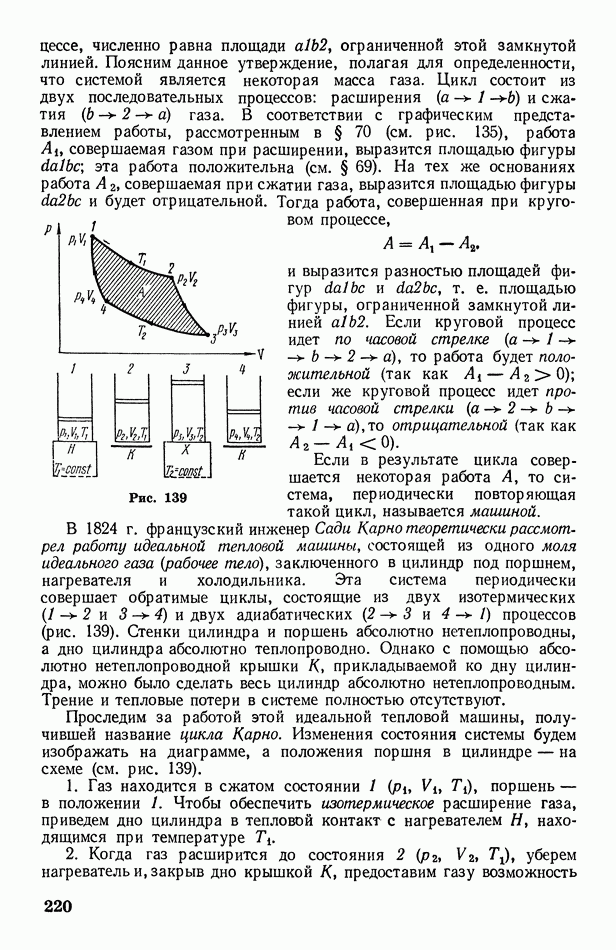
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
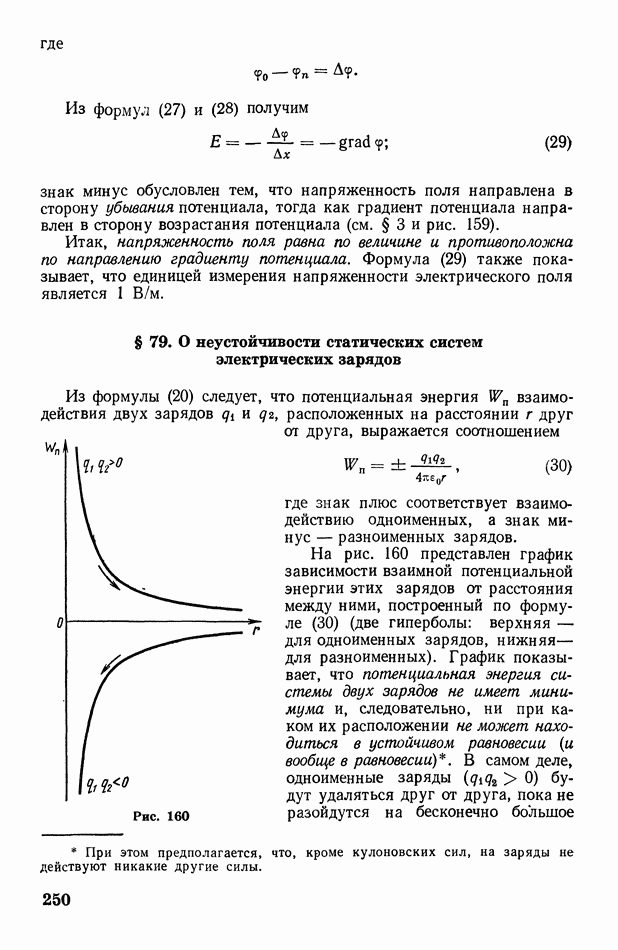
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
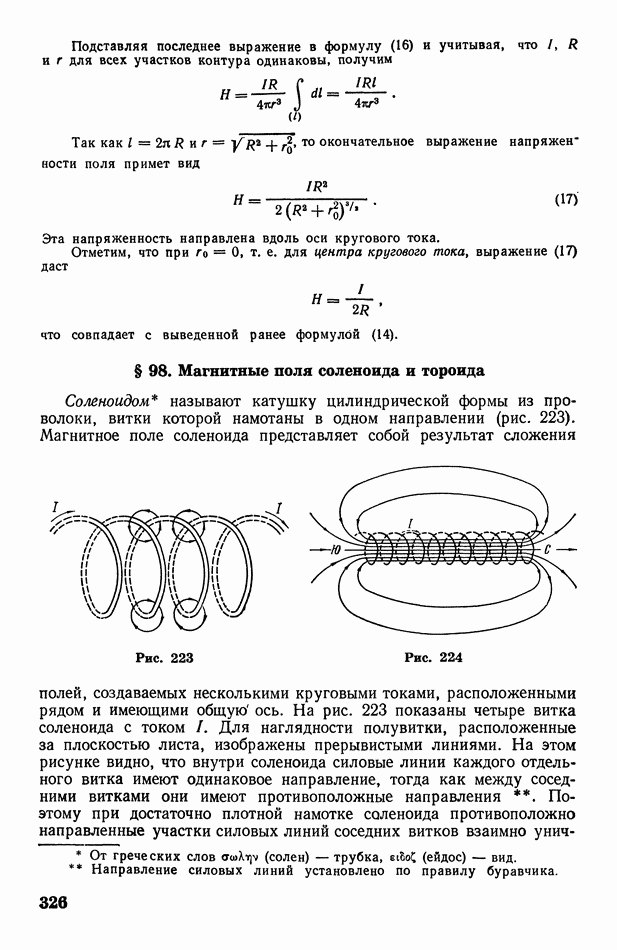
- § 87. Контактная разность потенциалов. Термоэлектрические явления
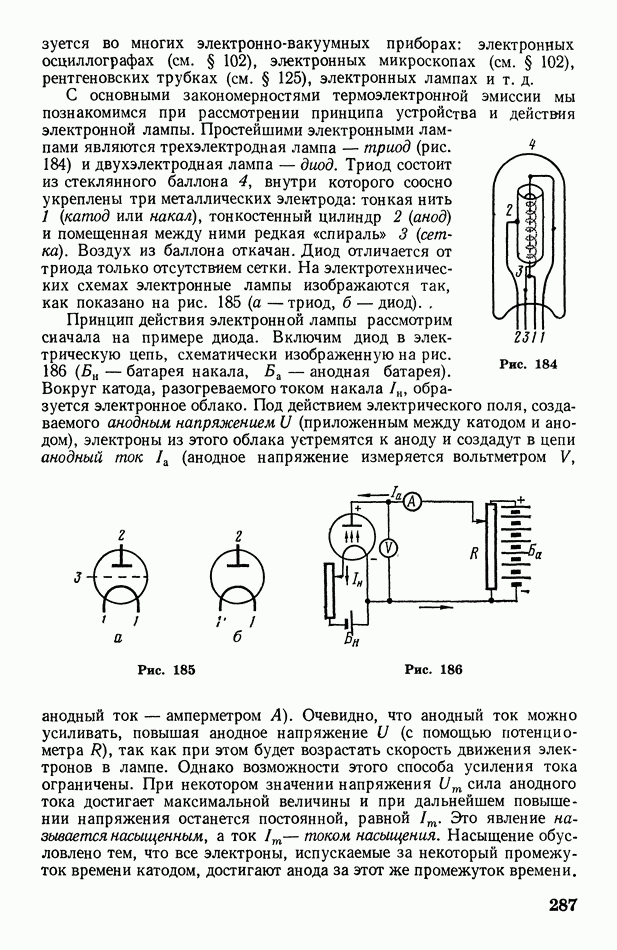
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
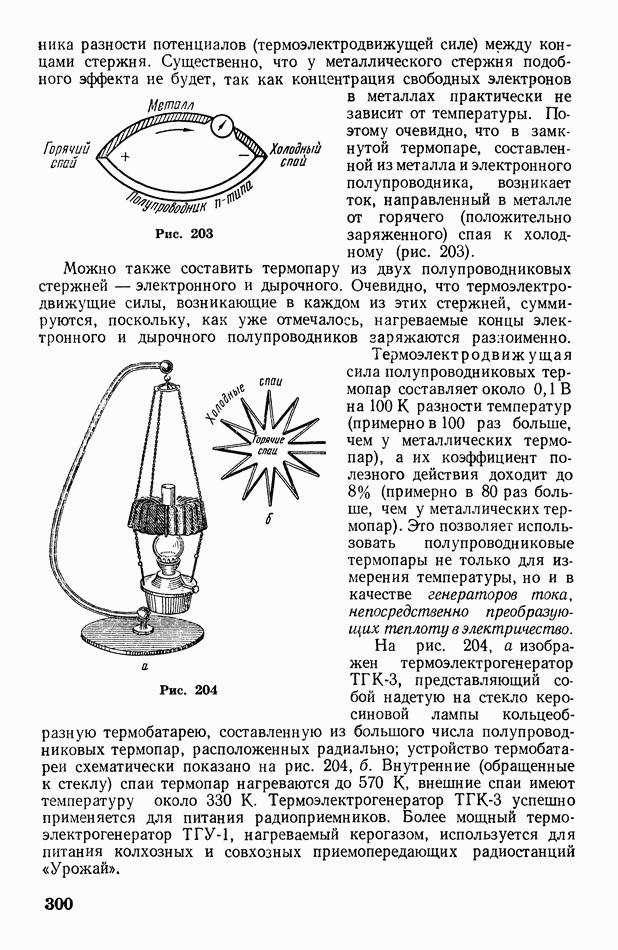
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
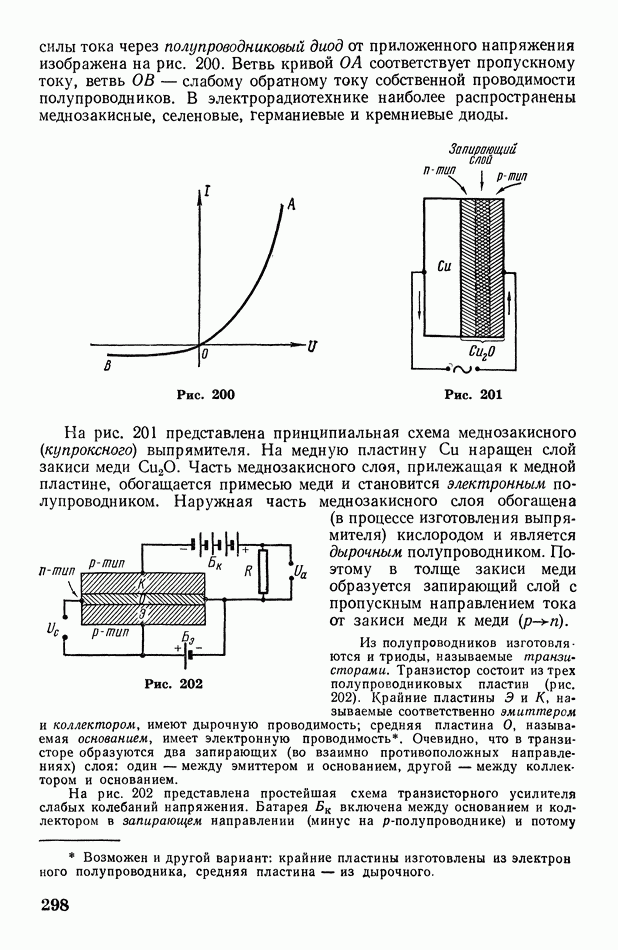
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
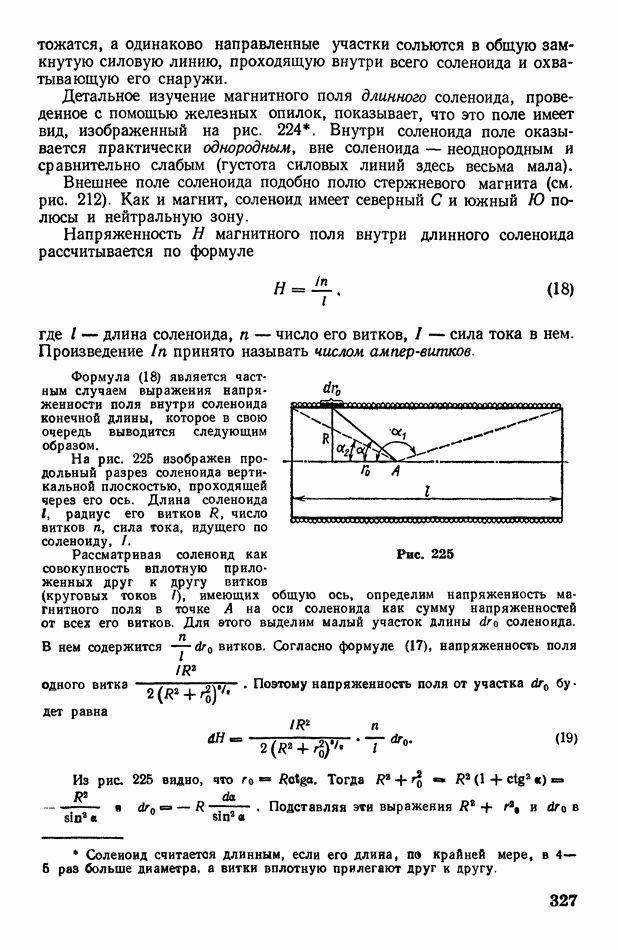
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
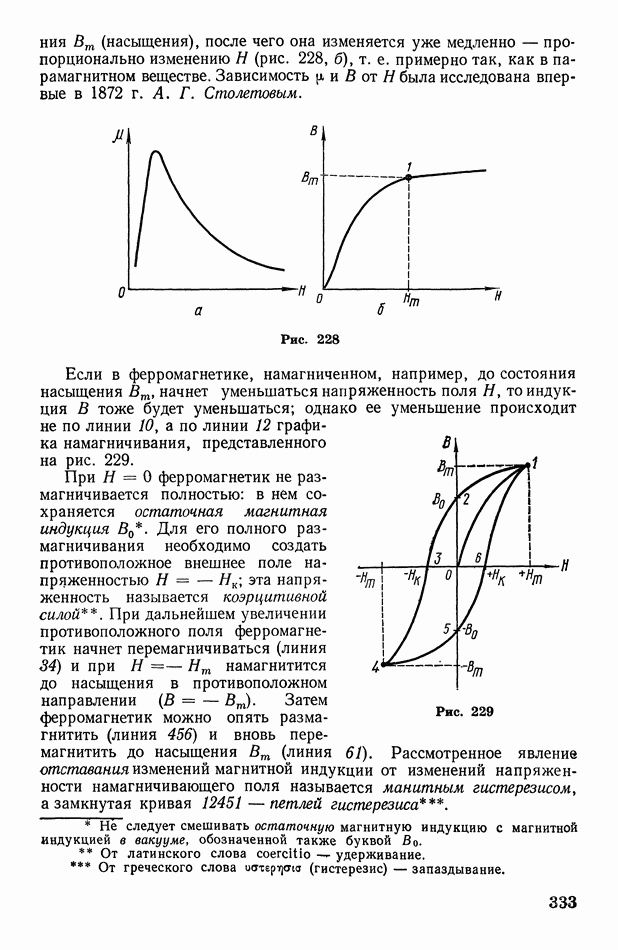
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
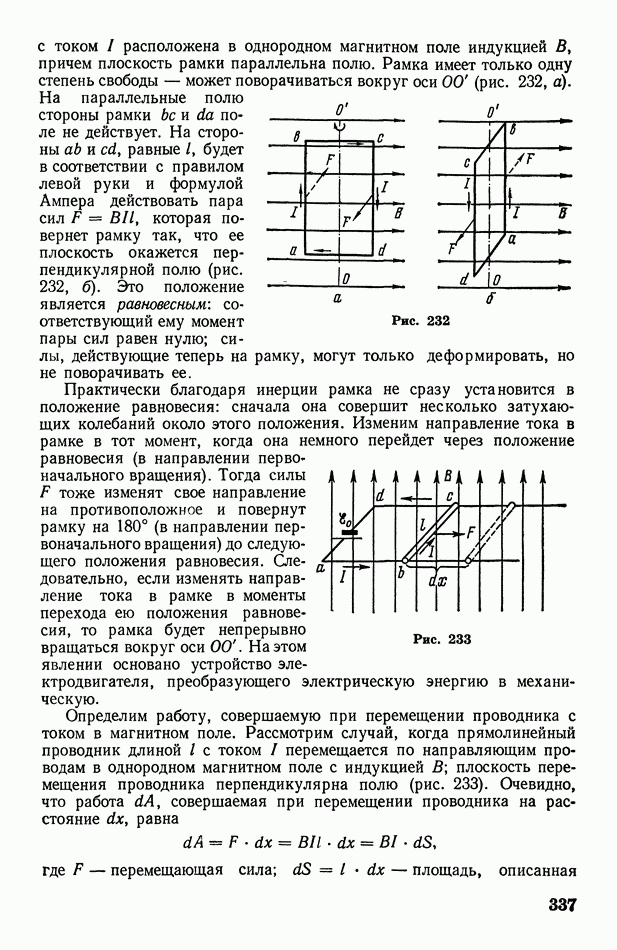
- § 100. Действие магнитного поля на проводник с током. Определение ампера
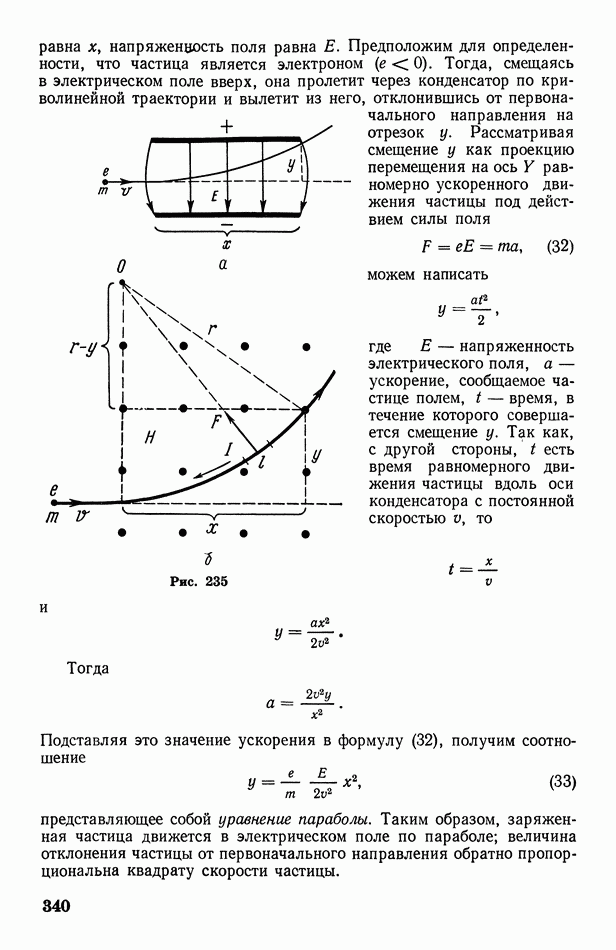
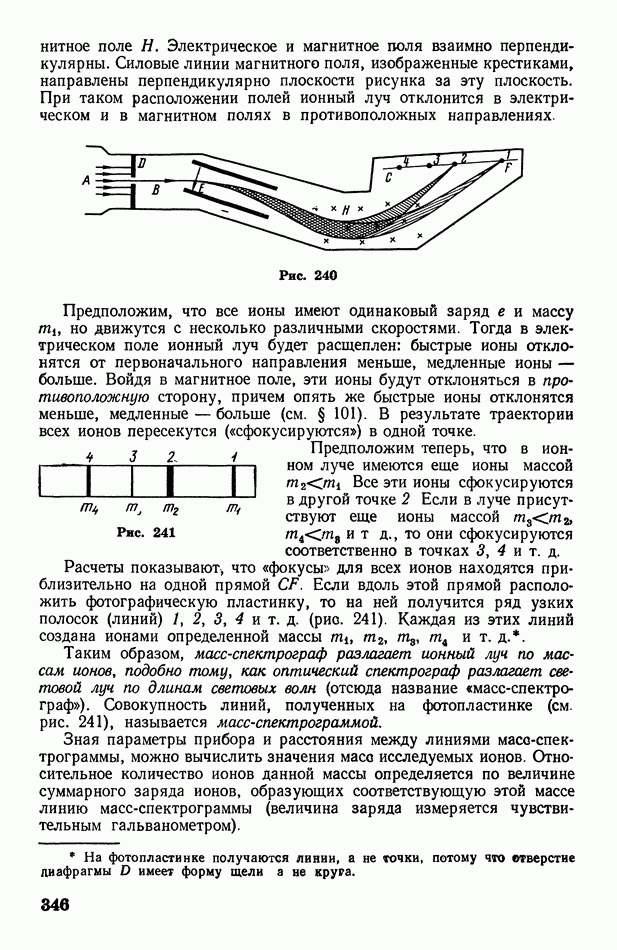
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
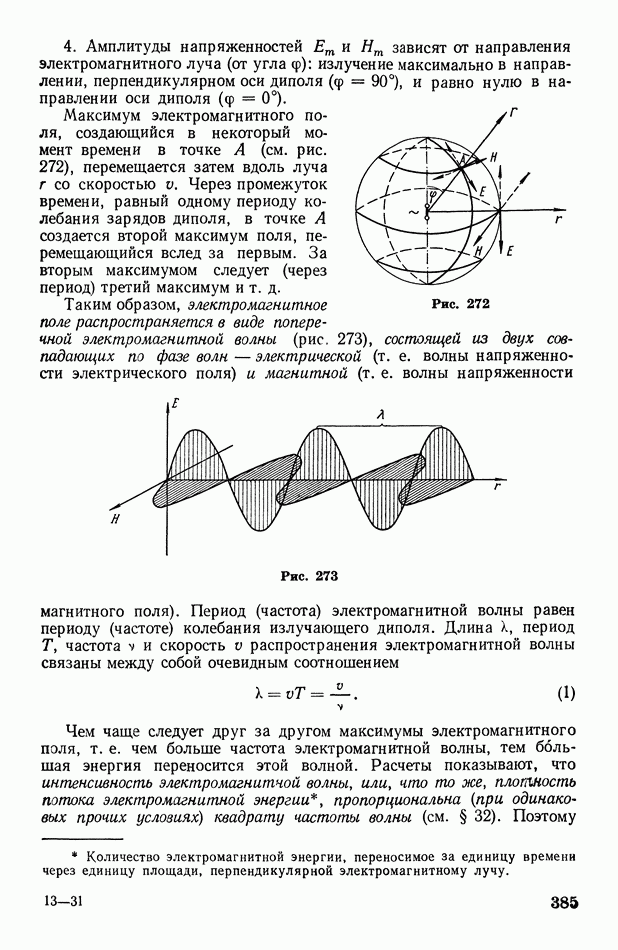
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
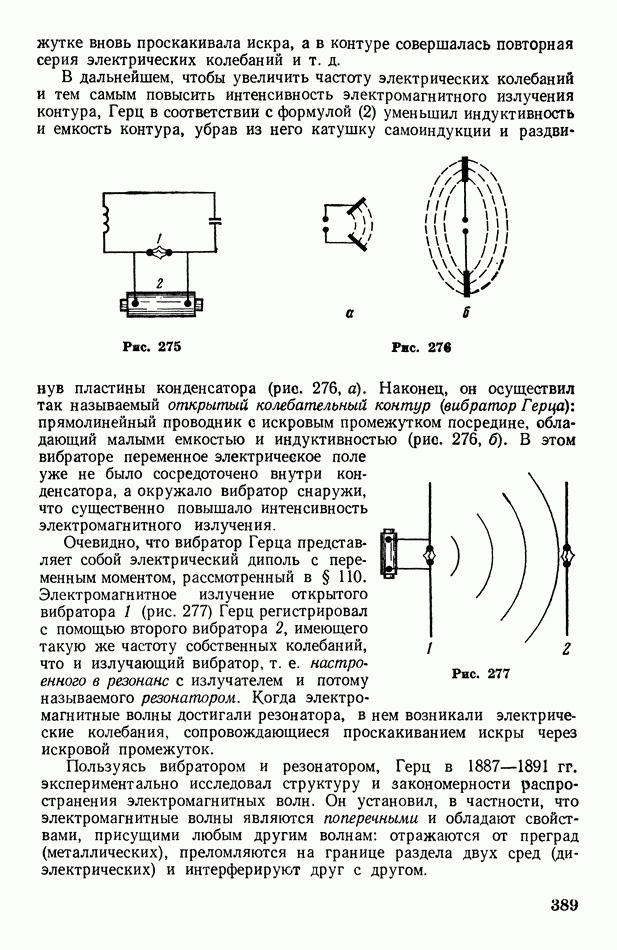
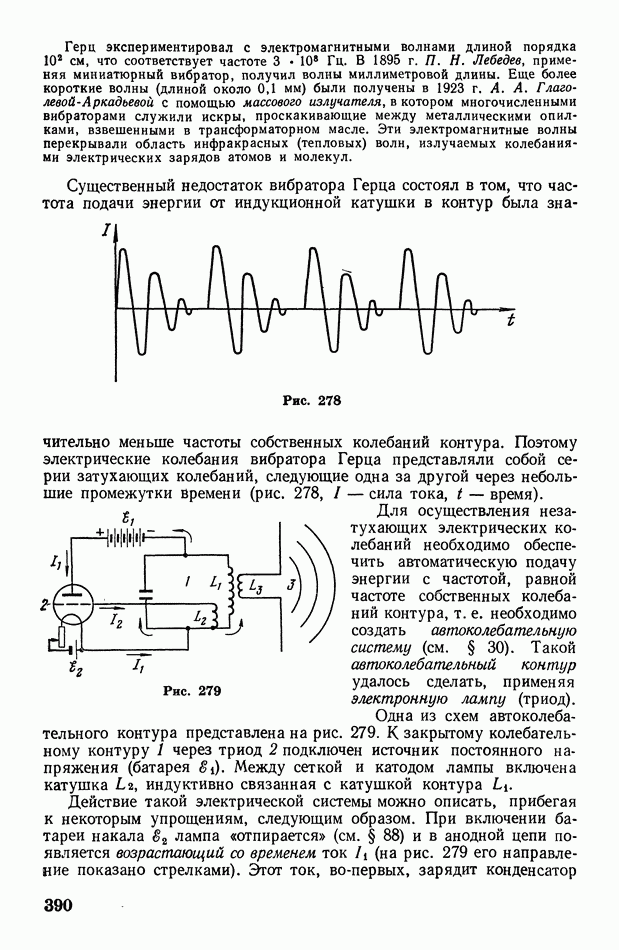
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
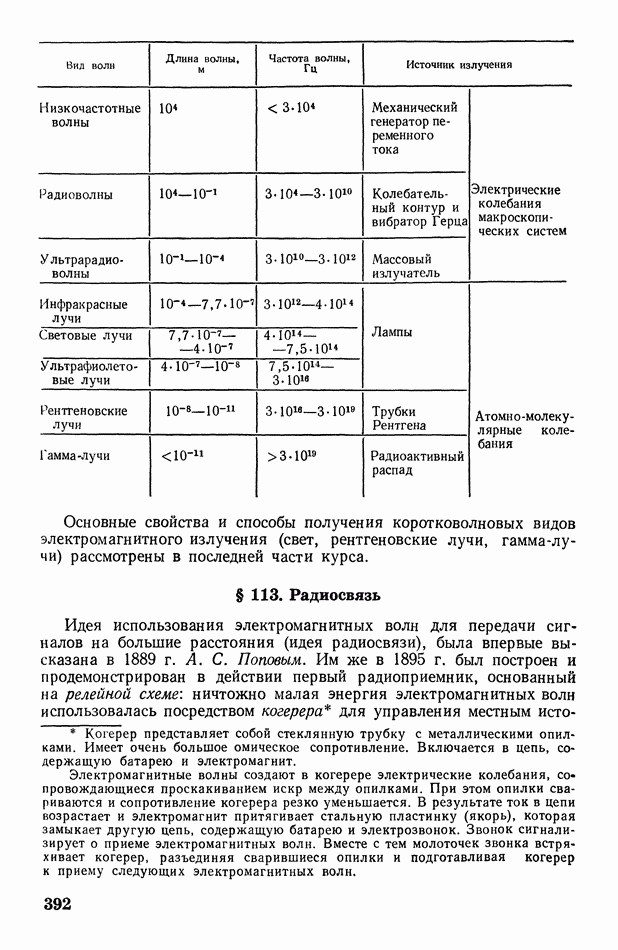
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
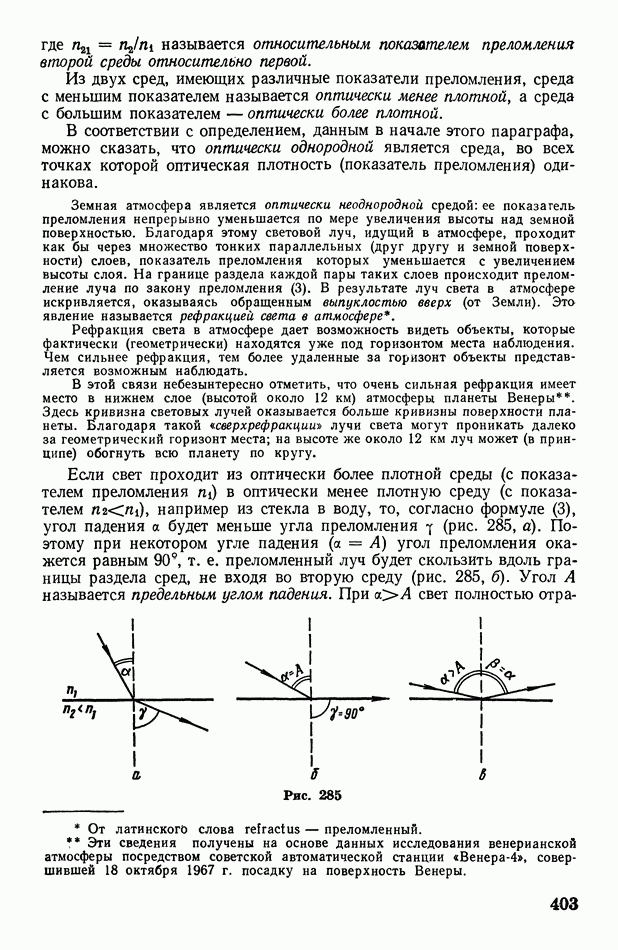
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
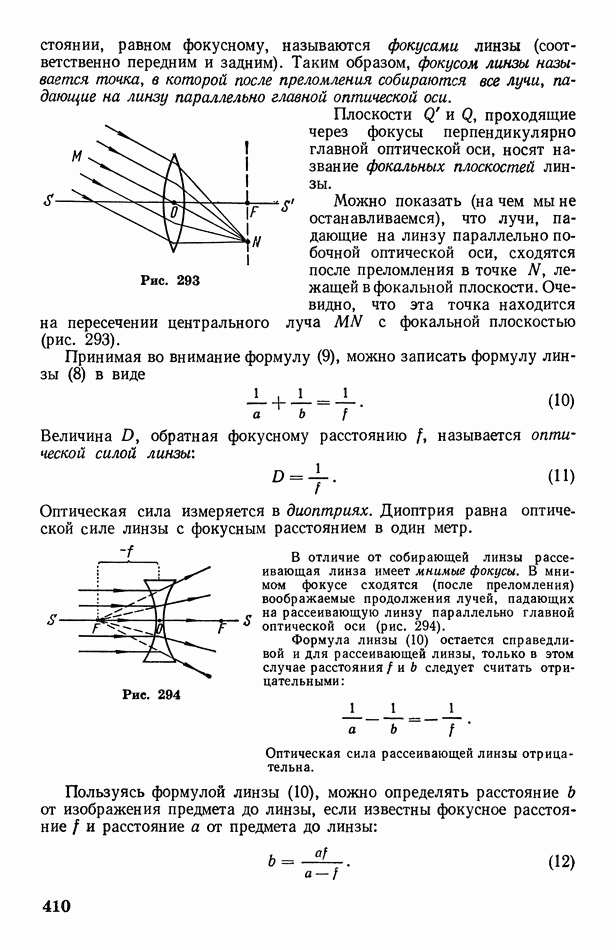
- § 117. Тонкие линзы. Микроскоп
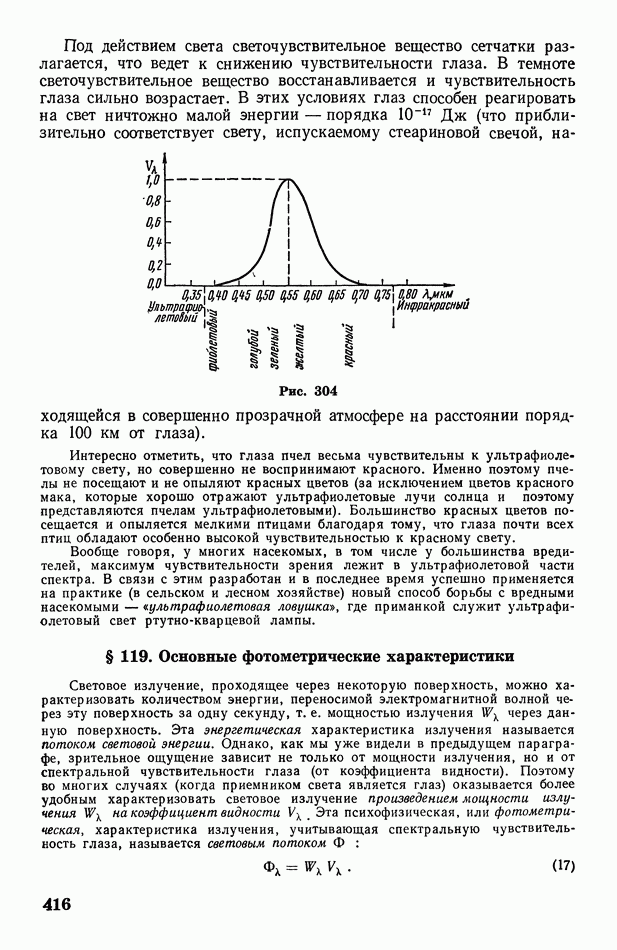
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
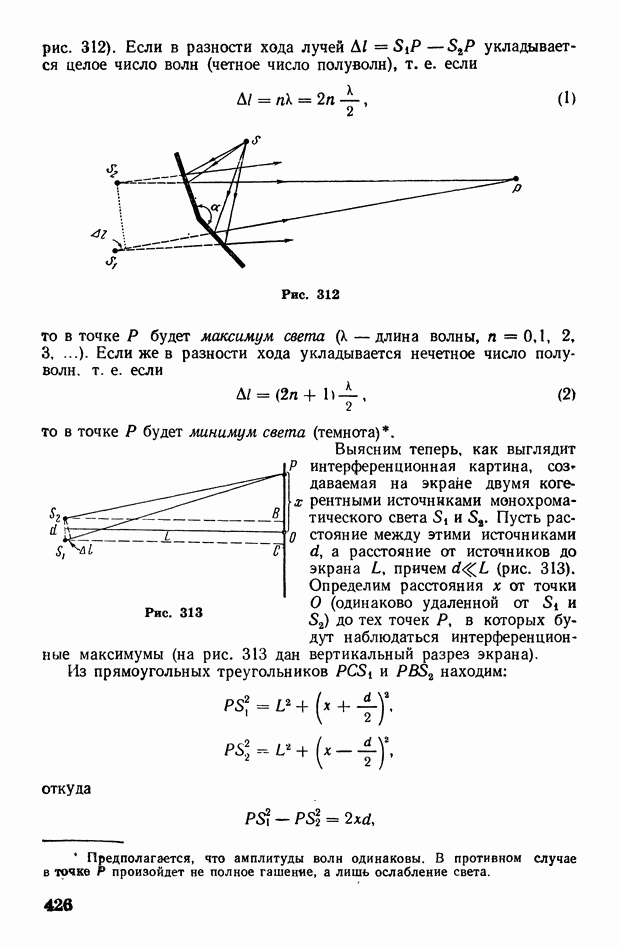
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
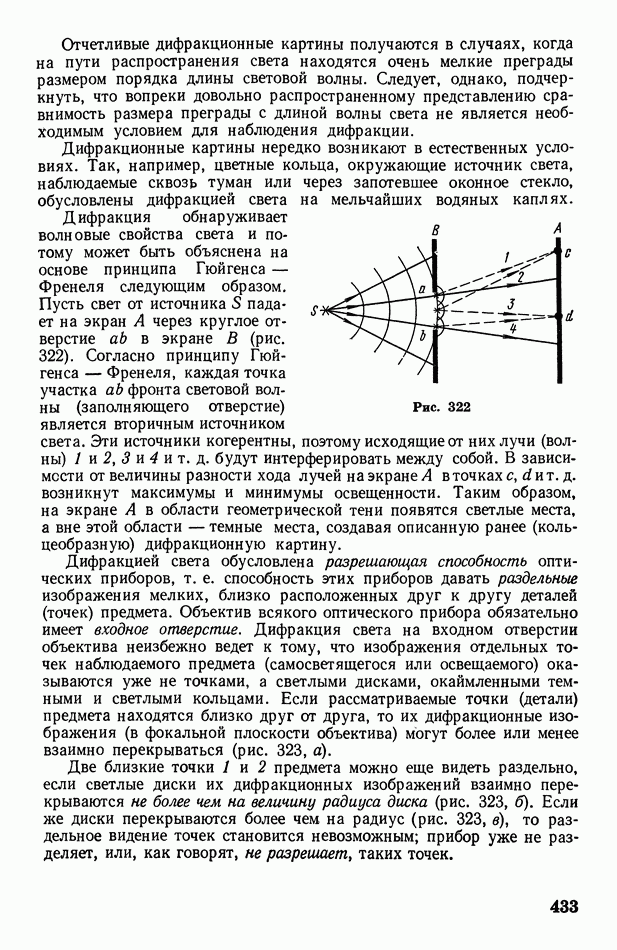
- § 123. Дифракция света. Разрешающая способность оптических приборов
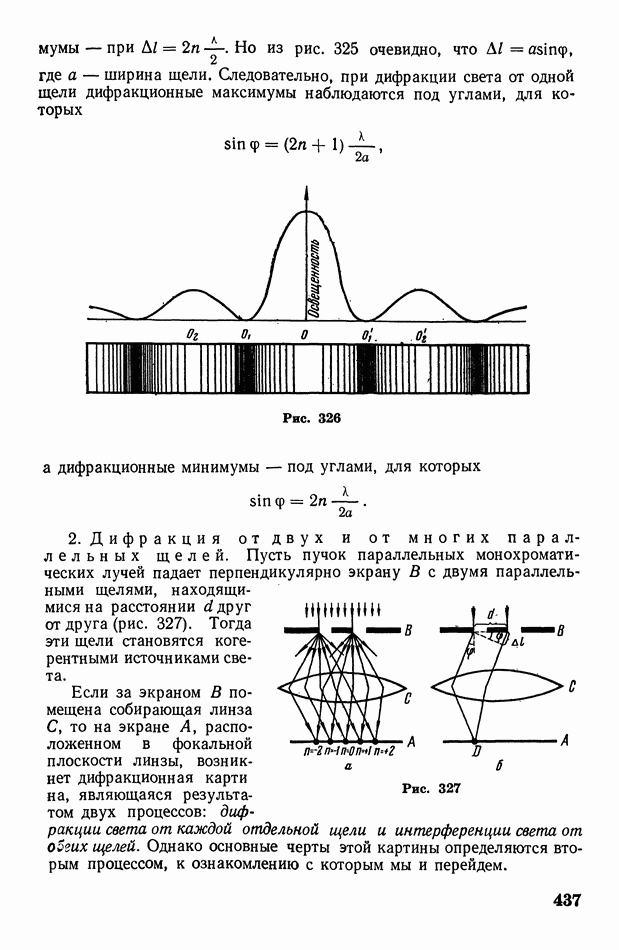
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
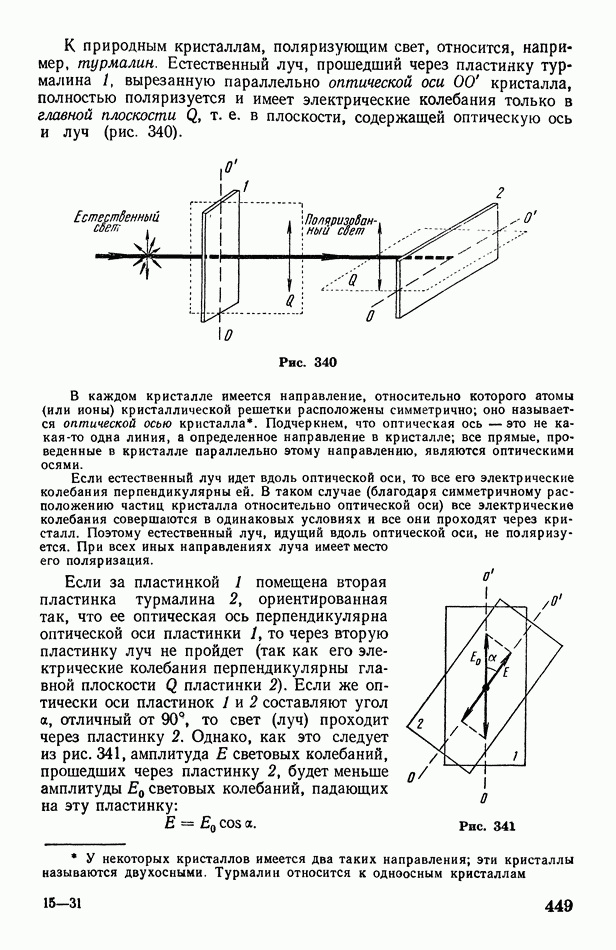
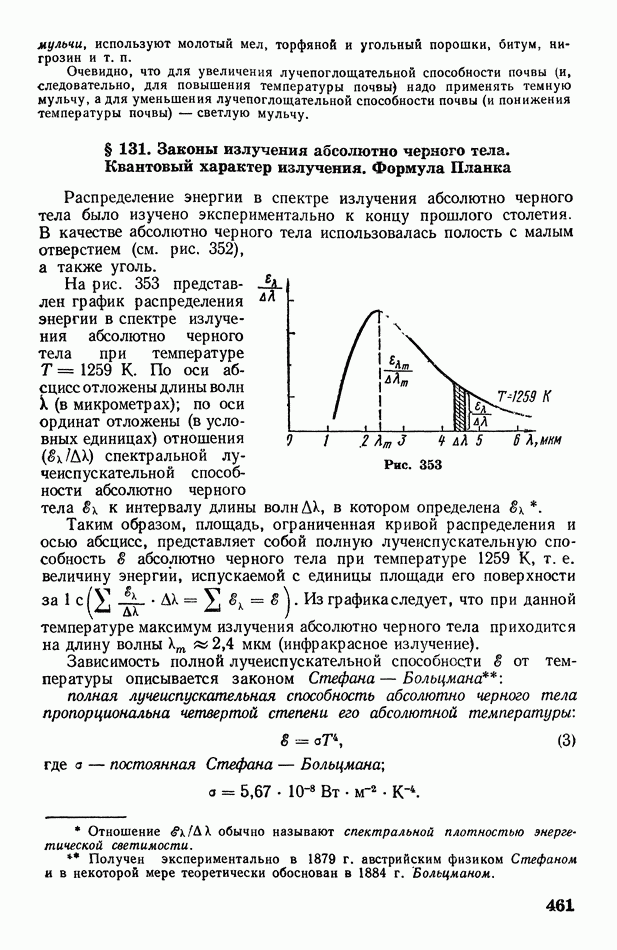
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
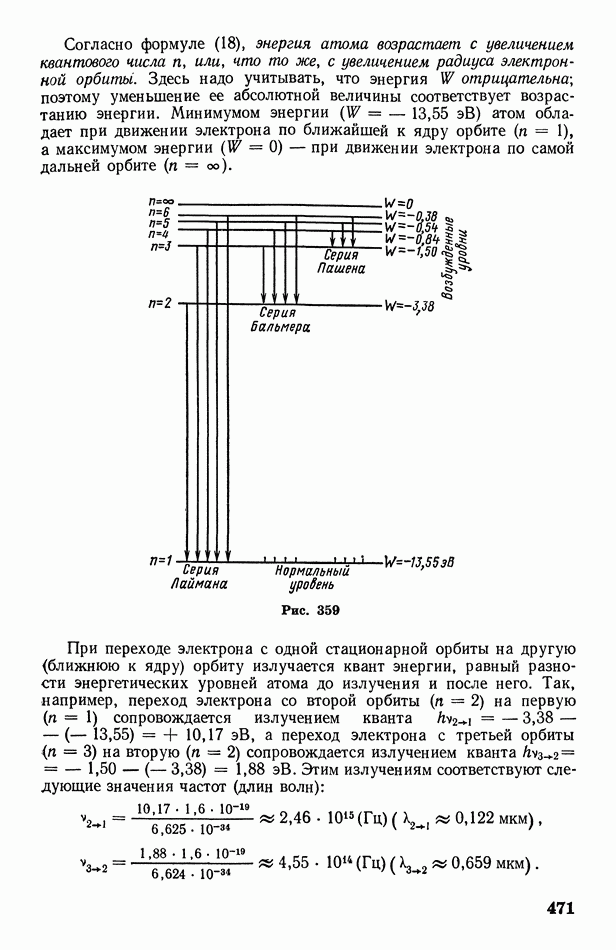
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
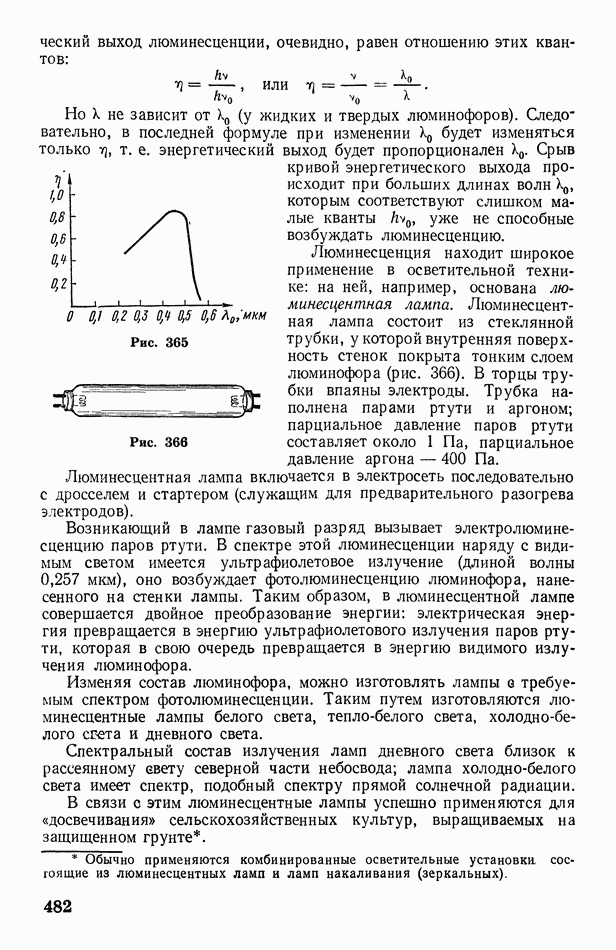
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
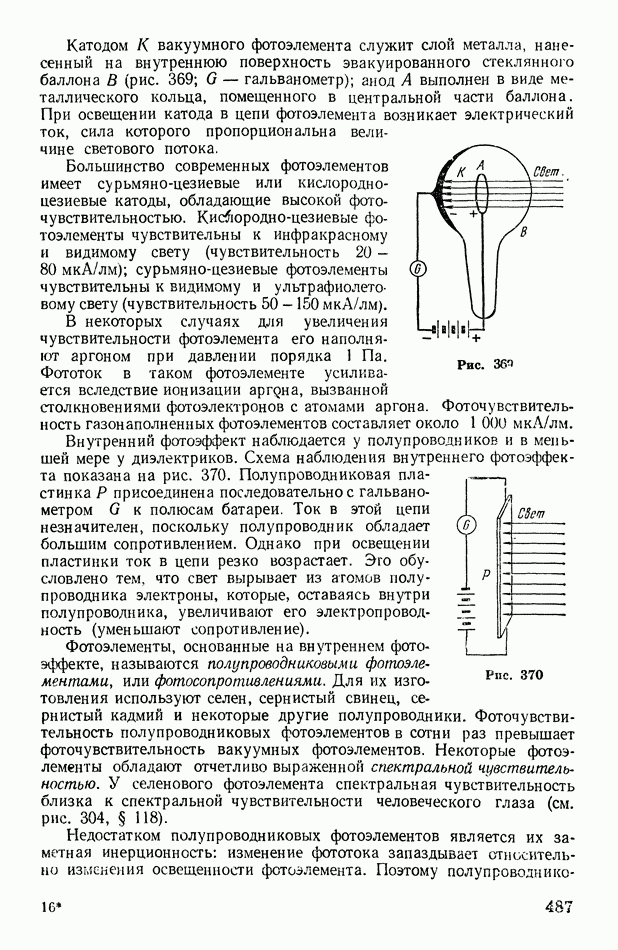
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
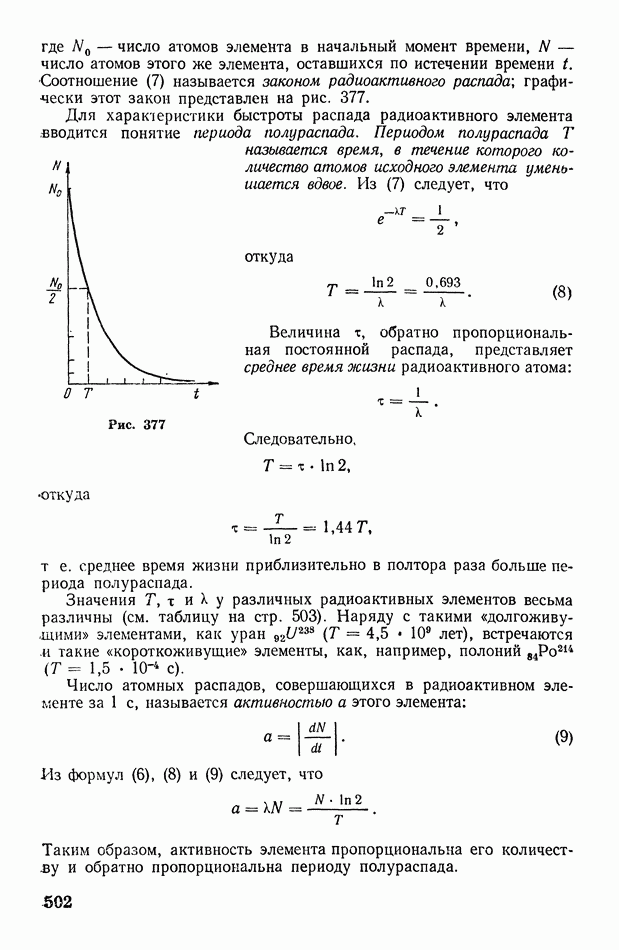
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
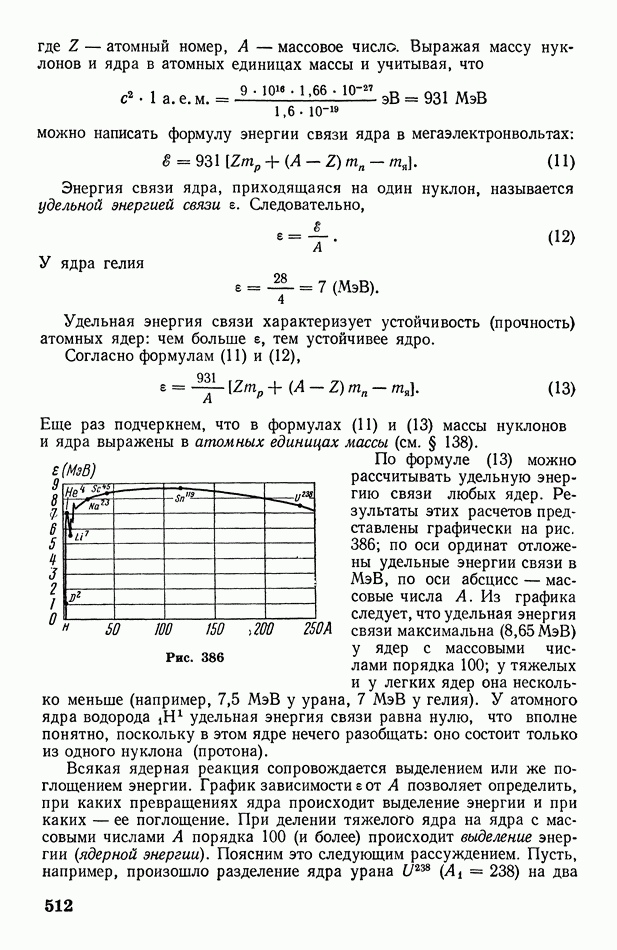
- § 142. Энергия связи и дефект массы атомного ядра
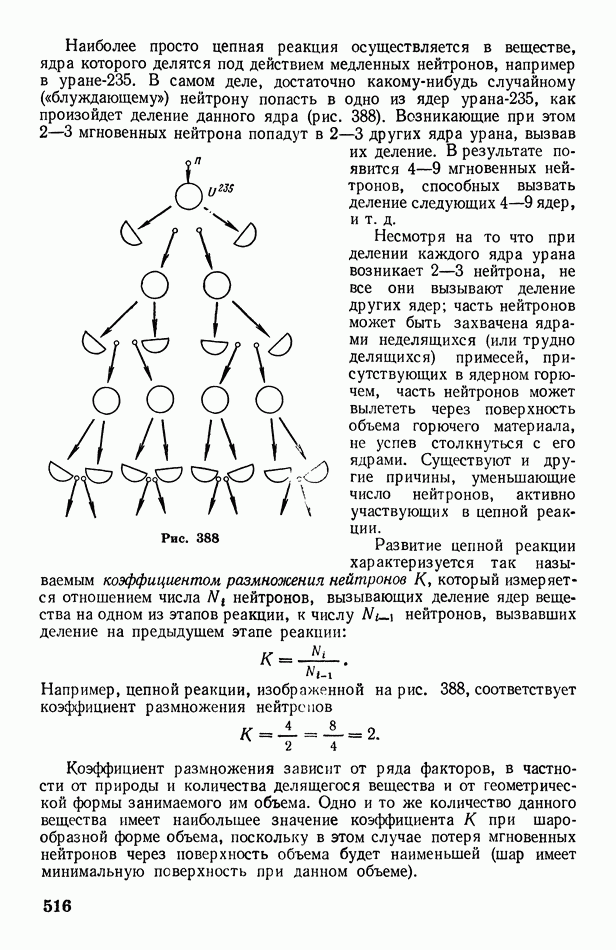
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
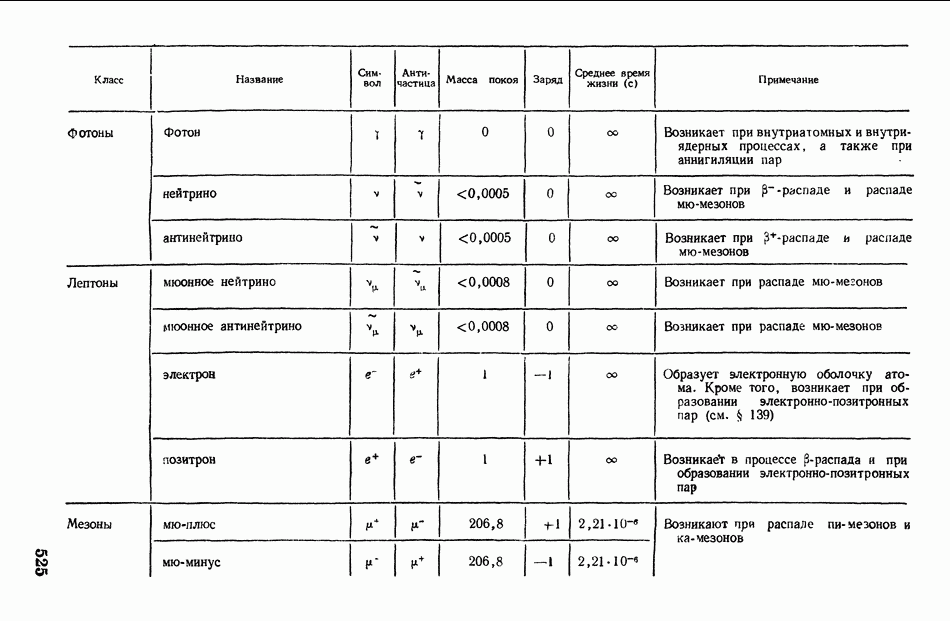
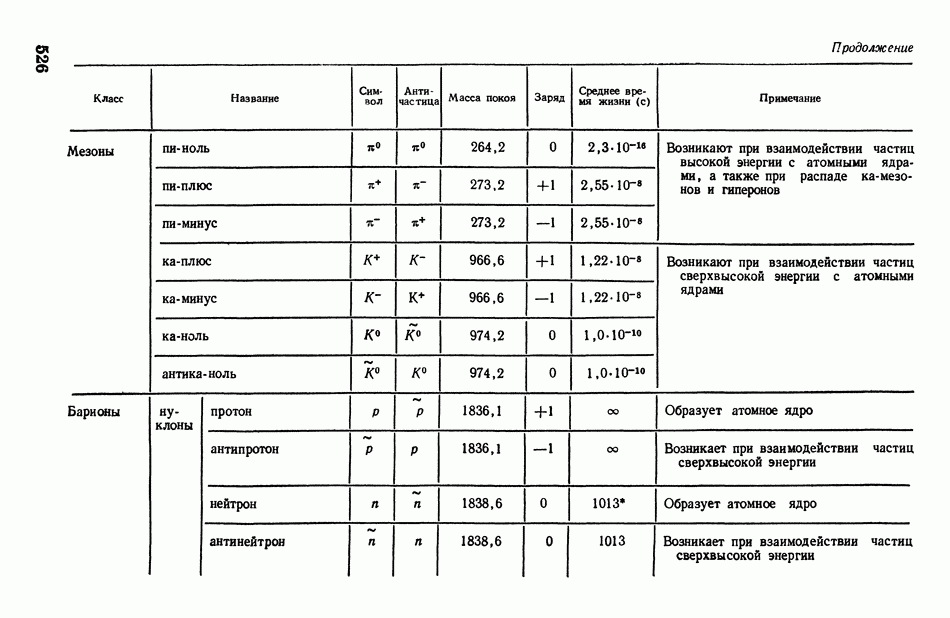
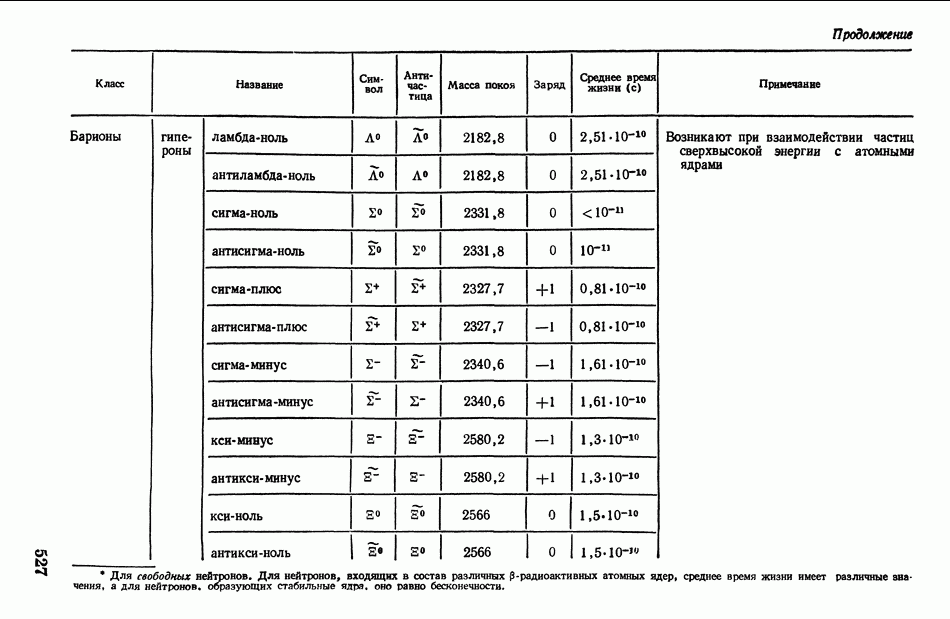
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии