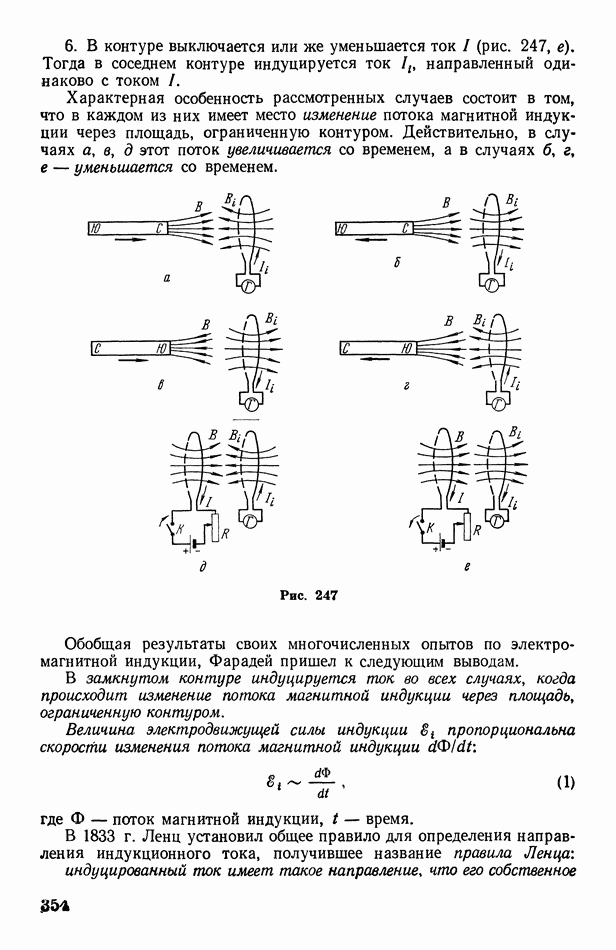
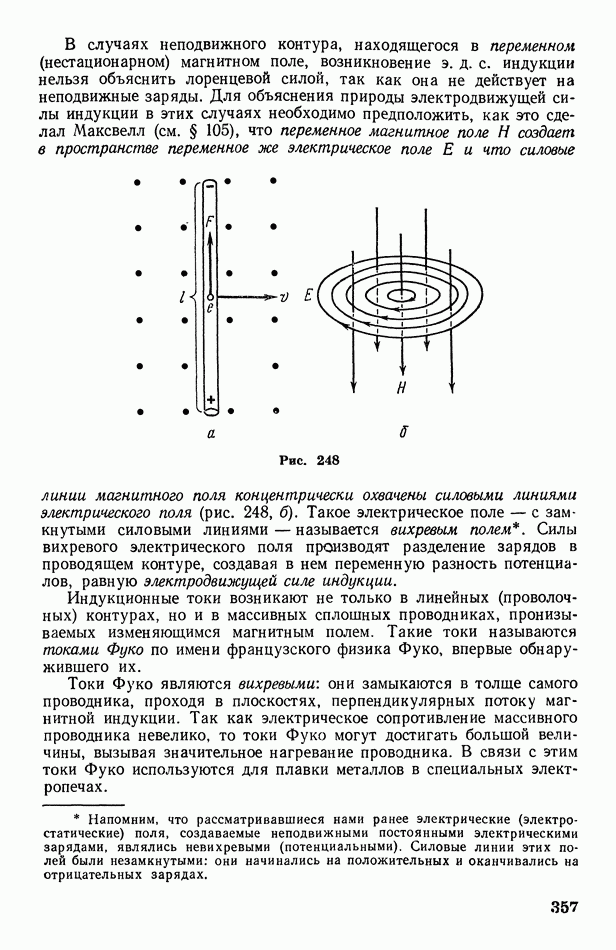
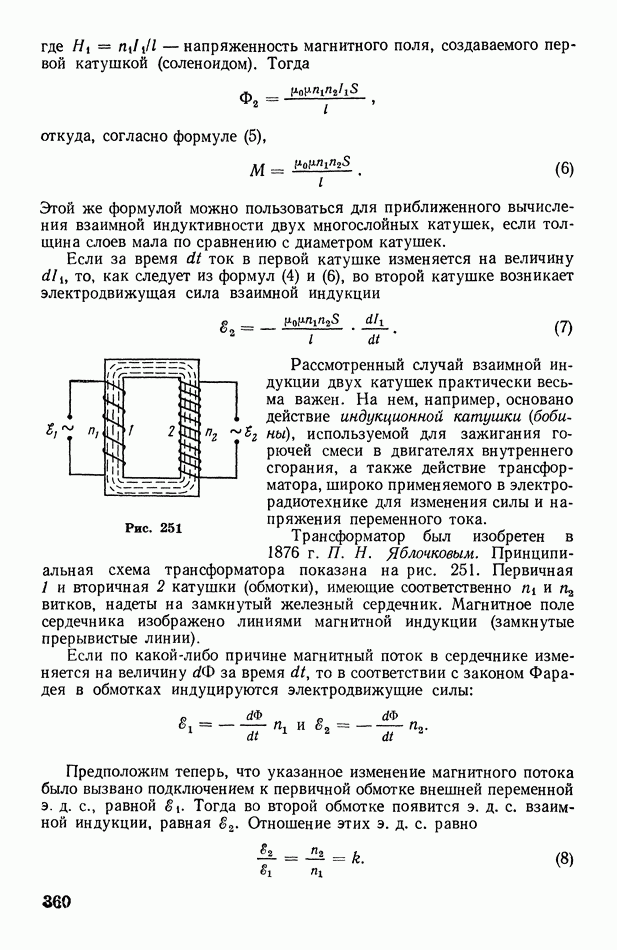
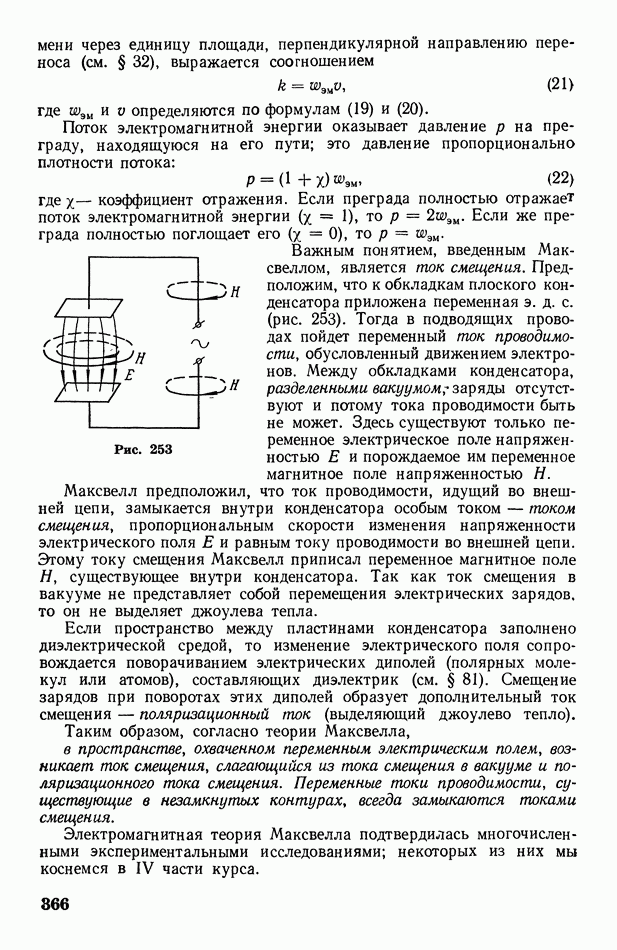
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
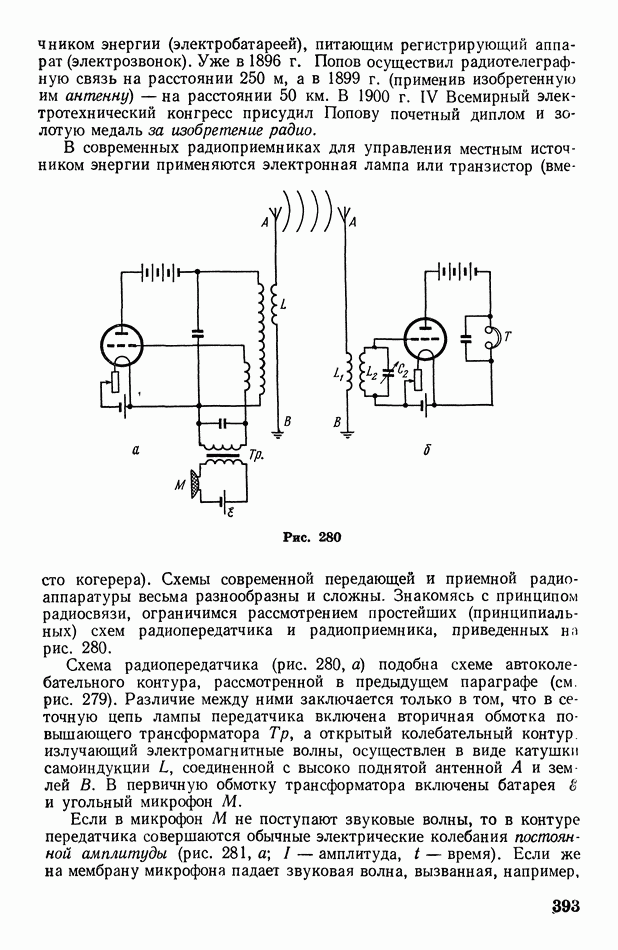
§ 25. Уравнение Бернулли
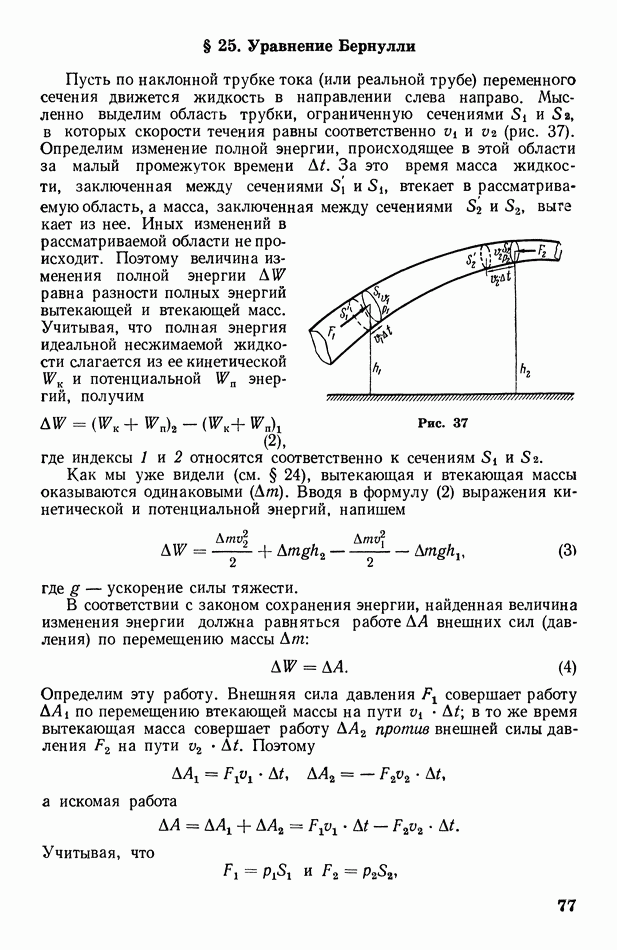
Пусть по наклонной трубке тока (или реальной трубе) переменного сечения движется жидкость в направлении слева направо. Мысленно выделим область трубки, ограниченную сечениями  в которых скорости течения равны соответственно
в которых скорости течения равны соответственно  и
и  (рис. 37). Определим изменение полной энергии, происходящее в этой области за малый промежуток времени
(рис. 37). Определим изменение полной энергии, происходящее в этой области за малый промежуток времени  За это время масса жидкости, заключенная между сечениями
За это время масса жидкости, заключенная между сечениями  втекает в рассматриваемую область, а масса, заключенная между сечениями
втекает в рассматриваемую область, а масса, заключенная между сечениями  выге кает из нее. Иных изменений в рассматриваемой области не происходит. Поэтому величина изменения полной энергии
выге кает из нее. Иных изменений в рассматриваемой области не происходит. Поэтому величина изменения полной энергии  равна разности полных энергий вытекающей и втекающей масс.
равна разности полных энергий вытекающей и втекающей масс.

Рис. 37
Учитывая, что полная энергия идеальной несжимаемой жидкости слагается из ее кинетической  и потенциальной
и потенциальной  энергий, получим
энергий, получим

где индексы 1 и 2 относятся соответственно к сечениям 
Как мы уже видели (см. § 24), вытекающая и втекающая массы оказываются одинаковыми  Вводя в формулу (2) выражения кинетической и потенциальной энергий, напишем
Вводя в формулу (2) выражения кинетической и потенциальной энергий, напишем

где  ускорение силы тяжести.
ускорение силы тяжести.
В соответствии с законом сохранения энергии, найденная величина изменения энергии должна равняться работе  внешних сил (давления) по перемещению массы
внешних сил (давления) по перемещению массы 

Определим эту работу. Внешняя сила давления  совершает работу
совершает работу  по перемещению втекающей массы на пути
по перемещению втекающей массы на пути  в то же время вытекающая масса совершает работу
в то же время вытекающая масса совершает работу  против внешней силы давления
против внешней силы давления  на пути
на пути  Поэтому
Поэтому

а искомая работа

Учитывая, что

где  и
и  -давления на сечениях
-давления на сечениях  получим
получим

Но

 объем каждой из рассматриваемых масс (см. § 24). Поэтому
объем каждой из рассматриваемых масс (см. § 24). Поэтому

Объединяя формулы (3), (4) и (5), получим после перегруппировки слагаемых

Поделив обе части последнего равенства на  и учитывая, что
и учитывая, что  плотность жидкости, получим
плотность жидкости, получим

Поскольку сечения  выбраны произвольно, можно окончательно написать
выбраны произвольно, можно окончательно написать

Это соотношение, выведенное в 1738 г. Д. Бернулли, называется уравнением Бернулли. Первое слагаемое левой части этого уравнения представляет собой удельную кинетическую энергию жидкости; второе — удельную потенциальную энергию жидкости в поле силы тяжести; третье — удельную энергию жидкости, обусловленную силами давления (удельная энергия — энергия, приходящаяся на единицу объема жидкости).
Единицей измерения давления является паскаль (Па). Паскаль — давление, вызываемое силой  равномерно распределенной на поверхности площадью
равномерно распределенной на поверхности площадью 

Следовательно, уравнение Бернулли выражает закон сохранения энергии (удельной) и может быть сформулировано так:
при установившемся движении идеальной несжимаемой жидкости сумма удельной энергии давления и кинетической и потенциальной удельных энергий остается постоянной на любом поперечном сечении потока.
Из приведенного преобразования единиц измерения давления в единицы измерения удельной энергии следует, что все члены левой части уравнения (6) можно еще рассматривать как величины давления. Величину  называют статическим давлением, величину
называют статическим давлением, величину  динамическим давлением, величину
динамическим давлением, величину  гидравлическим давлением. Следовательно, уравнению Бернулли можно дать еще такую формулировку:
гидравлическим давлением. Следовательно, уравнению Бернулли можно дать еще такую формулировку:
в установившемся потоке идеальной несжимаемой жидкости полное давление, слагающееся из динамического, гидравлического и статического давлений, постоянно на любом поперечном сечении потока.
Для горизонтальной трубки тока (или реальной трубы) уравнение Бернулли принимает вид

(так как 
Из уравнений Бернулли и неразрывности следует, что в местах сужения трубопровода скорость течения жидкости возрастает, а давление понижается.
В заключение остановимся на следующем важном положении. Уравнения (1) и (6) применимы не только к жидкостям, но и к газам в случаях, когда сжимаемостью и вязкостью газа можно пренебрегать. Оказывается, что это можно делать при небольших скоростях движения газа, когда в газовом потоке обычно не возникает больших градиентов скорости, а следовательно, и больших сил вязкости (см. § 50). Что касается сжимаемости газа, то, как показывают теория и опыт, ею можно пренебречь при скоростях движения газа, меньших скорости распространения звука в нем. Скорость звука в воздухе составляет около  Поэтому воздух, движущийся со скоростью, не превышающей
Поэтому воздух, движущийся со скоростью, не превышающей  допустимо считать идеальной несжимаемой жидкостью и применять к нему уравнение неразрывности и уравнение Бернулли.
допустимо считать идеальной несжимаемой жидкостью и применять к нему уравнение неразрывности и уравнение Бернулли.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- § 1. Предмет физики. Связь физики с другими науками и производством
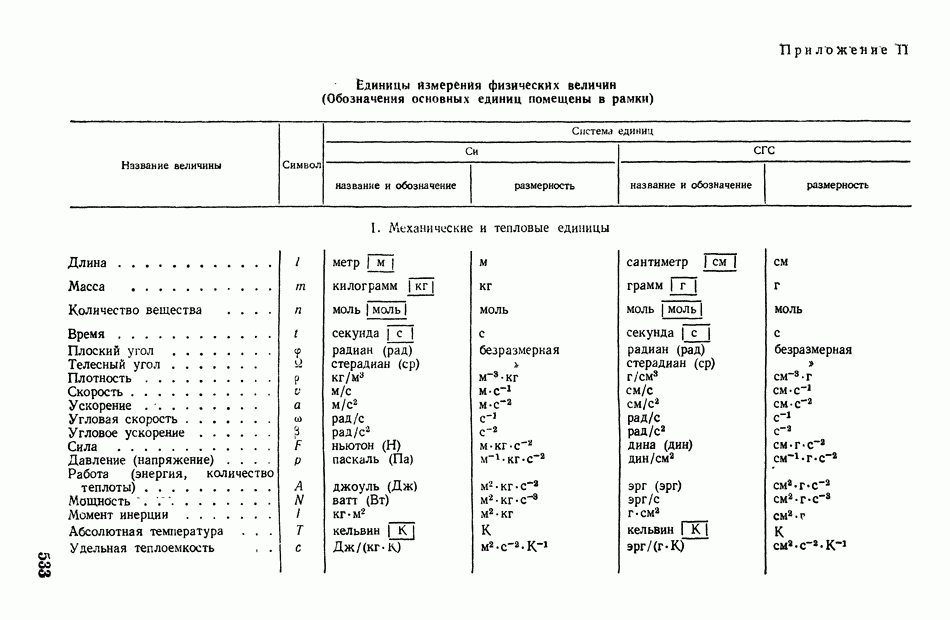
- § 2. О единицах измерения и размерности физических величин
- § 3. О некоторых математических понятиях и символах
- 1. Физические основы механики
- § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения
- § 5. Прямолинейное движение материальной точки
- § 6. Движение материальной точки по окружности
- Глава II. Основные законы динамики
- § 7. Законы Ньютона. Масса и сила
- § 8. Закон изменения количества движения (импульса)
- § 9. Закон сохранения количества движения в изолированной системе
- § 10. Силы упругости
- § 11. Силы трения
- § 12. Силы тяготения (гравитационные силы)
- § 13. Центростремительная сила
- § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции
- § 15. Вес тел. Ускорение силы тяжести. Невесомость
- Глава III. Работа и энергия
- § 16. Работа и мощность
- § 17. Энергия
- § 18. Закон сохранения и превращения энергии
- § 19. О космических скоростях
- § 20. Границы применимости классической механики
- Глава IV. Вращательное движение твердого тела
- § 21. Основной закон динамики вращения
- § 22. Моменты инерции некоторых тел
- § 23. Закон сохранения момента количества движения. Кинетическая энергия вращающегося тела
- Глава V. Движение жидкости
- § 24. Основные определения. Уравнение неразрывности
- § 25. Уравнение Бернулли
- § 26. О некоторых приложениях уравнения Бернулли
- Глава VI. Колебания и волны
- § 27. Гармоническое колебание и его характеристики
- § 28. Сложение гармонических колебаний
- § 29. Динамика колебательного движения. Маятник
- § 30. О затухающих и вынужденных колебаниях
- § 31. Волновой процесс
- § 32. Уравнение волны. Интенсивность волны
- § 33. Интерференция волн. Стоячие волны
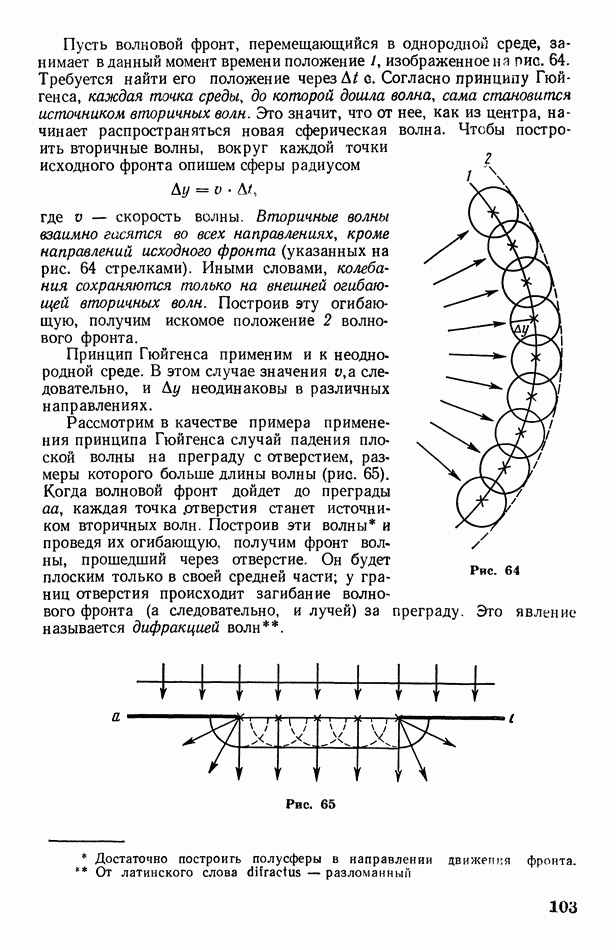
- § 34. Фронт волны. Принцип Гюйгенса-Френеля
- 2. Молекулярная физика и термодинамика
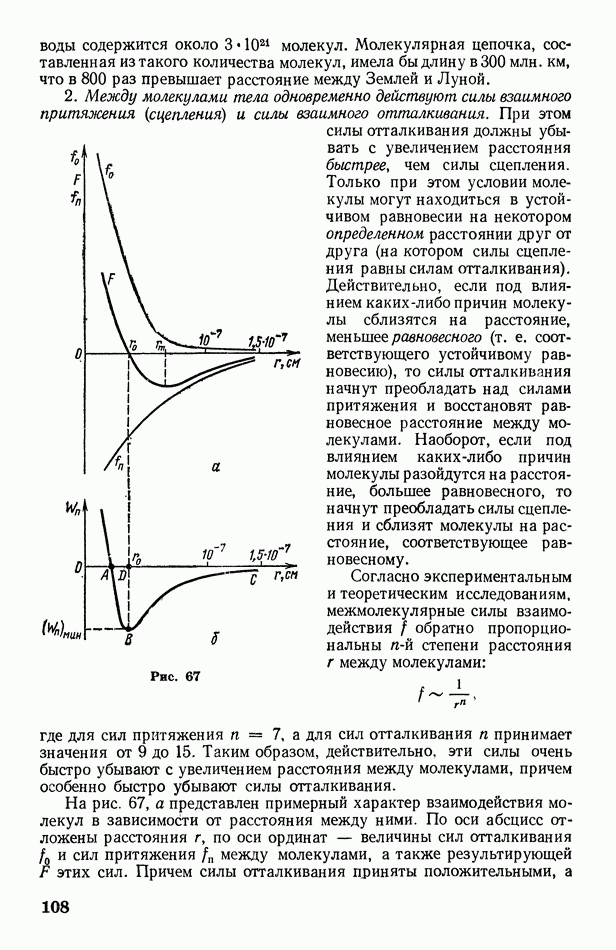
- § 35. Основные положения молекулярно-кинетической теории
- § 36. О некоторых явлениях, подтверждающих основные положения молекулярно-кинетической теории
- § 37. О теплоте и температуре
- § 38. О предмете и методах молекулярной физики
- Глава VIII. Газы
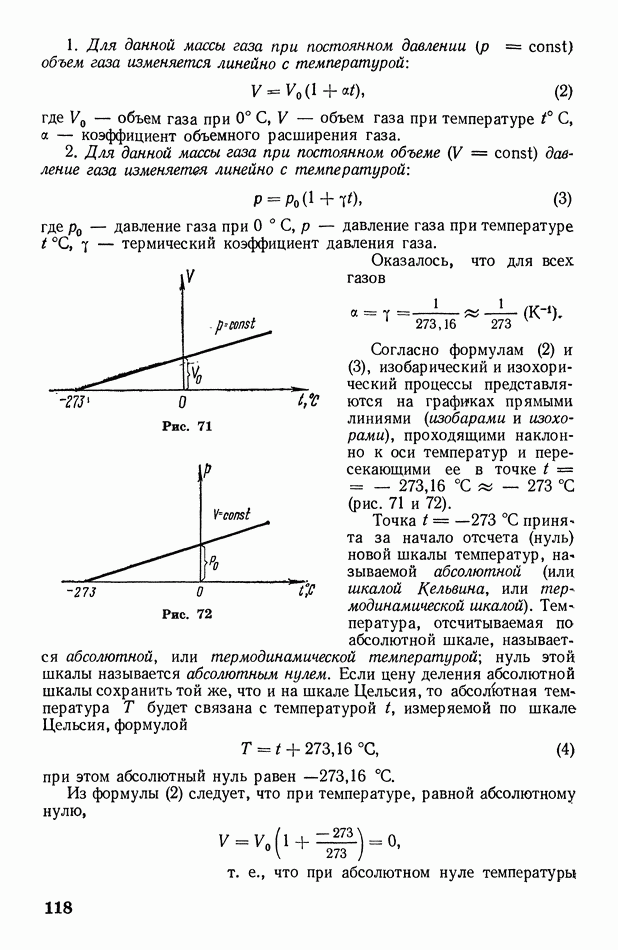
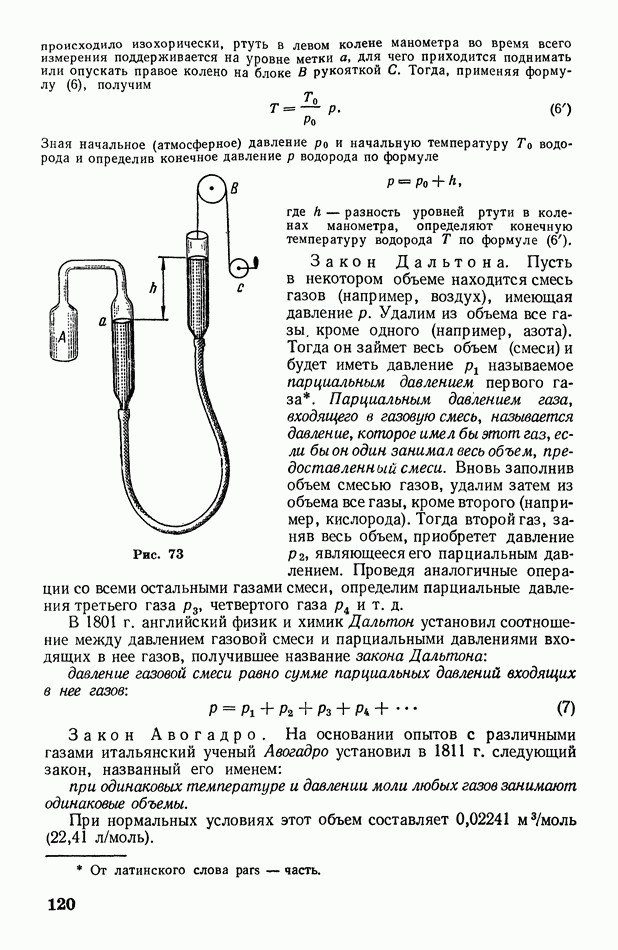
- § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура
- § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная
- § 41. Основное уравнение кинетической теории идеального газа
- § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа
- § 43. О числе степеней свободы. Внутренняя энергия газа
- § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной
- § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям
- § 46. Средняя длина свободного пробега молекул
- § 47. Явления переноса в газах. Уравнение переноса
- § 48. Диффузия
- § 49. Теплопроводность
- § 50. Внутреннее трение (вязкость)
- Глава IX. Жидкости и твердые тела
- § 51. Особенности строения жидкостей и твердых тел
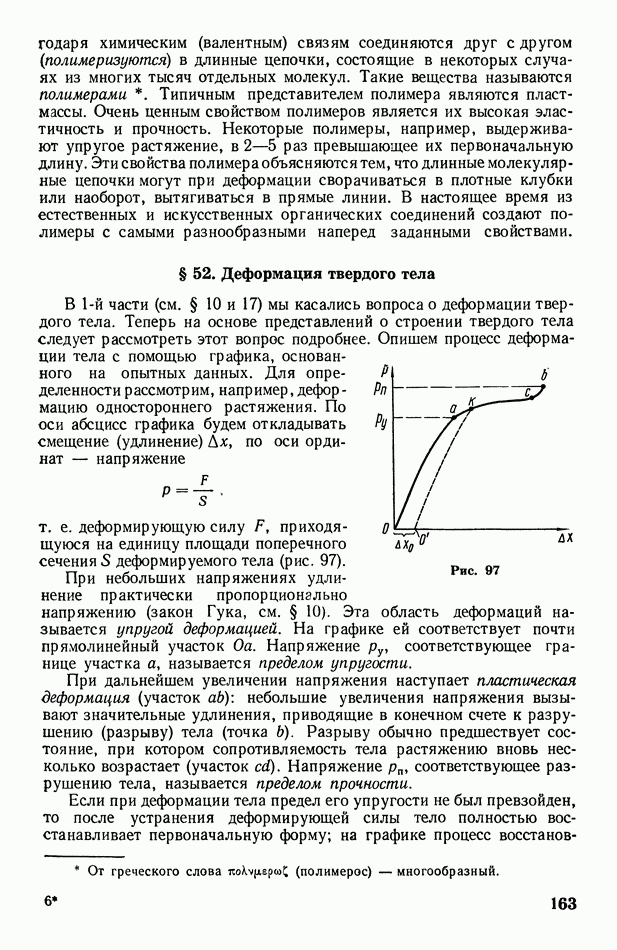
- § 52. Деформация твердого тела
- § 53. Тепловое расширение твердых и жидких тел
- § 54. Теплоемкость твердых и жидких тел
- § 55. Диффузия в жидких и твердых телах
- § 56. Осмос
- § 57. Теплопроводность жидких и твердых тел
- § 58. Вязкость жидкости. Турбулентное движение жидкости
- § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости
- § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа
- § 61. Капиллярные явления; формула Жюрена
- Глава X. Изменение агрегатного состояния вещества (фазовые превращения)
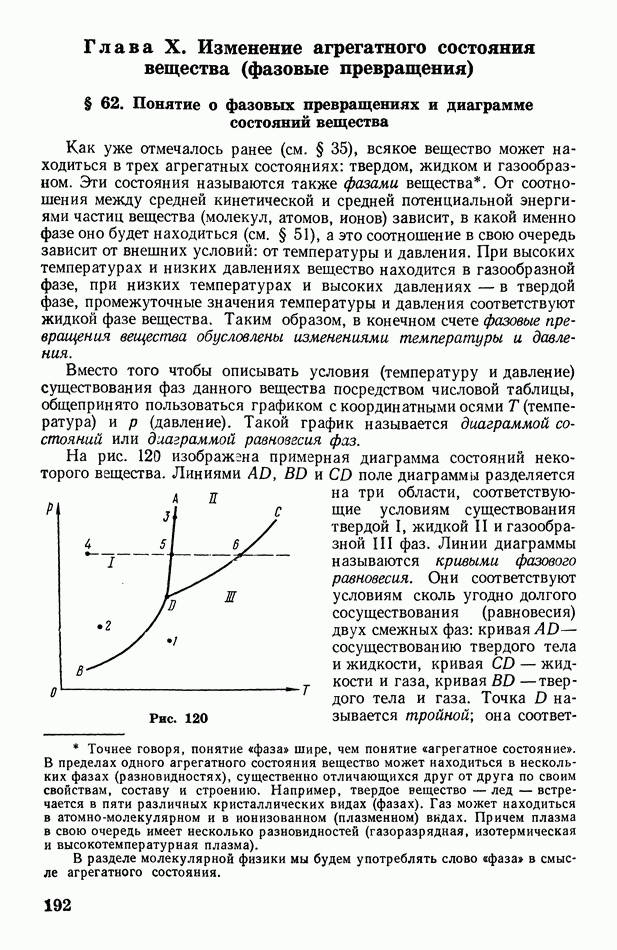
- § 62. Понятие о фазовых превращениях и диаграмме состояний вещества
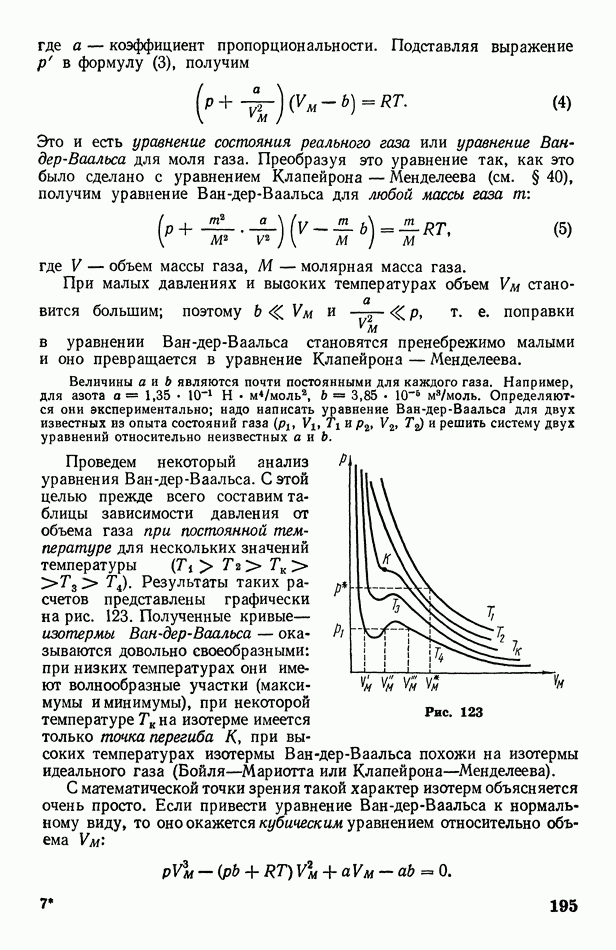
- § 63. Реальный газ. Уравнение Ван-дер-Ваальса
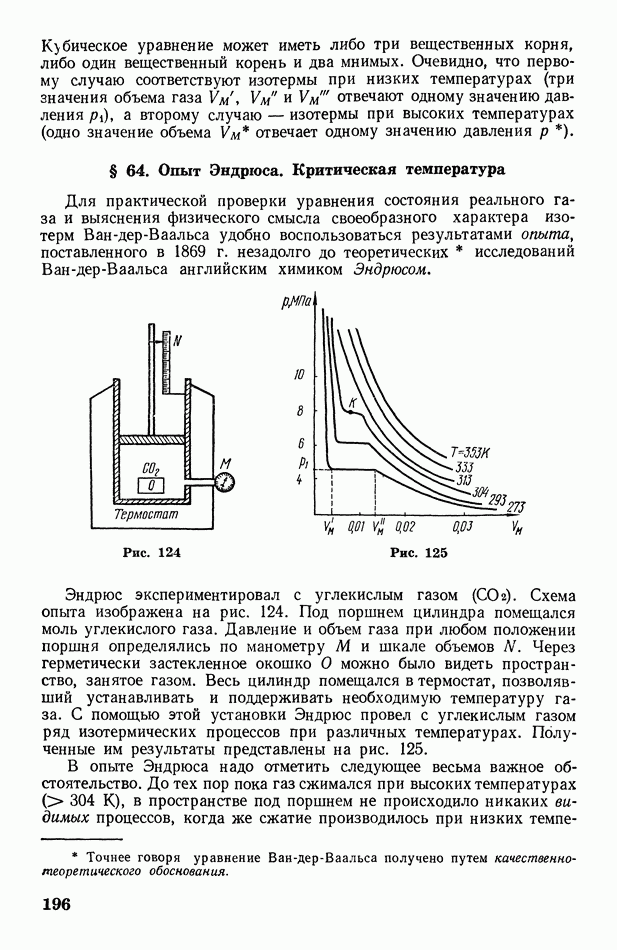
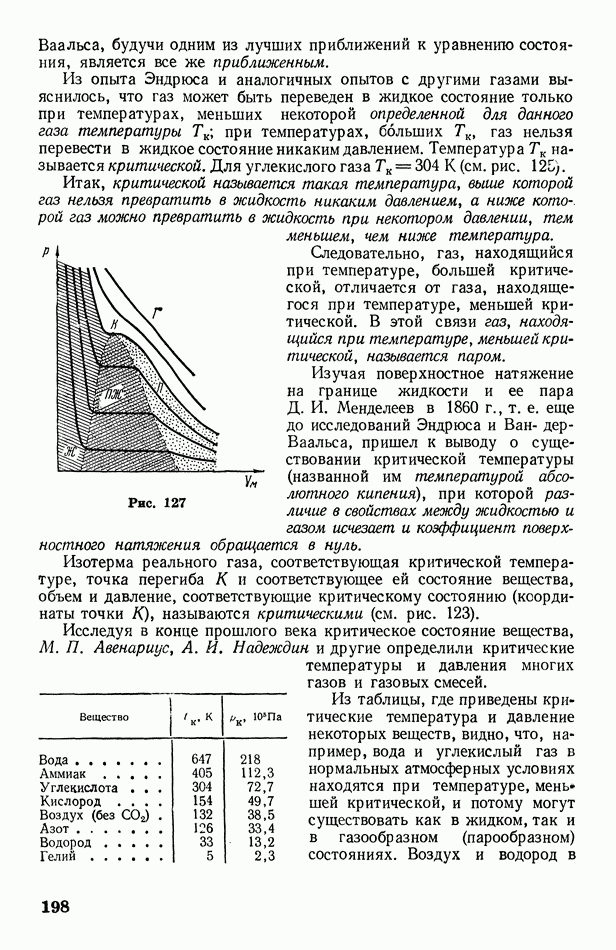
- § 64. Опыт Эндрюса. Критическая температура
- § 65. Сжижение газов. Эффект Джоуля-Томсона
- § 66. Испарение и конденсация. Кипение
- § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором
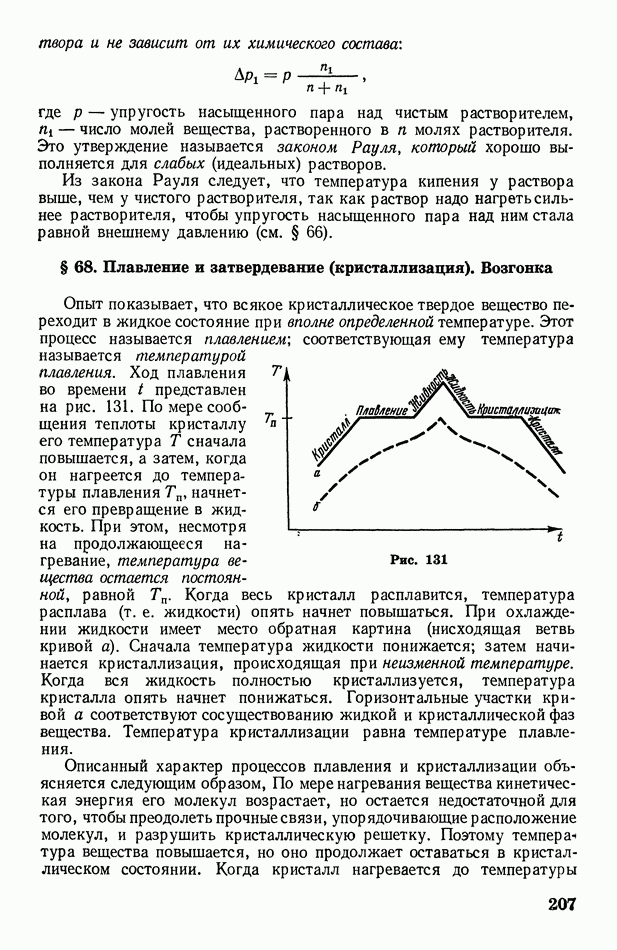
- § 68. Плавление и затвердевание (кристаллизация). Возгонка
- Глава XI. Основы термодинамики
- § 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики
- § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы
- § 71. Цикл Карно. Второе начало термодинамики
- § 72. Энтропия
- § 73. О статистическом смысле энтропии и второго начала термодинамики
- 3. Электричество и магнетизм
- § 74. Электризация тел. Электрический заряд
- § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность
- § 76 Электрический диполь. Поле диполя
- § 77. Теорема Остроградского-Гаусса и ее приложения
- § 78. Работа перемещения заряда в электрическом поле. Потенциал
- § 79. О неустойчивости статических систем электрических зарядов
- § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника
- § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков
- § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции
- § 83. Конденсатор. Энергия электрического поля
- Глава XIII. Постоянный электрический ток
- § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение
- § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока
- § 86. Разветвленная электрическая цепь. Правила Кирхгофа
- § 87. Контактная разность потенциалов. Термоэлектрические явления
- § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы
- § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников
- § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи
- § 91. Ток в жидкостях. Электролиз. Законы Фарадея
- § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды
- § 93. Типы самостоятельного газового разряда
- Глава XIV. Электромагнетизм
- § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов
- § 95. Магнитное взаимодействие токов в вакууме; закон Ампера
- § 96. Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа
- § 97. Некоторые приложения закона Био-Савара-Лапласа
- § 98. Магнитные поля соленоида и тороида
- § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции
- § 100. Действие магнитного поля на проводник с током. Определение ампера
- § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона
- § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях
- Глава XV. Электромагнитная индукция и переменный ток
- § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко
- § 104. Взаимная индукция и самоиндукция
- § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла
- § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока
- § 107. Емкостное и индуктивное сопротивления
- § 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи
- § 109. Понятие о трехфазном токе
- Глава XVI. Электрические колебания и электромагнитные волны
- § 110. Электромагнитные волны
- § 111. Закрытый колебательный контур
- § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн
- § 113. Радиосвязь
- 4. Оптика и атомная физика
- § 114. Природа света
- § 115. Отражение и преломление света. Полное отражение
- § 116. Дисперсия света. Спектры
- § 117. Тонкие линзы. Микроскоп
- § 118. Глаз как оптическая система. Спектральная чувствительность глаза
- § 119. Основные фотометрические характеристики
- § 120. Поглощение света. О физиологическом действии света
- Глава XVIII. Волновые свойства света
- § 121. Интерференция света. Интерферометр
- § 122. Об интерференции света, отраженного от прозрачных пленок
- § 123. Дифракция света. Разрешающая способность оптических приборов
- § 124. Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде
- § 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов
- § 126. О дифракции микрочастиц и волнах де-Бройля
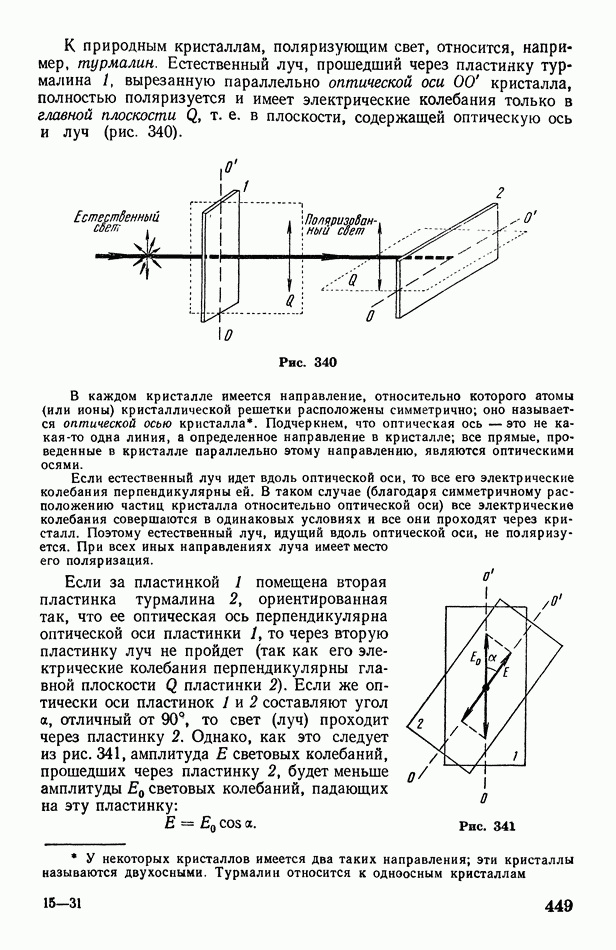
- § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды
- § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя
- 129. Вращение плоскости колебаний поляризованного света. Поляриметр
- Глава XIX. Квантовые свойства света и строение атома
- § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа
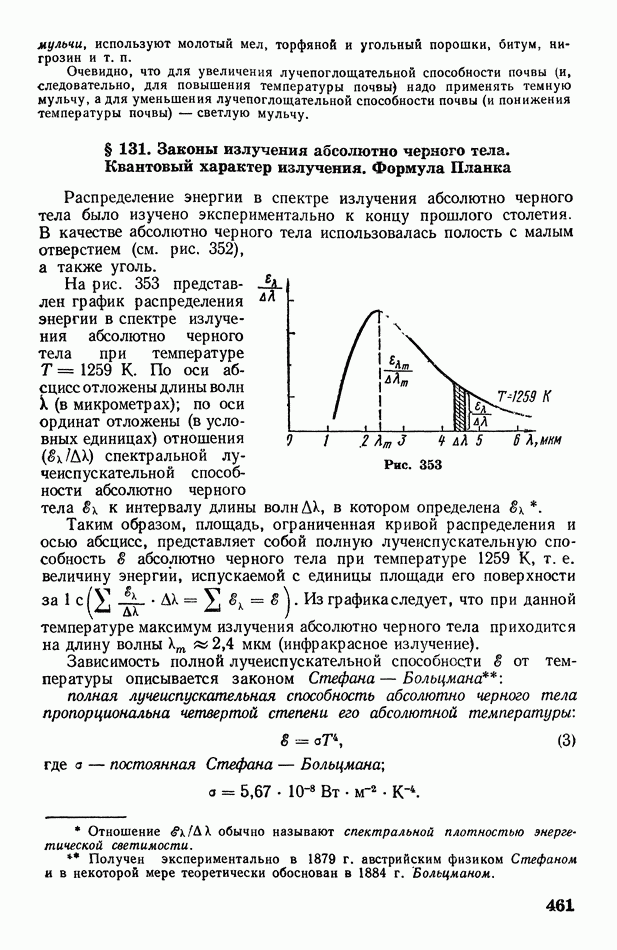
- § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка
- § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора
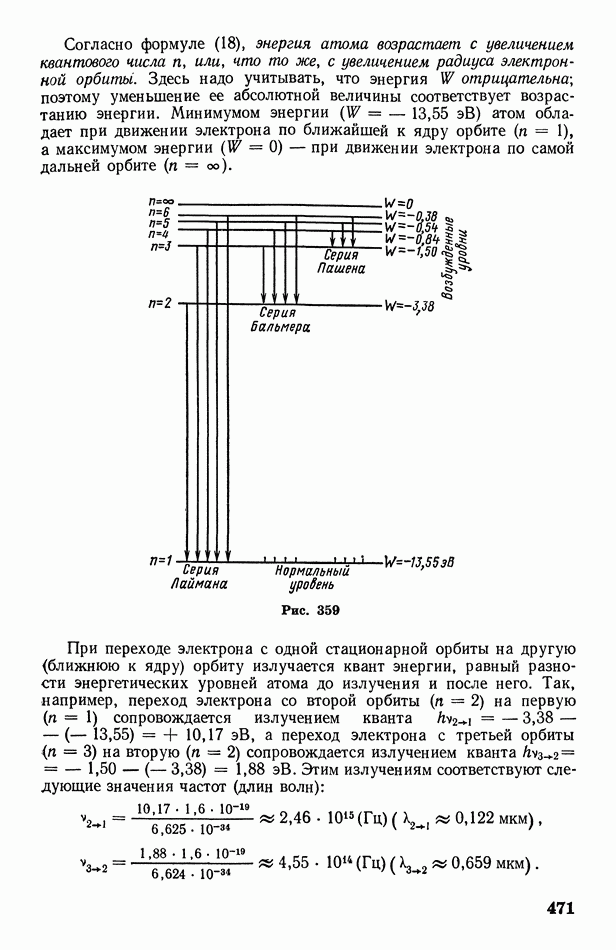
- § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода
- § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров
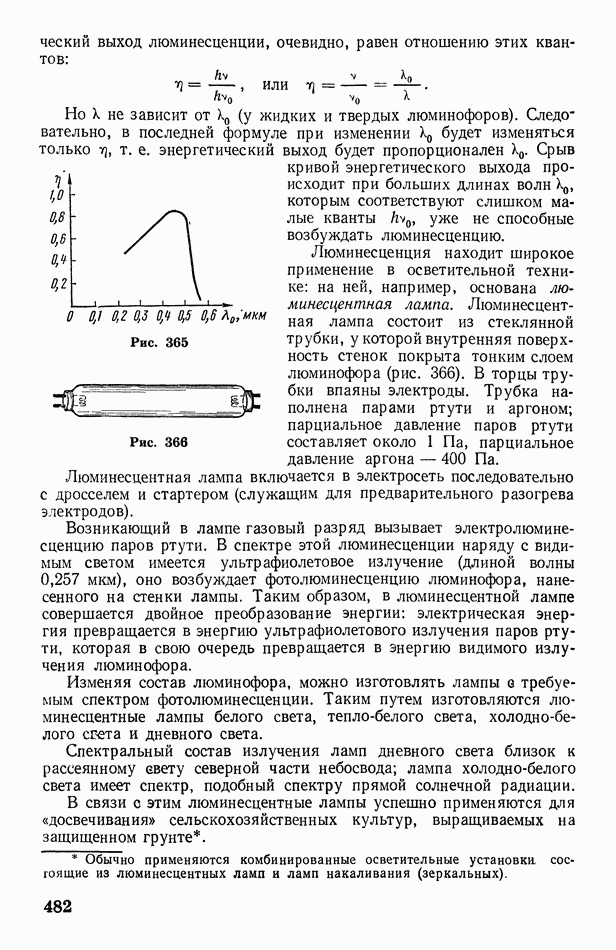
- § 135. Люминесценция. Законы фотолюминесценции и некоторые ее практические применения
- § 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы
- § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света
- Глава XX. Атомное ядро и внутриядерные процессы
- § 138. Общие сведения об атомных ядрах. Изотопы
- § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада
- § 140. О методах наблюдения и регистрации микрочастиц
- § 141. Ядерные реакции. Искусственная радиоактивность
- § 142. Энергия связи и дефект массы атомного ядра
- § 143. Реакция деления. Цепная реакция. Ядерный реактор
- § 144. Реакция синтеза (термоядерная реакция). Энергия звезд
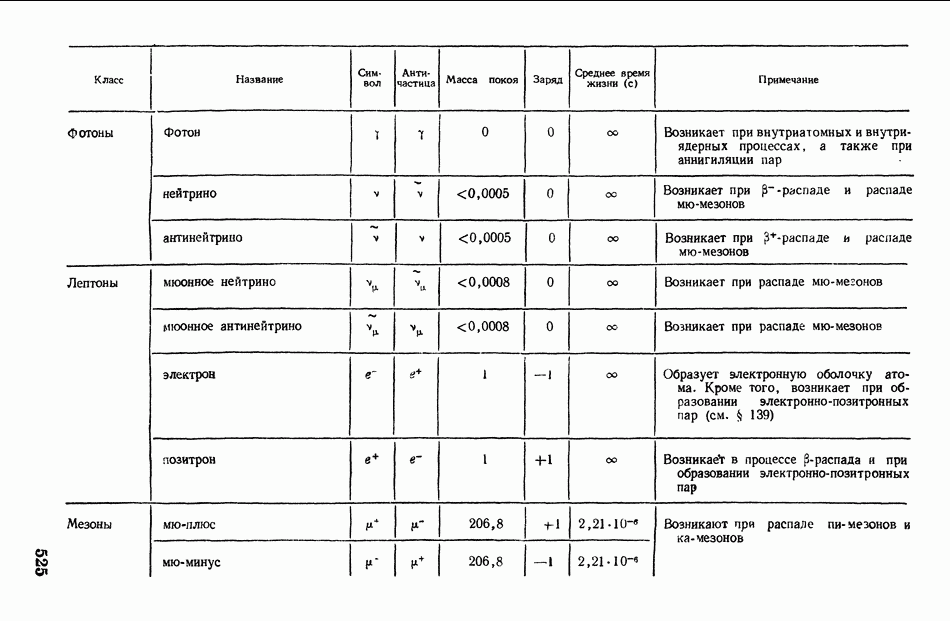
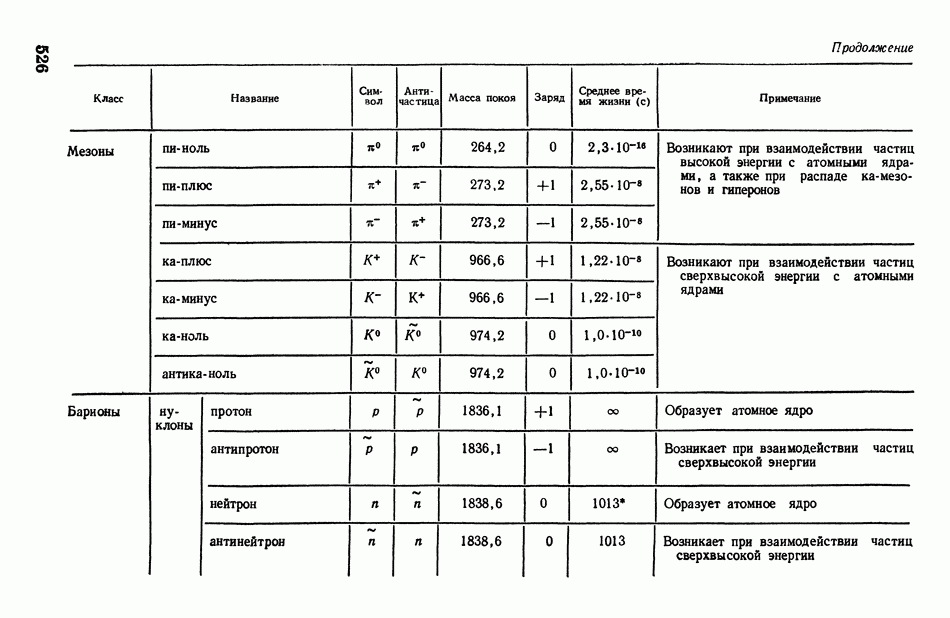
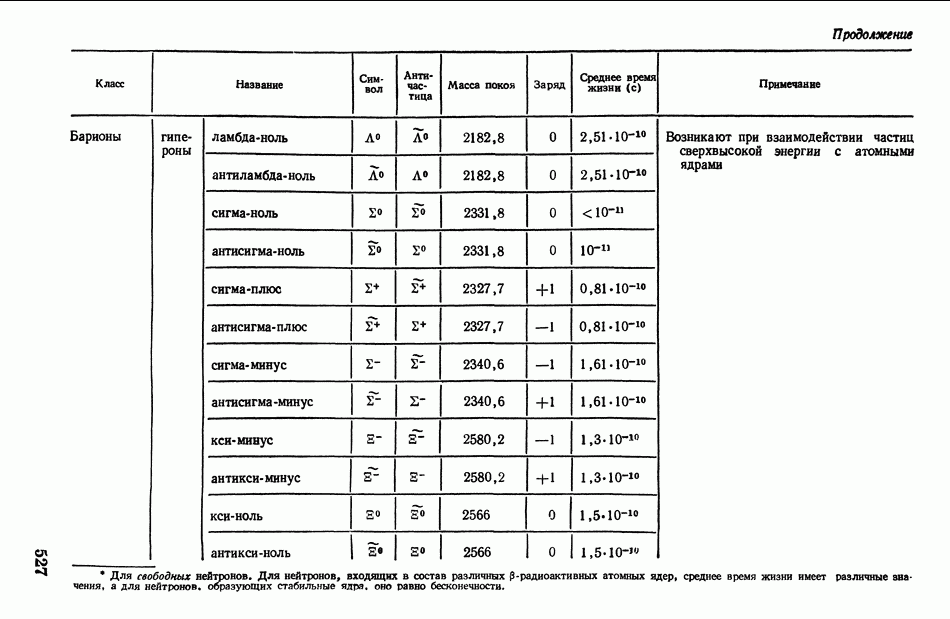
- § 145. Космические лучи. Элементарные частицы
- § 146. Об использовании ядерной энергии