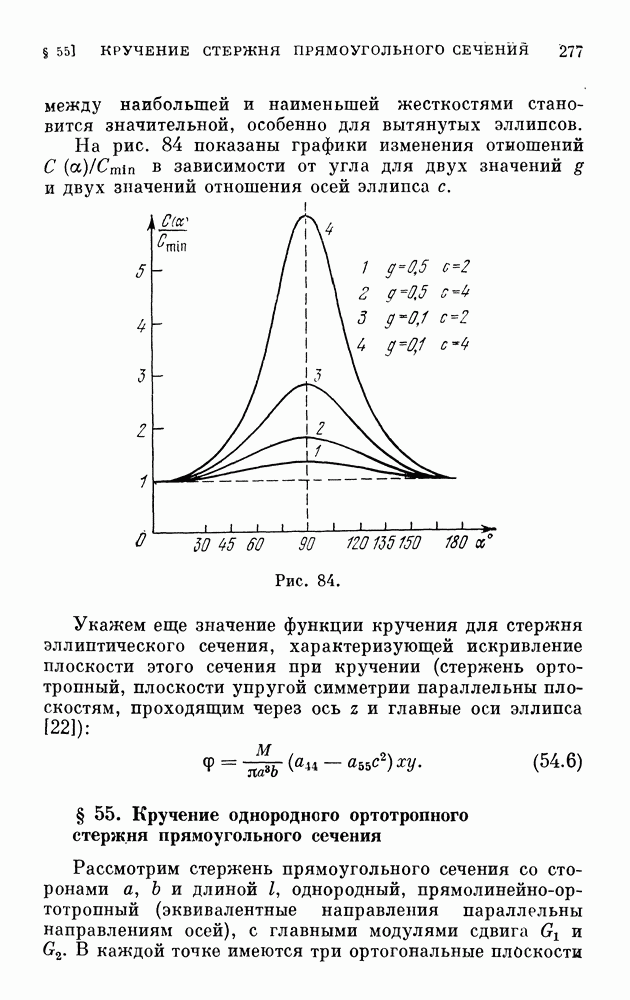
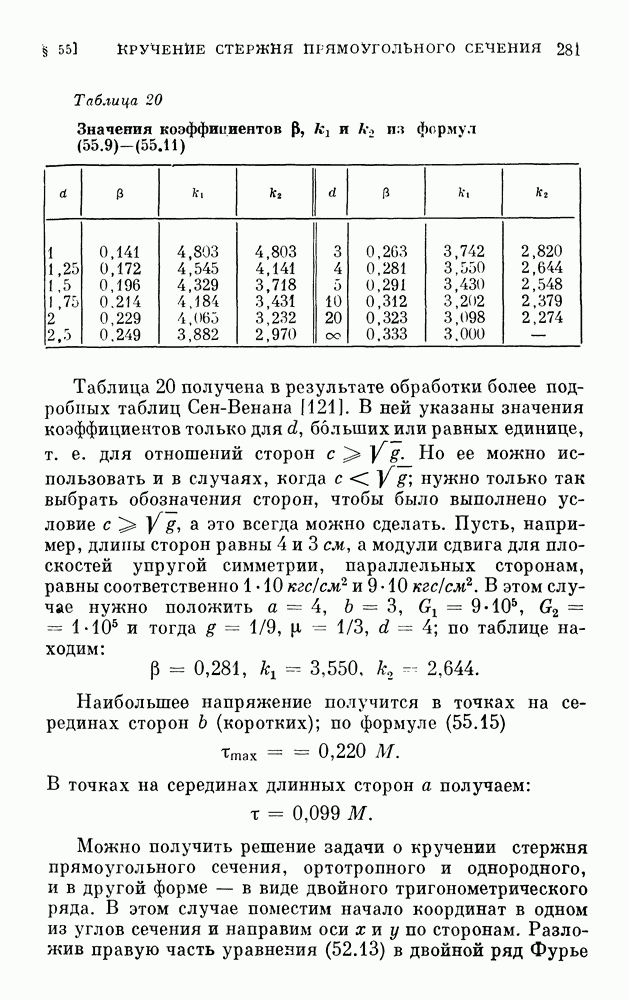
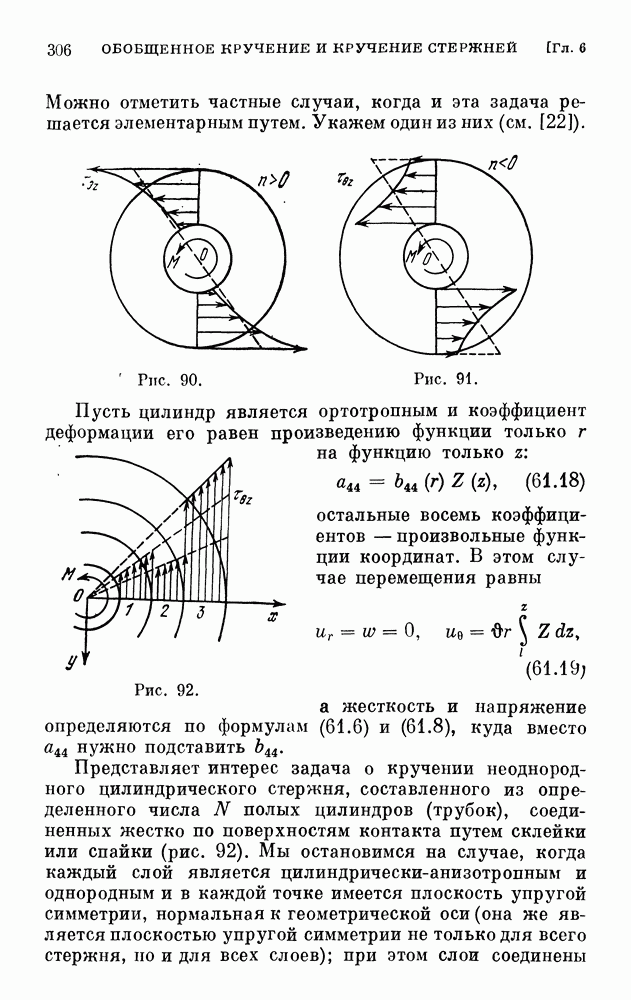
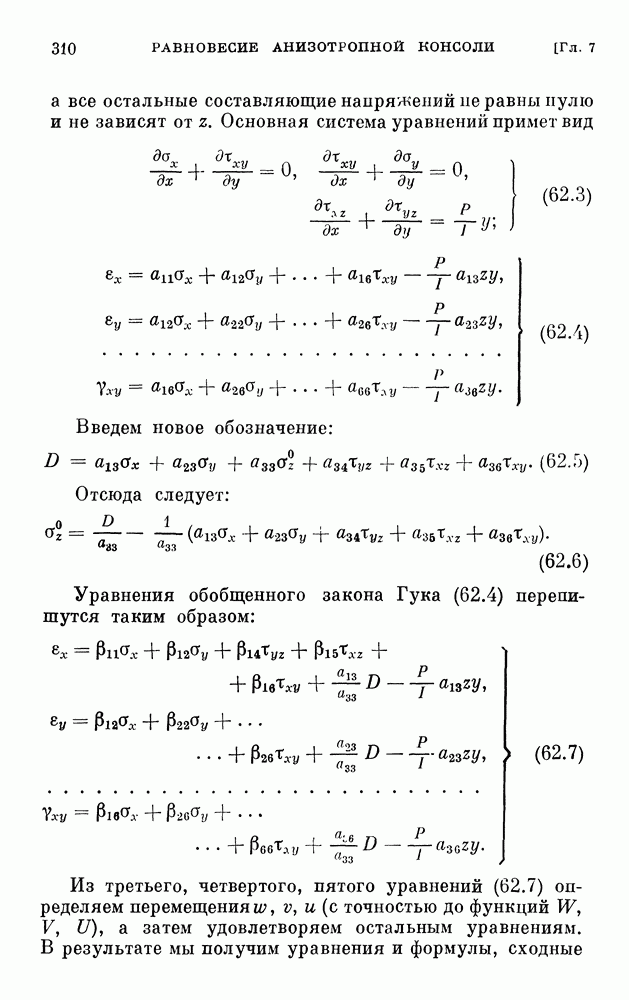| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 9. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ТЕЛА ВРАЩЕНИЯ
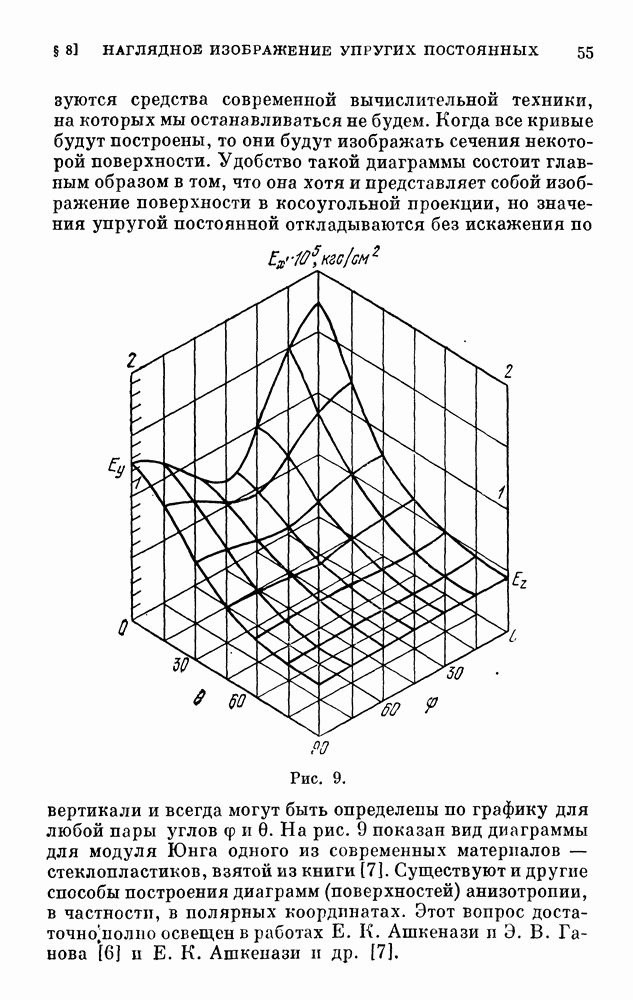
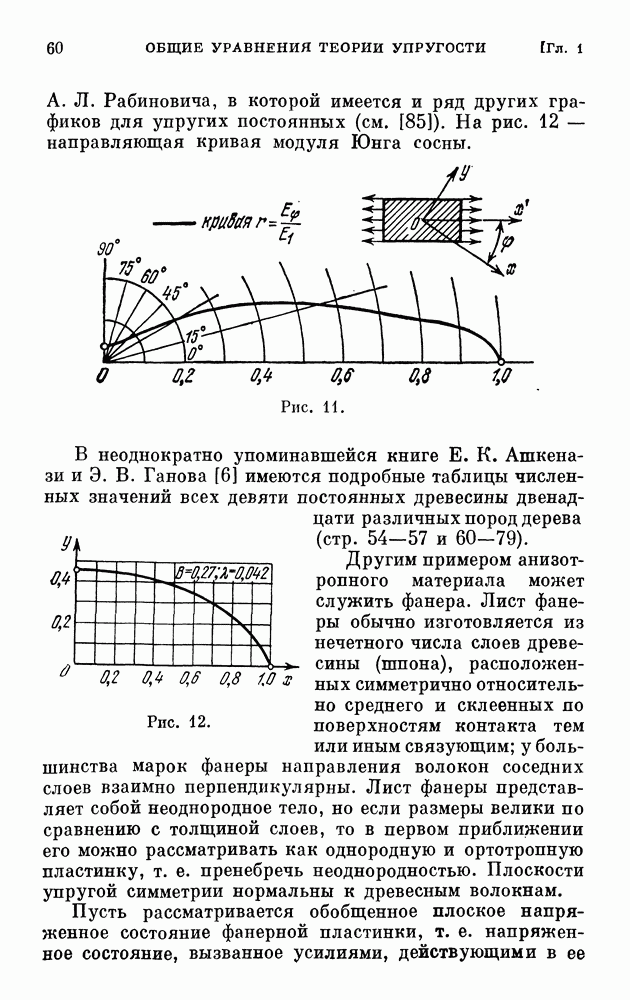
В последней, девятой главе рассматривается второй вид напряженно-деформированного состояния, при котором тело вращения, деформируясь, остается телом вращения; в этом случае говорят об осесимметричной деформации. Теория осесимметричной деформации разработана со всей полнотой только для тела изотропного и тела, обладающего анизотропией частного вида — трансверсально-изотропного. В этой главе мы всегда будем предполагать, что рассматриваемое тело является трансверсально-изотропным; из формул для него получаются формулы для изотропного тела как частные случаи.
§ 78. Общие уравнения осесимметричной деформации. Функция напряжений
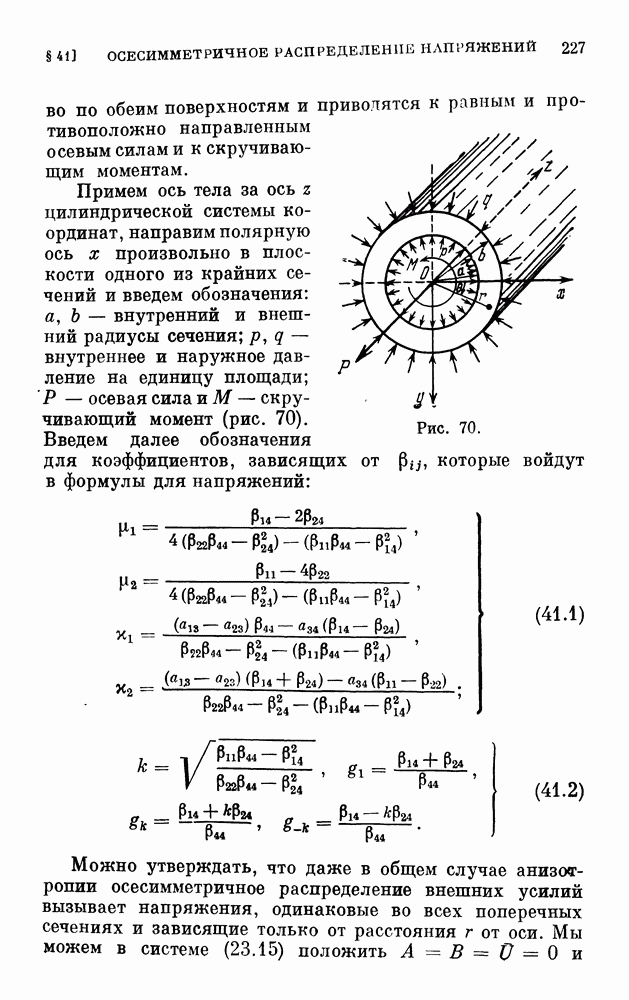
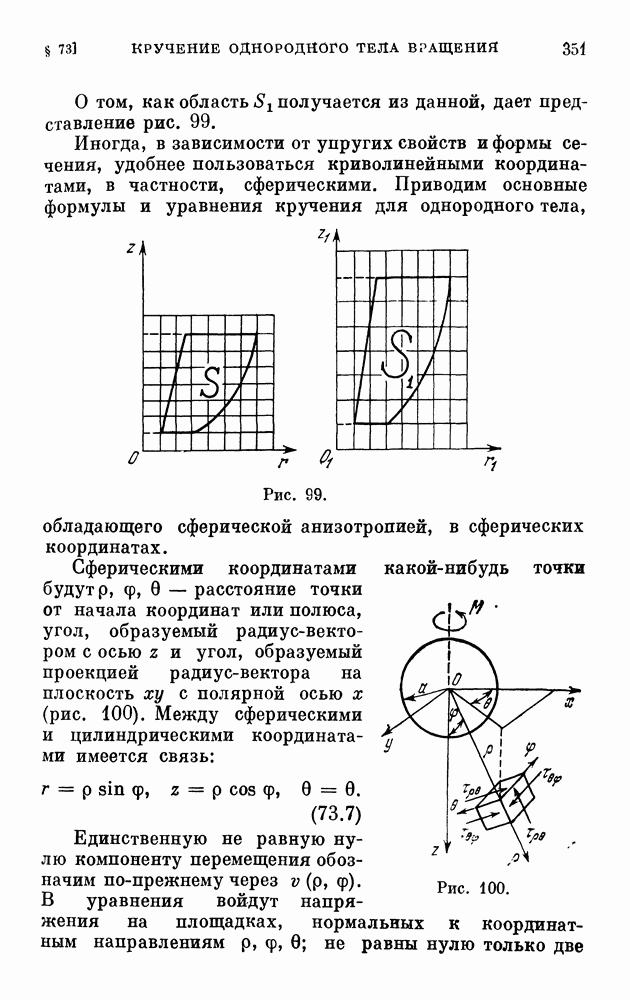
Представим себе тело из упругого однородного транссерсально-изотропного материала, ограниченное одной или несколькими коаксиальными поверхностями вращения, находящееся в равновесии под действием внешних усилий, поверхностных и объемных. Предположим, что плоскости изотропии, проходящие через каждую точку тела, нормальны к геометрической оси его (оси вращения), а распределение усилий обладает симметрией вращения относительно той же оси.
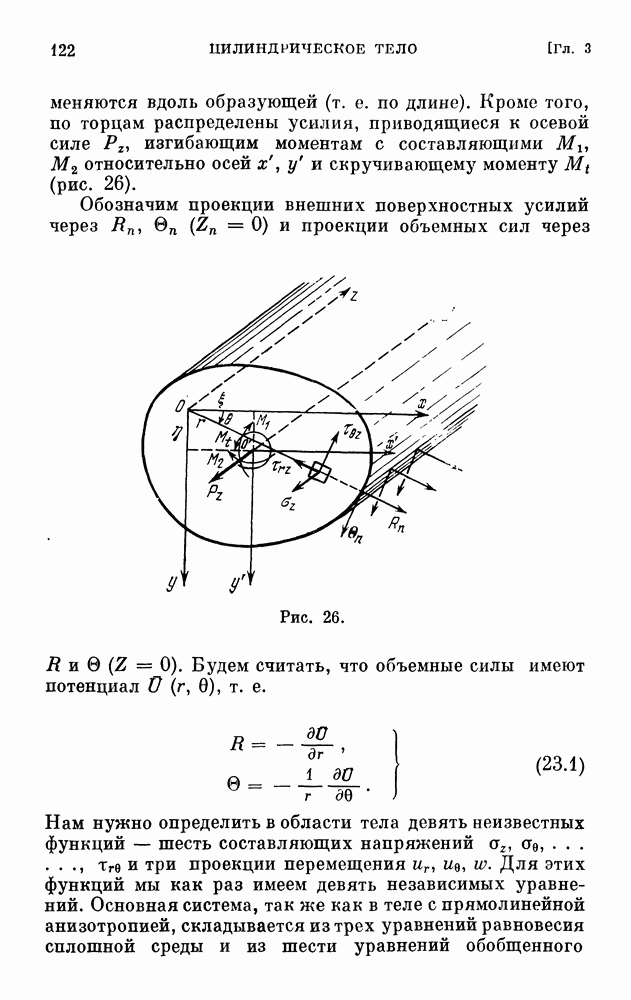
Отнесем тело к цилиндрической системе координат  , поместив начало координат в какой-нибудь точке на геометрической оси (например, в центре крайнего сечения) и направив ось z по этой оси, а полярную ось х
, поместив начало координат в какой-нибудь точке на геометрической оси (например, в центре крайнего сечения) и направив ось z по этой оси, а полярную ось х
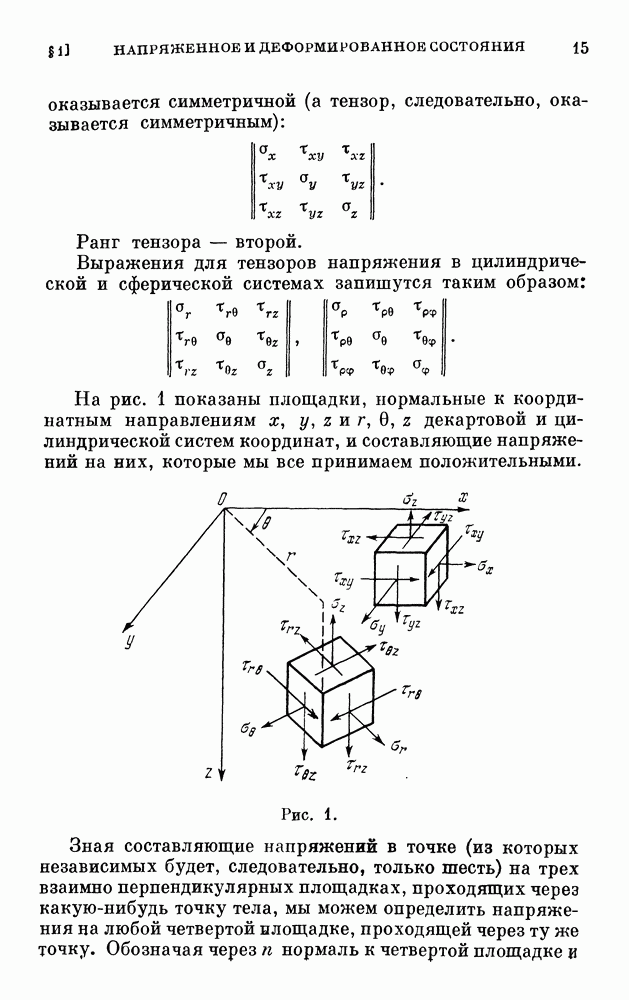
произвольно в плоскости поперечного сечения (рис. 104). Обозначим через  проекции поверхностных усилий на координатные направления
проекции поверхностных усилий на координатные направления  и через
и через  проекции объемных сил
проекции объемных сил  Как обычно, поверхностные силы относим к единице площади, а объемные — к единице объема. Уравнения обобщенного закона Гука запишутся так же, как и в декартовой системе
Как обычно, поверхностные силы относим к единице площади, а объемные — к единице объема. Уравнения обобщенного закона Гука запишутся так же, как и в декартовой системе 


Рис. 104.
Всего мы имеем пять независимых упругих постоянных. Решив (78.1) относительно составляющих напряжений, получим уравнения обобщенного закона Гука в другой форме:

Выражая коэффициенты  через
через  имеем:
имеем:

Здесь

Коэффициенты деформации  и модули упругости
и модули упругости
можно выразить и через технические константы (см. (4.9)):

где  модули Юнга для растяжения и сжатия в плоскости изотропии и в направлении, перпендикулярном к ней,
модули Юнга для растяжения и сжатия в плоскости изотропии и в направлении, перпендикулярном к ней,  коэффициент Пуассона, характеризующий сокращение в плоскости изотропии при растяжении в той же плоскости,
коэффициент Пуассона, характеризующий сокращение в плоскости изотропии при растяжении в той же плоскости,  коэффициент Пуассона, характеризующий сокращение в направлении, нормальном к плоскости изотропии при растяжении в этой плоскости,
коэффициент Пуассона, характеризующий сокращение в направлении, нормальном к плоскости изотропии при растяжении в этой плоскости,  модули сдвига для плоскостей изотропии и перпендикулярных (радиальных). Выражений А и через
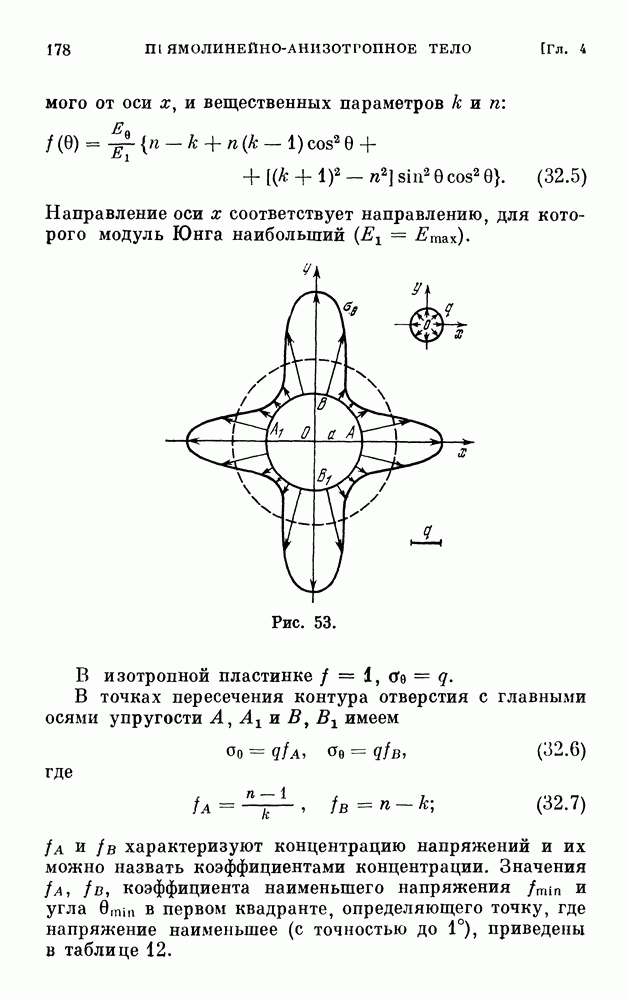
модули сдвига для плоскостей изотропии и перпендикулярных (радиальных). Выражений А и через  мы приводить не будем.
мы приводить не будем.
В силу симметрии в распределении усилий и упругой симметрии радиальные сечения останутся плоскими и тело останется телом вращения и в деформированном состоянии, т. е.

Отсюда следует, что  остальные составляющие деформации не будут зависеть от 0, причем
остальные составляющие деформации не будут зависеть от 0, причем

Четыре составляющие напряжений, не равные нулю, удовлетворяют двум уравнениям равновесия: 

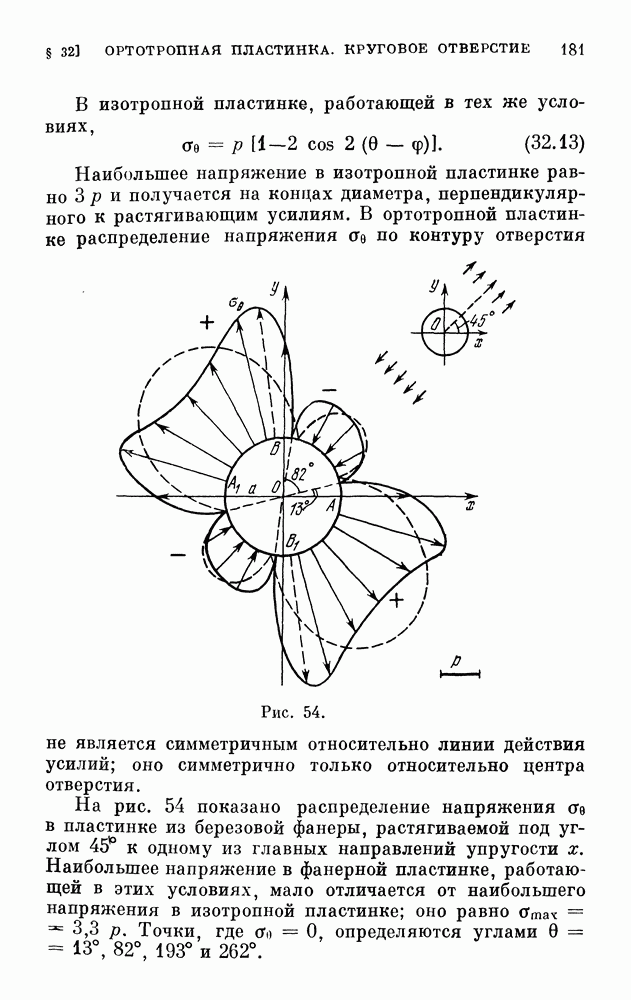
(третье уравнение превращается в тождество).
Присоединяя сюда первое, второе, третье и пятое уравнения обобщенного закона Гука (78.1) или (78.2), получим систему шести независимых уравнений для определения шести неизвестных функций 
Остановимся на случае отсутствия объемных сил, т. е. примем  Исключая перемещения
Исключая перемещения  из выражений для составляющих деформации (78.7), получим зависимости:
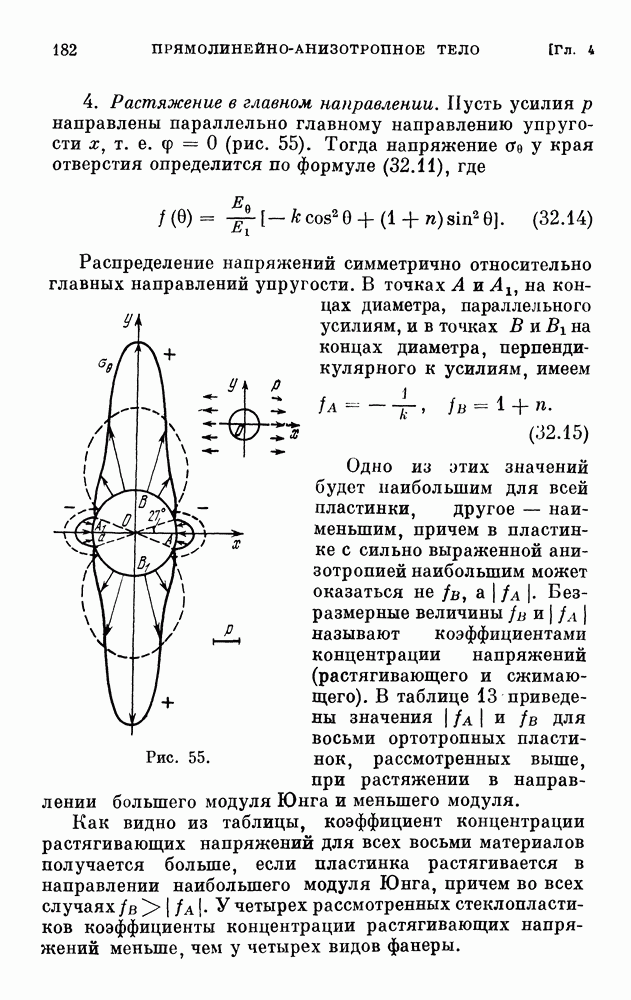
из выражений для составляющих деформации (78.7), получим зависимости:

Подставляя сюда выражения для деформаций из уравнений (78.1), получим

Присоединяя сюда (78.8), будем иметь четыре уравнения для четырех неизвестных — составляющих напряжений.
Первому уравнению равновесия (при  и уравнениям (78.10) мы можем удовлетворить, введя функцию напряжений
и уравнениям (78.10) мы можем удовлетворить, введя функцию напряжений  которая является обобщением функции напряжений для изотропного тела. Для транс-версально-изотропного тела выражения напряжений через
которая является обобщением функции напряжений для изотропного тела. Для транс-версально-изотропного тела выражения напряжений через  имеют вид:
имеют вид:

где

Из второго уравнения равновесия (78.8) (при  получаем уравнение для функции напряжений:
получаем уравнение для функции напряжений:

С дифференциальным уравнением четвертого порядка (78.13) связано алгебраическое уравнение

корни которого равны

Введя дифференциальные операторы

можно записать уравнение (78.13) очень просто (см. [20], стр. 259 и [58]):

Операторы  и
и  можно переставлять, так как легко убедиться, что
можно переставлять, так как легко убедиться, что 
Относительно чисел  зависящих от упругих постоянных
зависящих от упругих постоянных  можно доказать следующую теорему.
можно доказать следующую теорему.
Теорема. Числа  для любого трансеерсально-изотпропного упругого тела могут быть только
для любого трансеерсально-изотпропного упругого тела могут быть только
вещественными или комплексными (с вещественной частью, не равной нулю), но не могут быть чисто мнимыми.
Доказывается эта теорема тем же методом, что и теоремы 1—4, рассмотренные в § 20. Выражение упругого потенциала для трансверсально-изотропного тела запишется так:

 Задавая значения напряжений в виде
Задавая значения напряжений в виде

где к и  произвольные вещественные числа и
произвольные вещественные числа и  получим
получим

При всяких вещественных  имеем:
имеем:  Так как всегда
Так как всегда  (см. [8],
(см. [8],  или [47]), то мы получаем
или [47]), то мы получаем

при всяких вещественных  а следовательно, уравнение
а следовательно, уравнение

не может иметь вещественных корней. Но параметры  связаны с корнями уравнения
связаны с корнями уравнения  соотношениями:
соотношениями:

в чем можно убедиться, решив уравнение (78.22) и сопоставив решение с (78.15), а следовательно, они не могут быть чисто мнимыми. Квадраты параметров  и корней
и корней  могут быть вещественными или комплексными числами. Это следует из формул (78.23); они могут быть и чисто мнимыми (если вещественная часть
могут быть вещественными или комплексными числами. Это следует из формул (78.23); они могут быть и чисто мнимыми (если вещественная часть  равна по абсолютной величине мнимой).
равна по абсолютной величине мнимой).
Граничные условия в случае заданных на боковой поверхности усилий  сводятся к условиям на меридиане поверхности вращения и имеют вид
сводятся к условиям на меридиане поверхности вращения и имеют вид

При заданных на поверхности перемещениях  имеем условия:
имеем условия:

В том и другом случае заданные усилия или перемещения можно считать функциями дуги  меридиана радиального сечения или какого-нибудь другого параметра, определяющего положение точки на этой кривой.
меридиана радиального сечения или какого-нибудь другого параметра, определяющего положение точки на этой кривой.
Из приведенных уравнений и формул для трансверсально-изотропного тела, как частный случай, получаются уравнения и формулы для изотропного тела. В случае изотропного тела с модулем Юнга  и коэффициентом Пуассона
и коэффициентом Пуассона  имеем:
имеем:

Введя новую функцию

получим из (78.11) известные формулы:

где

Функция  удовлетворяет уравнению
удовлетворяет уравнению

т. е. является бигармонической (см. [24], стр. 288).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Глава 1. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ АНИЗОТРОПНОГО ТЕЛА
- § 1. Напряженное и деформированное состояния сплошного тела
- § 2. Преобразование составляющих напряжений к новым осям
- § 3. Обобщенный закон Гука
- § 4. Основные случаи упругой симметрии
- § 5. Преобразование упругих постоянных при переходе к новой системе координат
- § 6. Преобразование упругих постоянных при повороте координатной системы
- § 7. Преобразование комплексных параметров при повороте координатной системы
- § 8. Поверхности и кривые, изображающие изменение упругих постоянных с изменением направления
- § 9. Некоторые анизотропные упругие материалы
- § 10. Криволинейная анизотропия
- § 11. Общие уравнения теории упругости и постановка основных задач. Важнейшие вариационные принципы
- Глава 2. ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ
- § 12. Растяжение стержня под действием осевой силы и собственного веса
- § 13. Сдвиг
- 14. Всестороннее сжатие
- § 15. Изгиб стержня моментами, приложенными к концам
- § 16. Изгиб прямоугольной пластинки моментами, распределенными равномерно по сторонам
- § 17. Растяжение и изгиб стержня, обладающего цилиндрической анизотропией
- Глава 3. УПРУГОЕ РАВНОВЕСИЕ ТЕЛА, ОГРАНИЧЕННОГО ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТЬЮ, В КОТОРОМ НАПРЯЖЕНИЯ НЕ МЕНЯЮТСЯ ВДОЛЬ ОБРАЗУЮЩЕЙ
- § 18. Распределение напряжений в однородном теле с прямолинейной анизотропией, зависящее только от двух координат
- § 19. Функции напряжений
- § 20. Общие выражения для функций напряжений в однородном прямолинейно-анизотропном теле
- § 21. Общие формулы для составляющих напряжений и проекций перемещения; граничные условия
- § 22. Распределение напряжений в непрерывнонеоднородном прямолинейно-анизотропном теле, зависящее от двух координат
- § 23. Распределение напряжений в однородном теле, обладающем цилиндрической анизотропией, зависящее от двух координат
- § 24. Распределение напряжений в непрерывно-неоднородном теле, обладающем цилиндрической анизотропией, зависящее от двух координат
- Глава 4. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ И ПЛОСКАЯ ЗАДАЧА ДЛЯ ТЕЛА С ПРЯМОЛИНЕЙНОЙ АНИЗОТРОПИЕЙ
- § 25. Обобщенная плоская деформация однородного прямолинейно-анизотропного тела
- § 26. Плоская деформация и обобщенное плоское напряженное состояние
- § 27. Плоская задача для непрерывнонеоднородного прямолинейно-ортотропного тела. Растяжение и изгиб моментами
- § 28. Распределение напряжений в упругом однородном полупространстве под действием усилий, приложенных к ограничивающей плоскости
- § 29. Случай нагрузки, распределенной равномерно по прямой
- § 30. Распределение напряжений в упругом однородном пространстве с полостью в виде эллиптического цилиндра
- § 31. Растяжение однородной ортотропной пластинки с эллиптическим отверстием
- § 32. Некоторые случаи распределения напряжений в ортотропной пластинке с круговым отверстием
- § 33. Определение напряжений в однородной пластинке с эллиптическим и круглым ядром
- § 34. Растяжение ортотропной пластинки с круговым ядром
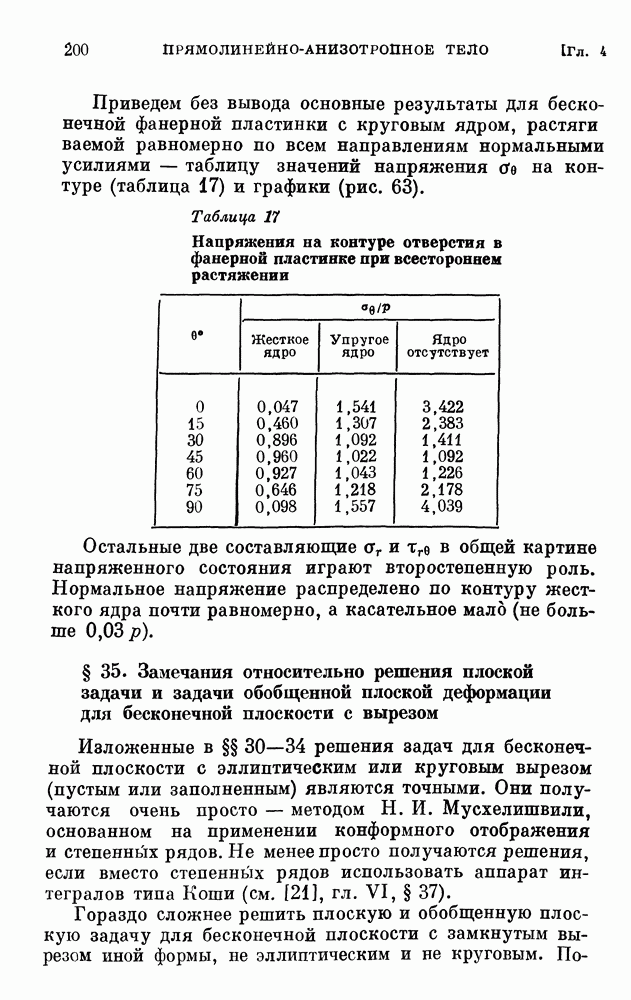
- § 35. Замечания относительно решения плоской задачи и задачи обобщенной плоской деформации для бесконечной плоскости с вырезом
- § 36. Радиальное распределение напряжений в непрерывно-неоднородней упругой полуплоскости
- § 37. Растяжение и изгиб моментами прямоугольной пластинки
- Глава 5. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ, ПЛОСКАЯ ЗАДАЧА И РОДСТВЕННЫЕ ЗАДАЧИ ДЛЯ ОДНОРОДНОГО И НЕПРЕРЫВНО-НЕОДНОРОДНОГО ТЕЛ, ОБЛАДАЮЩИХ ЦИЛИНДРИЧЕСКОЙ АНИЗОТРОПИЕЙ
- § 38. Обобщенная плоская деформация в однородном теле, обладающем цилиндрической анизотропией
- § 39. Задача о плоской деформации тела с цилиндрической анизотропией и родственные задачи
- § 40. Плоская задача для непрерывно-неоднородного тела, обладающего цилиндрической анизотропией
- § 41. Осесимметричное распределение напряжений в однородном полом цилиндре, обладающем цилиндрической анизотропией
- § 42. Распределение напряжений в полом однородном цилиндре под действием внутреннего и наружного давлений
- § 43. Распределение напряжений в полом однородном цилиндре под действием осевой силы и изгибающего момента
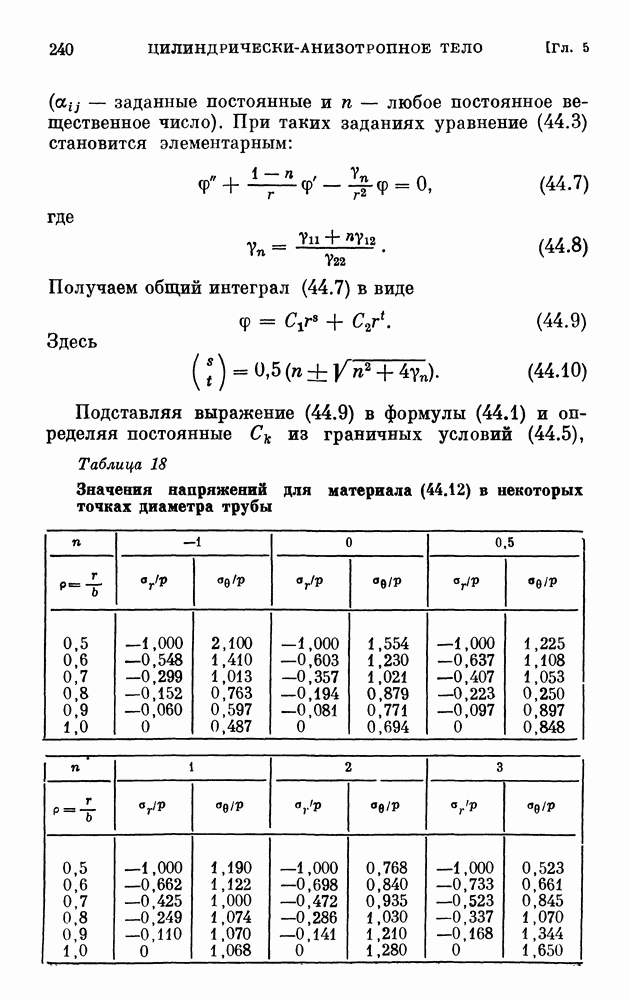
- § 44. Распределение напряжений в непрерывно-неоднородном полом цилиндре под действием давления
- § 45. Распределение напряжений в круговом неоднородном цилиндре, обладающем цилиндрической анизотропией, под действием осевой силы и изгибающего момента
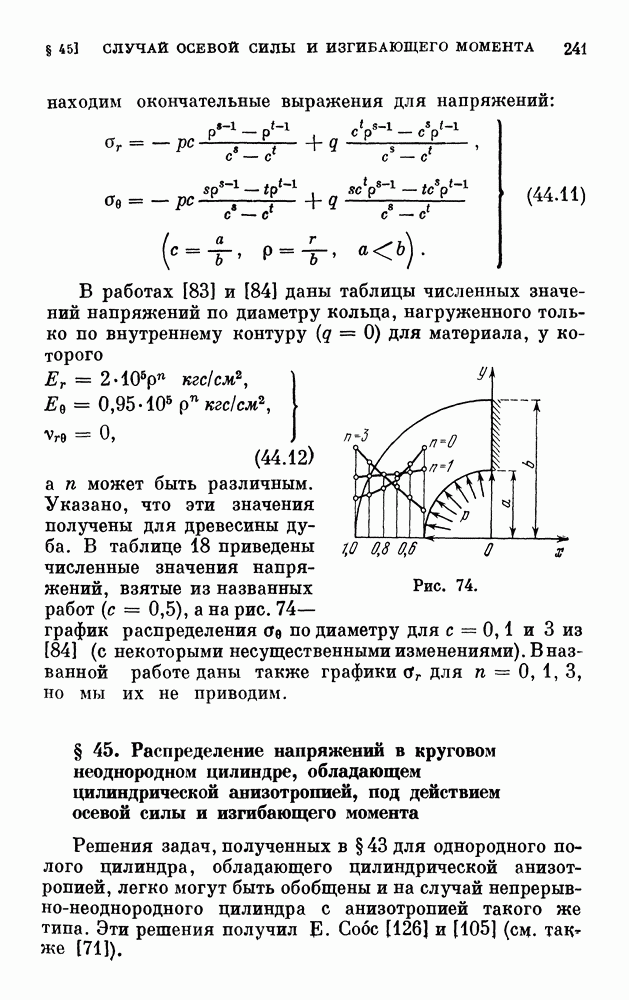
- § 46. Осесимметричное распределение напряжений в круговом цилиндре с упругими характеристиками, меняющимися вдоль радиуса и по длине
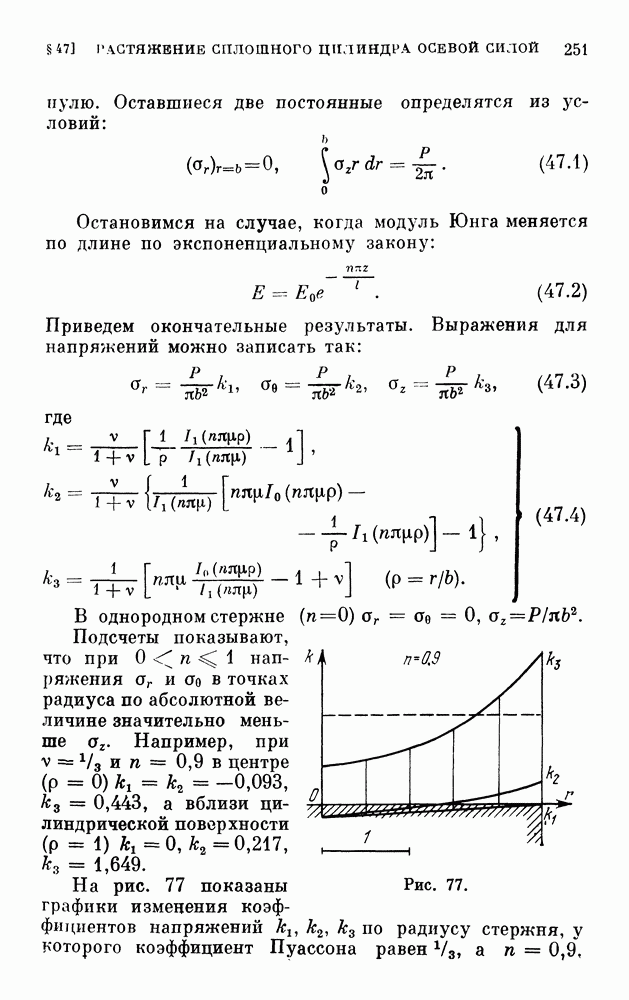
- § 47. Растяжение сплошного цилиндра с модулем, меняющимся только по длине, осевой силой
- § 48. Изгиб плоского кривого бруса моментами и силой, приложенными на концах
- Глава 6. ОБОБЩЕННОЕ КРУЧЕНИЕ И КРУЧЕНИЕ СТЕРЖНЕЙ
- § 49. Обобщенное кручение однородных стержней с прямолинейной анизотропией
- § 50. Совместное действие скручивающих и изгибающих моментов
- § 51. Простое или чистое кручение однородного стержня
- § 52. Связь напряжений и перемещений с функцией усложненной комплексной переменной
- § 53. Упругое равновесие стержня эллиптического сечения под действием скручивающих и изгибающих моментов
- § 54. Чистое кручение однородного ортотронного стержня эллиптического или кругового сечения
- § 55. Кручение однородного ортотропного стержня прямоугольного сечения
- § 56. Приближенные методы решения задач о кручении
- § 57. Кручение непрерывно-неоднородного стержня с прямолинейной анизотропией
- § 58. Кручение ортотропного стержня прямоугольного сечения с переменными модулями сдвига
- § 59. Некоторые другие случаи неоднородного ортотропного стержня прямоугольного сечения
- § 60. Кручение цилиндрического или призматического стержня, обладающего цилиндрической анизотропией
- § 61. Кручение неоднородного полого кругового цилиндра, обладающего цилиндрической анизотропией
- Глава 7. РАВНОВЕСИЕ АНИЗОТРОПНОЙ КОНСОЛИ ПОД ДЕЙСТВИЕМ ИЗГИБАЮЩЕЙ НАГРУЗКИ ПРОСТЕЙШЕГО ВИДА
- § 62. Обобщенный изгиб однородной консоли под действием поперечной силы
- § 63. Общие выражения для функций напряжений, составляющих напряжений и проекций перемещения. Граничные условия
- § 64. Изгиб однородной прямолинейно-анизотропной консоли поперечной силой
- § 65. Распределение напряжении в однородной консоли эллиптического и кругового сечения
- § 66. Изгиб однородной ортотропной консоли прямоугольного сечения
- § 67. Приближенные методы решения задачи об изгибе консоли поперечной силой
- § 68. Изгиб неоднородной ортотропной консоли
- § 69. Изгиб неоднородной ортотропной консоли прямоугольного сечения
- § 70. Равновесие консоли, обладающей цилиндрической анизотропией, под действием поперечной силы
- § 71. Распределение напряжений в консоли, имеющей форму полого или сплошного цилиндра
- Глава 8. КРУЧЕНИЕ ТЕЛ ВРАЩЕНИЯ
- § 72. Общие уравнения теории кручения непрерывно-неоднородных тел вращения, обладающих цилиндрической анизотропией
- § 73. Кручение однородного тела вращения
- § 74. Кручение криволинейно-анизотропного конуса
- § 75. Влияние сферического и сфероидального включения и полости на распределение напряжений в скрученном стержне
- § 76. Точное решение задачи о кручении кругового цилиндра
- § 77. Кручение цилиндра, у которого модули сдвига меняются пропорционально степени расстояния r (точное решение)
- Глава 9. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ТЕЛА ВРАЩЕНИЯ
- § 78. Общие уравнения осесимметричной деформации. Функция напряжений
- § 79. Общие выражения для напряжений и перемещений через две функции. Общий случай деформации трансверсально-изотропного тела
- § 80. Распределение напряжений в цилиндре под действием произвольной осесимметричной нагрузки
- § 81. Распределение напряжений в тяжелом массиве с вертикальной полостью
- § 82. Распределение напряжений в упругом полупространстве под действием осесимметричной нормальной нагрузки
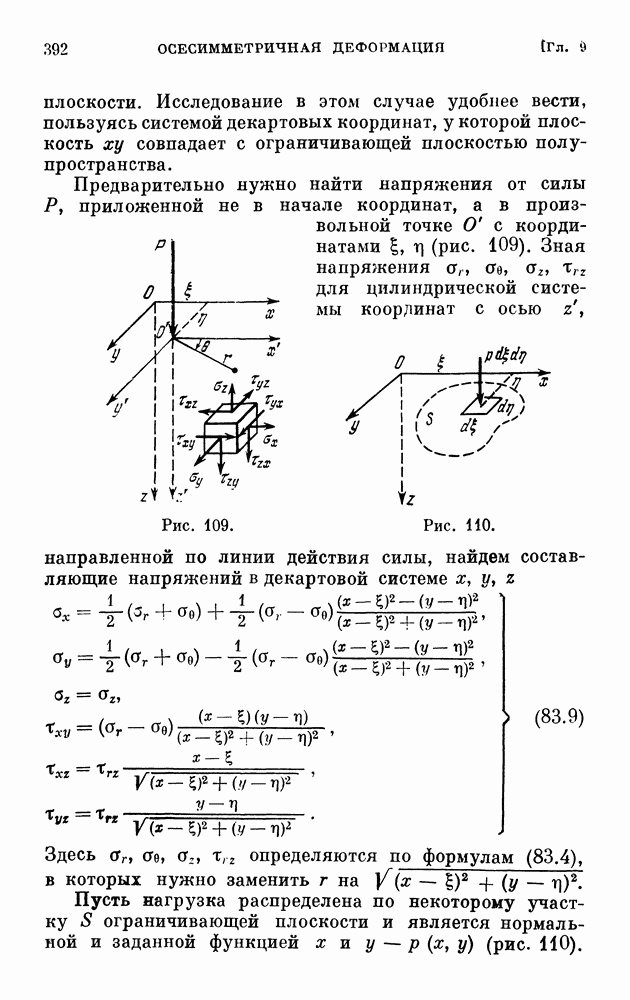
- § 83. Распределение напряжений в полупространстве под действием сосредоточенной силы и произвольной нормальной нагрузки
- § 84. Растяжение упругого конуса
- § 85. Распределение напряжений вблизи эллипсоидального и сферического включения или полости при одностороннем и всестороннем растяжении
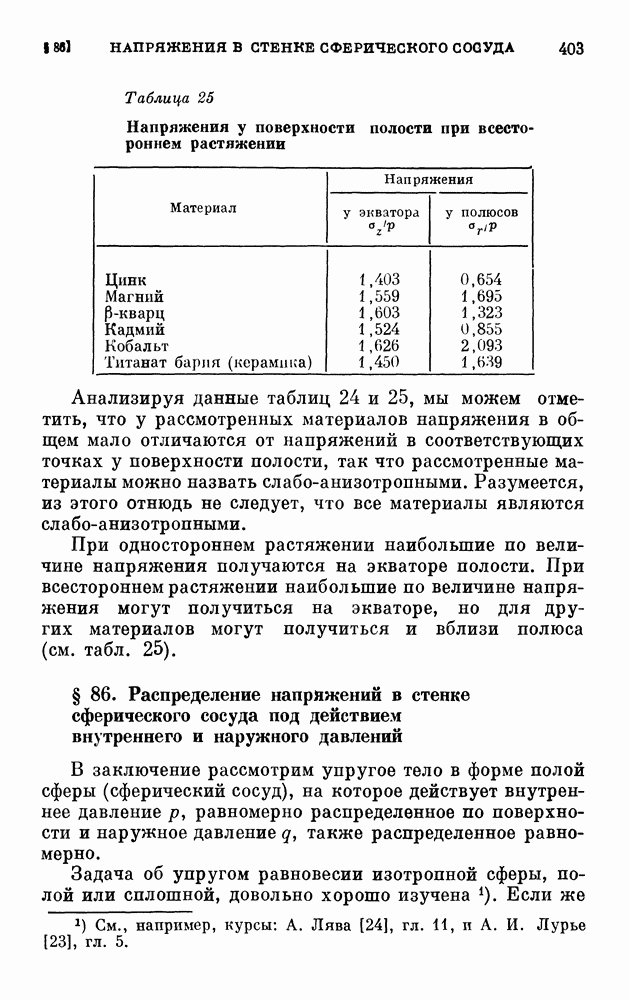
- § 86. Распределение напряжений в стенке сферического сосуда под действием внутреннего и наружного давлений
- ЛИТЕРАТУРА