| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
Для удобства изложения существа метода ограничимся вначале частным случаем этой задачи, когда объект описывается уравнением первого порядка  . Кроме того, заменим приближенно этот непрерывный объект дискретным. В связи с этим разобьем интервал
. Кроме того, заменим приближенно этот непрерывный объект дискретным. В связи с этим разобьем интервал  на
на  равных участков достаточно малой длины Т и будем рассматривать лишь дискретные значения
равных участков достаточно малой длины Т и будем рассматривать лишь дискретные значения  в моменты времени
в моменты времени  соответственно (далее будем полагать
соответственно (далее будем полагать  ).
).
Дифференциальное уравнение можно приближенно заменить уравнением в конечных разностях

или

где  , и кроме того, здесь и далее нижний индекс в обозначении
, и кроме того, здесь и далее нижний индекс в обозначении  , а также число Т опущены.
, а также число Т опущены.
Начальные условия для этого разностного уравнения остаются прежними:

Для удобства изложения примем  где
где  - заданные функции. Заменим приближенно интеграл (2.3.3) суммой
- заданные функции. Заменим приближенно интеграл (2.3.3) суммой

Принимая во внимание, что  и Т суть константы, запишем функционал качества в виде
и Т суть константы, запишем функционал качества в виде

Задача П.3.1. Определить функцию управления

такую, чтобы на решениях системы  при любых начальных условиях
при любых начальных условиях  минимизировалась сумма
минимизировалась сумма  . При этом искомая функция должна удовлетворять ограничению
. При этом искомая функция должна удовлетворять ограничению  .
.
Для определенности будем полагать, что эти ограничения на управления имеют вид

Сформулированная задача является, в сущности, задачей условного экстремума функции  . Независимыми переменными являются числа
. Независимыми переменными являются числа  .
.
Синтез на основе классических методов математического анализа. Используя связи  , исключим
, исключим  из
из  , тогда
, тогда

Если абсолютный минимум этой функции  переменных
переменных  достигается при
достигается при  , т. е. внутри множества U, то необходимые условия относительного экстремума функции
, т. е. внутри множества U, то необходимые условия относительного экстремума функции  записываются системой
записываются системой  нелинейных алгебраических уравнений
нелинейных алгебраических уравнений

К сожалению, подобные системы нелинейных уравнений трудно решить даже при сравнительно небольших  .
.
Откажемся от аналитических методов и обратимся к прямым численным методам. Пусть  . Будем определять минимум функции
. Будем определять минимум функции  путем подсчета ее значения при различных значениях
путем подсчета ее значения при различных значениях  .
.
Разобьем интервал  возможных значений
возможных значений  на 10 частей и подсчитаем значения для каждого из полученных таким образом 10 наборов значений
на 10 частей и подсчитаем значения для каждого из полученных таким образом 10 наборов значений  . Если вычислительной машине требуется 1 с на вычисление функции
. Если вычислительной машине требуется 1 с на вычисление функции  в одной точке, то для вычисления ее значений в
в одной точке, то для вычисления ее значений в  потребуется
потребуется  (более 10 лет). Таким образом, и этот подход оказывается мало пригодным для решения задачи
(более 10 лет). Таким образом, и этот подход оказывается мало пригодным для решения задачи  .
.
Более того, если бы даже эти пути и привели к числам  , при которых функция
, при которых функция  принимает наименьшее значение, то эти числа не разрешили бы полностью задачу
принимает наименьшее значение, то эти числа не разрешили бы полностью задачу  , поскольку в последней требуется найти функцию
, поскольку в последней требуется найти функцию  , зависящую от текущих значений
, зависящую от текущих значений  . Полученные же числа
. Полученные же числа  зависят только от
зависят только от  .
.
Синтез на основе принципа оптимальности. Будем полагать, что  не фиксировано, и рассмотрим различные случаи задачи
не фиксировано, и рассмотрим различные случаи задачи  , соответствующие различным значениям параметра N, характеризующего время, в течение которого исследуется качество процессов в системе.
, соответствующие различным значениям параметра N, характеризующего время, в течение которого исследуется качество процессов в системе.
Эти частные случаи будем называть  -шаговыми процессами.
-шаговыми процессами.
Обозначим  значение функционала качества
значение функционала качества  при
при  -шаговом оптимальном процессе.
-шаговом оптимальном процессе.
Пусть  Для этого одношагового процесса уравнения
Для этого одношагового процесса уравнения  и функционал
и функционал  имеют вид
имеют вид

Нетрудно видеть, что

Опишем вычислительную процедуру определения оптимального управления  в одношаговом процессе.
в одношаговом процессе.
Процедура 1. Положим  , где
, где  есть некоторое фиксированное число. Тогда
есть некоторое фиксированное число. Тогда

Разобьем интервал  допустимых изменений
допустимых изменений  на i отрезков длиной
на i отрезков длиной  и вычислим значение функции
и вычислим значение функции  в точках разбиения. При некотором значении
в точках разбиения. При некотором значении  эта функция принимает наименьшее значение
эта функция принимает наименьшее значение  . Запомним
. Запомним  .
.
Положим теперь  . Тогда
. Тогда  . При некотором
. При некотором  эта функция принимает наименьшее значение.
эта функция принимает наименьшее значение.
Таким образом, задаваясь различными значениями  , получим значения
, получим значения  . Эта зависимость оптимальных значений
. Эта зависимость оптимальных значений  от начальных условий
от начальных условий  и является искомой функцией
и является искомой функцией

задаваемой таблично.
Используя эту функцию, получим наименьшее значение функционала  :
:

Рассмотрим теперь двухшаговый процесс  . В этом случае
. В этом случае 

Представим  где
где  .
.
Значение  зависит от выбора
зависит от выбора  . При этом
. При этом  зависит от
зависит от  — от
— от  так как
так как  зависит от
зависит от  , которое в свою очередь определяется выбором
, которое в свою очередь определяется выбором  .
.
Положим  где
где  — некоторое произвольное, но фиксированное число. Это управление отклоняет
— некоторое произвольное, но фиксированное число. Это управление отклоняет  на величину
на величину  .
.
Почти очевидно, что если требуется получить наименьшее значение  при
при  то необходимо выбирать
то необходимо выбирать  так, чтобы
так, чтобы  принимало наименьшее значение.
принимало наименьшее значение.
Управление  , доставляющее минимум
, доставляющее минимум  , является управлением в одношаговом процессе (так как
, является управлением в одношаговом процессе (так как  ) зафиксировано) и определяется формулой
) зафиксировано) и определяется формулой  , т. е.
, т. е.

При этом

Значение функционала  при
при  определяется выражением
определяется выражением

Минимизируя эту сумму по  , получим
, получим

Выражение в фигурных скобках является функцией одной переменной  Используя процедуру 1, получим функцию
Используя процедуру 1, получим функцию  , при которой это выражение принимает наименьшее значение.
, при которой это выражение принимает наименьшее значение.
Таким образом, оптимальное управление в двухшаговом процессе имеет

При этом экстремальное значение функционала 

Пусть  . Для этого случая
. Для этого случая

Представим  , где
, где  .
.
Пусть  , где
, где  - произвольное, но фиксированное число.
- произвольное, но фиксированное число.
Для оптимальности управления в этом трехшаговом процессе при условии, что управление на первом шаге фиксировано, необходимо определить  так, чтобы
так, чтобы  принимало наименьшее значение. Для определения
принимало наименьшее значение. Для определения  воспользуемся результатами, полученными для двухшагового процесса с начальным условием
воспользуемся результатами, полученными для двухшагового процесса с начальным условием  .
.
На основе  получим
получим

Значение функционала  при управлении
при управлении  определяется выражением
определяется выражением

Минимизируя его по  , получим
, получим

Выражение в фигурных скобках является функцией одной переменной  . Используя процедуру 1, находим
. Используя процедуру 1, находим

Таким образом, оптимальное управление в трехшаговом процессе описывается выражениями  .
.
Повторяя эти рассуждения для  , получим соотношение
, получим соотношение

которое является функциональным уравнением для дискретных систем.
Вывод этого уравнения опирался на принцип оптимальности, который можно переформулировать так:
оптимальное уравнение обладает тем свойством, каковы бы ни были начальное состояние (условие) и управление на первом шаге (или нескольких первых шагах), управление на последующих шагах должно быть оптимальным относительно состояния, возникшего в результате управления на первом шаге.
Какие же трудности в решении задачи  мы преодолели, используя подход, основанный на принципе оптимальности? Главной трудностью являлась минимизация функции
мы преодолели, используя подход, основанный на принципе оптимальности? Главной трудностью являлась минимизация функции  переменных
переменных  . Функциональное уравнение
. Функциональное уравнение  позволило свести задачу минимума функции N переменных к значительно более простой задаче минимизации функций одной переменной. Действительно, используя
позволило свести задачу минимума функции N переменных к значительно более простой задаче минимизации функций одной переменной. Действительно, используя  при
при  , получим функции:
, получим функции:

Отметим еще раз, что функции  получены в результате минимизации функции
получены в результате минимизации функции  одной переменной
одной переменной  .
.
В задаче  требуется найти управление вида
требуется найти управление вида 

Очевидно, что искомые и полученные управления связаны соотношениями

Таким образом, искомые функции управления

Второй вариант применения принципа оптимальности. Приведем еще одну систему рассуждений, основанных на принципе оптимальности, позволяющих определить управления  . Определение этих управлений начнем с последнего интервала времени
. Определение этих управлений начнем с последнего интервала времени  , предполагая, что состояние
, предполагая, что состояние  известно. Согласно принципу оптимальности, управление
известно. Согласно принципу оптимальности, управление  на этом интервале должно минимизировать частичную сумму, соответствующую этому интервалу:
на этом интервале должно минимизировать частичную сумму, соответствующую этому интервалу:

Учитывая, что  , получим
, получим

Это выражение с точностью до обозначений совпадает с  и поэтому, применяя процедуру 1, получаем оптимальное управление на последнем участке:
и поэтому, применяя процедуру 1, получаем оптимальное управление на последнем участке:

Минимальное значение  определяется выражением
определяется выражением

Рассмотрим интервал времени  , состоящий из последнего и предпоследнего интервалов Этому интервалу соответствует частичная сумма
, состоящий из последнего и предпоследнего интервалов Этому интервалу соответствует частичная сумма

Состояние  будем предполагать известным. Из принципа оптимальности следует, что лишь состояние
будем предполагать известным. Из принципа оптимальности следует, что лишь состояние  и цель управления (минимизация
и цель управления (минимизация  ) определяют оптимальное управление на интервале
) определяют оптимальное управление на интервале  .
.
Найдем минимум по  . Учтем при этом
. Учтем при этом

Первые два слагаемых в  не зависят от
не зависят от  и поэтому
и поэтому

Применяя к последнему выражению в фигурных скобках, совпадающему с точностью до обозначений с  , процедуру 1, получим оптимальное управление на предпоследнем интервале
, процедуру 1, получим оптимальное управление на предпоследнем интервале  .
.

Перейдем теперь к интервалу времени  , состоящему из трех последних интервалов. Этому интервалу соответствует частичная сумма
, состоящему из трех последних интервалов. Этому интервалу соответствует частичная сумма

Предполагая состояние  известным, определим управления
известным, определим управления  , минимизирующие сумму
, минимизирующие сумму  . В соответствии с принципом оптимальности, эти управления являются оптимальными для трех последних интервалов времени движения.
. В соответствии с принципом оптимальности, эти управления являются оптимальными для трех последних интервалов времени движения.
Учитывая, что первые два слагаемых в  не зависят от
не зависят от  , запишем
, запишем

Применяя процедуру 1, получим оптимальное управление на интервале 

Продолжая этот процесс, получим общую рекуррентную формулу

Используя процедуру 1, получаем оптимальное уравнение на интервале  :
:

Это выражение совпадает с  , а функциональное уравнение
, а функциональное уравнение  при
при  совпадает с
совпадает с  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
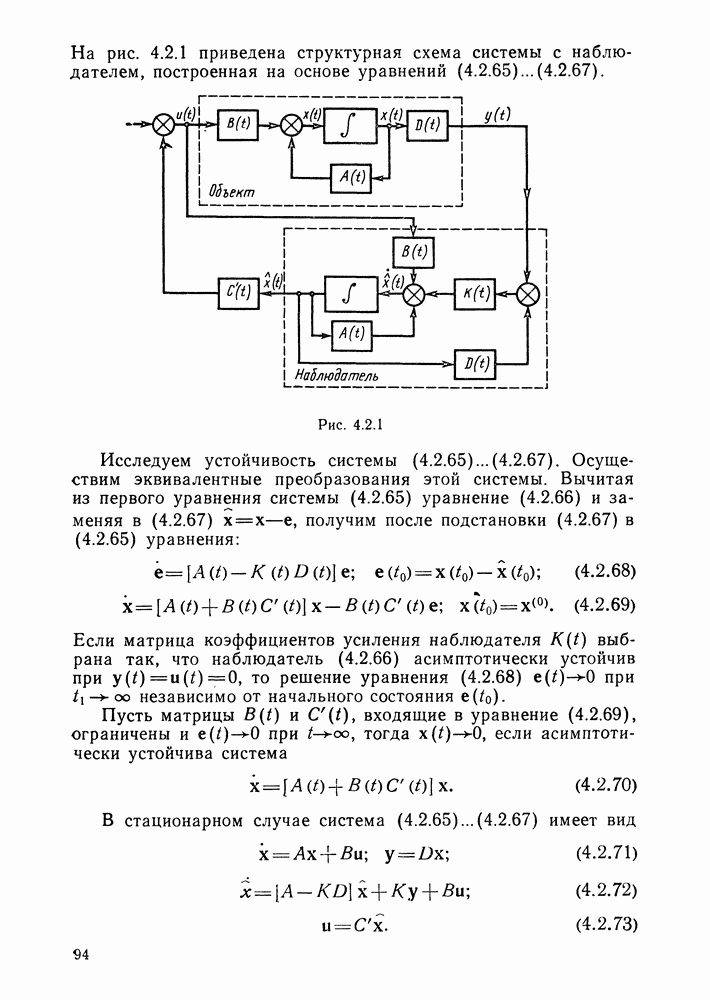
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
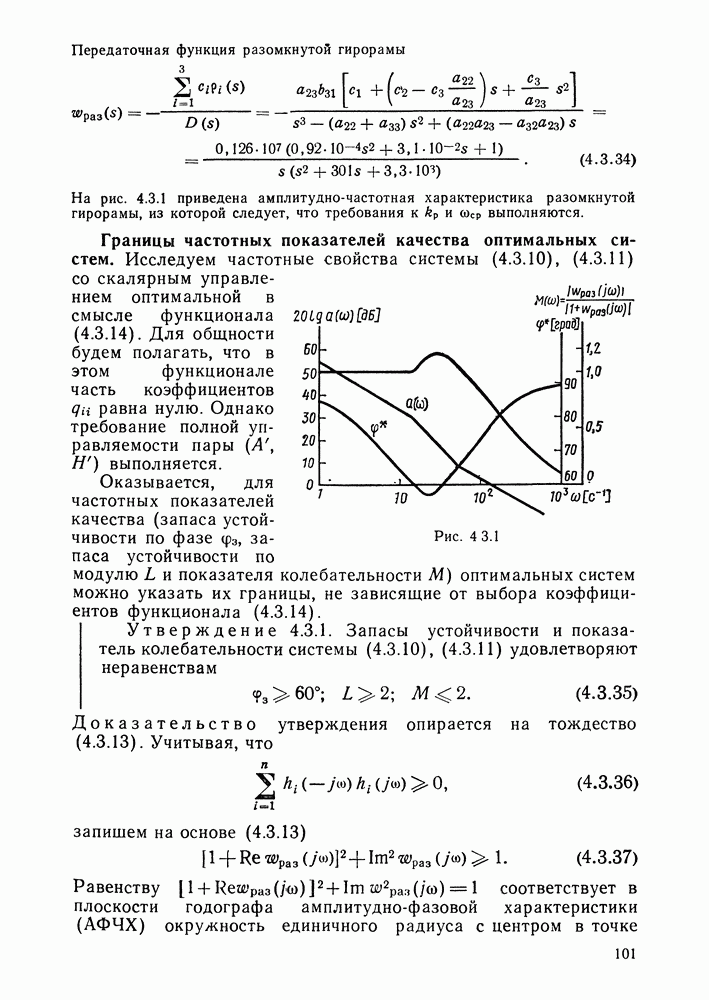
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
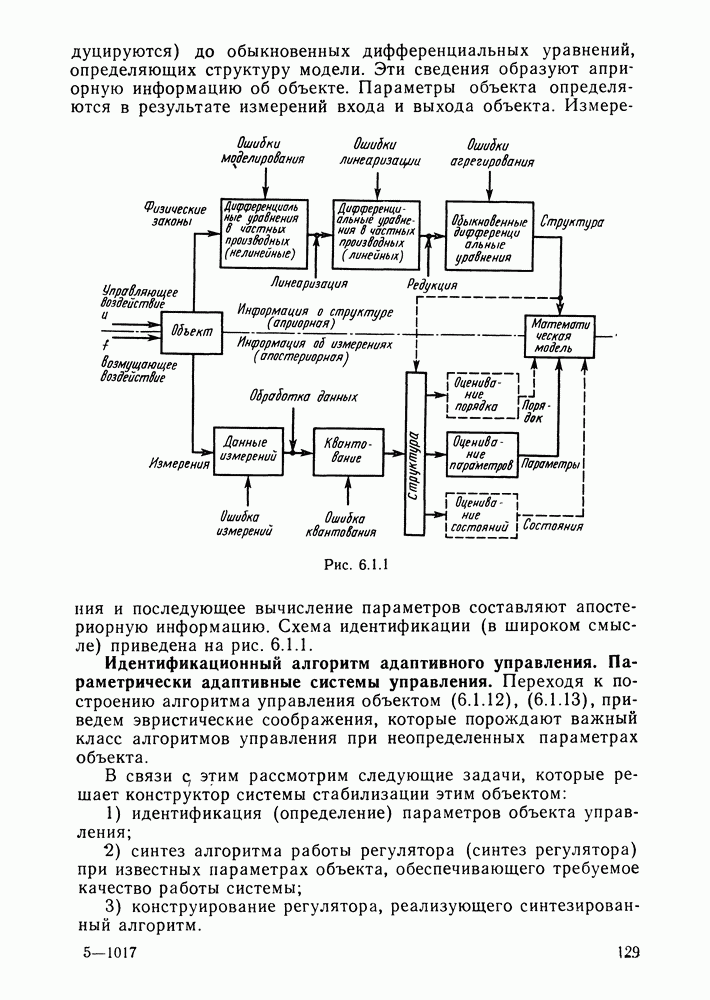
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
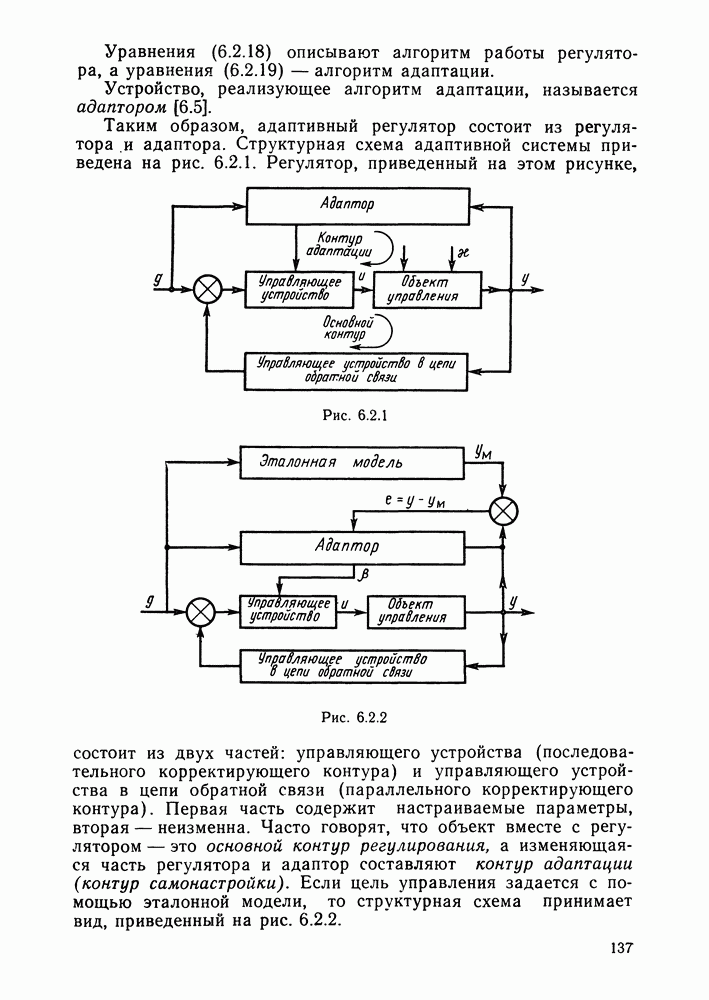
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
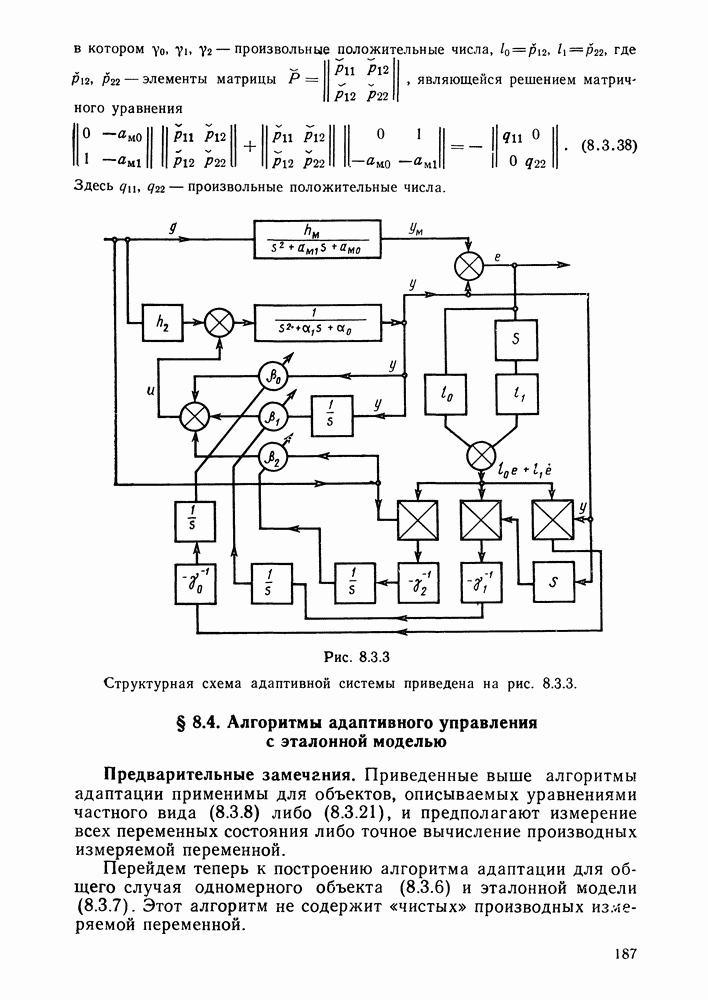
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
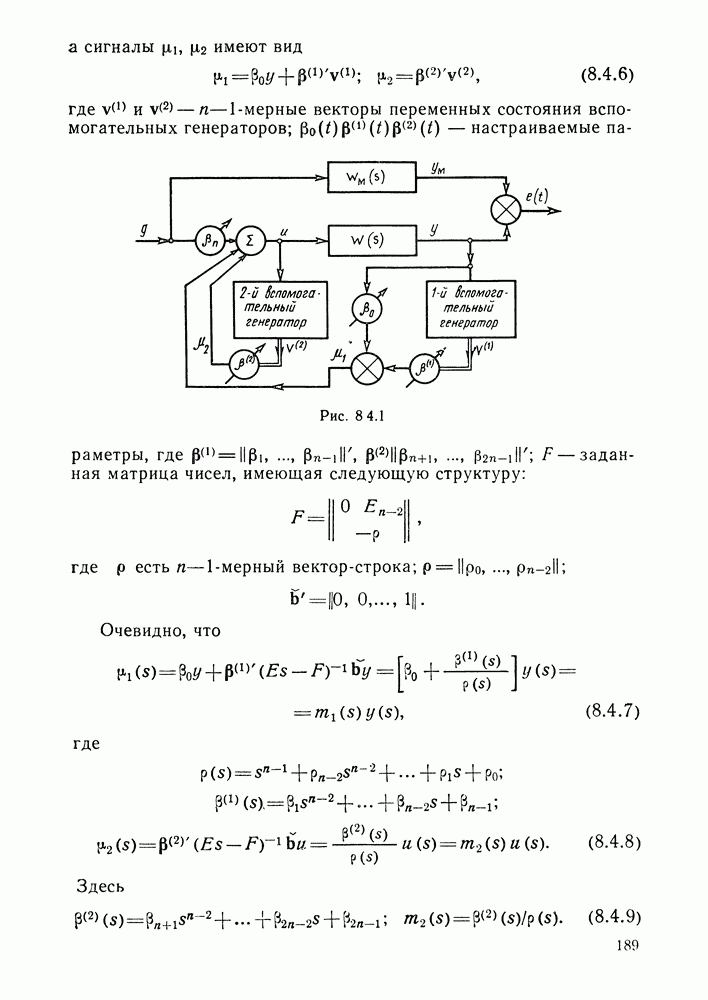
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
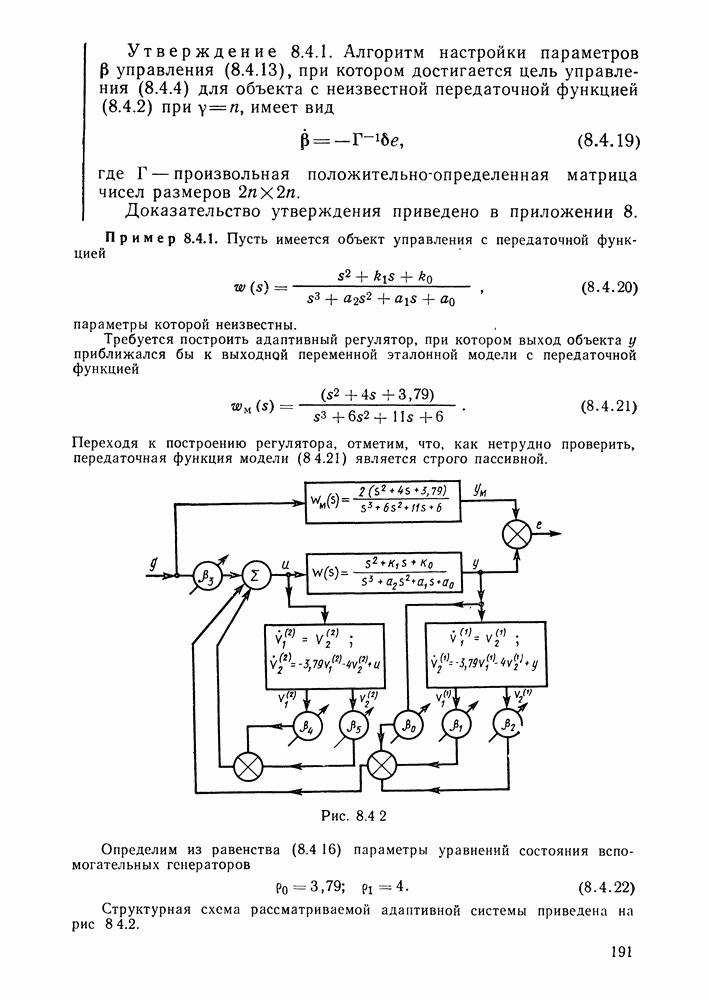
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
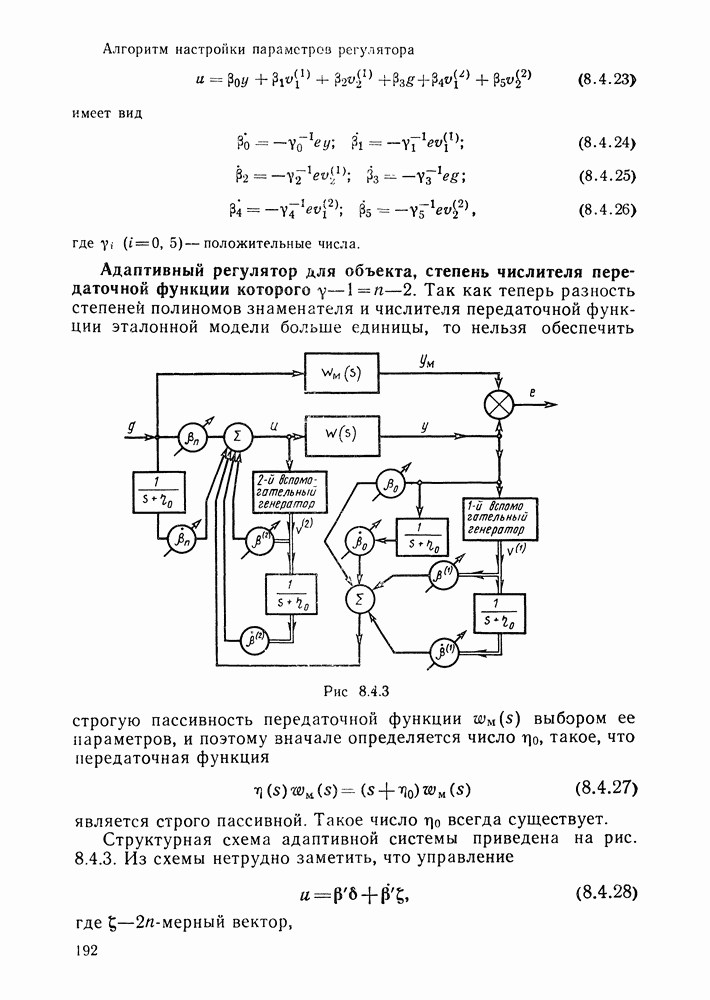
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ