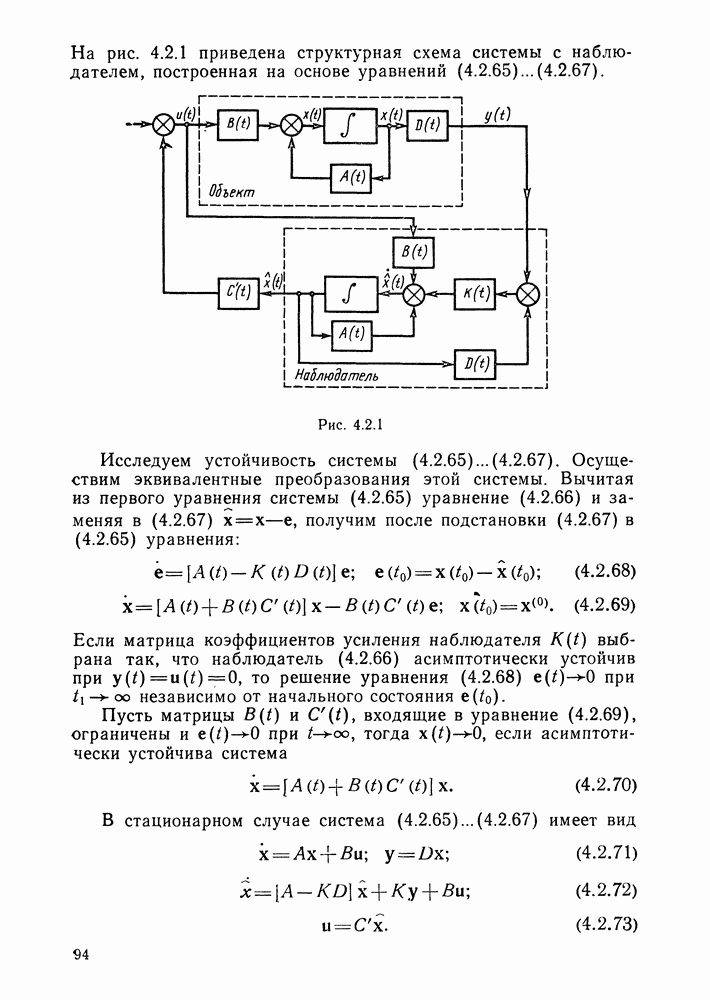
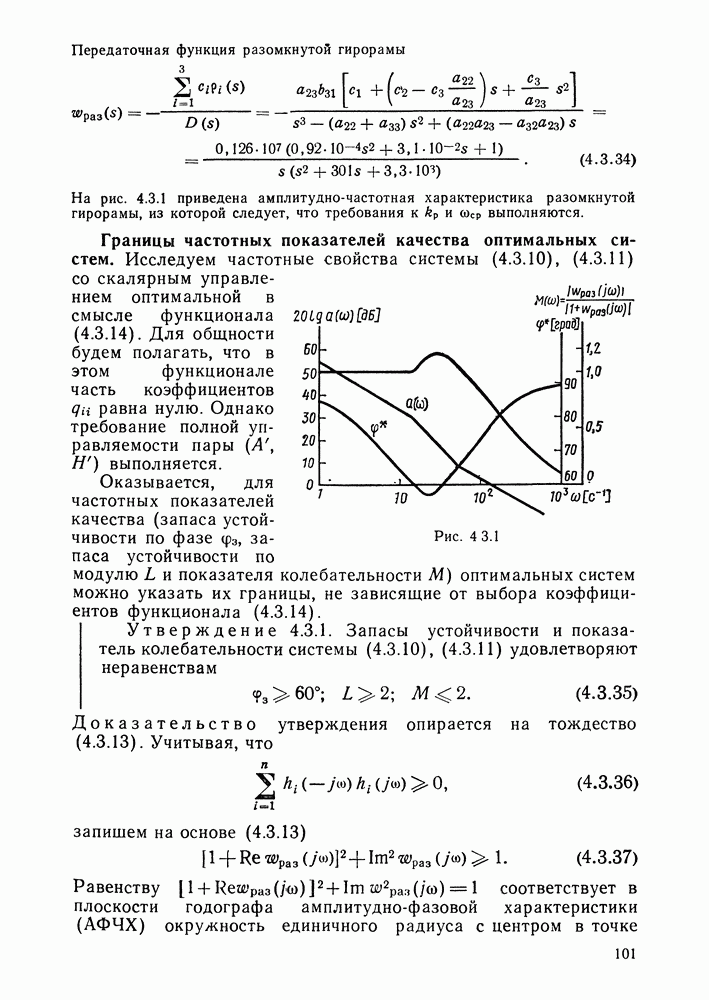
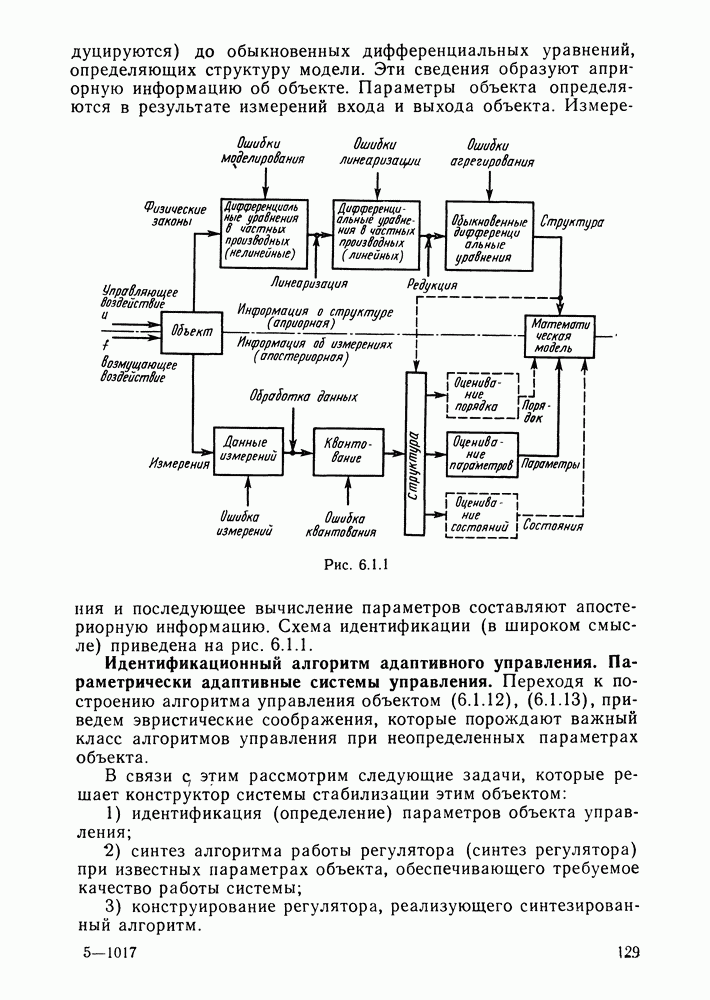
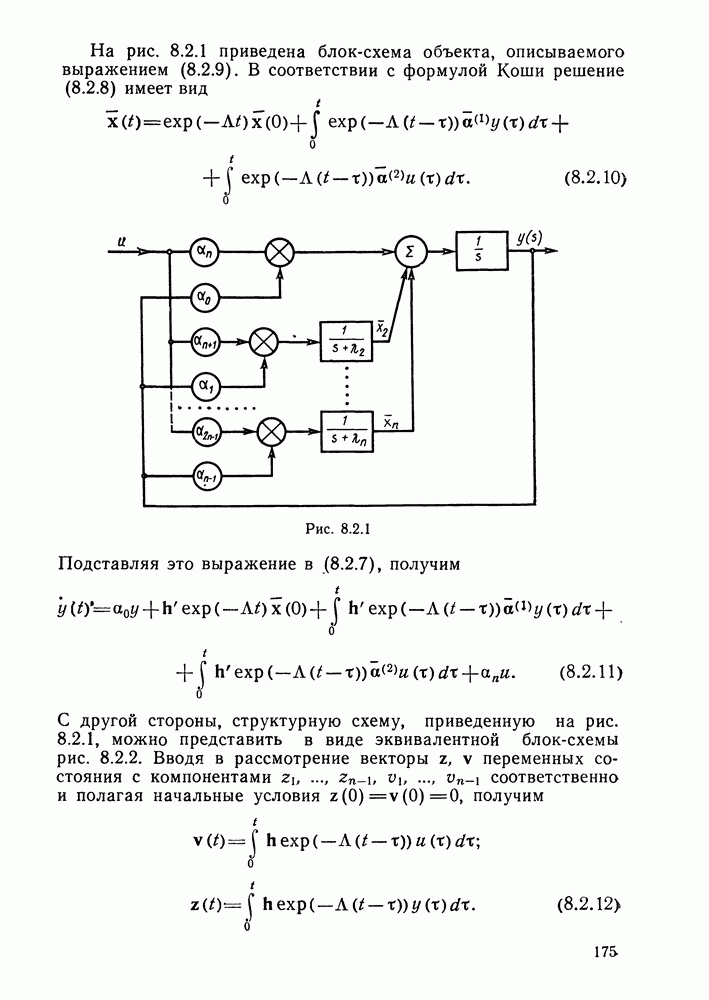
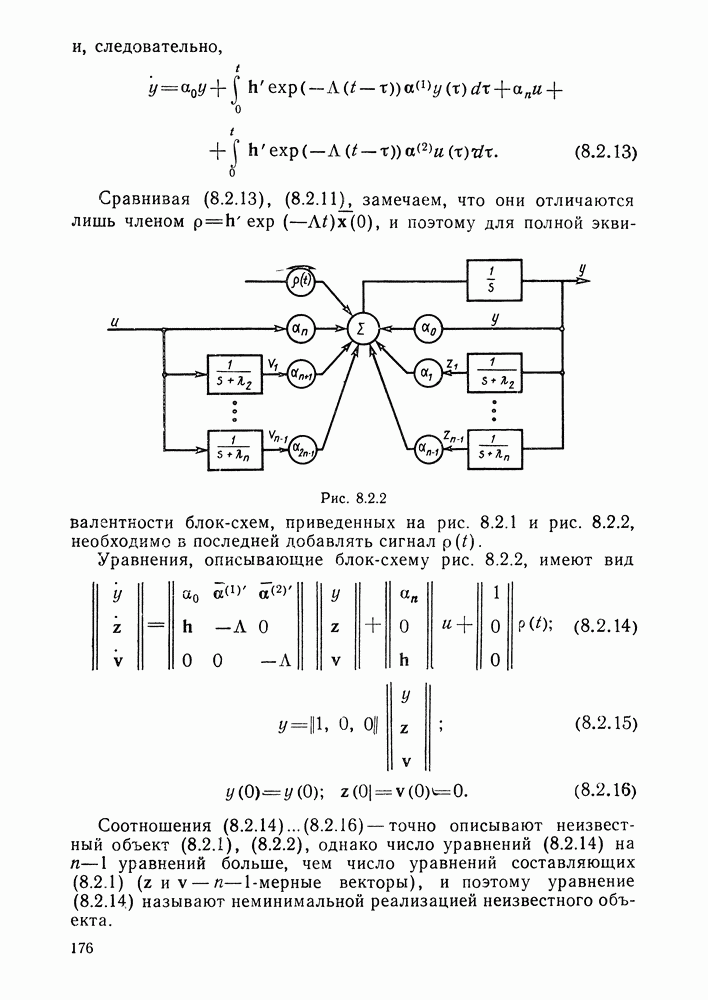
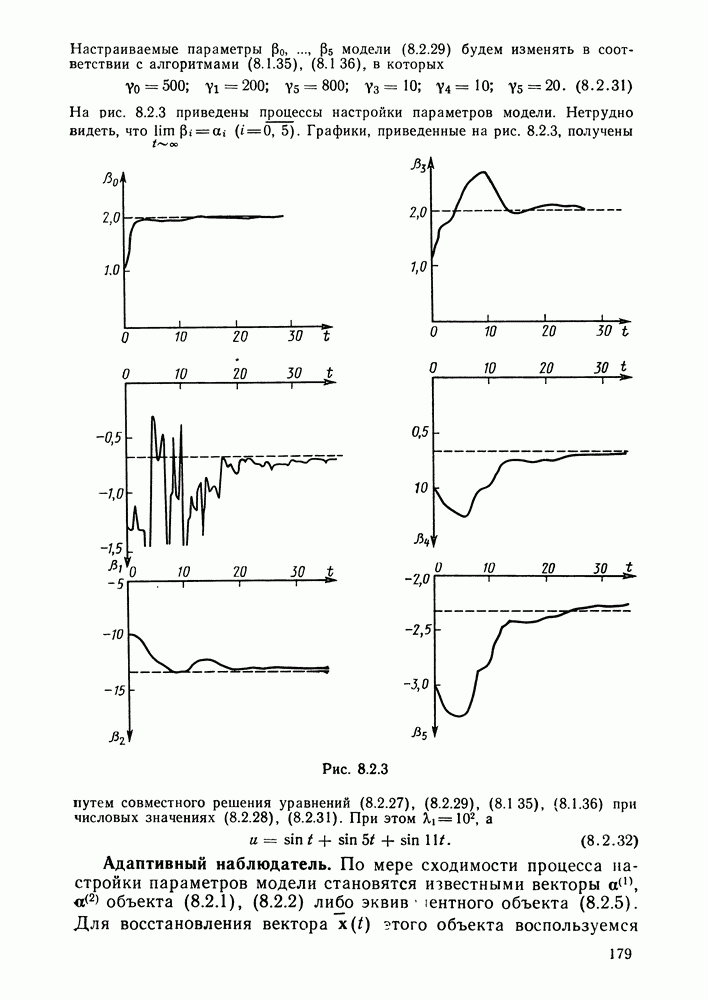
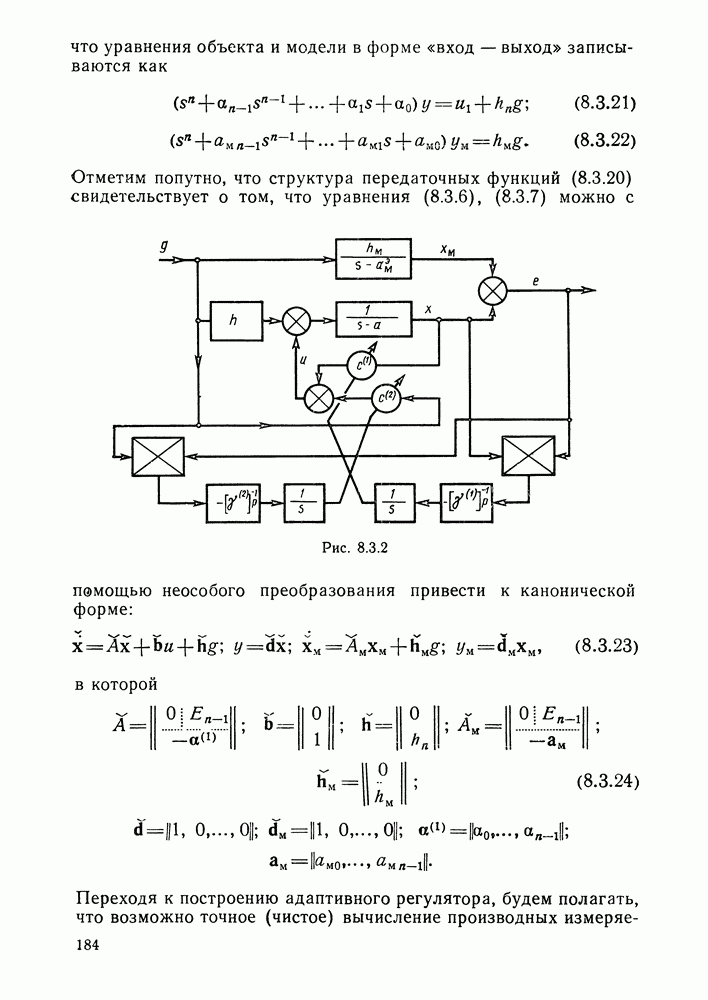
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
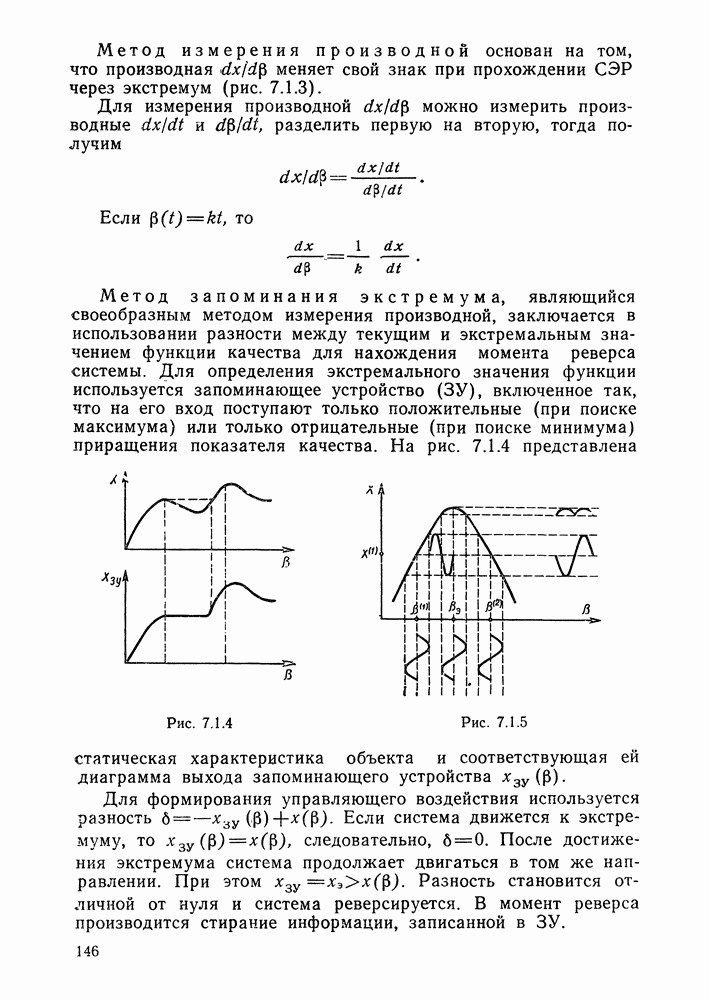
145
146
147
148
149
150
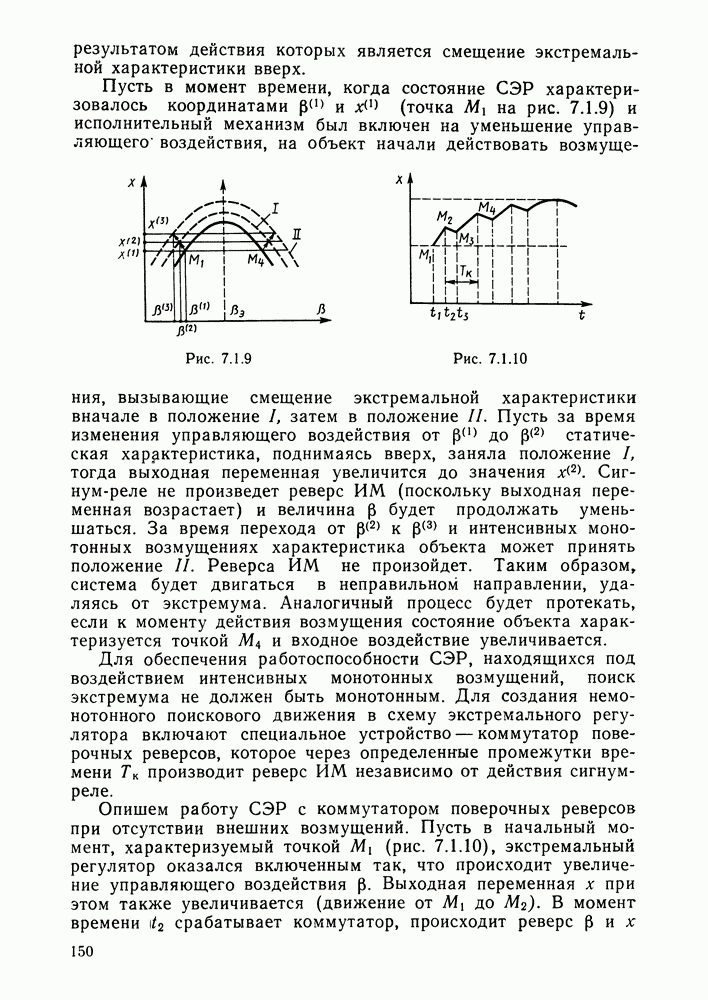
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
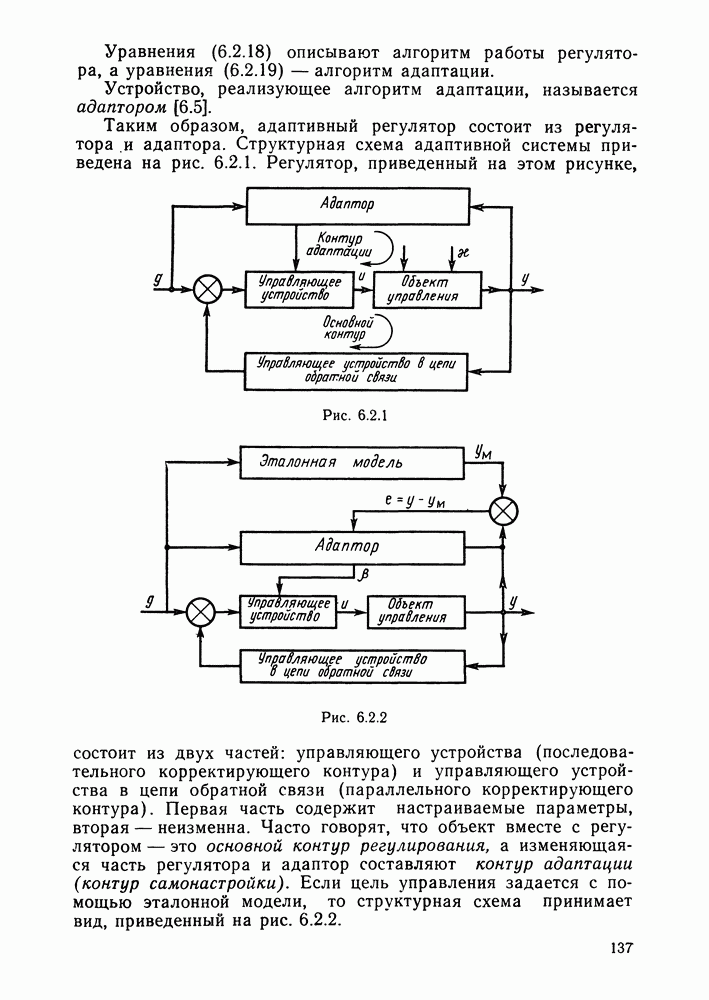
§ 6.2. Структура адаптивных систем
Цели управления. Рассмотрим объект управления, описываемый уравнениями
 (6.2.1)
(6.2.1)
в которых  — неизвестный вектор чисел.
— неизвестный вектор чисел.
Требуется найти алгоритм адаптивного управления объектом (6.2.1), при котором достигается цель управления. Эта задача, которой посвящена вторая часть книги, точно не определена, пока не задана цель управления.
Для задания цели управления используются оценочные функции
 (6.2.2)
(6.2.2)
где  - некоторая выпуклая функция, часто
- некоторая выпуклая функция, часто  - ошибка (невязка), малость которой соответствует достижению цели управления. Выражение ошибки зависит от назначения системы управления. Приведем некоторые из этих выражений для непрерывных и дискретных систем.
- ошибка (невязка), малость которой соответствует достижению цели управления. Выражение ошибки зависит от назначения системы управления. Приведем некоторые из этих выражений для непрерывных и дискретных систем.
1. Стабилизация. В этом случае
 (6.2.3)
(6.2.3)
2. Стабилизация с заданной динамикой. Пусть требуется, чтобы выходная переменная системы  изменялась наперед заданным образом, который задается уравнением
изменялась наперед заданным образом, который задается уравнением
 (6.2.4)
(6.2.4)
в котором числа  заданы так, чтобы решение уравнения (6.2.4) было асимптотически устойчивым.
заданы так, чтобы решение уравнения (6.2.4) было асимптотически устойчивым.
Тогда в непрерывном случае
 (6.2.5)
(6.2.5)
а в дискретном
 (6.2.6)
(6.2.6)
3. Идеальное слежение. Если требуется отработать задающее воздействие  то невязку принимают в виде
то невязку принимают в виде
 (6.2.7)
(6.2.7)
4. Системы с эталонной моделью. Системы с эталонной моделью составляют обширный класс адаптивных систем, в которых желаемое движение задается эталонной моделью, являющейся физическим устройством, описываемым уравнениями
 (6.2.8)
(6.2.8)
либо в общем случае нелинейным уравнением
 (6.2.8)
(6.2.8)
в которых  —
—  -мерный вектор переменных состояния эталонной модели;
-мерный вектор переменных состояния эталонной модели;  заданная матрица чисел;
заданная матрица чисел;  — заданные векторы чисел, которые определяются с использованием обычных методов синтеза. Это относится и к вектор-функции
— заданные векторы чисел, которые определяются с использованием обычных методов синтеза. Это относится и к вектор-функции  и функции
и функции  . Выход
. Выход  эталонной модели описывает желаемое движение (цель управления) системы при заданном (измеряемом) задающем воздействии
эталонной модели описывает желаемое движение (цель управления) системы при заданном (измеряемом) задающем воздействии  . Отклонение от желаемого движения
. Отклонение от желаемого движения
 (6.2.9)
(6.2.9)
Зависимость оценочной функции (критерия качества) (6.2.2) от ошибки  принимается различной в зависимости от объема информации о внешних возмущениях и помехах, действующих на объект (6.2.1).
принимается различной в зависимости от объема информации о внешних возмущениях и помехах, действующих на объект (6.2.1).
Если упорядочить сведения о внешних возмущениях и помехах по мере возрастания информации о них, то можно различить:
а) неопределенные, ограниченные по модулю внешние возмущения и помехи, когда  суть произвольные неизвестные функции, удовлетворяющие неравенствам
суть произвольные неизвестные функции, удовлетворяющие неравенствам
 (6.2.10)
(6.2.10)
где  — заданные числа;
— заданные числа;
б) случайные внешние воздействия и помехи с неизвестным законом распределения, но ограниченными математическими ожиданиями и дисперсиями:
 (6.2.12)
(6.2.12)
где  — заданные числа;
— заданные числа;
в) внешние воздействия и помехи — случайные процессы, законы распределения которых известны, но не известны параметры этих законов распределения. Эти параметры включают в множество  и тогда оно описывает класс допустимых объектов и возмущений;
и тогда оно описывает класс допустимых объектов и возмущений;
г) внешние воздействия и помехи — случайные процессы с известными законами распределения и заданными параметрами этих законов.
Если внешние воздействия и помехи — неопределенные, ограниченные по модулю, то цель управления задается неравенством
 (6.2.13)
(6.2.13)
где  — заданное положительное число, согласованное с уровнем помех и внешних воздействий.
— заданное положительное число, согласованное с уровнем помех и внешних воздействий.
При случайных воздействиях цели управления принимают вид
 (6.2.14)
(6.2.14)
Естественно, что из-за недостатка информации о параметрах объекта целевые условия (6.2.13) или (6.2.14) не будут выполняться на начальном этапе функционирования объекта, поэтому требуют, чтобы цель достигалась асимптотически — при достаточно большом t (или k) или при  .
.
Таким образом, приходим к заданию цели в виде предельных неравенств
 (6.2.15)
(6.2.15)
при неопределенных воздействиях и неравенств
 (6.2.16)
(6.2.16)
при случайных внешних воздействиях и помехах.
Отметим, что наряду с «локальными» критериями вида (6.2.13) иногда используют интегральные критерии с переменным верхним пределом
 (6.2.17)
(6.2.17)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
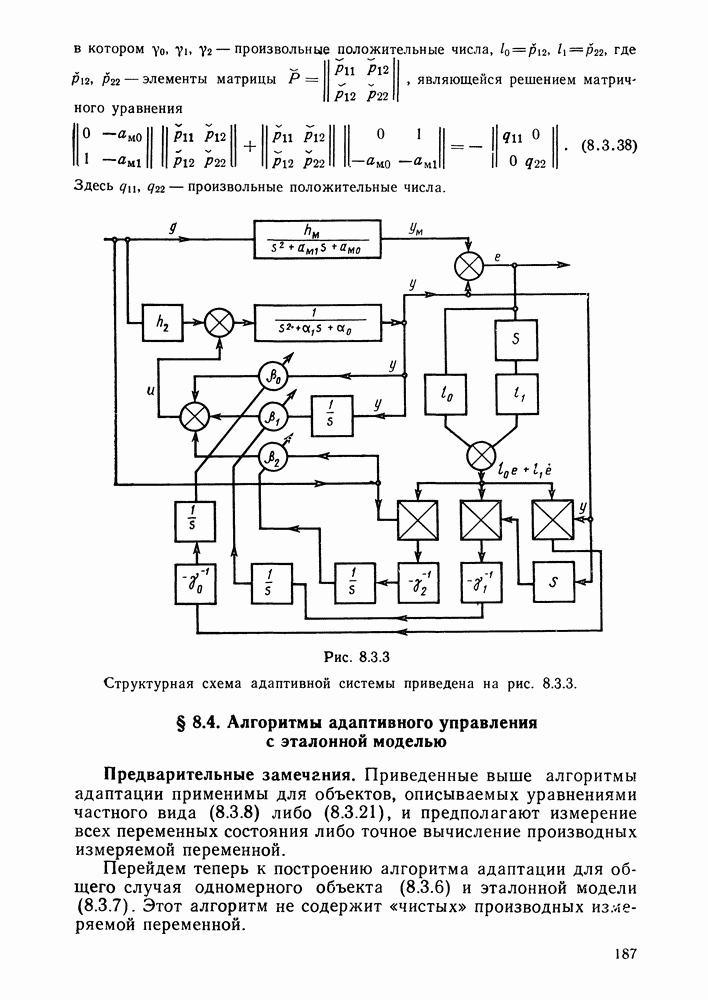
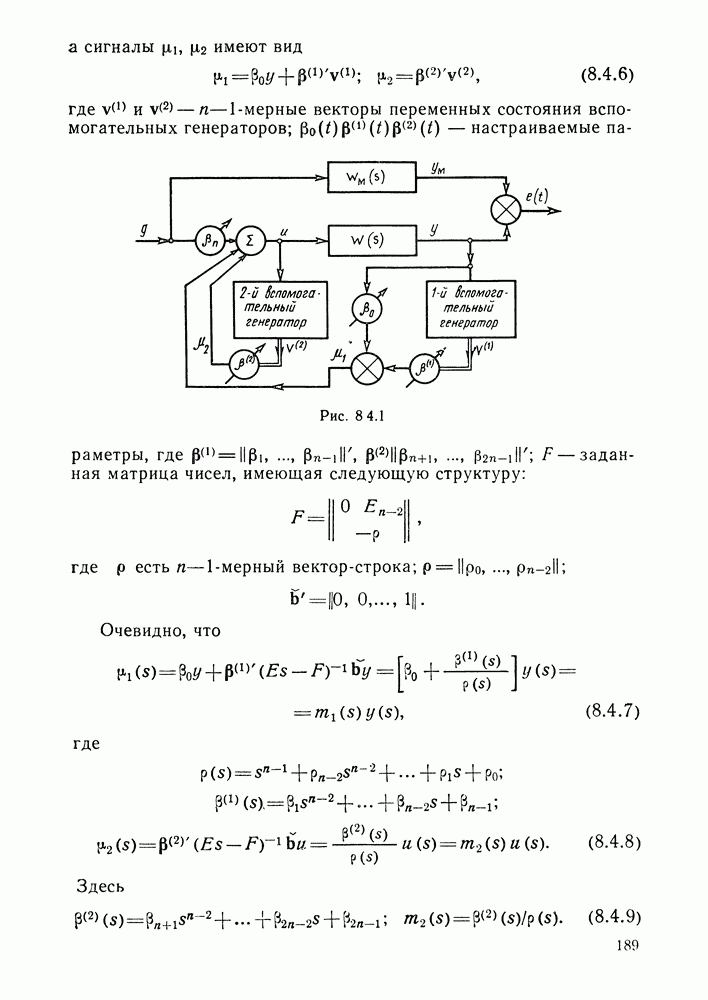
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
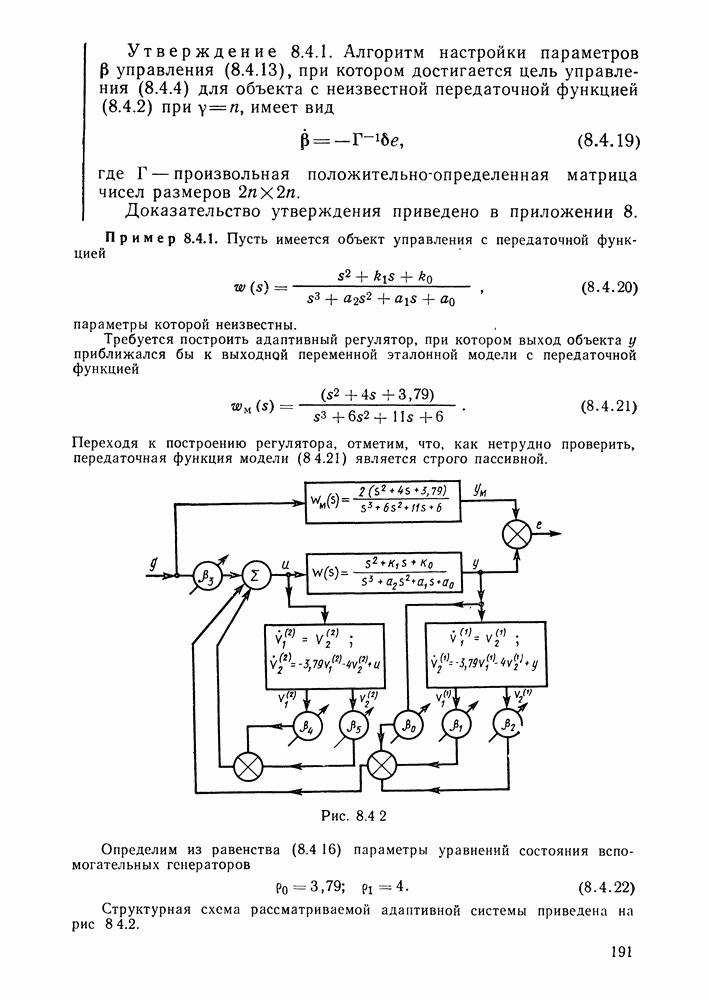
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
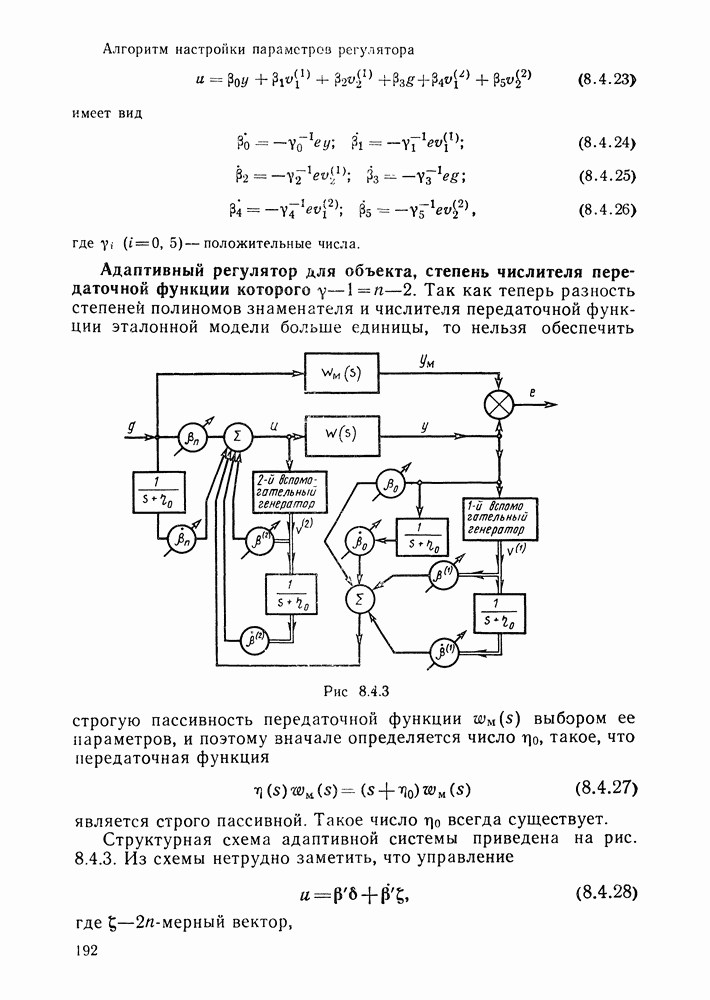
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
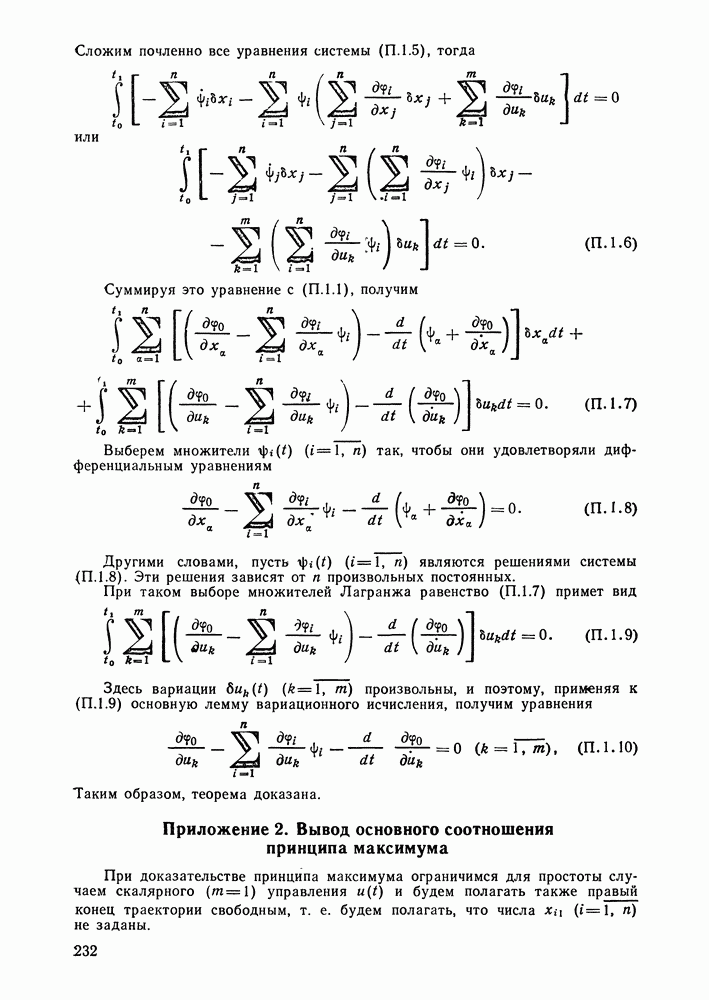
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ