| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
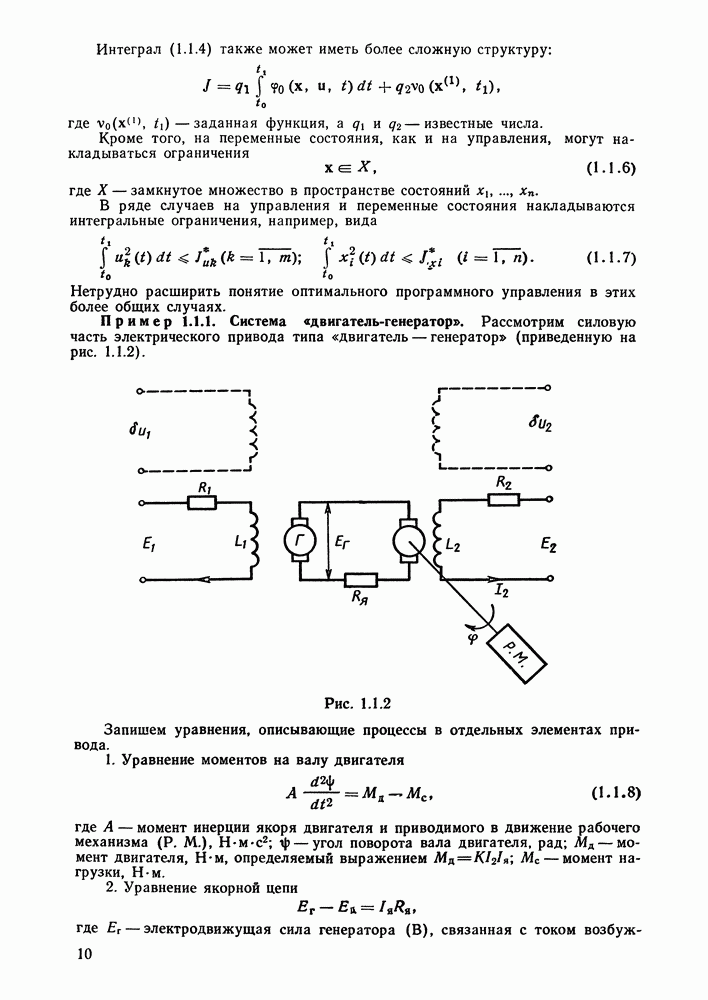
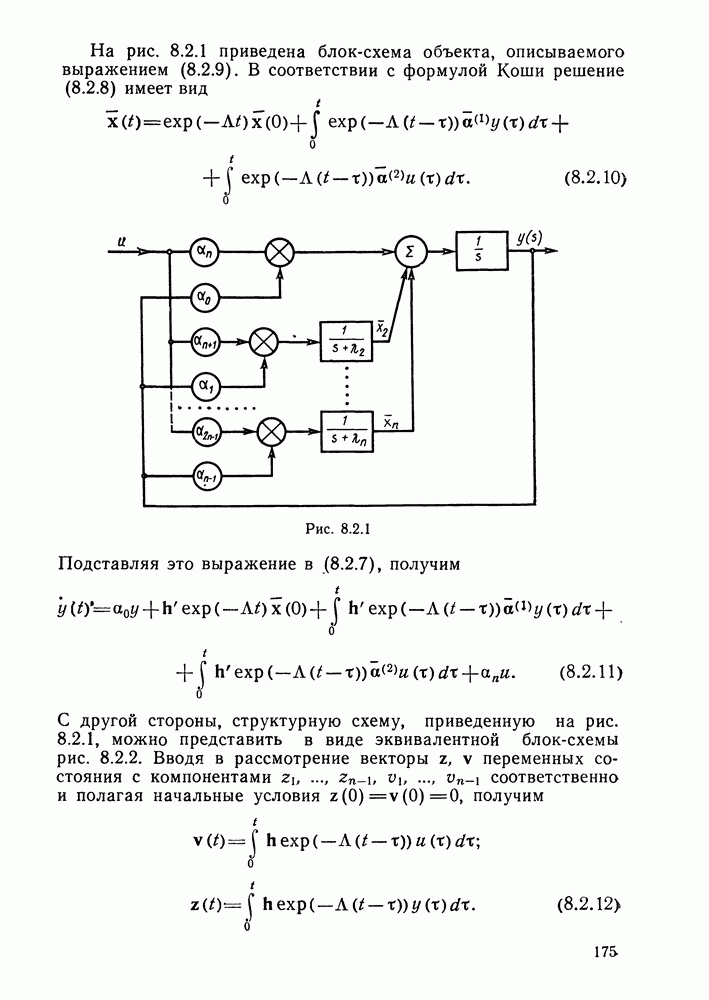
Границы частотных показателей качества оптимальных систем.
Исследуем частотные свойства системы (4.3.10), (4.3.11) со скалярным управлением оптимальной в смысле функционала (4.3.14). Для общности будем полагать, что в этом функционале часть коэффициентов  равна нулю. Однако требование полной управляемости пары
равна нулю. Однако требование полной управляемости пары  выполняется.
выполняется.
Оказывается, для частотных показателей качества (запаса устойчивости по фазе  , запаса устойчивости по модулю L и показателя колебательности М) оптимальных систем можно указать их границы, не зависящие от выбора коэффициентов функционала (4.3.14).
, запаса устойчивости по модулю L и показателя колебательности М) оптимальных систем можно указать их границы, не зависящие от выбора коэффициентов функционала (4.3.14).
Утверждение 4.3.1. Запасы устойчивости и показатель колебательности системы (4.3.10), (4.3.11) удовлетворяют неравенствам

Доказательство утверждения опирается на тождество (4.3.13). Учитывая, что

запишем на основе (4.3.13)

Равенству  соответствует в плоскости годографа амплитудно-фазовой характеристики (АФЧХ) окружность единичного радиуса с
соответствует в плоскости годографа амплитудно-фазовой характеристики (АФЧХ) окружность единичного радиуса с  в точке
в точке  .
.

Рис. 4.3.1.
Эта окружность показана на рис. 4.3.2. Неравенство (4.3.37) означает, что годограф АФЧХ оптимальной системы не пересекает зоны (это запретная зона на рис. 4.3.2 заштрихована), ограниченной окружностью единичного радиуса с центром в точке  .
.
Опираясь на такую геометрическую интерпретацию условия оптимальности в частотной форме (4.3.13) и неравенства (4.3.36), нетрудно доказать соотношения (4.3.35) для границ частотных показателей качества.
Действительно, пересечение запретной зоны с кругом единичного радиуса с центром в начале координат образует сегмент, в который вписываются два равносторонних треугольника  (сторонами этих треугольников являются радиусы пересекающихся окружностей), которые опираются на дугу, отмеченную на рисунке крестиками, а поэтому угол
(сторонами этих треугольников являются радиусы пересекающихся окружностей), которые опираются на дугу, отмеченную на рисунке крестиками, а поэтому угол  равен 120°. Это означает, что запас по фазе
равен 120°. Это означает, что запас по фазе  .
.
Переходя ко второму из неравенств (4.3.35), отметим, что отрезок вещественной оси  отмеченный на рисунке крестиками, находится внутри запретной зоны. Это означает, что запас устойчивости по модулю для оптимальных систем с АФЧХ второго рода не менее двух, а с АФЧХ первого рода — бесконечно велик. Последнее следует из того, что участок
отмеченный на рисунке крестиками, находится внутри запретной зоны. Это означает, что запас устойчивости по модулю для оптимальных систем с АФЧХ второго рода не менее двух, а с АФЧХ первого рода — бесконечно велик. Последнее следует из того, что участок  вещественной оси не может пересекаться АФЧХ оптимальной системы.
вещественной оси не может пересекаться АФЧХ оптимальной системы.
Граница показателя колебательности оптимальных систем находится следующим образом. На рис. 4.3.2 штрихпунктирной линией нанесена окружность радиуса  с центром в точке
с центром в точке  , где
, где  Эта окружность составляет геометрическое место точек, запретных для АФЧХ с показателем колебательности
Эта окружность составляет геометрическое место точек, запретных для АФЧХ с показателем колебательности  . Так как эта окружность находится внутри запретной зоны, касаясь границы этой зоны изнутри, то
. Так как эта окружность находится внутри запретной зоны, касаясь границы этой зоны изнутри, то  и, таким образом, утверждение доказано.
и, таким образом, утверждение доказано.

Рис 4.3.2.
Отметим, что доказательство опиралось на неравенство (4.3.37), которое не содержит коэффициентов функционала оптимизации. Правда, при этом требуется, чтобы  , так как в этом случае выполняется (4.3.36), поэтому границы (4.3.35) не зависят от выбора этих коэффициентов.
, так как в этом случае выполняется (4.3.36), поэтому границы (4.3.35) не зависят от выбора этих коэффициентов.
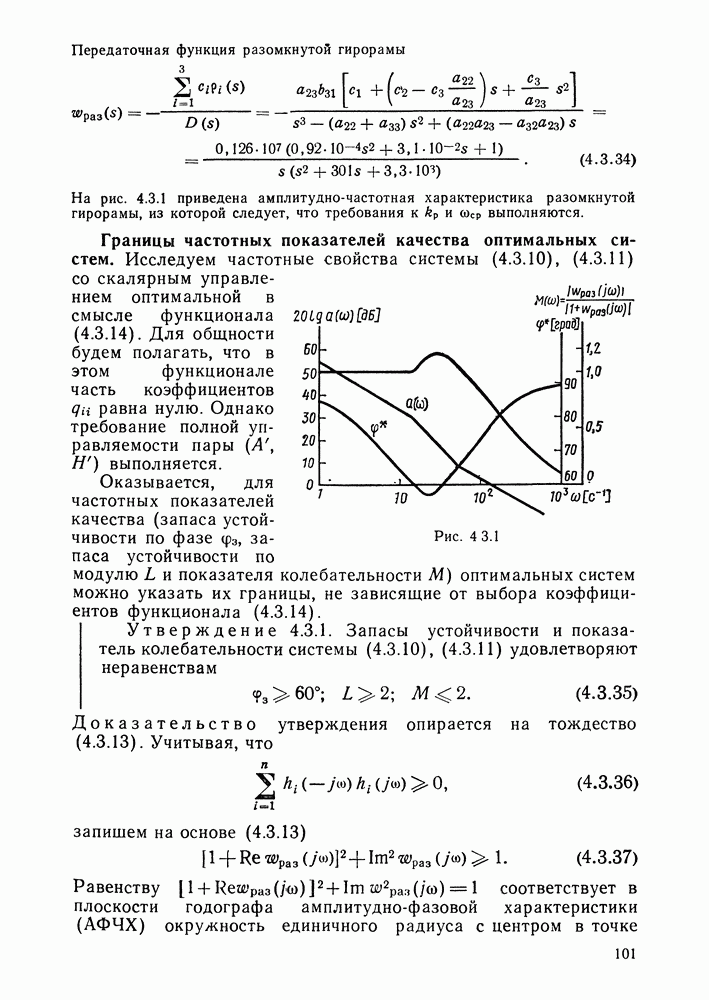
Пример 4.3.2. Определим запасы устойчивости и показатель колебательности гирорамы с законом управления, полученным в примере 4.3.1. Передаточная функция гирорамы в разомкнутом состоянии определяется выражением (4.3.34). На рис. 4.3.1 приведены логарифмическая амплитудно-частотная характеристика  и функция
и функция  (где
(где  - фазочастотная характеристика), соответствующие передаточной функции (4.3.34). Нетрудно видеть, что
- фазочастотная характеристика), соответствующие передаточной функции (4.3.34). Нетрудно видеть, что  . На этом же рисунке приведен график
. На этом же рисунке приведен график

из которого следует, что показатель колебательности

Отметим, что в более общем случае функционал (4.3.14) содержит произведения  и
и  :
:

в матричной форме он принимает вид

где  —
—  -мерный вектор.
-мерный вектор.
Условие неотрицательности подинтегральной квадратичной формы  переменного
переменного  . Вводя новые переменные
. Вводя новые переменные  нетрудно привести функционал (4.3.38) к форме (4.3.14) и использовать процедуру АКОР. Однако для частотных показателей качества систем, оптимальных в смысле функционала (4.3.38), уже нельзя указать границ (4.3.35). Более того, можно показать, что для любой (в том числе и сколь угодно «плохой» по частотным показателям) системы (4.3.10), (4.3.11) можно построить неотрицательный функционал вида (4.3.38), в смысле которого эта система является оптимальной.
нетрудно привести функционал (4.3.38) к форме (4.3.14) и использовать процедуру АКОР. Однако для частотных показателей качества систем, оптимальных в смысле функционала (4.3.38), уже нельзя указать границ (4.3.35). Более того, можно показать, что для любой (в том числе и сколь угодно «плохой» по частотным показателям) системы (4.3.10), (4.3.11) можно построить неотрицательный функционал вида (4.3.38), в смысле которого эта система является оптимальной.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
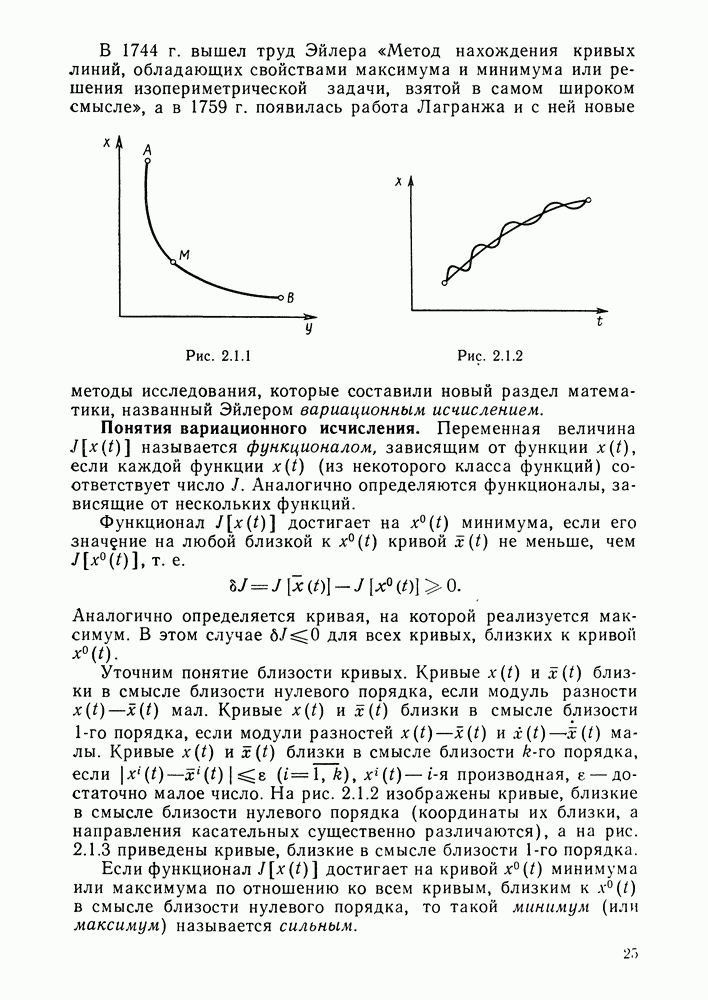
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
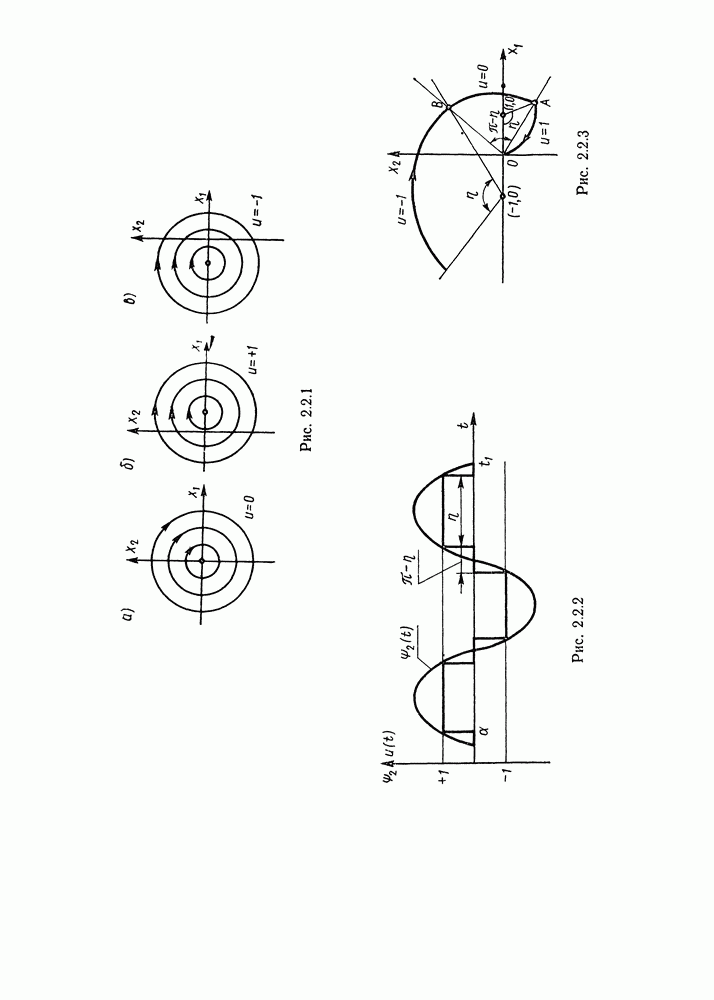
- § 2.2. Принцип максимума
- Принцип максимума.
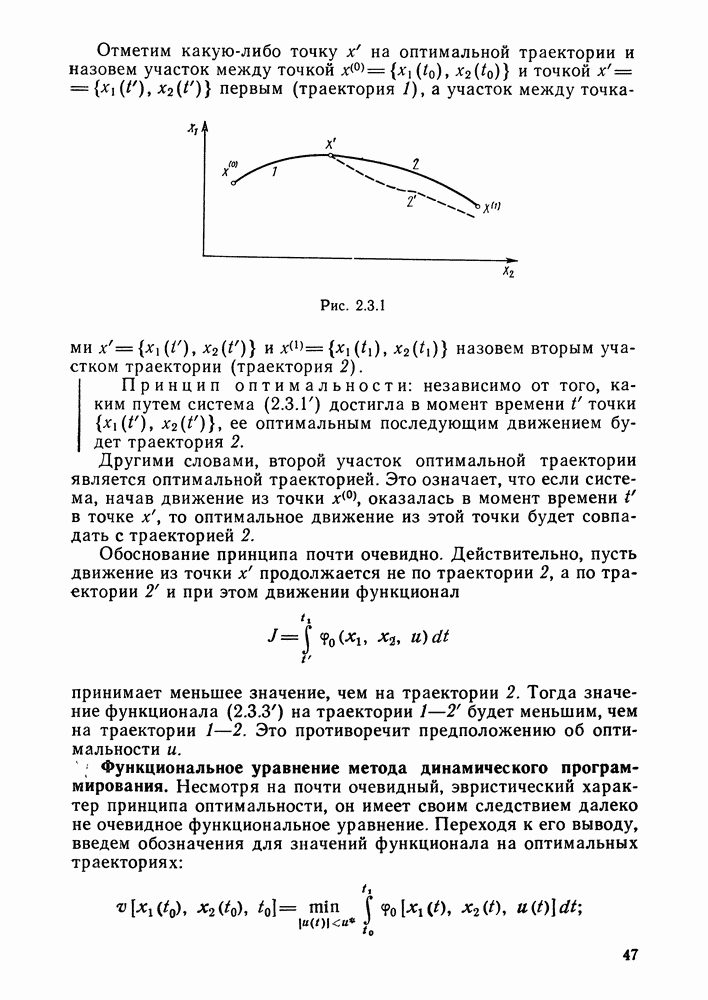
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
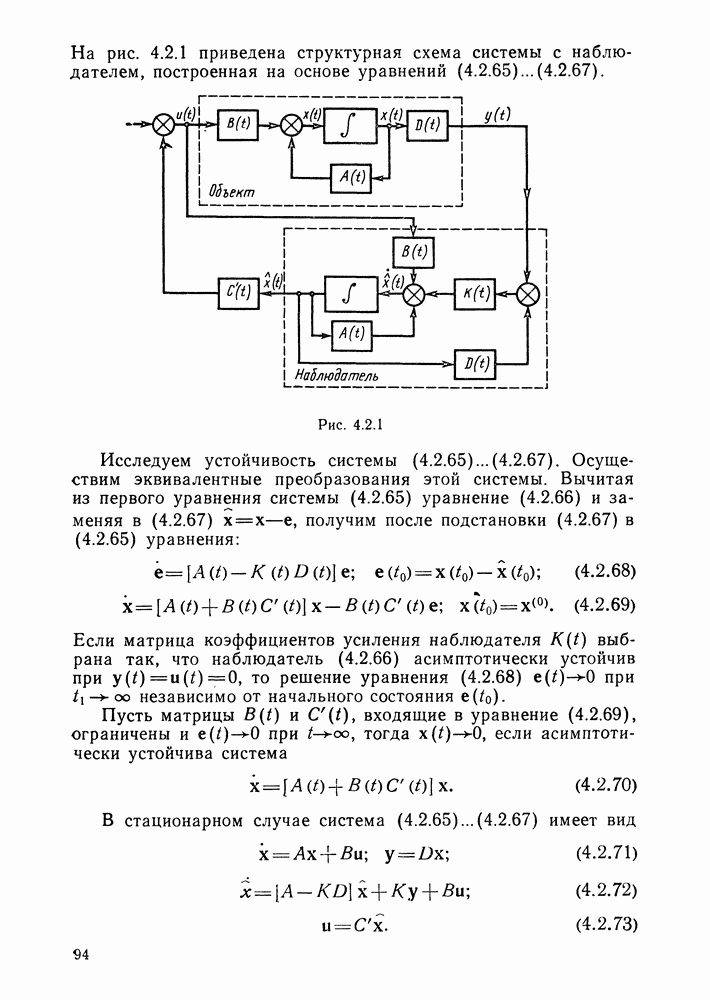
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
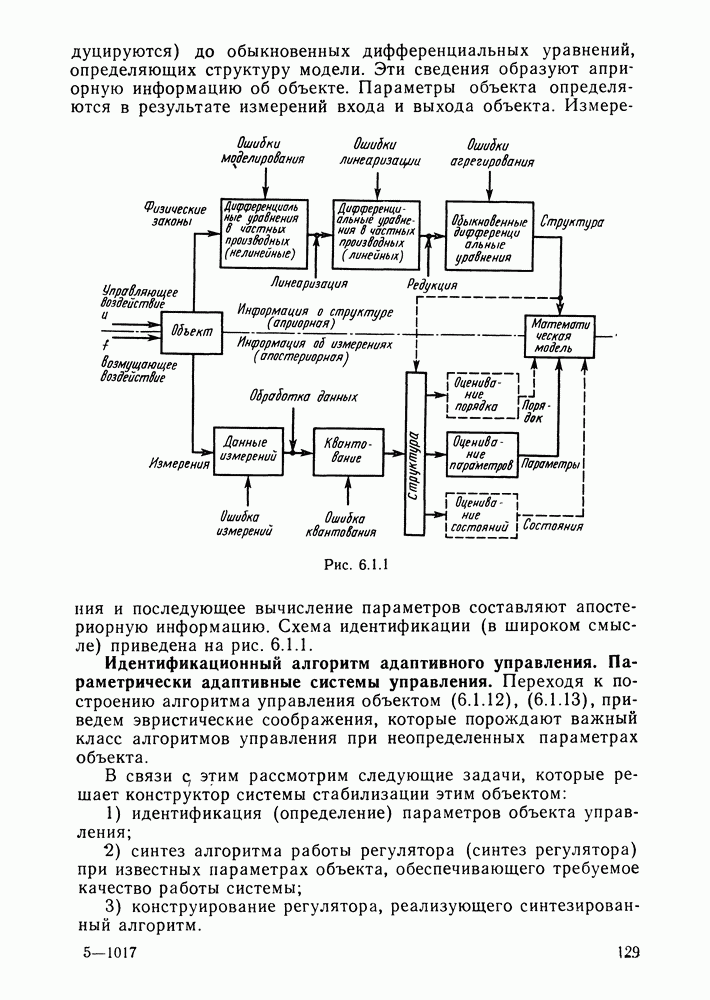
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
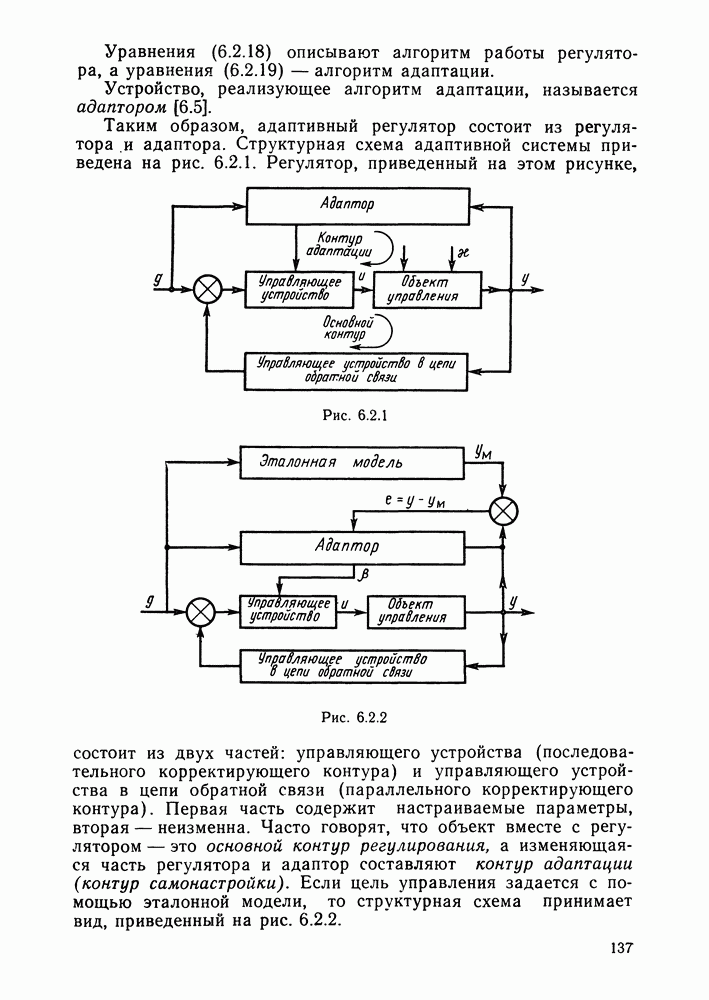
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
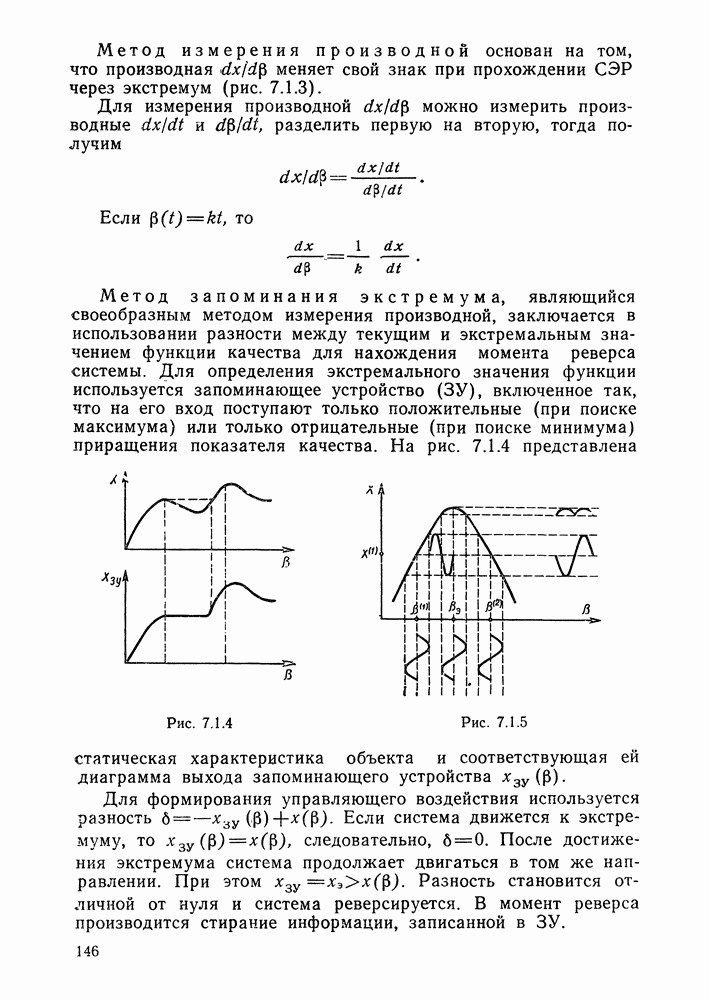
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
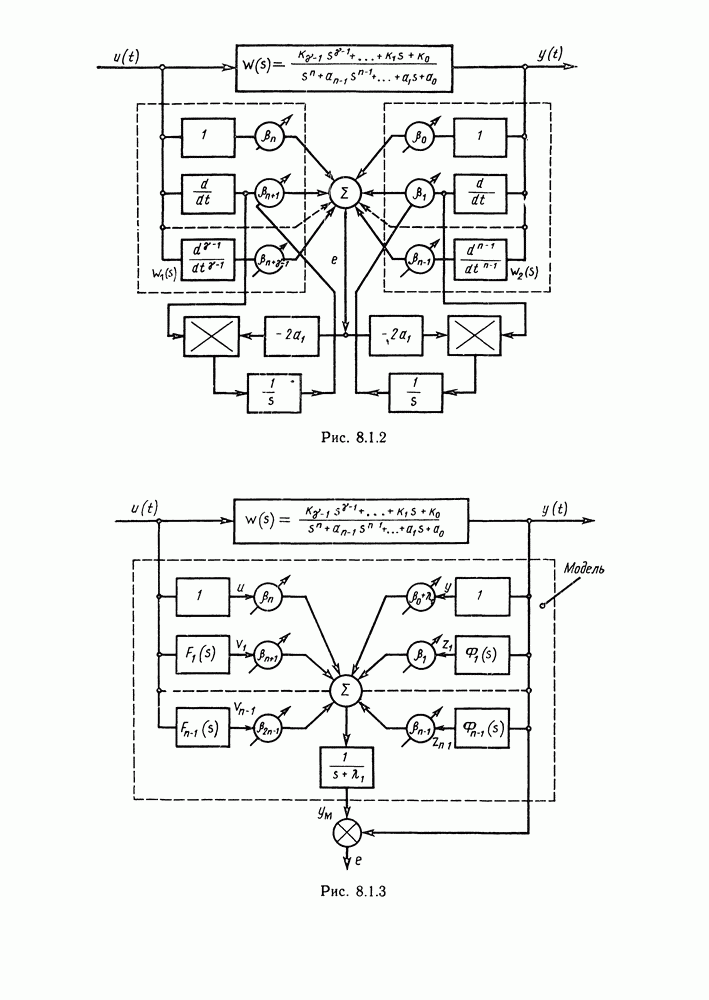
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
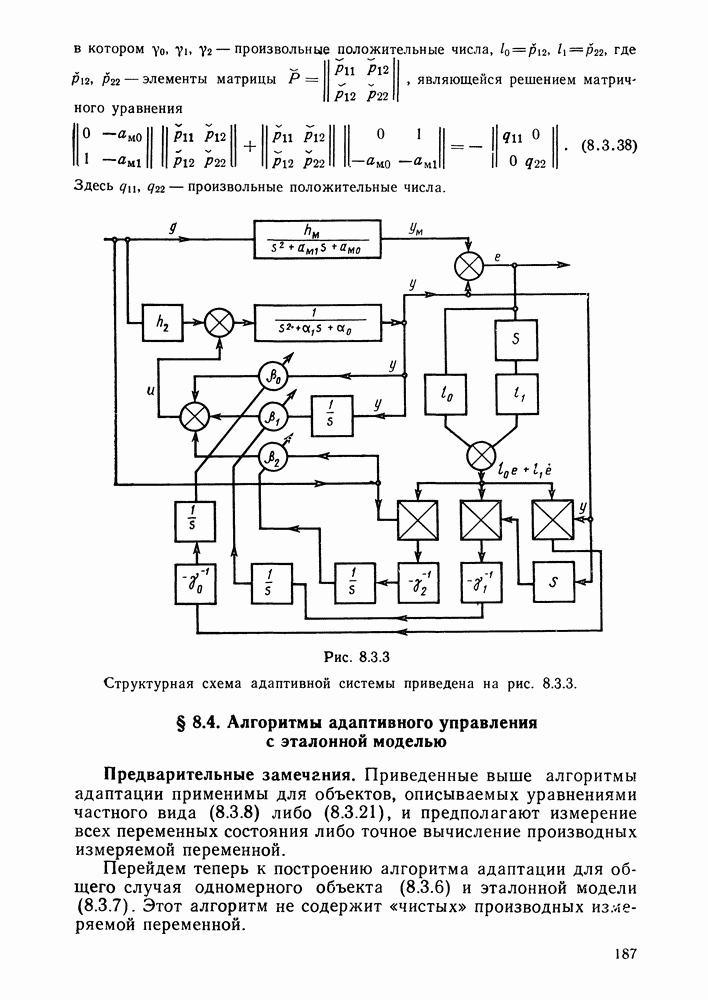
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
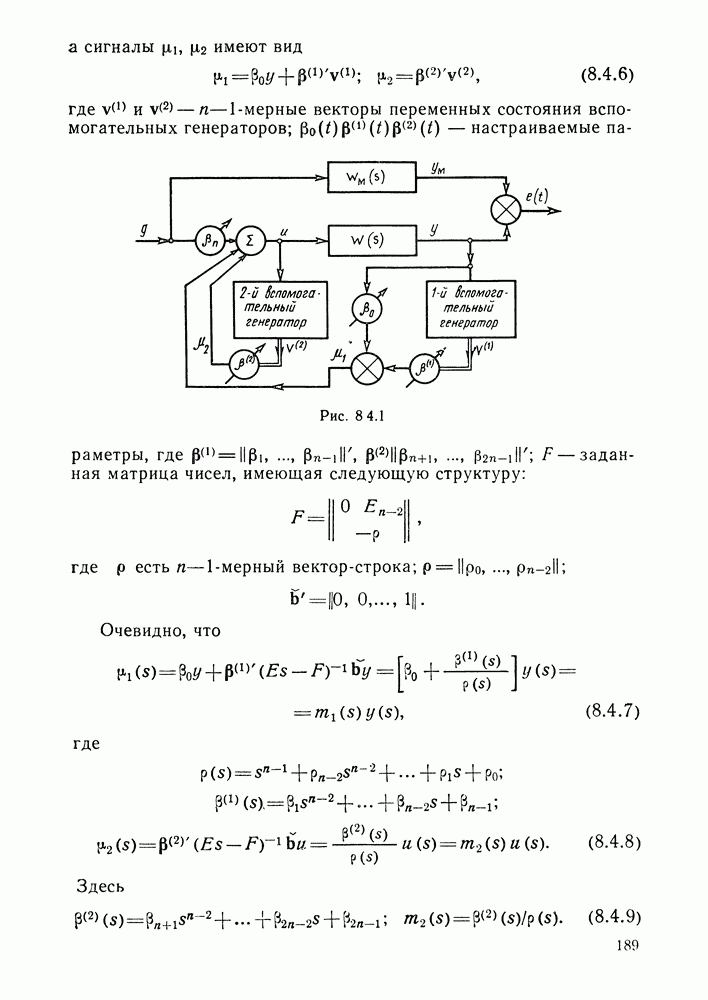
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
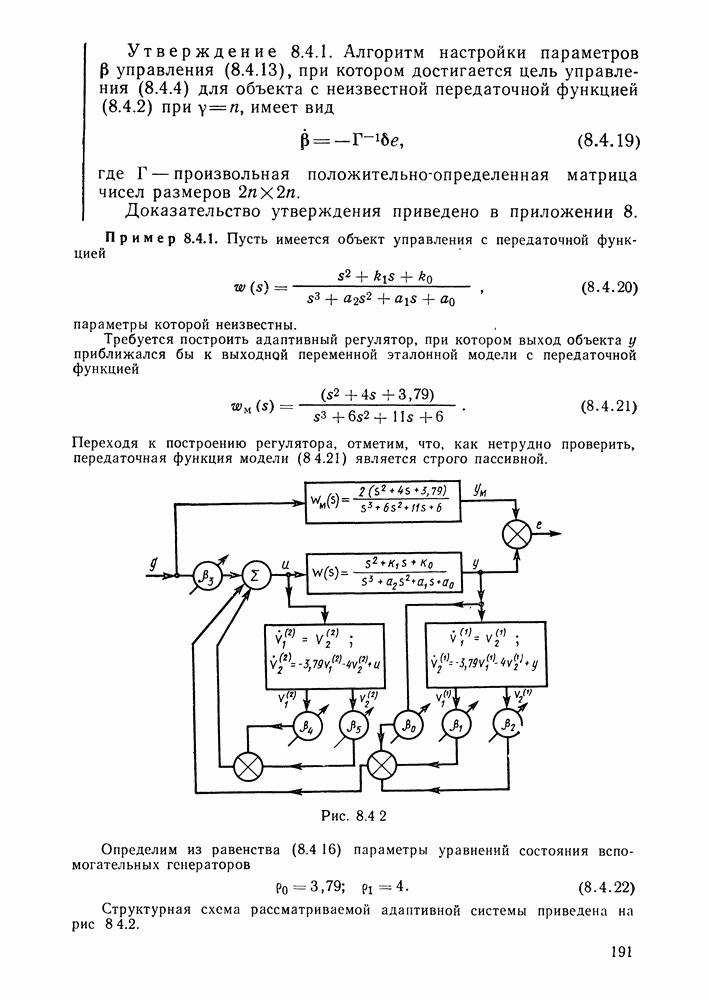
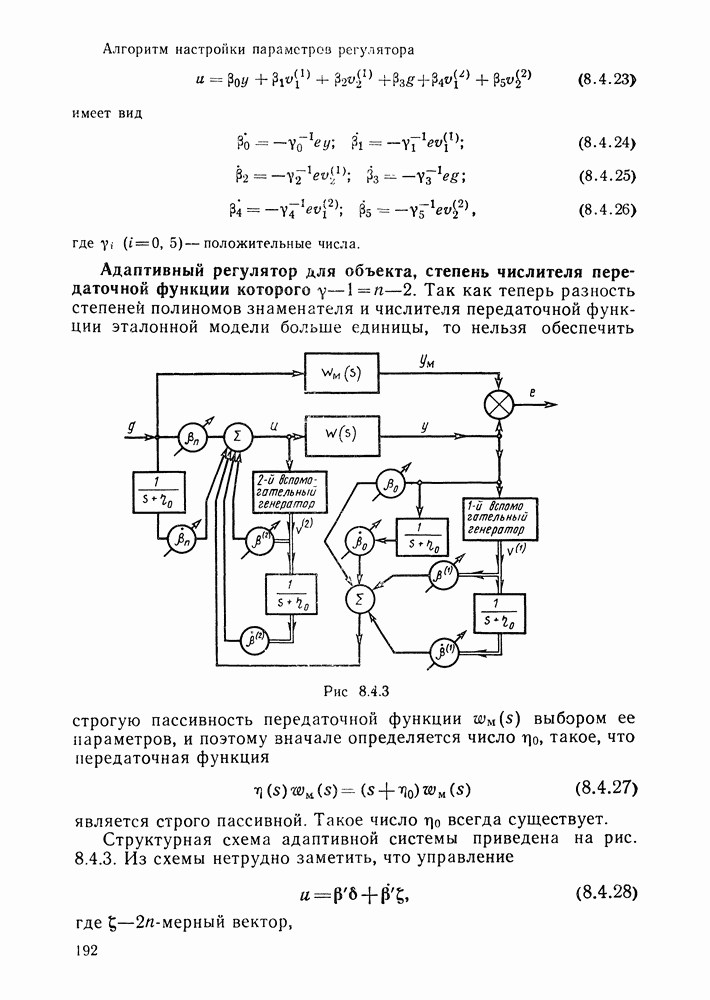
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ