| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Поисковые алгоритмы экстремального управления однопараметрическими объектами.
Откажемся теперь от первой операции (идентификации параметра а) рассматриваемого алгоритма экстремального управления. Тогда правая часть (7.2.6) содержит неопределенный параметр а. В связи с этим запишем приближенно выражение производной

где  — достаточно малое число, называемое величиной пробного шага.
— достаточно малое число, называемое величиной пробного шага.
При  выражение в правой части (7.2.10) совпадает с производной
выражение в правой части (7.2.10) совпадает с производной  .
.
Значения  доступны непосредственному измерению, и поэтому приближенное значение производной
доступны непосредственному измерению, и поэтому приближенное значение производной  может быть получено путем вычитания результатов измерений при двух значениях управляющего параметра (отстоящих друг от друга на величину
может быть получено путем вычитания результатов измерений при двух значениях управляющего параметра (отстоящих друг от друга на величину  ) и делении разности на число
) и делении разности на число  . Так как испытания объекта пробными шагами управляющего воздействия требуют определенного времени Т, то используется дискретный алгоритм адаптации вида (7.2.6), называемый далее дискретным алгоритмом поиска экстремума:
. Так как испытания объекта пробными шагами управляющего воздействия требуют определенного времени Т, то используется дискретный алгоритм адаптации вида (7.2.6), называемый далее дискретным алгоритмом поиска экстремума:
 (7.2.11)
(7.2.11)
Введем в рассмотрение число  , называемое параметром рабочего шага. Отметим, что часто этот термин будем использовать и для числа
, называемое параметром рабочего шага. Отметим, что часто этот термин будем использовать и для числа  . Таким образом, поисковый алгоритм экстремального управления состоит из операций: 1) в момент времени
. Таким образом, поисковый алгоритм экстремального управления состоит из операций: 1) в момент времени  к экстремальному объекту прикладываются пробные воздействия
к экстремальному объекту прикладываются пробные воздействия  ,
,  и измеряются значения выхода объекта; 2) на основе (7.2.11) формируется первый рабочий шаг
и измеряются значения выхода объекта; 2) на основе (7.2.11) формируется первый рабочий шаг  (
( ) к объекту прикладывается управляющее воздействие
) к объекту прикладывается управляющее воздействие  .
.
Затем вновь прикладываются пробные воздействия  , измеряется выход объекта и вычисляется значение управляющего параметра на втором шаге
, измеряется выход объекта и вычисляется значение управляющего параметра на втором шаге  и т. д. Отметим, что величина второго рабочего шага
и т. д. Отметим, что величина второго рабочего шага  .
.
Выбор параметра рабочего шага.
Алгоритм адаптации (7.2.11) содержит пока неопределенный параметр рабочего шага . Требования, которые предъявляются к его величине, противоречивы. С одной стороны, для увеличения скорости сходимости к экстремальному значению
. Требования, которые предъявляются к его величине, противоречивы. С одной стороны, для увеличения скорости сходимости к экстремальному значению  значения
значения  следует выбирать большими. Однако при этом можно «проскочить» экстремум на значительную величину, затем при возврате вновь происходит «проскок» экстремума и в системе возникают колебания большой амплитуды. Выходом из этого противоречия является выбор больших значений
следует выбирать большими. Однако при этом можно «проскочить» экстремум на значительную величину, затем при возврате вновь происходит «проскок» экстремума и в системе возникают колебания большой амплитуды. Выходом из этого противоречия является выбор больших значений  в начале поиска экстремума и назначение малых
в начале поиска экстремума и назначение малых  при приближении к экстремуму. Но так как значение
при приближении к экстремуму. Но так как значение  неизвестно, то выбор оптимальных значений
неизвестно, то выбор оптимальных значений  можно производить адаптивно. Для этого достаточно увеличивать
можно производить адаптивно. Для этого достаточно увеличивать  при совпадении знаков двух последовательных рабочих шагов поиска и уменьшать в противном случае. Примером алгоритма адаптации величины рабочего шага может служить алгоритм
при совпадении знаков двух последовательных рабочих шагов поиска и уменьшать в противном случае. Примером алгоритма адаптации величины рабочего шага может служить алгоритм
 (7.2.12)
(7.2.12)
в котором  — значения
— значения  рабочих шагов алгоритма (7.2.11) экстремального управления; v — некоторое положительное число, выбираемое из условия устойчивости процесса (7.2.11), (7.2.12).
рабочих шагов алгоритма (7.2.11) экстремального управления; v — некоторое положительное число, выбираемое из условия устойчивости процесса (7.2.11), (7.2.12).
Исследуем сходимость решения (7.2.11) к числу  . Будем полагать, что пробный шаг Др достаточно мал, так что величина
. Будем полагать, что пробный шаг Др достаточно мал, так что величина
 (7.2.13)
(7.2.13)
вычисляется точно. Тогда (7.2.11) примет вид
 (7.2.14)
(7.2.14)
Наложим на функцию  некоторые ограничения. Потребуем, чтобы эта функция удовлетворяла неравенству
некоторые ограничения. Потребуем, чтобы эта функция удовлетворяла неравенству
 (7.2.15)
(7.2.15)
где  — неизвестные положительные постоянные числа.
— неизвестные положительные постоянные числа.
Для пояснения геометрического смысла этого неравенства рассмотрим графики, приведенные на рис. 7.2.1. На этом рисунке приведены типичные зависимости  при различных значениях параметра
при различных значениях параметра  .
.

Рис 7.2.1.
Пунктиром показана граничная линия, описываемая правой частью (7.2.15), где для простоты далее полагаем  . Определим эффективность
. Определим эффективность  шага числом
шага числом
 (7.2.16)
(7.2.16)
модуль которого характеризует скорость приближения к экстремуму при  рабочем шаге. Действительно, если
рабочем шаге. Действительно, если  , то произошло удаление от
, то произошло удаление от  , а если
, а если  , то приближение к экстремуму. Найдем условия, при которых
, то приближение к экстремуму. Найдем условия, при которых
 (7.2.17)
(7.2.17)
Подставляя в (7.2.17) выражение (7.2.14), получим

Отсюда получаем условие сходимости

или
 (7.2.19)
(7.2.19)
Непосредственно из рис. 7.2.1 следует, что  , и поэтому
, и поэтому  .
.
На основе (7.2.15) получим  , и, таким образом, условие сходимости процесса поиска экстремума
, и, таким образом, условие сходимости процесса поиска экстремума
 (7.2.20)
(7.2.20)
Если величина s известна, то выбор
 (7.2.21)
(7.2.21)
обеспечивает устойчивость процесса поиска экстремума.
Пример 7.2.3. Найдем условия сходимости процесса поиска экстремума объекта (7.2 3). Дискретный алгоритм поиска (7.2.11) имеет в рассматриваемом случае вид
 (7.2.22)
(7.2.22)
где

определяется для каждого рабочего шага по результатам пробных шагов, так как а — неизвестное число. Для выбора параметра  рабочего шага определим
рабочего шага определим  . График функции
. График функции  является прямой линией, совпадающей с граничной.
является прямой линией, совпадающей с граничной.
Действительно, представим  , тогда
, тогда
 (7.2.23)
(7.2.23)
и, таким образом,  .
.
Используя это значение  , определим в формуле (7.2.21) постоянное значение рабочего шага
, определим в формуле (7.2.21) постоянное значение рабочего шага
 (7.2.24)
(7.2.24)
при котором процесс поиска экстремума устойчив.
Отметим, что значение параметра рабочего шага можно получить непосредственно, исследуя устойчивость линейного разностного уравнения (7.2 22). Действительно, его можно записать как

Решение этого уравнения сходится к значению  , если
, если

Отсюда следует
 (7.2.26)
(7.2.26)
Если величина s неизвестна, то значения  изменяются на каждом рабочем шаге, причем с ростом к значения должны монотонно уменьшаться до нуля:
изменяются на каждом рабочем шаге, причем с ростом к значения должны монотонно уменьшаться до нуля:
 (7.2.27)
(7.2.27)
Тогда для любого конечного s всегда существует шаг  , после которого выполняется условие сходимости (7.2.20). Однако при монотонно уменьшающихся
, после которого выполняется условие сходимости (7.2.20). Однако при монотонно уменьшающихся  может случиться так, что рабочие шаги (которые с ростом k становятся все меньше и меньше) не смогут покрыть исходное расстояние
может случиться так, что рабочие шаги (которые с ростом k становятся все меньше и меньше) не смогут покрыть исходное расстояние  , которое неизвестно и может быть очень большим. Тогда процесс поиска прекратится, не достигнув
, которое неизвестно и может быть очень большим. Тогда процесс поиска прекратится, не достигнув  . Это накладывает ограничения на выбор
. Это накладывает ограничения на выбор  , которые выражаются условием
, которые выражаются условием
 (7.2.28)
(7.2.28)
Убедимся в достаточности этого условия. Будем полагать, что процесс поиска экстремума протекает без перерегулирования. Путь  , проходимый за N шагов поиска, определяется по формуле
, проходимый за N шагов поиска, определяется по формуле
 (7.2.29)
(7.2.29)
где

Так как должно выполняться неравенство
 (7.2.30)
(7.2.30)
где  велико, то (7.2.28) является достаточным для его выполнения.
велико, то (7.2.28) является достаточным для его выполнения.
Примером последовательности чисел  , удовлетворяющих условиям (7.2.27), (7.2.28), может служить гармонический ряд
, удовлетворяющих условиям (7.2.27), (7.2.28), может служить гармонический ряд  которого равна бесконечности.
которого равна бесконечности.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
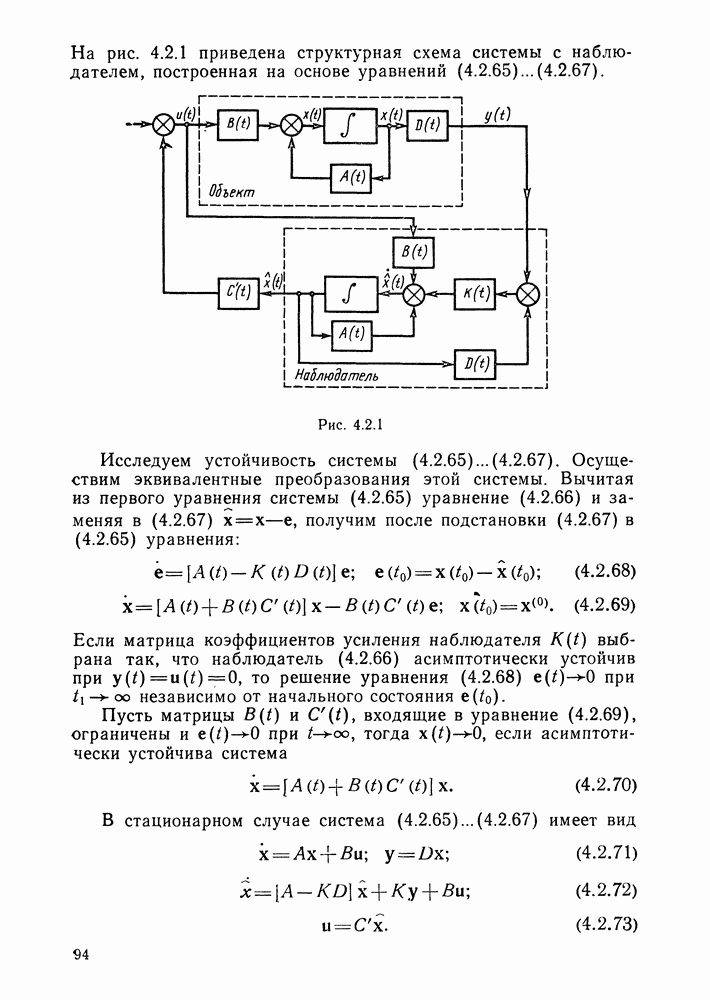
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
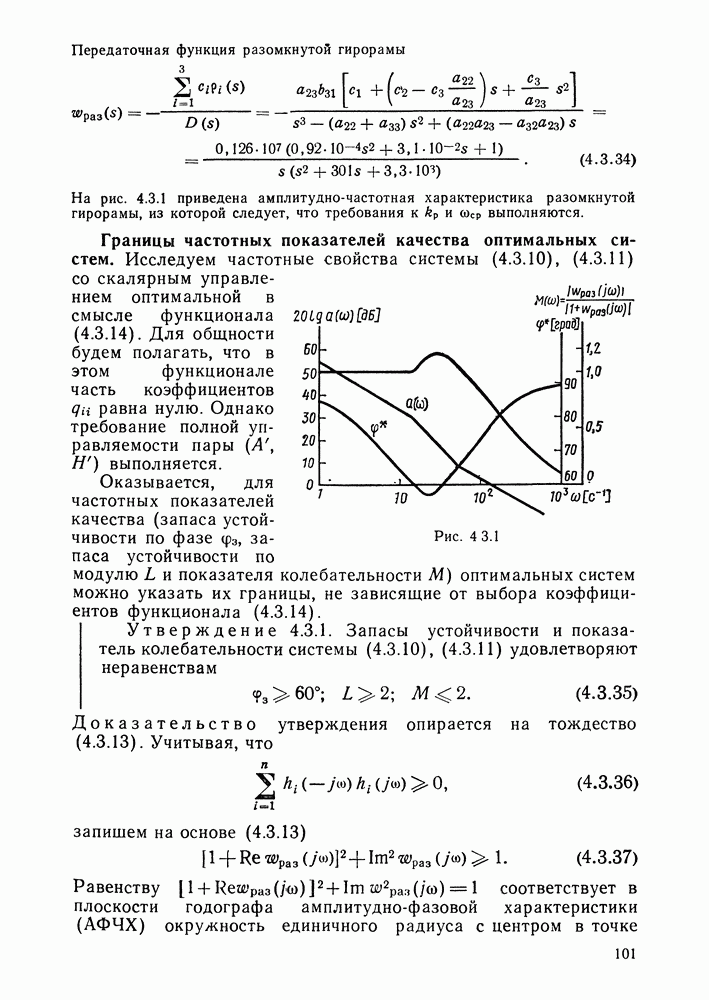
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
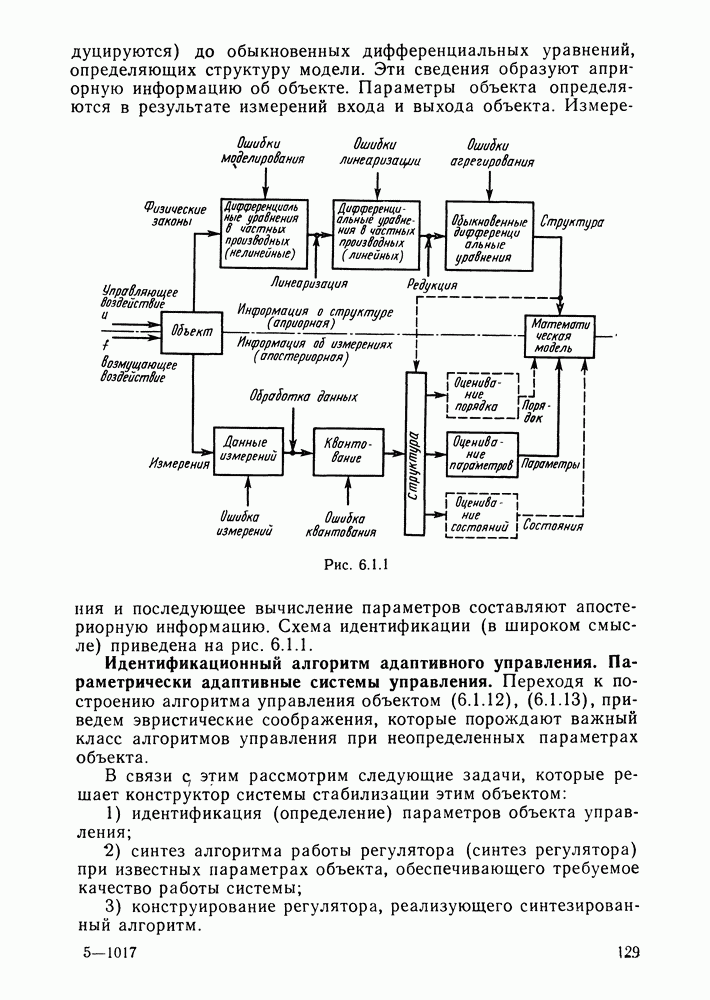
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
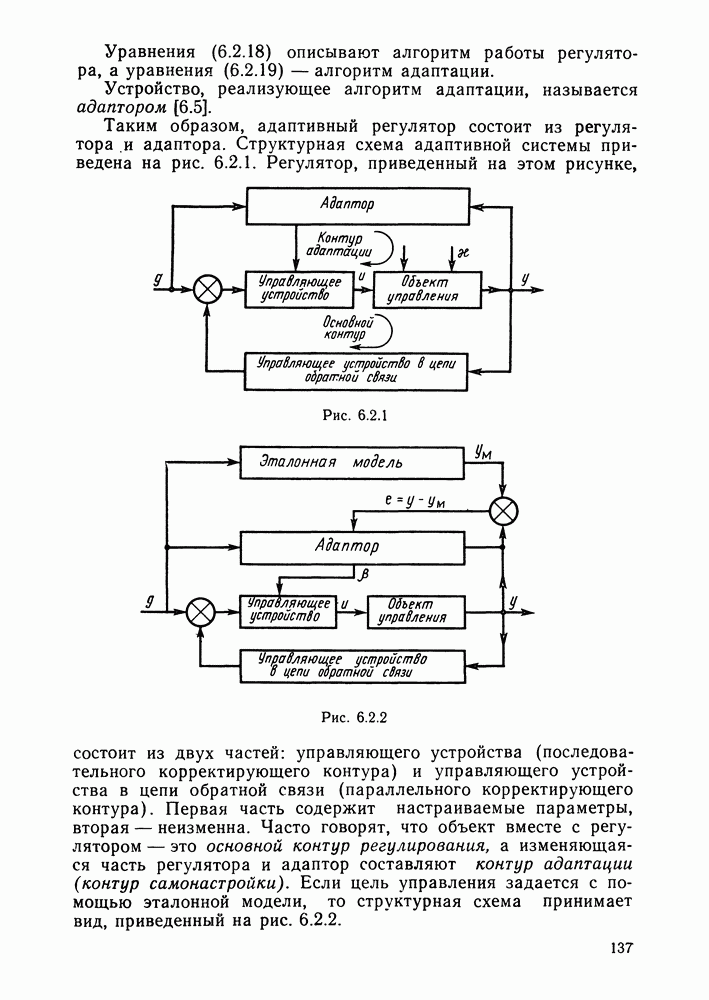
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
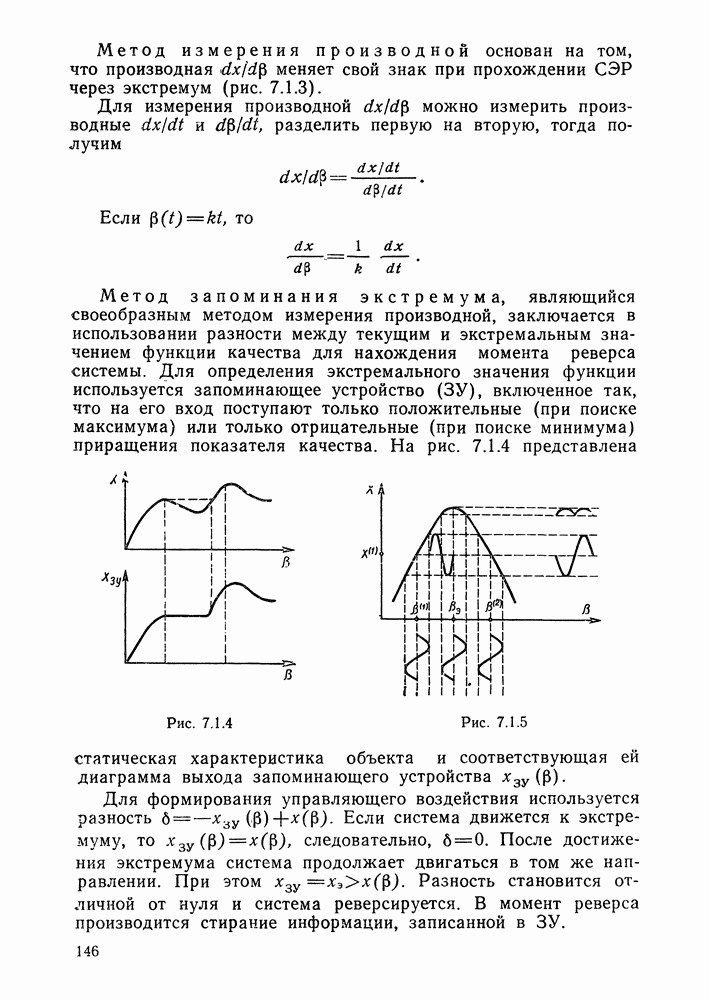
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
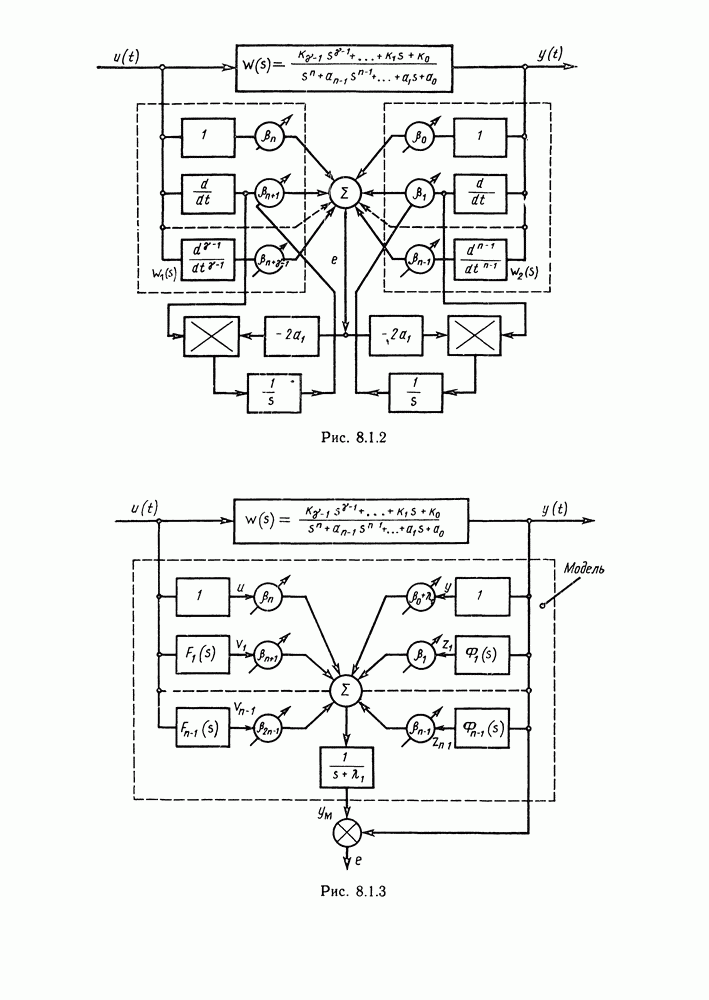
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
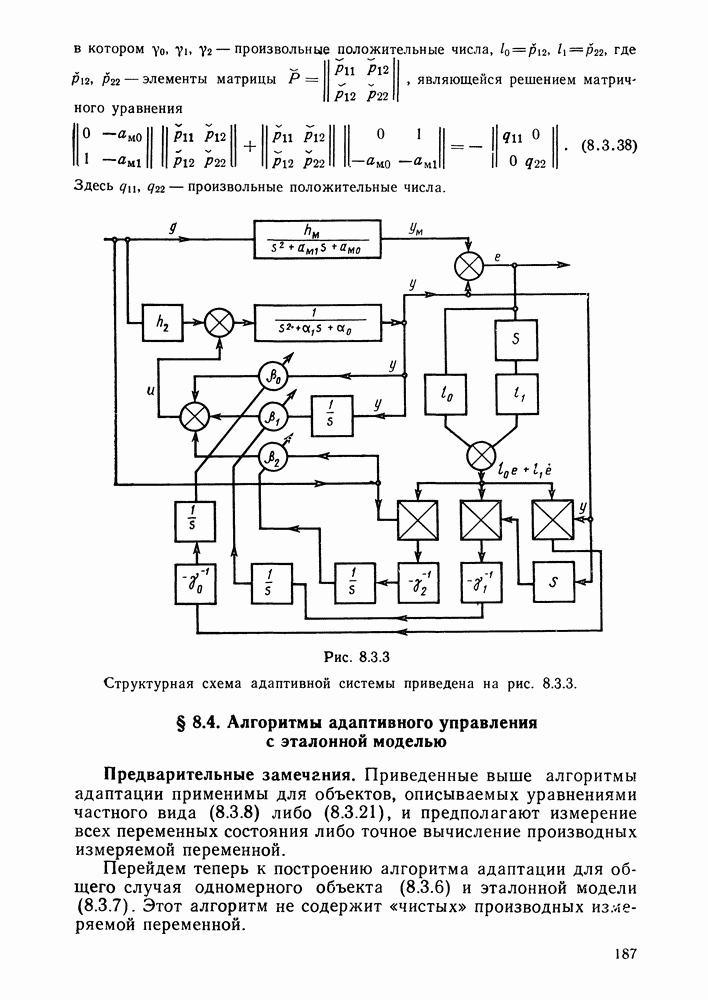
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
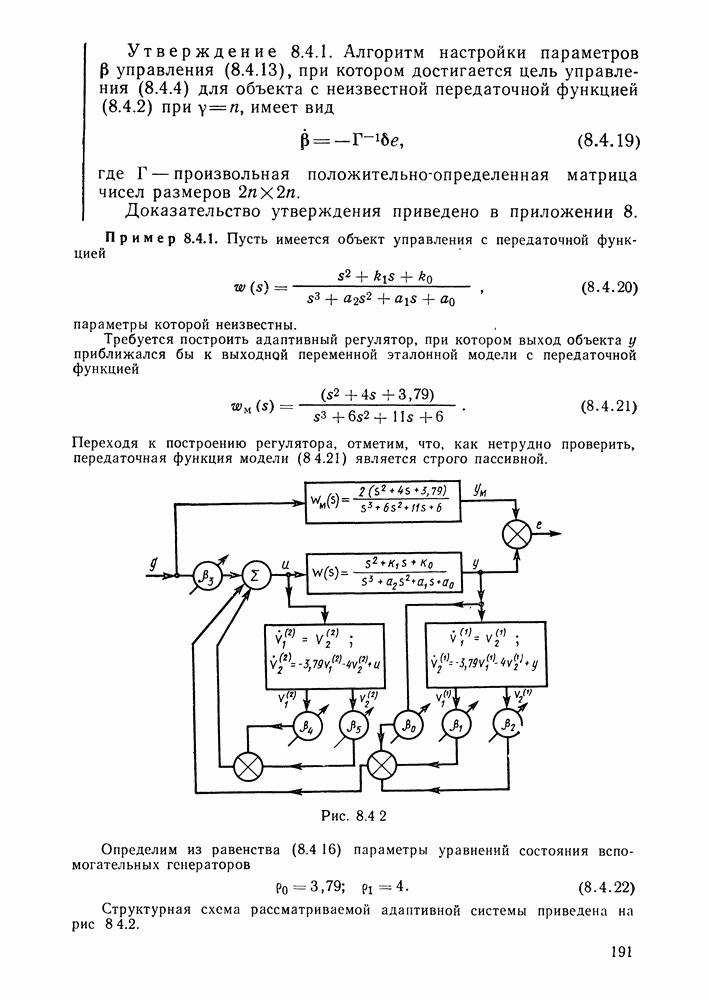
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
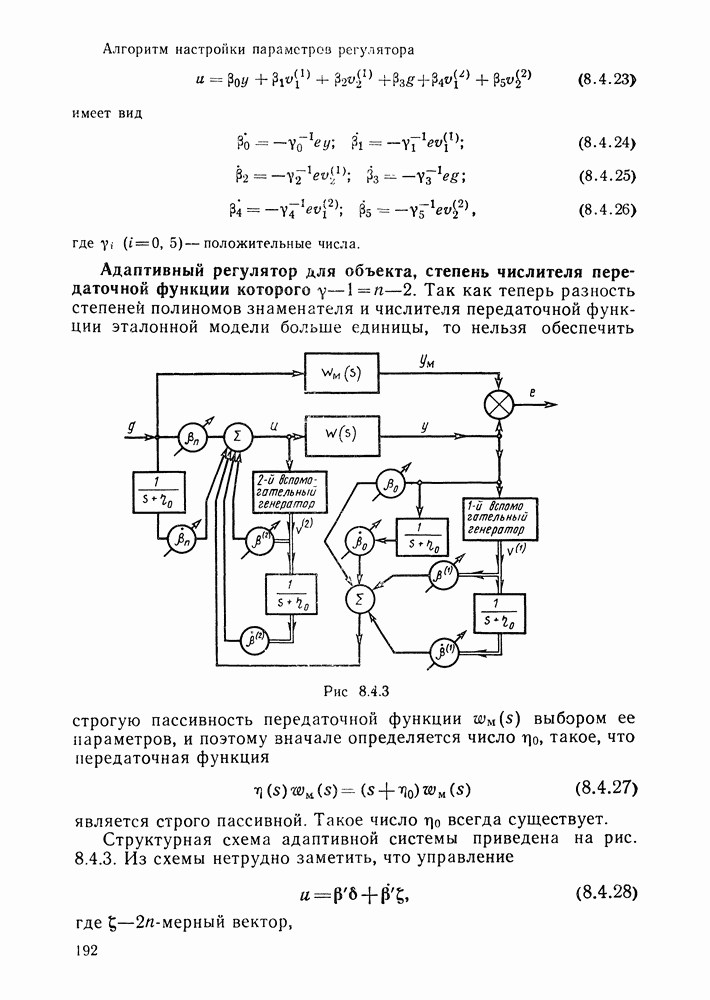
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ