| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Понятие об оптимальном стабилизирующем управлении.
Решения уравнения (1.2.4) при начальных условиях из множества (1.2.2) описывают отклонения реального движения от программного в каждый момент времени.
Для количественной характеристики этих отклонений часто используют значение интеграла

в котором  -положительные числа. Интеграл (1.2.6) представляет собой взвешенную с помощью коэффициентов
-положительные числа. Интеграл (1.2.6) представляет собой взвешенную с помощью коэффициентов  сумму площадей, ограниченных квадратом отклонений истинного движения от программного по каждой переменной состояния. Он характеризует «расстояние» реального движения и программного и является «мерой» близости этих движений.
сумму площадей, ограниченных квадратом отклонений истинного движения от программного по каждой переменной состояния. Он характеризует «расстояние» реального движения и программного и является «мерой» близости этих движений.
Используем  для сближения этих движений, тогда
для сближения этих движений, тогда  называются стабилизирующими управлениями. Таким образом, результирующие управления
называются стабилизирующими управлениями. Таким образом, результирующие управления  состоят из программных и стабилизирующих управлений. Подставляя это выражение в (1.1.5), получим ограничения на стабилизирующее управление:
состоят из программных и стабилизирующих управлений. Подставляя это выражение в (1.1.5), получим ограничения на стабилизирующее управление:

Обычно  . Это объясняется тем, что программное управление обеспечивает основное (программное) движение системы, а стабилизирующее управление лишь «парирует» малые отклонения от программного движения, обеспечивая, если
. Это объясняется тем, что программное управление обеспечивает основное (программное) движение системы, а стабилизирующее управление лишь «парирует» малые отклонения от программного движения, обеспечивая, если  , устойчивость (отсюда термин «стабилизирующее управление») и требуемую точность осуществления программного движения. В связи с этим часто вместо ограничений (1.2.7), определяющих допустимый «расход» стабилизирующего управления в каждый момент времени, накладывают на стабилизирующие управления интегральные ограничения (ограничения на «энергию»)
, устойчивость (отсюда термин «стабилизирующее управление») и требуемую точность осуществления программного движения. В связи с этим часто вместо ограничений (1.2.7), определяющих допустимый «расход» стабилизирующего управления в каждый момент времени, накладывают на стабилизирующие управления интегральные ограничения (ограничения на «энергию»)

Для учета ограничений (1.2.8) будем вместо (1.2.6) рассматривать критерии качества стабилизации

где числа  определяются значениями
определяются значениями  .
.
Стабилизирующее управление предназначено для минимизации интеграла (1.2.9). Кроме того, если  , то для существования этого интеграла стабилизирующее управление должно обеспечивать асимптотическую устойчивость нулевого решения системы (1.2.4).
, то для существования этого интеграла стабилизирующее управление должно обеспечивать асимптотическую устойчивость нулевого решения системы (1.2.4).
Если отыскивать стабилизирующее управление как явную функцию времени (по аналогии с программным управлением), то для каждого начального условия из множества (1.2.2) получим управления  для реализации которых необходимо измерять переменные состояния в момент времени
для реализации которых необходимо измерять переменные состояния в момент времени  , так как числа
, так как числа  неизвестны. Кроме того, функции
неизвестны. Кроме того, функции  будут различными для каждого набора
будут различными для каждого набора  из множества (1.2.2).
из множества (1.2.2).
В связи с этим естественно отыскивать стабилизирующее управление не как явную функцию времени, а как функцию переменных состояния

Заметим, что вид этих функций не зависит от начальных условий из множества (1.2.2). Поясним это обстоятельство подробнее.
Допустим, что найдено управление  при котором (1.2.9) принимает наименьшее значение на движениях системы (1.2.4), и пусть в начале движения оптимальной системы реализовались начальные условия
при котором (1.2.9) принимает наименьшее значение на движениях системы (1.2.4), и пусть в начале движения оптимальной системы реализовались начальные условия  . Подставляя в
. Подставляя в  решим это уравнение и, подставляя его решения в (1.2.9), вычислим значение интеграла. Получим число
решим это уравнение и, подставляя его решения в (1.2.9), вычислим значение интеграла. Получим число  . Оно является наименьшим из всех значений интеграла (1.2.9) при
. Оно является наименьшим из всех значений интеграла (1.2.9) при  . Допустим теперь, что в начале движения системы (1.2.4) реализовались начальные условия
. Допустим теперь, что в начале движения системы (1.2.4) реализовались начальные условия  тогда при
тогда при  получим другое значение (1.2.9), определяемое как
получим другое значение (1.2.9), определяемое как  . Это число опять должно быть наименьшим по сравнению со значениями интеграла на траекториях системы (1.2.4) при
. Это число опять должно быть наименьшим по сравнению со значениями интеграла на траекториях системы (1.2.4) при  и начальных условиях
и начальных условиях  .
.
Теперь можно определить понятие оптимального стабилизирующего управления как функции переменных состояния и времени, при которых на движениях системы (1.2.4), возбужденных произвольными начальными отклонениями из множества (1.2.2), показатель качества, например (1.2.9), принимает наименьшее  . Если в (1.2.9) верхний предел
. Если в (1.2.9) верхний предел  не ограничен, то стабилизирующее управление должно также обеспечивать асимптотическую устойчивость системы.
не ограничен, то стабилизирующее управление должно также обеспечивать асимптотическую устойчивость системы.
Примечание 121 Стабилизирующее управление реализуется регулятором, который является сложным динамическим устройством, состоящим обычно из трех компонент измерительных органов, устройства реализации алгоритма управления (корректирующих контуров), исполнительных органов.
Здесь и далее известные дифференциальные уравнения, описывающие измерительные и исполнительные органы, включаются в уравнения (1.2 4) Другими словами, уравнения ( - это уравнения физического объекта вместе с измерительными и исполнительными устройствами регулятора.
- это уравнения физического объекта вместе с измерительными и исполнительными устройствами регулятора.
Тогда  - выходы, измерительных устройств, а
- выходы, измерительных устройств, а  - входы исполнительных органов.
- входы исполнительных органов.
Уравнения (1.2.10) описывают устройство реализации алгоритмов управления.
Для упрощения терминологии будем по-прежнему называть уравнениями объекта уравнения (1.2.4) известной (неизменяемой) части системы, состоящей из объекта и элементов регулятора, а уравнениями регулятора - (1.2.10) - называть неизвестную (подлежащую определению) часть системы, состоящую лишь из устройства реализации алгоритма управления.
Пример 1.2.1. Оптимальное стабилизирующее управление в системе «генератор — двигатель». Пусть в системе «генератор — двигатель» найдено оптимальное программное управление  . Эти функции порождают программное движение
. Эти функции порождают программное движение  , которое находится путем численного интегрирования уравнений (1.1.18), (1.1 19) на ЭВМ, используя какой-либо из методов численного интегрирования (например, метод Рунге — Кутта). При эгом в (1.1.18),(1,1,19)
, которое находится путем численного интегрирования уравнений (1.1.18), (1.1 19) на ЭВМ, используя какой-либо из методов численного интегрирования (например, метод Рунге — Кутта). При эгом в (1.1.18),(1,1,19)  .
.
Реальные значения начальных значений положения вала двигателя, его скорости, токов в обмотках возбуждения отличаются от расчетных из-за погрешностей при «выставке» угла или скорости двигателя в начальный момент времени. Поэтому реальное движение будет отличаться от расчетного (программного). Переходя к уравнениям возмущенного движения, отметим, что по построению невозмущенное движение удовлетворяет уравнениям:

Так как возмущенное движение удовлетворяет уравнениям (1.1 18). (1.1.19), то

Учитывая уравнения невозмущенного движения, получим
 (1.2.11)
(1.2.11)
В качестве показателя отклонения реального движения от расчетного примем интеграл

в котором  -заданные положительные числа.
-заданные положительные числа.
Оптимальное стабилизирующее управление  должно минимизировать этот функционал на движениях системы (1.2.11) при начальных условиях
должно минимизировать этот функционал на движениях системы (1.2.11) при начальных условиях
 (1.2.13)
(1.2.13)
где  определяется погрешностями реализации начальных состояний
определяется погрешностями реализации начальных состояний  .
.
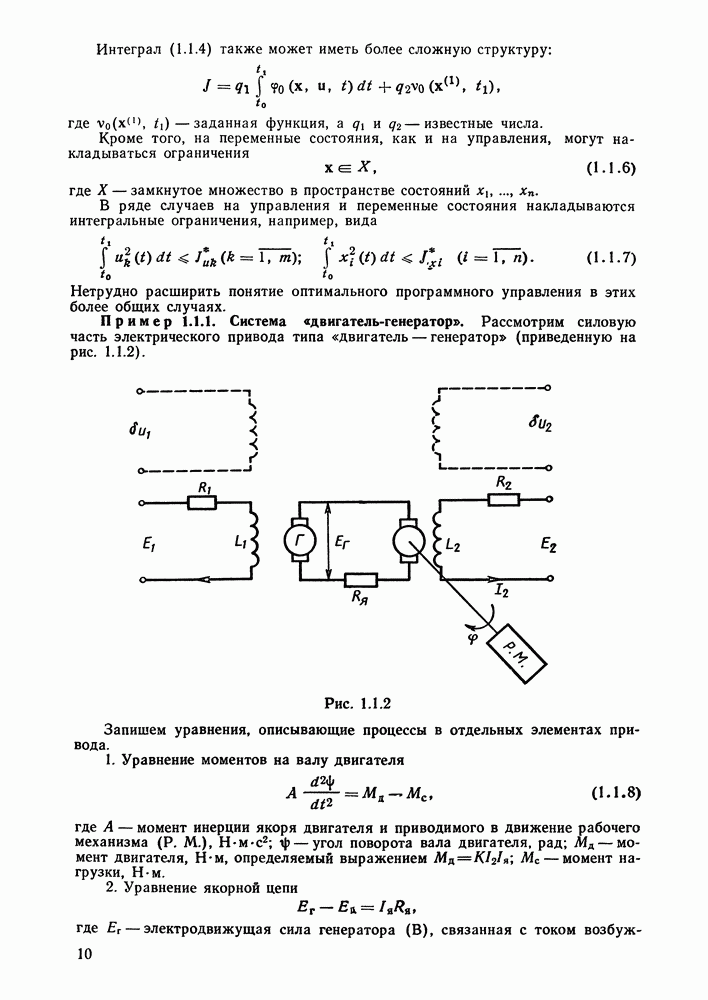
Физическая реализация стабилизирующих управлений осуществляется с помощью дополнительных обмоток возбуждения, показанных на рис. 1.1.2 пунктиром.
Во многих случаях контроль отклонений истинного движения от программного осуществляется не по переменным состояния, а по переменным, называемым регулируемыми (управляемыми) переменными. Они связаны с отклонениями по каждой переменной состояния соотношением

где  — регулируемые переменные.
— регулируемые переменные.
Критерий, с помощью которого оцениваются эти отклонения, имеет вид 

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
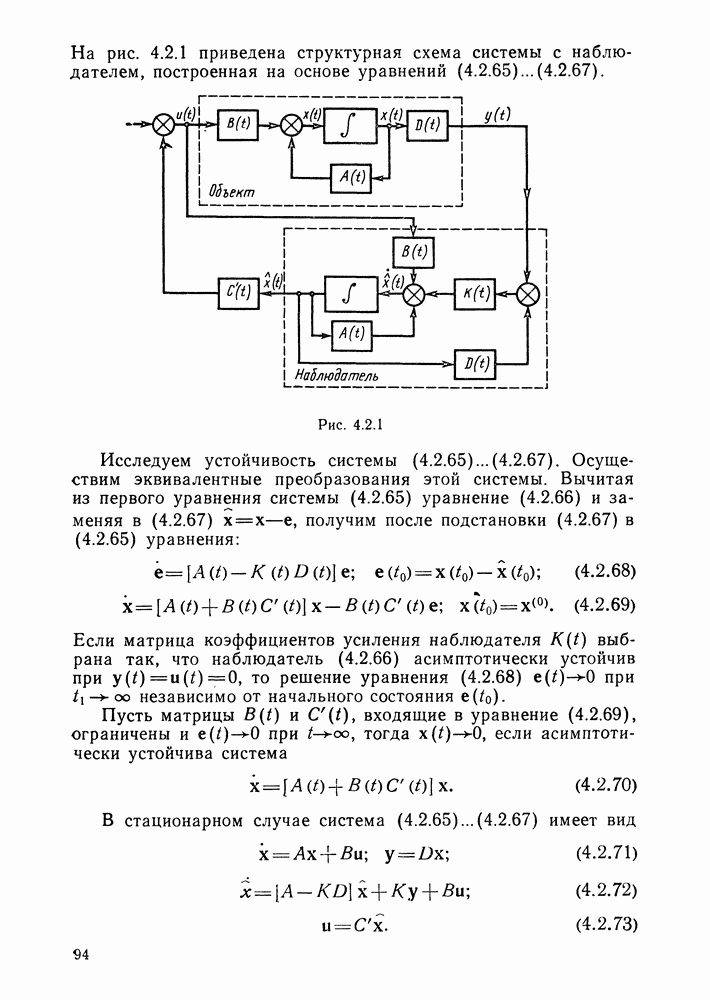
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
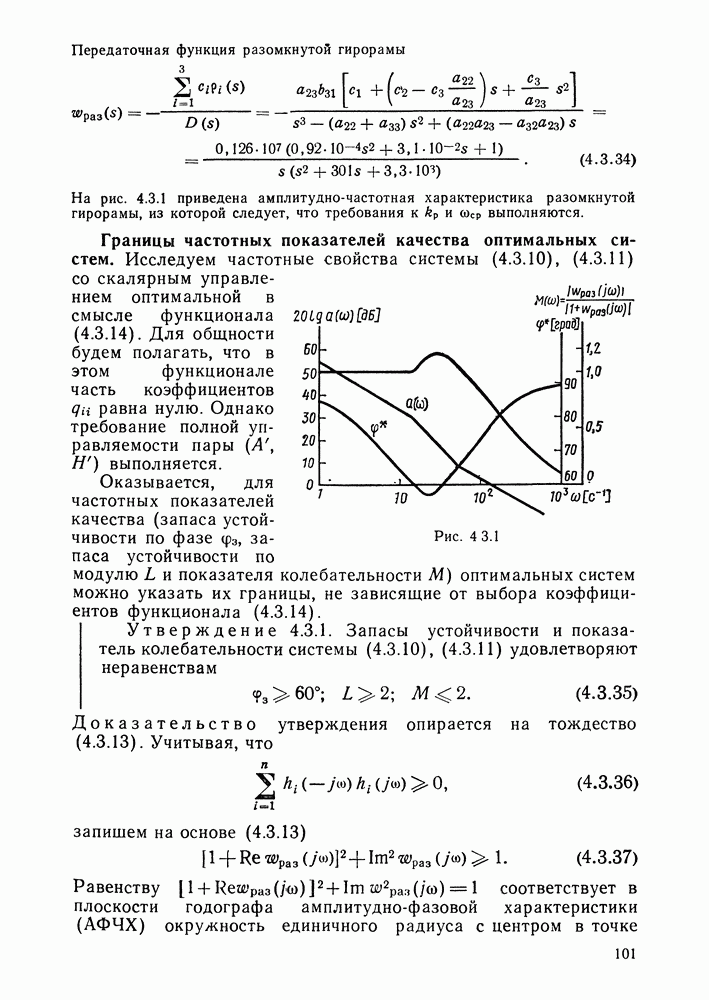
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
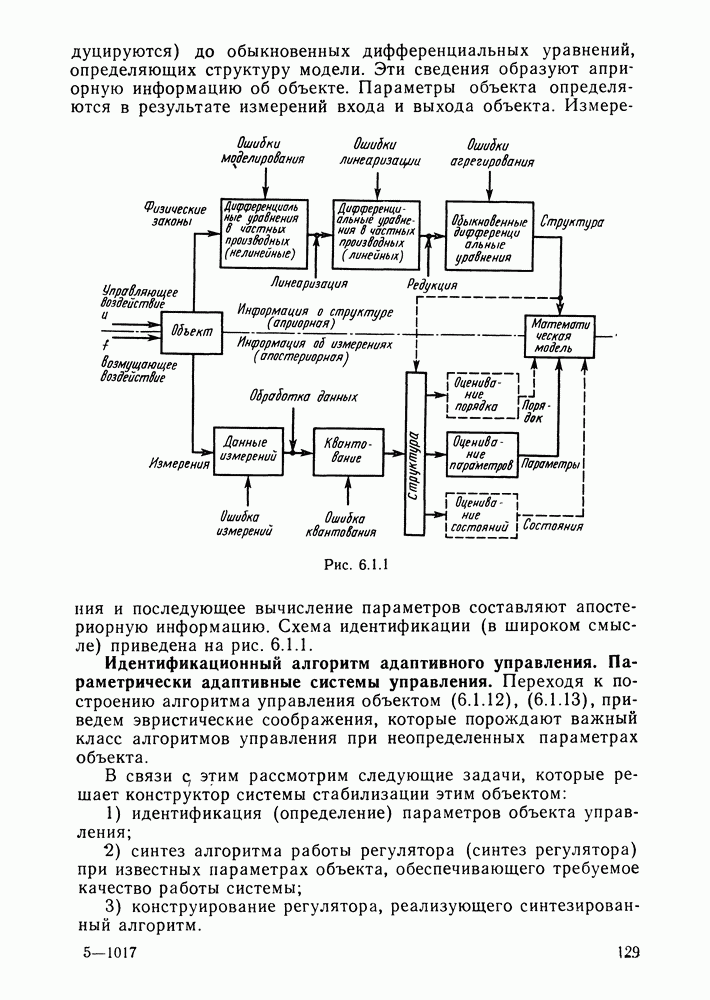
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
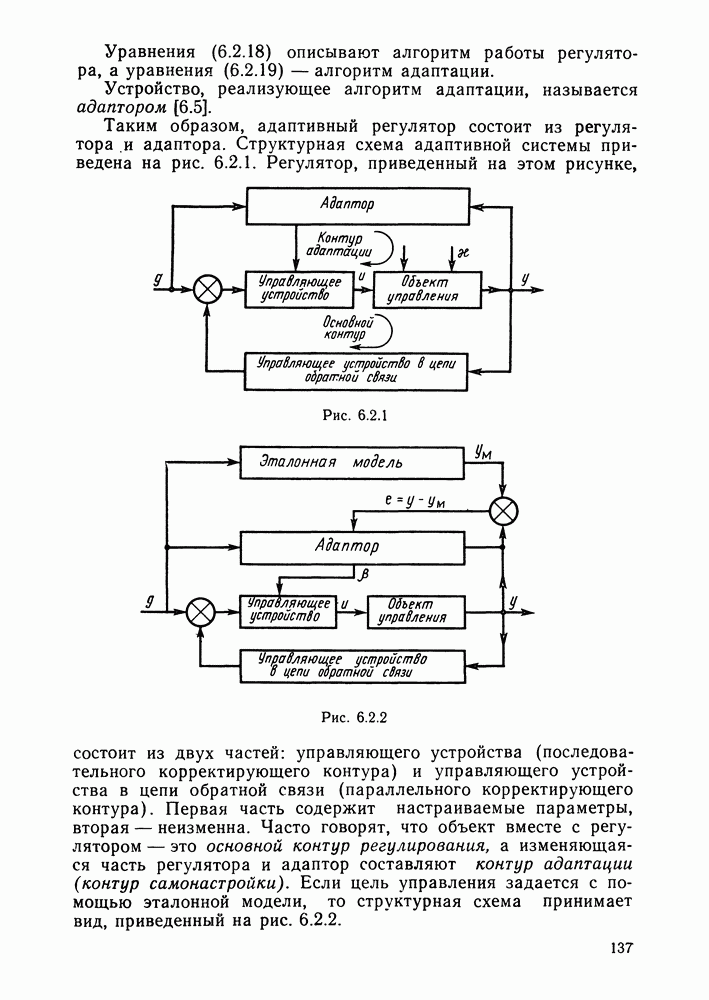
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
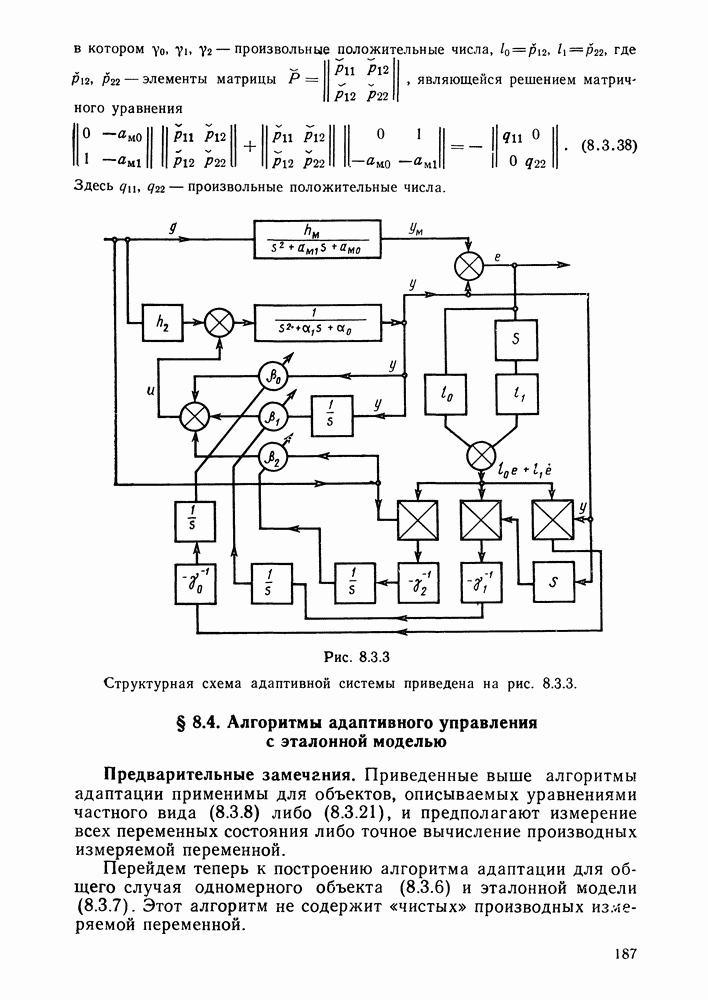
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
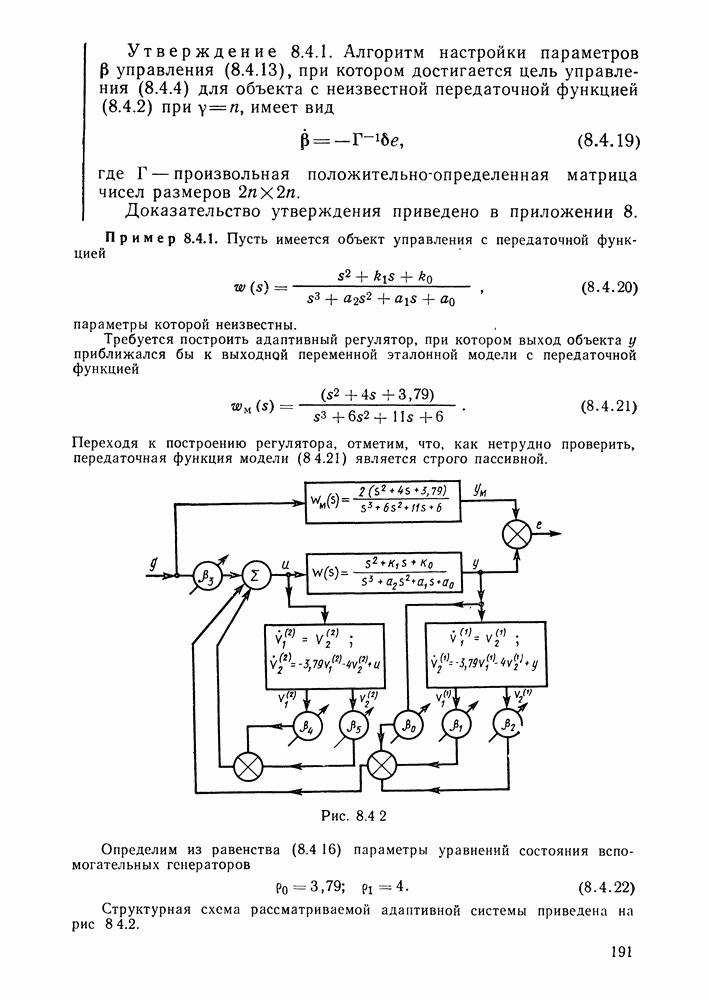
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
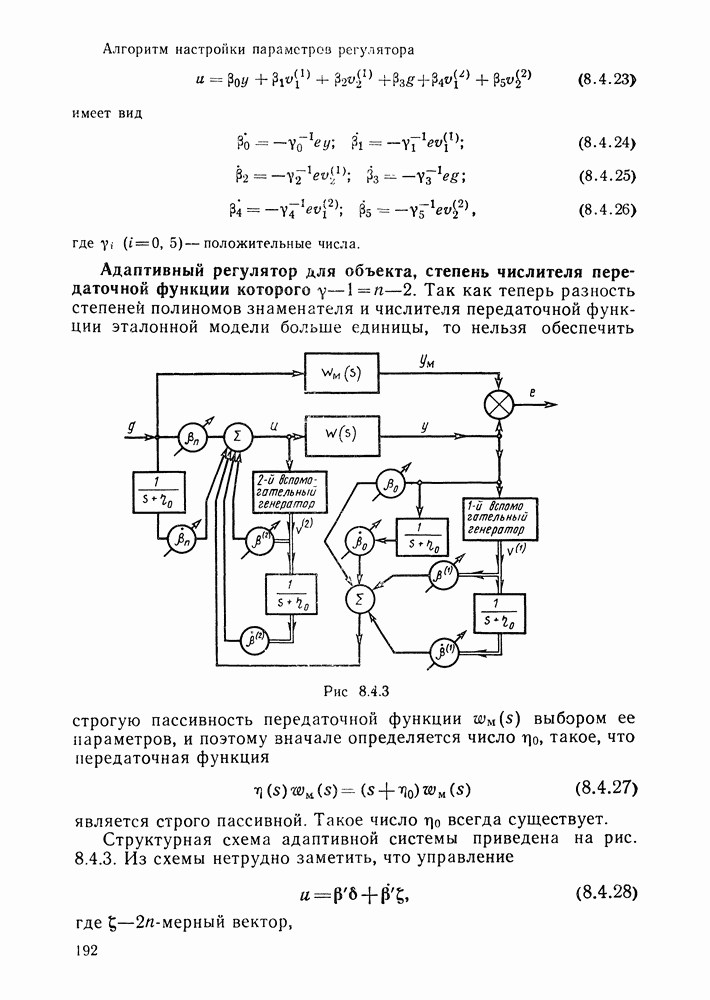
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ