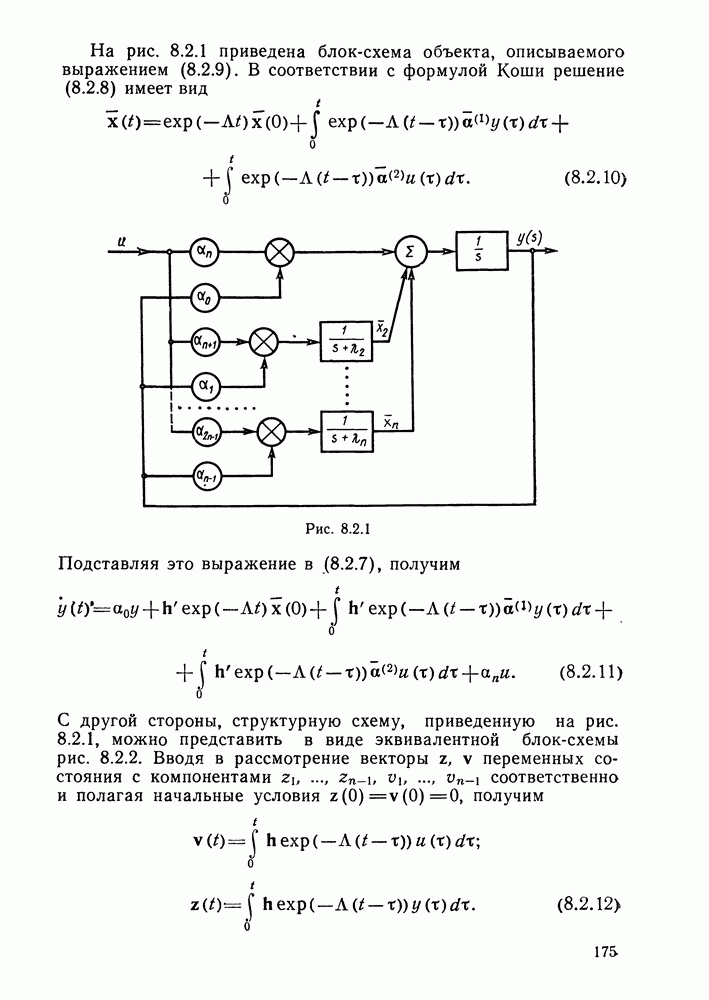
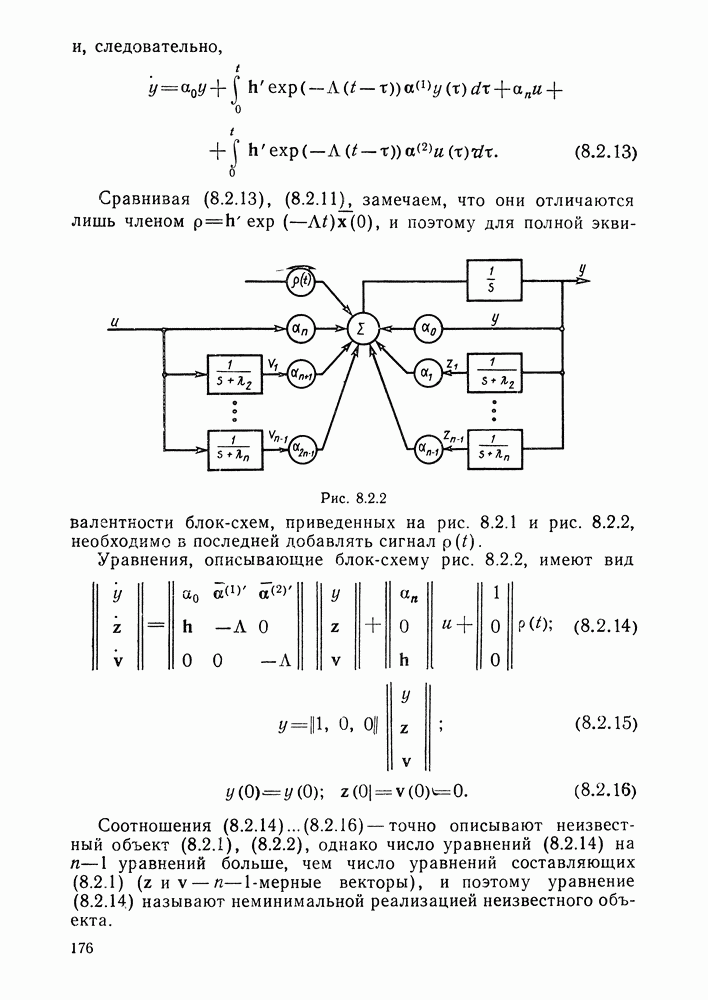
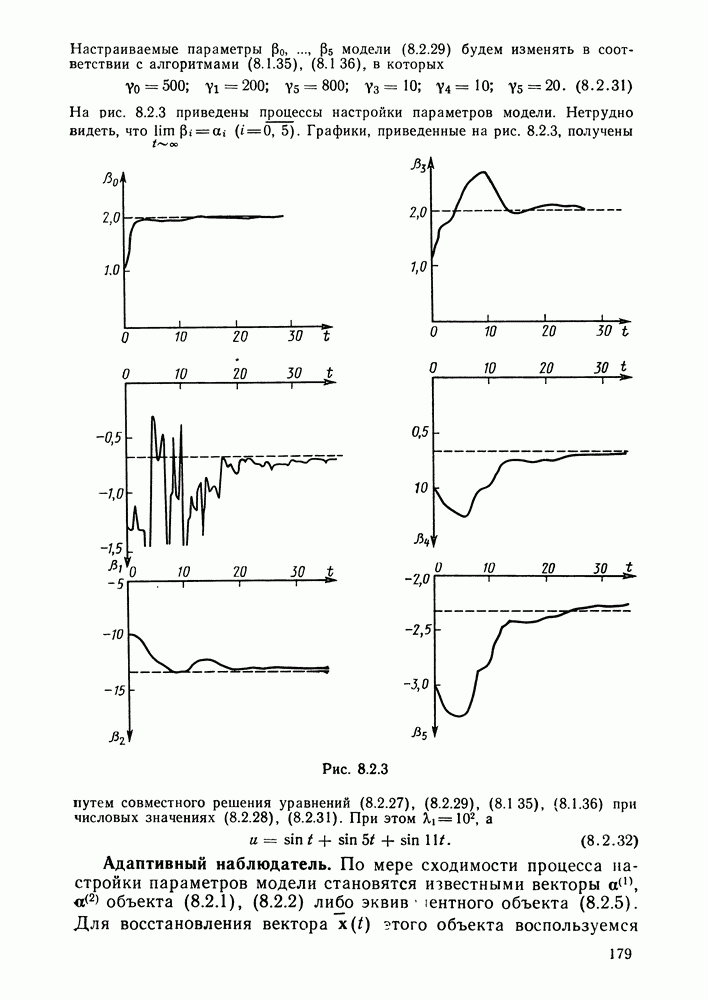
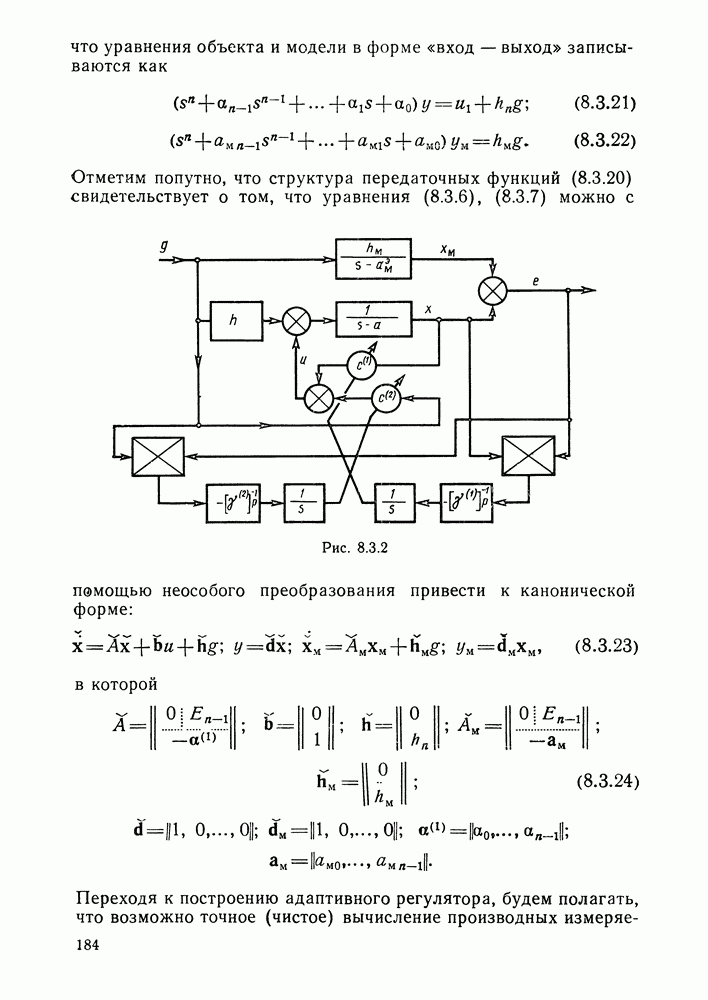
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6.3. Методы адаптивного управления
Две группы методов адаптивного управления.
Переходя к рассмотрению третьего этапа синтеза адаптивного регулятора — выбору алгоритма адаптации, отметим, что в зависимости от объема априорной информации о параметрах объекта, внешних возмущениях и помехах, можно выделить две группы методов, с помощью которых строятся алгоритмы адаптации.Первую группу составляют градиентные методы, которые используются при малых объемах информации о параметрах объекта, когда они являются неопределенными, ограниченными функциями, удовлетворяющими неравенствам (6.1.9). При этом сведения о внешних возмущениях и помехах могут быть различными. Это могут быть неопределенные ограниченные функции, удовлетворяющие неравенствам (6.2.10), и случайные процессы с известными или неизвестными законами распределения.
Вторую группу составляют методы, основанные на теории статистических решений. Они применяются, когда имеются априорные сведения о законе распределения параметров объекта. Эта плотность распределения уточняется в процессе работы системы. При этом предполагаются известными законы распределения случайных внешних воздействий и помех.
Наиболее полное изложение первой и второй групп методов можно найти соответственно в книгах [6.5, 6.6].
Здесь и в последующих главах основное внимание будет уделено градиентным методам построения алгоритма адаптации, причем здесь приведены эвристические соображения по применению этих методов, а в последующих главах получены условия и определены параметры алгоритмов адаптации, при которых эти алгоритмы приводят к достижению цели управления. Отметим, что наиболее трудным из всех этапов синтеза адаптивного регулятора является четвертый этап.
Интерпретация задачи оптимального адаптивного управления [6.11].
Рассмотрим устойчивую адаптивную систему, описываемую уравнениями (6.2.1), (6.2.18), (6.2.19) при известных функциях в правых частях уравнений (6.2.18) и известных (заданных) функциях . При некоторой функции
. При некоторой функции  в (6.2.19) и фиксированных начальных условиях на движениях адаптивной системы функционал
в (6.2.19) и фиксированных начальных условиях на движениях адаптивной системы функционал
 (6.3.1)
(6.3.1)
является функцией некоторого вектора чисел  , к которому сходятся решения уравнения (6.2.19).
, к которому сходятся решения уравнения (6.2.19).
Требуется найти такую функцию  , чтобы функция
, чтобы функция  достигала своего наименьшего значения.
достигала своего наименьшего значения.
Для этого построим процедуру нахождения минимума функции  . Экстремальное значение
. Экстремальное значение  аргумента этой функции удовлетворяет уравнениям
аргумента этой функции удовлетворяет уравнениям
 (6.3.2)
(6.3.2)
Алгоритм решения уравнений (6.3.2), основанный на методе градиента, имеет вид

где  — некоторая функция (параметр алгоритма), выбираемая из условий сходимости
— некоторая функция (параметр алгоритма), выбираемая из условий сходимости

Алгоритм (6.3.3) позволяет найти настраиваемые параметры  после того, как процесс управления объектом закончился, поскольку значение критерия
после того, как процесс управления объектом закончился, поскольку значение критерия  было определено при
было определено при  . Для устранения этого недостатка заметим, что значение
. Для устранения этого недостатка заметим, что значение  не зависит от траектории
не зависит от траектории  , входящей в функцию
, входящей в функцию  , и поэтому в алгоритм (6.3.3) подставляют вместо
, и поэтому в алгоритм (6.3.3) подставляют вместо  не предельное, а текущее значение
не предельное, а текущее значение  , и тогда (6.3.3) принимает вид
, и тогда (6.3.3) принимает вид
 (6.3.5)
(6.3.5)
В тех случаях, когда выражения  имеют явную (аналитическую) форму, как, например, уравнения (6.1.41) в примере (6.1.2), уравнения (6.3.5) являются уравнениями алгоритма адаптации (6.2.19). Таким образом, интерпретация задачи оптимального адаптивного управления как задачи о минимуме функции приводит при детерминированных внешних возмущениях и помехах к искомому алгоритму адаптации. Этот алгоритм содержит не определенный пока параметр
имеют явную (аналитическую) форму, как, например, уравнения (6.1.41) в примере (6.1.2), уравнения (6.3.5) являются уравнениями алгоритма адаптации (6.2.19). Таким образом, интерпретация задачи оптимального адаптивного управления как задачи о минимуме функции приводит при детерминированных внешних возмущениях и помехах к искомому алгоритму адаптации. Этот алгоритм содержит не определенный пока параметр  .
.
Покажем, что для идентификационного, адаптивного управления можно указать явный вид правой части алгоритма адаптации (6.3.5).
Рассмотрим объект (6.2.1), описанный уравнением в форме «вход—выход»:
 (6.3.6)
(6.3.6)
где  — заданная функция своих аргументов.
— заданная функция своих аргументов.
Допустим, что эта функция с достаточной точностью может быть аппроксимирована конечной суммой
 (6.3.7)
(6.3.7)
где  — линейно независимые известные функции;
— линейно независимые известные функции;  — неизвестные числа.
— неизвестные числа.
Примем в качестве критерия точности идентификации функцию
 (6.3.8)
(6.3.8)
где невязка
 (6.3.9)
(6.3.9)
и будем определять числа  из условия минимума критерия (6.3.8).
из условия минимума критерия (6.3.8).
Алгоритм решения уравнений  на основе метода градиента имеет вид
на основе метода градиента имеет вид
 (6.3.10)
(6.3.10)
где  — параметр, выбираемый из условия сходимости процесса идентификации,
— параметр, выбираемый из условия сходимости процесса идентификации,
 (6.3.11)
(6.3.11)
Допустим для простоты, что  , тогда
, тогда
 (6.3.12)
(6.3.12)
Нетрудно видеть, что правая часть этого уравнения является известной функцией измеряемых переменных объекта и их производных.
Отметим, что алгоритм адаптации (идентификации) (6.3.12) был получен исходя из выражения критерия оптимизации (6.3.8), а не из выражения для цели управления, которая достигается, если выбран соответствующий алгоритм регулирования, например вида (6.1.24), в котором оценками вектора а являются переменные  . Критерий (6.3.8) иногда называют (6.10] целью адаптации.
. Критерий (6.3.8) иногда называют (6.10] целью адаптации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
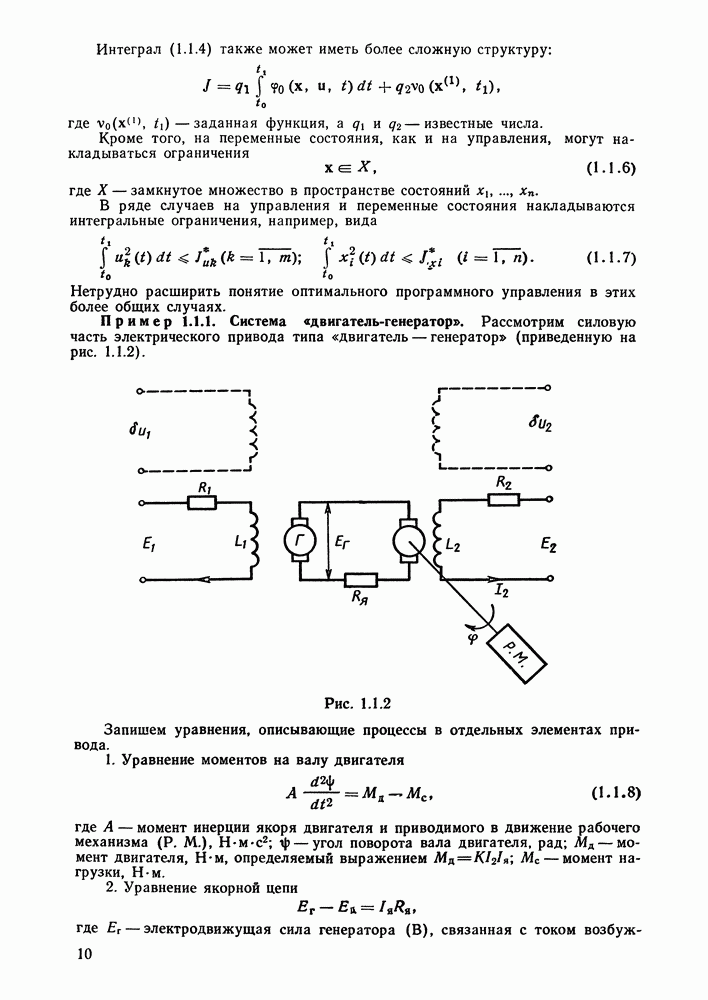
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
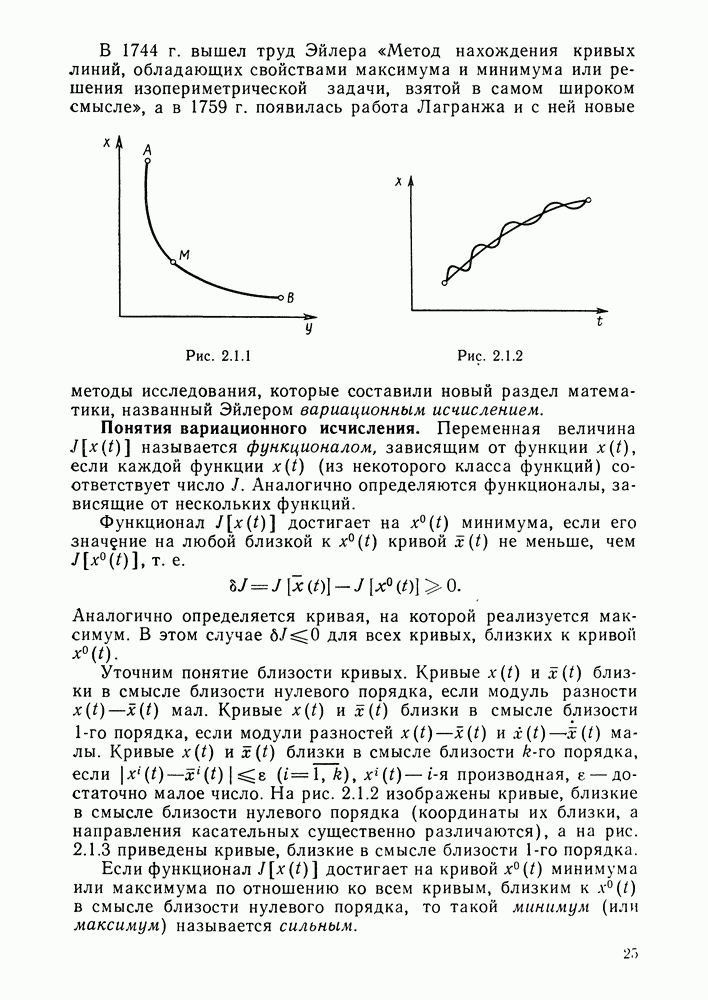
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
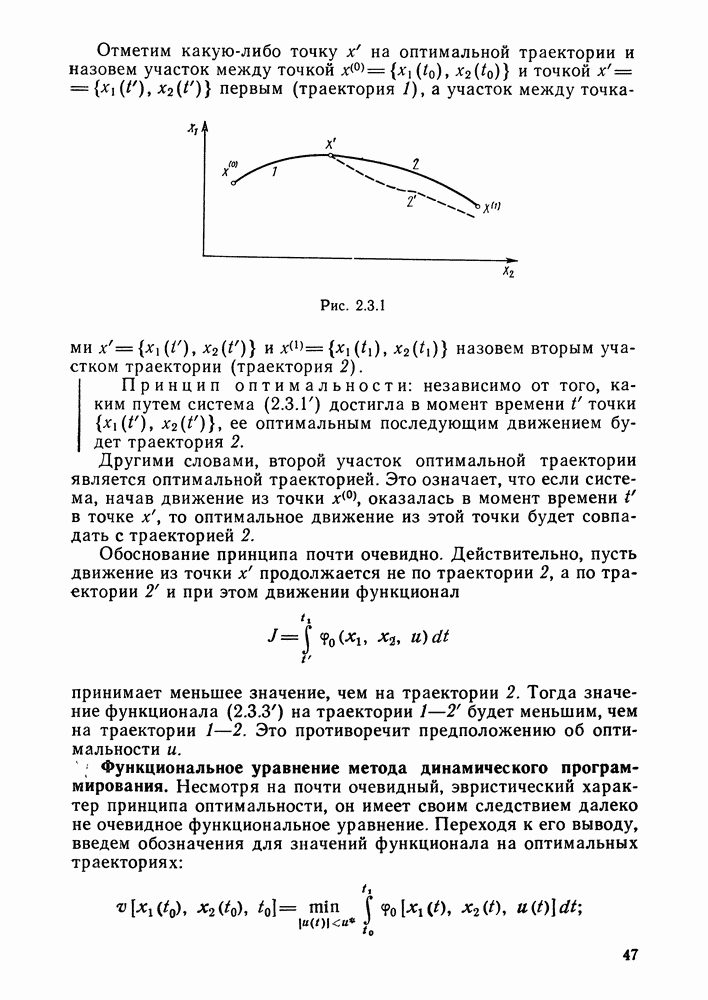
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
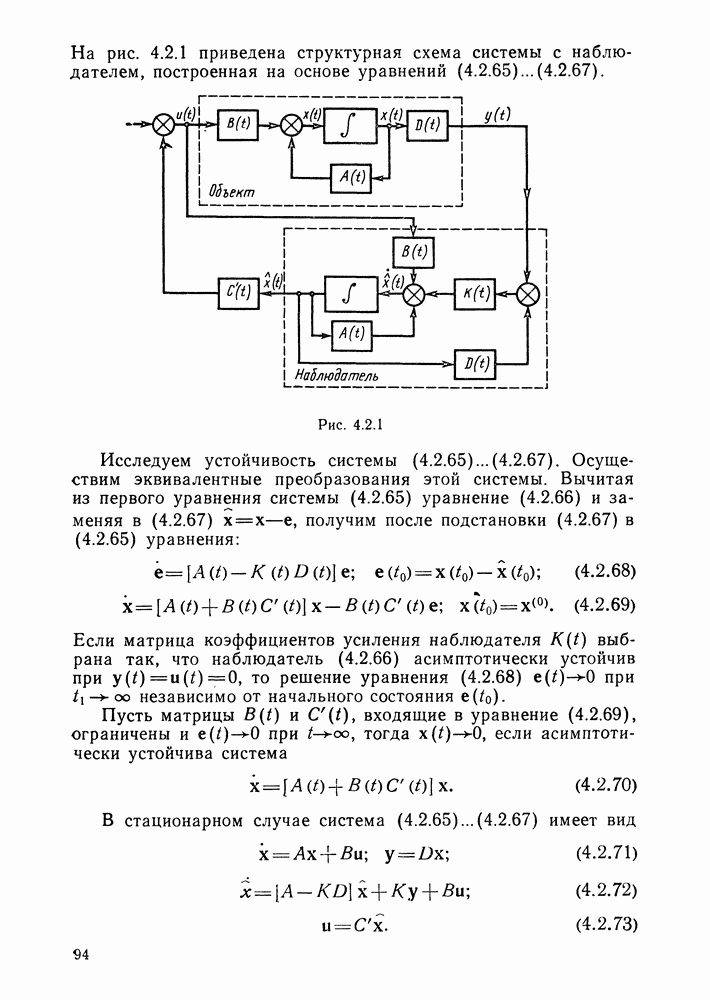
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
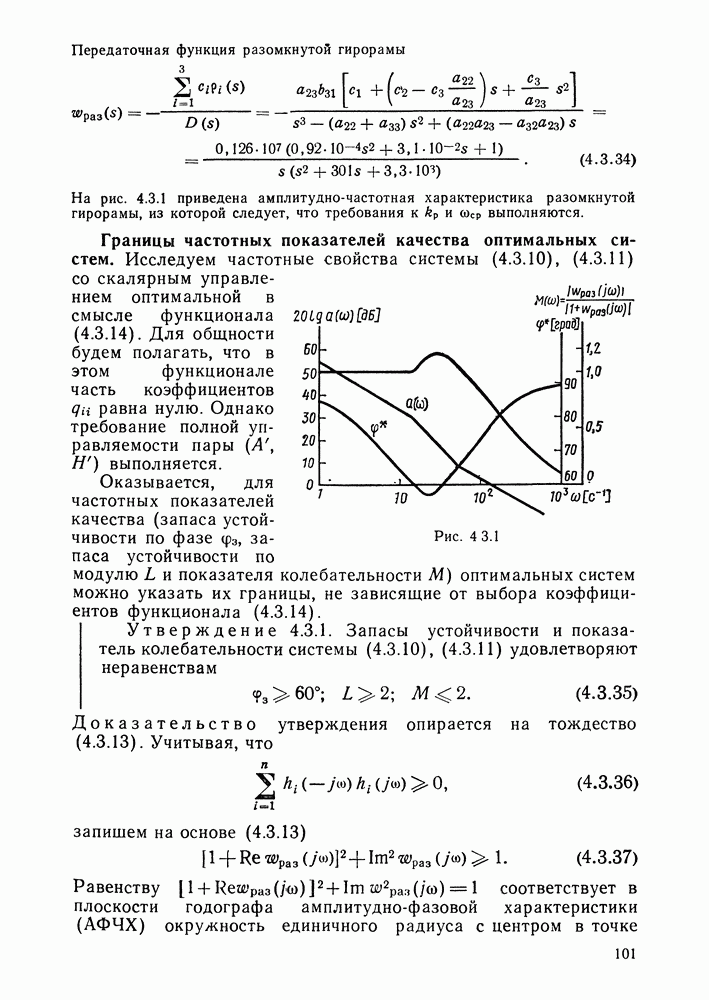
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
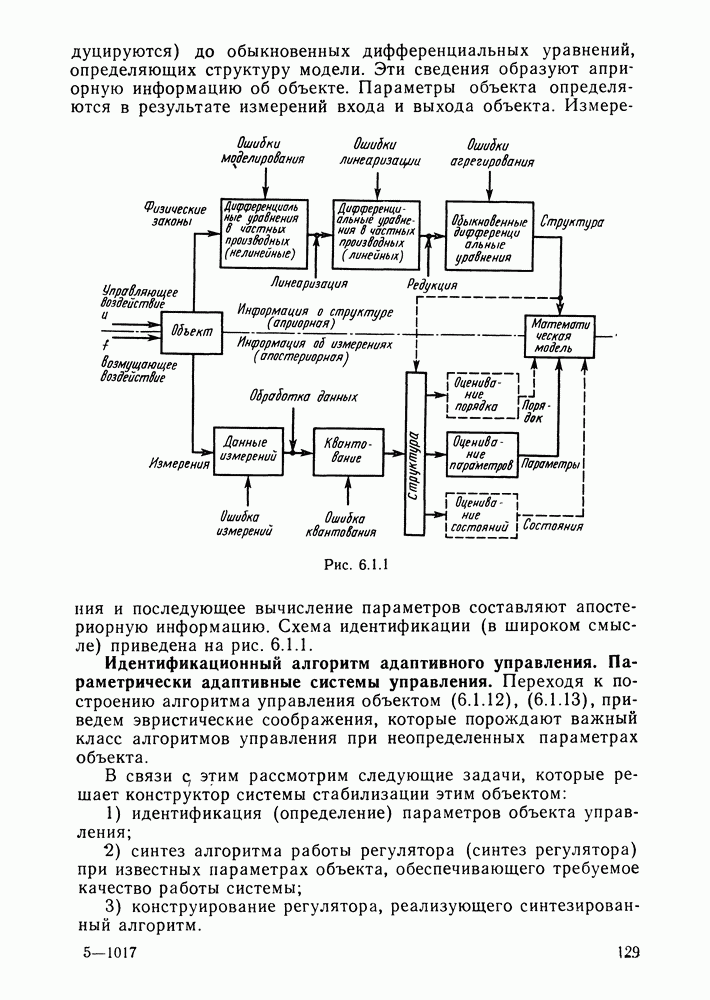
- Понятие об идентификации.
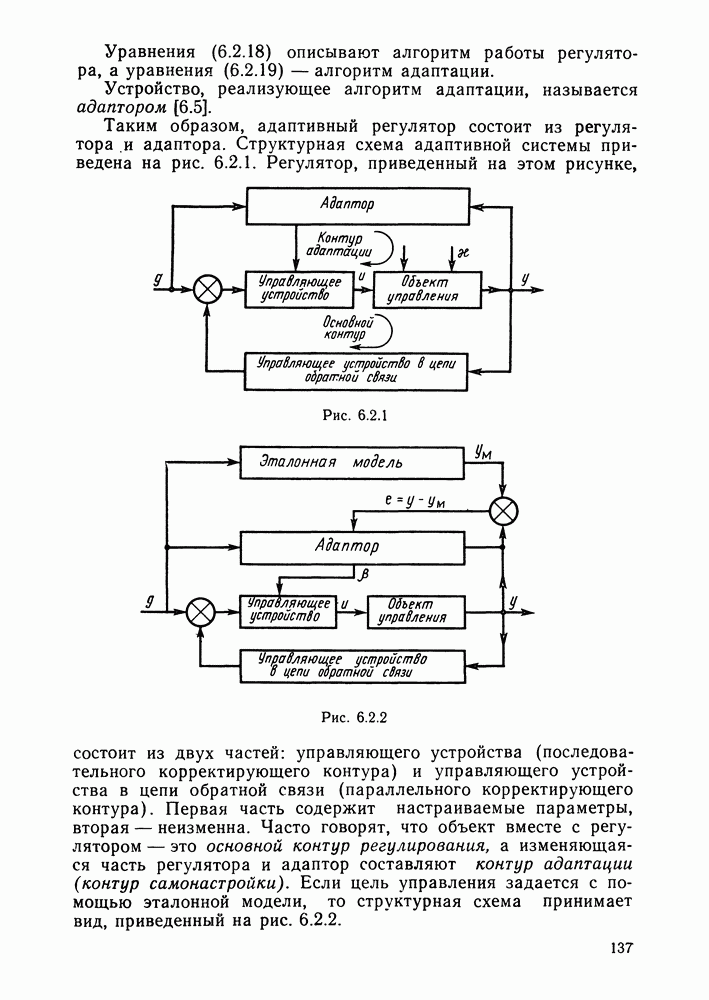
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
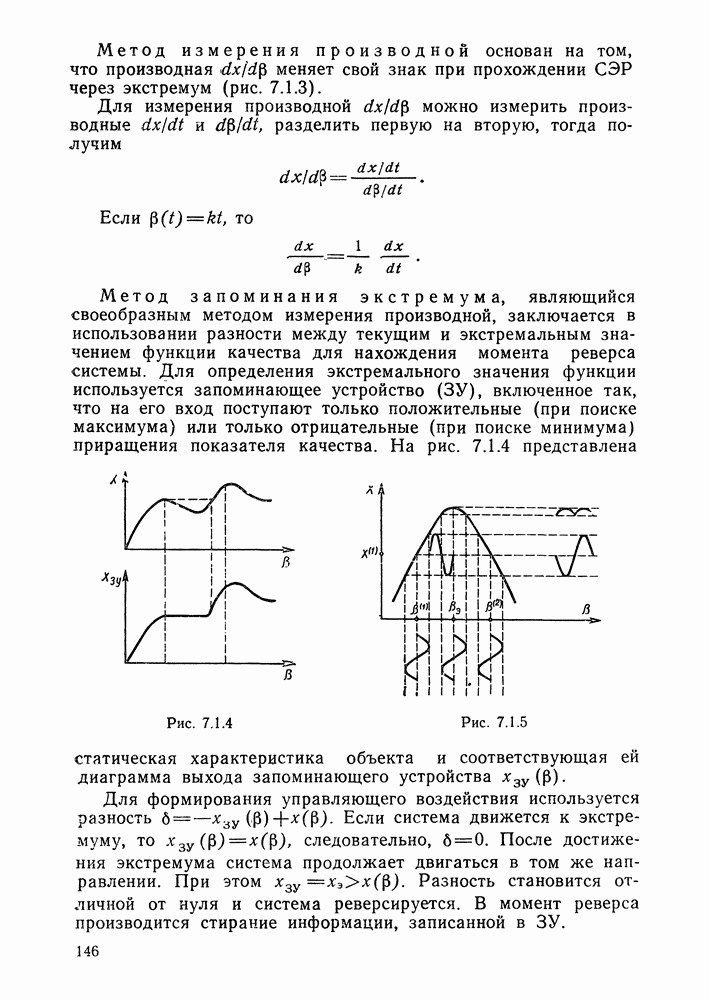
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
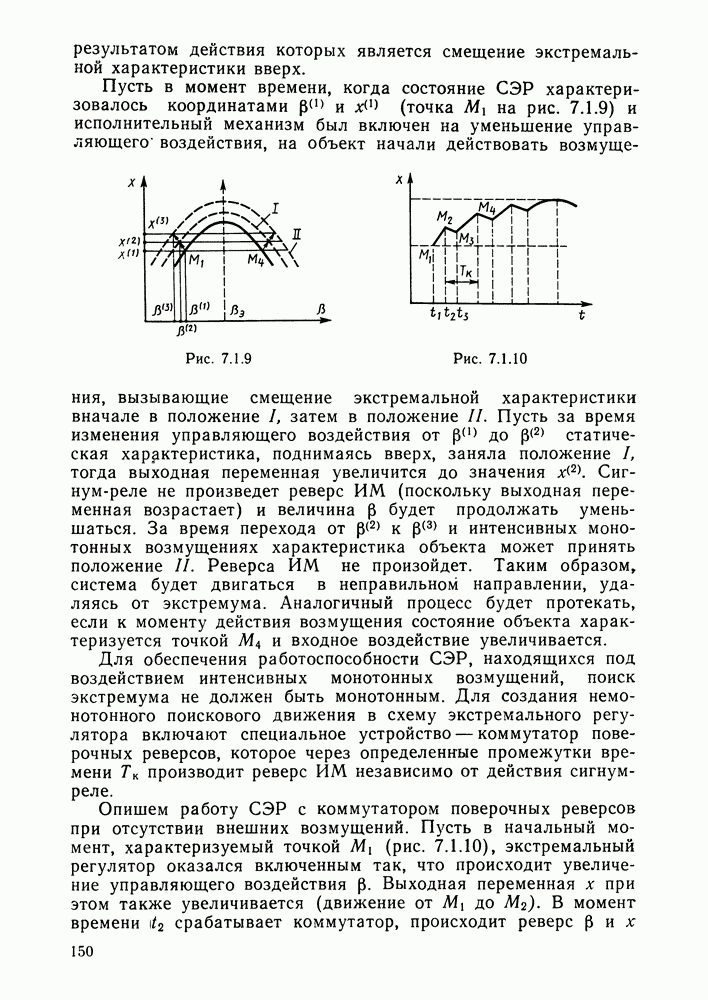
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
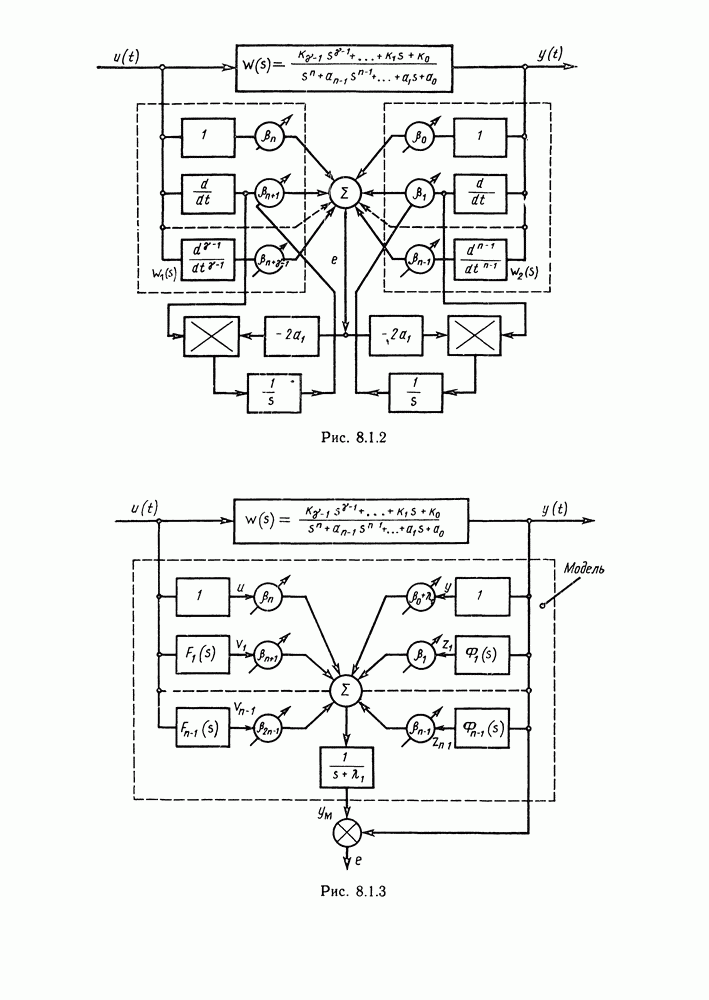
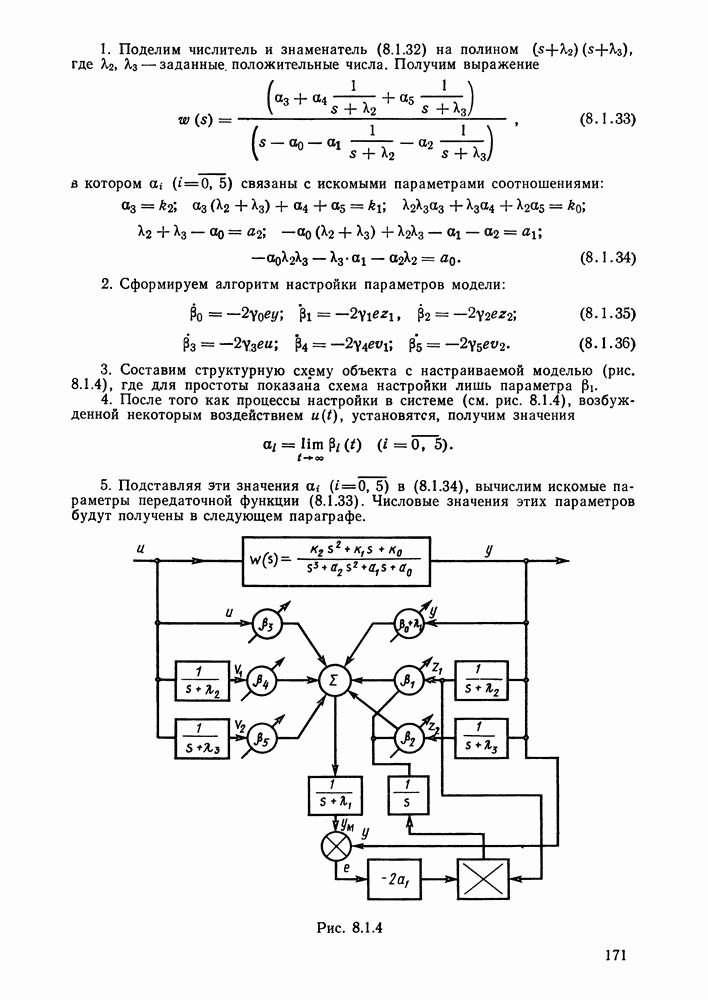
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
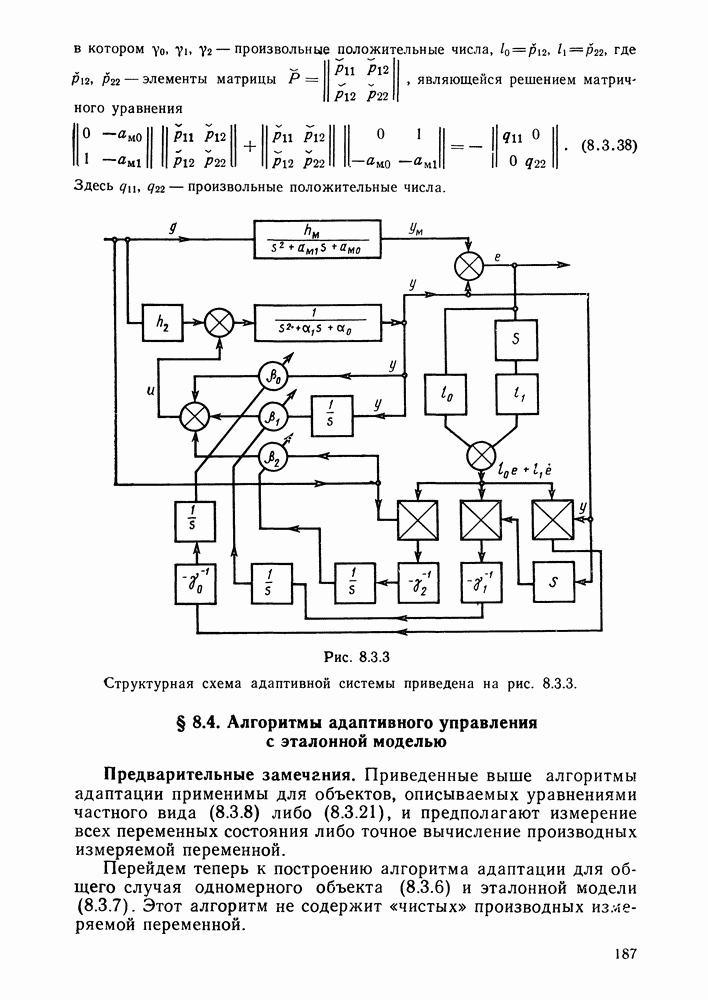
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
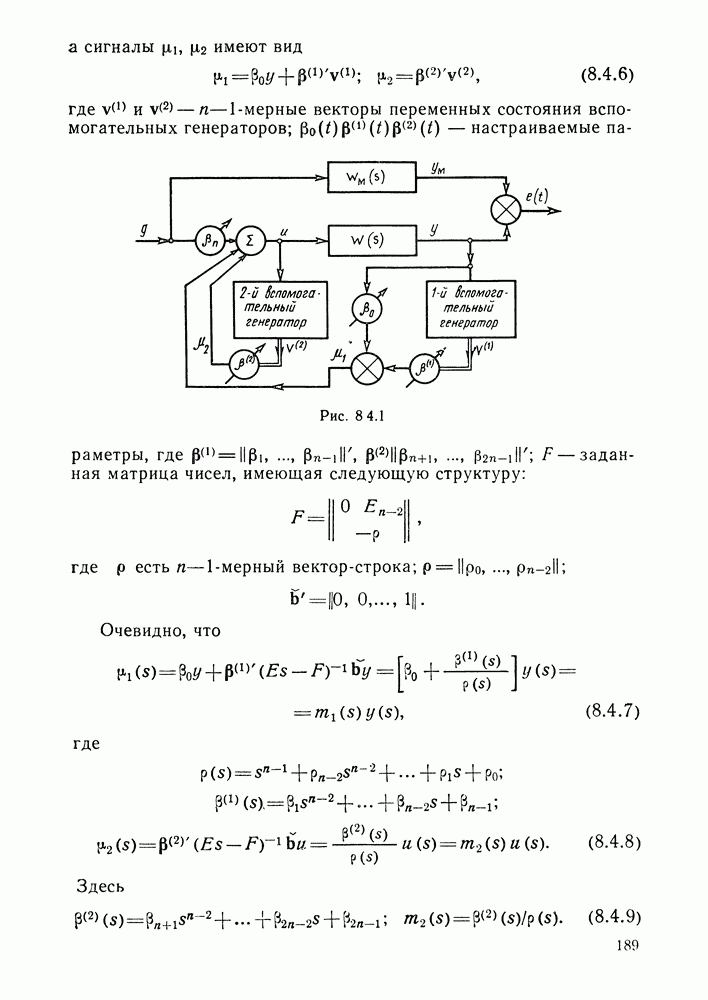
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
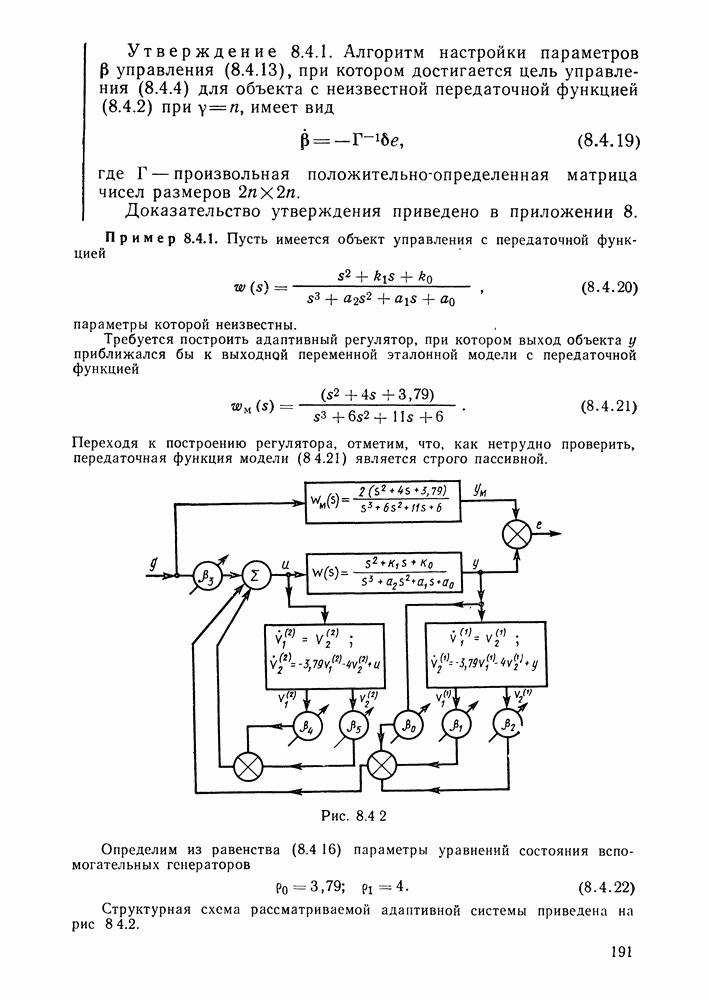
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
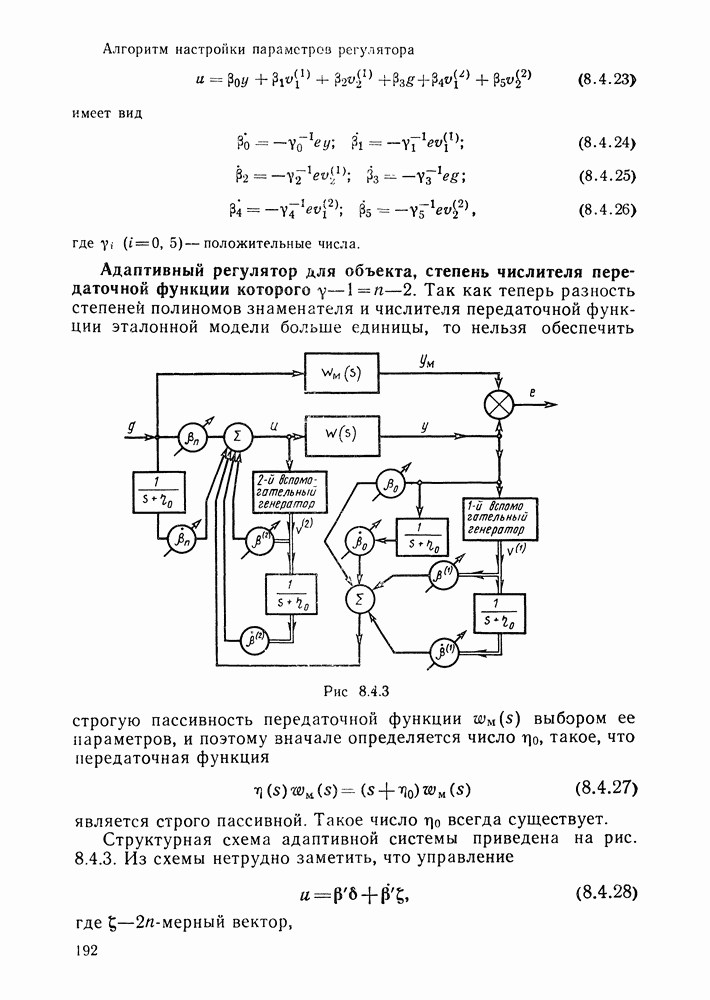
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ