| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
§ 1.1. Оптимальное программное управление
Рассмотрим объект управления, движение которого описывается уравнением
 (1.1.1)
(1.1.1)
где  -мерный вектор переменных состояния объекта,
-мерный вектор переменных состояния объекта,  -мерный вектор управлений.
-мерный вектор управлений.
В развернутой форме  имеет вид
имеет вид

где  -заданные функции. Они предполагаются непрерывными и необходимое число раз дифференцируемыми по
-заданные функции. Они предполагаются непрерывными и необходимое число раз дифференцируемыми по  .
.
В уравнении (1.1.1) управления являются неизвестными функциями времени, которые определяются исходя из следующих условий.
1. Задано начальное
 (1.1.2)
(1.1.2)
и конечное
 (1.1.3)
(1.1.3)
состояния объекта (1.1.1), где  — время начала, а
— время начала, а  — время окончания функционирования объекта.
— время окончания функционирования объекта.
2. Эффективность управления оценивается с помощью интеграла

где  — заданная непрерывная функция своих аргументов. Для определенности далее будем полагать, что эффективность управления тем выше, чем меньше значение этого интеграла.
— заданная непрерывная функция своих аргументов. Для определенности далее будем полагать, что эффективность управления тем выше, чем меньше значение этого интеграла.
3. На управления и переменные состояния накладываются ограничения, выражающие ограниченные ресурсы управления и допустимые пределы изменения переменных состояния. Часто ограничения на управления имеют вид

где  — заданные числа.
— заданные числа.
При  точки вектора
точки вектора  , координаты которого удовлетворяют этим неравенствам, заполняют заштрихованный прямоугольник, приведенный на рис. 1.1.1.
, координаты которого удовлетворяют этим неравенствам, заполняют заштрихованный прямоугольник, приведенный на рис. 1.1.1.
В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано замкнутое множество U в пространстве переменных  и управления могут принимать в каждый момент времени лишь значения из этого множества.
и управления могут принимать в каждый момент времени лишь значения из этого множества.
Замкнутость множества U означает, что управления могут находиться не только внутри, но и на его границе (например,  ).
).
Далее будем называть оптимальным программным управлением функции времени  , принимающие значения из множества
, принимающие значения из множества  , при которых объект (1.1.1) переводится из состояния (1.1.2) в состояние (1.1.3) и при этом функционал (1.1.4) принимает наименьшее значение.
, при которых объект (1.1.1) переводится из состояния (1.1.2) в состояние (1.1.3) и при этом функционал (1.1.4) принимает наименьшее значение.
Часто краевые условия имеют более общий, чем (1.1.2), (1.1.3), вид: а) моменты времени  в (1 1.2), (1.1.3) либо один из них не заданы (тогда говорят о задаче с нефиксированным временем), б) вектор
в (1 1.2), (1.1.3) либо один из них не заданы (тогда говорят о задаче с нефиксированным временем), б) вектор  не задан (задана со свободным правым (или левым) концом траектории с фиксированным либо нефиксированным временем
не задан (задана со свободным правым (или левым) концом траектории с фиксированным либо нефиксированным временем  или 11); в) в (1.1.2), (1.1 3) компоненты
или 11); в) в (1.1.2), (1.1 3) компоненты  m) векторов
m) векторов  не заданы, а лежат на гиперповерхностях
не заданы, а лежат на гиперповерхностях

(задача с подвижными концами).

Рис. 1.1.1.
Интеграл (1.1.4) также может иметь более сложную структуру:

где  -заданная функция,
-заданная функция,  и
и  -известные числа.
-известные числа.
Кроме того, на переменные состояния, как и на управления, могут накладываться ограничения
 (1.1.6)
(1.1.6)
где X — замкнутое множество в пространстве состояний  .
.
В ряде случаев на управления и переменные состояния накладываются интегральные ограничения, например, вида
 (1.1.7)
(1.1.7)
 Нетрудно расширить понятие оптимального программного управления в этих более общих случаях.
Нетрудно расширить понятие оптимального программного управления в этих более общих случаях.
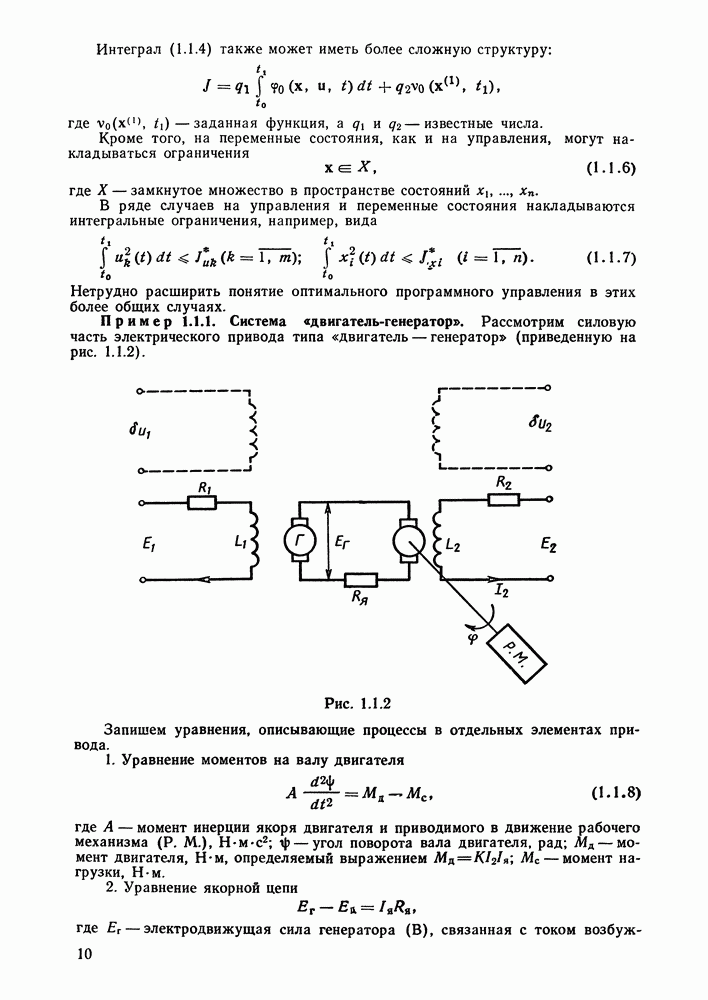
Пример 1.1.1. Система «двигатель-генератор». Рассмотрим силовую часть электрического привода типа «двигатель — генератор» (приведенную на рис. 1.1.2).

Рис. 1.1.2.
Запишем уравнения, описывающие процессы в отдельных элементах привода.
1. Уравнение моментов на валу двигателя
 (1.1.8)
(1.1.8)
где А — момент инерции якоря двигателя и приводимого в движение рабочего механизма (Р. М.),  — угол поворота вала двигателя, рад;
— угол поворота вала двигателя, рад;  — момент двигателя,
— момент двигателя,  , определяемый выражением
, определяемый выражением  — момент нагрузки,
— момент нагрузки,  .
.
2. Уравнение якорной цепи

где  — электродвижущая сила генератора (В), связанная с током возбуждения
— электродвижущая сила генератора (В), связанная с током возбуждения  (А) кривой намагничивания
(А) кривой намагничивания  электродвижущая сила двигателя, связанная с током возбуждения двигателя: h (А) зависимостью
электродвижущая сила двигателя, связанная с током возбуждения двигателя: h (А) зависимостью  , в которой С — коэффициент пропорциональности.
, в которой С — коэффициент пропорциональности.
Подставляя эти зависимости в уравнение якорной цепи, получим
 (1.1.9)
(1.1.9)
3. Уравнение цепей возбуждения генератора и двигателя имеют соответственно вид
 (1.1.10)
(1.1.10)
где  — напряжение, ток, сопротивление и индуктивность цепи возбуждения генератора и двигателя соответственно.
— напряжение, ток, сопротивление и индуктивность цепи возбуждения генератора и двигателя соответственно.
В зависимости от назначения рабочего механизма, связанного с валом двигателя, возникают различные режимы управления рабочим механизмом, который должен:
а) за минимальное время разогнаться до заданной скорости либо
б) совершить заданную работу за минимальное время, либо
в) переместиться из одного положения в другое за заданное время при минимальных потерях в цепях управления и якорной цепи.
Осуществление каждого из этих режимов управления затруднено целым рядом ограничений, к числу которых относятся следующие:
1. Перегрев якоря, определяемый потерями в якорной цепи, которые пропорциональны квадрату тока в этой цепи. Температура перегрева пропорциональна числу

и, следовательно, ограничение температуры перегрева описывается соотношением

где Т — заданное число, характеризующее допустимую температуру.
2. Напряжение, прикладываемое к обмотками возбуждения генератора и двигателя, ограничено напряжением источников питания —  :
:
 (1.1.12)
(1.1.12)
3. Максимальные значения скоростей и ускорений движения ограничены из условий прочности рабочего механизма либо комфорта, если, например, рабочим механизмом является лифт с людьми. Эти ограничения имеют вид
 (1.1.13)
(1.1.13)
где  и
и  -заданные числа.
-заданные числа.
Время осуществления названных выше режимов управления  выступает в рассматриваемом случае как мера эффективности управления. Эту меру можно описать с помощью интеграла
выступает в рассматриваемом случае как мера эффективности управления. Эту меру можно описать с помощью интеграла
 (1.1.14)
(1.1.14)
Действительно, из (1.1.14) следует  .
.
Начальными и конечными состояниями системы «генератор — двигатель» являются положение, частота вращения вала двигателя, ток в обмотках возбуждения генератора и двигателя в начальный  и конечный
и конечный  моменты времени.
моменты времени.

Оптимальным программным управлением являются законы изменения напряжений  , удовлетворяющих ограничениям (1 1 12), при которых система «генератор — двигатель» переходит из состояния (1.1.15) в состояние (1.1.16) и при этом функционал (1.1 14) принимает наименьшее значение и выполняются ограничения (1 1 13), (1.1.11)
, удовлетворяющих ограничениям (1 1 12), при которых система «генератор — двигатель» переходит из состояния (1.1.15) в состояние (1.1.16) и при этом функционал (1.1 14) принимает наименьшее значение и выполняются ограничения (1 1 13), (1.1.11)
Для режима  , когда требуется переместить рабочий механизм из одного положения в другое за заданное время
, когда требуется переместить рабочий механизм из одного положения в другое за заданное время  при минимальных потерях в цепях управления и якорной цепи, минимизируемый функционал имеет вид
при минимальных потерях в цепях управления и якорной цепи, минимизируемый функционал имеет вид

и выражает энергию, выделяемую в этих цепях.
Для удобства последующего изложения запишем уравнения системы «генератор — двигатель» и ограничения в стандартной форме. В связи с этим введем обозначения

где  — номинальные значения угла поворота двигателя (рад), частота его вращения (
— номинальные значения угла поворота двигателя (рад), частота его вращения ( ), токов в обмотках возбуждения (А) (для простоты полагаем, что числовые значения
), токов в обмотках возбуждения (А) (для простоты полагаем, что числовые значения  равны).
равны).
С учетом этих обозначений запишем уравнения (1.1.8), (1.1.9), (1.1.10) в безразмерной форме (полагая далее  :
:

где

Ограничения  примут вид:
примут вид:

где

Оптимальным программным управлением в рассматриваемом случае будут (например, для режима  ) функции
) функции  , такие, что рабочий механизм за минимальное время при выполнении ограничений (1,1.11) - (1.1.13) переместится из состояния
, такие, что рабочий механизм за минимальное время при выполнении ограничений (1,1.11) - (1.1.13) переместится из состояния  в состояние
в состояние  , где
, где

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
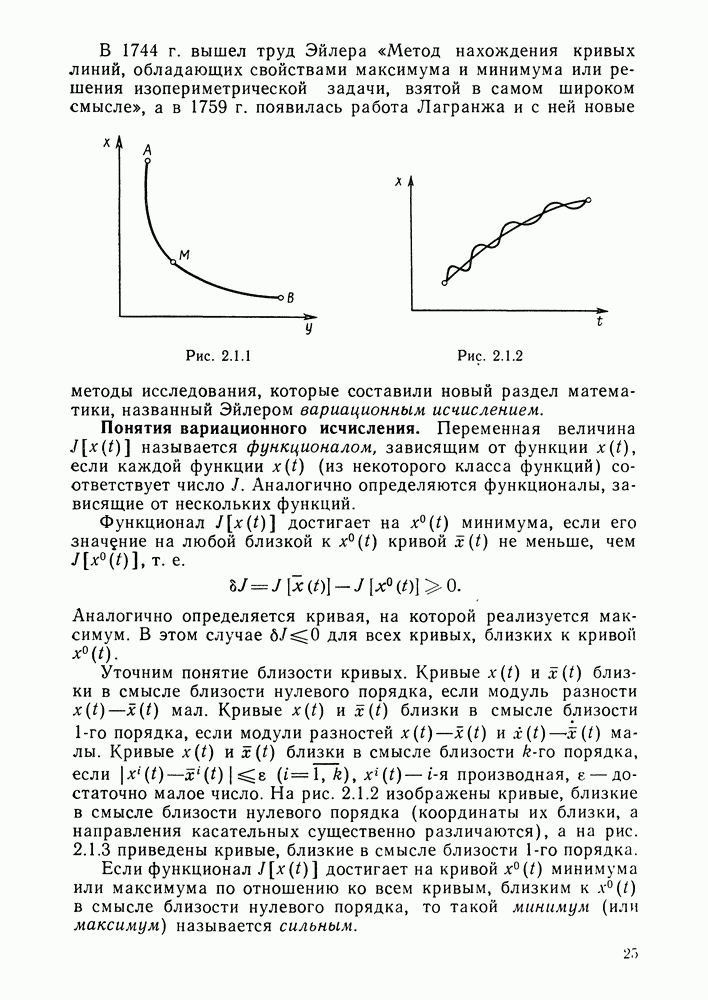
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
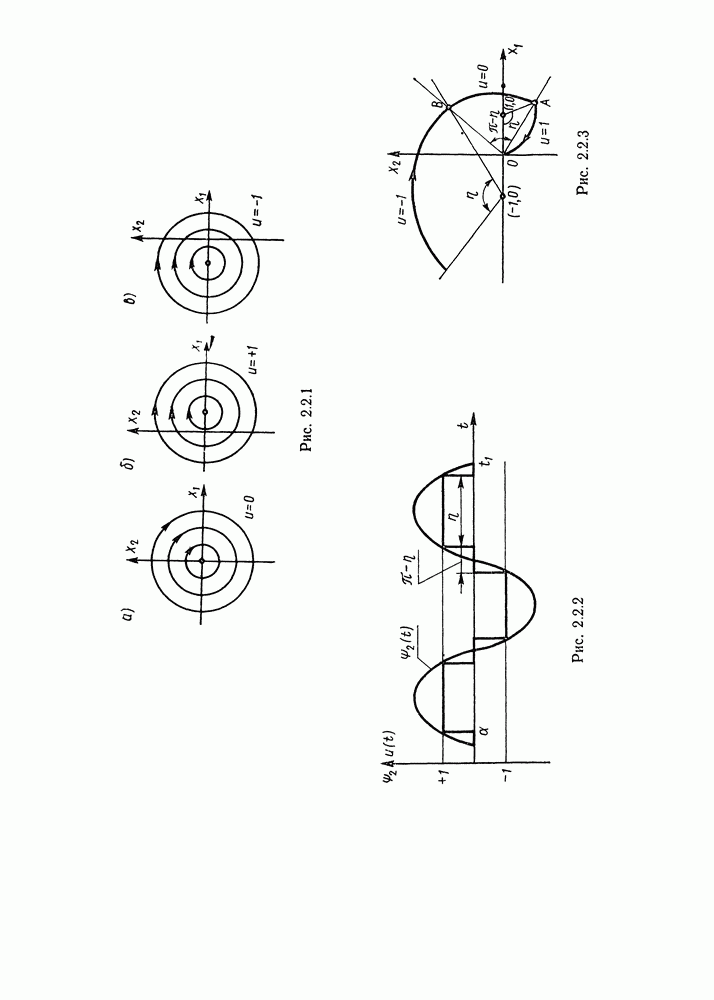
- § 2.2. Принцип максимума
- Принцип максимума.
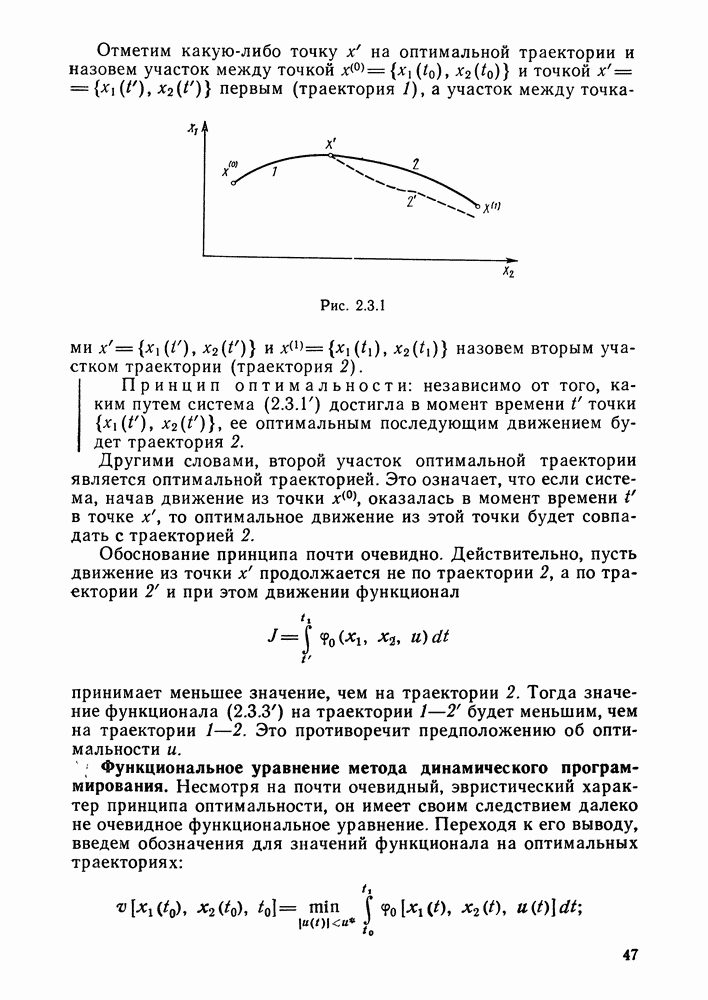
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
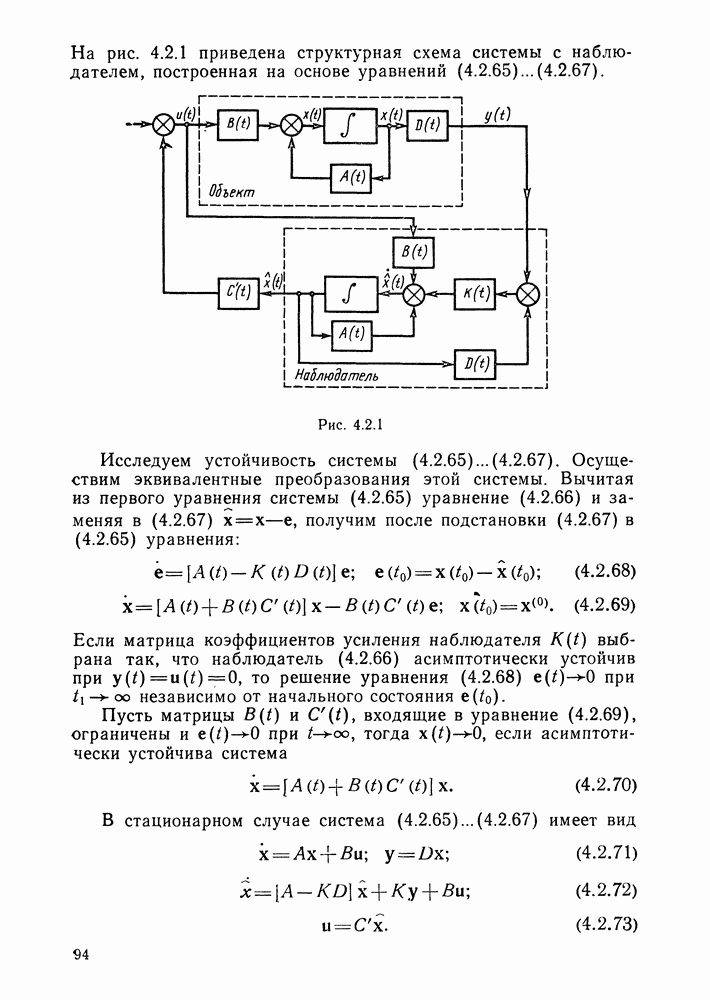
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
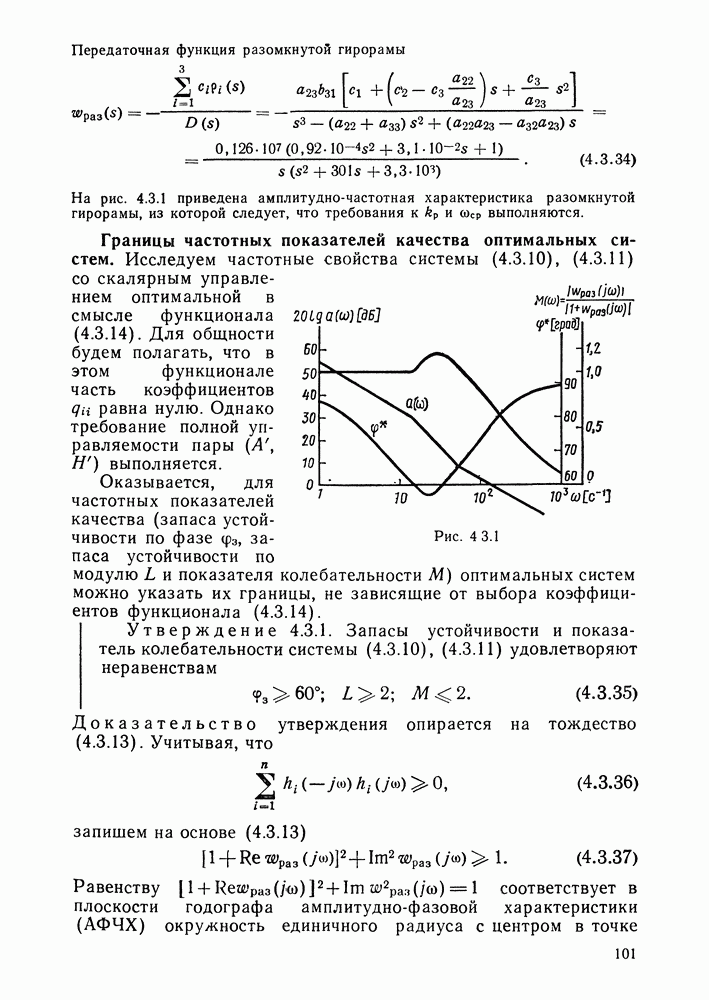
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
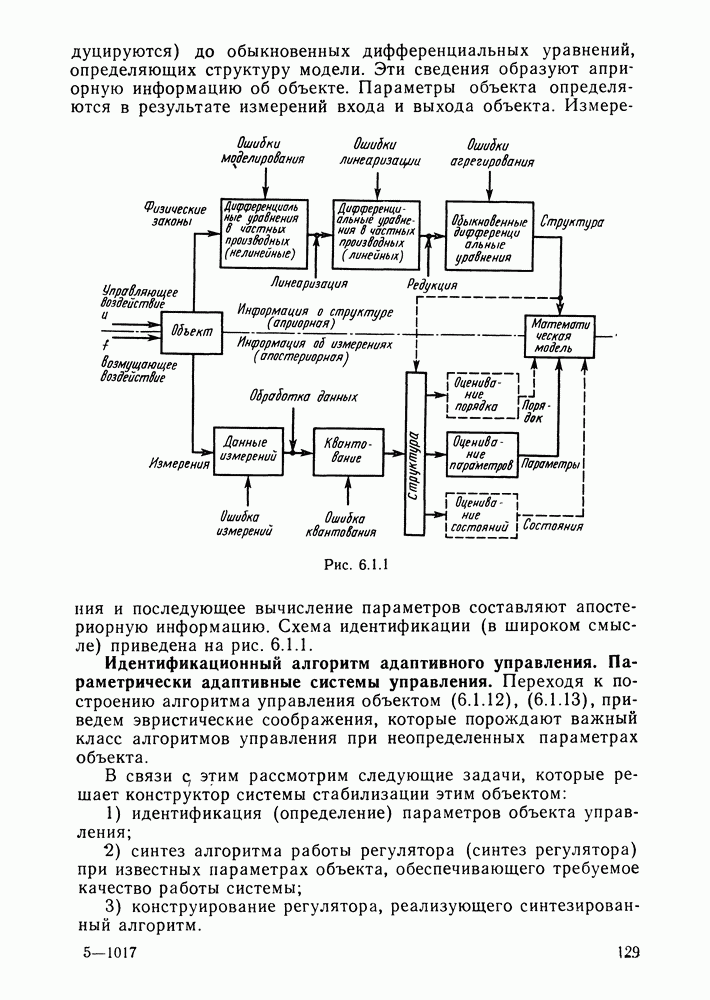
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
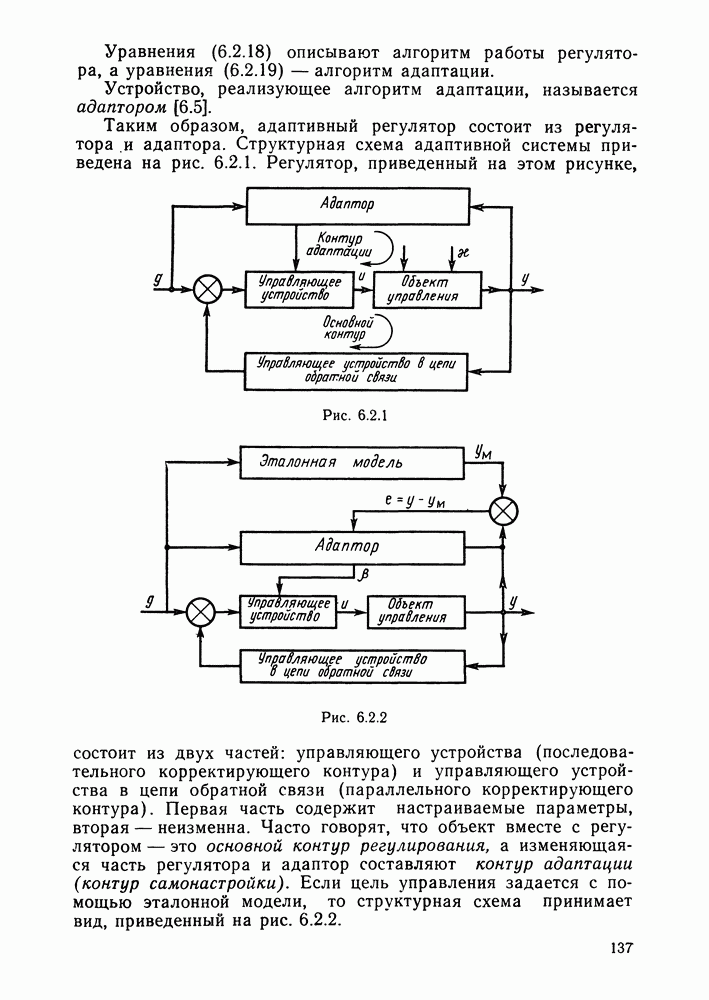
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
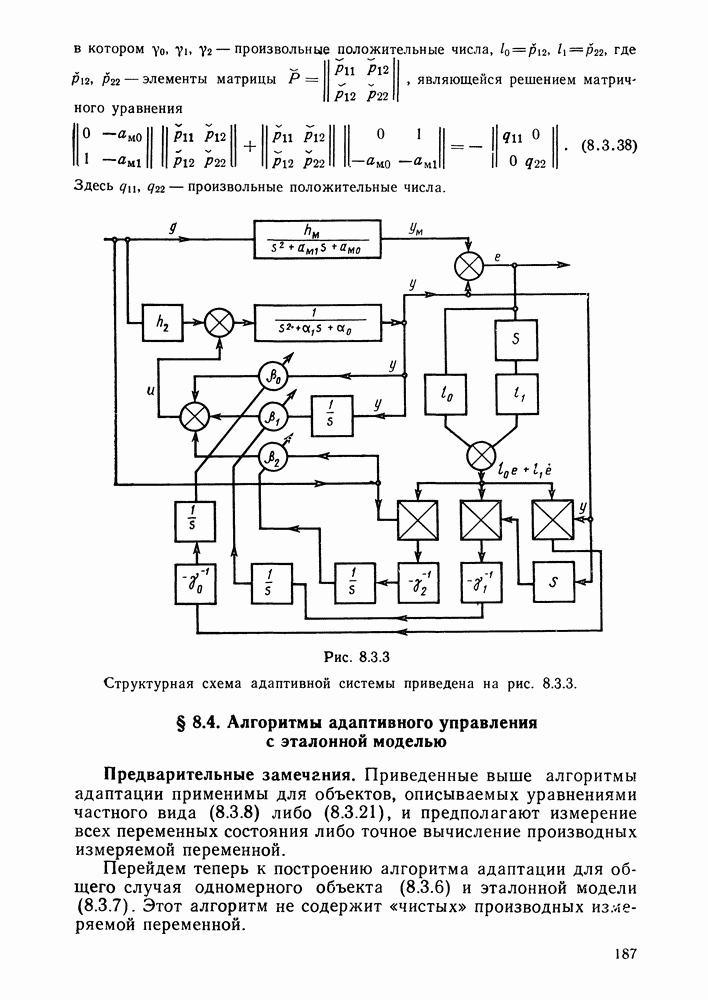
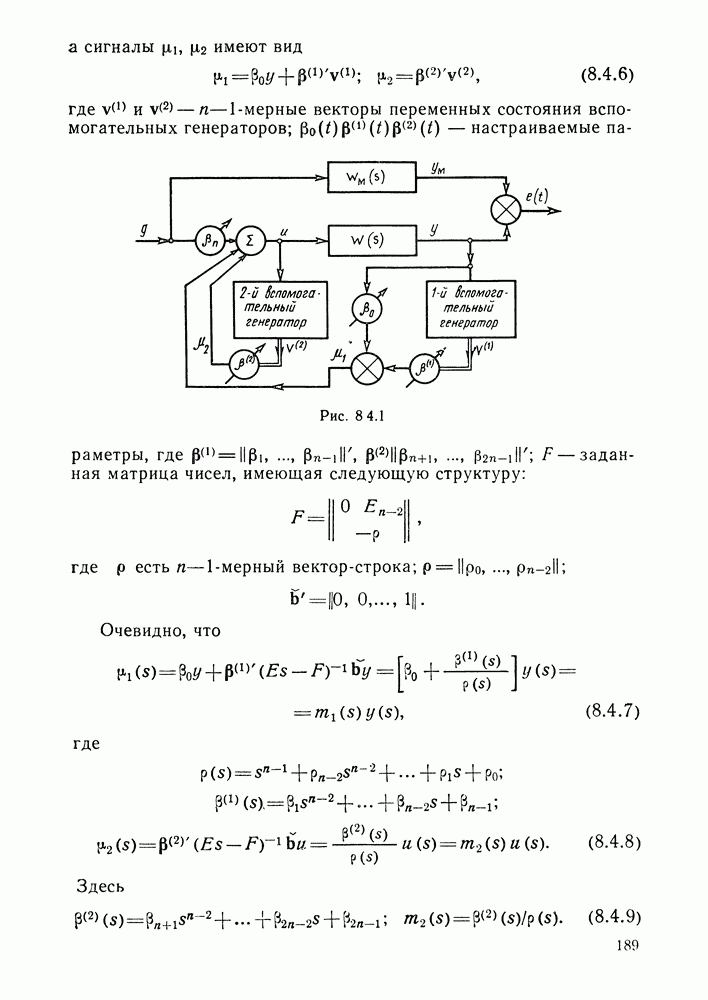
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
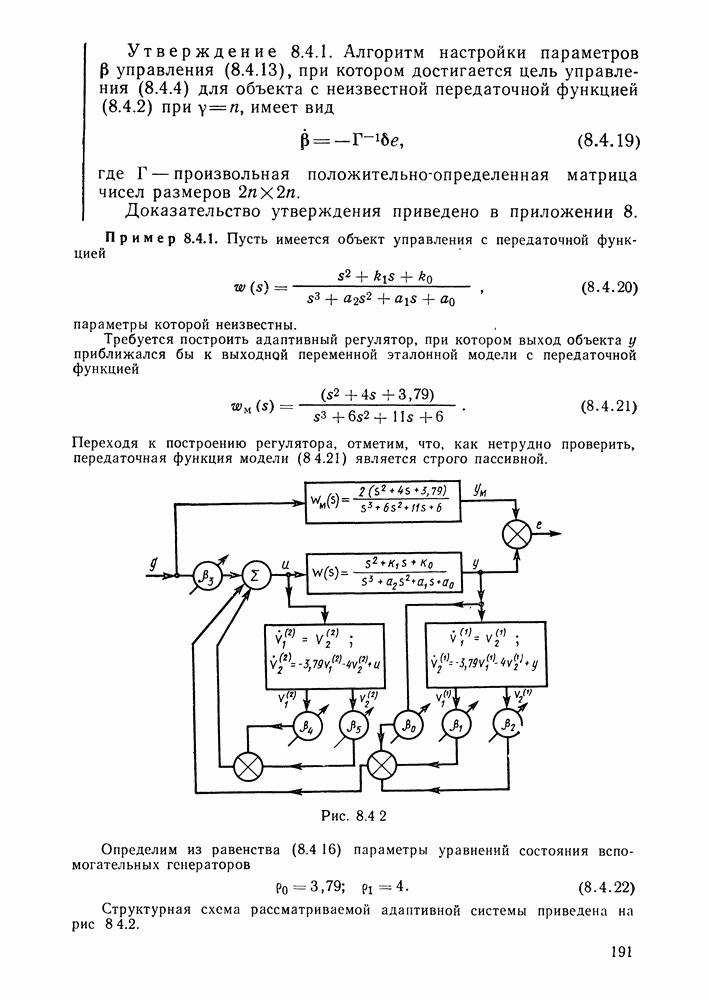
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
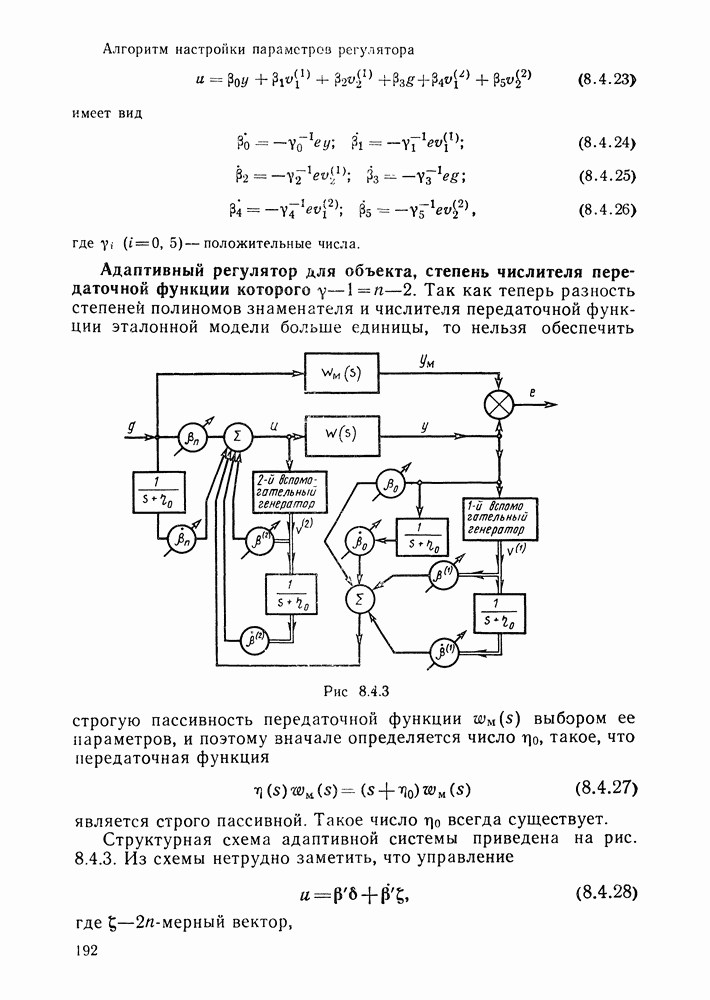
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ