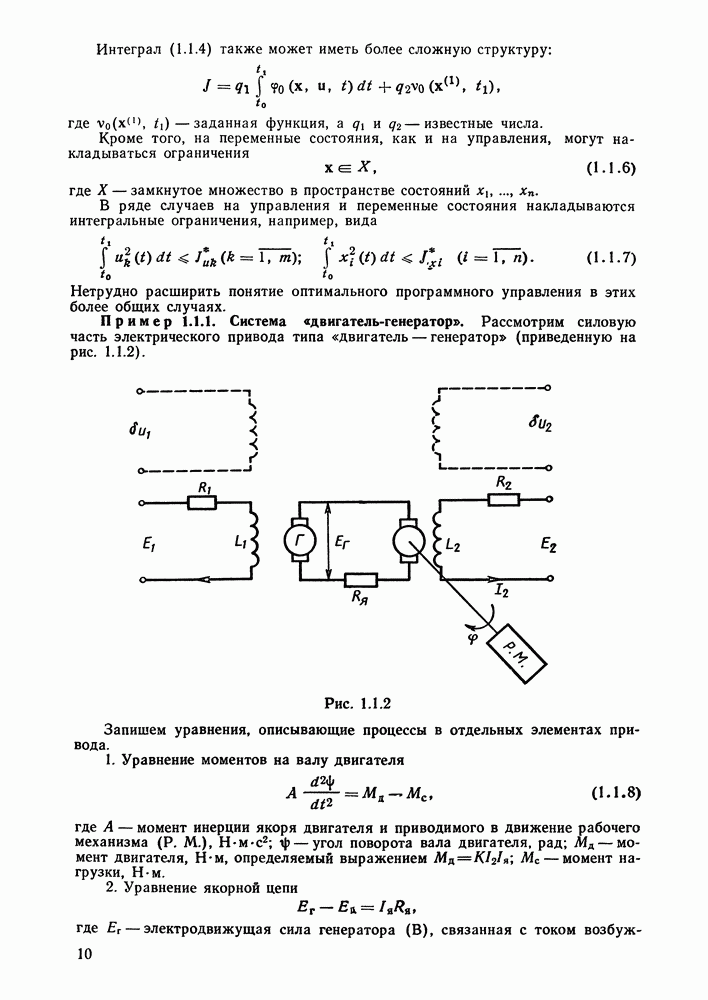
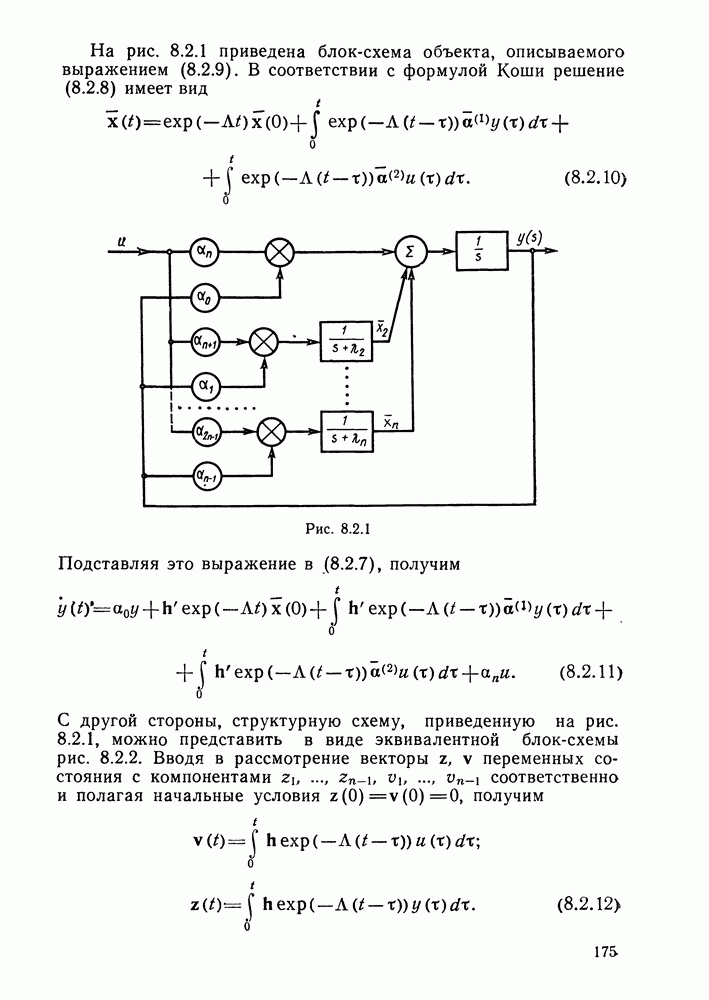
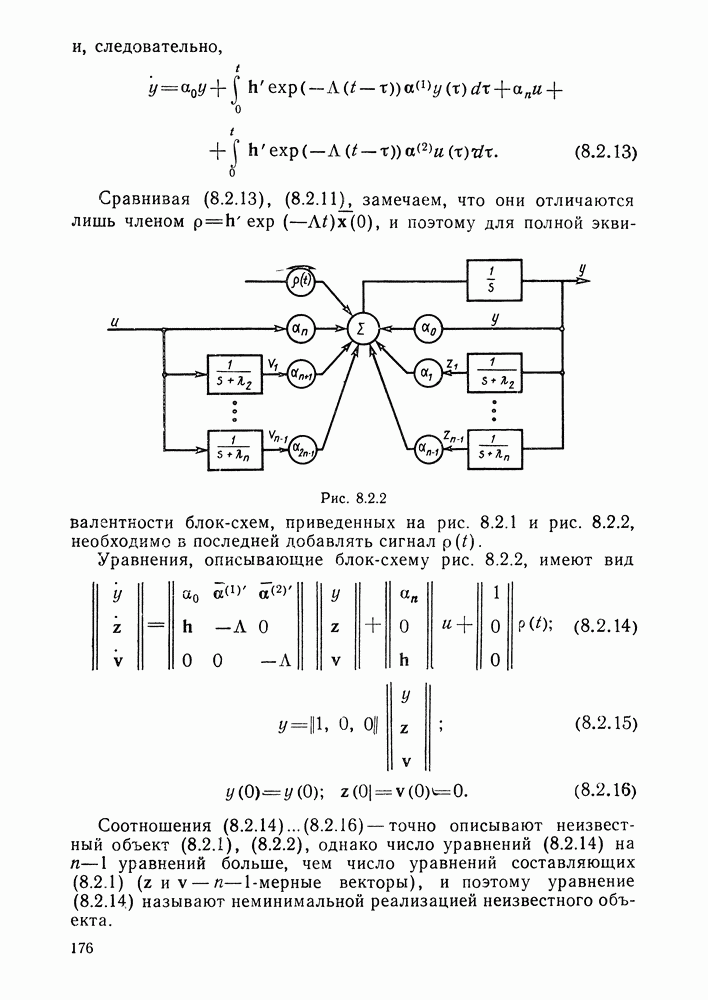
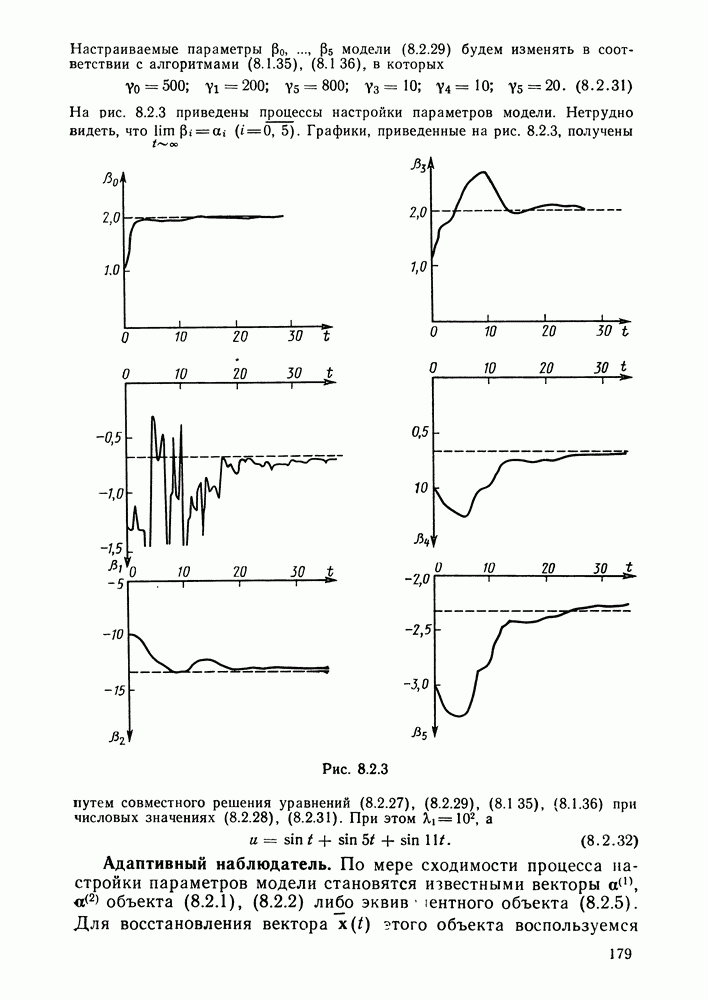
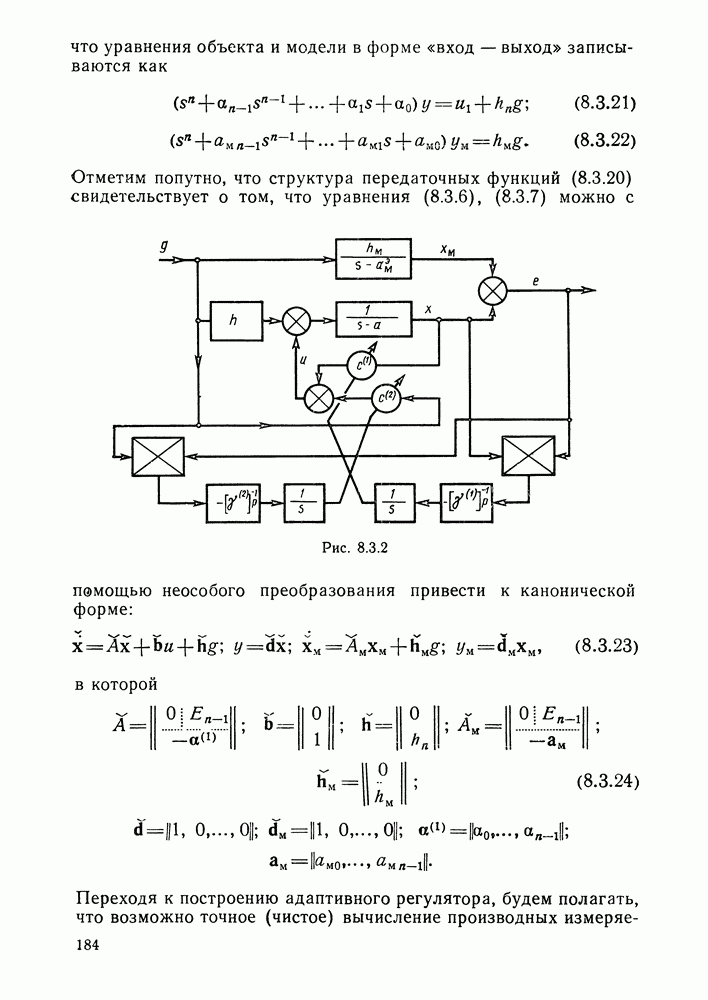
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
Переходя к построению алгоритма управления объектом (6.1.12), (6.1.13), приведем эвристические соображения, которые порождают важный класс алгоритмов управления при неопределенных параметрах объекта.
В связи с этим рассмотрим следующие задачи, которые решает конструктор системы стабилизации этим объектом:
1) идентификация (определение) параметров объекта управления;
2) синтез алгоритма работы регулятора (синтез регулятора) при известных параметрах объекта, обеспечивающего требуемое качество работы системы;
3) конструирование регулятора, реализующего синтезированный алгоритм.
Поскольку параметры объекта (6.1.12), (6.1.13) изменяются, то эти три задачи должны решаться в процессе работы объекта, притом решаться автоматически, без участия человека. Другими словами, если при неизвестных, но постоянных параметрах объекта указанные задачи решались в процессе проектирования системы, то при изменяющихся во времени параметрах они должны решаться в естественных условиях работы объекта («на борту» объекта) и в темпе работы объекта. Это означает, что алгоритм регулятора должен изменяться в процессе работы системы, приспосабливаясь (самонастраиваясь, адаптируясь) за время f к изменяющимся параметрам объекта так, чтобы качество работы системы оставалось неизменным. Для построения такого алгоритма запишем уравнение регулятора для объекта (6.1.18) с неопределенными параметрами
 (6.1.23)
(6.1.23)
где  —
—  -мерный вектор состояния регулятора,
-мерный вектор состояния регулятора,  — матрица,
— матрица,  — векторы,
— векторы,  — скаляр, зависящие от неизвестного вектора параметров (а). Зависимости параметров регулятора (6.1.23) от параметров объекта (6.1.18) могут быть как аналитическими (заданными с помощью формул), так и алгоритмическими.
— скаляр, зависящие от неизвестного вектора параметров (а). Зависимости параметров регулятора (6.1.23) от параметров объекта (6.1.18) могут быть как аналитическими (заданными с помощью формул), так и алгоритмическими.
Последнее следует понимать в том смысле, что существует алгоритм (процедура), с помощью которого для каждого фиксированного вектора а можно найти матрицу  вектора
вектора  и скаляр
и скаляр  . В качестве таких алгоритмов могут выступать, в частности, процедуры синтеза оптимальных регуляторов, приведенные в главах 4 и 5.
. В качестве таких алгоритмов могут выступать, в частности, процедуры синтеза оптимальных регуляторов, приведенные в главах 4 и 5.
Если в результате идентификации определено истинное значение  вектора а, то, полагая в
вектора а, то, полагая в  , получим искомый регулятор.
, получим искомый регулятор.
При таком подходе процесс управления не может быть начат, пока не закончится идентификация параметров и не будут вычислены (по формулам либо на основе процедур) матрица  , векторы
, векторы  и скаляр
и скаляр  регулятора (6.1.23).
регулятора (6.1.23).
Естественно, не дожидаясь окончания процесса идентификации, использовать оценки а, доставляемые алгоритмом (6.1.22), и тогда уравнение (6.1.23) примет вид
 (6.1.24)
(6.1.24)
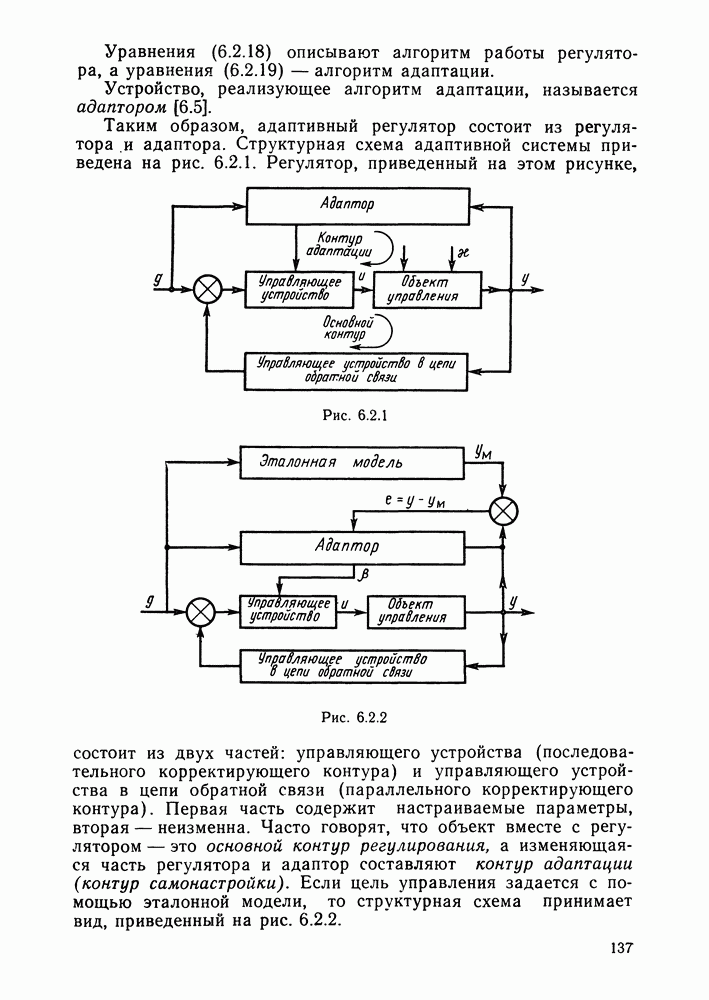
Уравнения (6.1.22), (6.1.24) описывают идентификационный алгоритм адаптивного управления. Системы с идентификационным алгоритмом называют параметрически адаптивными системами.
Отметим, что уравнения (6.1.24) также можно записать в форме «вход — выход»:

В дискретном случае уравнение принимает вид

Пример 6.1.1. Пусть объектом управления является некоторый химикотехнологический процесс, протекающий в замкнутом резервуаре-реакторе [6.10]. В моменты времени  в реактор поступает сырье, имеющее температуру
в реактор поступает сырье, имеющее температуру  (параметр Т, как и ранее, опускаем), и доза катализатора
(параметр Т, как и ранее, опускаем), и доза катализатора  . Количество продукта реакции
. Количество продукта реакции  зависит от концентрации промежуточного вещества
зависит от концентрации промежуточного вещества  :
:
 (6.1.26)
(6.1.26)
а величина  определяется значениями
определяется значениями  :
:
 (6.1.27)
(6.1.27)
Величины  доступны непосредственному измерению, а доза катализатора
доступны непосредственному измерению, а доза катализатора  является управляющим воздействием, которое влияет на ход процесса.
является управляющим воздействием, которое влияет на ход процесса.
Коэффициенты a, b, d соотношений (6.1.26), (6.1.27) зависят от активности катализатора, скорости протекания реакции, конструкции установки и т. п.
Пусть целью управления является поддержание выходного продукта  на заданном уровне
на заданном уровне  . Если значения параметров а,
. Если значения параметров а,  известны точно, то легко построить алгоритм работы регулятора, обеспечивающего достижение цели управления. Этот алгоритм имеет вид
известны точно, то легко построить алгоритм работы регулятора, обеспечивающего достижение цели управления. Этот алгоритм имеет вид
 (6.1.28)
(6.1.28)
Действительно, подставляя (6.1.28) в (6.1.27), получим, что
 (6.1.29)
(6.1.29)
В реальных условиях многие факторы, от которых зависят параметры  , недоступны непосредственному измерению либо могут изменяться во времени неизвестным образом (например, активность катализатора меняется при его отравлении, при переходе на новую партию катализатора и т. д.). Поэтому управление осуществляется в условиях неопределенности, когда законом управления (6.1.28) воспользоваться нельзя.
, недоступны непосредственному измерению либо могут изменяться во времени неизвестным образом (например, активность катализатора меняется при его отравлении, при переходе на новую партию катализатора и т. д.). Поэтому управление осуществляется в условиях неопределенности, когда законом управления (6.1.28) воспользоваться нельзя.
Переходя к построению идентификационного алгоритма адаптивного управления, обозначим
 (6.1.30)
(6.1.30)
и запишем закон управления (6.1.28) как функцию неопределенных параметров 

Для определения коэффициентов закона управления (6.1.31) идентифицируем параметры объекта (6.1.26), (6.1.27), уравнения которого можно с учетом введенных обозначений записать в виде
 (6.1.32)
(6.1.32)
При  получим систему из трех алгебраических уравнений:
получим систему из трех алгебраических уравнений: 
 (6.1.33)
(6.1.33)
решая которую найдем числа  . Подставляя эти числа в (6.1.31), получим управление, обеспечивающее достижение цели (6.1.29).
. Подставляя эти числа в (6.1.31), получим управление, обеспечивающее достижение цели (6.1.29).
Уравнение (6.1.31) вместе с процедурой решения алгебраических уравнений (6.1 33) образуют алгоритм идентификационного адаптивного управления.
Заметим, что столь простой алгоритм адаптивного управления обусловлен во многом доступностью для измерения  и отсутствием помех в измерении
и отсутствием помех в измерении  . Если
. Если  недоступно непосредственному измерению либо присутствуют помехи в измерении, это приводит к процессу идентификации, описываемому уравнением вида (6.1 22).
недоступно непосредственному измерению либо присутствуют помехи в измерении, это приводит к процессу идентификации, описываемому уравнением вида (6.1 22).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
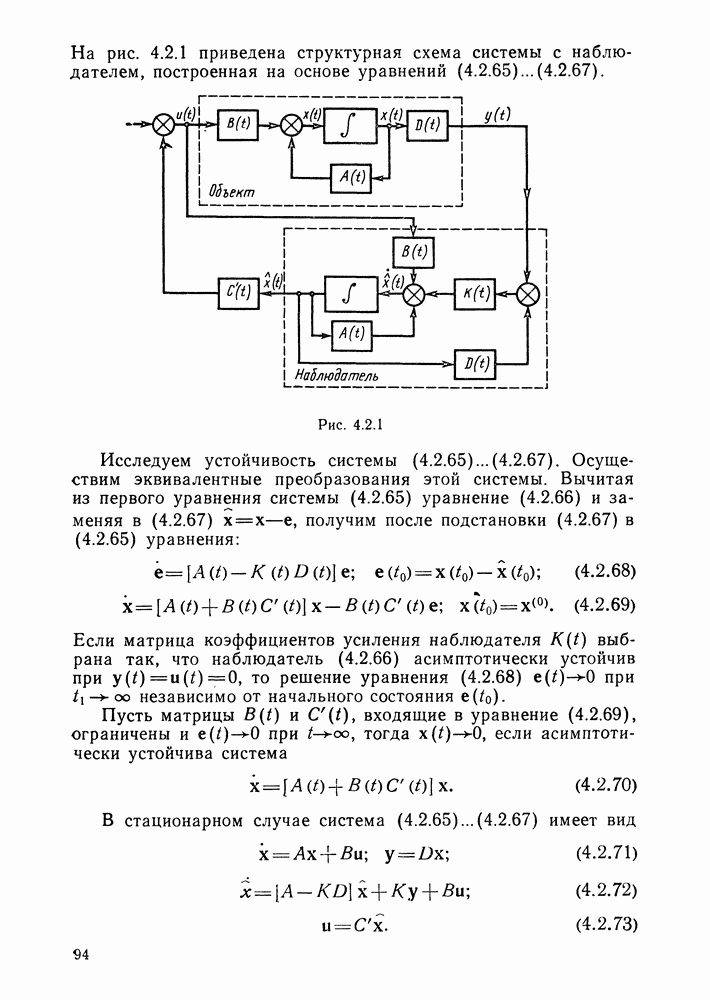
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
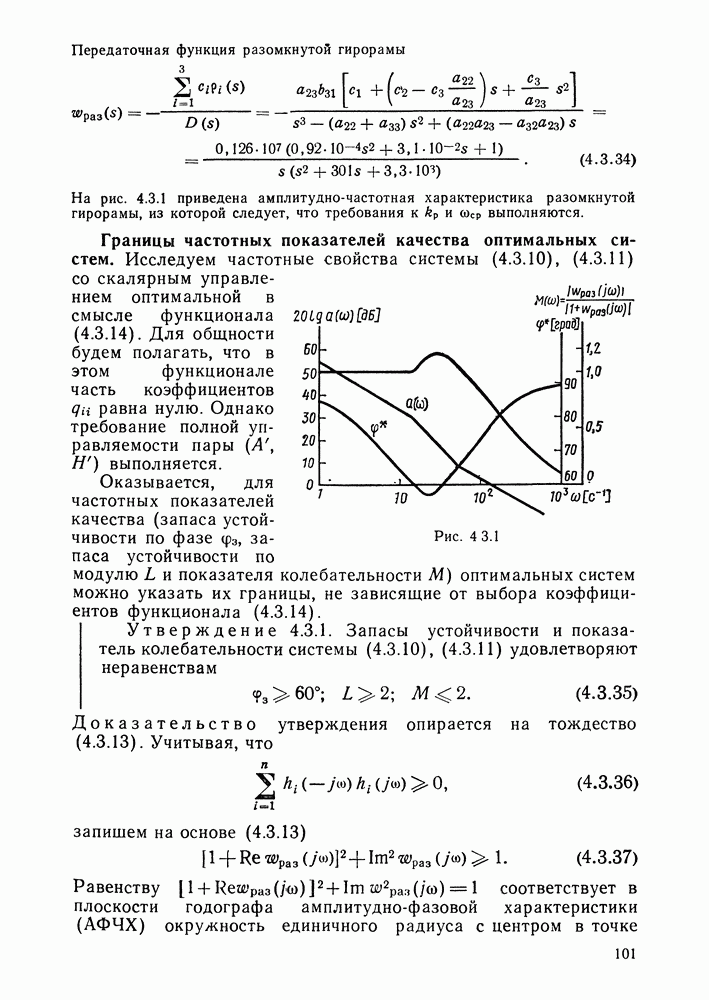
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
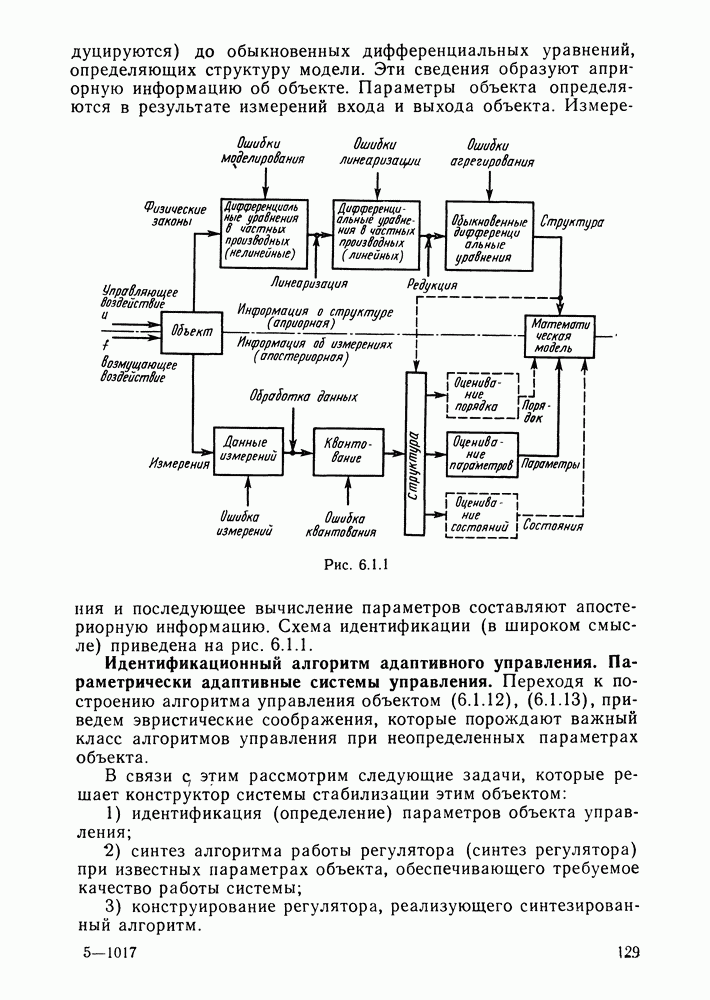
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
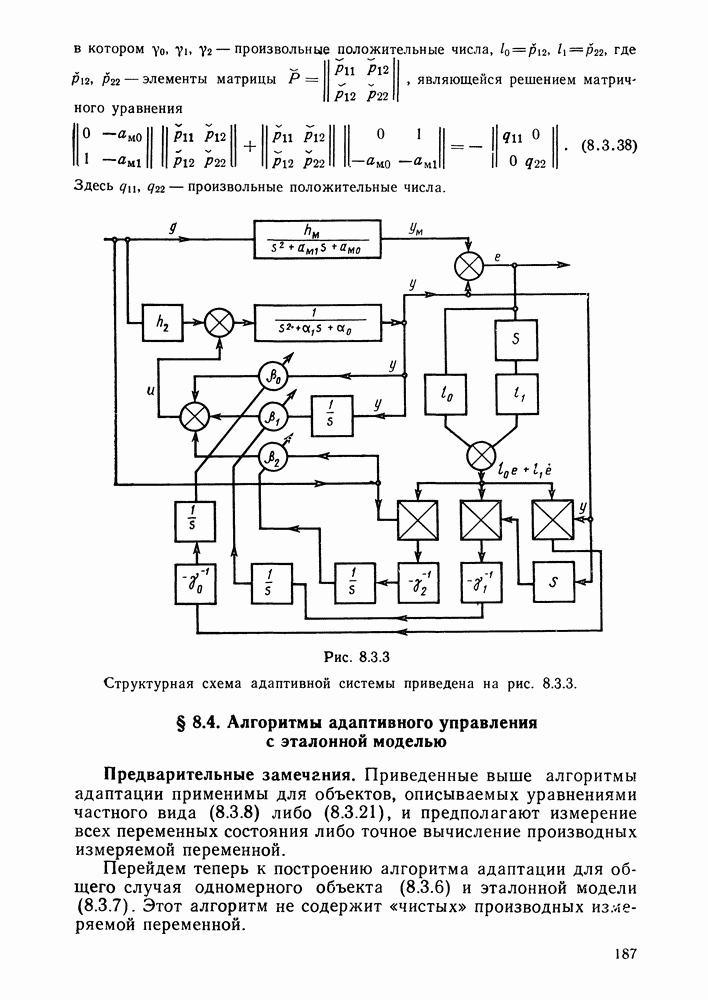
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
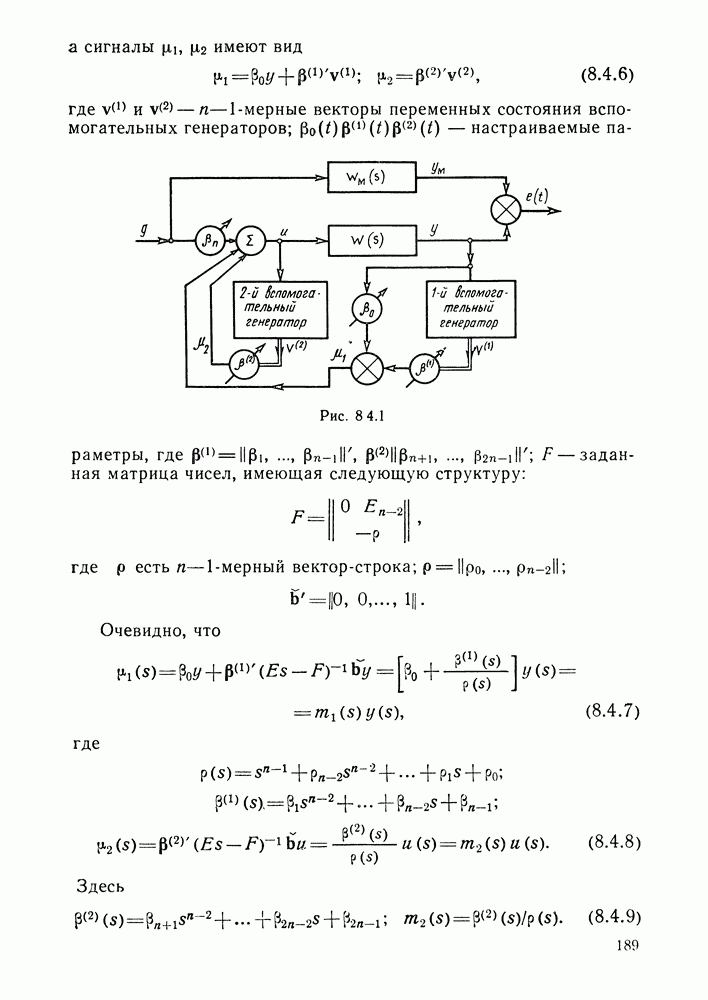
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
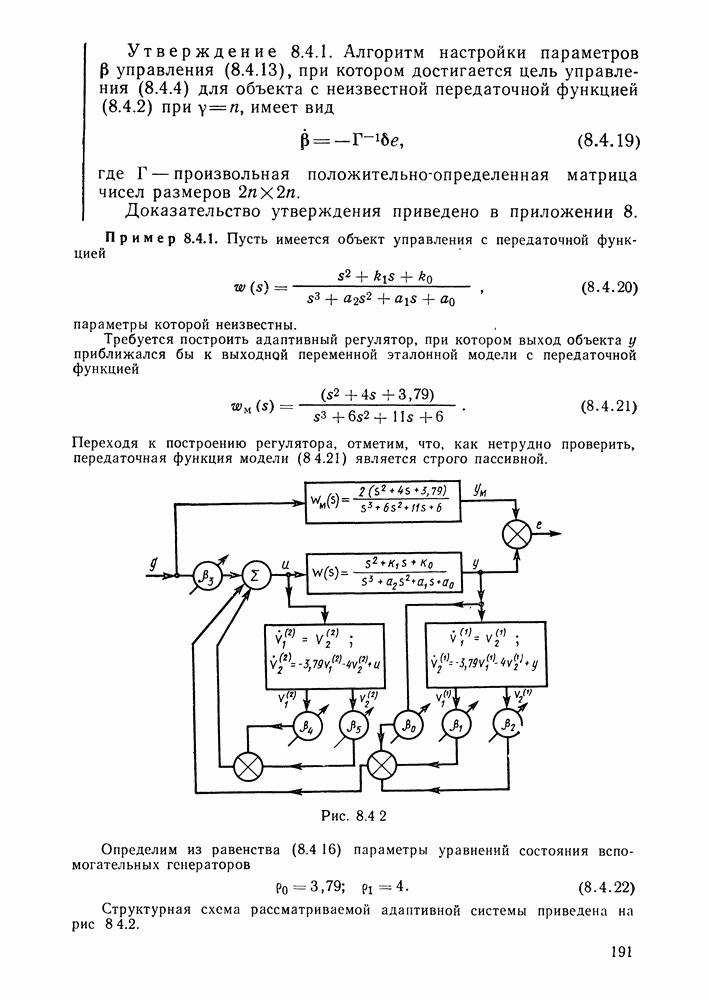
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
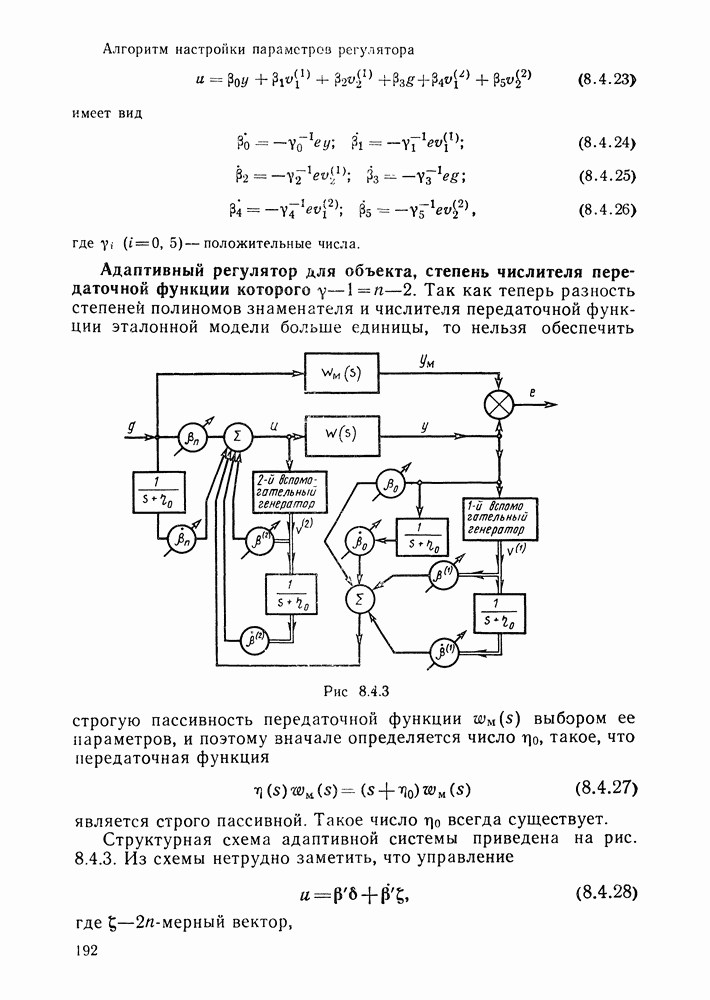
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ