| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Принцип максимума.
Учтем теперь ограничения (2.2.2) на управление. Если в процессе оптимального управления функции  не достигают границ множества (2.2.2) (что означает
не достигают границ множества (2.2.2) (что означает  )
)  то для них выполняются соотношения (2.2.13), (2.2.14). Однако часто оптимальное управление принимает граничные значения
то для них выполняются соотношения (2.2.13), (2.2.14). Однако часто оптимальное управление принимает граничные значения  либо —
либо —  , более того, оптимальное управление может скачком переходить с одной границы на другую. Такие управления уже являются кусочно-непрерывными функциями времени.
, более того, оптимальное управление может скачком переходить с одной границы на другую. Такие управления уже являются кусочно-непрерывными функциями времени.
При попадании оптимального управления на границу множества U соотношения (2.2.13), (2.2.14) нарушаются. Оптимальные управления удовлетворяют в этом случае принципу максимума Л. С. Понтрягина, установленного и доказанного в форме приведенной ниже - теоремы.
Переходя к этой теореме, сделаем некоторые пояснения. Возьмем произвольное допустимое управление  и при начальных условиях
и при начальных условиях  найдем решение системы (2.2.1):
найдем решение системы (2.2.1):  .
.
Подставляя это решение и управление  в (2.2.8), определим, пока при некоторых произвольных начальных условиях
в (2.2.8), определим, пока при некоторых произвольных начальных условиях  , решение (2.2.8):
, решение (2.2.8):  . При фиксированных (постоянных) значениях векторов
. При фиксированных (постоянных) значениях векторов  функция Н становится функцией вектора
функция Н становится функцией вектора  . Максимум этой функции по и обозначим через
. Максимум этой функции по и обозначим через  :
:

Максимум (наибольшее значение) непрерывной функции  может достигаться как в точках локального максимума этой функции, в которых
может достигаться как в точках локального максимума этой функции, в которых

так и на границах  множества
множества  .
.
Теорема 2.2.1 (принцип максимума Л. С. Понтрягина). Пусть  , — такое допустимое управление, что соответствующие ему решения
, — такое допустимое управление, что соответствующие ему решения  уравнения (2.2.11), исходящие в момент
уравнения (2.2.11), исходящие в момент  из состояния (2.2.3), (2.2.7), проходят в момент времени
из состояния (2.2.3), (2.2.7), проходят в момент времени  через точку
через точку  .
.
Для оптимальности управления (при котором  ) принимает наименьшее значение) необходимо существование таких ненулевых непрерывных функций
) принимает наименьшее значение) необходимо существование таких ненулевых непрерывных функций  удовлетворяющих уравнениям (2.2.12), что при любом
удовлетворяющих уравнениям (2.2.12), что при любом  функция
функция  переменного
переменного  достигает при
достигает при  максимума
максимума

при этом в конечный момент времени  выполняются соотношения
выполняются соотношения

Если  удовлетворяют (2.2.11), (2.2.12) и (2.2.17), то функции
удовлетворяют (2.2.11), (2.2.12) и (2.2.17), то функции  переменного t являются постоянными и поэтому проверку соотношений (2.2.18) можно проводить не обязательно в момент времени
переменного t являются постоянными и поэтому проверку соотношений (2.2.18) можно проводить не обязательно в момент времени  а в любой момент
а в любой момент  .
.
Доказательство теоремы является достаточно сложным, и поэтому в приложении 2 приведен лишь вывод основного соотношения (2.2.17) теоремы для случая свободного правого конца ( не задан) и фиксированного
не задан) и фиксированного  .
.
Соотношения (2.2.17) и (2.2.18) можно записать в более простой форме:

Таким образом, центральным в теореме 2.2.1 является условие максимума (2.2.19). Оно означает, что если  — оптимальные управления, а
— оптимальные управления, а  -оптимальные траектории, то непременно найдутся такая постоянная
-оптимальные траектории, то непременно найдутся такая постоянная  и такие решения
и такие решения  ),
),  системы (2.2.12), что функция
системы (2.2.12), что функция  их,
их,  переменных
переменных  при всех
при всех  будет достигать максимума на U именно при оптимальных управлениях
будет достигать максимума на U именно при оптимальных управлениях  . Поэтому теорему 2.2.1, дающую необходимое условие оптимальности в задачах оптимального управления, принято называть принципом максимума. Отметим, что во внутренних точках множества U для оптимального управления выполняются условия (2.2.13), (2.2.14), которые являются необходимыми для (2.2.19).
. Поэтому теорему 2.2.1, дающую необходимое условие оптимальности в задачах оптимального управления, принято называть принципом максимума. Отметим, что во внутренних точках множества U для оптимального управления выполняются условия (2.2.13), (2.2.14), которые являются необходимыми для (2.2.19).
Практическое применение принципа максимума.
Как же практически воспользоваться условием (2.2.19), ведь функции и постоянная
и постоянная  , входящие в это условие, неизвестны?
, входящие в это условие, неизвестны?
Здесь поступают следующим образом: рассматривая функцию  ) как функцию
) как функцию  переменных
переменных  и считая переменные
и считая переменные  параметрами, решают задачу максимизации функции
параметрами, решают задачу максимизации функции  и находят функцию
и находят функцию

на которой достигается наибольшее значение функции  .
.
В ряде случаев функция (2.2.20) может быть записана в явном виде. Например, если правые части (2.2.1) имеют структуру

а подынтегральное выражение функционала (2.2.5)

множество описывается U неравенствами (2.2.2), то

и эта функция достигает [2.8] наибольшего значения на U в точке с координатами

или

Формула (2.2.22) дает большой объем информации о структуре оптимального управления:  координата оптимального управления является ступенчатой (кусочно-постоянной) функцией со значениями
координата оптимального управления является ступенчатой (кусочно-постоянной) функцией со значениями  при этом моменты переключения определяются условием
при этом моменты переключения определяются условием

Итак, допустим, что функция (2.2.20) известна. Рассмотрим систему  дифференциальных уравнений
дифференциальных уравнений


Функции  и
и  , входящие в правые части этих уравнений, известны. Общее решение системы (2.2.24), (2.2.25) зависит от произвольных постоянных, которые определяются из краевых условий (2.2.3), (2.2.4). Задача интегрирования уравнений (2.2.24), (2.2.25) при краевых условиях (2.2.3), (2.2.4) называется краевой задачей (двухточечной краевой задачей).
, входящие в правые части этих уравнений, известны. Общее решение системы (2.2.24), (2.2.25) зависит от произвольных постоянных, которые определяются из краевых условий (2.2.3), (2.2.4). Задача интегрирования уравнений (2.2.24), (2.2.25) при краевых условиях (2.2.3), (2.2.4) называется краевой задачей (двухточечной краевой задачей).
Таким образом, принцип максимума позволяет свести решение задачи об оптимальном программном управлении к решению краевой задачи.
Трудность ее решения состоит в том, что интегрирование уравнений (2.2.24), (2.2.25) в «прямом времени» не представляется возможным, так как неизвестны начальные условия  Один из возможных подходов к решению краевой задачи заключается в следующем. Задаваясь произвольным вектором
Один из возможных подходов к решению краевой задачи заключается в следующем. Задаваясь произвольным вектором  и интегрируя (2.2.24), (2.2.25) при известных начальных условиях
и интегрируя (2.2.24), (2.2.25) при известных начальных условиях  , найдем функции
, найдем функции  и при
и при  проверим выполнение равенства (2.2.4). Если оно нарушается, задаемся другим вектором
проверим выполнение равенства (2.2.4). Если оно нарушается, задаемся другим вектором  и, интегрируя (2.2.24), (2.2.25) при начальных условиях
и, интегрируя (2.2.24), (2.2.25) при начальных условиях  , получим при
, получим при  вектор
вектор  .
.
Если он не совпадает с заданным, продолжаем процесс до тех пор, пока не найдется такой вектор  что условия (2.2.4) будут выполняться с приемлемой точностью. При этом подходе используются градиентные методы, когда
что условия (2.2.4) будут выполняться с приемлемой точностью. При этом подходе используются градиентные методы, когда  определяется из условия минимума «расстояния»
определяется из условия минимума «расстояния»  от заданного вектора
от заданного вектора  .
.
В вычислительной математике разработан ряд методов приближенного численного решения краевых задач: метод стрельбы, метод прогонки, ряд итерационных методов [2.10], [2.11]. Во многих случаях не представляется возможным найти из условия (2.2.19) явный вид (2.2.22) оптимального управления. Тогда уравнения (2.2.1), (2.2.6), сопряженная система (2.2.12) и условия максимума (2.2.19) образуют краевую задачу принципа максимума. Эта задача имеет ряд специфических особенностей, затрудняющих применение стандартных численных методов решения краевых задач. К числу таких особенностей относятся разрывы функций  удовлетворяющих условию максимума (2.2.14), их неединственность, нелинейный характер зависимости (2.2.20) даже в линейных системах. Кроме того, особенностью краевых задач, связанных с принципом максимума даже в случаях, когда удается найти явный вид управлений (2.2.20), является их плохая сходимость, вызванная неустойчивостью системы (2.2.24), (2.2.25). Ряд приемов решения краевых задач принципа максимума изложен, например, в [2.12, 2.13].
удовлетворяющих условию максимума (2.2.14), их неединственность, нелинейный характер зависимости (2.2.20) даже в линейных системах. Кроме того, особенностью краевых задач, связанных с принципом максимума даже в случаях, когда удается найти явный вид управлений (2.2.20), является их плохая сходимость, вызванная неустойчивостью системы (2.2.24), (2.2.25). Ряд приемов решения краевых задач принципа максимума изложен, например, в [2.12, 2.13].
Отметим в заключение, что, несмотря на различные методы численного решения краевой задачи принципа максимума, процесс решения каждой оптимизации на основе этого принципа является самостоятельной творческой задачей, решаемой в рамках той частной отрасли динамики, к которой относится объект управления, с учетом его специфических особенностей, используемых для улучшения сходимости численного решения краевой задачи.
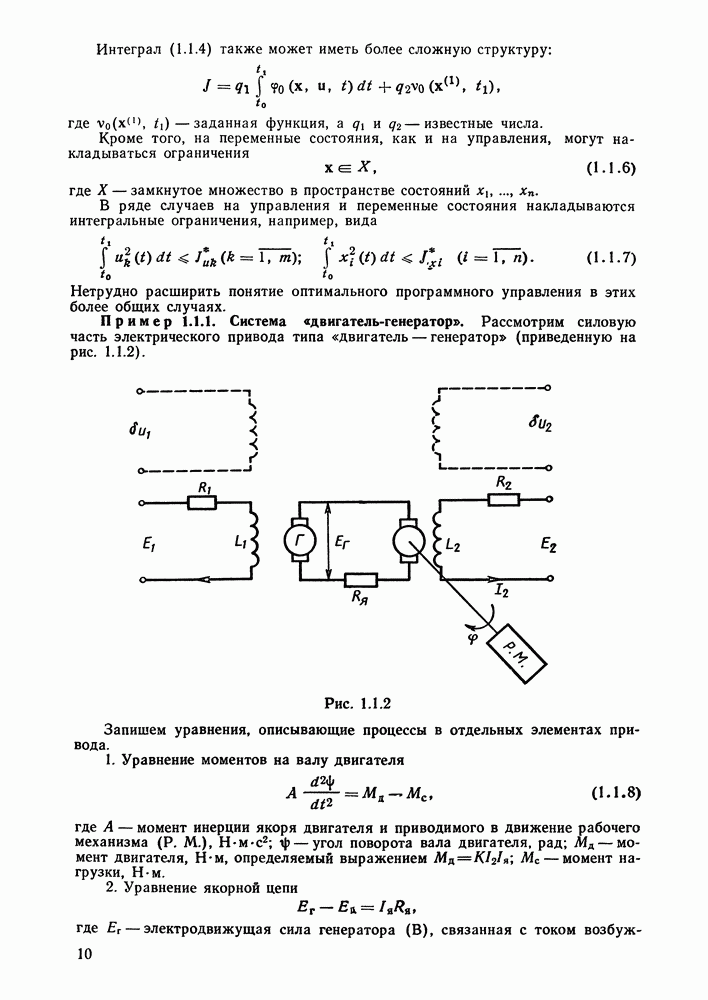
Пример 2.2.1. Построение оптимального по расходу топлива управления [2.3].
Рассмотрим объект управления, описываемый уравнениями

Пусть на управление наложено ограничение

Функционал оптимизации, выражающий расход топлива, имеет вид

Заданы начальное состояние

и условие в момент времени 

Требуется найти  , при котором объект (2.2.26) переходит из состояния (2.2.29) в состояние (2.2.30), при этом выполняются ограничения (2.2.27), а функционал (2.2.28) принимает наименьшее значение.
, при котором объект (2.2.26) переходит из состояния (2.2.29) в состояние (2.2.30), при этом выполняются ограничения (2.2.27), а функционал (2.2.28) принимает наименьшее значение.
Переходя к определению оптимального управления на основе принципа максимума, сформируем функцию

уравнения для вспомогательных переменных

Управление  , доставляющее максимум функции (2.2.31), определяется как
, доставляющее максимум функции (2.2.31), определяется как

Уравнения (2.2.26), (2.2.32), (2.2.33) составляют краевую задачу. Переходя к ее исследованию, запишем решение системы (2.2.32):

где  — неизвестные числа, которые необходимо определить так, чтобы управление (2.2.33) привело объект (2.2.26) в состояние (2.2.30).
— неизвестные числа, которые необходимо определить так, чтобы управление (2.2.33) привело объект (2.2.26) в состояние (2.2.30).
Найдем решение системы (2.2.26) при  и
и  . В первом случае решение этой системы имеет вид
. В первом случае решение этой системы имеет вид  . Оно зависит от постоянных R и р, при этом
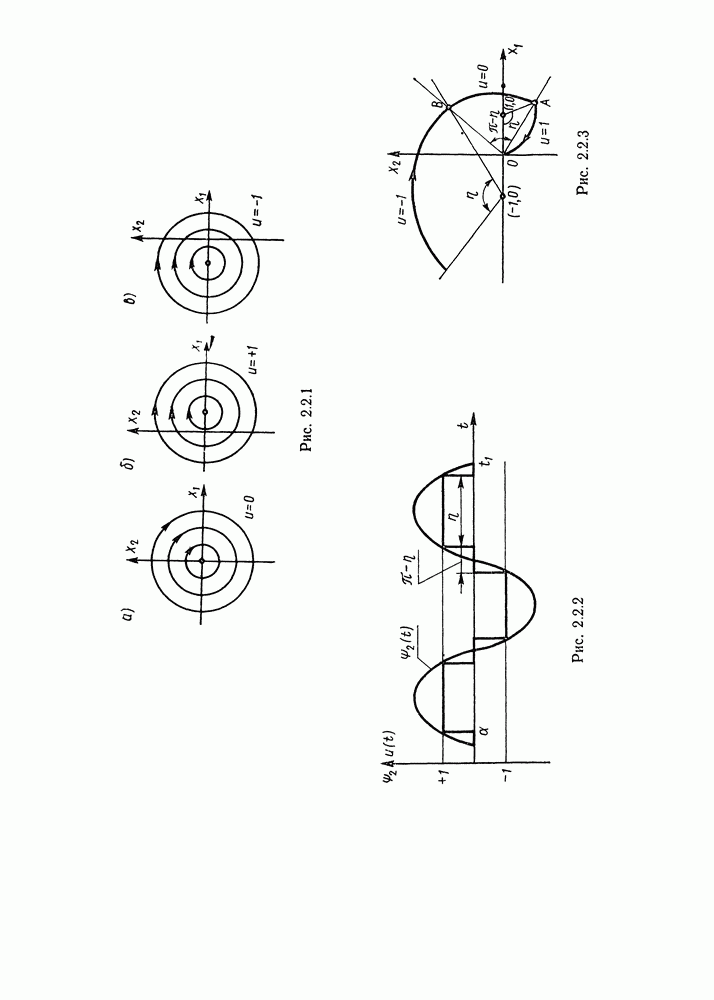
. Оно зависит от постоянных R и р, при этом  . Фазовые траектории этой системы представляют собой окружности с центром в начале координат (рис. 2.2.1, а). Фазовые траектории системы (2.2.26) при
. Фазовые траектории этой системы представляют собой окружности с центром в начале координат (рис. 2.2.1, а). Фазовые траектории системы (2.2.26) при  и
и  также являются окружностями, центры которых расположены в точках
также являются окружностями, центры которых расположены в точках  соответственно (рис. 2.2.1, б, в).
соответственно (рис. 2.2.1, б, в).

Рис. 2.2.1.

Рис. 2.2.2.

Рис. 2.2.3.
Пусть некоторым оптимальным управлениям  объект (2.2.26) переводится из начального состояния
объект (2.2.26) переводится из начального состояния  в начало координат. Тогда на последнем участке оптимальной траектории управление
в начало координат. Тогда на последнем участке оптимальной траектории управление  равно
равно  либо —1. Для определенности будем полагать, что оптимальное управление имеет вид, изображенный на рис. 2.2.2. В этом случае последний участок фазовой траектории представляет собой дугу величиной
либо —1. Для определенности будем полагать, что оптимальное управление имеет вид, изображенный на рис. 2.2.2. В этом случае последний участок фазовой траектории представляет собой дугу величиной  с центром в точке (1, 0) (рис. 2.2.3). Управление
с центром в точке (1, 0) (рис. 2.2.3). Управление  при
при  , и поэтому соответствующий участок фазовой траектории является дугой с центром в точке (0, 0) и центральным углом
, и поэтому соответствующий участок фазовой траектории является дугой с центром в точке (0, 0) и центральным углом  .
.
В точке А происходит переключение управления  на
на  , а в точке
, а в точке  на
на  . Задаваясь различными значениями чисел
. Задаваясь различными значениями чисел  и
и  , получим различные числа
, получим различные числа  . Строя для каждого числа
. Строя для каждого числа  траекторию методом «попятного движения (каким была построена траектория на рис. 2 2.3), определяем, «попал» ли левый конец этой траектории в точку
траекторию методом «попятного движения (каким была построена траектория на рис. 2 2.3), определяем, «попал» ли левый конец этой траектории в точку  . Пусть для некоторого
. Пусть для некоторого  траектория ОАВ прошла через точку
траектория ОАВ прошла через точку  . Для такого числа
. Для такого числа  нетрудно определить числа
нетрудно определить числа  и
и  , а через них начальные условия
, а через них начальные условия  , которые и разрешают краевую задачу.
, которые и разрешают краевую задачу.
Условия трансверсальности.
Пусть в задаче об оптимальном программном управлении начальное (2.2.3) и конечное (2.2.4) состояния не фиксированы ( заданы) и могут перемещаться по поверхностям: левый конец траектории
заданы) и могут перемещаться по поверхностям: левый конец траектории  по поверхности
по поверхности  , а правый — по поверхности
, а правый — по поверхности  .
.
Теорема 2.2.2 (принцип максимума) в этом случае в основном сохраняется (так как управление, оптимальное при подвижных концах траектории  , является оптимальным и в частном случае, когда концы закреплены), однако
, является оптимальным и в частном случае, когда концы закреплены), однако  граничных условий для системы (2.2.24), (2.2.25), решения которой содержат
граничных условий для системы (2.2.24), (2.2.25), решения которой содержат  произвольных постоянных, определяются из условий трансверсальности:
произвольных постоянных, определяются из условий трансверсальности:

Если один из концов траектории  , например правый, закреплен, то граничные условия имеют вид
, например правый, закреплен, то граничные условия имеют вид

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
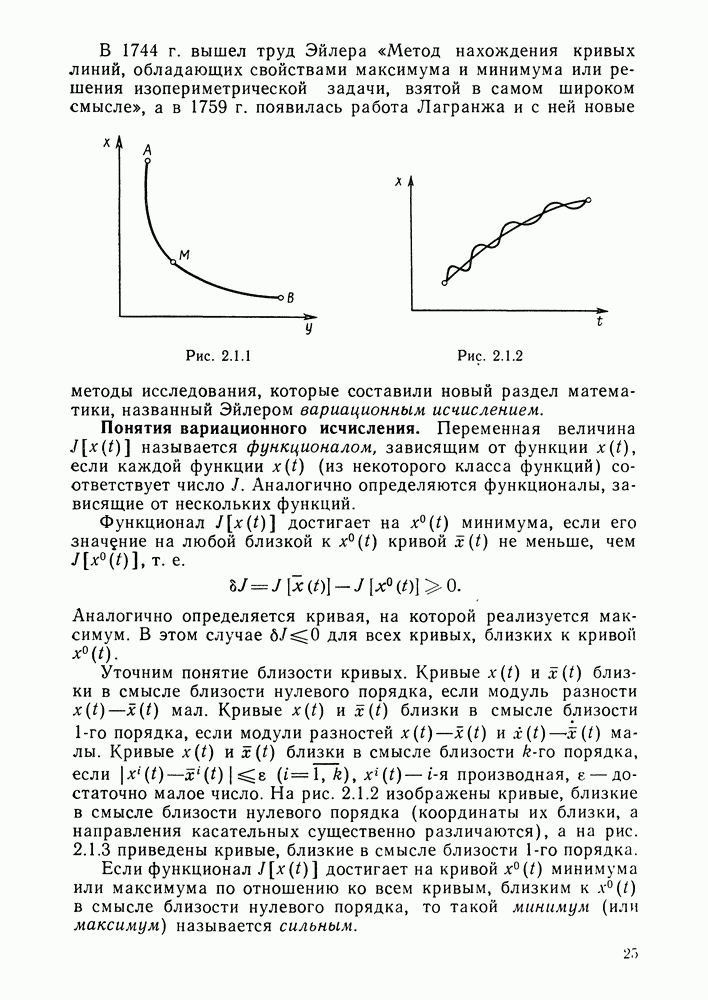
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
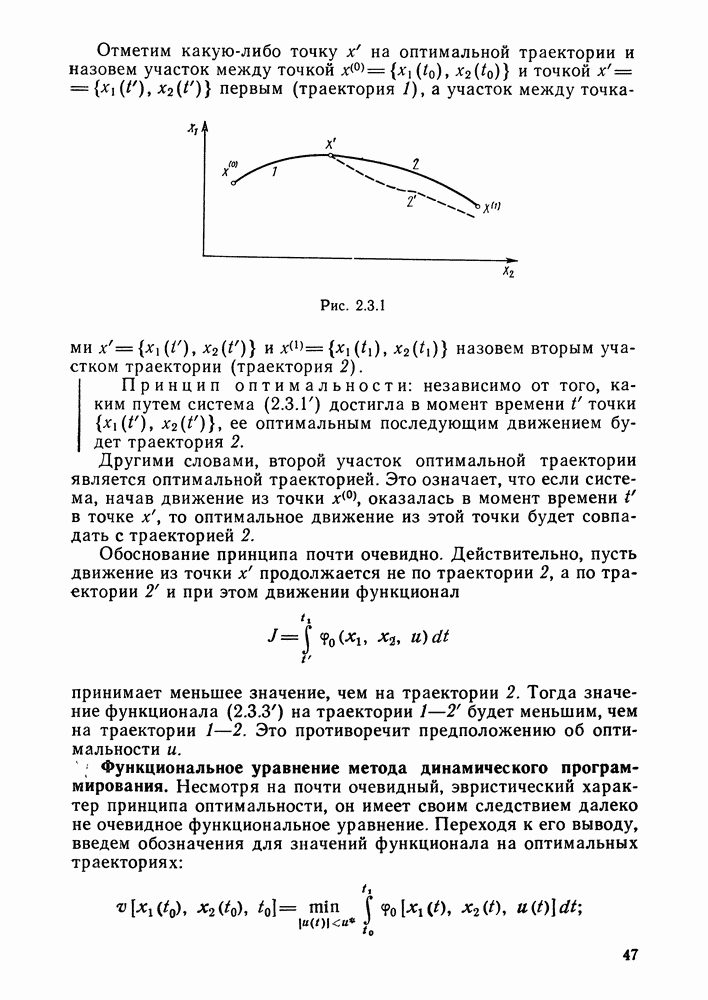
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
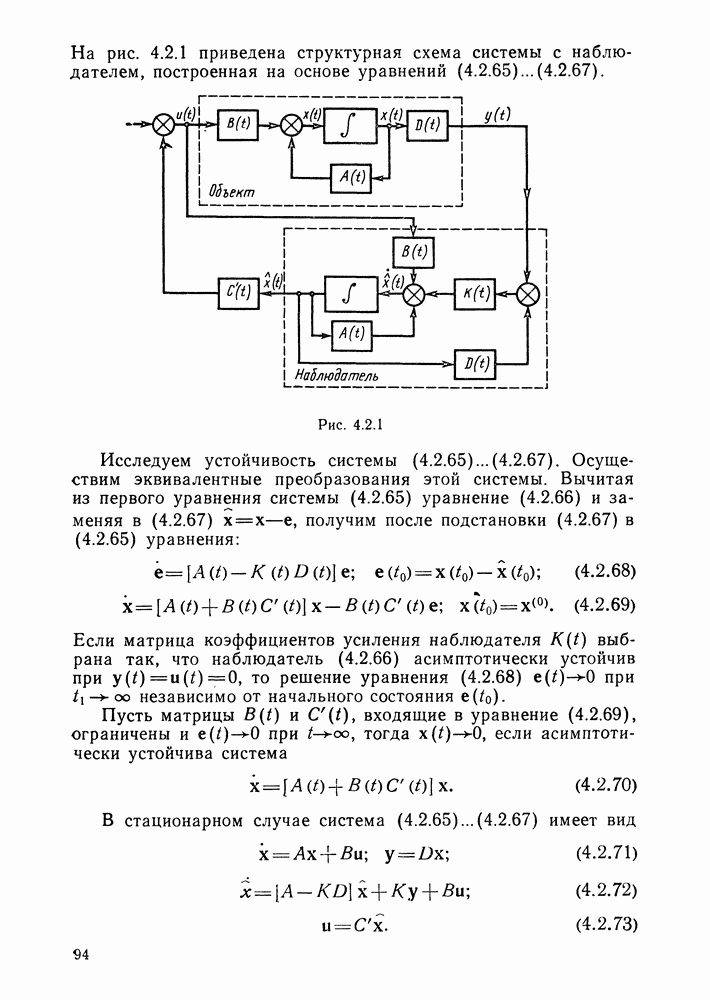
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
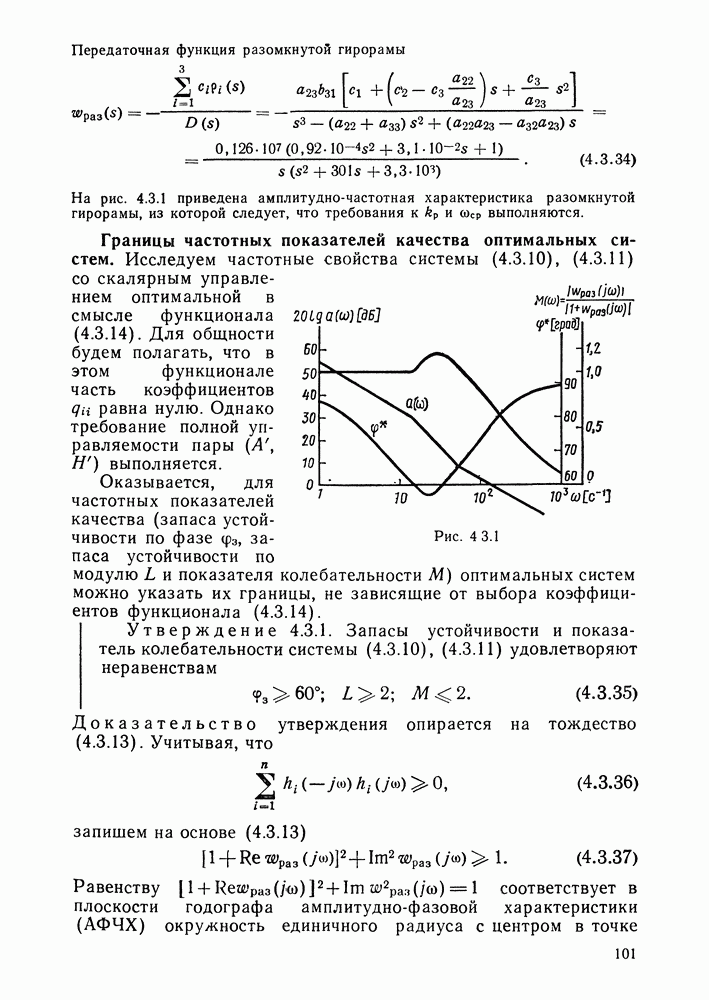
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
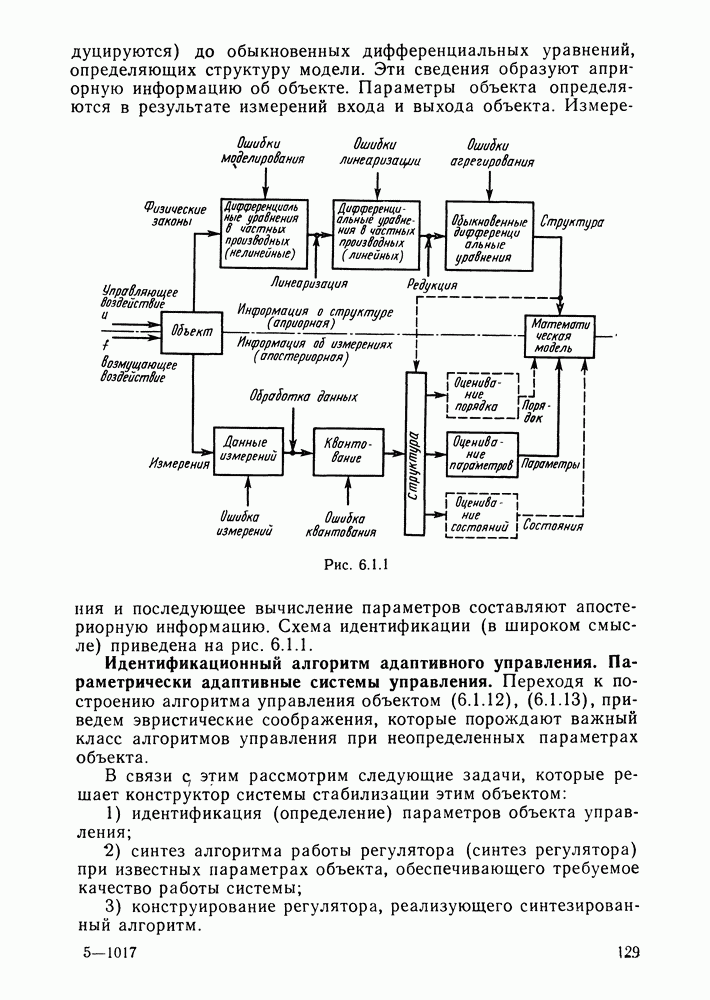
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
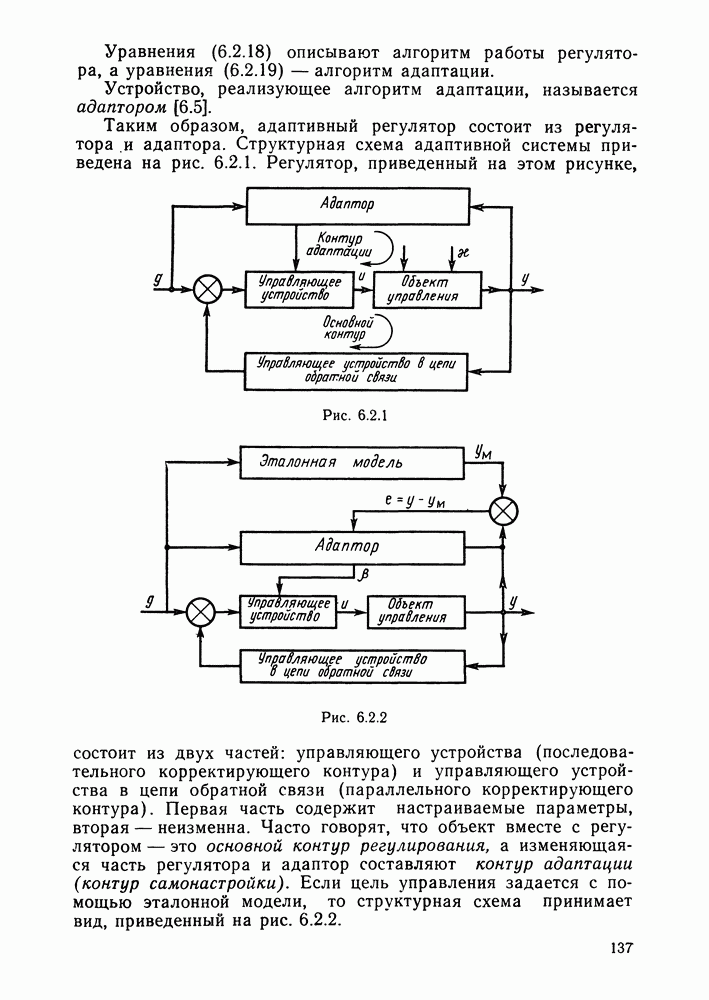
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
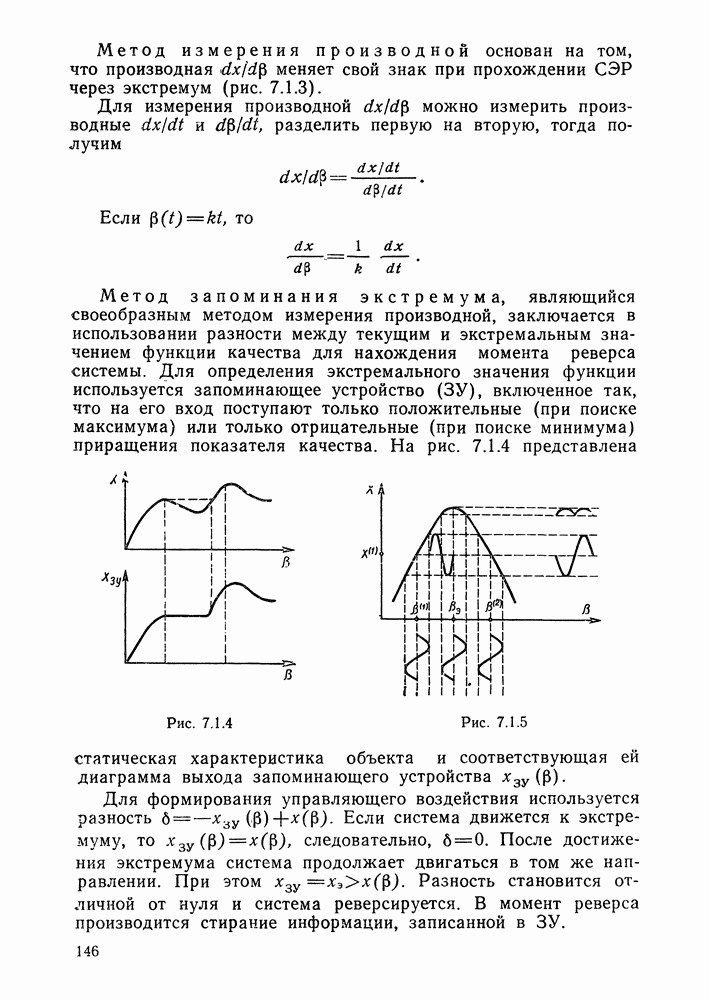
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
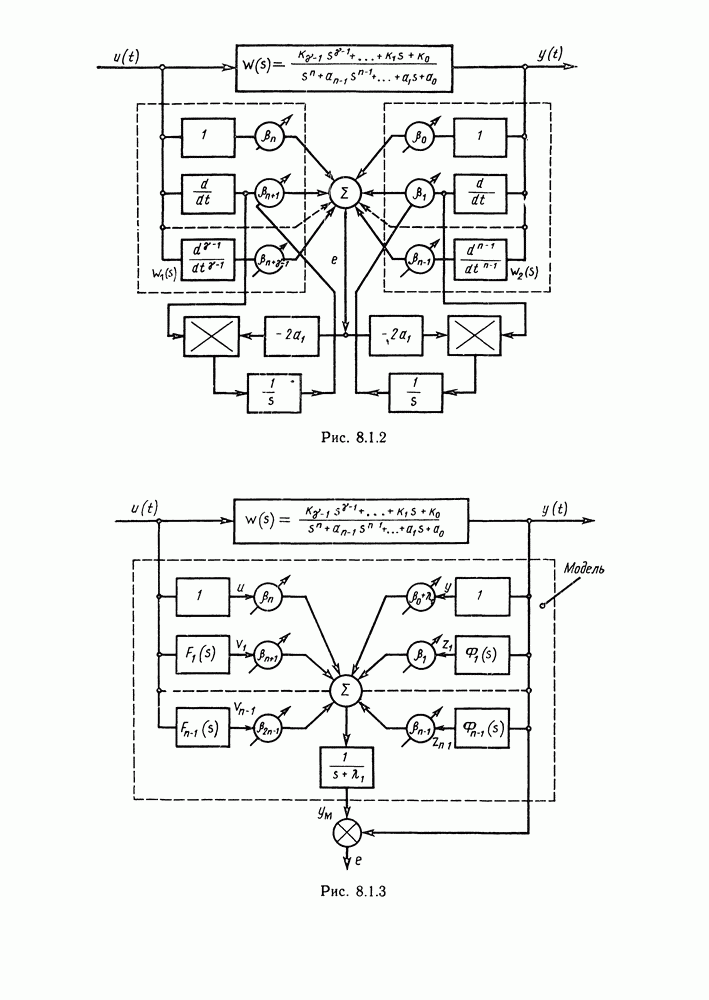
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
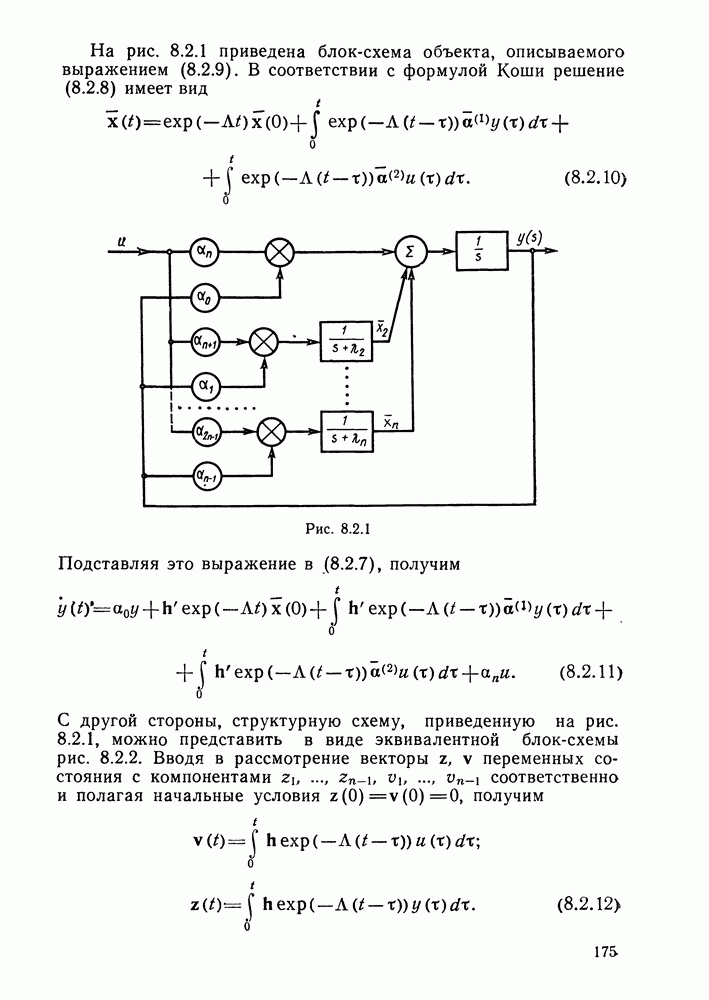
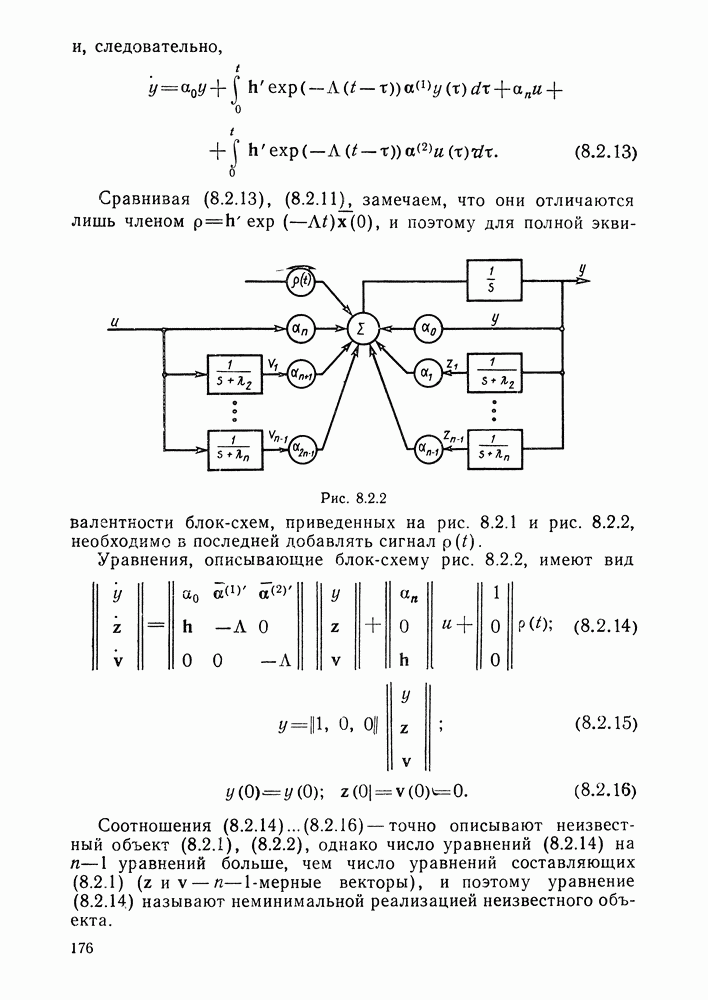
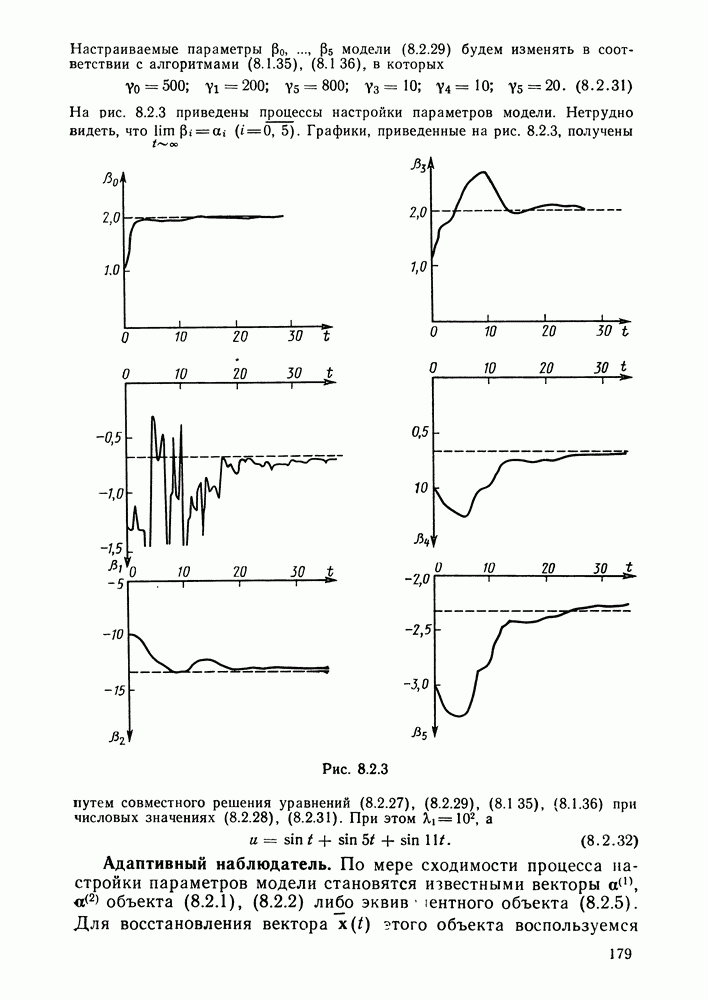
- Адаптивный наблюдатель.
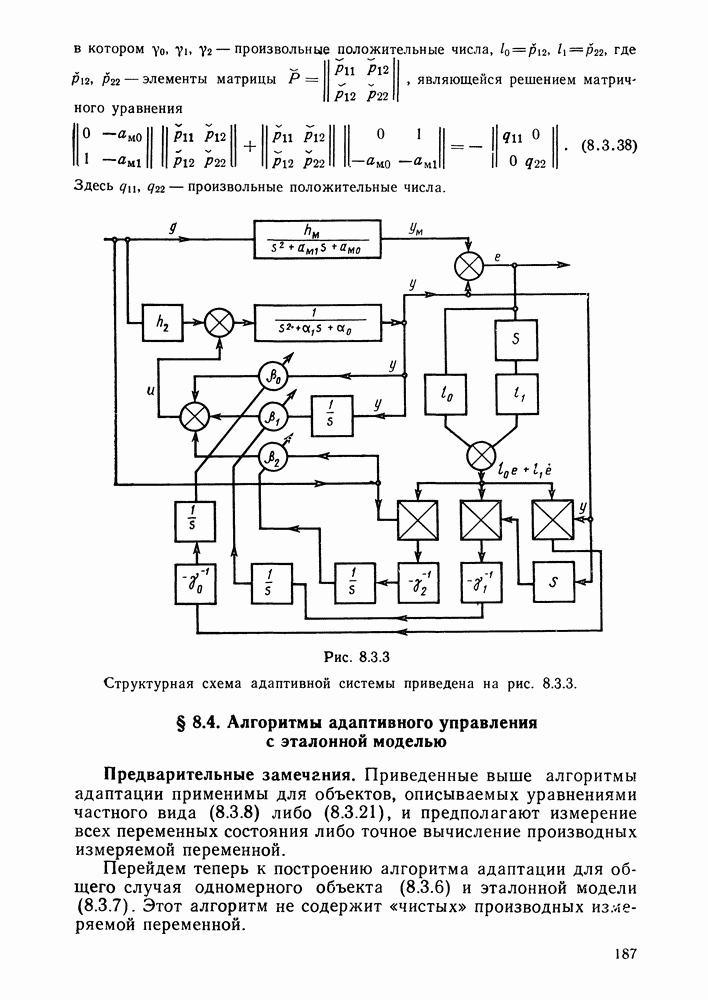
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
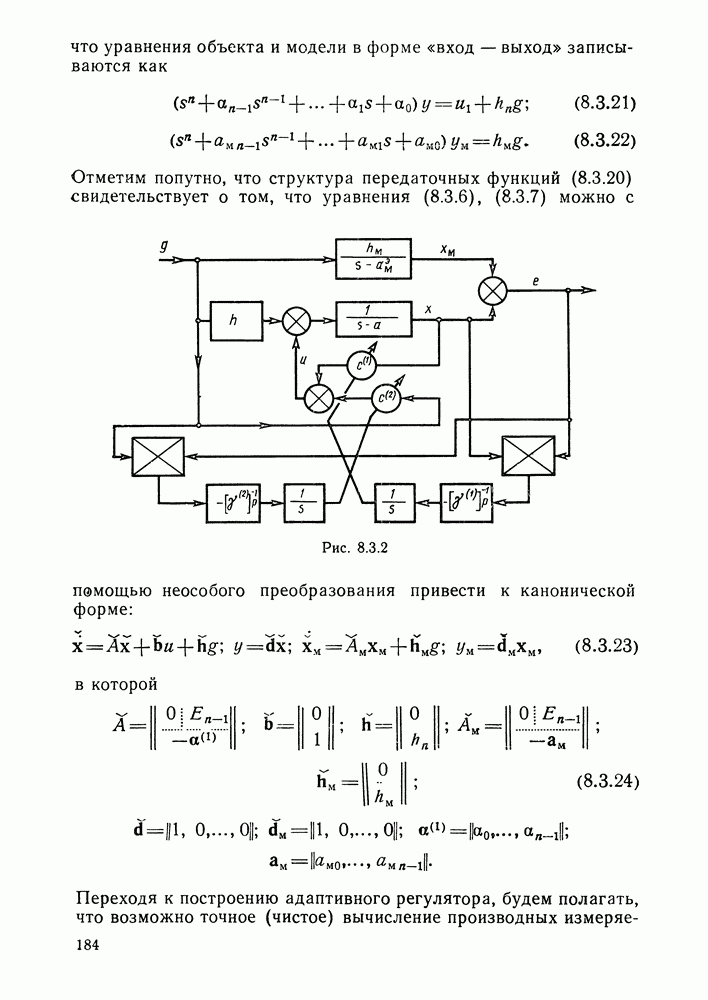
- Алгоритм адаптации с использованием чистых производных выхода объекта.
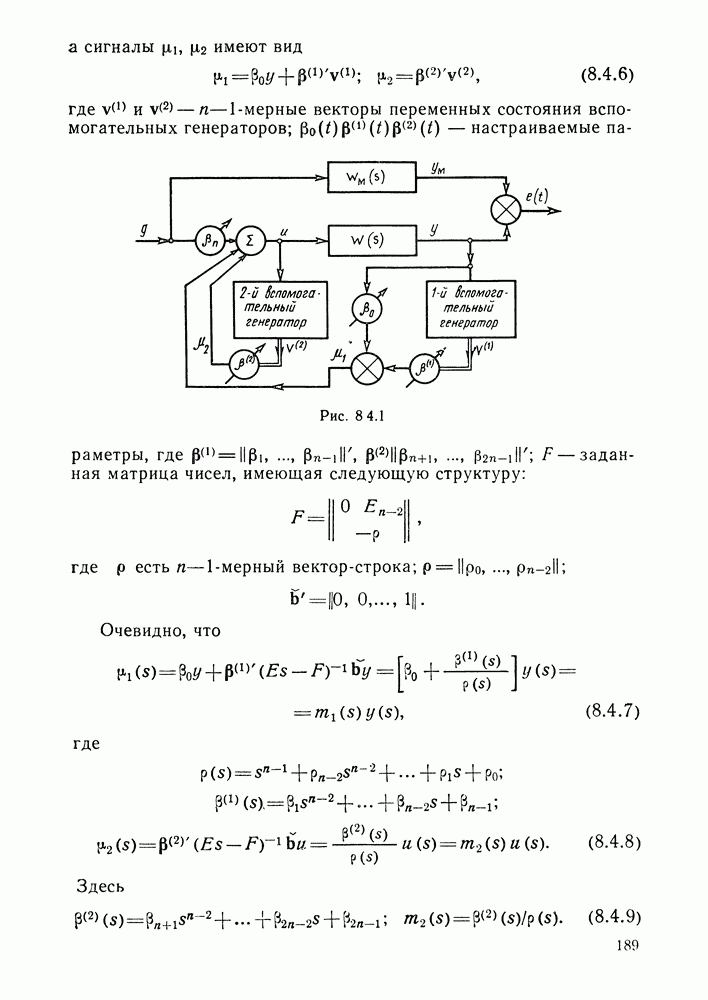
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
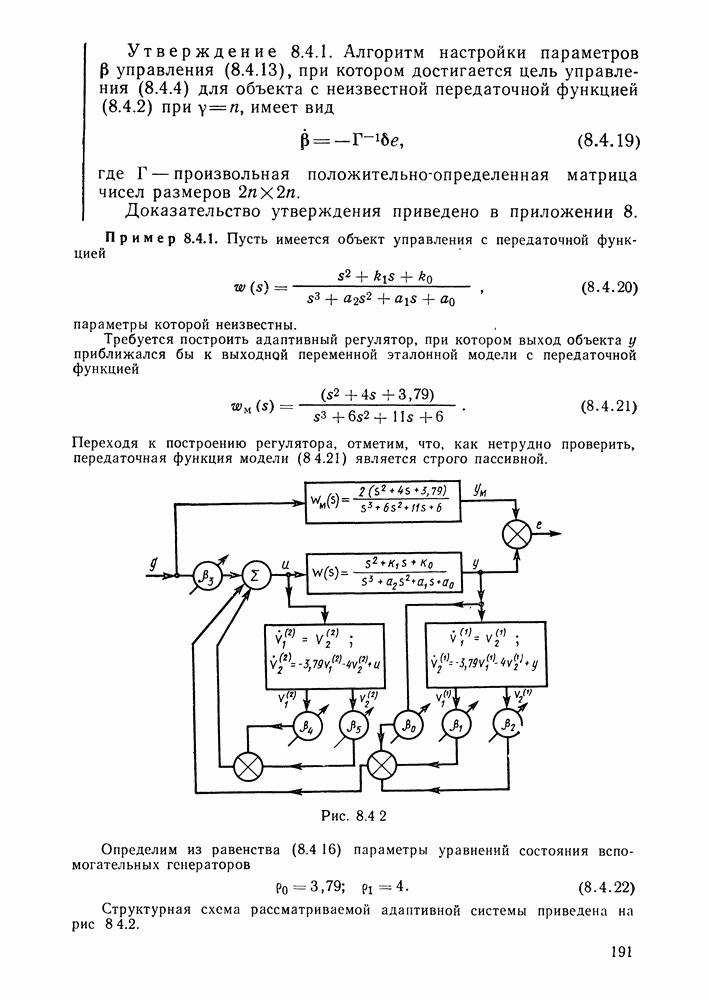
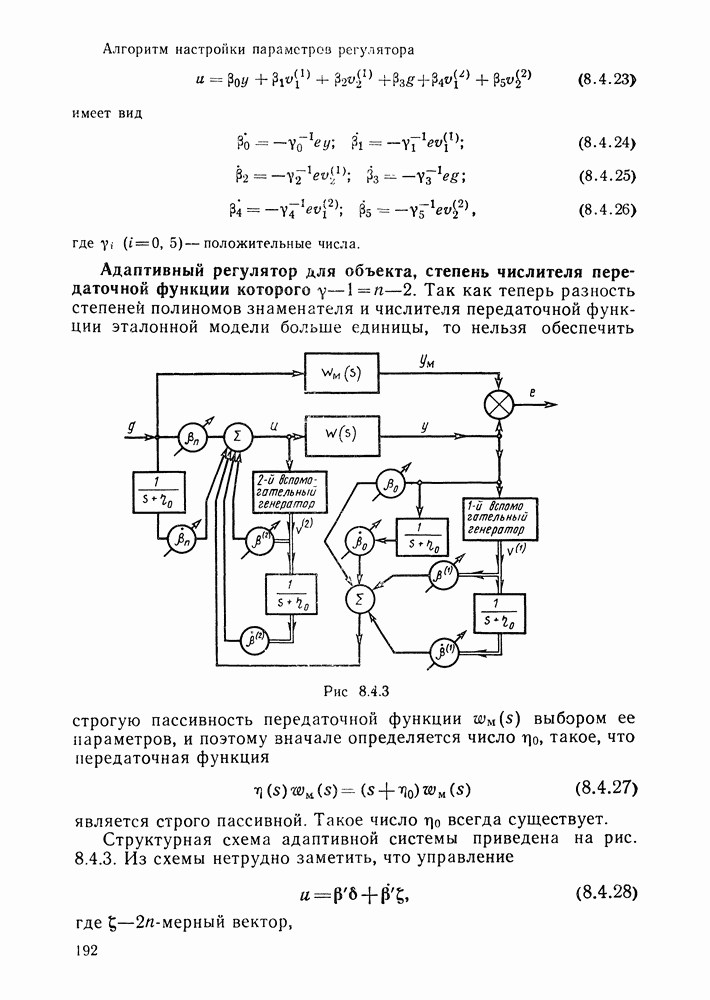
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ