| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
В этой главе приводятся методы синтеза адаптивных регуляторов. Глава состоит из двух частей.
В первой части (§ 10.1) строится два вида параметрически адаптивных систем. Алгоритм регулирования первого вида систем основывается на модальном управлении, а в качестве идентификационного алгоритма адаптации используются процедуры метода наименьших квадратов. Второй вид параметрически адаптивных систем основан на хметоде стохастической аппроксимации.
Определяются параметры алгоритмов адаптации, при которых достигается цель управления при белошумных внешних возмущениях.
Параграф 10.2 посвящен синтезу функционально-адаптивных систем. В качестве закона регулирования используется компенсационный алгоритм. Для определения параметров градиентного алгоритма адаптации применяется метод рекуррентных целевых неравенств, обеспечивающий достижение цели адаптации в условиях неизвестных, но ограниченных внешних возмущений.
§ 10.1. Параметрически-адаптивные системы
Проблема синтеза параметрических адаптивных систем. Рассмотрим полностью управляемый дискретный объект управления, описываемый уравнением
 (10.1.1)
(10.1.1)
где  - измеряемая (выходная) переменная объекта;
- измеряемая (выходная) переменная объекта;  — внешнее воздействие, являющееся случайным процессом с независимыми значениями (случайным процессом типа «белый
— внешнее воздействие, являющееся случайным процессом с независимыми значениями (случайным процессом типа «белый  ), причем
), причем
 (10.1.2)
(10.1.2)
( некоторое число), параметры
некоторое число), параметры  — неизвестные числа.
— неизвестные числа.
Требуется найти алгоритм управления, при котором достигается цель управления, задаваемая критерием
 (10.1.3)
(10.1.3)
в котором  — заданное число.
— заданное число.
В соответствии с этапами процедуры синтеза адаптивного регулятора вначале необходимо построить алгоритм регулирования. Методы его построения будут приведены ниже. Второй этап синтеза состоит в выборе класса алгоритмов адаптивного управления. Напомним, что для параметрически адаптивных систем этот класс составляют идентификационные алгоритмы. Перейдем к третьему этапу синтеза — выбору алгоритма адаптации. Таким алгоритмом в принятом классе выступают алгоритмы идентифиции. Рассмотрим возможности различных методов идентификации: а) идентификации с настраиваемой моделью; б) корреляционного способа; в) метода наименьших квадратов; г) алгоритма стохастической аппроксимации; д) расширенного фильтра, е) метода максимального правдоподобия [9.2], ж) бейсовских оценок [9.3].
Первые два метода отпадают, поскольку в них предполагается возможность измерения возмущающего воздействия, а в рассматриваемом случае  предполагается не доступной измерению. Последние два метода мало пригодны, так как отсутствуют какие-либо сведения о законах распределения неизвестных параметров.
предполагается не доступной измерению. Последние два метода мало пригодны, так как отсутствуют какие-либо сведения о законах распределения неизвестных параметров.
Выбираем для дальнейшего рассмотрения в качестве алгоритмов идентификации (адаптации) алгоритмы метода наименьших квадратов и стохастической аппроксимации.
Отметим некоторые обстоятельства, которые существенно затрудняют выполнение четвертого этапа синтеза — определения параметров алгоритма адаптации из условия сходимости процесса адаптации. Рассмотрим вначале случай, когда используется метод наименьших квадратов. В этом случае процесс идентификации сходится к истинным значениям параметров при условии, что  белошумные случайные процессы. Для переменной
белошумные случайные процессы. Для переменной  это условие не выполняется, так как управление
это условие не выполняется, так как управление  является решением дифференциального уравнения, описывающего адаптивный регулятор, на вход которого поступает выходная переменная
является решением дифференциального уравнения, описывающего адаптивный регулятор, на вход которого поступает выходная переменная  объекта (10.1.1), что означает определенную зависимость чисел
объекта (10.1.1), что означает определенную зависимость чисел  для различных значений к. Это приводит к смещению оценок параметров от их истинных значений.
для различных значений к. Это приводит к смещению оценок параметров от их истинных значений.
Использование алгоритма стохастической  , описанного в утверждении 9.3.1, для идентификации параметров объекта (10.1.1) не приводит к смещению оценок, однако этот алгоритм применим лишь для устойчивых объектов. Это условие в процессе работы адаптивной системы может нарушаться. Действительно, поскольку алгоритм регулирования строится с использованием текущих оценок параметров объекта, может случиться так, что на каком-то шаге идентификации эти оценки будут таковы, что закон управления, построенный с их использованием, приводит к неустойчивости всей системы. Последнее явится причиной нарушения процесса идентификации, поскольку при построении алгоритма идентификации предполагалась малость чисел
, описанного в утверждении 9.3.1, для идентификации параметров объекта (10.1.1) не приводит к смещению оценок, однако этот алгоритм применим лишь для устойчивых объектов. Это условие в процессе работы адаптивной системы может нарушаться. Действительно, поскольку алгоритм регулирования строится с использованием текущих оценок параметров объекта, может случиться так, что на каком-то шаге идентификации эти оценки будут таковы, что закон управления, построенный с их использованием, приводит к неустойчивости всей системы. Последнее явится причиной нарушения процесса идентификации, поскольку при построении алгоритма идентификации предполагалась малость чисел  при достаточно больших
при достаточно больших  , что возможно лишь при условии асимптотической устойчивости.
, что возможно лишь при условии асимптотической устойчивости.
Отметим попутно, что в методе наименьших квадратов отсутствует ограничение на устойчивость системы, и поэтому нарушение устойчивости не приводит к ошибкам оценивания параметров (если и  )
)  белошумные процессы), а тогда при приближении оценок к истинным значениям параметров синтезируется алгоритм регулирования, обеспечивающий асимптотическую устойчивость системы.
белошумные процессы), а тогда при приближении оценок к истинным значениям параметров синтезируется алгоритм регулирования, обеспечивающий асимптотическую устойчивость системы.
Таким образом, основной проблемой синтеза идентификационных алгоритмов адаптивного управления является доказательство сходимости процесса адаптации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
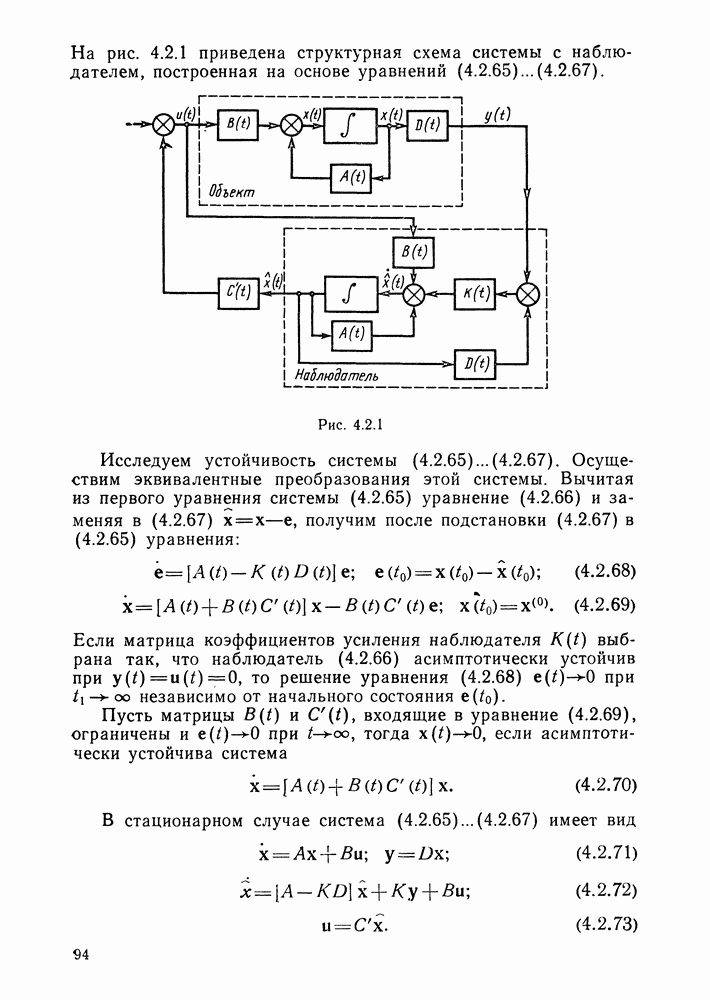
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
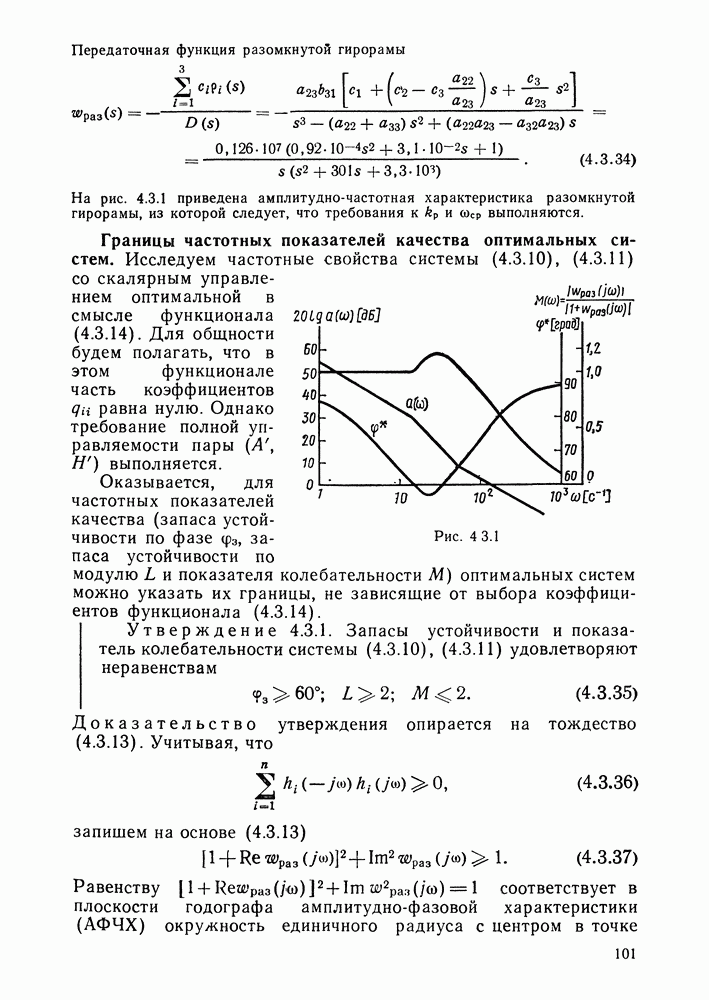
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
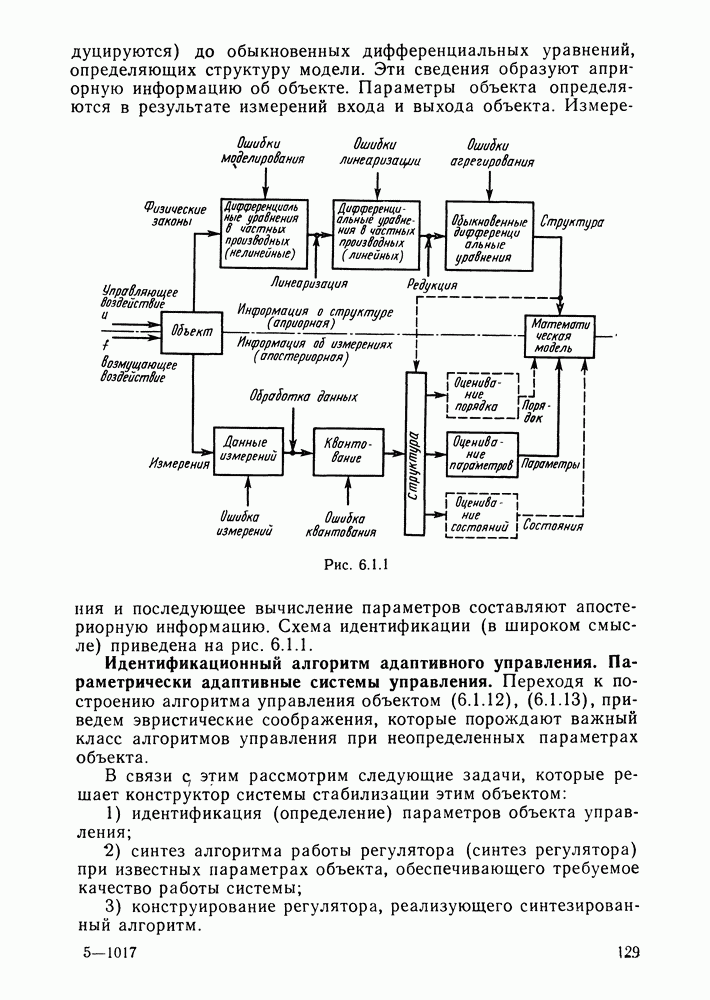
- Понятие об идентификации.
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
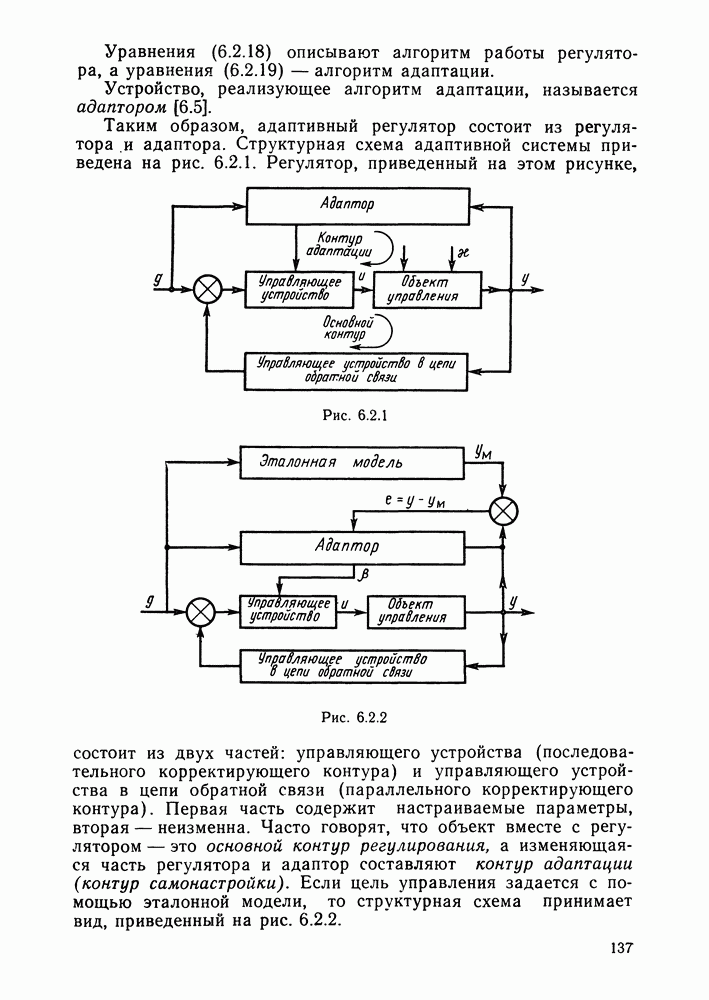
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
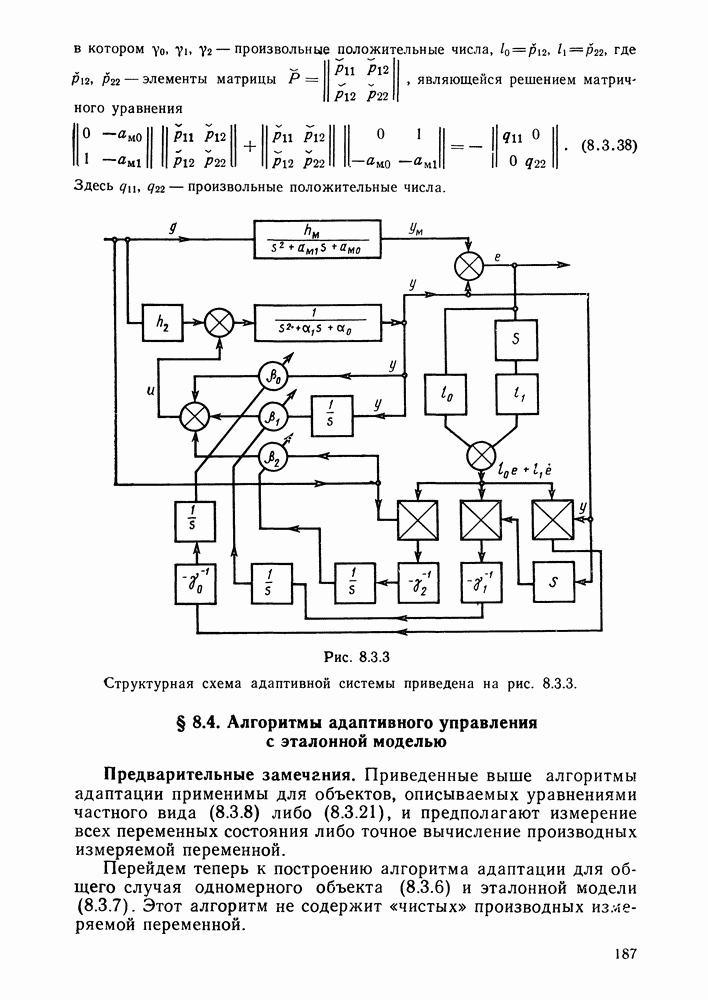
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
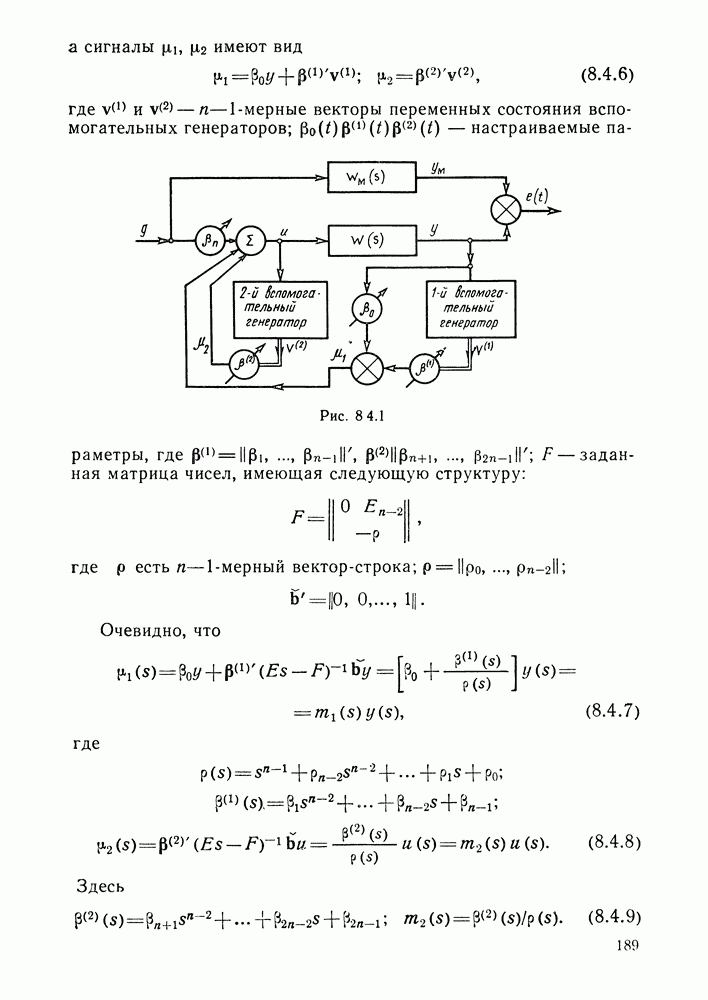
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
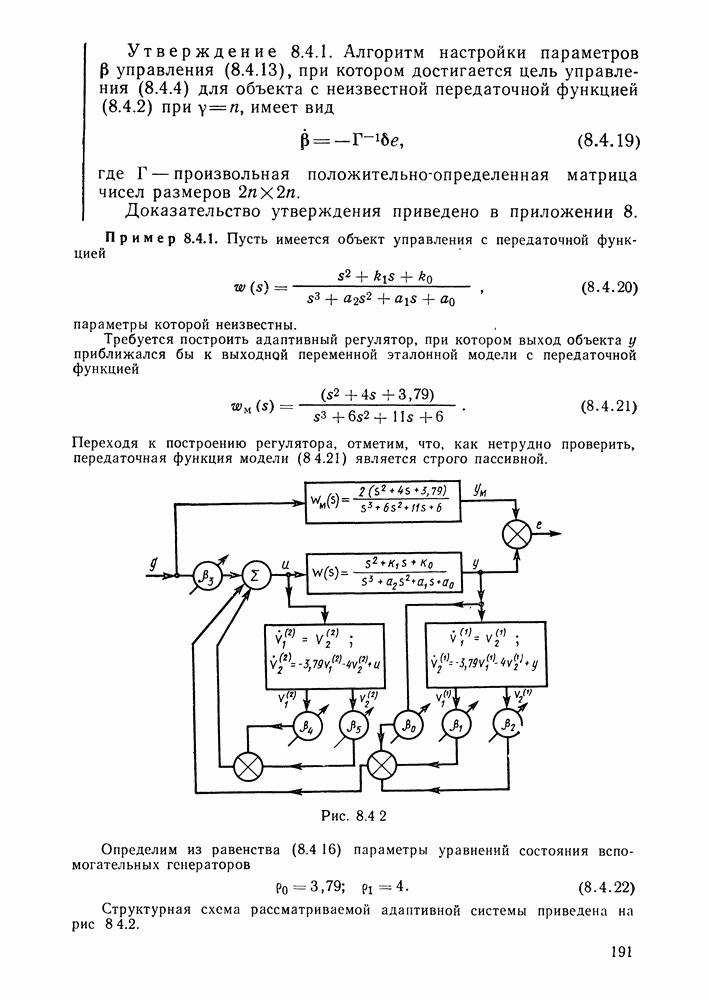
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
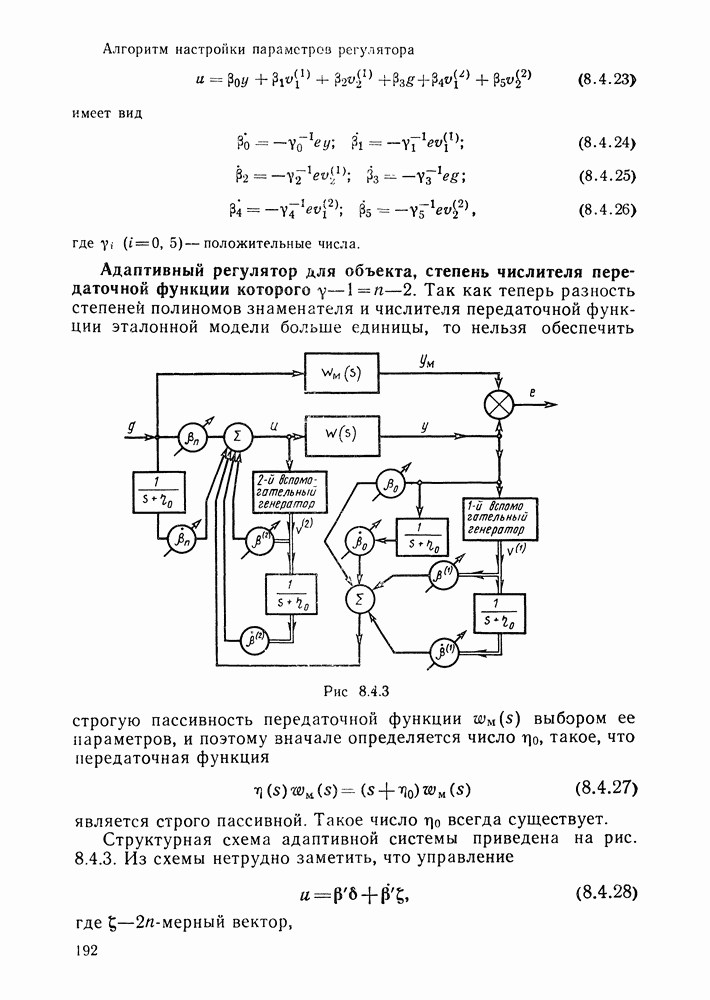
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ