| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
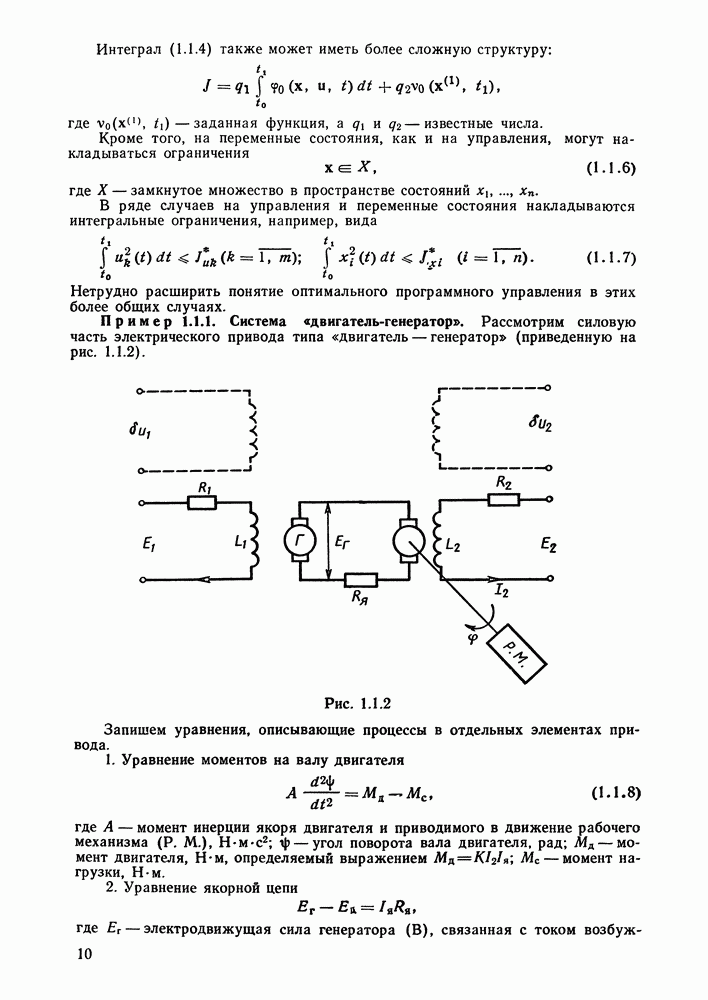
Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
Исследуем на экстремум (максимум или минимум) функционал

где  - непрерывная и трижды дифференцируемая функция своих аргументов.
- непрерывная и трижды дифференцируемая функция своих аргументов.
Искомая функция (для которой этот функционал принимает экстремальное значение) удовлетворяет краевым условиям

Задача о нахождении экстремума функционала (2.1.1) при условиях (2.1.2), в которых  — заданные числа, называется вариационной задачей с закрепленными граничными точками. Непрерывно дифференцируемые функции
— заданные числа, называется вариационной задачей с закрепленными граничными точками. Непрерывно дифференцируемые функции  , определенные на
, определенные на  и удовлетворяющие условиям (2.1.2), называются допустимыми функциями.
и удовлетворяющие условиям (2.1.2), называются допустимыми функциями.
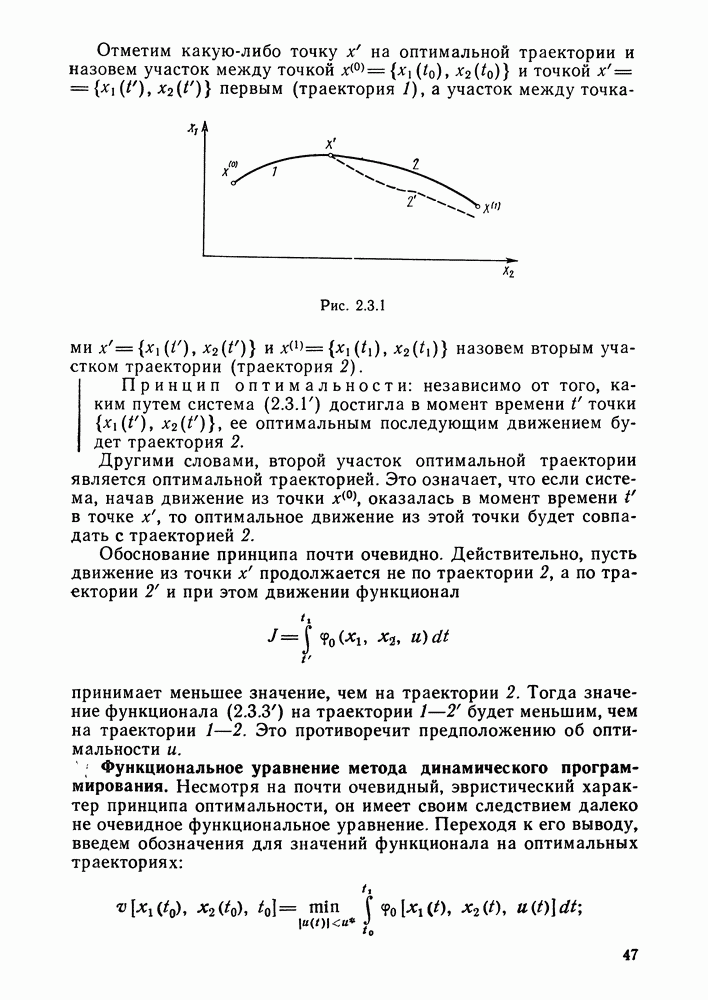
Переходя к решению вариационной задачи, допустим, что ее решение — кривая  - найдено. Возьмем некоторую функцию
- найдено. Возьмем некоторую функцию  и включим ее в однопараметрическое семейство кривых
и включим ее в однопараметрическое семейство кривых

где а — некоторое число.

Рис. 2.1.3

Рис. 2.1.4
Концы варьируемых кривых естественно также закреплять в точках (2.1.2) (рис. 2.1.4), и поэтому

Рассмотрим значения, которые принимает функционал (2.1.1) на кривых семейства (2.1.3),

где  .
.
Нетрудно видеть, что при известных кривых  функционал (2.1.1) становится функцией
функционал (2.1.1) становится функцией  . Эта функция достигает своего экстремума при
. Эта функция достигает своего экстремума при  , так как, по определению,
, так как, по определению,  .
.
Необходимым условием экстремума функции  при
при  является, как известно, равенство
является, как известно, равенство

Подставляя в это условие выражение (2.1.5), получим t 1

После интегрирования по частям

и тогда запишем (2.1.6) окончательно с учетом краевых условий  в виде
в виде

В этом выражении сомножитель  является на кривой
является на кривой
 , реализующей экстремум, заданной непрерывной функцией, а второй сомножитель
, реализующей экстремум, заданной непрерывной функцией, а второй сомножитель  - произвольная (в силу произвола при выборе функции
- произвольная (в силу произвола при выборе функции  ) дифференцируемая функция.
) дифференцируемая функция.
При этих условиях из (2.1.7) следует тождество
 (2.1.8)
(2.1.8)
которое выполняется на экстремалях  .
.
Доказательство того, что (2.1.8) следует из (2.1.7), опирается на основную лемму вариационного исчисления, которая формулируется так: если для каждой непрерывной функции  (удовлетворяющей условию
(удовлетворяющей условию  )
)
 (2.1.9)
(2.1.9)
где  - непрерывная на отрезке
- непрерывная на отрезке  функция, то
функция, то  на том же отрезке.
на том же отрезке.
Для доказательства  предположим (в противоречии с ее утверждением), что в точке
предположим (в противоречии с ее утверждением), что в точке  значение
значение  . Тогда придем к противоречию с утверждением леммы. Действительно, из непрерывности функции
. Тогда придем к противоречию с утверждением леммы. Действительно, из непрерывности функции  следует, что если
следует, что если  , то
, то  сохраняет знак в некоторой окрестности
сохраняет знак в некоторой окрестности  точки t. Выбирая функцию
точки t. Выбирая функцию  сохраняющей знак на отрезке
сохраняющей знак на отрезке  и равной нулю вне этого отрезка, заключаем, что произведение
и равной нулю вне этого отрезка, заключаем, что произведение  сохраняет знак на отрезке
сохраняет знак на отрезке  и равно нулю вне этого отрезка и, следовательно,
и равно нулю вне этого отрезка и, следовательно,

а это противоречие и доказывает Лемму. Таким образом,  является решением уравнения
является решением уравнения
 (2.1.10)
(2.1.10)
которое называется уравнением Эйлера.
Принимая во внимание, что

запишем (2.1.10) в развернутой форме:
 (2.1.11)
(2.1.11)
Его решения  , где
, где  постоянные, определяемые краевыми условиями (2.1.2), называются экстремалями.
постоянные, определяемые краевыми условиями (2.1.2), называются экстремалями.
Пример 2.1.1. Найдем кривую  , проходящую через заданные точки
, проходящую через заданные точки  в моменты времени
в моменты времени  на которой достигает экстремума функционал
на которой достигает экстремума функционал

где  — заданное число.
— заданное число.
В рассматриваемом случае  , поэтому
, поэтому

и уравнение Эйлера для экстремалей функционала (2 1.12) имеет вид

Решением этого уравнения является (как нетрудно проверить непосредственной подстановкой) кривая

Используя граничные условия, определим значения постоянных  из уравнений
из уравнений

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
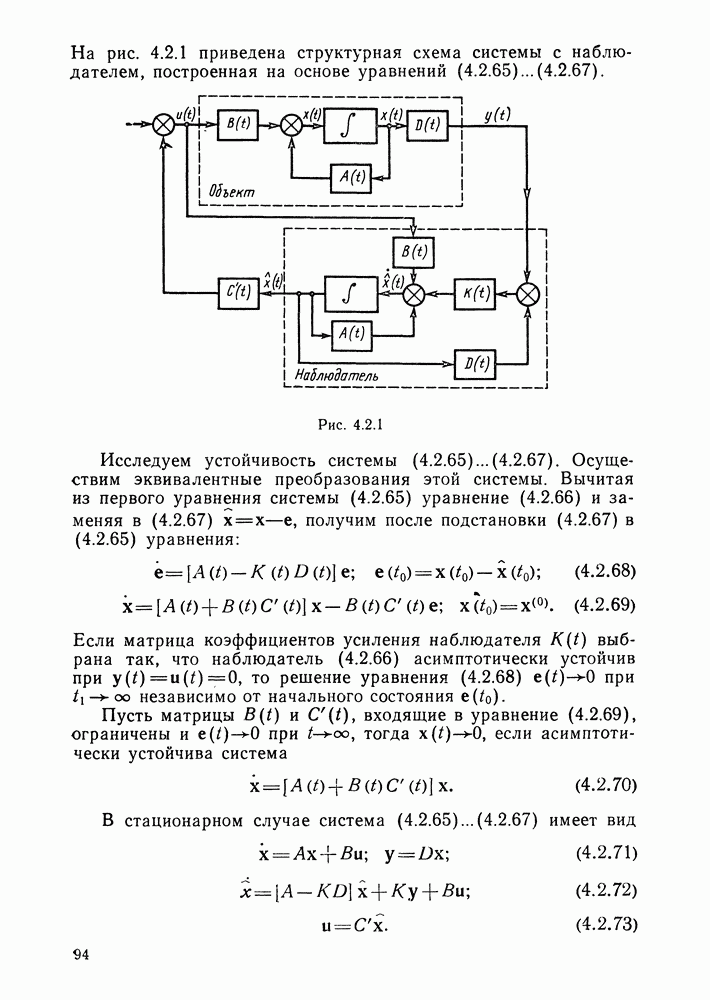
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
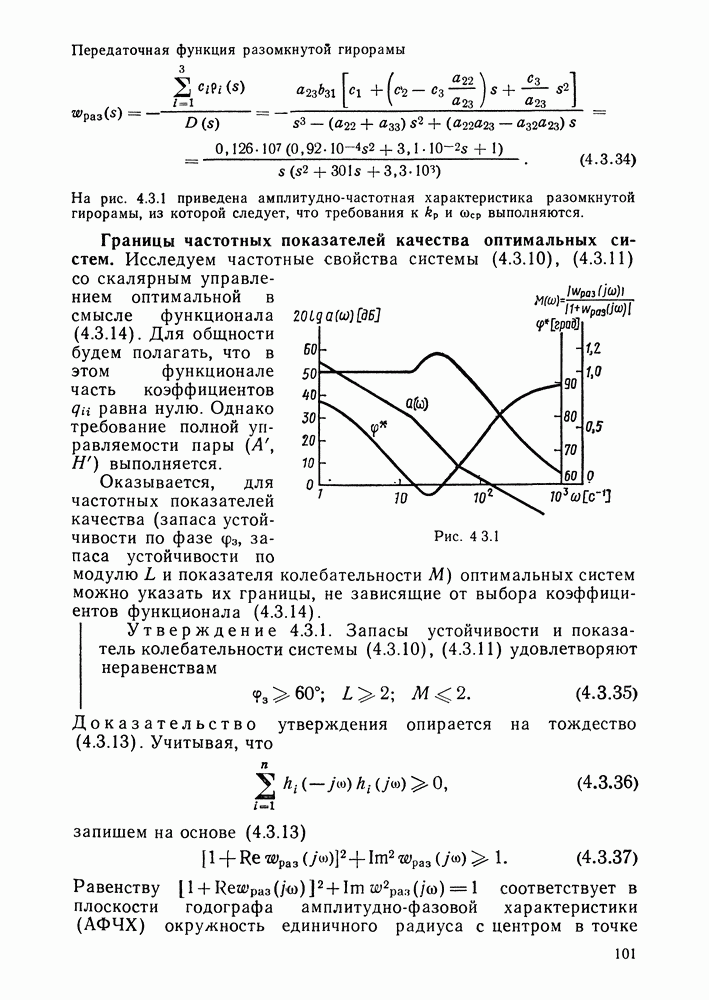
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
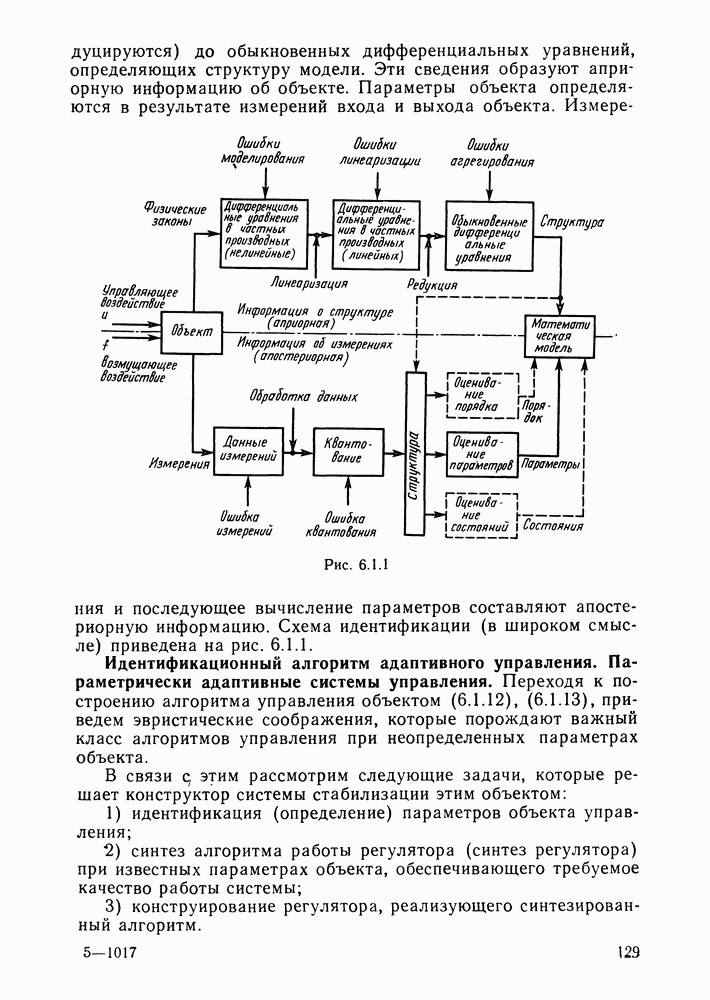
- Понятие об идентификации.
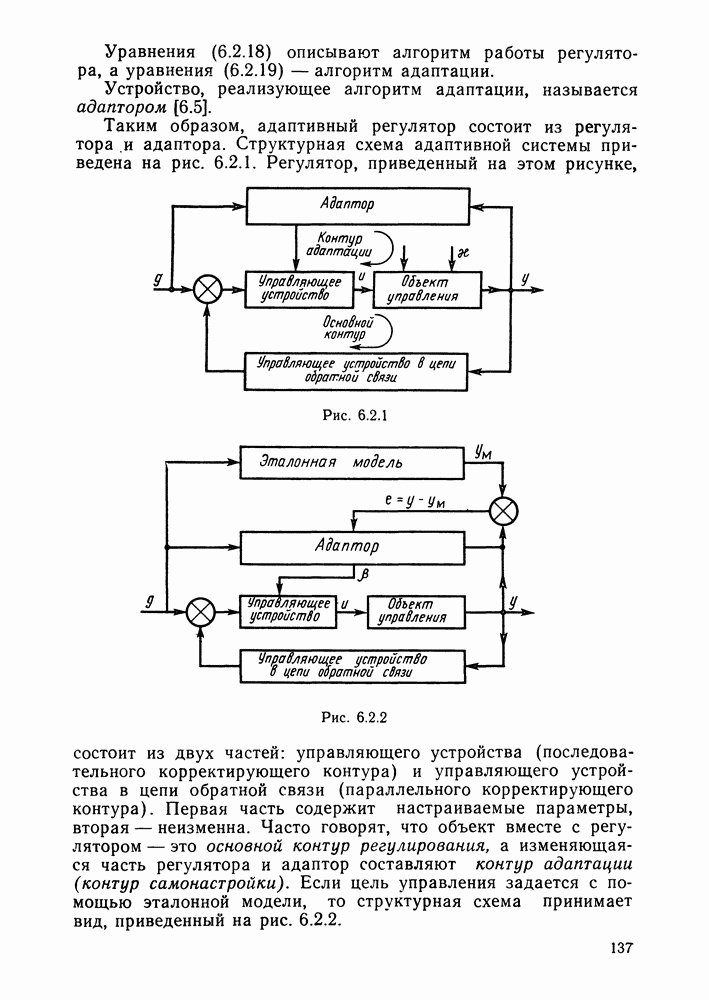
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
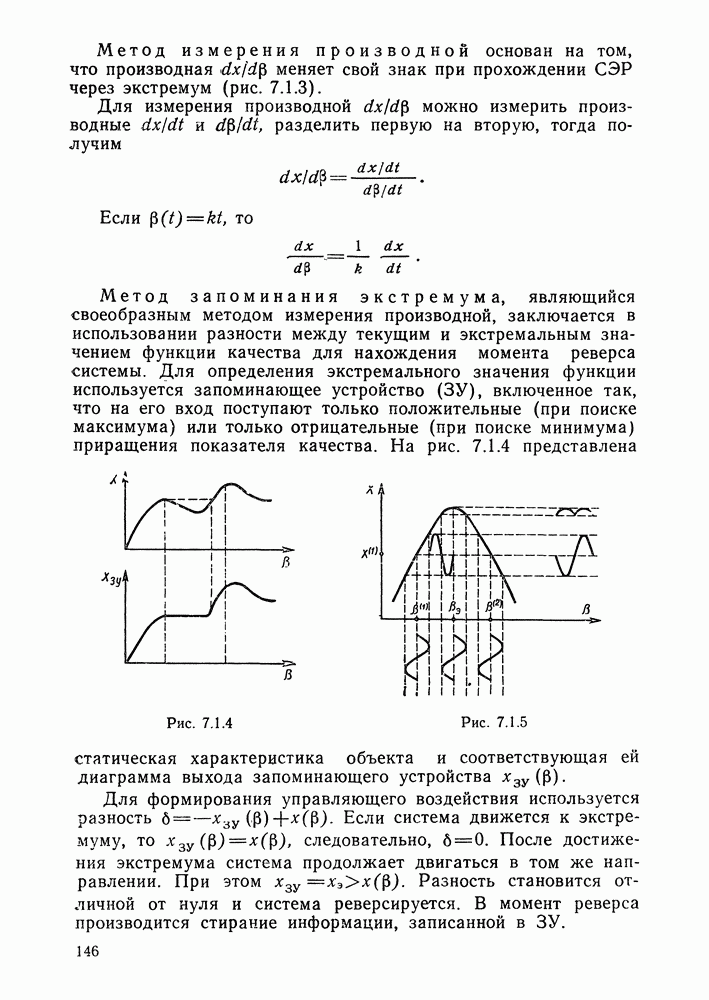
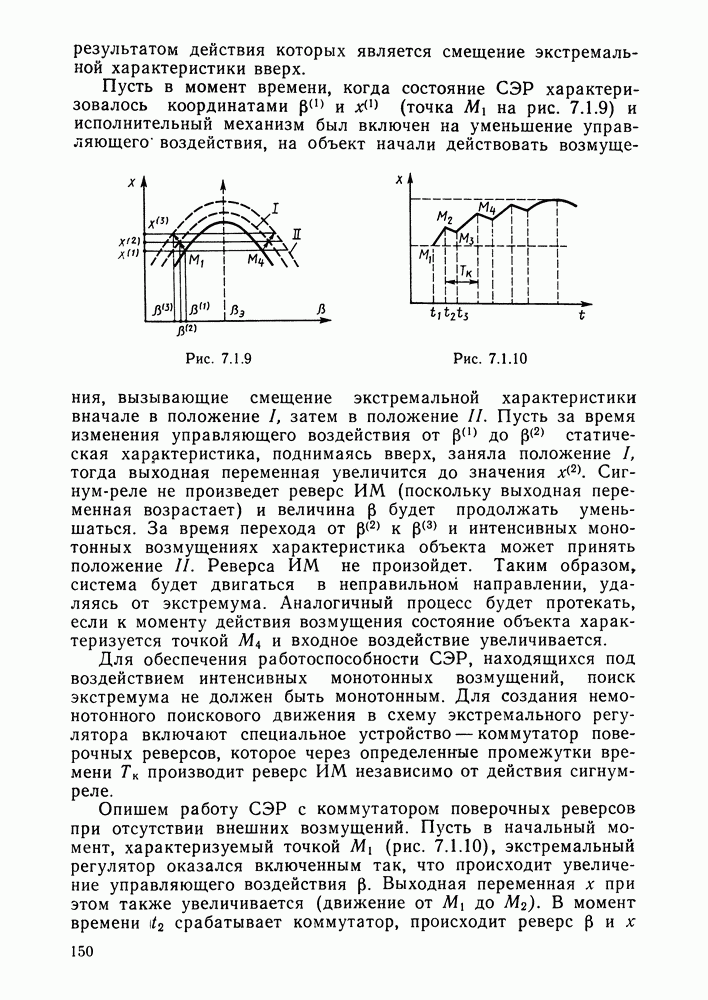
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
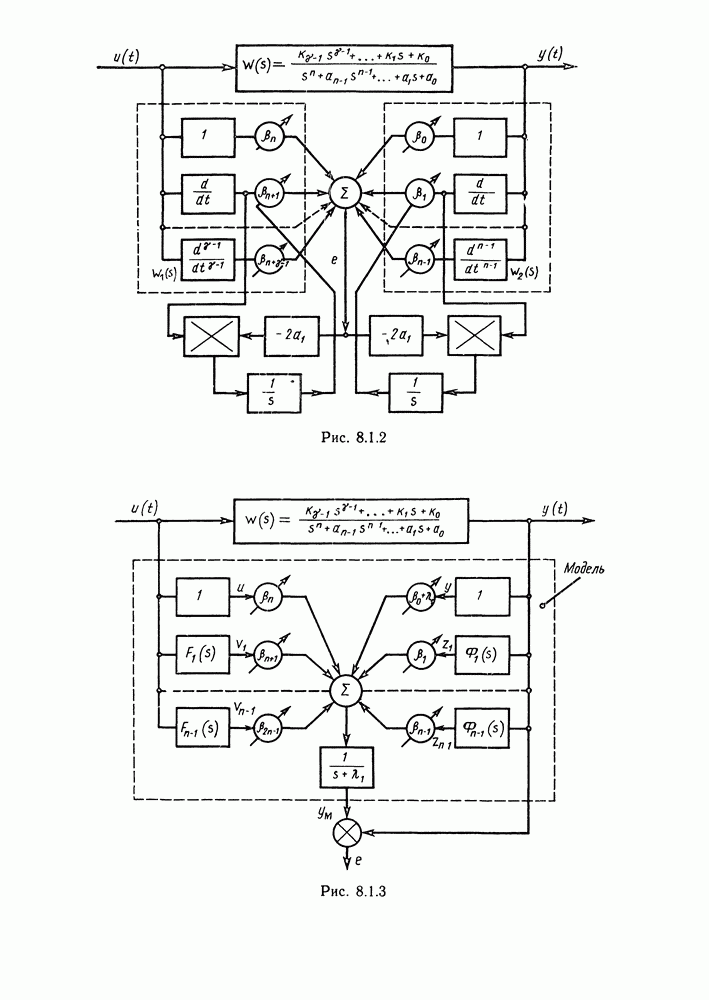
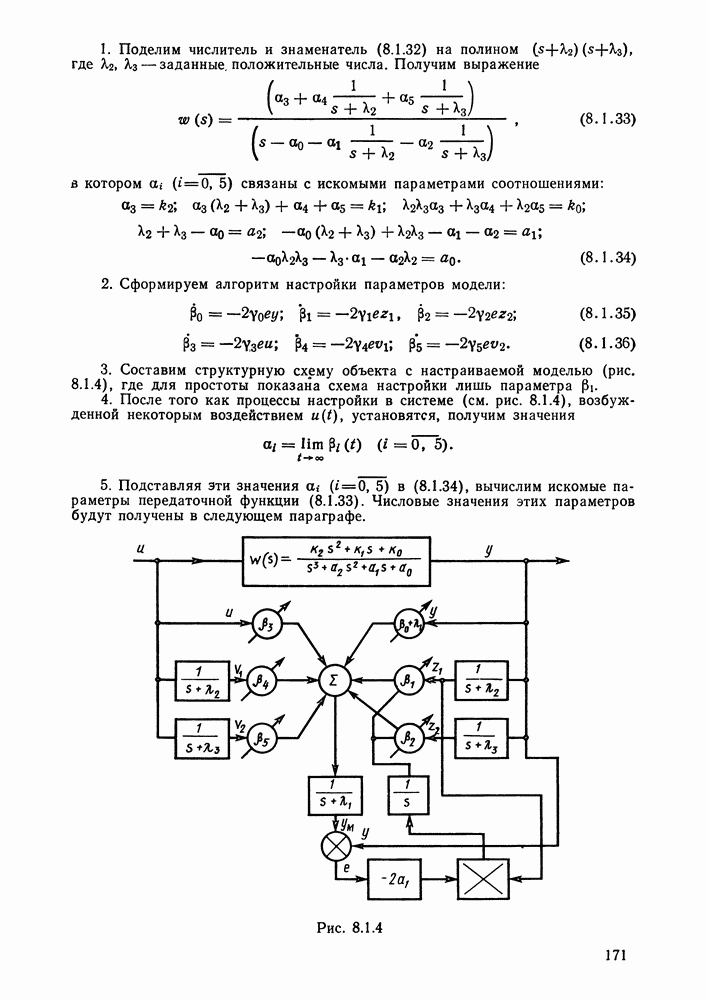
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
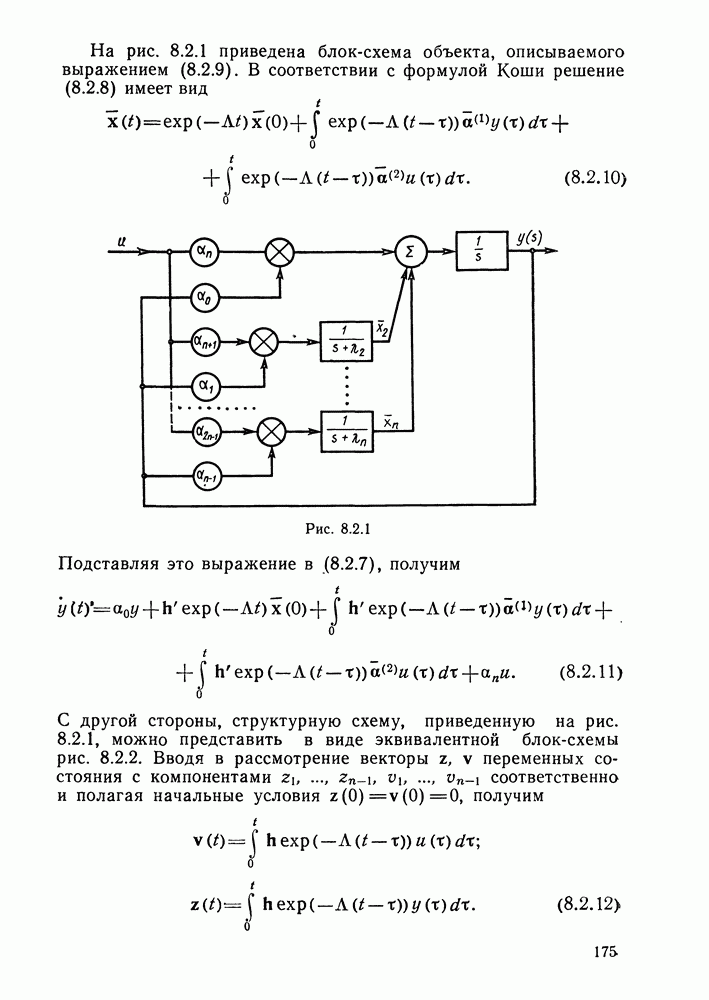
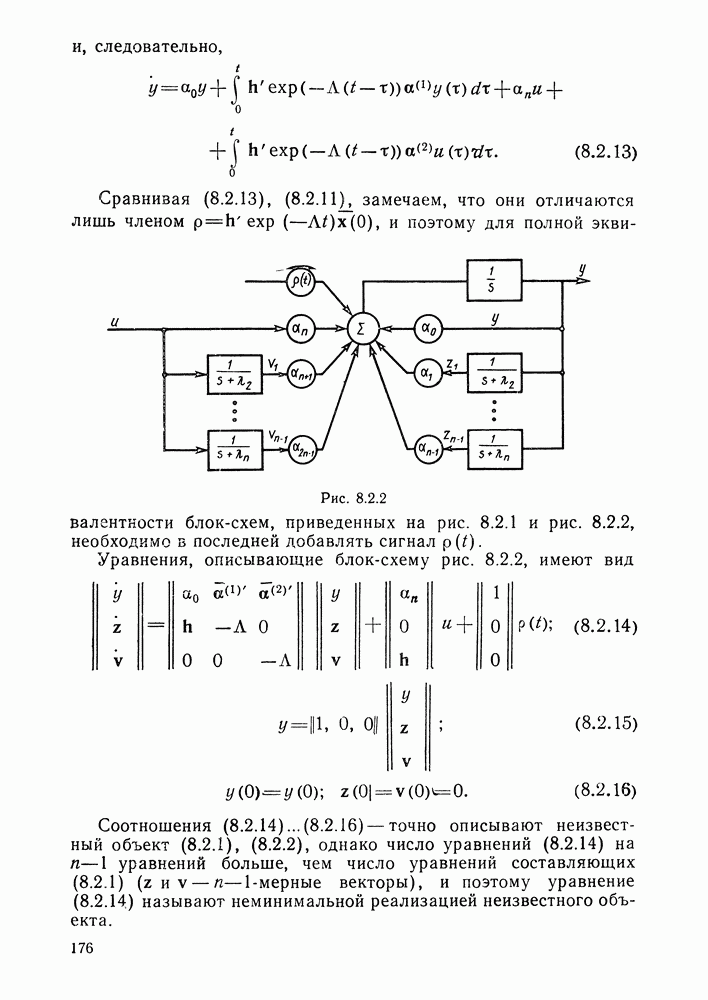
- § 8.2. Адаптивные наблюдатели
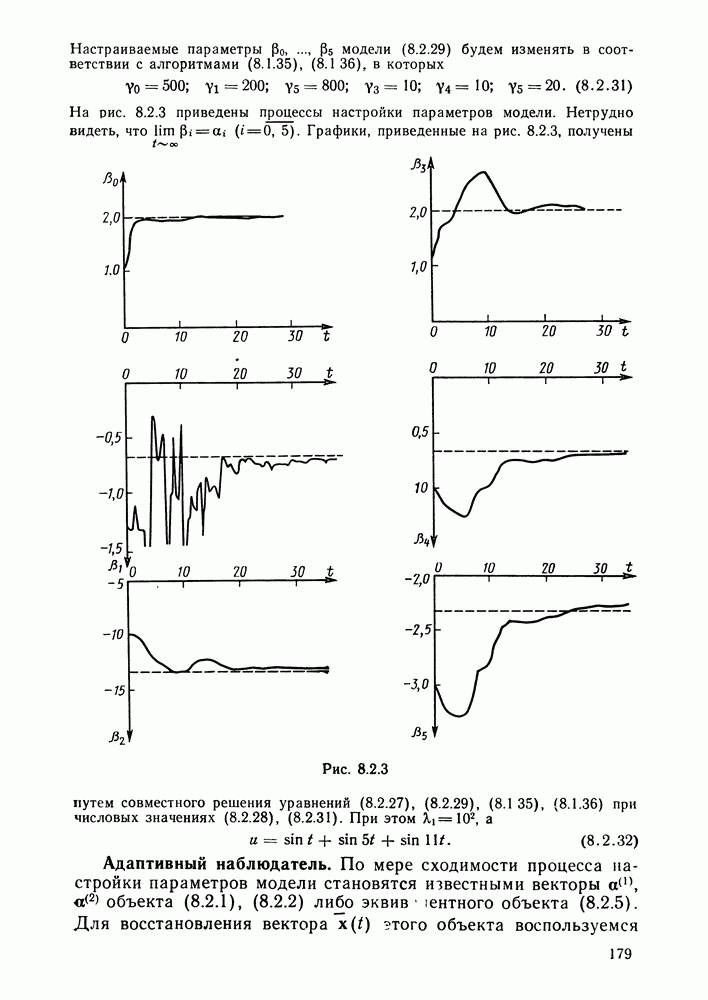
- Адаптивный наблюдатель.
- § 8.3. Адаптивные системы с эталонной моделью
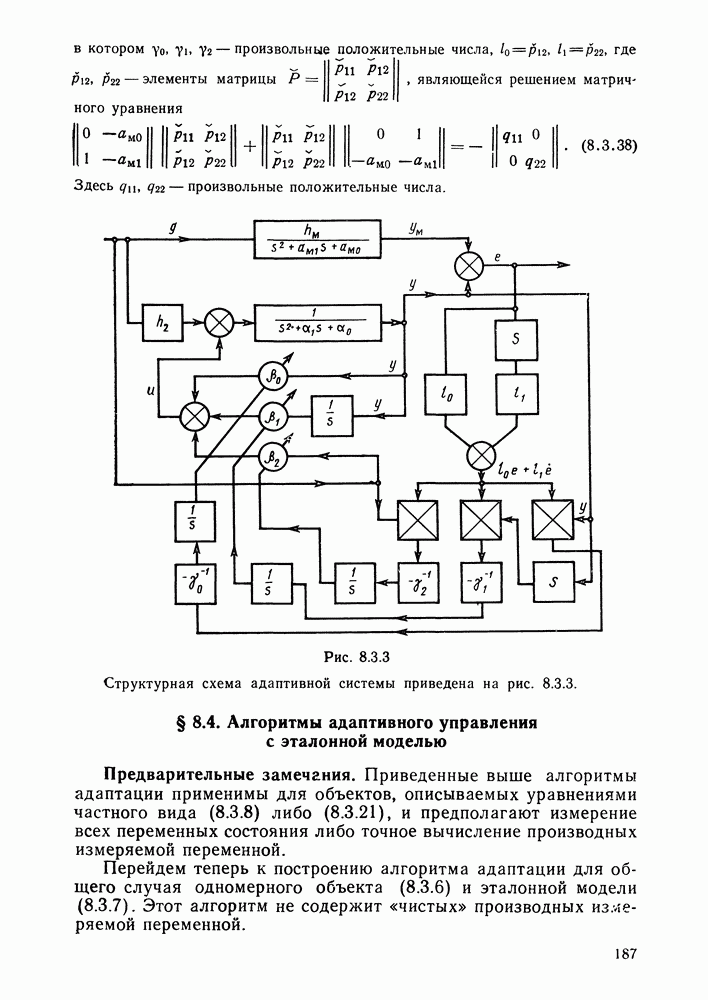
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
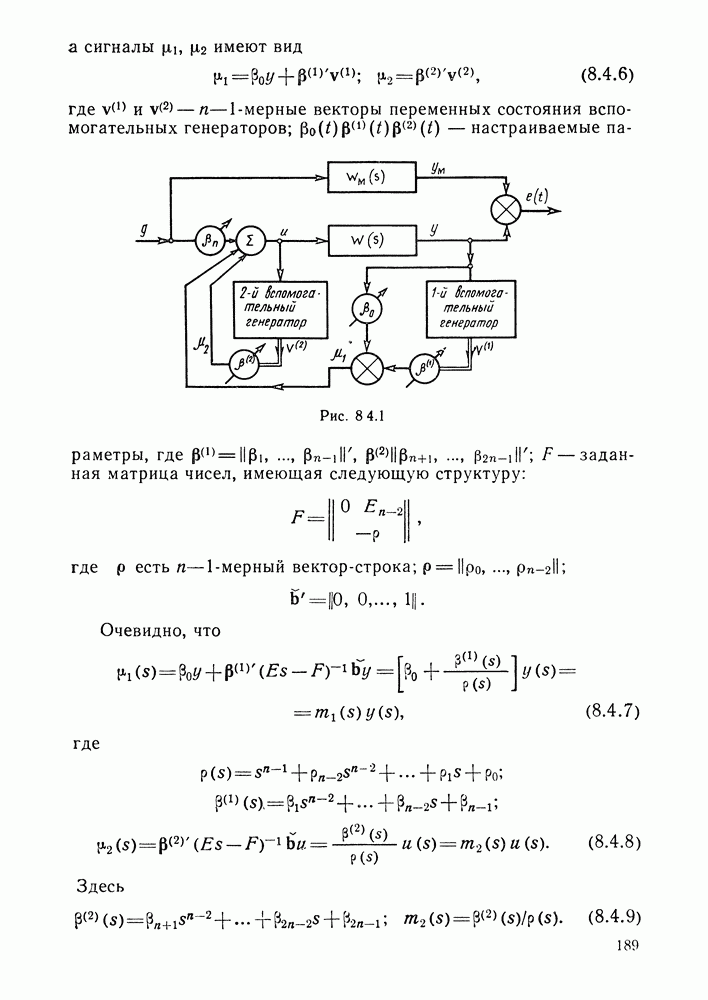
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
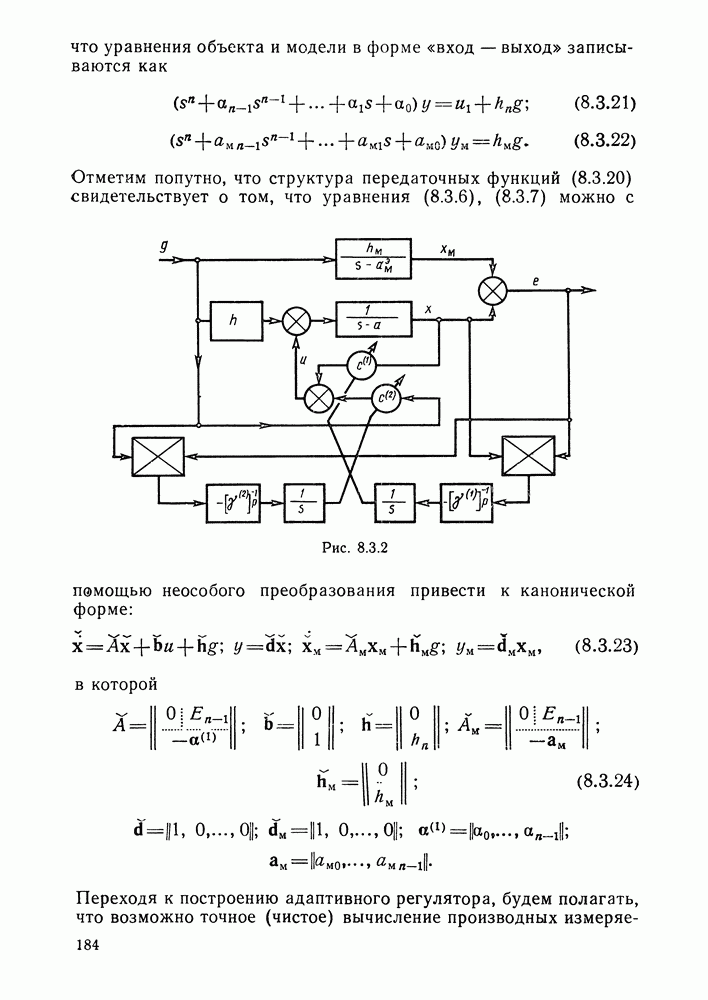
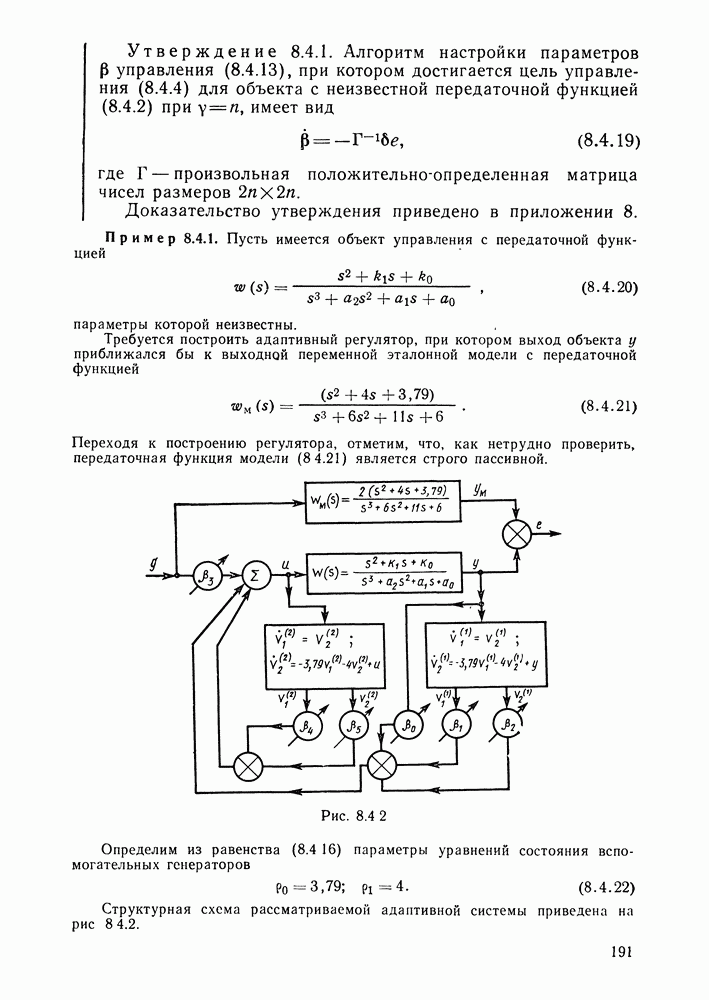
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
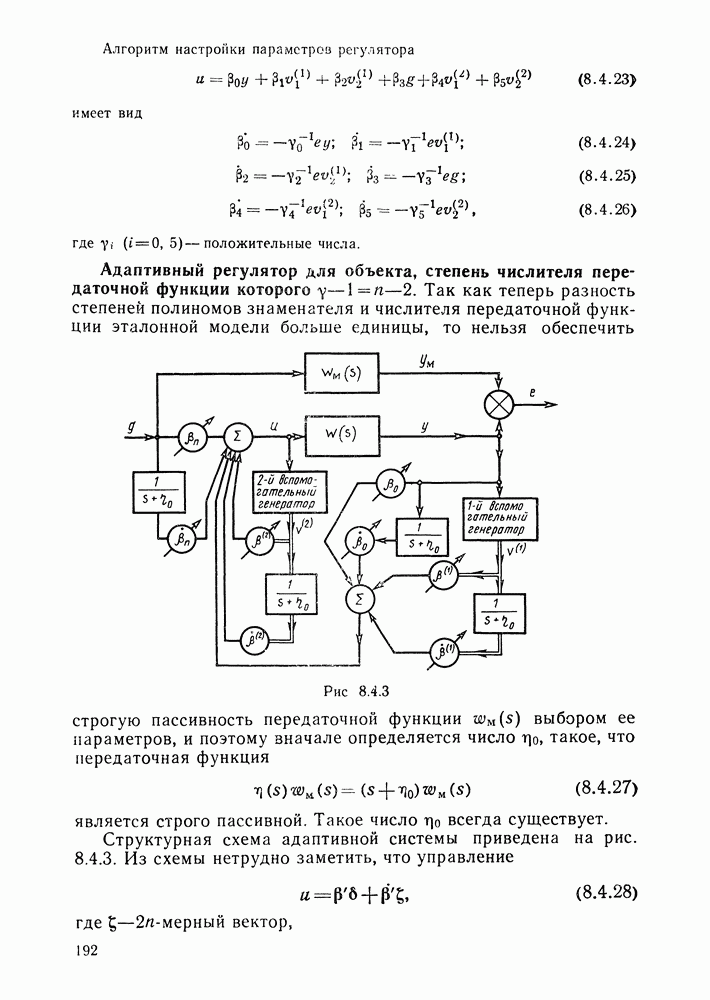
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ