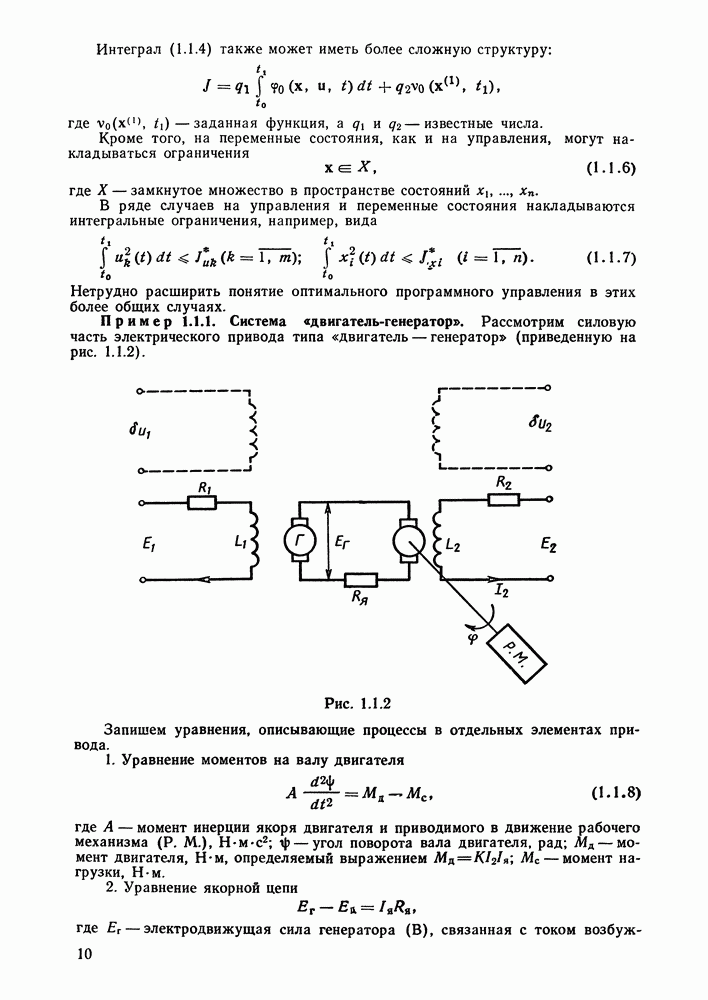
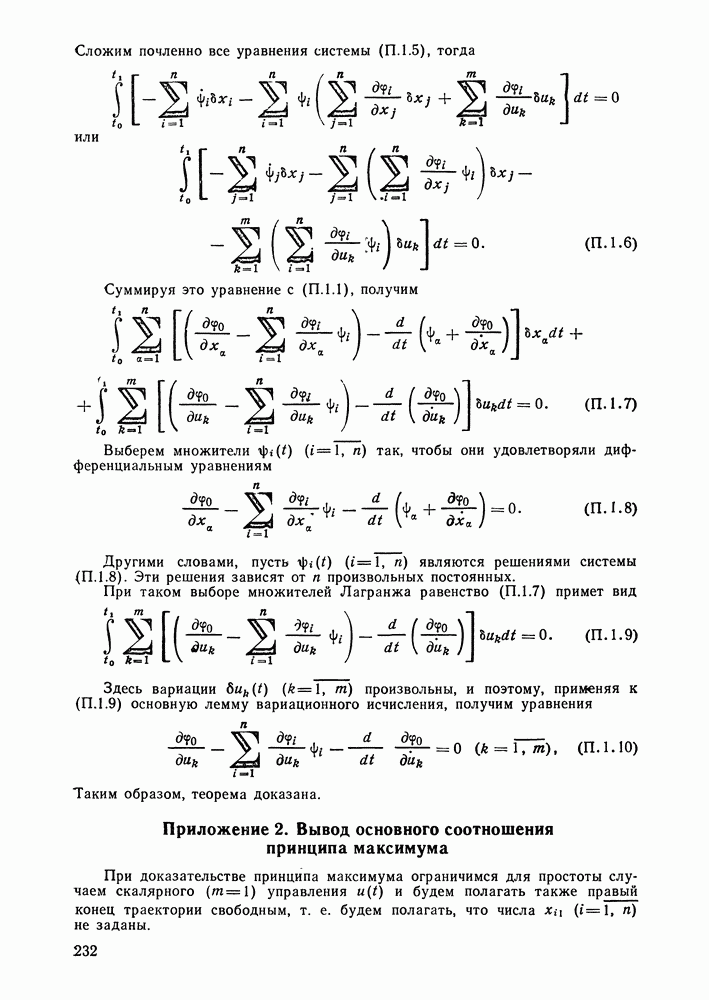
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оптимальное по быстродействию управление линейными объектами.
Рассмотрим важный для практики частный случай задачи об оптимальном быстродействии, когда уравнения (3.1.1) объекта линейны и имеют вид

В этом случае функция

Сопряженная система (3.1.7) записывается так:
 (3.1.14)
(3.1.14)
Для линейных объектов принцип максимума является не только необходимым, но и достаточным условием оптимальности по быстродействию. В соответствии с (3.1.8) для оптимальности управления необходимо и достаточно, чтобы функция (3.1.13) принимала наибольшее значение при ограниченном  . Эта функция достигает максимума, если
. Эта функция достигает максимума, если
 (3.1.15)
(3.1.15)
При  и ограничении
и ограничении  это условие примет вид
это условие примет вид
 (3.1.16)
(3.1.16)
где  .
.
Необходимым условием экстремума всякой гладкой функции, заданной в открытой области изменения ее аргумента, является равенство нулю ее производной. Если функция задана в замкнутой области, то ее экстремум может достигаться как внутри, так и на границе этой области. В рассматриваемом случае функция  — линейная относительно
— линейная относительно  , ее производная не зависит от
, ее производная не зависит от  , и поэтому если на
, и поэтому если на  не наложено ограничение, то не существует точки
не наложено ограничение, то не существует точки  , в которой функция
, в которой функция  достигает экстремума. Если функция
достигает экстремума. Если функция  рассматривается в замкнутом интервале
рассматривается в замкнутом интервале  изменения переменной
изменения переменной  , то в этом интервале она достигает максимума и минимума на границах интервала (рис. 3.1.1).
, то в этом интервале она достигает максимума и минимума на границах интервала (рис. 3.1.1).
Спрашивается, каково же должно быть  , чтобы функция
, чтобы функция  достигала максимума? Как следует из рис. 3.1.1, и определяется выражением
достигала максимума? Как следует из рис. 3.1.1, и определяется выражением

Это выражение справедливо для каждого момента времени, и поэтому оптимальное управление имеет вид
 (3.1.17)
(3.1.17)
Возвращаясь к общему случаю  замечаем, что каждая составляющая
замечаем, что каждая составляющая  вектора и изменяется независимо от остальных составляющих, поэтому (3.1.15) выполняется, если
вектора и изменяется независимо от остальных составляющих, поэтому (3.1.15) выполняется, если

Таким образом, для линейных объектов принцип максимума дает явный вид (3.1.18) оптимального управления, а краевая задача состоит в определении вектора  , при котором решения системы
, при котором решения системы

( - столбец матрицы
- столбец матрицы  );
);

удовлетворяют краевым условиям (3.1.2), (3.1.3).
Заметим, что корни характеристического уравнения объекта (3.1.12) и сопряженной системы (3.1.14) равны по модулю, однако противоположны по знаку. Действительно, характеристический полином объекта имеет вид  , а сопряженной системы имеет вид
, а сопряженной системы имеет вид  , и если, например, объект асимптотически устойчив, то сопряженная система неустойчива. Это приводит к трудностям при численном решении краевой задачи. В связи с этим были разработаны специальные методы (изложенные, например, в [3.4]) решения краевых задач для системы
, и если, например, объект асимптотически устойчив, то сопряженная система неустойчива. Это приводит к трудностям при численном решении краевой задачи. В связи с этим были разработаны специальные методы (изложенные, например, в [3.4]) решения краевых задач для системы  .
.
Трудности решения краевой задачи для системы  к которой сводится задача об оптимальном программном управлении при использовании принципа максимума, привели к разработке нового метода [2.6], предложенного Н. Н. Красовским.
к которой сводится задача об оптимальном программном управлении при использовании принципа максимума, привели к разработке нового метода [2.6], предложенного Н. Н. Красовским.

Рис. 3.1.1.
Этот метод сводит задачу об оптимальном программном управлении в линейных системах к так называемой проблеме моментов, изучаемой в функциональном анализе. Доступное изложение метода приведено в [3.5].
Пример 3.1.2. Пусть объект управлении описывается уравнением

Требуется определить функцию управления  , удовлетворяющую неравенству
, удовлетворяющую неравенству  , которое переводит этот объект из состояния
, которое переводит этот объект из состояния

в нулевое положение

за минимальное время.
Вводя обозначения  запишем уравнение объекта в форме
запишем уравнение объекта в форме

Функция

а сопряженная система (3.1.14) имеет вид

Из (3.1.23) заключаем, что искомое оптимальное управление имеет вид

Разрешая последнюю систему трех уравнений относительно  , получим дифференциальное уравнение
, получим дифференциальное уравнение

для определения функции  .
.
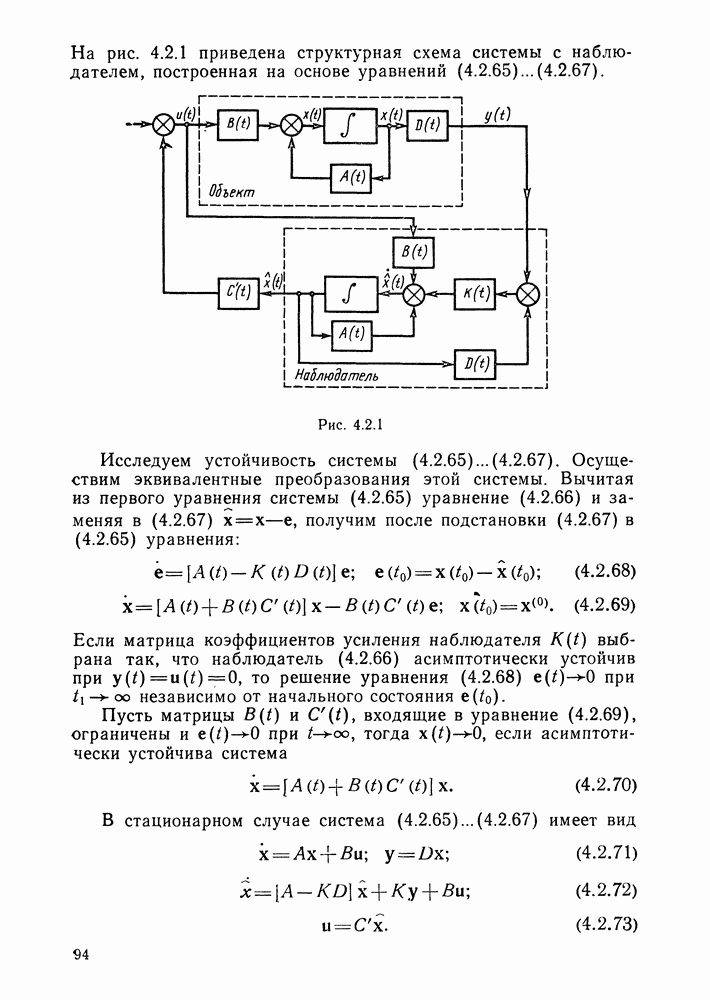
Теорема об  -интервалах. Из (3.1.18) следует, что каждая из компонент оптимального управления представляет собой кусочно-постоянную функцию, точками разрыва которой являются точки обращения в нуль функции
-интервалах. Из (3.1.18) следует, что каждая из компонент оптимального управления представляет собой кусочно-постоянную функцию, точками разрыва которой являются точки обращения в нуль функции

На рис. 3.1.2 приведен график изменения во времени одной из этих функций.
Каждую точку разрыва оптимального управления будем называть точкой переключения. Число переключений каждого из управлений  определяется числом нулей функции
определяется числом нулей функции  и может быть очень большим. Существует, однако, один важный случай, когда число переключений этих управлений допускает точную оценку.
и может быть очень большим. Существует, однако, один важный случай, когда число переключений этих управлений допускает точную оценку.
Этот случай составляет содержание теоремы об  -интервалах.
-интервалах.
Теорема 3.1.1 (об  -интервалах). Если корни характеристического уравнения объекта (3.1.12) действительны, то число переключений каждого из управлений
-интервалах). Если корни характеристического уравнения объекта (3.1.12) действительны, то число переключений каждого из управлений  не превышает
не превышает  .
.
При доказательстве теоремы ограничимся для простоты случаем  Кроме того, будем полагать, что объект управления описывается системой (3.1.22), при этом корни уравнения
Кроме того, будем полагать, что объект управления описывается системой (3.1.22), при этом корни уравнения  объекта (3.1.22) попарно различны. Однако приводимое ниже доказательство полностью повторяется для общего случая, описанного теоремой.
объекта (3.1.22) попарно различны. Однако приводимое ниже доказательство полностью повторяется для общего случая, описанного теоремой.
Обозначим через  — корни характеристического уравнения объекта. Тогда очевидно, что корни характеристического полинома уравнения (3.1.26) равны
— корни характеристического уравнения объекта. Тогда очевидно, что корни характеристического полинома уравнения (3.1.26) равны  и, следовательно, функция
и, следовательно, функция  являющаяся решением этого уравнения, имеет вид
являющаяся решением этого уравнения, имеет вид

где  — постоянные интегрирования.
— постоянные интегрирования.
Поскольку число корней (нулей) функции  определяет число переключений оптимального управления, то теорема 3.1.1 будет доказана, если справедливо следующее утверждение.
определяет число переключений оптимального управления, то теорема 3.1.1 будет доказана, если справедливо следующее утверждение.
Утверждение 3.1.1. Если  попарно различные действительные числа, то функция (3.1.27) не может иметь более двух действительных корней. Доказательство. При
попарно различные действительные числа, то функция (3.1.27) не может иметь более двух действительных корней. Доказательство. При  утверждение справедливо (уравнение
утверждение справедливо (уравнение  не имеет действительных корней). Предположим, что утверждение доказано для случая, когда в (3.1.27) имеется лишь два слагаемых, и докажем ее для трех слагаемых.
не имеет действительных корней). Предположим, что утверждение доказано для случая, когда в (3.1.27) имеется лишь два слагаемых, и докажем ее для трех слагаемых.
Допустим противное, что функция  имеет не менее трех действительных корней. Умножив ее на
имеет не менее трех действительных корней. Умножив ее на  , получим функцию
, получим функцию

которая также имеет не менее трех действительных корней. Из математического анализа (теорема Ролля) следует, что между двумя действительными корнями функции лежит по крайней мере один корень ее производной.

Рис. 3.1.2.
Следовательно, производная функции (3.1.28) имеет не менее двух действительных корней. С другой стороны, эта производная определяется выражением

в которой числа  попарно различны, и, следовательно, она имеет не более одного действительного корня (выше полагалось, что утверждение доказано для случая, когда (3.1.27) содержит менее трех слагаемых). Полученное противоречие доказывает утверждение и теорему 3.1.1.
попарно различны, и, следовательно, она имеет не более одного действительного корня (выше полагалось, что утверждение доказано для случая, когда (3.1.27) содержит менее трех слагаемых). Полученное противоречие доказывает утверждение и теорему 3.1.1.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ЧАСТЬ ПЕРВАЯ. ОПТИМАЛЬНЫЕ СИСТЕМЫ
- Глава 1. ПОНЯТИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 1.1. Оптимальное программное управление
- § 1.2. Оптимальное стабилизирующее управление
- Понятие об оптимальном стабилизирующем управлении.
- Особенности оптимальных систем программного управления и стабилизации.
- § 1.3. Развитие понятий оптимального управления
- Общий вид уравнений стабилизирующего управления.
- Глава 2. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
- § 2.1. Элементы классического вариационного исчисления
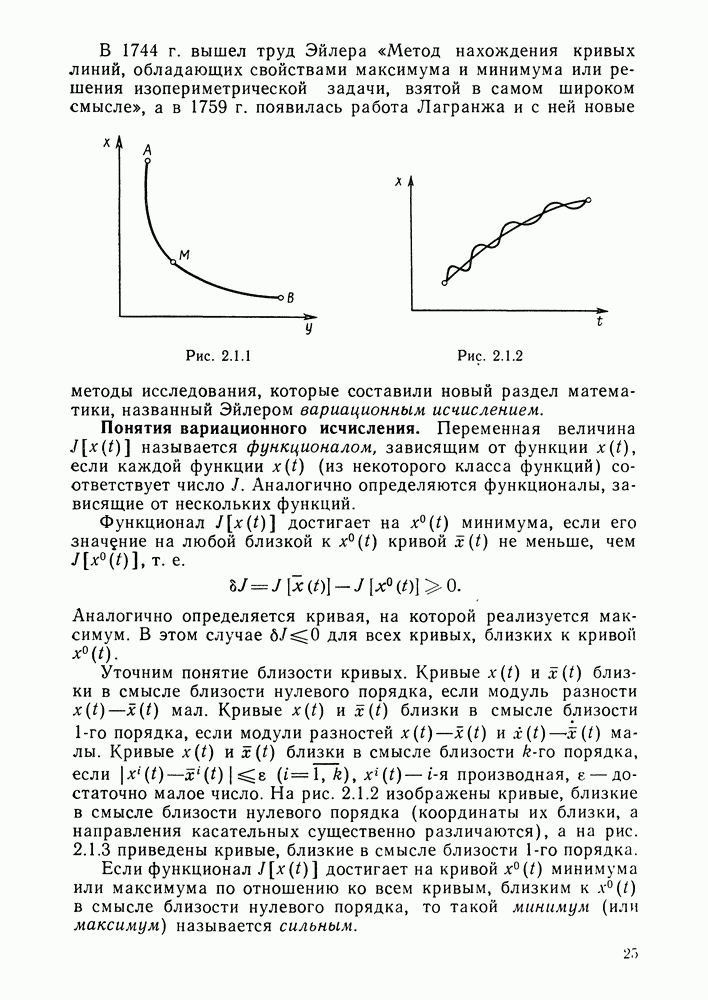
- Понятия вариационного исчисления.
- Вариационная задача с закрепленными граничными точками. Первое необходимое условие экстремума (уравнение Эйлера).
- Уравнения Эйлера — Пуассона.
- Вариационные задачи с подвижными границами.
- Второе необходимое условие экстремума (условие Лежандра) [2.3].
- Вариационные задачи на условный экстремум. Уравнения Эйлера — Лагранжа.
- Задачи Майера и Больца.
- § 2.2. Принцип максимума
- Принцип максимума.
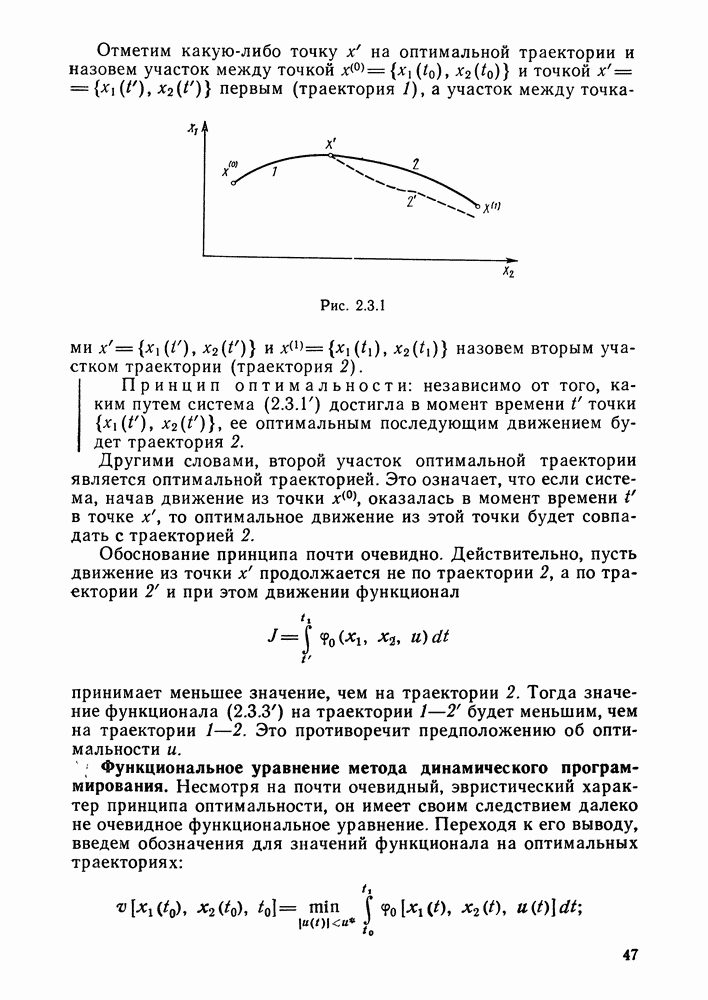
- § 2.3. Метод динамического программирования
- Функциональное уравнение метода динамического программирования.
- Численное решение задачи об оптимальном стабилизирующем управлении.
- Связь метода динамического программирования и принципа максимума.
- Глава 3. ОПТИМАЛЬНЫЕ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМЫ УПРАВЛЕНИЯ
- § 3.1. Системы программного управления, оптимальные по быстродействию
- Оптимальное по быстродействию управление линейными объектами.
- § 3.2. Синтез оптимальных по быстродействию систем
- Синтез оптимальных регуляторов систем второго порядка.
- Глава 4. АНАЛИТИЧЕСКОЕ КОНСТРУИРОВАНИЕ РЕГУЛЯТОРОВ
- § 4.1. Процедуры аналитического конструирования регуляторов
- Аналитическое конструирование регуляторов нестационарных систем.
- Численное решение матричного алгебраического уравнения Риккати. Метод Репина — Третьякова.
- Аналитическое конструирование по критерию обобщенной работы.
- Аналитическое конструирование регуляторов для нелинейных объектов.
- Аналитическое конструирование при детерминированных внешних возмущениях [4.12].
- Задача о слежении [4.13].
- Аналитическое конструирование дискретных (цифровых) регуляторов.
- § 4.2. Построение регуляторов при неполной информации о векторе состояния
- Построение наблюдателя полного порядка на основе модального управления.
- Построение модального управления.
- Структура оптимальной системы с наблюдателем.
- § 4.3. Применение процедур аналитического конструирования регуляторов
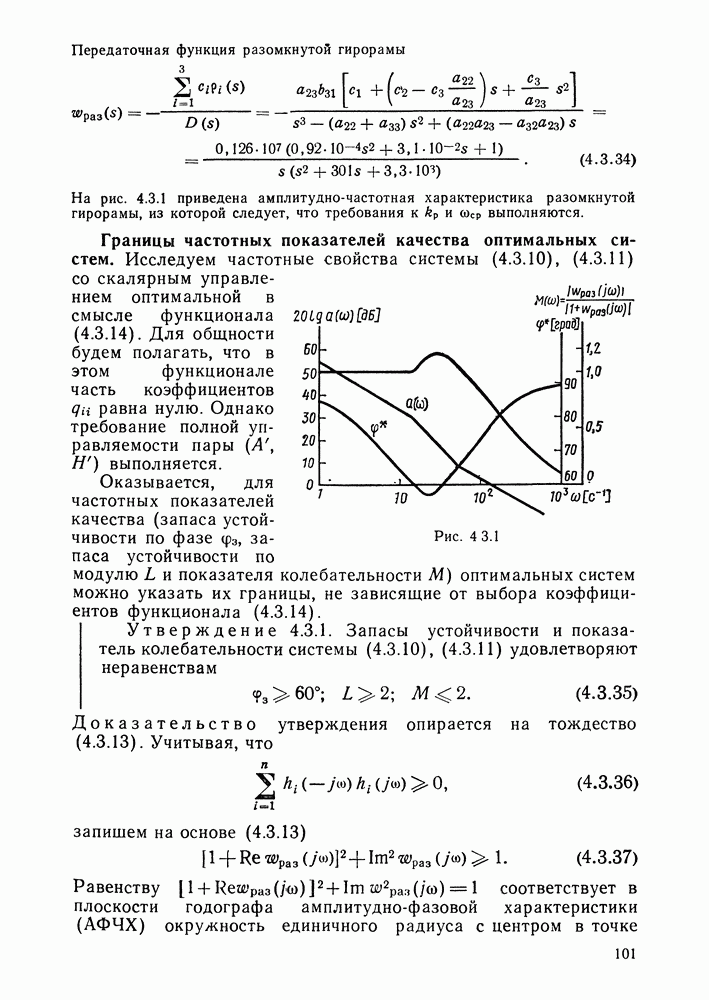
- Коэффициент передачи и частота среза оптимальных систем со скалярным управлением.
- Границы частотных показателей качества оптимальных систем.
- Точность и качество оптимальных систем.
- Глава 5. ОПТИМАЛЬНЫЕ СТОХАСТИЧЕСКИЕ СИСТЕМЫ СТАБИЛИЗАЦИИ
- § 5.1. Оптимальное управление при случайных внешних возмущениях и измеряемом векторе состояний
- § 5.2. Синтез стохастических систем при неполной информации о векторе переменных состояния.
- Оптимальный наблюдатель (оптимальный фильтр Калмана — Бьюси).
- Теорема разделения.
- Восстановление переменных состояния нелинейных объектов.
- § 5.3. Оптимальные стохастические дискретные системы
- Оптимальные дискретные наблюдатели (оптимальный дискретный фильтр Калмана — Бьюси).
- Оптимальные системы с обратной связью по выходу объекта.
- Дальнейшее развитие теории оптимального стохастического управления.
- ЧАСТЬ ВТОРАЯ. АДАПТИВНЫЕ (САМОНАСТРАИВАЮЩИЕСЯ) СИСТЕМЫ
- Глава 6. ВВЕДЕНИЕ В АДАПТИВНОЕ УПРАВЛЕНИЕ
- § 6.1. Понятия об адаптивных (самонастраивающихся) системах
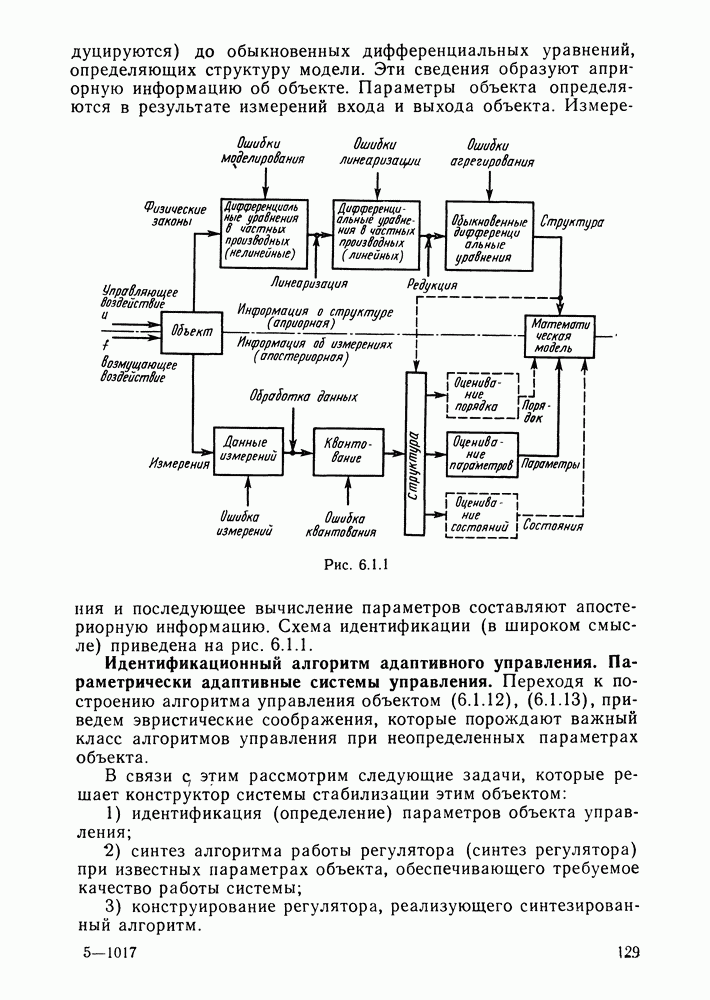
- Понятие об идентификации.
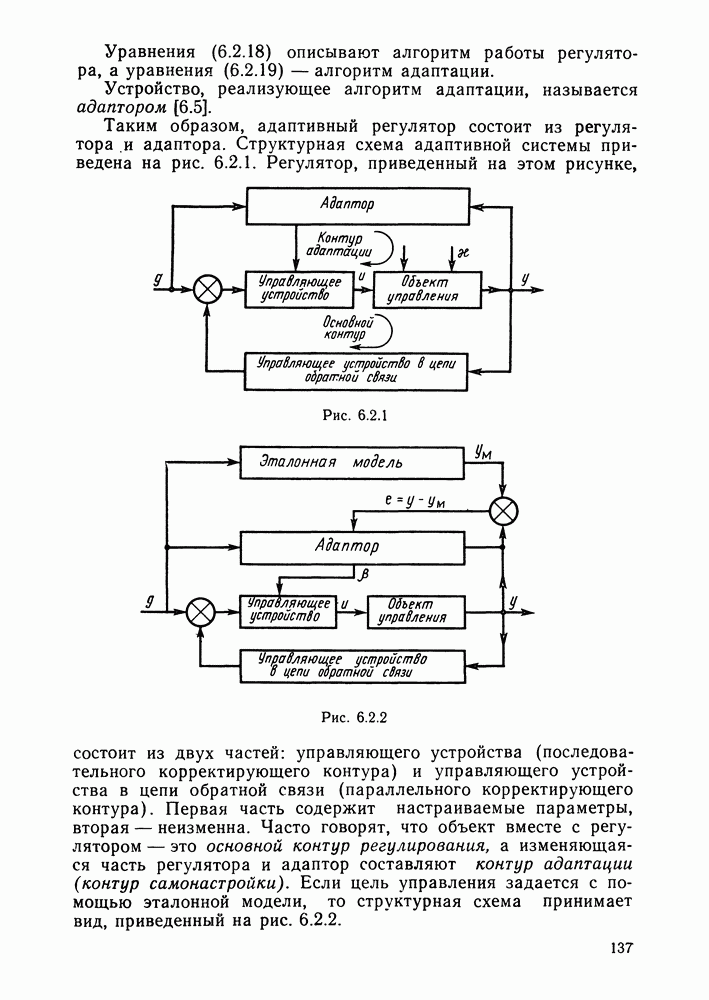
- Идентификационный алгоритм адаптивного управления. Параметрически адаптивные системы управления.
- Прямой алгоритм адаптивного управления. Функциональноадаптивные системы.
- § 6.2. Структура адаптивных систем
- Структура адаптивных систем.
- Постановка задачи синтеза адаптивного регулятора и этапы ее решения.
- § 6.3. Методы адаптивного управления
- Глава 7. СИСТЕМЫ ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- § 7.1. Принципы экстремального регулирования
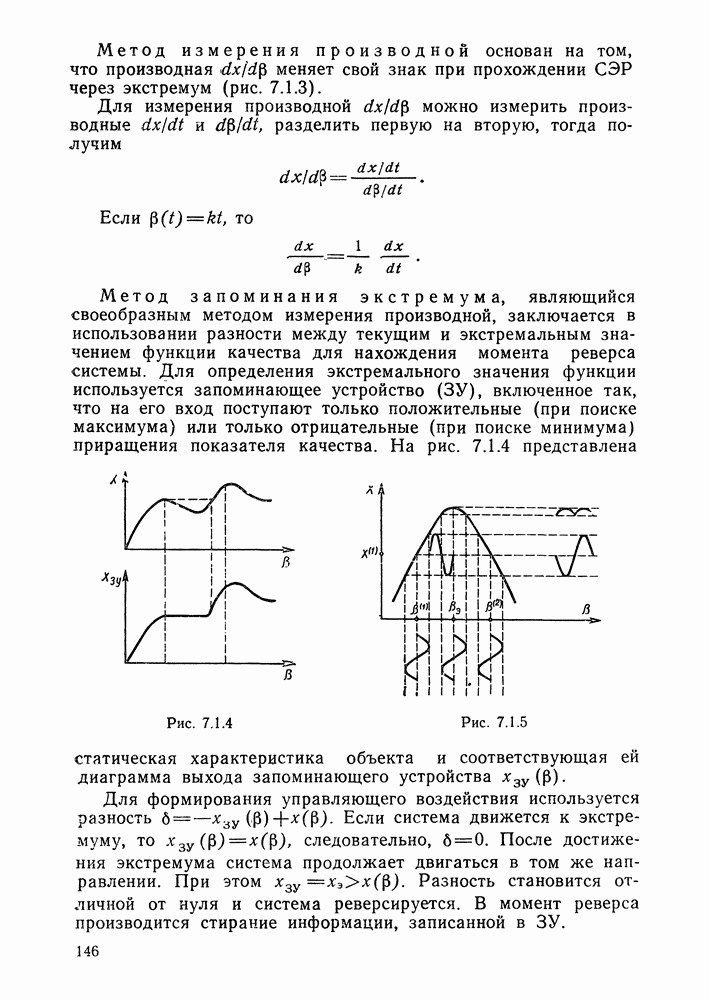
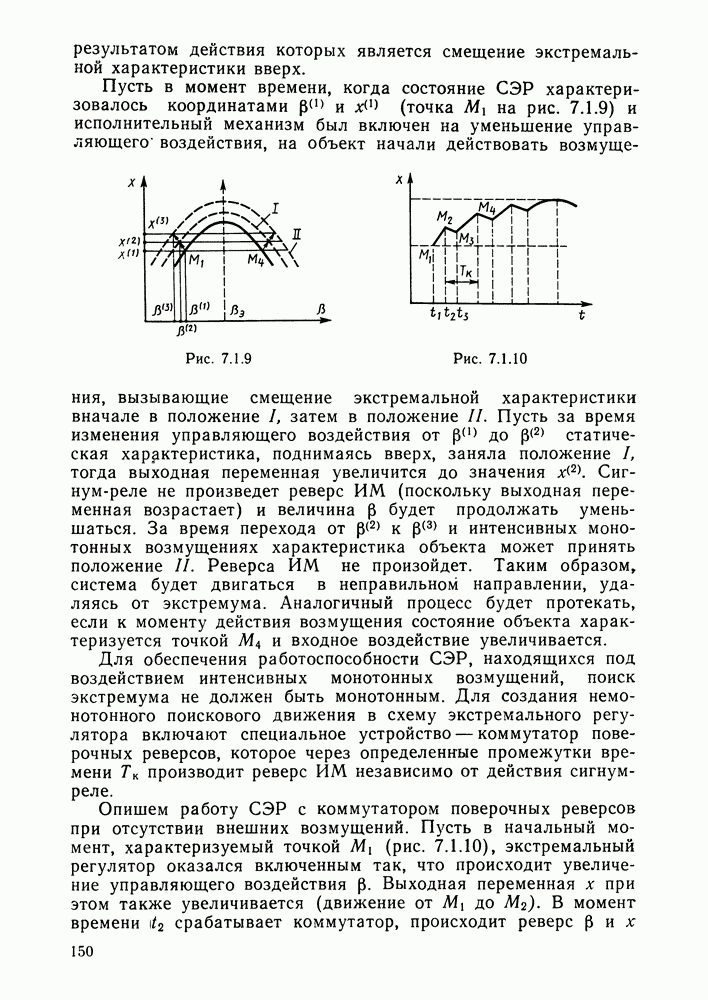
- Методы (принципы) нахождения экстремума однопараметрических объектов.
- § 7.2. Алгоритмы шаговых систем экстремального управления
- Поисковые алгоритмы экстремального управления однопараметрическими объектами.
- Градиентные алгоритмы поиска экстремума многопараметрических объектов.
- § 7.3. Экстремальное управление в условиях помех. Стохастическая аппроксимация
- Поиск экстремума многопараметрических объектов в условиях помех.
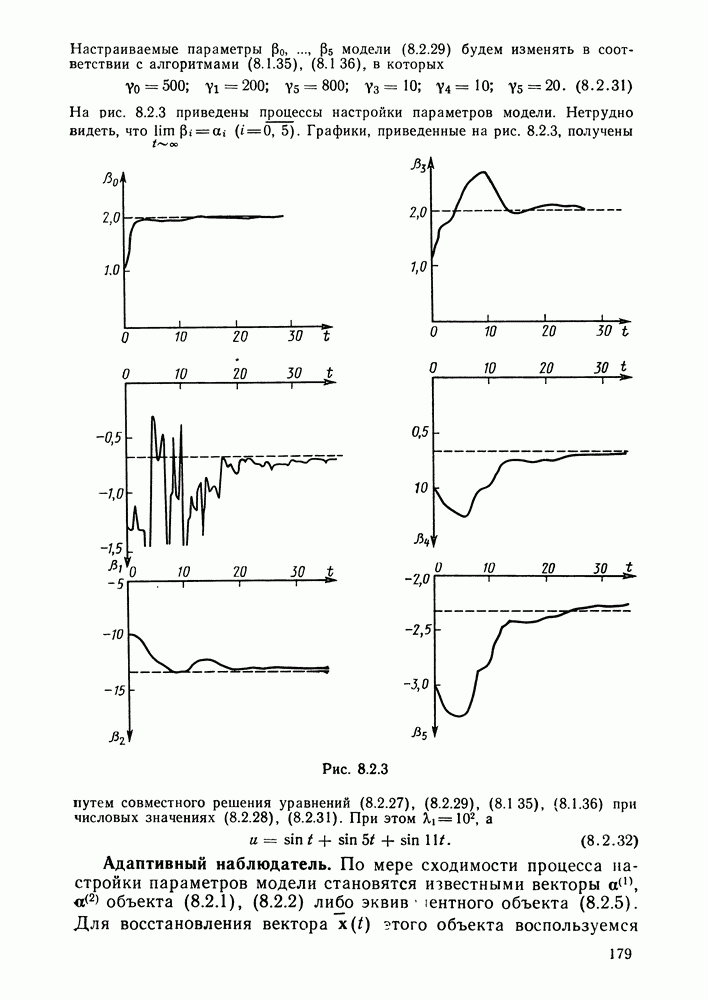
- Глава 8. СИСТЕМЫ С МОДЕЛЬЮ
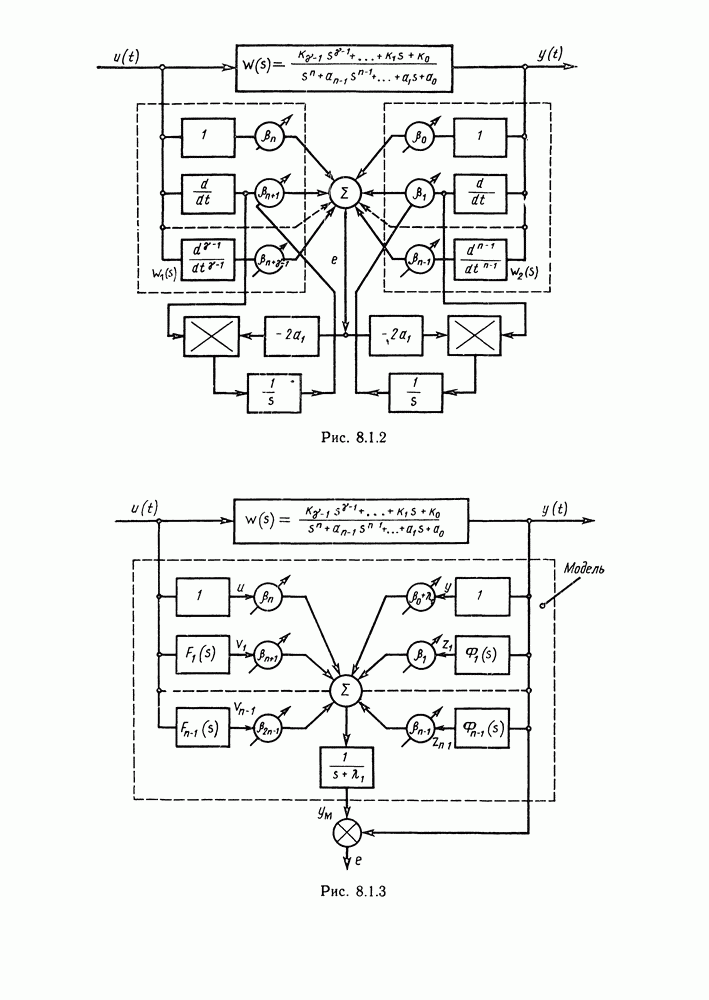
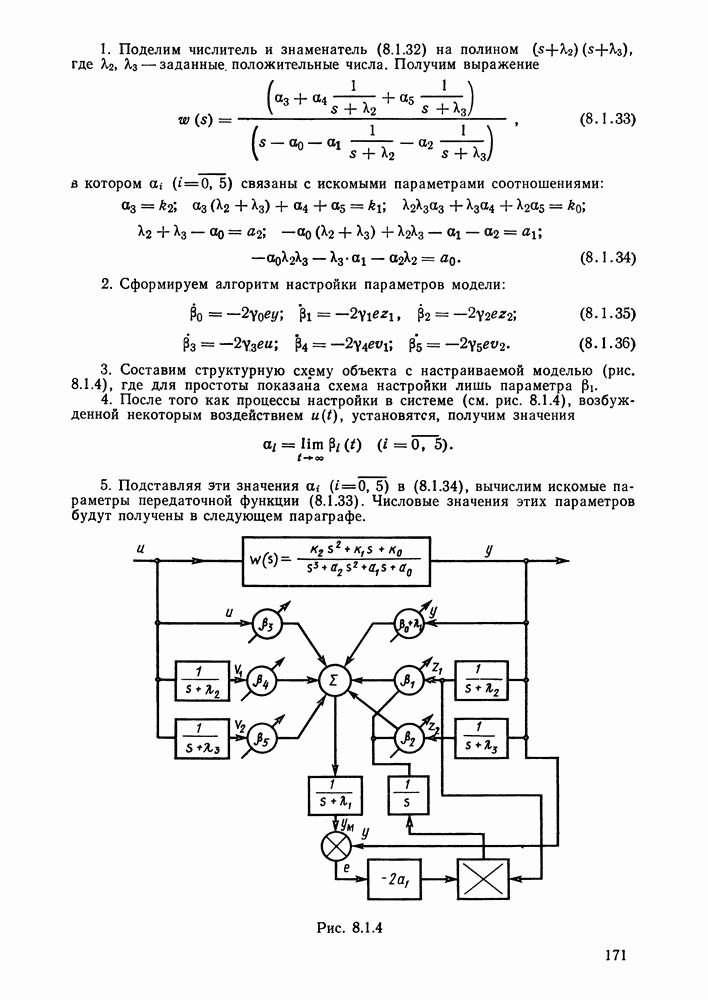
- § 8.1. Методы идентификации объектов управления при детерминированных воздействиях и отсутствии помех. Настраиваемые модели
- Идентификация на основе частотных характеристик.
- Идентификация с помощью настраиваемой модели.
- Идентификация при полностью измеряемом векторе переменных состояний.
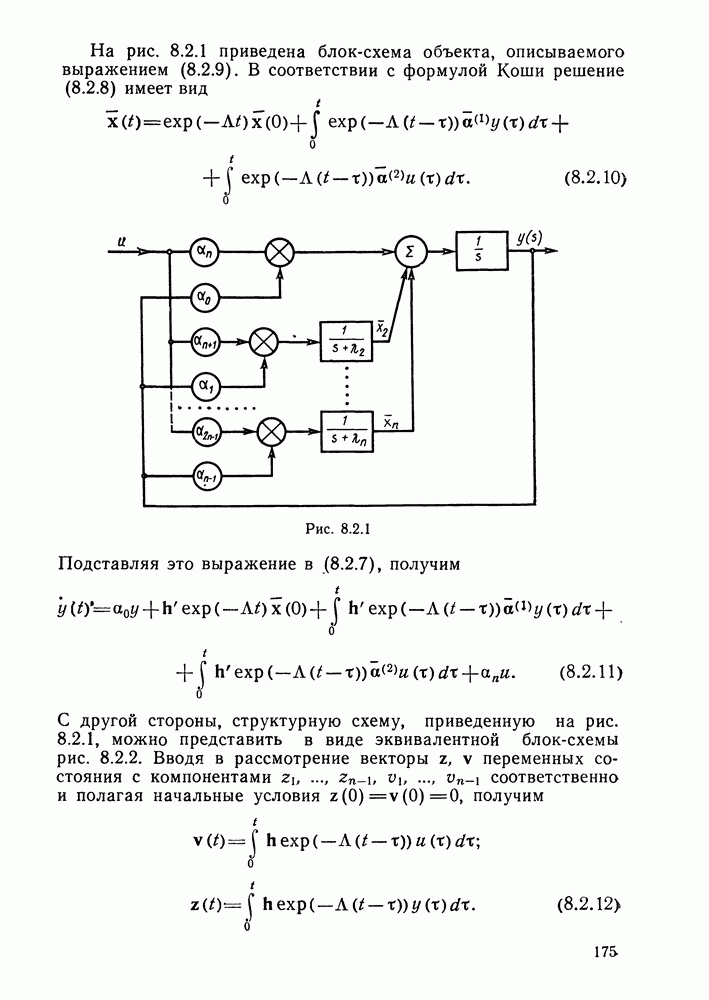
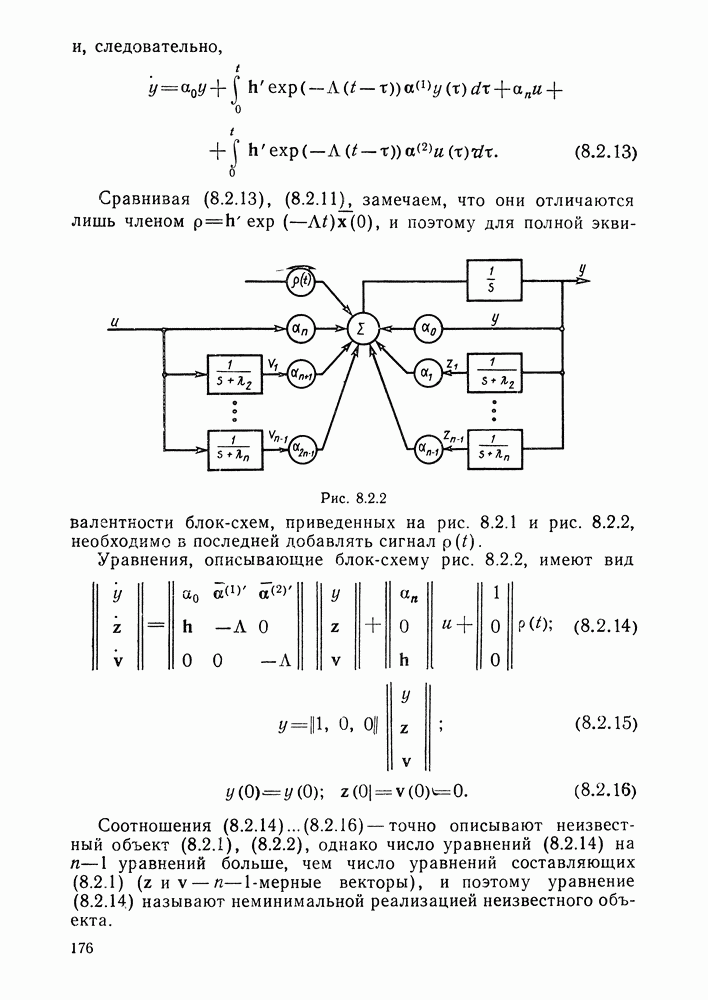
- § 8.2. Адаптивные наблюдатели
- Адаптивный наблюдатель.
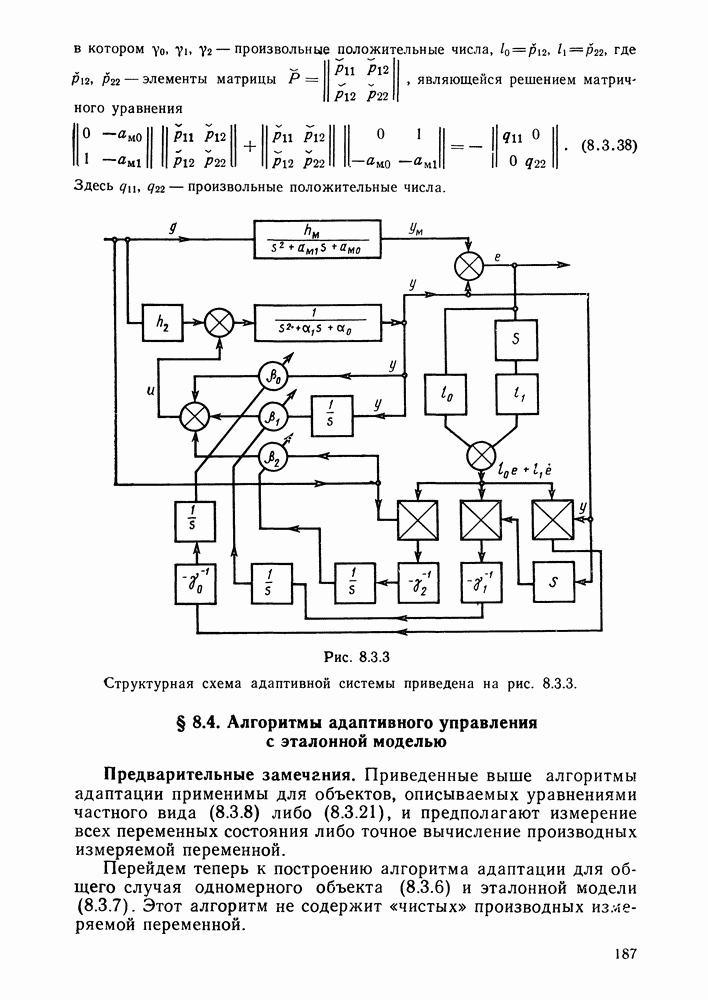
- § 8.3. Адаптивные системы с эталонной моделью
- Алгоритм настройки коэффициентов уравнения состояния.
- Алгоритм адаптации с использованием чистых производных выхода объекта.
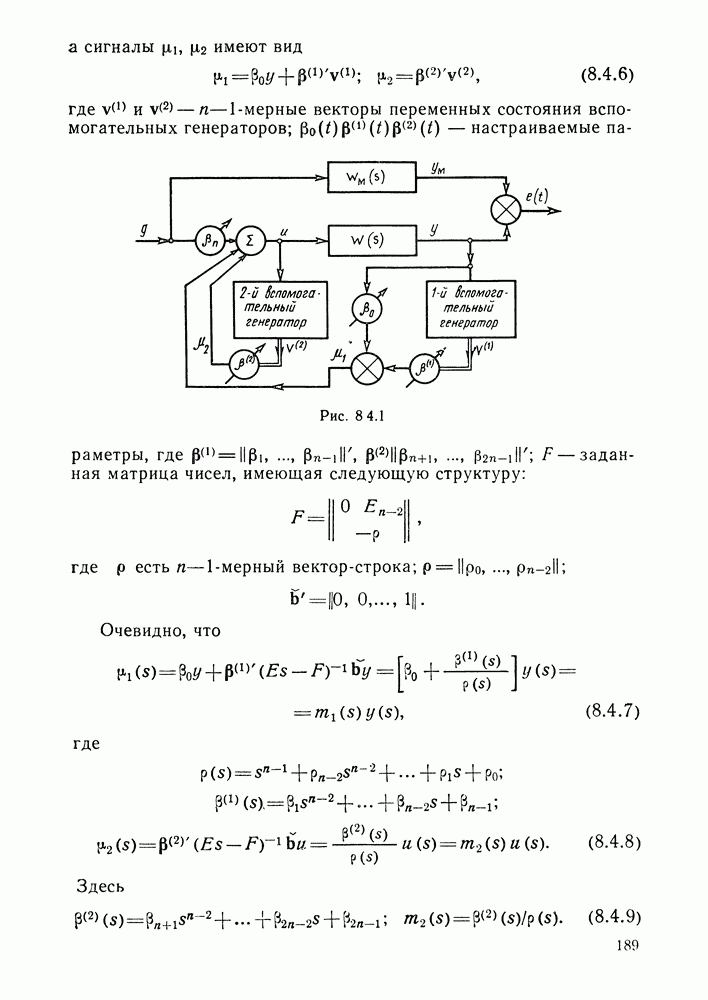
- § 8.4. Алгоритмы адаптивного управления с эталонной моделью
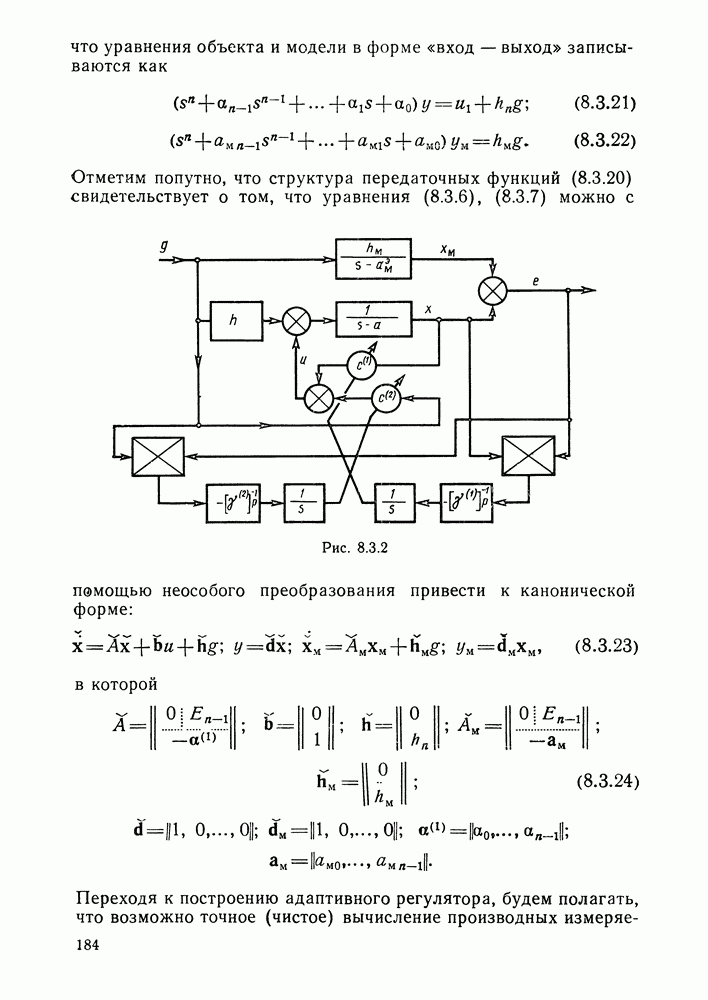
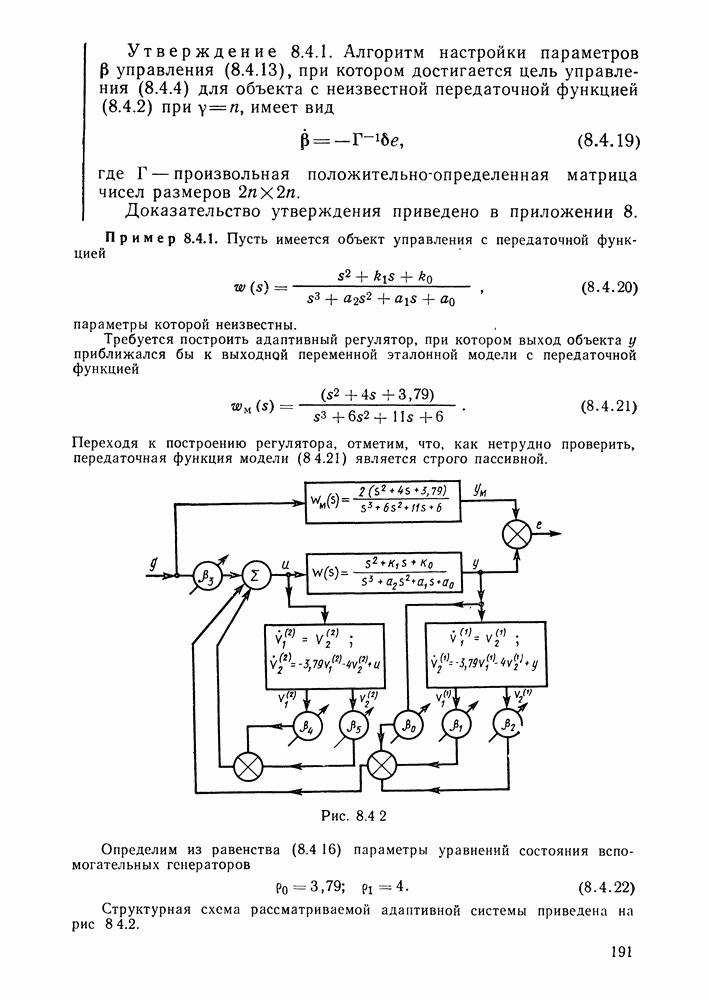
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого на единицу меньше степени знаменателя.
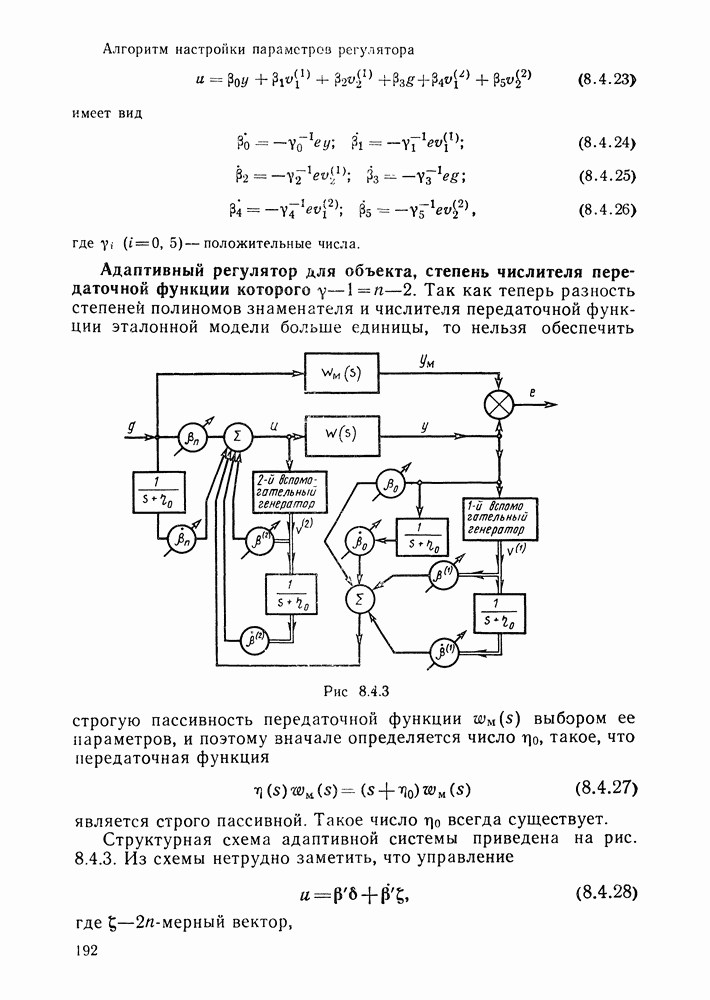
- Адаптивный регулятор для объекта, степень числителя передаточной функции которого.
- Глава 9. ИДЕНТИФИКАЦИЯ
- § 9.1. Идентификация при внешних возмущениях и помехах. Корреляционный способ
- Алгоритм корреляционного способа идентификации [9.1].
- § 9.2. Метод наименьших квадратов
- Метод наименьших квадратов [9.1].
- Рекуррентный алгоритм метода наименьших квадратов (последовательный регрессионный метод).
- Оценка параметров СС-модели.
- Оценка параметров АРСС-модели.
- Связь рекуррентного алгоритма метода наименьших квадратов и алгоритма фильтрации.
- § 9.3. Стохастическая аппроксимация. Идентификация параметров и переменных состояния
- Идентификация параметров и переменных состояния.
- Глава 10. ИДЕНТИФИКАЦИОННЫЙ И ПРЯМОЙ АЛГОРИТМЫ АДАПТИВНОГО УПРАВЛЕНИЯ
- § 10.1. Параметрически-адаптивные системы
- Построение алгоритма регулирования на основе модального управления.
- Построение алгоритма адаптации (идентификации) на основе метода наименьших квадратов.
- § 10.2. Функционально-адаптивные системы
- Синтез регулятора (построение компенсационного алгоритма регулирования).
- Построение алгоритма адаптации при отсутствии внешних возмущений.
- Построение алгоритма адаптации с учетом внешних возмущений.
- Приложение 1. Доказательство теоремы Лагранжа
- Приложение 2. Вывод основного соотношения принципа максимума
- Приложение 3. Метод динамического программирования для дискретных систем. Численное решение функционального уравнения
- Приложение 4. Вывод алгебраического уравнения Риккати
- Приложение 5. Аналитическое конструирование регуляторов дискретных систем
- Приложение 6. Вывод уравнений оптимального наблюдения (уравнений фильтра Калмана — Бьюси)
- Приложение 7. Доказательство теоремы разделения
- Приложение 8. Вывод алгоритма настройки параметров регулятора
- Приложение 9. Вывод алгоритма настройки регулятора
- СПИСОК ЛИТЕРАТУРЫ